Input-Gain Control Produces Feature-Specific Surround Suppression

Abstract

In primary visual cortex (V1), neuronal responses are sensitive to context. For example, responses to stimuli presented within the receptive field (RF) center are often suppressed by stimuli within the RF surround, and this suppression tends to be strongest when the center and surround stimuli match. We sought to identify the mechanism that gives rise to these properties of surround modulation. To do so, we exploited the stability of implanted multielectrode arrays to record from neurons in V1 of alert monkeys with multiple stimulus sets that more exhaustively probed center-surround interactions. We first replicated previous results concerning center-surround similarity using gratings representing all combinations of center and surround orientation. With this stimulus set, the surround simply scaled population responses to the center, such that the overall population tuning curve had the same shape and peak response. However, when the center contained two superimposed gratings (i.e., a visual “plaid”), one component of which always matched the surround orientation, suppression selectively affected the portion of the response driven by the matching center component, thereby producing shifts in the peak of the population orientation tuning curve. In effect, the surround caused neurons to respond predominantly to the component grating of the center plaid that was unmatched to the surround grating, as if by reducing the effective strength of whichever stimulus attributes were matched to the surround. These results provide key physiological support for theoretical models that propose feature-specific, input-gain control as the mechanism underlying surround suppression.

Introduction

Neuronal responses to stimuli confined to the receptive field (RF) center are modulated by the simultaneous presentation of stimuli in the RF surround (McIlwain, 1964; Hubel and Wiesel, 1965; Allman et al., 1985). In primary visual cortex (V1), one common manifestation of such spatial modulation is a decreased neuronal response to stimuli extending beyond the RF center (Sceniak et al., 1999, 2001; Cavanaugh et al., 2002a), a phenomenon generically referred to as “surround suppression.” This operation is thought to enhance the efficiency of visual information processing by reducing the redundancy inherent in natural images (Barlow, 1959; Mumford, 1992; Rao and Ballard, 1999; Vinje and Gallant, 2000, 2002; Schwartz and Simoncelli, 2001; Haider et al., 2010).

The surround, like the center, exhibits selectivity for orientation (Bair et al., 2003; Ozeki et al., 2009; Hashemi-Nezhad and Lyon, 2012), but, interestingly, the surround tuning does not appear to be fixed. Instead, suppression is usually strongest when the center and surround stimuli match (Sillito et al., 1995; Cavanaugh et al., 2002b; Jones et al., 2002; Shushruth et al., 2012). We replicated these results by recording V1 responses to gratings representing all combinations of center and surround orientation. We show that, under these conditions, the surround effectively scaled population responses to the center according to its orientation similarity to the surround.

We further sought to identify the type of mechanism that gives rise to this behavior of the surround. One possibility suggested by the above result is that the surround simply modulates neural outputs according to the similarity between the center and the surround. Alternatively, recent theoretical studies have proposed that the mechanism of surround suppression is a form of input-gain control (Spratling, 2010, 2011; Lochmann and Deneve, 2011; Lochmann et al., 2012). This mechanism produces efficient coding by allowing the surround to suppress predictable inputs and unifies a number of observations regarding surround modulation (Lochmann et al., 2012).

To evaluate these different possibilities, we measured the effect of the surround on center stimuli composed of visual plaids. The orientations of each center component varied independently, but the orientation of the surround grating was matched to one of the center components. We found that suppression from the surround selectively affected the portion of the responses driven by the matched center component, such that the peak of the population tuning curve shifted toward the orientation of the unmatched center component, consistent with the predictions of input-gain control (Lochmann et al., 2012). These findings demonstrate that the surround is capable of modulating the representation of central stimuli in a highly selective way to better represent informative stimulus features at the expense of spatially redundant ones.

We offer a simple, quantitative model to account for our results, showing that the full range of surround behaviors observed by us and others can be explained by an input-gain control mechanism in which suppression selectively targets the effective strength of central features that match the surround.

Materials and Methods

Multiunit activity recordings.

Two male macaque monkeys (Macaca mulatta; Monkey P and Monkey R) were each implanted with a 10 × 10 electrode array (400 μm spacing) in the right hemisphere of V1 as well as a head post on the anterior portion of the skull. Monkeys were trained to fixate a 1.5° window for ∼3 s while stimuli were presented. Completed fixations resulted in a liquid reward. Multiunit activity (MUA) was sampled using a Cerebus 128-channel system (Blackrock). At the start of each recording day, activity thresholds were set for each electrode as −3.6 root mean square background noise; MUA events were logged as threshold crossings.

Experimental design.

All stimuli used for the present experiments consisted of stationary, sinusoidal gratings and were presented on a CRT monitor (100 Hz refresh rate), using mean luminance as background. Stimuli included a central grating/plaid, an annular surround, or both. To simplify pooling the data, the diameter of the central stimulus and the inner and outer diameters of the annular surround were fixed across sessions (at 0.3°, 0.6°, and 2.0°, respectively), as was the spatial frequency of the gratings (at 3.33 Hz). Orientation was sampled at a spacing of 30°. For each session, the stimulus location was approximately aligned to the RF center(s) of one or more multiunit sites. Whether a given site was included for analysis depended on how well its RF boundaries aligned with the stimulus boundaries, as assessed using the criteria described below. Once selected, experimental sessions consisted of three distinct portions. First, surround-only activity was recorded by measuring responses to all orientations of the full-contrast (100% Michelson contrast) surround with the center contrast set to 0%. Second, we recorded responses to the plaid-only/plaid+surround stimulus set (described below). Last, we recorded responses to the center-only/center+surround stimulus set (described below). Within each portion, stimuli were presented in a random block interleaved design. For each portion, the goal was to repeat each stimulus 20 times. Occasionally, this goal was not met for the final portion; data were included provided that at least 10 blocks had been completed. A trial began when the monkey achieved fixation; 300–500 ms after fixation began the stimulus appeared and remained on screen for another 500 ms, after which the trial ended. If the monkey broke fixation before the end of the trial, the trial was aborted without reward.

Center/surround stimuli.

For the center-only/center+surround portion of the experiments, we measured responses to all combinations of center and surround orientations, presented in pseudorandom order. The center was always presented at 100% contrast. In half the trials, the center was presented in isolation (giving center-only data); and in the other half, a full-contrast surround was included (giving center+surround data).

Plaid/surround stimuli.

For the plaid-only/plaid+surround portion, we presented the central stimulus as a “plaid,” drawn by summing two component gratings (termed Center₁ and Center₂), each at 50% contrast. We measured responses to all Center₁/Center₂ orientation combinations. As with the center-only/center+surround stimuli, half of the trials presented the center in isolation (giving plaid-only data). The other half of trials included a 100% contrast surround (giving plaid+surround data) with the added manipulation that the surround orientation was always set equal to that of Center₂.

Inclusion criteria.

We wanted to restrict our analysis to data from multiunits whose RFs overlapped the central stimulus and only minimally overlapped the annular surround. To that end, we applied a set of inclusion criteria to ensure the interpretability of our analyses. For the plaid-only/plaid+surround dataset, inclusion required that: (1) surround-only responses showed no significant tuning to surround orientation; (2) responses to plaid-only stimuli significantly exceeded spontaneous activity; (3) responses to plaid-only stimuli significantly exceeded responses to plaid+surround stimuli; and (4) evoked activity was significantly tuned to center orientation (assessed using plaid-only trials where component orientations were identical). For the center-only/center+surround dataset, multiunits that met all 4 plaid-only/plaid+surround criteria were included, provided that center-only responses were also significantly tuned to the orientation of the center. Significance of tuning was tested using a permutation test (1000 iterations, α = 0.05). This yielded a total of 97 and 61 multiunits for the plaid-only/plaid+surround and center-only/center+surround datasets, respectively. However, some sites met all criteria on more than one session. To prevent any potential miscounting of data, we determined that the most conservative approach was to only allow each site to enter the analysis once. Therefore, if a given site met criteria for multiple sessions, its data were included only for the session in which its RF most overlapped the center. We used the ratio of the average center-only (plaid-only) to the average center+surround (plaid+surround) activity as a benchmark for this overlap. (Because the sites included for the plaid-only/plaid+surround and center-only/center+surround experiments only partly overlapped, we performed this final exclusion step separately for the two sets of data). These steps resulted in plaid-only/plaid+surround and center-only/center+surround sample sizes of 71 and 47 multiunit sites, respectively. The qualitative outcome of our analyses remained the same if this final exclusion step was omitted.

Analysis.

Responses were analyzed over the final 350 ms of stimulus presentation (chosen to include only the sustained portion of the response). Before data were pooled, spontaneous activity was first subtracted from responses, which were then normalized to their grand mean response to all stimuli in the no-surround conditions. Where applicable, stimuli orientations are reported relative to the preferred orientations of the measured multiunits. Preferred orientation was calculated as the vector average of the responses to the no-surround stimuli (for the plaid-only data, specifically the conditions where the orientations of Center₁ and Center₂ were identical). For simplicity, preferred orientations were binned before analysis (bin width: 30°).

MUA fitting.

Population responses (see Figs. 2 and 3C) were fit according to the equations and approaches described in Results. The underlying templates used in these fits were themselves acquired by fitting the population response with a circular Gaussian (two free parameters: width and height). Importantly, these template fits were acquired before attempting to fit the remaining data and were therefore not optimized for the entire dataset. Where different models were compared, the significance associated with the improved fit of the full model was determined using Sequential F-testing. Any data used to fit the underlying templates were excluded from such significance calculations.

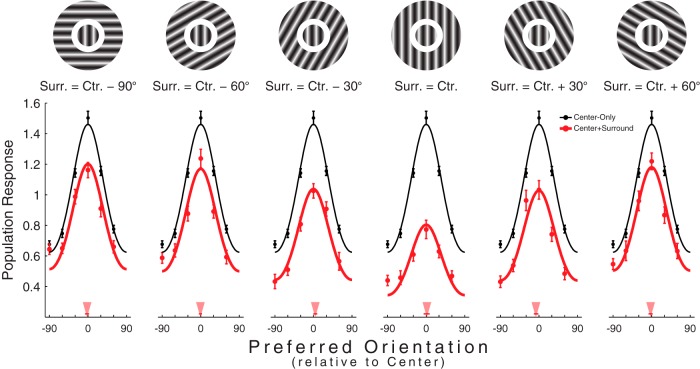
Figure 2.

Scaling of population responses. Population responses under each of the six relative center/surround configurations (a stimulus exemplifying the relevant configuration is illustrated above each subplot). Data points indicate mean ± SEM. Smooth black curves indicate the circular Gaussian fit to the center-only population response. Smooth red curves indicate the center-only Gaussian, scaled to best fit the center+surround data depicted in red. Red triangles point to the orientations of the mean vectors calculated from the center+surround population responses. The thin red lines superimposed on the triangles indicate the 95% confidence intervals obtained from the bootstrapping procedure described in the main text. Stimuli are shown for illustration and are not to scale.

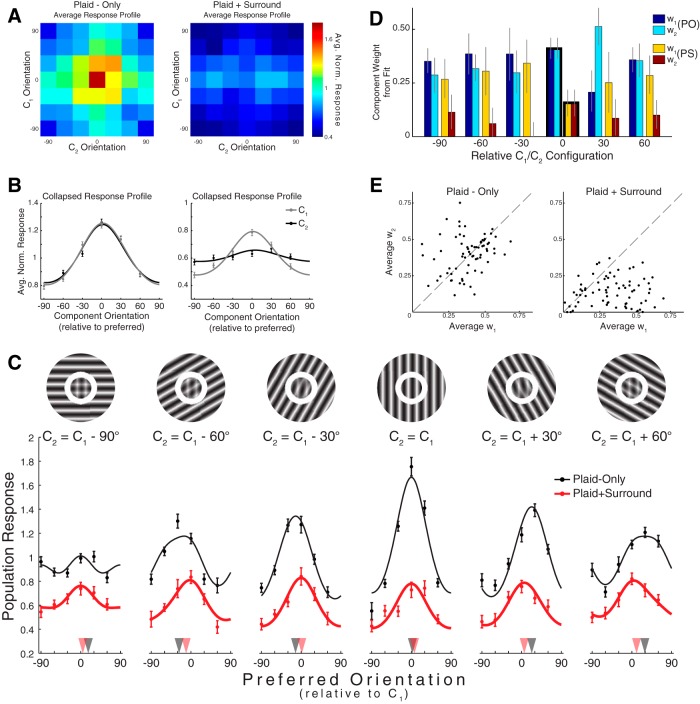
Figure 3.

Component-specific suppression with plaid center stimuli. A, Average response maps measured under the two surround conditions. B, Response maps in A, collapsed across stimulus dimensions, showing the average tuning to each of the center components with (right) and without (left) a surround. C, Population responses under each of the six relative configurations (a stimulus exemplifying the relevant configuration is illustrated above each subplot). Data points indicate mean ± SEM. Smooth curves indicate the results of the fitting procedure described in the main text (Eq. 2). Black (red) triangles point to the orientations of the mean vectors calculated from the plaid-only (plaid+surround) population responses. Stimuli are shown for illustration and are not to scale. D, Best-fitting component weights (Eq. 2). For fitting the two C₂ = C₁ population responses, w₁ and w₂ were constrained to be equal. The 95% confidence intervals (black) were obtained using bootstrapping. E, Scatter plots comparing the mean weight assigned to each component for fits to the plaid-only data (left) and fits to the plaid+surround data (right). Each data point corresponds to an individual multiunit.

Model parameter fitting.

Our entire dataset (the center-only, center+surround, plaid-only, and plaid+surround data) was fit to a single model with six free parameters (Eq. 3). During fitting, these parameters were chosen to minimize the squared adjusted error between the observed population responses (see Figs. 2, 3C) and those produced by the model (see Fig. 4). The adjusted error refers to an additional step where the error on each data point was normalized by the grand mean of the dataset to which it belonged. (For example, the errors in the fit to the plaid+surround data were normalized by the grand mean of the actual plaid+surround data.) We observed that the standard least squared error fitting approach (where this normalization does not occur) underfit the center+surround and plaid+surround data, likely because some model parameters only applied to the half of the data where a surround was present and this half of the data contained less variance. Normalizing the error as we described ameliorated this bias and produced better qualitative fits.

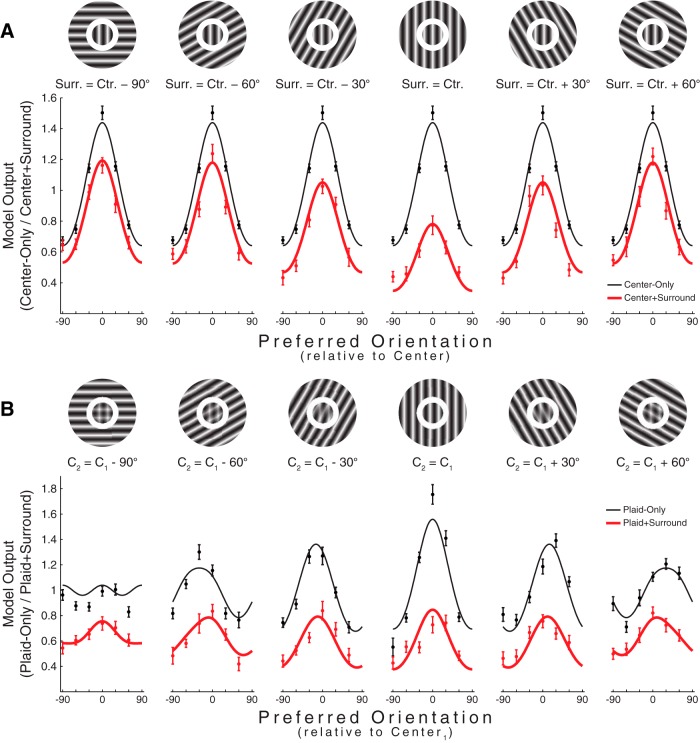
Figure 4.

Population responses predicted by input-gain model (Eq. 3). Continuous lines indicate model responses. Dots indicate actual data. A, Population responses under each of the six relative center/surround configurations, shown for the center-only (black) and center+surround (red) data. Conventions are identical to Figure 2. B, Same as A, for the plaid-only (black) and plaid+surround (red) data. Conventions are identical to Figure 3C.

Results

We measured multiunit activity in primary visual cortex (V1) of two awake male macaque monkeys during a fixation task involving the presentation of stimuli designed to probe center/surround interactions (see Materials and Methods). Responses were recorded using chronically implanted 10 × 10 microelectrode arrays. Our experimental procedure involved two distinct stimulus sets (see Materials and Methods): data collected using a single, full-contrast grating in the center are referred to as “center-only” and “center+surround”; data collected using two superimposed half-contrast gratings are referred to as “plaid-only” and “plaid+surround.” For each stimulus set, a given electrode was only allowed to enter analysis on at most one session, yielding sample sizes of 47 multiunit sites for the center-only/center+surround data and 71 for the plaid-only/plaid+surround data.

Surround suppression scales population responses to single-grating center stimuli

Previous studies characterizing center/surround interactions in V1 have shown that surround suppression is greatest when surround features (i.e., orientation, direction, color) match those of the center (Sillito et al., 1995; Zipser et al., 1996; Cavanaugh et al., 2002b; Shen et al., 2007). With the goal of identifying the surround mechanism underlying this form of context-dependent response modulation, we first sought to replicate these findings by measuring V1 responses to stationary sinusoidal gratings representing all combinations of center and surround orientation. Consistent with previous reports, we found that tuned surround suppression was a common property of the multiunits recorded: in the subset of trials with the center at the preferred orientation, suppression was significantly tuned to surround orientation (p < 0.05, permutation test) in a majority of the analyzed units (25 of 47) and the average suppression from the preferred surround (46%) significantly exceeded the average suppression from the anti-preferred surround (19%). In addition, the orientation tuning of the surround depended on the orientation contained in the center. This trend was often visible in the responses of individual multiunits (see example in Fig. 1A) and was clearly visible in the combined population data (Fig. 1B). Each of these plots shows the tuning to the orientation of the center when no surround was present (plotted in black) as well as the tuning to the orientation of the surround (plotted in red) measured when the center was held at a particular orientation. The six subplots show the surround tuning measured for each of the fixed center orientations, which is indicated by the title of the plot and by the black asterisk along the abscissa. For each center condition (i.e., for each surround tuning curve), the red triangle represents the maximally suppressive surround orientation, which clearly tracks the orientation in the center.

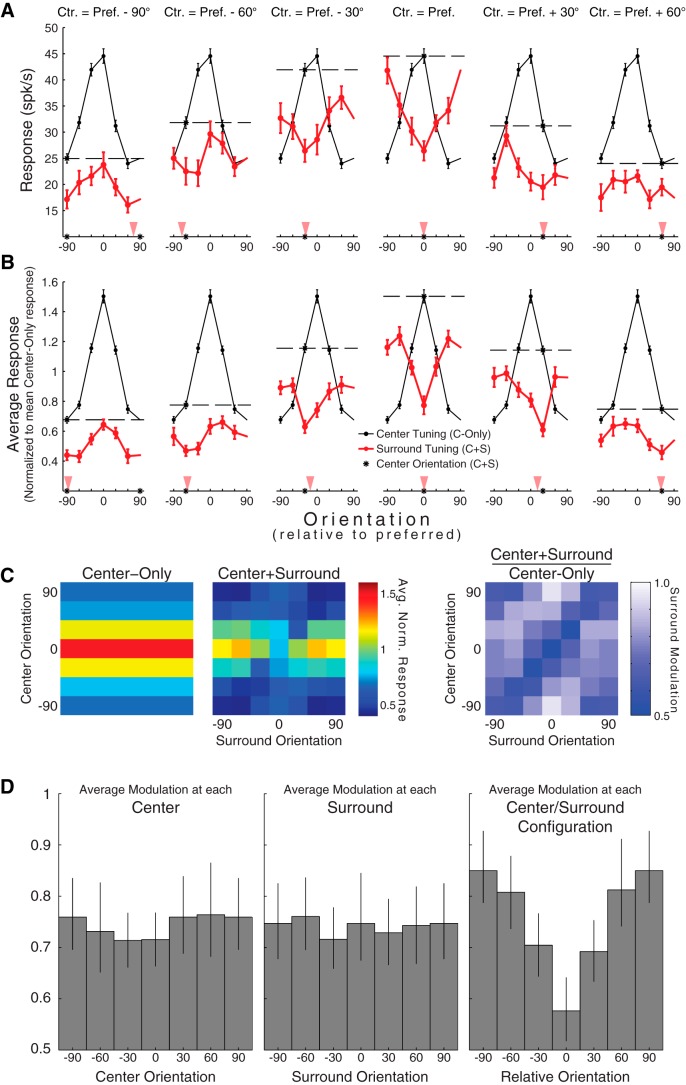
Figure 1.

Tuning of surround suppression is sensitive to stimulus context. A, Tuning of an example MU to center orientation with no surround (black curve) and to surround orientation (red curves). Data points indicate mean ± SEM. Data plotted in black indicate the orientation tuning of the example MU to center orientation. These data serve as a visual reference and are identical across the six subplots. Data plotted in red indicate the orientation tuning of the MU to the orientation of the surround (with the center orientation fixed at a particular orientation). Each plot represents the surround tuning measured using a specific center orientation (indicated by the title and again as a black asterisk along the abscissa). Dashed line indicates the response to the relevant center when presented without a surround. Red triangles represent the orientation of the maximally suppressive surround, calculated from the mean vector of the difference between the center-only response (dashed line) and the surround tuning. B, Same as A, for population-averaged data. C (left), Same data in B, represented as response maps. C (right), Surround modulation map obtained by dividing (element-wise) the center+surround response map by the center-only response map. Smaller values indicate greater suppression. D, Collapsed representations of the modulation map, showing the average relationships between surround modulation and center (left), surround (middle), and relative center/surround orientations (right). The 95% confidence intervals (black) were obtained using bootstrapping.

We compared responses to center-only stimuli and responses to center+surround stimuli after aligning responses by preferred orientation and pooling across units (Fig. 1C; n = 47; see Materials and Methods for details). From there, we estimated the condition-by-condition effect of the surround by normalizing the response to each center+surround stimulus by the response to the center-only stimulus with the same center (Fig. 1C). Collapsing the resulting suppression profile across surround orientations failed to reveal any systematic relationship between center orientation and degree of modulation, and the same was true for surround orientation when collapsing across center orientations (Fig. 1D). Instead, the pattern of modulation was almost entirely determined by the relative orientation (i.e., the absolute orientation difference) between the center and surround (Fig. 1D, right). Therefore, although the surround may have exhibited orientation tuning at a given center, the full set of center+surround responses suggested that suppression was not concentrated toward any particular orientation of the surround itself (nor of the center itself); rather, the key variable for describing suppression at the population level appeared to be the degree of orientation similarity between the center and surround (i.e., the relative center/surround configuration).

We rerepresented the combined center-only/center+surround data as a series of population responses under each of the relative center/surround configurations (Fig. 2). This illustrates how the presence of a surround affected the representation of center orientation, demonstrating that, for the center-only/center+surround dataset, the addition of a surround resulted in a scaling of the center-only population response (black curves). To confirm this intuition, we fit the center+surround population response in each configuration (red curves) with a scaled version of the center-only population response, which itself was fit as a circular Gaussian centered on 0° (the preferred orientation). As such, the center+surround population responses were expressed as follows:

where R_θ is the center+surround population response for relative center/surround configuration θ, w_θ is the scaling factor for that configuration, and T is the Gaussian template fit to the center-only population response. This analysis resulted in six unique weights, one for each of the six relative center/surround configurations and their respective population responses. The best fitting weights very closely approximate the average surround modulation measured at each relative configuration (Fig. 1D, right). We compared this reduced model (Eq. 1) with a full model in which T was allowed to shift (to accommodate potential shifts in the peak orientation) and found that the fit improvements offered by the full model were not significant (r_full² = 0.96; r_reduced² = 0.94; p = 0.15, Sequential F test), suggesting that, within the center+surround data, the surround did not shift the center tuning curves. One corollary of the scaling effect is that the orientations of the population responses' mean vectors continue to be 0°. We might fail to detect shifting behavior because the orientations in fact remain at 0° or because the data were too noisy. To estimate our confidence in the mean vector orientations measured for each of the six center+surround population responses, we iteratively resampled (with replacement) the underlying units in the complete dataset and remeasured the mean vectors at each iteration (n = 10,000) to determine the 95% confidence intervals. These intervals are plotted as red horizontal bars in Figure 2 and were quite small. As such, any shifting effects of the surround that we failed to detect using the Sequential F test were unlikely to be of more than a few degrees in magnitude.

Last, we adapted a fitting procedure used by Benucci et al. (2013; their Fig. 4) to quantitatively compare how center/surround orientation difference and neuronal orientation preference each contribute to the suppression patterns we measured. In essence, this approach fits surround modulation (Fig. 1C, right) as the product of two Gaussian-shaped gain factors: one tuned to the difference between the center and surround orientations (“stimulus” gain) and one tuned to the difference between the preferred orientation and the surround orientation (“neuronal” gain). The data were fit by adjusting the magnitude of each gain factor, which revealed that ∼84% of the observed suppression was attributable to stimulus gain (data not shown). Importantly, stimulus gain should scale population responses and neuronal gain should shift them (Benucci et al., 2013). As such, this analysis supports the conclusion that, when the center consists of a single grating, the surround acted primarily to scale population responses to the center.

Surround suppression shifts population responses to plaid center stimuli

The goal of this study was to understand the surround mechanism that gave rise to the suppression patterns illustrated in Figures 1 and 2 and reported previously (Sillito et al., 1995; Cavanaugh et al., 2002b; Jones et al., 2002; Shushruth et al., 2012). In particular, we wanted to distinguish between two alternative classes of models. The first possibility that we considered was that the surround acts as a global modulator of activity, and suppression similarly affects the output of all neurons whose receptive fields cover the “center,” regardless of each neuron's feature selectivity, thereby scaling the population response. This mechanism assumes that the pool of neurons controlling suppression is most active when the center and surround stimuli match. The second possibility we considered was that the surround acts to modulate the input strengths of specific features within the center stimulus, specifically those features that match the surround (Spratling, 2010; Lochmann et al., 2012). Accordingly, this mechanism would cause neurons to respond predominantly to the stimulus attributes that were unmatched to the surround stimulus. For example, a vertical surround stimulus would act to suppress whatever portion of the neurons' response was driven by vertical components of the center stimulus. Comparing these potential mechanisms more generally amounted to asking whether surround suppression is best understood as a form of output- or input-gain control.

The data presented thus far are useful for motivating the two hypothetical mechanisms described above but do not provide any evidence for one over the other. To distinguish between them, we performed an additional experiment using a “plaid” center stimulus, created by superimposing two 50%-contrast component gratings (termed Center₁ and Center₂, abbreviated in figures as C₁ and C₂), and recorded V1 responses to all Center₁/ Center₂ orientation combinations. On half of the trials, the plaid was presented by itself (“plaid-only”), and in the other half a surround was added whose orientation always matched that of Center₂ (“plaid+surround”). In this way, the center+surround and plaid+surround stimulus sets were quite similar; the difference was that, for the plaid+surround stimuli, the orientation presented in the surround also contributed to the center. This allowed us to measure responses under a similar range of center/surround configurations but introduced the manipulation that, at all times, at least one component orientation would match the surround.

Critically, this experiment allowed us to directly compare our two hypotheses because they make distinct predictions for how the surround should affect responses to the plaid centers. According to the first hypothesis, the surround mechanism is sensitive to center/surround similarity and globally modulates neuronal responses in proportion to this similarity, which would predict scaling of population responses similar to what was seen in the previous experiment (Fig. 2). According to the second hypothesis, the surround mechanism modulates the input strength of each feature of the center stimulus according to how much that feature matches the surround. Importantly, this predicts that the surround should shift population responses toward the orientation of the unmatched component of the center.

When examining the combined population data (n = 71) to the plaid-only stimulus set, we found that, on average, responses appeared equally tuned to the two component orientations (Fig. 3A,B, left). Unsurprisingly, the average plaid-only response curves to the two components were nearly identical because, without a surround, the distinction between Center₁ and Center₂ was arbitrary. Interestingly, the complementary response profile for the plaid+surround dataset revealed that the responses were more tuned to the orientation of Center₁ than to the orientation of Center₂, indicating that the surround had disproportionately suppressed the responses driven by the matched Center₂ component (Fig. 3A,B, right).

To investigate this possibility more closely, we examined population responses measured for the plaid-only/plaid+surround stimuli under each of the relative configurations (Fig. 3C). We reasoned that the measured population responses should be describable as a weighted sum of the responses to each center component alone (Busse et al., 2009; MacEvoy et al., 2009). To approximate this, we created a template by fitting a circular Gaussian to the plaid-only population response measured when the orientations of Center₁ and Center₂ were the same. For each of the remaining 11 curves, we fit the population response as a weighted sum of two such templates: one centered on the orientation of Center₁ and the other on the orientation of Center₂. When applied to the population responses, each curve could be expressed as follows:

where R_θ is the population response for a given configuration (identified by the Center₁/Center₂ orientation difference, θ), T₀ is the Gaussian template centered on 0° (representing the response to Center₁), T_θ is the Gaussian template shifted by θ° (representing the response to Center₂), and w₁ and w₂ are the weights assigned to Center₁ and Center₂, respectively. To reduce the tradeoff between fitting the mean versus the shape of the data, we allowed a constant offset, k. This model was then fit simultaneously to all 12 of the population response curves shown in Figure 3C (to ensure that the term k was the same across fits).

As stated above, our goal was to identify the class of mechanism underlying surround modulation, and we focused on two possibilities. The first was that the surround globally scales neuronal outputs in proportion to center/surround similarity. The second was that the surround effectively modulates the input strength of distinct center features depending on whether they match the surround. The most obvious difference between these two hypotheses is that they explain the surround mechanism as a form of output-gain control and as a form of input-gain control, respectively. That is, they differ in whether the effect of the surround occurs after or before inputs are combined into a neuronal response. In the context of Equation 2, this difference could be expressed as whether the surround modulates the response itself (R_θ; output-gain control) or whether the surround modulates the specific weight given to each component (w₁/w₂; input-gain control). The advantage of fitting our data with Eq. 2 was that it allowed us to compare these two mechanisms simply by asking whether the surround differentially affected the weights associated with each center component.

The set of weights obtained by fitting the data to Equation 2 is plotted in Figure 3D. The fits to the plaid-only data produced approximately equal weights, on average, between the two components, as expected. The fits to the plaid+surround data show that the surround disproportionately reduced the contribution of the matched center component to the population responses: w₁ exceeded w₂ for all plaid+surround fits where they were not constrained to be equal. We additionally performed this fitting procedure for each multiunit individually. The plots in Figure 3E compare, for each unit, average w₁ to average w₂ for the plaid-only data (left) and for the plaid+surround data (right). (For averaging, we ignored data from conditions where the two center components had the same orientation.) As one would expect, there was not any systematic difference between the average component weights in the plaid-only data (p > 0.5, paired t test). In contrast, the average weight given to the unmatched Center₁ component consistently exceeded that given to the matched Center₂ component, and this trend was highly significant (p ≪ 0.00001, paired t test).

These analyses show that the surround effectively suppressed the portion of the response specifically driven by the matched component. This effect is evident not only in the combined data (Fig. 3C,D) but also in the responses of individual multiunits (Fig. 3E). The specificity of this suppression is further visible in Figure 3C, where plaid-only population responses appear to represent the approximate average orientation of the two plaid components but plaid+surround population responses instead appear to represent almost exclusively the orientation of Center₁. These representational shifts, caused by a selective suppression of the response to Center₂, directly contradict the hypothesis that the surround performs population scaling as a function of center/surround similarity. Instead, our findings provide strong physiological evidence in support of input-gain control as the mechanism underlying surround suppression (Spratling, 2010; Lochmann and Deneve, 2011).

Suppression as feature-selective input gain

From this perspective, our entire dataset should be easily describable by a model with two simple stages: one in which the surround modulates the weighting of specific inputs and another in which inputs are combined into a response according to their weighting. Here, we formalize such a model to demonstrate how an input-gain control mechanism can recapitulate the modulation patterns we observe.

The first stage, implementing input-gain control, can be written as follows:

where c_θ is the stimulus contrast of the center component with orientation θ. The term inside the brackets represents the effects of the surround. Within this term, G_surround (θ − θ_s) is a circular Gaussian function tuned to the difference between the orientation of the center component, θ, and the orientation of the surround, θ_s. G_surround implements feature-selective input-gain control by modulating the component contrast according to how much the orientation of that component matches the surround. The magnitude of this feature-selective input gain is determined by a scaling factor α; additionally, the term β is a constant offset that allows the surround to control input gain in a feature-nonselective manner. The result of this modulation is represented as w_θ, which can intuitively be thought of as the effective strength or “weight” of the center component with orientation θ. To model responses when no surround is present, α and β are simply set to 0.

The second stage of the model is then the neuron's response function, where each input is combined (summed) into a net output according to its weighting and the neuron's orientation preference:

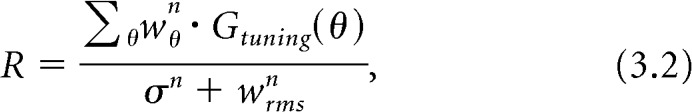where w_θ is the weight of the center component with orientation θ (from Eq. 3.1), and G_tuning(θ) is a circular Gaussian representing the orientation tuning of the neuron. The weighting of each center component is multiplied by the neuron's preference for the orientation of that component; the neuron's response, R, is taken as the sum of these products, normalized by a constant, σ, plus the root mean square of the weights of all center components. The exponent, n, is a constant. We chose this response function for our model because it has been shown to account for population responses to plaids as a function of their component contrasts (Busse et al., 2009). Although our Equation 3.2 similarly expresses population responses as a function of the components' “weight,” we do not intend to equate these weights to contrast, per se. That is, we cannot say with certainty that the effect of the surround on a given component is the same as changing that component's contrast (see Discussion).

The model given by Eq. 3 is described by six free parameters: the width of G_surround, the width of G_tuning, α, β, σ, and n. We used this model to simulate the full range of experiments we performed. We chose parameter values based on what produced the best agreement between the population responses returned by the model and those observed experimentally (see Materials and Methods). This model, which relies on feature-specific input-gain control, provided an excellent fit to the data and produced population response patterns qualitatively identical to what we observed (Fig. 4, original data replotted as dots for comparison). When simulating the center-only/center+surround data, the effect of the surround was to scale population responses (Fig. 4A; compare with Fig. 2), whereas, when simulating the plaid-only/plaid+surround data, the effect of the surround was to shift population responses away from the orientation of the surround (Fig. 4B; compare with Fig. 3C). Therefore, the full range of surround effects that we observed experimentally is explained by a mechanism that functions to reduce the effective input strength of specifically those stimulus features that are matched to their surroundings.

Eye movement controls

Given that perifoveal V1 receptive fields are of similar spatial scale to fixational eye movements, we wanted to be certain that our results were not affected by such eye movements. First, although the fixation window we used was on the generous side (1.5 degrees in diameter), both animals maintained fixation over a much smaller range: the median within-trial variability in eye position was 0.07 degrees (root mean square), well within the scale of the center stimulus (generally a diameter of 0.3 degrees). Second, we reanalyzed the plaid data after removing half of the trials with the largest variance in eye position and obtained results that were qualitatively identical to those from the full dataset. Finally, we note that any deviations in eye position would have the effect of moving the stimulus surround into the RF center, a manipulation that would produce responses favoring the orientation of the surround stimulus: opposite to the effects we observed. We are thus confident that small fixational eye movements did not influence our results.

Discussion

We investigated the effect of surround suppression on population coding in V1 of alert macaque monkeys under a range of stimulus configurations. Previous studies have found that the effect of a surround stimulus on neuronal responses depends on the center stimulus with which is it presented (Sillito et al., 1995; Cavanaugh et al., 2002b; Shen et al., 2007; Shushruth et al., 2012). The common result throughout these studies is that, in general, suppression follows the degree of feature-similarity between the center and surround. This tendency was readily visible in the V1 responses we measured to all combinations of center and surround orientation (Figs. 1 and 2). In addition, we measured V1 center/surround interactions using stimuli in which the center consisted of plaids. The effect of the surround in this dataset was to specifically reduce the portion of the response driven by the central plaid component whose orientation matched that of the surround (Fig. 3). These seemingly distinct suppression patterns were both consistent with a single input-gain control mechanism that reduces the effective strength of center features that match the surround (Fig. 4).

The response function used to model our data (Eq. 3.2) is adapted from the normalization model previously shown to account for population responses to plaids as a function of their component contrasts (Busse et al., 2009). Whereas Busse et al. (2009) systematically varied the contrast of the plaid components, in our experiments it was kept constant. As such, we do not really know whether the surround's effect on the center components behaves exactly like contrast (i.e., shows the same characteristic nonlinearity). Although it is intriguing to interpret our result in the context of the contrast-weighted normalization model (Busse et al., 2009) by saying that the addition of the surround lowers the effective contrast of the matched plaid component, the experiments needed to make that claim have not been done. We thus emphasize the common feature of the two models that we think is necessary for explaining our results, which is the relative weighting of the inputs (i.e., input-gain control). However, we do note that normalization (the denominator of Eq. 3.2) improves the performance of our model; this mechanism exaggerates the shifting effect of the surround when responses are driven by multiple orientations with unequal weights, producing an output that is closer to “winner-take-all,” with the unmatched component winning.

Although the results obtained using the plaid stimuli are, to our knowledge, novel, the observation that surround tuning depends on the contents of the center is well established. Despite this, relatively little is known about the biophysical mechanisms directing this form of contextual modulation. The most successful biophysical model to date (Shushruth et al., 2012) derives its explanatory power from the assumption that the feedforward activity evoked by a given center stimulus engages recurrent activity in an orientation-nonspecific manner; each neuron receives the strongest suppression when the surround contains its preferred orientation but only when the center and surround stimuli match does the suppression inhibit the primary source of recurrent drive to the network. Although this model is capable of replicating the nonfixed suppression patterns observed previously and in our center+surround data, it is not intuitively obvious whether it could reproduce the results of our plaid experiment. Thus, our data provide an important benchmark for future biophysical models.

The impact of future research directed toward understanding the circuit mechanisms that control input gain will likely extend beyond the scope of surround suppression. For one thing, the firing rate changes observed in studies of selective attention are well captured when attention is modeled as changes in the effective strength of inputs into a normalization mechanism (Lee and Maunsell, 2009; Ni et al., 2012). This description reconciles the finding that attention performs multiplicative scaling with a single center stimulus (McAdams and Maunsell, 1999) with the finding that attention often has nonlinear effects with multiple stimuli in the RF center (Reynolds et al., 1999; Reynolds and Desimone, 2003). Interestingly, the effects of a surround on the population responses we observed with either one or two orientations in the RF center resemble the effects of attention under similar conditions (Lee and Maunsell, 2010). This similarity is further evidenced by the ability of the same basic model (where attentional or surround context controls a feature-selective input-gain mechanism) to explain both the effects of attention and the full range of surround behavior reported above. Although this descriptive overlap may hint at a common mechanism, one has yet to be identified experimentally. Nevertheless, a unified explanation of attentional and surround modulation (based on context-dependent input-gain control) seems within reach (Spratling, 2008, 2010).

The common link between surround suppression and selective attention may be that both mechanisms serve to enhance the representation of relevant information. In the case of attention, relevance is behaviorally determined, whereas, in the case of surround suppression, relevance appears to be determined by the statistics of natural stimuli. That is, a given surround may establish predictions regarding the contents of the center based on learned statistics of naturally occurring stimuli (Schwartz and Simoncelli, 2001; Coen-Cagli et al., 2012). Elements of the center that violate the predictions established by the surround are more relevant by virtue of the added information that they carry (Rao and Ballard, 1999). This fact appears to be exploited by the surround mechanism, as evidenced by the observation that, when the center contains both redundant and informative elements (i.e., orientations that do and do not, respectively, match the surround), representation is specifically biased toward the more informative (i.e., less spatially redundant) element. This feature of the surround likely explains its observed tendency to decorrelate and “sparsify,” and thereby increase the information content of representations of natural stimuli in V1 (Vinje and Gallant, 2000, 2002; Haider et al., 2010). Importantly, our conclusions support those of theoretical studies that approached surround suppression as a form of input-gain control, especially with regard to their implications for how the surround enhances efficient coding (Spratling, 2010; Lochmann et al., 2012).

The idea that the surround promotes efficient processing is not new (Barlow, 1959; Mumford, 1992), nor is the idea that top-down mechanisms interact with surround suppression (Bair et al., 2003; Roberts et al., 2007; Sundberg et al., 2009; Nassi et al., 2013, 2014). However, these ideas bear further investigation because they underscore the notion that contextual modulation (in the form of context-dependent, feature-selective, input gain) is a solution to the inherent challenges of representing natural stimuli. With this in mind, our findings constitute key physiological evidence supporting a framework for understanding contextual modulation and its role in information processing. According to this framework, “context” (in the case of passive sensing) is determined by the surround (rather than by its continuity with the center); modulation occurs through a form of feature-specific input-gain control that can fundamentally tailor the representation of context-embedded stimuli; and this mechanism prioritizes the efficient representation of the most informative features of the sensory input. Identifying the circuit mechanisms that perform this type of input-gain control remains a crucial step toward understanding how the cortex implements contextual modulation.