Simulation method for calculating the entropy and free energy of peptides and proteins

Abstract

A method called complete hypothetical scanning Monte Carlo has been introduced for calculating the absolute entropy, S, and free energy, F, of fluids. Here, the method is extended to peptide chains in vacuum. Thus, S is calculated from a given sample by reconstructing each conformation step-by-step by using transition probabilities (TPs); at each step, part of the chain coordinates have already been determined (the “frozen past”), and the TP is obtained from a Monte Carlo simulation of the (future) part of the chain whose TPs as yet have not been calculated. Very accurate results for S and F are obtained for the helix, extended, and hairpin microstates of a simplified model of decaglycine (Gly)₁₀ and (Gly)₁₆. These results agree well with results obtained by the quasiharmonic approximation and the local states method. The complete HSMC method can be applied to a macromolecule with any degree of flexibility, ranging from local fluctuations to a random coil. Also, the difference in stability, ΔF_mn = F_m - F_n between significantly different microstates m and n can be obtained from two simulations only without the need to resort to thermodynamic integration. Our long-term goal is to extend this method to any peptide and apply it to a peptide immersed in a box with explicit water.

In ref. 1, White and Meirovitch discuss the importance and difficulties of calculating the absolute free energy, F, and entropy, S; however, their role in computational structural biology should be further emphasized. The energy surface of a protein, commonly defined by a force field, is highly rugged, consisting of a tremendous number of local minima (2), where the native structure corresponds to the localized energy well with the lowest F. However, molecular dynamics simulations have shown (3, 4) that even a protein with a well defined structure fluctuates significantly within a region called wide microstate (e.g., the conformational region of an α-helix of a peptide) that typically consists of many localized energy wells. A peptide or protein, or protein segments such as surface loops, can exhibit an intermediate flexibility, where several wide microstates are populated significantly at thermodynamic equilibrium. It is essential to be able to identify these wide microstates, m, and to calculate F_m, which lead to their relative populations and to weighted averages of various quantities that can be compared with experimental values (5, 6). F_m is useful particularly if m and n differ significantly; then, calculating the difference, ΔF_mn = F_m - F_n is straightforward, whereas calculating it by thermodynamic integration might be prohibitive (see refs. 7–12 and references therein).

In ref. 1, the hypothetical scanning (HS) method for calculating the absolute F and S (10) has been further developed and applied to liquid argon and water. This method, named complete hypothetical scanning Monte Carlo (HSMC), is extended here to a peptide in vacuum or peptide described by an implicit solvation. As a first step, we treat a simplified model of decaglycine (Gly)₁₀ simulated by Monte Carlo (MC) (13) at three wide microstates: helix, extended, and hairpin. Each sample conformation is reconstructed gradually by calculating transition probabilities (TP) for the dihedral angles and fixing the related atoms at their positions. A TP is obtained by an MC simulation of the future (yet unfixed) part of the chain and, to avoid the escape of a future sample from the corresponding microstate, we impose restrictions obtained from the local states (LS) method for calculating S (5, 6, 14–18). Therefore, the entire procedure is a hybrid of two techniques and, to test its performance for larger peptides, we also study a 16-residue polyglycine (Gly)₁₆ in the helix and extended wide microstates. The complete HSMC results for S and F are found to be in a very good agreement with results obtained by the LS method and the quasiharmonic (QH) approximation (19, 20). Our long-term goal is to extend the complete HSMC method to any peptide and to apply it to a peptide immersed in a box with explicit water.

Theory and Methodology

The Model and Statistical Mechanics Considerations. We have first studied decaglycine, NH₂(Gly)₁₀CONH₂, modeled by the amber96 force field in vacuum (21), where the charges of the end groups were neutralized. For simplicity, we denote the dihedral angles ϕ_i,Ψ_i, and ω_i ordered along the chain by α_k, k = 1,3N = 30, where N is the number of residues [the extension for (Gly)₁₆ is straightforward]. The partition function, Z, is an integral over the function exp(-E/k_BT) (E is the potential energy and k_B, the Boltzmann constant) with respect to the Cartesian coordinates over the whole conformational space, Ω. However, for a stable wide microstate, the integration is carried out only over the limited region Ω₀ that defines the wide microstate. To apply the HS or LS methods, one has to change the variables of integration from Cartesian to internal coordinates, which makes the integral dependent also on the Jacobian, J. For a linear chain, J has been shown to be independent of the dihedral angles and is a simple function of the bond angles and bond lengths. Thus, if the potentials of these “hard variables” are strong, their average values can be assigned to J, which to a good approximation can be taken out of the integral (see refs. 19, 22, and 23).

For the same reason, one can assume a more restrictive model (see below), where the bond angles and bond lengths are kept constant at their average values and thus the corresponding exp(-E/k_BT) values can be taken out of the integral as well. In particular, notice that, although the contribution of bond stretching to the absolute entropy is not small, it is expected to be similar for different wide microstates of the same molecule. Therefore, to a good approximation, the contribution of bond stretching to the differences ΔS_m,n and ΔF_m,n between wide microstates m and n cancels out. Assuming that the bond lengths are not correlated with the bond and dihedral angles enables one to carry out the integration over the bond lengths; if a similar assumption is made for the bond angles, the remaining integral becomes a function of the 3N dihedral angles (22, 23) The partition function is

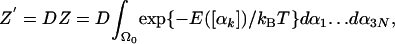[1]

where the prefactor D is a product of J and the integral over the bond lengths and bond angles; D depends on T and the units in which the bond lengths and bond angles are expressed. For calculating ΔS_m,n and ΔF_m,n of two wide microstates of the same molecule, lnD cancels and can be ignored (notice, however, that D contributes to the absolute F and S). The probability density corresponding to Z (Eq. 1) is

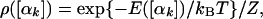[2]

and the exact entropy (defined up to an additive constant) is

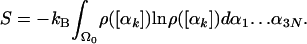[3]

Thus far we have described the transformation from a peptide model represented by Cartesian coordinates to a model represented by dihedral angles. This is needed for applying both the LS and HS methods. However, we have found MC simulations in Cartesian coordinates to be extremely inefficient; therefore, we have studied a relatively simple model of ployglycine based on the amber96 force field with constant bond lengths and bond angles, an option available in the program tinker (http://dasher.wustl.edu/tinker). Thus, the dihedral angles ϕ_i, Ψ_i, and ω_i become the variables of an MC procedure significantly more efficient than that based on Cartesian coordinates; for the present model of rigid geometry, the application of the LS and HS methods is therefore direct. Obviously, keeping the bond angles constant is a temporary restriction applied only in this initial study of the complete HSMC method. In what follows, for simplicity, the various methods will be described as applied to this model of polyglycine.

The Exact Scanning Method. The exact scanning method is a step-by-step construction procedure for polymer chains (24) and thus is equivalent to the MC and MD procedures in the sense that large samples generated by all these methods lead to the same averages and fluctuations within the statistical errors. With the exact scanning method an N-residue conformation of polyglycine in the helical region (Ω₀), is built by defining the dihedral angles α_k step by step with TPs and adding the related atoms; for example, the angle ϕ determines the coordinates of the two hydrogens connected to C^α, and the position of C′ (16, 25). Thus, at step k, k-1 dihedral angles α_1,..., α_k-1 have already been determined, they and the related structure (the past) are kept constant, and α_k should be defined with the exact TP density ρ(α_k|α_k-1... α₁),

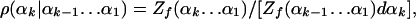[4]

where dα_k is a small segment centered at α_k, and Z_f(α_k... α₁) is a future partition function defined over the helical region Ω₀ by integrating over the future conformations defined by α_k+1... dα_3N (within Ω₀), where the past angles, α₁... α_k, are held fixed,

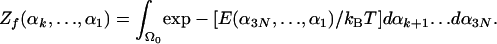[5]

The probability density of the entire conformation is

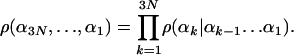[6]

Because of the equivalence between the MC and the scanning method mentioned above, one can assume that a given MC sample has rather been generated by the scanning method, which enables one to reconstruct each conformation and to calculate the TP densities that hypothetically were used to create it step-by-step. This idea can be implemented in two different ways, by the LS and HS methods. Because some elements of the LS method are implemented within the framework of the complete HSMC method, we describe the LS method first.

The LS Method. In the first step, the MC sample (of a given wide microstate) is visited, and the variability range Δα_k is calculated (5, 6, 14–18).

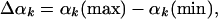[7]

where α_k(max) and α_k(min) are the maximum and minimum values of α_k found in the sample, respectively. Next, the ranges Δα_k are divided into l equal segments, where l is the discretization parameter. We denote these segments by ν_k, (ν_k = 1, l). Thus, an angle α_k is now represented by the segment ν_k to which it belongs, and a conformation i is expressed by the corresponding vector of segments [ν₁(i), ν₂(i),..., ν_3N(i)]. Under this discretization approximation, ρ(α_k|α_k-1... α₁) can be estimated by

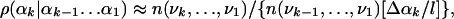[8]

where n(ν_k,..., ν₁) is the number of times the LS [i.e., the partial vector (ν_k,...,ν₁) representing (α_k,...,α₁)] appears in the sample. Because the number of local states increases exponentially with k, one has to resort to approximations based on smaller LSs that consist of ν_k and the b angles preceding it along the chain, i.e., the vector (ν_k, ν_k-1,..., ν_k-b); b is called the correlation parameter. The sample is visited for the second time, and for a given b, one calculates the number of occurrences n(ν_k, ν_k-1,..., ν_k-b) of all of the local states from which a set of TP ρ(ν_k|ν_k-1,..., ν_k-b) are defined. The sample is then visited for the third time, and for each member i of the sample, one determines the 3N local states and the corresponding TP, whose product defines an approximate probability density ρ_i(b, l) for conformation i:

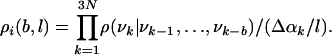[9]

The larger are b and l, the better the approximation (given enough statistics). ρ_i(b, l) allows defining an approximate entropy and free energy functional, S^A and F^A, which constitute rigorous upper and lower bounds for the correct values, respectively (25),

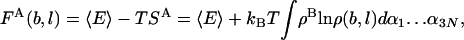[10]

where 〈E〉 is the Boltzmann average of the potential energy, estimated from the MC sample, and ρ^B is the Boltzmann probability density with which the sample was created.

S^A is estimated from a Boltzmann sample of size n by S̄^A:

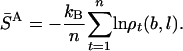[11]

As discussed in ref. 1, the fluctuation ΔF of the correct free energy is zero, whereas the approximate F^A has finite fluctuation, ΔF^A (estimated by 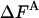), which is expected to decrease as the approximation improves (17).

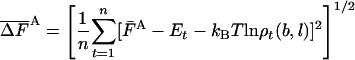[12]

The LS method can be applied to any chain flexibility, i.e., it is not limited to harmonic or QH fluctuations (19, 20, 22, 23, 26). Thus, free energy differences between wide microstates with significant structural differences can be calculated, which is a difficult task with methods based on thermodynamic integration.

Approximate HS Method. The idea of the HS method is to reconstruct each sample conformation step by step, obtaining the TP density of each α_k (Eq. 4) by calculating the future partition functions Z_f. However, a systematic integration of Z_f within the limits of Ω₀ is difficult and becomes impractical for a large peptide where Ω₀ is unknown; therefore, thus far, HS was applied only to self-avoiding walks (SAWs) on a lattice, where Ω₀ is the entire space and Z_f is calculated approximately by enumerating only future SAWs of f steps (i.e., α_k,..., α_k+f-1), rather than of N - k + 1 steps (27, 28).

The Complete HSMC Method. With the complete HSMC method applied to peptides (like for fluids), one calculates at each reconstruction step k of conformation i the TP density, ρ(α_k|α_k-1... α₁), from n_f MC steps (trials) (13), where the entire future of the peptide can move by changing the future angles α_k,..., α_3N, whereas the dihedral angles α₁,..., α_k-1 (defining the past) are kept fixed at their values in conformation i. A small segment (bin) δα_k (see Eq. 4) is centered at α_k, and the number of MC visits to this bin during the simulation, n_visit, is calculated; one obtains

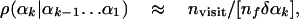[13]

where the relation becomes exact for a very large n_f. The product of these TP densities leads to the probability density of the entire chain (Eqs. 6 and 10). Notice that, unlike the systematic calculation of Z_f, where the limits of Ω₀ are in practice unknown, with the complete HSMC procedure, the future structures generated by MC at each step k remain in general within the limits of the wide microstate Ω₀ defined by the analyzed MC sample. In some cases, however, the future samples were found to escape from this region; therefore, before applying the complete HSMC method, the LS method is applied to the analyzed sample and the α_k(min) and α_k(max) values (Eq. 7) are calculated; they are then used to keep the future structures within Ω₀ by rejecting MC moves with angle values beyond those of α_k(min) and α_k(max). Although complete HSMC considers the entire future, in practice ρ(α_k|α_k-1... α₁) (Eq. 13) will be somewhat approximate due to insufficient future sampling, imperfect random number generator, etc.; therefore, the corresponding free energy, F^A (Eqs. 10 and 11), will underestimate slightly the correct value, where its fluctuation ΔF^A (Eq. 12) does not vanish.

Results and Discussion

We have first studied three wide microstates of (Gly)₁₀: helix, hairpin, and extended. Samples of these wide microstates were generated by the Metropolis MC procedure (13) at 100 K where a trial structure is obtained by randomly changing all of the 30 dihedral angles, each within ±1° of its current value. These simulations were started from helical, extended, and hairpin structures obtained by minimizing the energy of the corresponding structures, ϕ_k = Ψ_k = -55°, and ω_k = 180°, ϕ_k = Ψ_k = ω_k = 180°, and two extended strands of four residues connected by a type I′ turn. The first 5,000 MC steps were used for equilibration, and from the following 50,000 steps, after every 100 steps the current structure was retained for future analysis; in this way, three equal samples of 500 structures were generated. It should be pointed out that preliminary simulations at 300 K resulted in unstable samples (i.e., the structures escaped from their wide microstates); therefore, the temperature was decreased to 100 K, where the helix and extended simulations were found to be very stable, whereas the hairpin sample remained stable only up to the first 50,000 MC steps. The corresponding Δα_k values (Eq. 7) are relatively small (see Table 1), representing relatively concentrated samples. Notice, however, that due to correlations, each wide microstate is significantly smaller than the corresponding region, Δα_1×Δα_2×.... ×Δα₃₀.

Table 1.

The differences (in degrees) between the minimum and maximum values of the dihedral angles of (Gly)₁₀ in three MC samples of 500 structures (Eq. 4)

	Extended			Helix			Hairpin
Number	Δυ	Δυ	Δω	Δυ	Δψ	Δω	Δυ	Δψ	Δω
1	47	142	23	43	48	23	35	57	21
2	61	55	23	20	43	21	37	30	21
3	57	43	23	28	33	22	37	36	26
4	68	51	26	22	25	21	54	89	21
5	58	46	25	30	35	19	59	65	24
6	68	46	24	25	29	20	31	27	18
7	61	45	23	22	46	16	30	43	32
8	66	42	25	27	34	19	39	31	22
9	60	54	25	30	48	19	41	37	23
10	65	47	26	49	360	26	56	32	28

To apply the complete HSMC method, each conformation was reconstructed step by step by TPs obtained from MC simulations of the future part carried out in the same way as described above with the additional restriction that a trial conformation with α_k larger than α_k(max) or smaller than α_k(min) is rejected. To check the convergence of the results, they were calculated for four future sample sizes, n_f = 20,000, 40,000, 80,000, and 160,000. For the same reason, we studied for each dihedral angle four bin sizes, δ = Δα_k/15, Δα_k/10, Δα_k/5, and 20° centered at α_k. Notice that as for the LS method, the bin size is proportional to Δα_k. If the counts of the smallest bin are smaller than 50, the bin size is increased to the next size and, if necessary, to the next one (δ = Δα_k/5); the same is applied to the second size bin. In the case of zero counts, n_visit is taken to be 1; notice, however, that zero counts is a very rare event.

Results for the entropy (TS) appear in Table 2 for various n_f values and bin sizes; the results for the largest bin (of 20°) are not provided, because they are significantly worse than those obtained for the smaller bins. All of the HSMC results are based on samples of 400 structures (of the entire samples of 500 conformations), and the statistical errors were obtained from the fluctuations and results based on partial samples. The accuracy of complete HSMC can always be improved by decreasing the bin size and increasing the future sample size, meaning that correspondingly S^A (Eq. 11) is expected to decrease [provided that the probability density is defined on the same conformational space (i.e., the wide microstate) as the Boltzmann probability density used to generate the sample]. Indeed, for each bin, the entropy decreases (or remain constant) as n_f increases, where the only exception is the entropy for the helix based on the smallest sample, n_f = 20,000, which is smaller than the entropies of the larger samples; this probably stems from an HSMC probability density that is defined on only a partial region of the helical wide microstate due to insufficient sampling.

Table 2.

Entropy, TS^A (T = 100 K) in kcal/mol (Eqs. 10 and 11) for (Gly)₁₀ for various bin sizes (Eq. 4) and future sample sizes, n_f, obtained with the complete HSMC method

Bin size	nf	Extended	Helix	Hairpin
Δαk/5	20,000	20.30	16.33	18.32
	40,000	20.14	16.36	18.15
	80,000	20.06	16.34	18.02
	160,000	20.03	16.35	17.97
Δαk/10	20,000	20.24	16.08	18.17
	40,000	20.11	16.16	18.03
	80,000	20.04	16.16	17.90
	160,000	20.01	16.16	17.86
Δαk/15	20,000	20.23	16.01	18.14
	40,000	20.11	16.10	18.02
	80,000	20.04	16.10	17.89
	160,000	20.01	16.11	17.85
QH		19.83	16.13	17.76
LS		20.05	17.50	19.29

Δα_k is defined in Eq. 7. The HSMC results are based on a sample of 400 conformations. The statistical errors are not larger than ±0.05 kcal/mol for the HSMC and QH results (Eq. 14) and are not larger than ±0.03 kcal/mol the LS results (b = 1, l = 10). The entropy is defined up to an additive constant.

The entropy results for the extended microstate for a given n_f are the same for the different bin sizes, and the results for n_f = 80,000 and 160,000 are converged within the error bars. The same applies to the hairpin results for the two smallest bins. The helix results behave differently, where for each bin they are constant for the three largest n_f values, whereas they decrease with decreasing the bin size and probably have not yet completely converged. However, within the accuracy of the usual force fields, entropy and free energy differences smaller than 0.1 kcal/mol are in general ignored; therefore, even the helix results can be considered as converged.

It is of interest to compare the complete HSMC results with those obtained by other methods. For that, we increased the samples of the three wide microstates from 500 to 30,000 structures by imposing the restriction on the MC procedure that a trial conformation with α_k larger than α_k(max) or smaller than α_k(min) obtained for the initial sample (Table 1) is rejected. We applied the QH approximation (19, 20) to a subsample of 4,000 conformations, where

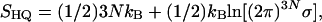[14]

and σ is the determinant of the covariance matrix of the 3N dihedral angles. We also applied the LS method (with correlation parameter, b = 1 and l = 10) to the entire increased sample. The QH results presented in Table 2 are very close to the complete HSMC values, probably because the three samples are approximately QH. The LS and HSMC entropies are equal for the extended microstate, because the angular correlations along the chain are short, and b = 1 already captures most of them. On the other hand, the range of these correlations increases for the helix and the hairpin, and the LS entropies, as expected, become slightly larger (upper bounds) than the HSMC values.

In Table 3, complete HSMC results are presented for the free energy, which is defined by F^A (Eq. 10), as discussed for the entropy above. These results are given only for the smallest bin, because the free energies for the other bins can be obtained from the entropies of Table 2; as expected, the free energy increases as the approximation improves (i.e., as n_f is increased). Again, the QH results are close to the HSMC values, and the LS result is close to the HSMC value for the extended microstate and smaller for the other two microstates. Notice, however, that the energy components of QH and LS are calculated from the corresponding larger samples (see previous paragraph). We also provide in Table 3 results for the average energy (obtained from 400 structures) and the fluctuations of the energy and free energy. As expected, the free energy fluctuations decrease as n_f is increased, and for n_f = 160,000, they are four times smaller than the corresponding fluctuations of the energy, except for the hairpin where the ratio is ≈2.

Table 3.

Results for the free energy, F^A (Eqs. 10 and 11) and its fluctuation 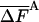(Eq. 12) obtained for (Gly)₁₀ by the complete HSMC method

	Extended		Helix		Hairpin
HSMC/nf	—FA		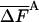—FA		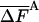—FA
20,000	74.75 (4)	0.61 (3)	98.48 (3)	0.50 (4)	84.57 (3)	0.84 (4)
40,000	74.64 (4)	0.39 (3)	98.57 (2)	0.32 (4)	84.45 (3)	0.63 (3)
80,000	74.57 (3)	0.26 (3)	98.58 (2)	0.23 (4)	84.32 (3)	0.45 (3)
160,000	74.53 (2)	0.18 (3)	98.59 (2)	0.18 (4)	84.27 (3)	0.36 (3)
QH	74.48 (8)		98.69 (8)		84.64 (8)
LS	74.68 (1)		100.08 (1)		86.14 (1)
—Energy	54.53 (7)	0.73 (4)	82.48 (5)	0.80 (5)	66.43 (7)	0.68 (5)

All results are in kcal/mol. T = 100 K. The first result in the last line is for the average energy, and the second is for its fluctuation. The HSMC results are presented only for the smallest bin size, δ = Δα_k/15, but for all the future samples sizes, n_f. F is defined up to an additive constant. The free energy obtained with the QH approximation (Eq. 14) and the LS method is based on larger samples. The statistical error is given in parentheses, e.g., 82.48 (5) = 82.48 ± 0.05.

The main interest in this study is to determine the relative stability of the three wide microstates. In the upper part of Table 4, we present results for the differences, TΔS, ΔF, and ΔE between these microstates for (Gly)₁₀. Within their uncertainty of 0.1–0.2 kcal/mol, the differences are very stable for the three bin sizes, for n_f = 40,000–160,000, for samples as small as 200 conformations, and for the helix-extended differences also for 100 conformations. This demonstrates that, in practice, complete HSMC can be quite efficient. For the model studied, the helix is the most stable, where its free energy is lower by 14.3 and 24.1 kcal/mol than that of the hairpin and extended microstates, respectively. These differences are mostly governed by the energy differences, 11.9 and 27.95 kcal/mol, where the TΔS values are only 1.7 and 3.9 kcal/mol, respectively.

Table 4. Differences in the entropy, TΔS^A, the free energy, ΔF^A, and the energy, ΔE, among the three wide microstates (these properties are denoted R).

	TΔSA	ΔFA	ΔE
	(Gly)10
R(extended) — R(hairpin)	2.2 (1)	9.7 (1)	16.1 (1)
R(extended) — R(helix)	3.9 (1)	24.1 (1)	27.95 (6)
R(hairpin) — R(helix)	1.7 (2)	14.3 (2)	11.9 (1)
	(Gly)16
R(extended) — R(helix)	7.1 (2)	55.7 (2)	62.9 (3)

Results are in kcal/mol. TΔS^A and ΔF^A were obtained by the complete HSMC method at T = 100 K. The statistical error is defined in Table 3.

It is of interest to test the performance of complete HSMC for larger peptides, and we therefore also applied it to (Gly)₁₆. Two samples of size 600 each spanning the extended and helical wide microstates were generated by MC [as described for (Gly)₁₀], where 400 and 600 conformations of them were reconstructed by HSMC, respectively. The dihedral angle values of these samples are concentrated around their canonical values with deviations Δα_k (Eq. 4) very close to those obtained for (Gly)₁₀ in Table 1, where significant differences exist only for ΔΨ of the first and last residues. Results for TS^A, F^A, and its fluctuation, ΔF^A, appear in Tables 5 and 6, which are structured as Tables 2 and 3. The corresponding results for TS^A are basically unchanged (i.e., converged) as bin size decreases, i.e., in going from Δα_k/5 (results not shown) to Δα_k/10, and to Δα_k/15. Within each bin size, the helix results are constant as well, meaning that already a future sample size of n_f = 40,000 is sufficient. On the other hand, for the extended microstate, the results for each bin size decrease as n_f is increased and larger n_f is needed to reach convergence; for n_f = 320,000, the expected extrapolated result is TS^A = 31.90, which is used in calculating the differences for (Gly)₁₆ in Table 4.

Table 5. Results for the entropy, TS^A, of (Gly)₁₆.

		Extended	Helix
Bin size	nf	TSA	TSA
Δαk/10	20,000	33.26 (8)	24.54 (4)
	40,000	32.48 (6)	24.73 (5)
	80,000	32.13 (6)	24.74 (5)
	160,000	31.96 (5)	24.73 (5)
Δαk/15	20,000	33.26 (8)	24.50 (4)
	40,000	32.52 (6)	24.72 (5)
	80,000	32.15 (6)	24.74 (5)
	160,000	31.97 (5)	24.73 (5)
QH		32.5 (2)	25.8 (2)
LS		32.80 (4)	26.90 (6)

All results are in kcal/mol and T = 100 K. The QH and LS results were obtained from samples of 2.5 × 10⁴ and 5 × 10⁴ conformations, respectively. The parameters and statistical error are defined in Tables 2 and 3. The entropy is defined up to an additive constant.

Table 6. Results for the free energy, F^A, of (Gly)₁₆.

		Extended		Helix
Bin size	nf	—FA		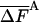—FA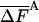
Δαk/15	20,000	100.70 (6)	1.20 (6)	154.81 (3)	0.69 (7)
	40,000	99.96 (4)	0.81 (4)	155.03 (2)	0.47 (6)
	80,000	99.59 (3)	0.57 (3)	155.05 (2)	0.33 (4)
	160,000	99.41 (2)	0.42 (3)	154.03 (1)	0.24 (2)
QH		99.8 (1)		155.2 (1)
LS		100.34 (4)		157.60 (7)
—Energy		67.44 (6)	0.94 (10)	130.31 (8)	1.13 (10)

All results are in kcal/mol and T = 100 K. The QH and LS results were obtained from samples of 2.5 × 10⁴ and 5 × 10⁴ conformations, respectively. The parameters and statistical error are defined in Tables 2 and 3. The free energy is defined up to an additive constant.

As expected, for both microstates, the LS results (b = 1, l = 10) slightly overestimate the HSMC values, whereas the QH results are equal to the HSMC values within a relatively large statistical error. The free energy fluctuations, as expected, decrease monotonically as the approximation improves, and they are smaller than the energy fluctuations by a factor of 4.7 and 2.2 for the helix and extended microstates, respectively. The LS and QH results were obtained from relatively large samples of 5·10⁴ and 25·10³ conformations, respectively, hence the corresponding energies are slightly different from those based on the smaller HSMC samples; thus, whereas the F^A(LS) and F(QH) are close to F^A(HSMC), a strict comparison is not straightforward. In Table 4 the differences, TΔS, ΔF, and ΔE for the extended and helix microstates are presented with acceptable errors of 0.2–0.3 kcal/mol (see above). It should be pointed out that the results for S^A and the energy of the helix scale with increasing peptide size, whereas the energy of the extended state does not; therefore, ΔE, and ΔF, do not scale in going from (Gly)₁₀ to (Gly)₁₆.

At this stage of development of the complete HSMC method, reconstructing a single conformation of (Gly)₁₀ based on n_f = 160,000 requires ≈90-min central processing unit (CPU) time on a 2.6-GHz Athlon processor, meaning that a n_f = 40,000 run, which is sufficient for providing the 0.1–0.2 kcal/mol accuracy, requires 23-min CPU time; for (Gly)₁₆, the time increases by a factor of ≈2.2. However, one can increase the efficiency further by decreasing the amount of sampling (n_f) for the smaller future peptides and using importance sampling methods to enhance the number of counts.

Summary

We have introduced here the complete HSMC method for a peptide chain in vacuum. In this initial study, we sought to treat a simple model with minimal degrees of freedom and therefore chose a polyglycine model with constant bond lengths and bond angles described by the amber force field. Although ignoring the contribution of the bond lengths to differences in entropy is a valid approximation, the contribution of the bond angles is significant and should not be ignored; however, adding this contribution is straightforward and is currently being studied by us. To be able to generate stable wide microstates around helix, extended, and hairpin structures, the temperature was decreased to 100 K; the corresponding samples were approximately QH, which allowed comparing the HSMC results with those obtained by the QH method. However, unlike the QH method, the complete HSMC is general, in the sense that it can be applied to any chain flexibility, where side chains visit all of the available rotamers, for example. Complete HSMC is probably the only method for calculating the absolute entropy of peptide chains that, practically, is exact.