Repeatability of adaptation in experimental populations of different sizes

Abstract

The degree to which evolutionary trajectories and outcomes are repeatable across independent populations depends on the relative contribution of selection, chance and history. Population size has been shown theoretically and empirically to affect the amount of variation that arises among independent populations adapting to the same environment. Here, we measure the contribution of selection, chance and history in different-sized experimental populations of the unicellular alga Chlamydomonas reinhardtii adapting to a high salt environment to determine which component of evolution is affected by population size. We find that adaptation to salt is repeatable at the fitness level in medium (N_e = 5 × 10⁴) and large (N_e = 4 × 10⁵) populations because of the large contribution of selection. Adaptation is not repeatable in small (N_e = 5 × 10³) populations because of large constraints from history. The threshold between stochastic and deterministic evolution in this case is therefore between effective population sizes of 10³ and 10⁴. Our results indicate that diversity across populations is more likely to be maintained if they are small. Experimental outcomes in large populations are likely to be robust and can inform our predictions about outcomes in similar situations.

1. Introduction

The repeatability of evolution has important implications. If evolution is repeatable, evolutionary trajectories taken by different lineages and the final evolutionary outcomes in given conditions will be the same. In other words, high repeatability will reduce the extent of diversification and/or lead to the loss of diversity across independent populations. Thus, the repeatability of evolution affects our understanding of the nature of biodiversity [1] and can inform the extent to which evolutionary theory can be used to make predictions [2,3].

Ultimately, the relative contributions of selection, chance and history to adaptation will determine whether trajectories and outcomes are repeatable across independent populations. Using the metaphor of the fitness landscape [4] (i.e. the regression of individual fitness over genotypic space), we describe adaptation as a climb up a fitness peak. In an isogenic population, this will occur through the fixation of novel beneficial mutations. If every possible mutation is generated each generation, selection will lead to the increase in frequency of the one with largest beneficial effect at every step [5–8], assuming there is always a single mutation with largest effect. In such cases, genetic changes will be attributable entirely to selection, and adaptation will be highly deterministic, always following the quickest path up the fitness peak.

In reality, all possible mutations will not be generated and/or established in each generation. Stochasticity in the supply of mutations will increase the probability that different populations fix different mutations, and therefore follow different paths up a fitness peak. If there is only one fitness peak, such as on a ‘smooth’ fitness landscape, the divergence in evolutionary trajectories will be temporary, as all populations will eventually converge on the same outcome. However, if there are multiple peaks, such as on a ‘rugged’ fitness landscape, this stochasticity can lead to long-term divergence (e.g. [9,10]).

Finally, populations with different evolutionary histories are unlikely to be starting at the same place on the fitness landscape. History can reduce the repeatability of evolutionary trajectories and outcomes among genetically different populations by altering the accessibility of certain paths [11]. We expect history to have minimal impact on the final outcomes of adaptation on smooth landscapes, as all populations will converge on the same peak. By contrast, on rugged landscapes, different populations will remain constrained to the peak nearest their starting location, unless they are able to cross fitness valleys through variance-induced peak shifts [12], drift [4,13], double mutants [14,15] or recombination [15–17]. History could thus potentially cause long-term divergence in adaptive outcomes.

The importance of chance and history as opposed to selection during adaptation is likely to be affected by population size. In the absence of standing genetic variation, small populations are expected to explore more trajectories than larger populations because of the low supply of beneficial mutations, and variation in what particular mutation arises across populations [18–20]. Trajectories and outcomes in small populations are therefore predicted to be less repeatable than in large populations because of the higher contribution of chance. In large populations, the higher supply of mutations will increase the probability of there being multiple different individuals each carrying a different beneficial mutation. Clonal interference [5–7] will tend to lead to the fixation of the mutations with largest beneficial effect [21,22] and to a reduction in the number of different trajectories taken by independent lineages [18]. As such, adaptation in large populations is predicted to be more repeatable because of the greater efficiency of selection and lower contribution of chance [18–20].

Microbial experiments have shown that selection is usually the most important driver of evolutionary change relative to history and chance after at least 200 generations of evolution in a novel environment [23–28]. Similar results have been obtained in sexual and initially diverse experimental populations of Drosophila after 20–30 generations [29,30]. While the effect of population size on the contribution of selection, chance and history has not, to our knowledge, been empirically determined, smaller population sizes do generally lead to greater among-population variation than do large population sizes [31], although this effect depends on the environment [32] and time scale [33].

Here we quantify the contribution of selection, chance and history to adaptation to a novel environment of initially isogenic, asexual experimental populations of different sizes. We predict that chance and history will play a greater role in small populations while selection will be more efficient in larger populations.

2. Material and methods

(a). Base populations

The experiment was started using six different genotypes of the unicellular green alga Chlamydomonas reinhardtii: CC-1690 (wild-type, mating type+); CC-1952 (wt, mt−); backcrossed CC-2342 (strain created in our laboratory by backcrossing to the wild-type CC-2342 a total of 12 times, mt−); backcrossed CC-2344 (same as above using wild-type CC-2344, mt−); backcrossed CC-2931 (same as above using wild-type CC-2931, mt+); dark line DD C8 (obtained from G. Bell, mt+). These genotypes are genetically [34] and/or ecologically distinct. We propagated each genotype individually, such that all growth during the experiment was vegetative, and adaptation occurred via de novo mutations.

(b). Selection experiment

For each combination of genotype and population size, we had six replicate lines, for a total of 6 × 3 × 6 = 108 independent lines. A single colony from each genotype was expanded in standard growth medium. Six samples from each well-mixed culture were used to initiate each replicate line. The amount of genetic variation is minimal and expected to be the same across replicates. The replicates were then propagated independently. Each line was exposed to a constant novel environment consisting of Bold's minimal medium [35] supplemented with 5 gl⁻¹ NaCl. High salt imposes strong osmotic and oxidative stresses in C. reinhardtii by disrupting the homeostasis of ions (Na⁺, Cl⁻, K⁺ and Ca²⁺), degrading proteins, and thus reducing rates of photosynthesis and cell division [36,37]. We chose 5 gl⁻¹ NaCl because salinities between 5 and 7 gl⁻¹ NaCl (0.085 and 0.120 M) reduce growth by about 50% [38–40] and induce adaptive responses within short evolutionary time scales [40].

Population size was manipulated by varying the volume of growth medium in which the lines were growing. Small lines were cultured in 0.1 ml of medium (96-well plate), medium lines in 1 ml (48-well plate) and large lines in 8 ml (6-well plate). Lines were serially transferred using the same relative inoculum size (5%) at the end of each cycle (i.e. every 4 days). This means that the number of cells at the end of a growth cycle and the number of cells transferred are greater in larger volumes than in small volumes. Using the same relative inoculum size ensures that the number of cell divisions within a growth cycle, population density and the relative amount of spent media transferred are the same across treatments initially, although small differences (i.e. about 1.3-fold difference in cell density at the end of the experiment compared with 10-fold differences in population size) will arise as populations adapt during the experiment. Using N_e = gN_o, where N_e is the effective population size, g is number of generations between transfers (here g = 4.3) and N_o is the initial population size [41], the effective population sizes for the small, medium and large lines at the start of the experiment are approximately 5 × 10³, 5 × 10⁴ and 4 × 10⁵ cells, respectively. Lines were maintained at 24.5°C, 60% air humidity, 8000 Lux constant light intensity, shaking at 130 r.p.m. with a 3 mm rotation diameter. The experiment lasted 40 cycles (about 200 generations). Note that since our focus is on general adaptation to the selection environment, rather than any specific adaptation to the salt stress, it was not necessary for us to maintain control lines evolving in the absence of salt.

(c). Fitness assay

To estimate fitness, we calculated the maximum growth rate of ancestral and evolved lines when grown in 5 gl⁻¹ NaCl. The ancestors had been maintained in dim light on Bold's agar throughout the experiment, conditions which limit growth and selection [35]. Six cultures were set up per ancestor to match the number of evolved lines generated per ancestor per population size treatment. All lines were cultured in Bold's medium for two cycles to minimize physiological differences, and then transferred to 5 gl⁻¹ NaCl. Each line was assayed three times.

Growth was monitored during the second growth cycle in 5 gl⁻¹ NaCl by measuring optical density at 750 nm every 9 ± 1 h. We transformed the measurements (log10 of (optical density × 10 000)) to allow the models to be fitted. Growth parameters were extracted from a nonlinear model using nonlinear least squares in the nlstools R package [42]. We first fitted a baranyi model [43,44]. This model returned a fit for 83% of the lines. The remaining lines were fitted with either a baranyi model without N_max, a baranyi model without lag or a linear model, as appropriate. Model fits were visually inspected to ensure the proper model had been applied.

(d). Determining the contribution of selection, chance, and history

Generally speaking, the effect of selection is to increase fitness. As such, the difference between the ancestors and evolved lines is the contribution of selection on beneficial alleles and any associated alleles that may be hitchhiking. Note here that we are investigating sources of variation in fitness. Differences between the phenotype or genotype of ancestors and evolved lines could be attributable to factors other than selection. Any variation in fitness among evolved lines descending from the same starting genotype will be the result of chance. Finally, if history affects adaptation, we expect lines from different starting genotypes to reach different outcomes. As such, variation in final fitness among starting genotypes is the contribution of history.

More specifically, we quantified components of variation in fitness by calculating sums of squares, which provides a phenomenological description of the structure of variation that is entirely additive [25]. The effect of selection was estimated as mnr(F − I)², where F and I are the final and initial grand mean growth rates, respectively, m is the number of lines descending from each ancestor, n is the number of ancestors and r is the number of assay replicates. The effect of history was estimated as mrΣ(A − F)², where A is the mean growth rate of all lines from a given ancestor. The effect of chance was estimated as rΣΣ(L − A)², where L is the mean growth rate of each replicates from a given line. Finally, the variation due to error measurement was estimated as ΣΣΣ(R − L)², where R is the growth rate of each replicate. Each sum of squares estimate was divided by the sum of all estimates to obtain the relative contribution of each factor. We prefer this method to alternative variance component-based approaches [23,26,29] since our design does not permit a full additive partition of variation using these methods. Nevertheless, a variance component analysis of our data produced similar results.

(e). Statistical analyses

Variance in growth rates among the starting genotypes was estimated by equating observed and expected mean squares from a nested analysis of variance, with genotype and line within genotype as random effects. To determine whether adaptation had occurred, and whether it had occurred to different extents in populations of different sizes, multiple comparisons were done using Tukey's HSD following a general linear model on population size (with four levels representing the ancestors, and the small, medium and large evolved lines), as a fixed effect. To further investigate the effect of population size on growth and its interaction with starting genotype and line, we performed an analysis of variance on the growth of the evolved lines. The model included population size as a fixed factor, starting genotype as a random factor, line within genotype as a random factor and their interactions.

The significance of the difference in relative contribution of selection, chance and history between two sizes of populations was determined by a randomization test. We randomly allocated each evolved line to a population size and initial genotype without replacement, and then calculated the relative sums of squares. We compared the ratio of relative sums of squares for each pair of population sizes to the observed ratios. The number of times where the random ratios were as large or larger than those observed over the total number of randomizations (10 000) is our significance statistic.

3. Results

(a). The ancestors differ in their response to the novel environment

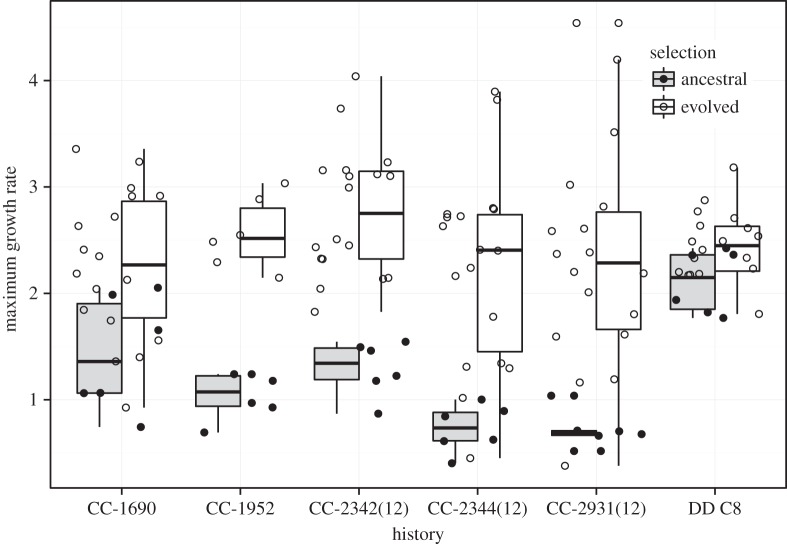
There is a significant amount of variation in growth rates among the six starting genotypes (figure 1; variance among genotypes = 0.26, mean = 1.22).

Figure 1.

Maximum growth rate of ancestors and evolved lines in 5 gl⁻¹ NaCl. History corresponds to the different starting genotypes.

(b). Small populations adapt to a lesser degree than larger populations

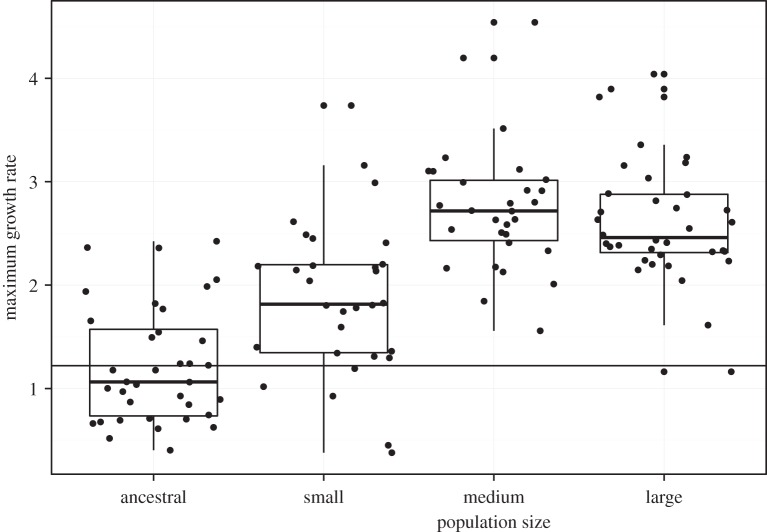
All six replicate lines of ancestor CC-1952 went extinct in small and medium populations. These lines were not included in the following analyses. Among the surviving lines, all population sizes have greater growth rates on average than their ancestors, meaning that adaptation to 5 gl⁻¹ NaCl has occurred over the course of 200 generations of evolution (figure 2; effect of population size F_3,392 = 88.72, p < 0.001; TukeyHSD comparisons between ancestors and small or medium or large evolved lines all have p < 0.001). The growth rate of small lines is significantly lower than that of the medium and large lines (p < 0.001 for both comparisons) while the growth rates of medium and large lines do not differ (p = 0.62).

Figure 2.

Maximum growth rate in 5 gl⁻¹ NaCl of the ancestral line, and of the small, medium and large evolved lines.

The growth of each genotype, as well as the growth of each line within genotype, varies depending on which size of population they evolved in (effect of population size F_2,192 = 70.86, p < 0.001; effect of population size × starting genotype interaction F_8,192 = 13.02, p < 0.001; effect of population size × line within history interaction F_50,192 = 3.36, p < 0.001).

(c). Population size affects the contributions of selection, chance and history to evolution

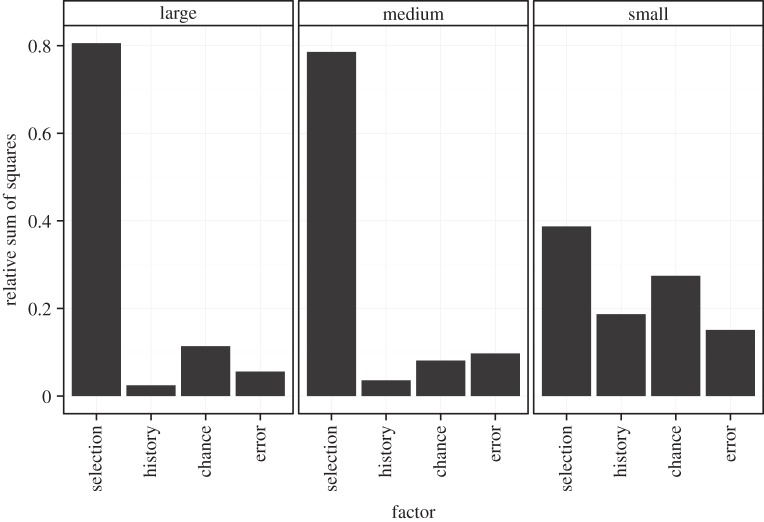
Selection plays a significantly greater role in medium and large lines than in small lines during evolution in 5 gl⁻¹ NaCl (figure 3, tables 1 and 2). Selection explains about 80% of the changes in growth rates in medium and large lines, whereas it explains less than 40% in small lines.

Figure 3.

Relative contribution of selection, chance and history after 200 generations of selection in 5 gl⁻¹ NaCl. Error here corresponds to variation among assay replicates.

Table 1.

The effect of population size on the contribution of selection, history and chance to variation in growth rates after 200 generations of evolution in 5 gl⁻¹ NaCl. Error here corresponds to variation among assay replicates.

population size	effect	sum of squares	total sum of squares	relative sum of squares
small	selection	38.1	98.4	0.387
	history	18.4		0.187
	chance	27.0		0.275
	error	14.8		0.151
medium	selection	210	267	0.786
	history	9.60		0.0359
	chance	21.7		0.0810
	error	26.0		0.0974
large	selection	210	261	0.806
	history	6.40		0.0245
	chance	29.8		0.114
	error	14.6		0.0560

Table 2.

Significance of the difference between population sizes in the relative contribution of selection, history and chance. p-values were determined from a randomization test.

factor	comparison	p-values
selection	small–medium	0
	small–large	0
	medium–large	0.38
history	small–medium	0.064
	small–large	0.015
	medium–large	0.26
chance	small–medium	0.0017
	small–large	0.012
	medium–large	0.19
error	small–medium	0.042
	small–large	0
	medium–large	0.0098

History explains less than 4% of the variation in medium and large lines, but explains close to 20% of the variation in small lines. This difference is significant when comparing small with large lines, but not when comparing small with medium lines (table 2). The variance among initial genotypes (σ² = 0.26) is maintained after evolution in small populations (σ² = 0.30), but much reduced after evolution in medium (σ² = 0.13) and large (σ² = 0.016) populations.

Finally, chance explains about 10% of the variation in medium and large lines, which are significantly less than the approximately 30% that it explains in small lines (table 2).

It is also interesting to look at the absolute amount of variation, because it tells us about the diversity that is present for a given component irrespective of mean growth or the amount of variation for another component. Small amounts of variation in growth, whether for low mean growth or high mean growth, means that growth is very similar across lines. The absolute variation among replicate lines with the same starting genotype is very similar for all population sizes (table 1). However, there is two to three times more variation among genotypes evolved in small than in medium and large populations. Finally, the variation between ancestors and evolved lines is more than five times smaller in small lines than in medium and large lines.

We can define the repeatability of adaptation as the ratio of the difference between deterministic and stochastic contributions to evolutionary change over total variation. That is, (SS_selection – (SS_chance + SS_history))/(SS_selection + SS_chance + SS_history). A value of 1 indicates completely deterministic dynamics, and a value of −1 indicates completely stochastic dynamics. Repeatability is –0.087 in small lines, 0.74 in medium lines and 0.71 in large lines.

4. Discussion

We propagated experimental populations of small, medium and large size (N_e = 5 × 10³, 5 × 10⁴ and 4 × 10⁵ cells, respectively) in a novel environment for 200 generations. By partitioning the variation in growth among lines into selection, chance and history, we determined which components depend on population size and how this affects the repeatability of evolution at the fitness level. Initial diversity among larger populations was lost as they converged on the same growth rate, whereas diversity among small populations was maintained as they diverged during adaptation. Thus, adaptation is less repeatable in small populations than in larger populations because history is more constraining and selection less efficient in the former.

(a). The transition from stochastic to deterministic dynamics

The main differences in the relative contributions of selection, chance and history arise between small and medium populations, although we cannot rule out the possibility that a more powerful study would have shown a more continuous effect of population size. This suggests that the transition between stochastic and deterministic dynamics occurs between effective population sizes of 10³ and 10⁴. This is lower than an estimate from microvirid bacteriophages, where the transition occurred between bottleneck sizes of 10⁴ and 10⁵ [31]. Stochastic dynamics occur when mutations fix more rapidly than they arise—that is, when N_eμ_b ≪ ln(N_es) [8]—and so depend on the effective population size as well as the rate (μ_b) and fitness effects (s) of beneficial mutations. While in C. reinhardtii the estimated mutation rate is 3.23 × 10⁻¹⁰ [45] or 6.76 × 10⁻¹¹ per site per generation [46], the rate per genome could be much greater than in viruses, and could explain why the transition point was observed at lower N_e. In addition, μ_b will depend on the number of genes involved in fitness for a particular environment as well as the specific type of gene interactions, and so the difference may reflect differences in the evolutionary challenge set by different selective environments. Without details of the genetic basis of adaptation in these experiments, it is difficult to speculate further.

The greater contribution of selection in medium and large lines than in small lines could be because of higher supply rate or probability of fixing beneficial mutations. It cannot be explained by effects of dilution ratio on the probability of fixing beneficial mutations [47,48] since the dilution ratio was maintained constant across population size treatments in this experiment. Rather, it is likely to result from a reduced supply of beneficial mutations in small lines. Selection was not more effective in large than in medium lines, perhaps because of clonal interference slowing down the rate of fixation of beneficial mutations [7,49,50].

The similar absolute contribution of chance across population sizes contrasts with the prediction that chance should be greater in smaller populations because of their lower supply of mutations and higher degree of drift [5,13]. It is possible that such effects will only occur in much smaller populations than used here.

(b). The importance of historical contingency

Differences in the amount of convergence or divergence in fitness among populations of different sizes could be due to differences in rates of adaptation [19,33] or the ability to cross fitness valleys in rugged fitness landscapes [18]. The initial variance among starting genotypes was reduced after evolution in medium and large populations, which is expected if the different histories were converging on the same trait combination. There may be a single fitness peak in this environment, and medium and large lines could have climbed it faster than small lines. However, we cannot exclude the possibility that the lines have reached different peaks of similar heights. Yet the maintenance of variance among genotypes evolving in small lines and the fact that some small lines achieved similar fitness to larger lines suggest that the differences in fitness between small and larger lines are not due entirely to slower rates of adaptation, but result from epistatic interactions. Large and medium lines appear to have ended up on the same peak, whereas small lines have remained trapped on different peaks.

In small populations, the lower supply of mutations can limit the exploration of the fitness landscape and increase the probability of getting trapped on local fitness optima. Larger populations are more likely to find the global fitness optimum because their higher supply of double or double-step mutants makes available a larger proportion of the landscape [51,52]. Convergence in medium and large lines could also have occurred if higher genetic or phenotypic variance within the populations led to flattening the adaptive landscape, enabling them to move across the landscape more easily than small lines [53].

The population sizes investigated here cover a limited range. They are much smaller than most microbial populations [54]. However, many isolated microbial populations, such as pathogens initiating an infection, will have their effective population sizes in the range investigated here following environmental change or colonization of new habitats. While they are of the same order as species such as Caenorhabditis elegans (with an estimate of 8 × 10⁴) [54] and many plant populations (with estimates of 10³–10⁴) [55], our results are probably only directly relevant to asexual populations without standing genetic variation.

Our populations were maintained entirely asexually. In sexual organisms, recombination generally increases the efficiency of selection [5,6,56–60] and should therefore increase repeatability. Thus, the threshold between deterministic and stochastic dynamics seen in our study might be pushed further down in sexual populations. However, whether recombination will reduce the effects of chance and history will depend, in part, on the amount of linkage disequilibrium and the type of gene interactions [16,17]. Experiments directly examining the effect of sex on the repeatability of adaptation would be valuable.

Another aspect of our system is the lack of initial standing genetic variation. In the short term, adaptation will generally be faster when there is standing genetic variation for fitness [5]. This may affect both the repeatability of adaptation and also the interaction with population size. That is, genetic variation could have a disproportionate effect in small populations which are limited by variation compared with large populations, where alleles present at the start will also arise through mutation at some point because of the high supply of mutations. Moreover, the effect might depend on the time scale. Over short time scales, selection will act on the standing alleles rather than the novel mutations because of their greater frequencies [61], while over longer time scales the contribution of standing genetic variation to adaptation will not be easily distinguishable from that of novel mutations.

On short evolutionary time scales, our results indicate that adaptation will be repeatable in large populations. If the mechanism of adaptation is well understood, then predictions about outcomes in large populations will be accurate. On the other hand, adaptation will be less repeatable and diversity will be maintained among independent populations if they are of small size. It will therefore be difficult to use evolutionary theory to make predictions about the outcome of environmental change in small populations. The strong effect of history underlines the importance of using different starting genotypes in experiments to investigate the range of potential responses of small populations to environmental change.

Data accessibility

The data associated with this manuscript are archived in Dryad (doi:10.5061/dryad.6m150).

Author contributions

J.L. conceived the study, designed the experiment, participated in the laboratory work, carried out the statistical analyses and wrote the manuscript. J.R. contributed in designing the experiment and participated in the laboratory work. N.C. coordinated the study and contributed to writing the manuscript. All authors gave final approval for publication.

Funding statement

J.L. is funded by NSERC of Canada as well as by a studentship from the School of Biological Sciences, University of Edinburgh. N.C. is funded by BBSRC of the UK.

Competing interests

The authors declare no competing interests.