Spatial synchrony of local populations has increased in association with the recent Northern Hemisphere climate trend

Abstract

According to ecological theory, populations whose dynamics are entrained by environmental correlation face increased extinction risk as environmental conditions become more synchronized spatially. This prediction is highly relevant to the study of ecological consequences of climate change. Recent empirical studies have indicated, for example, that large-scale climate synchronizes trophic interactions and population dynamics over broad spatial scales in freshwater and terrestrial systems. Here, we present an analysis of century-scale, spatially replicated data on local weather and the population dynamics of caribou in Greenland. Our results indicate that spatial autocorrelation in local weather has increased with large-scale climatic warming. This increase in spatial synchrony of environmental conditions has been matched, in turn, by an increase in the spatial synchrony of local caribou populations toward the end of the 20th century. Our results indicate that spatial synchrony in environmental conditions and the populations influenced by them are highly variable through time and can increase with climatic warming. We suggest that if future warming can increase population synchrony, it may also increase extinction risk.

Considerable effort has been devoted recently to extensive documentation of the responses of local populations to climatic variability on hemispheric or global scales. These efforts have revealed effects of large-scale climatic fluctuation on the population dynamics of birds, mammals, and amphibians throughout the Northern Hemisphere (1, 2). However, a central challenge inherent to attempts to foresee and mitigate responses of populations to future climate change arises from the scarcity of studies of sufficient length to compare responses of populations to climatic variability before and after the onset of the recent large-scale warming trend (3, 4).

The multicentury analyses of ecological dynamics in relation to climate necessary for such comparisons are rare (5), but they have the potential to contribute critical insight into the question of whether climatic influences on population processes have strengthened, weakened, or remained constant as global temperatures have risen (3, 6). A recent analysis of the occurrence of cholera in Bangladesh, for instance, revealed a strengthening in recent decades of the role of the El Niño Southern Oscillation in the temporal dynamics of this disease (6). That study is relevant to investigations of ecological effects of climate change because it indicates that the relationship between climate and ecological dynamics may not be constant through time but may strengthen with future warming.

Here, we present an analysis of nearly two centuries of data on multiple populations of caribou (Rangifer tarandus) spanning 10° of latitude in western Greenland (7) to investigate the potential for such nonstationary links between climate change and large-scale spatial synchrony in population dynamics. Our previous analyses of a subset of these data have revealed that large-scale climate, specifically the North Atlantic Oscillation (NAO), influences both temporal dynamics (8) and spatial synchrony of these populations (9). We focus on the role of climate in spatial synchrony of populations because numerous theoretical studies have concluded that the risk of global extinction is greater in synchronously fluctuating than in asynchronously fluctuating populations (10, 11) and an increase in spatial autocorrelation in the environment increases extinction risk (12). We focus on caribou not only because of the spatio-temporal extent of the population data for this species in Greenland, but also because caribou are one of the few Arctic large mammals to survive the rapid warming at the Pleistocene–Holocene transition (13). Moreover, caribou and reindeer have assumed an importance in human settlement of the far north that is perhaps unparalleled by any other mammal species, and they remain the most important means by which humans exploit primary productivity in the Arctic (14). Although caribou formerly occupied the entire continent, their present distribution in Greenland is restricted to the west coast (7), and the demise of many isolated Greenlandic populations has been attributed to freeze–thaw cycles during episodes of regional warming (15).

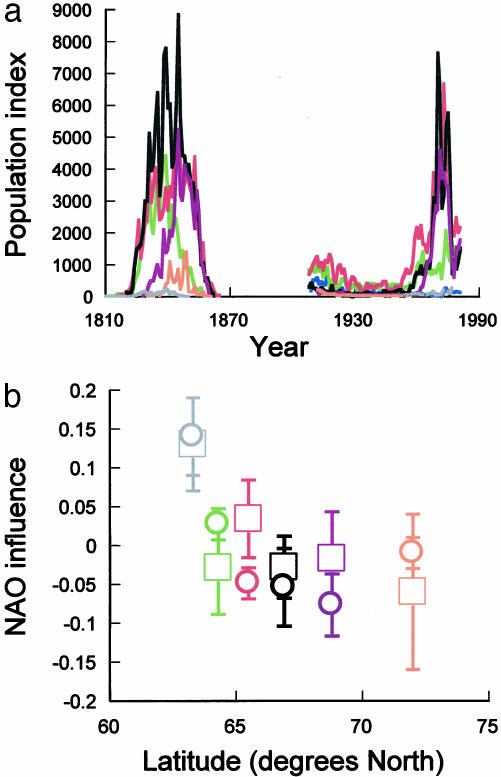
As is evident in the long-term caribou data from western Greenland, all of the extant populations have progressed through two multidecadal periods of increase and decline since 1810, strongly reminiscent of population cycles (Fig. 1a). A cursory evaluation of correlation among all seven populations during these two periods indicates that, during the more recent period, the average pairwise population correlation (0.53 ± 0.08) was ≈50% more than that during the earlier period (0.35 ± 0.08), suggesting an increase in population synchrony toward the end of the 20th century. Focusing on the subset of populations that are influenced by the NAO (8, 9), the average pairwise population correlation is higher in both periods and still ≈50% greater in the more recent period (0.75 ± 0.09) than in the earlier period (0.50 ± 0.09). These and other observations (16–18) suggest that population synchrony is not constant through time. However, the extent to which such temporal variability in population synchrony reflects similar temporal variation in spatial autocorrelation in weather due to climate change has not been addressed and is therefore a major focus of this paper.

Fig. 1.

Caribou population dynamics and response to NAO over two centuries in Greenland. (a) Dynamics of caribou populations, as indexed by fur trading and harvest data, between 1810 and 1981. Each color represents the same population in both periods. (b) Coefficients quantifying the strength of the NAO's influence on population dynamics in a plotted against the latitudes of these populations for the periods 1810–1865 (□) and 1910–1981 (○).

Materials and Methods

Temporal Changes in Spatial Synchrony of Populations. Time series data on the population indices for caribou in western Greenland cover the period 1810–1981 (Fig. 1a) and comprise annual skin-trading data (1810–1863, six populations) and harvest data (1908–1981, seven populations) compiled by the Danish National Archives and the Ministry of Greenland, respectively. We cannot be sure of the extent to which human hunting may have influenced year-to-year or longer-term changes in these population indices. However, data on the size of the human population in Greenland are available for 7 years at approximately 20-year intervals between 1840 and 1980 (19) and do not correlate with the caribou data for all populations combined or any population individually (all Pearson correlation coefficient P values > 0.50). Furthermore, for one of these populations, Paamiut, there exists a 35-year period of contemporary skin trading and harvest data that are highly correlated (r = 0.94, P < 0.0001). We assume that annual numbers of skins traded and animals harvested scale approximately linearly with population sizes (8, 20). Indeed, 7 years of aerial census data for two of these populations (Sisimiut and Manitsoq) overlap and correlate positively with data on numbers shot in those populations (r = 0.61, P = 0.14, df = 5).

One potential mechanism underlying increased population synchrony in the 20th century compared with the 19th century is a strengthening of the influence of climate on all populations in the more recent period. This hypothesis is consistent with the Moran theorem (21), which predicts that the degree of synchrony between any pair of populations should scale with the degree of correlation between environmental variables influencing their dynamics (22). To test for a change in the strength of climatic influence on population dynamics (Fig. 1a) between the two periods covered by the data, we applied autoregressive models to each time series in each period. These models were consistent in structure and included a lagged term for the NAO (8). We used an approximation of the t test (23) to compare the coefficients quantifying the NAO influence between the two periods for each population.

Linking Changes in Population Synchrony to Weather. An alternative contribution to temporal variation in population synchrony, also consistent with the Moran theorem (21, 22), might derive from an increase in spatial autocorrelation in local environmental variables influencing the dynamics of these populations (24), which, in this case, might ultimately be winter temperature and its effects on winter precipitation (15, 25, 26). Lacking long-term, spatially replicated data on winter precipitation, we used data on local winter temperatures. We used two approaches to test the hypothesis that temporal changes in spatial synchrony of caribou populations might be associated with similar changes in spatial autocorrelation of local winter temperatures. First, we used a 25-year sliding window (17) to construct time series on population correlation and correlation in local winter temperatures. This approach, however, has two obvious limitations. First, it produces observations that are highly autocorrelated in time because of pseudoreplication of the data between time steps (27). Second, we should expect population correlation to scale linearly with environmental correlation only for populations with identical density-dependent structure (22, 28). Hence, this stage of the analysis was limited to only two populations, Paamiut and Nuuk, which share identical first-order density dependence (8).

Another approach to testing this hypothesis, which is amenable to statistical analysis and allows us to include more populations in our analysis, is to use time series quantifying interannual variation in spatial autocorrelation in local populations and winter temperatures that do not suffer from pseudoreplication through time. Using data extending back to 1912, we constructed such time series indices of spatial autocorrelation of caribou population densities (hereafter referred to as caribou spatial synchrony) and local winter temperatures (hereafter referred to as temperature synchrony) across all available weather stations located within the ranges of the caribou populations along the west coast of Greenland. The indices of spatial synchrony were calculated as the inverse of the coefficient of variation across all observations in each year (29–31). For caribou spatial synchrony, this index would reflect only changes in the mean density calculated across all populations if the SD of the mean was constant over the period of analysis. However, there is significant covariation between the SD of these populations and the spatial synchrony index through time (r = -0.95, P = 0.001). The index of temperature synchrony was calculated from winter temperature data to which a constant was added in all years to remove negative observations, which would otherwise confound the calculation of the index (32).

Annual estimates of caribou abundance were not continuous for all populations. We wanted to avoid any potential bias in our calculation and analysis of caribou spatial synchrony that might arise because of the uneven spatio-temporal distribution of the full data set. Therefore, we limited our analyses to the four populations influenced by the NAO (8) and with the longest continuous and overlapping time series: Nuuk, Manitsoq, Sisimiut, and Aasiaat, all of which are continuous over the periods 1828–1860 and 1912–1981. Results of analyses that included a fifth population, Upernavik, which was not influenced by the NAO (8), did not differ from results focusing on the other four populations.

We analyzed temporal variation in the spatial synchrony of these populations in relation to temporal variation in spatial synchrony of local temperatures in a nonlinear scenario. Allowing for nonlinear effects of independent variables (X_i) on response variables (Y), we used generalized additive models (GAMs) applying the backfitting algorithm of smoothing splines, s(X_i): Y = α + Σ s_j(X_i) + ε (33). A smoothing spline minimizes the compromise between fit and degree of smoothness (df) of s_j(X_i). dfs were chosen by crossvalidation (33). When the use of GAM, compared to linear relationships, failed to significantly reduce the model's residual sum of squares, we used generalized linear models. We used a natural logarithm (ln) transformation of the caribou population indices to stabilize variance. Results using raw (non-ln-transformed) caribou data did not differ (see Results and Discussion). Because nonlinear analyses may be sensitive to outliers, we identified such data points in both dependent (caribou spatial synchrony) and independent (temperature synchrony) variables and repeated the GAM excluding them.

Having previously identified a relationship between large-scale climatic fluctuation and the dynamics of these caribou populations (8, 9, 34), we adopted a GAM of caribou spatial synchrony that, in its full form, included as independent variables spatial autocorrelation of local winter temperatures at lags of 0–2 years, the winter (December to March) NAO index at lags of 0–2 years, and annual data on wintertime Northern Hemisphere temperature anomalies (35). We also included “year” as an independent variable to account for temporal trends in the data. We note that GAMs provide only approximate significance tests on nonparametric F values (33). Therefore, we checked the goodness-of-fit and significance of our best-fit GAM using a linear-regression approximation with quadratic and cubic predictors as appropriate on the basis of partial plots of the GAM functions.

Linking Changes in Temperature Synchrony to Regional Warming. To test for a relationship between regional warming and spatial synchrony of local temperatures, we used a time series on the annual mean of the average winter temperatures at each local weather station located near the caribou populations as the independent variable in a regression with temperature synchrony as the dependent variable. We tested for both nonlinear and linear associations and included year as an independent variable to account for changes in temperature synchrony through time.

Linking Regional Warming to Global Climate. Because winter temperatures correlate negatively with the NAO index in western Greenland (8), the mechanism potentially underlying any relationship between spatial autocorrelation in local temperatures and regional warming might be the influence of the NAO on regional warming. Thus, we applied a GAM and a linear regression of regional mean winter temperature in western Greenland with the NAO and Northern Hemisphere temperature anomalies as predictors.

Results and Discussion

Analysis of caribou population dynamics during the periods 1810–1865 and 1908–1981 revealed that the influence of the NAO on each population has been remarkably consistent over two centuries. For all but one population, there is overlap of the 95% confidence intervals of the coefficient quantifying the strength of the NAO influence on population dynamics during the two periods, and all pairwise comparisons failed to reject the null hypothesis of overlap between periods (Fig. 1b). Hence, the increase in population synchrony toward the end of the 20th century is not directly attributable to an increase in strength of the NAO influence on the population dynamics.

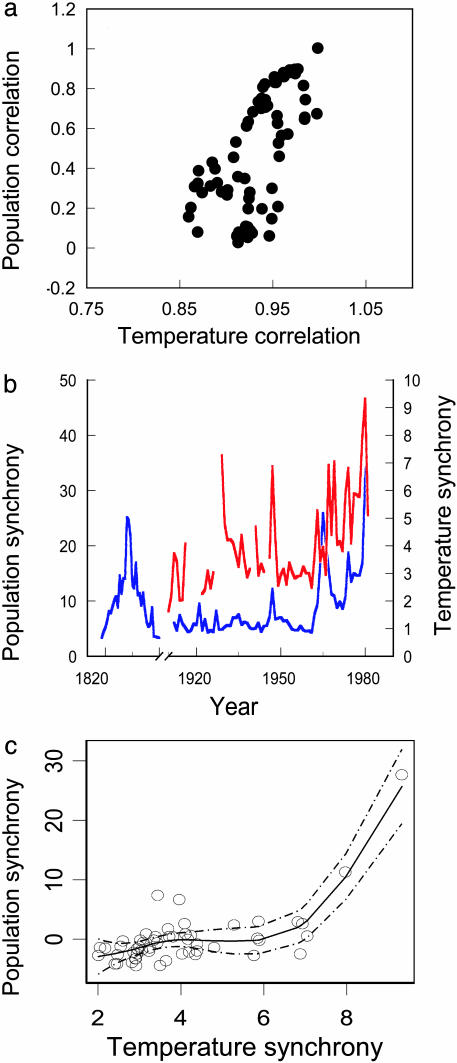
However, the 25-year sliding-window analysis revealed a strong positive association between caribou population correlation and winter temperature correlation contributing to the dynamics of those populations (Fig. 2a), supporting a key prediction of the Moran theorem (21, 22). Although not statistically robust because of massive autocorrelation in the 25-year window time series, this association suggests that, as local temperatures become more spatially correlated, the populations influenced by them display greater correlation. This result is corroborated by our GAM of the spatial synchrony index of the caribou populations (see below).

Fig. 2.

Variation in caribou population synchrony with temperature synchrony in Greenland. (a) Relation between pairwise population correlation for caribou populations Nuuk and Paamiut and pairwise temperature correlation for local winter temperatures measured at stations on the ranges of those populations, 1908–1981. Pairwise correlations were calculated for 25-year windows moved down each time series in 1-year steps. (r² = 0.64). (b) Indices of spatial synchrony of local winter temperatures (red) and caribou populations (blue) in western Greenland (see Materials and Methods). (c) Partial residual plot of the relationship between winter temperature synchrony and caribou spatial synchrony from the GAM. The solid line represents the nonlinear spline function, and the dashed lines are the 95% confidence intervals.

The time series for spatial synchrony among the caribou populations matches closely with temperature synchrony for the period 1912–1981 (Fig. 2b). Indeed, the GAM revealed a significant, nonlinear association between local temperature synchrony and caribou spatial synchrony for this period (nonparametric F = 11.24, df = 3, approximate P < 0.001) (Fig. 2c). Because the analysis in Fig. 2c may be sensitive to the two most extreme values for spatial synchrony in both variables, we repeated the GAM excluding them and the term remained significant (t = 3.12, P = 0.003). The most parsimonious GAM, reduced to significant predictors only, included temperature synchrony lagged 1 year, the winter NAO index lagged 1 year (nonparametric F = 6.62, df = 3, approximate P < 0.001), and year (nonparametric F = 8.87, df = 3, approximate P < 0.001). We checked our analysis to determine whether the period of low densities in all populations (1924–1948) influenced our results; reanalyzing the data with those years excluded, we found that all three terms remained significant (all approximate P values < 0.003). Moreover, results using raw caribou data were similar to results obtained using ln-transformed caribou data for all three independent variables: local temperature synchrony, nonparametric F = 10.9 (approximate P < 0.001); NAO, nonparametric F = 6.08 (approximate P = 0.001); and year, nonparametric F = 5.87 (approximate P = 0.002). The linear-regression approximation of the best-fit GAM was also significant (r² = 0.59, P < 0.001).

As noted above, we recognize that winter precipitation, rather than winter temperature directly, may be the proximal factor influencing caribou dynamics. Although we lacked sufficient long-term data on winter precipitation to include in our GAMs, such data were available for the period 1967–1981. An index of spatial synchrony of winter precipitation calculated over the same stations indicates significant correlation with our index of temperature synchrony (r = 0.39, P = 0.04) and with the index of caribou spatial synchrony (r = 0.58, P = 0.03) for this period.

These results indicate that the recent increase in caribou spatial synchrony is associated with increasingly spatially autocorrelated local weather overlain by large-scale environmental forcing through the NAO, a scenario that has been predicted (24) but not, to our knowledge, empirically demonstrated. However, this scenario does not explain the increase in spatial synchrony of local winter temperatures evident in Fig. 2b.

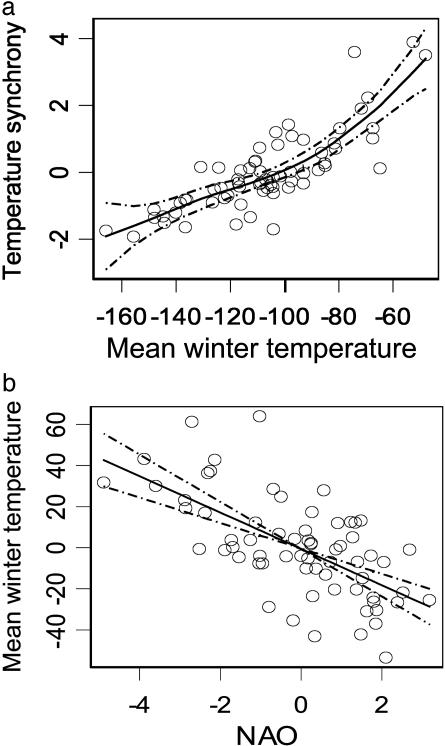
Local weather variables display significant spatial correlation over considerable distances, in some cases up to several hundred kilometers, throughout the Northern Hemisphere (36), including western Greenland (9). Our analysis also indicates that such spatial correlation is highly variable among years and, in western Greenland, has increased considerably toward the end of the 20th century (GAM of temperature synchrony vs. year: nonparametric F = 11.24, df = 3, approximate P < 0.001). The GAM of local temperature synchrony as a function of regional warming revealed a strong, nonlinear association with regional mean winter temperature (nonparametric F = 2.97, df = 3, approximate P = 0.039) (Fig. 3a) that was significant alone as well as after accounting for the temporal trend in temperature synchrony by including a nonlinear spline function for year in the model (nonparametric F = 17.69, approximate P < 0.001). These results indicate that, as regional temperatures rise, spatial autocorrelation of local winter temperatures increases, with an associated increase in spatial synchrony of local caribou populations.

Fig. 3.

Relations between local temperature synchrony, winter temperatures, and the NAO in western Greenland. (a) Partial residual plot from the GAM of spatial synchrony of local winter temperatures as a function of mean winter temperature (in tenths of a degree Celsius) in western Greenland. (b) Relation between the winter NAO index and mean winter temperature in western Greenland; shown is the partial correlation plot from the multivariate generalized linear model (partial r² = 0.40) that also included Northern Hemisphere temperature anomalies and year. The solid line represents the nonlinear spline function, and the dashed lines are 95% confidence intervals.

To trace these relationships further to large-scale climate, we turn to the results of the multivariate generalized linear model of regional mean winter temperature in relation to the NAO and the recent Northern Hemisphere warming trend. This model revealed that the dominant contribution to variation in regional mean winter temperature derives from the NAO (t = -6.63, P < 0.001) (Fig. 3b) with a concomitant, although weaker, influence of Northern Hemisphere winter temperature anomalies (t = 2.03, P = 0.047). Hence, hemispheric-scale climatic trends seem to drive regional warming trends in western Greenland, and, as regional winter temperatures rise, local winter temperatures become more spatially autocorrelated. In association with this recent increase in spatial autocorrelation in the environment, caribou populations in western Greenland have apparently become more spatially synchronized.

The picture presented here reveals many steps in a complex relationship among large-scale climatic variability and trends, regional weather, and spatio-temporal patterns in local weather that contribute to the dynamics of local populations. Among the more salient conclusions derived from these analyses is that spatial synchrony in animal population dynamics and local weather variables influencing them are highly variable through time and have increased recently in western Greenland (e.g., Fig. 2b and the significance of “year” in our multivariate GAMs above). Whereas temporal variability in the degree of correlation among animal populations has been documented previously (17, 18, 37), we demonstrate here a close association of this phenomenon with a similar pattern in local weather that is, notably, nonlinear. Although we cannot rule out a potential role of climate-mediated dispersal in the increase in caribou spatial synchrony, dispersal may have only a minor influence on spatial synchrony in systems in which the Moran effect (21, 22) is important (10).

The links among regional warming, increasing spatial synchrony in local temperatures, and increasing spatial synchrony of local populations emphasize the relevance of these results to potential future warming predicted in some scenarios of climate change (4). Recent theoretical work indicates that an increase in spatial correlation of environmental noise influencing population dynamics, as is evident in our analysis of local winter temperatures in Greenland, increases the risk of extinction of the populations influenced by that noise (12). We suggest that further large-scale climatic warming may have the potential to strengthen spatial synchrony among the caribou populations in western Greenland.