Reliability and Extension of Quantitative Prediction of CYP3A4-Mediated Drug Interactions Based on Clinical Data

Abstract

An approach was proposed in 2007 for quantitative predictions of cytochrome P450 (CYP)3A4-mediated drug-drug interactions. It is based on two characteristic parameters: the contribution ratio (CR; i.e., the fraction of victim drug clearance by CYP) and the inhibition ratio (IR) of the inhibitor. Knowledge of these parameters allows forecasting of the ratio between the area under the plasma concentration-time curve (AUC) of the victim drug when given with the inhibitor and the AUC of the victim drug when it is given alone. So far, these parameters were established for 21 substrates and 17 inhibitors. The goals of our study were to test the assumption of substrate independence of the potency of inhibitors in vivo and to estimate the CR and IR for an extended list of substrates and inhibitors of CYP3A4. The assumption of independence of IRs from the substrate was evaluated on a set of eight victim drugs and eight inhibitors. Forty-four AUC ratios were available. This assumption was rejected in four cases, but it did not result in more than a twofold error in AUC ratio predictions. The extended list of substrates and inhibitors was defined by a thorough literature search. Fifty-nine AUC ratios were available for the global analysis. Final estimates of CRs and IRs were obtained for 37 substrates and 25 inhibitors, respectively. The mean prediction error of the ratios was 0.02, while the mean absolute prediction error was 0.58. Predictive distributions for 917 possible interactions were obtained, giving detailed information on some drugs or inhibitors that have been poorly studied so far.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-014-9663-y) contains supplementary material, which is available to authorized users.

INTRODUCTION

Cytochrome P450 (CYP)3A4 is involved in the metabolism of more than 50% of all drugs (1). It plays a major role in the metabolism of, e.g., several antibiotics, antiviral drugs (anti-VIH and anti-VHC drugs), benzodiazepines, calcium channel blockers, statins, immunosuppressive drugs, and opioids, among others (2). Many instances of CYP3A4-mediated drug interactions have been studied, and many of them are of clinical relevance (3,4). However, only a small proportion of all possible combinations between substrates and inhibitors have been studied in vivo. An approach has been advocated to forecast the magnitude of metabolic interaction. This approach was introduced by Ohno et al. (5). It can be applied to inhibition and to induction (5,6). It is based solely on clinical data and uses two characteristic parameters: the contribution ratio (CR)_3A4 of the substrate, which is the fraction of drug clearance mediated by CYP3A4, and the inhibition ratio (IR)_3A4 of the inhibitor, which is a measure of its inhibiting power and is related to its inhibition constant K_i measured in vitro. The magnitude of the interaction is measured by the ratio between the area under the plasma concentration-time curve (AUC) of the victim drug when the inhibitor is coadministered and the AUC of the victim drug administrated alone. Any type of inhibitor (competitive, noncompetitive, mechanism based) may be accommodated in the same framework (5). The method has already been extended to predict quantitatively the drug interactions mediated by CYP2D6 (7), CYP2C9 (8), and CYP2C19 (9) and the interplay with genetic polymorphism (10) and evaluated by external validation in each case.

Drug interactions may be of clinical concern when the AUC ratio is "high," but the threshold value depends obviously on the therapeutic range of the victim drug. Drugs with which an AUC ratio greater than 5 is observed with a known inhibitor are considered as sensitive to drug interactions (2). In the CR-IR framework, such interactions are observed when a strong inhibitor (IR_3A4 >0.8) is combined with a substrate metabolized mainly by CYP3A4 (CR_3A4 >0.8).

The predictive performance of Ohno’s approach is very good for CYP3A4-mediated interactions, and the method is very easy to use, once the characteristic parameters have been established. However, in their seminal publications (5,6), Ohno et al. studied only 22 substrates and 18 inhibitors, whereas many other drugs are known as substrate or inhibitor of CYP3A4. Furthermore, the wide application of this method relies on a crucial assumption, namely the independence of the IRs from the victim drug. A number of in vitro studies (11–14) showed on the contrary that the K_i values were dependent on the substrates at least to some degree, but the clinical relevance of these observations remains unclear.

Therefore, the goals of this study were to test the assumption of substrate independence of the inhibitors in vivo, to estimate the CR and IR of an extended list of substrates and inhibitors of CYP3A4 and to forecast the magnitude of a large number of interactions that have not been studied so far. Emphasis was given to the identification of strong interactions, i.e., those leading to a large variation of AUC.

METHODS

The Interaction Model

The pharmacokinetic formulas have already been demonstrated for CYP3A4; we will not detail all the calculations (5,7). The ratio between the AUC of the victim drug when given with the inhibitor and the AUC of the victim drug when it is given alone at the same dose may be expressed by:

$$\mathrm{AUC}*/\mathrm{AUC}=1/\left[1-{\mathrm{CR}}_{\mathrm{CYP}3\mathrm{A}4}\times {\mathrm{IR}}_{\mathrm{CYP}3\mathrm{A}4}\right]$$ 1

The CR_CYP3A4 is the fraction of the victim drug metabolized in vivo by CYP3A4. The IR_CYP3A4 is a characteristic of the inhibitor and is independent of the substrate but depends on the dose of the inhibitor. In this equation, the asterisk denotes the parameters of the victim drug when the inhibitor is coadministered. When the CR of a substrate and the IR of an inhibitor are known, the change in the AUC of the substrate following inhibition of CYP3A4 can be calculated by Eq. 1. Likewise, rearrangement of Eq. 1 allows the calculation of CR_CYP3A4 of a substrate (Eq. 2) or the IR_CYP3A4 of an inhibitor (Eq. 3) when the other quantities are known:

$${\mathrm{CR}}_{\mathrm{CYP}3\mathrm{A}4}=\left[\left(\mathrm{AUC}*/\mathrm{AUC}\right)-1\right]/\left[\left(\mathrm{AUC}*/\mathrm{AUC}\right)\times {\mathrm{IR}}_{\mathrm{CYP}3\mathrm{A}4}\right]$$ 2

$${\mathrm{IR}}_{\mathrm{CYP}3\mathrm{A}4}=\left[\left(\mathrm{AUC}*/\mathrm{AUC}\right)-1\right]/\left[\left(\mathrm{AUC}*/\mathrm{AUC}\right)\times {\mathrm{CR}}_{\mathrm{CYP}3\mathrm{A}4}\right]$$ 3

Initial Estimates

Initial estimates of CRs and IRs may be obtained by using Eqs. 2 and 3. The initial values of the CRs and the IRs are given in Tables I and II, respectively. Expanding upon the work of Ohno et al. (5,6), relevant information are listed for 37 substrates (expanding the list with 16 additional substrates) and 25 inhibitors (including 8 additional inhibitors).

Table I.

Initial CRs and Their Methods of Obtaining

Victim drug	CRCYP3A4	Source	Reference
Alprazolam	0.75	Literature	(5)
Amitriptyline	0.25	Literature	(5)
Atorvastatin	0.68	Literature	(5)
Boceprevir	0.20	Calculation (clarithromycin)	(25)
Buspirone	0.99	Literature	(5)
Cerivastatin	0.18	Literature	(5)
Cyclosporin	0.80	Literature	(5)
Clarithromycin	0.35	Calculation (saquinavir)	(26,27)
Colchicine	0.67	Calculation (cyclosporin)	(28)
Dronedarone	0.90	Calculation (erythromycin)	(29)
Eplerenone	0.82	Calculation (erythromycin)	(30)
Felodipine	0.89	Literature	(5)
Gefitinib	0.39	Literature	(5)
Imatinib	0.28	Literature	(5)
Ketoconazole	0.58	Calculation (telaprevir)	(31)
Lovastatin	1.00	Literature	(5)
Mefloquine	0.44	Literature	(5)
Methylprednisolone	0.77	Calculation (diltiazem)	(32)
Midazolam	0.92	Literature	(5)
Nifedipine	0.78	Literature	(5)
Nisoldipine	0.96	Literature	(5)
Prednisolone	0.18	Literature	(5)
Quietapine	0.85	Literature	(5)
Quinidine	0.43	Calculation (diltiazem)	(33)
Rilpivirine	0.33	Calculation (ketoconazole)	(34)
Rivaroxaban	0.28	Calculation (erythromycin)	(35)
Saquinavir	0.73	Calculation (clarithromycin)	(26,27)
Sildenafil	0.79	Calculation (erythromycin)	(36)
Simvastatin	1.00	Literature	(5)
Sirolimus	0.77	Calculation (verapamil)	(37)
Tadalafil	0.50	Calculation (ketoconazole)	(38)
Telithromycin	0.49	Literature	(5)
Ticagrelor	0.79	Calculation (diltiazem)	(39)
Triazolam	0.93	Literature	(5)
Zopiclone	0.44	Literature	(5)
Zolpidem	0.40	Literature	(5)

CR contribution ratio

Table II.

Initial IRs in Drug-Drug Interaction Studies

Inhibitor	Inhibitor dosage(mg/day)	IRCYP3A4	Victim drug	AUC ratio	Reference
Boceprevir	800 × 3	0.88	Midazolam	5.30	(40)
Cyclosporin	100	0.80	Colchicine	2.15	(28)
Clarithromycin	500 × 2a	0.88	Boceprevir	1.21	(25)
Clarithromycin	500 × 2	0.88	Saquinavir	2.77	(26)
Diltiazem	60 × 3	0.80	Methylprednisolone	2.60	(32)
Diltiazem	90 × 2	0.80	Quinidine	1.53	(33)
Diltiazem	180a	0.80	Ticagrelor	2.70	(39)
Erythromycin	500 × 3	0.82	Dronedarone	3.80	(29)
Erythromycin	500 × 3	0.82	Rivaroxaban	1.30	(35)
Erythromycin	500 × 2	0.82	Sildenafil	2.82	(36)
Fluconazole	200	0.79	Midazolam	3.60	(14)
Grapefruit	RS	0.54	Midazolam	2.00	(14)
Grapefuit	DS	0.91	Midazolam	6.00	(14)
Itraconazole	200	0.92	Midazolam	6.60	(14)
Ketoconazole	400	1.00	Rilpivirine	1.49	(34)
Ketoconazole	200	1.00	Tadalafil	2.00	(38)
Ketoconazole	400	1.00	Tadalafil	4.00	(38)
Posaconazole	100	0.83	Midazolam	4.24	(41)
Ritonavir	100 × 2	1.00	Colchicine	3.96	(28)
Saquinavir	1,200 × 3	0.88	Clarithromycin	1.45	(26)
Telaprevir	750 × 3a	0.97	Ketoconazole	2.25	(31)
Telaprevir	750 × 3a	0.97	Midazolam	8.96	(31)
Ticagrelor	90 × 2a	0.36	Simvastatine	1.56	(39)
Verapamil	240	0.71	Colchicine	1.90	(28)
Verapamil	240a	0.71	Sirolimus	2.20	(37)

IR _CYP3A4 inhibition ratio, AUC area under the plasma concentration-time curve, RS regular strength, DS double strength

^aStandard dose due to the uncertainty of the AUC reports

The Regression Approach

Better estimates of the CRs and IRs may be obtained by a regression analysis using data from a set of interaction studies and the following regression model (7):

$$\mathrm{Observed}\mathrm{AUC}\mathrm{ratio}=\mathrm{Predicted}\mathrm{AUC}\mathrm{ratio}+\epsilon$$ 4

where the predicted AUC ratio is calculated by Eq. 1 and the residual error ε is assumed to have a normal distribution with zero mean. An orthogonal regression had to be used because the variables of interest—i.e., the AUC ratios, CRs, and IRs—were prone to uncertainty. A Bayesian approach, described in more detail in the Appendix, was used to fit the following model (15). Each AUC ratio, CR, and IR were assumed to follow normal and logistic distributions, respectively. The logistic distribution was retained in order to constrain the CRs and the IRs between 0 and 1. The mean of each distribution was set to the initial estimate found by Eqs. 2 and 3, while a common precision (the inverse of the variance) was attributed to the normal distribution (τ_AUC) and the logistic distributions for CRs (τ_CR) and IRs (τ_IR). A moderately informative gamma prior distribution was attributed to each of these precisions. The parameters of the gamma distributions were chosen so that the expected standard errors of CRs and IRs on the logit scale, and of AUC ratios, were 0.5, 0.5, and 5, respectively. The posterior distributions of the AUC ratios, CRs, and IRs were obtained by Monte Carlo Markov chain simulation by using Gibb's sampling in WinBugs 1.4 software (16). The number of sampling for burn-in and estimation was 4,000 and 20,000 or more, respectively. Sensitivity to assumptions about the precision of prior distributions was determined by fitting the model with different assumptions. Convergence was controlled by verifying the stability of the posterior distributions. Goodness of fit was assessed by visual examination of the residual scatter plots and the posterior distributions. Occurrence of a multimodality in any posterior distribution, revealing a conflict between the prior distribution and the data, was examined. The point estimates of the CRs, IRs, and the AUC ratios were taken as the means of their posterior distributions. Standard deviation (SD) and confidence interval (CI) of 90%, defined as the interval between the 5th and 95th percentiles of the posterior distribution of each variable were calculated.

Estimation of the Imprecision of AUC Ratios

SDs for interstudy differences in observed AUC are ratios needed to be estimated, because it determines the credibility interval of the estimated CRs and IRs, and thereby the significance of the difference between substrate-dependent and substrate-independent IR values. The imprecision of AUC ratios was estimated by using data gained with three substrates (alprazolam, midazolam, and triazolam) and three inhibitors (fluconazole, itraconazole, and ketoconazole). Thirty-five interaction studies between these substrates and inhibitors have been reported (17). Among these, 23 were suitable for our purpose (studies based on a single dose of fluconazole or itraconazole were excluded). The number of subjects in these 23 studies varied from 4 to 19, with a median of 9. It was considered unnecessary to adjust the analysis for sample size, because (1) 20 out of 23 values were in the range 7 to 12, and (2) the AUC ratios reported in the studies of minimal and maximal size were similar. The prediction model (Eq. 4) was fitted to these 23 AUC ratios by orthogonal regression. The residual error ε was assumed to have a variance (pred. σ²), where σ was to be estimated. The imprecision was characterized by σ.

Testing the Assumption of IR Independence from the Substrate

The assumption of independence of IRs from the substrate was evaluated on a set of eight victim drugs (midazolam, simvastatin, nifedipine, nisoldipine, felodipine, eplerenone, saquinavir, and cyclosporin) and eight inhibitors (clarithromycin, diltiazem, erythromycin, grapefruit juice, fluconazole, itraconazole, ketoconazole, and verapamil). These substrates and inhibitors were chosen because they belong to different clusters regarding their binding properties to or inhibiting properties for CYP3A4 (11–14) and there were enough clinical interaction studies with them: 44 AUC ratios were available.

In a first step, the prediction model was fitted to the 44 AUC ratios by orthogonal regression, in order to refine the eight CR and substrate-independent IR estimates with respect to their value determined in previous studies (5). Here, the IR of each inhibitor was assumed to be independent of the substrate and the imprecision σ was fixed to the value obtained above. In a second step, the assumption of independence was relaxed: the substrate-dependent IR values were calculated algebraically from the AUC ratio and the CR of the substrate (Eq. 3), yielding 44 IR values. In the third step, the substrate-independent IR values were compared with the substrate-dependent ones, by using the ratio of the substrate-dependent to substrate-independent IR value. The null hypothesis was that the substrate-dependent IR and the substrate-independent IR are equal. To test this assumption, we compared the ratio of these quantities to 1. The posterior distribution of this ratio is not expected to be Gaussian. Hence, the usual parametric test is not relevant. Given that a Bayesian procedure was used to estimate this ratio, the 90% CI of the ratio can be calculated as the interval between the 5th and the 95th percentiles of its posterior distribution. This interval was then compared with the reference value (i.e., 1). If the reference value was outside the CI, the null hypothesis was rejected at 5% level.

Estimation of New CRs and IRs

The second goal of the analysis was to estimate the CRs and the IRs of a number of drugs and inhibitors. After an extensive literature search of drug-drug interactions involving CYP3A4, a three-step approach was followed. First, initial estimates of CRs and IRs were determined by several methods, using published data. Second, an external validation of these initial estimates was made, by comparing the AUC ratios predicted by Eq. 1 with the observed values, using data not involved in the first step. Third, refined estimates of CRs and IRs were obtained by Bayesian orthogonal regression, using all the data (including Ohno’s) (5) and the initial estimates. The Bayesian approach allowed to combine the prior information stemming from the learning set with the data from the validation set.

Literature Search

The analysis was based on summaries of product characteristics and articles published up to March 2014. The references were extracted from PubMed. The main keywords were “pharmacokinetics” “interaction” “CYP3A4” “metabolism” and “drug name.” Only in vivo pharmacokinetic data obtained in humans after oral drug administration were retained. When a report of an in vivo interaction was found, articles supporting the involvement of CYP3A4 as the main mechanism were sought, such as in vitro studies. Victim drugs and inhibitors with an initial estimate of CR_3A5 or IR_3A4 less than 0.16 and 0.3, respectively, were excluded. Substrate associations (e.g., artemether-lumefantrine) (18) were excluded from the analysis. The metabolites of victim drugs, even active metabolites, were not taken into account in our approach. Drugs and inhibitors for which a single interaction study was available were excluded, because external validation was not possible.

• Step 1Estimation of initial values of CRs and IRs

  The first step consisted in the formation of two sets: a set of estimation and a validation set. The set of estimation was used to estimate the values of CRs or IRs from different ratios from the literature. The set of validation was used to validate or not the previous estimates by comparing the estimated values for calculating AUC to those observed. The allocation of the data to the learning and the validation data set was not made at random. In the learning set, there must be one interaction study for each substrate and inhibitor, preferably involving a single mechanism of interaction (as far as we know), and for which either CR or IR is already known, to allow calculation of IR or CR of the associated drug, respectively (see below). In the validation set, there must be at least one interaction study for each substrate and inhibitor.

  First, we took all CRs calculated from Ohno’s article (5). Then, the calculation of the other CRs was based on Eq. 2, using the AUC ratio determined in a drug-drug interaction study with an inhibitor whose IR is known. Similarly, the IRs were determined by Eq. 3, using the AUC ratio determined in a drug-drug interaction study with a substrate whose CR is known. The values of the CR and IR for various substrates and inhibitors constituting the learning data set were calculated sequentially, using the references listed in Tables I and II.

  Some drugs known as CYP3A4 substrates (at least in vitro) were not retained in the analysis, due to the lack of clinical studies to estimate their CR in vivo (amlodipine and quinidine). Ten interactions were excluded because they involved multiple mechanisms (carriers, PgP), for example the interactions between cyclosporin and statins. Darunavir data were excluded because all AUC values were from studies in which darunavir was given in combination with ritonavir.

• Step 2External validation of initial values

  External validation was based on the comparison of the AUC ratios predicted by Eq. 1 with the observed values, using all of the available data except those from the first step. The references used in the validation data set are listed in Table III. For the validation, a plot of predicted vs. observed AUC ratios was made. The initial values of the CRs and the IRs were considered valid if 90% of the predicted AUC ratios were in the range of 50–200% of the observed ratio. In the event of invalidation, step 1 would be repeated with another set of data. The accuracy of AUC ratio prediction was evaluated by the mean prediction error (MPE). The prediction error is the predicted value minus the observed value. The imprecision of the prediction was assessed by the mean absolute prediction error (MAPE).

• Step 3Final Estimation

  Refined estimates of CRs and IRs were obtained by orthogonal regression, using all data (learning and validation data sets combined), the initial estimates, and the model defined by Eq. 1.

Table III.

Published AUC Ratios in Drug-Drug Interaction Studies Involving CYP3A4, Used for External Validation

Victim drug	Inhibitor	Inhibitor dosage (mg/day)	Observed AUC ratio	Reference
Alprazolam	Ritonavir	200 × 2	2.50	(42)
Alprazolam	Telaprevir	750 × 3a	1.35	(31)
Atorvastatin	Boceprevir	800 × 3	2.30	(43)
Atorvastatin	Ticagrelor	90 × 2a	1.36	(39)
Boceprevir	Cyclosporin	100	1.16	(40)
Boceprevir	Ketoconazole	200a	2.31	(44,45)
Boceprevir	Ritonavir	100	0.81	(40)
Cyclosporin	Boceprevir	800 × 3	2.68	(40)
Cyclosporin	Telaprevir	750 × 3a	4.64	(31)
Clarithromycin	Fluconazole	200	1.18	(26)
Clarithromycin	Ritonavir	200 × 3	1.77	(26)
Colchicine	Azithromycin	500	1.40	(28)
Colchicine	Clarithromycin	250 × 2	3.40	(28)
Colchicine	Diltiazem	240	1.30	(28)
Colchicine	Ketoconazole	200 × 2	2.90	(28)
Dronedarone	Diltiazem	240 × 2	1.70	(29)
Dronedarone	Ketoconazole	200	17.00	(29)
Dronedarone	Verapamil	240	1.40	(24)
Ketoconazole	Ritonavir	500 × 2	3.40	(42)
Methylprednisolone	Itraconazole	200	3.14	(46)
Methylprednisolone	Ketoconazole	200	2.40	(47)
Prednisolone	Ritonavir	200 × 2	1.30	(42)
Quinidine	Erythromycin	250 × 4	1.30	(48)
Quinidine	Verapamil	240a	1.50	(49)
Rivaroxaban	Clarithromycin	500 × 2	1.50	(35)
Rivaroxaban	Ketoconazole	400	2.60	(35)
Saquinavir	Erythromycin	250 × 4	1.99	(27)
Saquinavir	Fluconazole	400a	1.50	(27)
Saquinavir	Ranitidine	300a	1.67	(27)
Sildenafil	Azithromycin	500	1.02	(36)
Sildenafil	Saquinavir	3,600a	3.10	(36)
Simvastatine	Posaconazole	100	7.42	(41)
Sirolimus	Diltiazem	120	1.60	(37)
Sirolimus	Erythromycin	250 × 4a	4.20	(37)
Tacrolimus	Posaconazole	400 × 2	4.58	(50)
Tadalafil	Ritonavir	200 × 2	2.24	(38)
Ticagrelor	Ketoconazole	200a	7.30	(39)
Triazolam	Ritonavir	200 × 4	20.00	(42)
Zolpidem	Ritonavir	200 × 4	1.28	(42)

AUC area under the plasma concentration-time curve

^aStandard dose due to the uncertainty of the AUC reports

Prediction

The AUC ratios were computed for an exemplary set of substrates and inhibitors, using Eq. 1 with the point estimates of the final values of the CRs and the IRs.

RESULTS

Imprecision of AUC Ratios

The range of AUC ratio was 1.63 to 16 (Supplemental Table I). There is an obvious variability of the magnitude of the interaction between a given substrate and inhibitor, when looking at the mean AUC ratio reported in different studies. For example, the combination of midazolam with ketoconazole 400 mg/day in four studies with similar design yielded an increase of midazolam exposure by 6.5-, 9.5-, 15.9-, and 16-fold. The imprecision σ of the AUC ratio, based on 23 interaction studies between 3 benzodiazepines and 3 azole antifungals, was estimated at 1.06 and was subsequently rounded to one. Hence, the SD of an AUC ratio of 1, 10, or 20 is equal to 1, 3.16, or 4.5, respectively.

Independence of IRs from the Substrate

The 90% credibility interval of the ratio of the substrate independent to the substrate-dependent IR for each of the 44 interaction studies between eight substrates and inhibitors is shown in Fig. 1 (Supplemental Table II). In 6 cases out of 44, this ratio was significantly different from unity; in four cases among them, this ratio was less than 0.67 or greater than 1.5. The corresponding substrate-inhibitor pairs were nifedipine-grapefruit juice, nifedipine-verapamil, cyclosporin-clarithromycin, and cyclosporin-diltiazem. However, the predicted AUC ratios, based on substrate-independent IRs, were all within the 50% to 200% interval around the observed AUC ratios (Supplemental Fig. 1). In the rest of the study, IRs were considered as substrate independent.

Fig. 1.

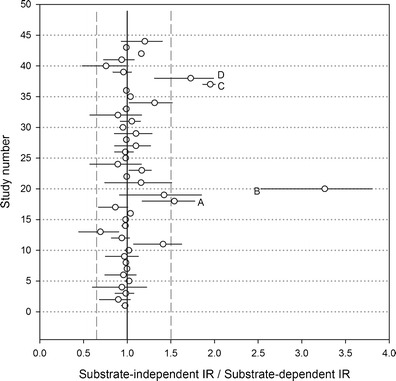
Ninety-percent credibility interval of the substrate-independent to substrate-dependent IR in 44 interaction studies between eight substrates and eight inhibitors. The vertical lines are set at 0.67, 1, and 1.5. A–D Important and statistically significant deviations from the assumption of IR independence from the substrate, corresponding to the substrate-inhibitor pairs nifedipine-grapefruit juice, nifedipine-verapamil, cyclosporin-clarithromycin, and cyclosporin-diltiazem, respectively. The inhibitor-substrate pairs are, by order of study number: (1) clarithromycin-midazolam, (2) diltiazem-midazolam, (3) erythromycin-midazolam, (4) grapefruit RS-midazolam, (5) grapefruit DS-midazolam, (6) fluconazole-midazolam, (7) itraconazole-midazolam, (8) ketoconazole-midazolam, (9) verapamil-midazolam, (10) clarithromycin-simvastatin, (11) diltiazem-simvastatin, (12) erythromycin-simvastatin, (13) grapefruit RS-simvastatin, (14) grapefruit DS-simvastatin, (15) itraconazole-simvastatin, (16) ketoconazole-simvastatin, (17) verapamil-simvastatin, (18) diltiazem-nifedipine, (19) grapefruit RS-nifedipine, (20) verapamil-nifedipine, (21) grapefruit RS-nisoldipine, (22) ketoconazole-nisoldipine, (23) erythromycin-felodipine, (24) grapefruit RS-felodipine, (25) itraconazole-felodipine, (26) erythromycin-eplerenone, (27) fluconazole-eplerenone, (28) ketoconazole-eplerenone, (29) verapamil-eplerenone, (30) clarithromycin-saquinavir, (31) erythromycin-saquinavir, (32) grapefruit RS-Saquinavir, (33) grapefruit DS-saquinavir, (34) fluconazole-saquinavir, (35) itraconazole-saquinavir, (36) ketoconazole-saquinavir, (37) clarithromycin-cyclosporin, (38) diltiazem-cyclosporin, (39) erythromycin-cyclosporin, (40) grapefruit RS-cyclosporin, (41) fluconazole-cyclosporin, (42) itraconazole-cyclosporin, (43) ketoconazole-cyclosporin, and (44) verapamil-cyclosporin

External Validation of Initial Estimates

References for the drug-drug interaction studies involving CYP3A4 that were used for the external validation are listed in Table III. Thirty-nine AUC ratios were available. Figure 2 shows a comparison of the observed and predicted AUC ratios. Two points (5%) were outside of the acceptable interval. The mean prediction error was −0.24, while the mean absolute prediction error was 1.03.

Fig. 2.

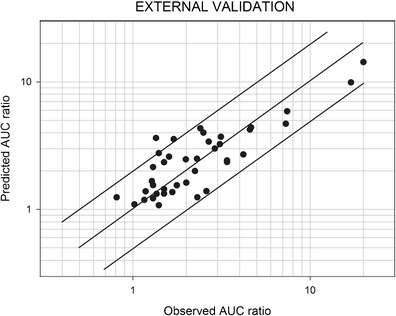
Predicted vs. observed AUC ratios in the external validation set. The references for the studies are listed in Table III. The predictions of the AUC ratios were made using Eq. 1 (see text). AUC area under the plasma concentration-time curve

Final Estimation of CRs and IRs

Fifty-nine AUC ratios were available for this analysis. The final estimates of the CRs and the IRs are shown in Tables IV and V, respectively. These final estimates were very similar to the initial estimates. Depending on the amount of data available for each substrate and inhibitor, the widths of the 90% CIs for the CRs and IRs were variable. The relationship between the observed and predicted AUC ratios is plotted in Fig. 3. Three points (5%) were outside the range of acceptable predictions. The mean prediction error was 0.02, and the mean absolute prediction error was 0.58. These figures showed that the refined estimates provided better prediction than the initial estimates.

Table IV.

Final Estimates of CR_CYP3A4 Values for Oral Clearance of 37 Substrates (Including 16 New CYP3A4 Substrates)

Drug	CRCYP3A4	New substrates
		SD	90%	CI
Lovastatin	1.00
Buspirone	0.99
Nisoldipine	0.97
Simvastatin	0.97
Dronedarone	0.95	0.005	0.94	0.96
Triazolam	0.93
Midazolam	0.91
Tacrolimus	0.91	0.028	0.86	0.95
Felodipine	0.87
Ticagrelor	0.87	0.013	0.84	0.89
Quietapine	0.85
Sirolimus	0.84	0.052	0.75	0.92
Eplerenone	0.79	0.064	0.68	0.88
Sildenafil	0.78	0.053	0.68	0.86
Alprazolam	0.75
Nifedipine	0.72
Colchicine	0.71	0.033	0.65	0.76
Atorvastatin	0.68
Cyclosporin	0.68
Methylprednisolone	0.68	0.046	0.59	0.74
Ketoconazole	0.63	0.062	0.51	0.71
Saquinavir	0.58	0.066	0.55	0.77
Tadalafil	0.50	0.080	0.36	0.62
Telithromycin	0.49
Mefloquine	0.44
Zopiclone	0.44
Quinidine	0.43	0.107	0.25	0.61
Zolpidem	0.40
Gefitinib	0.39
Clarithromycin	0.35	0.089	0.21	0.50
Rivaroxaban	0.35	0.101	0.19	0.52
Rilpivirine	0.33	0.096	0.18	0.49
Imatinib	0.28
Amitriptyline	0.25
Boceprevir	0.22	0.077	0.11	0.36
Cerivastatin	0.18
Prednisolone	0.18

CR contribution ratio, SD standard deviation, CI confidence interval

Table V.

Final Estimates of Apparent IR_CYP3A4 Values of 25 Inhibitors (Including Eight New CYP3A4 Inhibitors)

Inhibitor	Inhibitor dosage (mg/day)	IR	New inhibitors
			SD	90% CI
Ritonavir	800	0.99	0.004	0.98	1.00
Ketoconazole	200–400	0.98
Voriconazole	400	0.98
Telaprevir	2,250	0.97	0.012	0.95	0.99
Itraconazole	100–200	0.95
Clarithromycin	500–1,000	0.94
Grapefruit	DS	0.93	0.02	0.89	0.96
Telithromycin	800	0.91
Saquinavir	3,600	0.88
Boceprevir	2,400	0.87	0.026	0.83	0.91
Posaconazole	100–800	0.86	0.012	0.84	0.88
Nefazodone	400	0.85
Erythromycin	1,000–2,000	0.81
Diltiazem	90–270	0.80
Fluconazole	200	0.75
Cyclosporin	100	0.78	0.077	0.64	0.89
Verapamil	240–480	0.71
Grapefruit	RS	0.51	0.10	0.33	0.67
Cimetidine	800–1,200	0.44
Ranitidine	300–600	0.37
Roxithromycine	300	0.35
Ticagrelor	180	0.35	0.096	0.19	0.51
Fluvoxamine	100–2,00	0.30
Azithromycin	250–500	0.11
Gatifloxacine	400	0.08

IR inhibition ratio, SD standard deviation, CI confidence interval, RS regular strength, DS double strength

Fig. 3.

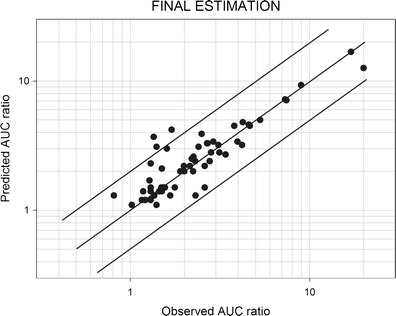
Predicted vs. observed AUC ratios with final estimates of the CRs and the IRs. The references for the studies are listed in Tables I, II, and III. The predictions of the AUC ratios were made using Eq. 1 (see text). AUC area under the plasma concentration-time curve, CR contribution ratio, IR inhibition ratio

Prediction

The AUC ratios of 917 possible interactions between the 37 substrates listed in Table IV and the 25 inhibitors listed in Table V were computed. The predicted AUC ratios greater than 5 are listed in Supplemental Table III. The AUC ratios for an exemplary set of substrates and inhibitors are shown in Fig. 4.

Fig. 4.

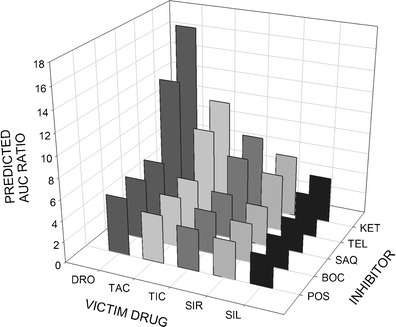
Predicted AUC ratios of victim drugs in the presence of various inhibitors. AUC area under the plasma concentration-time curve, SIL sildenafil, SIR sirolimus, TIC ticagrelor, TAC tacrolimus, DRO dronedarone, POS posaconazole, BOC boceprevir, SAQ saquinavir, TEL telaprevir, KET ketoconazole

The Case of Grapefruit Juice

The current equation of the CR-IR method (Eq. 1) may be established by considering that intestine wall and liver are lumped in a single presystemic compartment. Hence, metabolisms in the gut wall and in the liver, as well as inhibition of these processes, are not distinguished. As a consequence, the CRs and IRs calculated using Eqs. 2 and 3 are composite values. This may introduce some bias when predictions are made for an organ-selective inhibitor associated with a victim drug principally excreted either by the intestine or the liver. To evaluate the magnitude of this bias, we considered the interactions with grapefruit juice, known as a selective inhibitor of intestinal CYP3A4 (19), for a set of victim drugs with known intestinal availability (F_g): nisoldipine, tacrolimus, felodipine, midazolam, nifedipine, triazolam, and alprazolam (Supplemental Table IV). The F_g values ranged from 0.11 to 0.94. The IR value of grapefruit juice was calculated for each substrate by Eq. 3. The IR values varied from 0.14 with alprazolam (F_g = 0.94) to 0.58 with tacrolimus (F_g = 0.14). As expected, the apparent IR of grapefruit juice increased when F_g decreased. The value currently retained for grapefruit juice IR is 0.51 (Table V). With this value, the prediction error is always less than 1.5-fold.

DISCUSSION

In this study, the approach introduced by Ohno et al. for CYP3A4-mediated drug-drug interactions has been extended to a variety of substrates and inhibitors (5,6). Noteworthy, among 917 possible interactions between the substrates and inhibitors considered in the current work, only 98 had been evaluated in a clinical study. Among 917 interactions, 112 have a predicted AUC ratio greater than 5 (Supplemental Table III), which, even for drugs with a large therapeutic index, results in a potential risk of adverse effects. These strong interactions are expected when both CR_CYP3A4 and IR_CYP3A4 are greater than 0.8. The data listed in Tables IV and V may help to forecast and to select the interactions studies that should be made when a new drug that is a substrate or an inhibitor of CYP3A4 is developed.

Estimation of the dose to be given once the AUC ratio has been predicted is very simple:

$$\mathrm{Adjusted}\mathrm{dose}=\left(\mathrm{Current}\mathrm{or}\mathrm{usual}\mathrm{dose}\right)/\left(\mathrm{AUC}\mathrm{ratio}\right)$$ 5

However, the decision to adjust the dose depends on additional considerations, such as the therapeutic index of the victim drug (the dose will be adjusted only if the variation of AUC is considered clinically important). Also, the metabolites of the victim drug were not taken into account in our approach. Among the drugs studied here, active metabolites contributing significantly to drug action are encountered with amitriptyline and clarithromycin. Because both drugs are metabolized to a low extent by CYP3A4 (CR <0.4), the interactions with CYP3A4 inhibitors are weak anyway and not clinically significant.

This method of drug-drug interaction prediction relies on the assumption that the effect of an inhibitor at a given dose is the same whatever the victim drug is, i.e., IRs do not depend on the substrate. In vitro, weak and strong inhibitors provide a fairly consistent inhibition of substrates metabolism; variability of the inhibition constant K_i is observed more frequently with intermediate inhibitors, such as cyclosporin, nifedipine, fluconazole, and terfenadine (11,14). Regarding the substrates, benzodiazepines, dihydropyridines, steroids, and high molecular weight compounds (cyclosporin) seem to belong to different categories regarding their sensitivity to CYP3A4 inhibitors (11,13,14,20). At the molecular level, the reason for the variability of the K_is is ascribed to the existence of several binding domains within the active site of CYP3A4 and several types of interaction with them (13). However, the impact of these features on the magnitude of drug-drug interations in vivo is uncertain, because many interactions assessed in vitro were never evaluated in vivo. For example, we did not find any interaction study with testosterone and there are only three interaction studies with nifedipine (both drugs are frequently used for in vitro studies). In our conceptual framework, variation of the K_i of an inhibitor among substrates would translate into variability of its IR. Our analysis revealed only limited evidence of substrate dependence of the power of inhibitors. With cyclosporin as the substrate, only two inhibitors out of eight exhibited significant variability in the estimated IR value. Hence, cyclosporin per se does not seem to be the cause for IR variability. With nifedipine, two inhibitors out of three exhibited significant variability in the estimated IR value. Hence, nifedipine may behave differently from other substrates. However, the error on AUC ratio prediction, if any, induced by the assumption of substrate-independent IRs is less than 2-fold, as shown in Figs. 2 and 3. Noteworthy, strong interactions, which are the most clinically relevant, were always accurately forecasted.

An interesting feature of the method is the possibility that predictions of drug-drug interactions can be made even for a substrate or an inhibitor for which very few interactions have been documented. In this respect, we were particularly interested in predicting interactions of colchicine, a drug that is frequently prescribed, and interactions due to ritonavir (21–23) and telaprevir, which are strong inhibitors. These predictions showed that the interactions with colchicine result in AUC ratios that are never >3.5, whereas ritonavir and telaprevir were confirmed as strong inhibitors with an IR of 0.99 and 0.97, respectively. Because colchicine is a drug with a narrow therapeutic index (the optimal dose is in the range 0.015 to 0.030 mg/kg, (24), predicted AUC ratios greater than 2 may indicate a potentially clinically significant interaction where the prediction should either lead to avoiding the comedication with strong inhibitors of CYP3A4 or to a decrease in the colchicine dose. Of course, the point predictions should always be interpreted cautiously noting that the calculation of a CI for the predicted AUC ratio will allow the quantification of the uncertainty about the prediction.

The current analysis has some limitations. First, the method relies on the assumption that drug clearance is independent of the dose and the time, i.e., that all drugs have linear pharmacokinetics. If this assumption is violated, then the predicted AUC ratio is biased, because it is equal to the oral drug clearance ratio. Hence, the method should not be used for victim drugs that exhibit nonlinear pharmacokinetics at the intended dose level. Second, under the form of Eq. 1, the method is not applicable to interactions involving multiple mechanisms of action. For example, as stated above, darunavir was not included in the analysis, because it inhibits several CYPs. Ritonavir, which is not only a CYP3A4 inhibitor, was nevertheless included because its properties have been well characterized. Ritonavir is also an inhibitor of CYP2D6 and P-glycoprotein and an inducer of CYP2C9 and CYP2C19 (21–23). To estimate and validate the IR of ritonavir, we selected interaction studies for which CYP3A4 inhibition was thought to be the major mechanism. Third, with the current quantitative approach, the predicted AUC ratio for an interaction between a substrate that is almost exclusively cleared by CYP3A4 metabolism and a strong inhibitor is very imprecise. For example, if both the CR and the IR are assumed to be 0.98, the predicted AUC ratio is 25, but if the true values of the CR and the IR are 0.99, the AUC ratio will be 50 (7). Hence, small variations in the CR and IR may result in a large variation in the AUC ratio. The errors in the CR and the IR might result from a biased estimation in the current study or from interindividual variation. Fourth, the IR depends on the concentration profile of the inhibitor. As a result, the value of IR depends on both the dose per interval and the dosing interval. In the current study, the IRs could not be determined for different dosing schedules, but the IR values were obtained for repeated administration. It should realized that the IR is greater upon repeated administration of the inhibitor than upon a single administration, if the accumulation ratio is greater than 1. This issue is particularly relevant for drugs with a long elimination half-life. Finally, most if not all drugs metabolized by CYP3A4 are also metabolized by CYP3A5, but the contribution of each CYP is most often unknown. This is a problem because the inhibitors may have a different value of IR for CYP3A4 and CYP3A5 (25), and CYP3A5 is polymorphic (26), resulting in further variation of the expected AUC ratio, not accounted for with the current model.

CONCLUSIONS

The assumption of independence of the IR of the inhibitors from the victim drug seems to be generally valid, and in the rare cases where it was invalidated, the prediction error of the AUC ratio remained acceptable from a clinical point of view. The framework introduced by Ohno et al. for CYP3A4-mediated interactions has been extended successfully to a larger panel of substrates and inhibitors. The bias and the imprecision of the predicted AUC ratios were low, and in the final estimation, only one case of poor estimation was present among 59 cases. Finally, predictive distributions for 917 possible interactions were obtained, giving detailed information on some drugs or inhibitors that have been poorly studied so far, such as telaprevir, boceprevir, and ticagrelor. Because strong interactions involve combinations of a substrate with a CR_CYP3A4 greater than 0.8 and an inhibitor greater than 0.8, the data from this study may help to forecast clinically relevant interactions.

A Website based on the principles described in this article is dedicated to quantitative prediction of drug-drug interactions (http://www.ddi-predictor.org).

APPENDIX

The orthogonal regression was based on the following approach (7):

• CRs and IRs are the initial values found in the step 1 of the analysis.

• X’s and Y’s are the logit-transformed initial values.

• CRTs and IRTs are the “observed” logit-transformed initial values.

• CRZs and IRZs are the refined estimates.

• ~N (μ, τ) means “distributed as normal distribution, with a mean of μ and variance of 1/τ.”

• ~G (r,μ) means “distributed as gamma distribution, with a mean of r/μ and variance of r/μ².”

• i and j are the indexes of the substrate and the inhibitor, respectively.

• Preds are the predicted AUC ratios for each (CR and IR) couple.

• AUC ratios are the observed values, if any, for each (CR and IR) couple.

For each j:

$$\begin{array}{l}{Y}_j=\mathrm{Log}\left[{\mathrm{IR}}_j/\left(1-{\mathrm{IR}}_j\right)\right]\hfill \\ {\mathrm{IRT}}_j~N\left(Y_j,{\tau }_{\mathrm{IR}}\right)\hfill \\ {\mathrm{IRZ}}_j=\left[exp\left({\mathrm{IRT}}_j\right)\right]/\left[1+exp\left({\mathrm{IRT}}_j\right)\right]\hfill \end{array}$$

For each i:

$$\begin{array}{l}{X}_j=\mathrm{Log}\left[{\mathrm{CR}}_i/\left(1-{\mathrm{CR}}_i\right)\right]\hfill \\ {\mathrm{CRT}}_i~N\left(X_j,{\tau }_{\mathrm{CR}}\right)\hfill \\ {\mathrm{CRZ}}_i=\left[exp\left({\mathrm{CRT}}_j\right)\right]/\left[1+exp\left({\mathrm{CRT}}_j\right)\right]\hfill \end{array}$$

For each j:

$$\begin{array}{l}{\mathrm{Pred}}_{\mathit{ij}}=1/\left[1-{\mathrm{CRZ}}_i\times {\mathrm{IRZ}}_j\right]\hfill \\ {\mathrm{AUC}}_{\mathrm{ratio},\mathit{ij}}~N\left({\mathrm{pred}}_{\mathit{ij}},{\tau }_{\mathrm{AUC}}/{\mathrm{pred}}_{\mathit{ij}}\right)\hfill \end{array}$$

τ_CR~

G(4,1)

τ_IR~

G(4,1)

τ_AUC~G(0.2,1)

to estimate imprecision on AUC ratios.

τ_AUC =

1 otherwise.