Experimental and Modeling Study of Human Tympanic Membrane Motion in the Presence of Middle Ear Liquid

Abstract

Vibration of the tympanic membrane (TM) has been measured at the umbo using laser Doppler vibrometry and analyzed with finite element (FE) models of the human ear. Recently, full-field TM surface motion has been reported using scanning laser Doppler vibrometry, holographic interferometry, and optical coherence tomography. Technologies for imaging human TM motion have the potential to lead to using a dedicated clinical diagnosis tool for identification of middle ear diseases. However, the effect of middle ear fluid (liquid) on TM surface motion is still not clear. In this study, a scanning laser Doppler vibrometer was used to measure the full-field surface motion of the TM from four human temporal bones. TM displacements were measured under normal and disease-mimicking conditions with different middle ear liquid levels over frequencies ranging from 0.2 to 8 kHz. An FE model of the human ear, including the ear canal, middle ear, and spiral cochlea was used to simulate the motion of the TM in normal and disease-mimicking conditions. The results from both experiments and FE model show that a simple deflection shape with one or two major displacement peak regions of the TM in normal ear was observed at low frequencies (1 kHz and below) while complicated ring-like pattern of the deflection shapes appeared at higher frequencies (4 kHz and above). The liquid in middle ear mainly affected TM deflection shapes at the frequencies higher than 1 kHz.

INTRODUCTION

The tympanic membrane (TM) or eardrum separates the ear canal from the middle ear cavity and converts the sound pressure waves in the ear canal into mechanical vibrations of the ossicular chain in the middle ear. Sound-induced TM vibration has been measured at the umbo using laser Doppler vibrometry (LDV) (Goode 1994; Whittemore et al. 2004; Gan et al. 2004a; 2006b; Dai et al. 2007, 2008; Rosowski et al. 2003, 2008) and analyzed using finite element (FE) models of the ear (Funnell et al. 1987; Puria and Allen 1998; Koike et al. 2002; Sun et al. 2002; Gan et al. 2004b, 2007; Gan and Wang 2007; Wang et al. 2007; Zhang and Gan 2011). However, single-point measurements cannot provide information about complex TM surface motion and the properties of sound wave propagation across the TM. Measurements on a grid array with a large number of points on the TM provide a more complete validation for FE models of the human ear.

The pioneering measurement of the full-field TM motion in human temporal bones was reported by Tonndorf and Khanna (1972) using time-average holography. Recently, the full-field TM surface motion was measured using the multi-point LDV measurement (Fay et al. 2005; Maftoon et al. 2013), time-average (Furlong et al. 2009; Rosowski et al. 2009) or stroboscopic holographic interferometry (Aarnisalo et al. 2010; Del Socorro Hernandez-Montes et al., 2009; Cheng et al. 2010, 2013; Rosowski et al. 2011), optical coherence tomography (Djalilian, et al. 2008), and scanning laser Doppler vibrometry (Huber et al. 2001). The experimental measurements demonstrated that the TM motion pattern was relatively simple with one area of maximal displacement at low frequencies (below 2,000 Hz) dominating. The motion became more complicated at higher frequencies with multiple areas of maximal displacements and different phases at different locations on the TM. Rosowski et al. (2011) reported that both modal responses (standing waves) and traveling waves exist on the TM. The modal responses were present at low and high frequencies, while traveling waves were only apparent at higher frequencies (above 2 kHz). These experimental measurements are valuable for understanding of wave propagation across the TM and the mechanism of TM vibration induced by sound.

FE models of the ear have been reported for simulation of the full-field TM motion. Funnell and Laszlo (1978) published the first study on the full-field motion of the cat eardrum model, and the eardrum was modeled by shell elements. Wada et al. (1992) reported a preliminary study on FE modeling of the human TM vibration pattern (displacement amplitude) at two frequencies of 996 and 1,924 Hz. Wang et al. (2007) reported the TM motion as the displacement amplitude contour under middle ear static pressures (−2 and 2 kPa). However, there is a lack of studies in the literature that correlate the experimental measurements and FE modeling analysis on sound-induced full-field TM motion across a wide frequency range (from 0.2 to 8 kHz). The relationship between the TM surface wave propagation and the middle ear transfer function changes in diseased ears has not been fully investigated.

To gain a better understanding of TM motion in normal and diseased ears, a single-point Hearing Laser Vibrometer (HLV) has been used for in vivo measurements for gathering dynamic information at key locations on the TM (umbo, quadrants, light reflex, etc.) (Huber et al. 2001; Rosowski et al. 2003). Compared to the HLV measurement, some diagnostic tools currently used in clinics have shown limitations as reported by Rosowski et al., (2008). For example, the standard single frequency (226 Hz) tympanometry is insensitive to ossicular disorders and sometimes cannot provide accurate diagnosis before middle ear surgery. Thus, HLV eventually could be used as a clinical diagnosis tool for differentiating normal and diseased middle ears (Goode et al. 1996; Huber et al. 2001; Rosowski et al. 2003, 2008; Aarnisalo et al. 2010; Jakob et al. 2009).

In addition to single-point HLV, scanning laser Doppler vibrometry and holographic interferometry have been considered for potential clinical application for analyzing the location and frequency sensitivities of measurements in normal and diseased ears. For example, middle ear effusion is a very common disorder associated with otitis media, a common middle ear inflammatory or infectious disease that causes effusion to accumulate in the middle ear cavity (Rovers et al. 2004). To date, no literature addresses the effect of middle ear effusion on full-field TM motion studied using experimental measurement and correlated to FE modeling analysis. The best measurement locations on the TM and the range of frequencies that may help with differentiating the normal ear and the ear with middle ear effusion have yet to be identified.

The aim of this study was to investigate the full-field motion of the TM in normal cadaveric ears and in disease-mimicking cadaveric ears with middle ear liquid using a scanning laser Doppler vibrometer (SLDV) and an FE model of the human ear. The FE model of the human ear reported by Gan and Wang (2007) and Zhang and Gan (2011) was used to simulate the motion of the TM in normal and disease-mimicking conditions. Both experimental measurement and FE modeling may provide a better understanding of the full-field motion of the TM. There were two basic hypotheses for this study: (1) human TM vibration patterns measured in normal cadaveric ears differ from those measured in disease-mimicking cadaveric ears with liquid in the middle ear and (2) the FE model of the human ear consisting of the ear canal, TM, middle ear ossicular chain and cavity, and spiral cochlea can reproduce or predict the experimental TM vibration measurements in both normal and disease-mimicking conditions. The data reported in this study will help elucidate the complex TM motion with and without middle ear liquid.

METHODS

Human Temporal Bone Preparation

Four unfixed temporal bones (TB), obtained from cadavers through the Willed Body Program at the University of Oklahoma’s Health Sciences Center, were used in this study. The ages of donors ranged from 64 to 82, with a mean of 73 (all donors were male). To maintain soft tissue compliance and hydration in the 5 days between extraction of the TBs and the experiment, the bones were immersed in 0.9 % saline solution mixed with providine (15 % providine; 85 % saline) at 5 °C until use. Each TB was visually inspected under an operating microscope (OPMI-1, Zeiss, Thornwood, NY) to confirm the presence of a normal ear canal and intact TM. The four TBs reported in this paper were all from normal ears and showed no evidence of pathology in the middle ear after the post-experimental check.

The external ear canal was surgically removed until about 90 % of the TM surface was visible under the microscope. The Eustachian tube (ET) meatus was identified at the nasopharyngeal end. The cartilaginous portion of the ET was surgically removed up to the bone. A soft silicone tube (outer diameter of 1 mm) with a white tip was put through the ET into the middle ear cavity while visualizing through the TM with an operating microscope. When the white tip was visualized through the TM, the tube was glued in place using cyanoacrylate gel glue (Henkel Consumer Adhesives, Avon, OH) and connected to a syringe for injecting the liquid into the middle ear cavity (shown in Fig. 1). Another hole with a diameter of about 2 mm was drilled through the epitympanic tegmen. A second silicone tube was laced through this hole into the middle ear cavity, which served as the air outflow tube during the saline injection. In line with a method described by Cheng et al. (2010), the TM was coated with a solution of 3 % TiO₂ powder (Acros Organics, NJ, USA) suspended in saline to increase the backscattered light from its surface. The effect of the TiO₂ powder on the vibration of the TM can be neglected according to a study reported by Rosowski et al. (2009). During experiments, the TBs were wrapped in paper tissue wet with saline to ensure appropriate moisture levels.

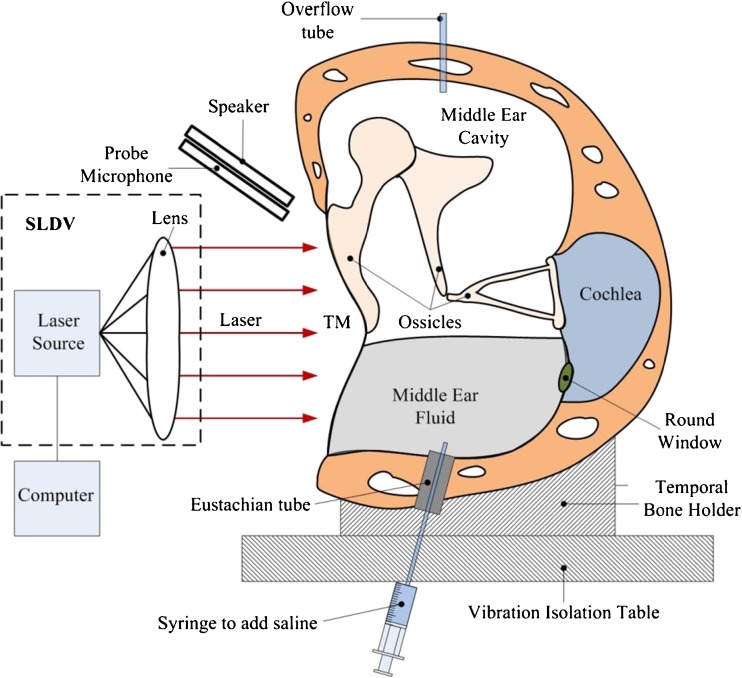
FIG. 1.

Schematic of the experimental set-up showing the scanning laser Doppler vibrometer (SLDV) and a human temporal bone.

Experimental Set-Up

The schematic diagram of the experimental set-up with an SLDV to measure the motion of the TM surface in the TB is shown in Figure 1. The TB was seated in a temporal bone holder and placed on a vibration isolation table. A chirp stimulus at 80 dB sound pressure level (SPL) with frequency range from 0.2 to 8 kHz was created with a function generator (HP 35670A, Hewlett-Packard, Palo Alto, CA) and an amplifier (RCA SA-155, Radio Shack, Fort Worth, TX). It was delivered onto the TM using a speaker (TDT CF1, Tucker-Davis Technologies, Alachua, FL) and a sound delivery tube with an inner diameter of 1 mm. A probe microphone (Model ER-7, Etymotic Research) used for monitoring the input SPL was secured parallel to the sound delivery tube and placed about 2 mm away from the TM. At high frequencies, the phase of sound pressure applied to different portions of the TM may vary due to the distance variation between the TM and the sound source. For example, at 8 kHz, the wavelength of sound is approximately 43 mm. The distance between the TM surface and the sound source can vary up to approximately 9 mm (the diameter of the TM) and may induce a sound pressure phase variation of up to 1/5 cycle. Background noise measurements were performed in the absence of an excitation source at several sites on the TM. The noise level was negligible for measurements conducted above 120 Hz.

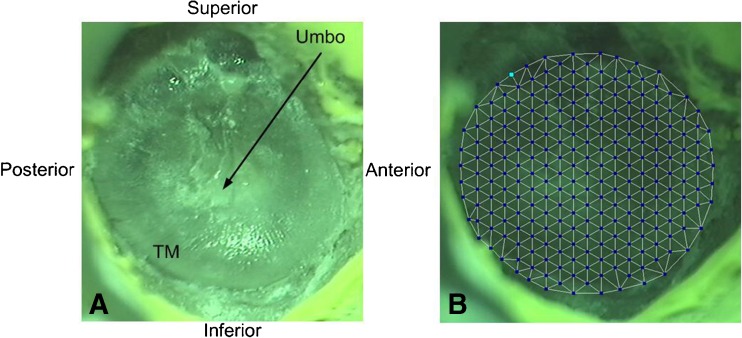
An SLDV (PSV-400, Polytec Inc., Irvine, CA) with a software package (PSV 8.8, Polytec Inc., Irvine, CA) was used to measure the full-field vibration of the TM. The orientation of the plane of the tympanic annulus was set perpendicular to the laser beam. Figure 2a shows a typical view of one TM sample captured by the SLDV. Scanning grids of measurement points were set and aligned by drawing them onto the TM live video image using the PSV 8.8 software. These points covered the entire surface of the TM (see Fig. 2b). The number of measurement points varied with the TB samples and was generally in the range of 250 to 300 points. The vibration velocity of each measurement point along with the sound pressure was recorded simultaneously by PSV 8.8 over the entire frequency range from 0.2 to 8 kHz. The vibration displacement amplitudes at different frequencies d(f) were simply calculated from the velocity v(f) using the equation d(f_i) = v(f_i)/2πf_i, where f_i is the bin frequency set by the data acquisition setting and resolution.

FIG. 2.

A One exposed TM sample image captured by the SLDV. B The typical scanning points defined on the TM surface.

Experimental Protocol

Three groups of experiments were performed sequentially on each TB to study the effect of the middle ear liquid on the TM motion. The first group was the ears without middle ear liquid. In group two, 0.3 ml normal saline solution was injected slowly into the middle ear cavity through the silicone tube of the previously “normal” measured ears. The saline level was observed through the TM image acquired by SLDV and did not change visibly after the injection. The amount of 0.3 ml was chosen because it was reported to be a critical volume of liquid in the middle ear, and about half of the middle ear cavity was filled (Gan et al. 2006a, b). In this study, it was observed that the 0.3 ml middle ear liquid level was just below the umbo. In group three, 0.6 ml saline solution was injected slowly into the middle ear cavity. The volume of liquid should almost fill up the middle ear cavity (Gan et al. 2006a, b) and cover the entire TM surface; this was confirmed by visual observation under the microscope. Middle ear effusion may have a higher viscosity than saline (Lupovich et al. 1971; Carrie et al. 1992) and the TM may also change in otitis media (von Unge and Bagger-Sjoback 1994). It is a limitation in this temporal bone study not to include these effects.

During experimental measurements for each group, the velocity or displacement of all defined scanning points on the TM were acquired by means of the SLDV across frequencies from 0.2 to 8 kHz. The scanning process took about 10 min, which was dependent on parameters such as the number of scanning points (generally, more scanning points meant longer acquisition times), the laser reflection signal level (a weaker signal level might require a little longer time), and the signal processing parameters (e.g., the sampling rate). When experiencing low signal reflection level (low backscattered level), the Signal Enhancement (SE) mode of the SLDV automatically kicks in. It works as follows: The SLDV dithers a few microns around the center of the original grid point site in a hexagonal pattern. The SLDV measures the backscatter light at all of these seven sites and automatically chooses the site with the highest backscattered intensity. The second part of the SE mode automatically increases the number of averages until the signal-to-noise ratio (SNR) for the measured scanned point is acceptable. If a scanned point does not reach the acceptable SNR, the scanned point on the grid is rejected and marked as such. That point will not enter into the results. This procedure increases the scanned time a little. Since our measurements were carried out under high magnification, the laser beam was highly focused. The TM’s geometry is similar to an asymmetric flattened cone; thus, it is necessary to change the focus of the laser beam while scanning the TM. A pre-measure auto-focus scanning process at each point was performed prior to measuring each point, which generally guarantees that all points get sufficient backscattered signal in order to get more than acceptable SNR even before the actual scanned measurement is performed. Statistical analysis was conducted on the three groups of experimental data measured from the specified nodes. One-way ANOVA was conducted in this study to analyze the differences of nodal displacements between the three experimental groups: no liquid, 0.3 ml, and 0.6 ml.

Finite Element Model of the Human Ear

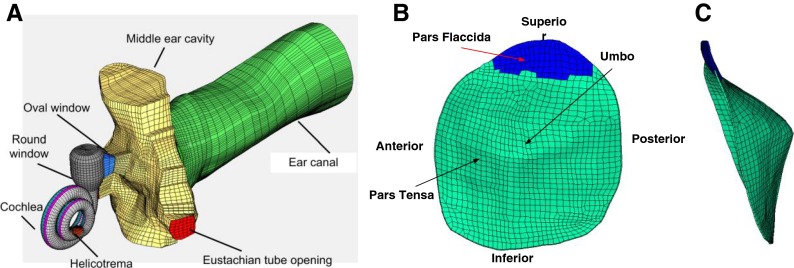
An FE model of the human ear with spiral cochlea was recently reported by Zhang and Gan (2011) and Gan et al. (2011). In brief, the model was created based on histological sections of a temporal bone (male, age 52, left ear), and consists of the ear canal, TM, ossicular chain, suspensory ligaments and muscle tendons, middle ear cavity, and spiral cochlea with three chambers. Figure 3a shows the anterior-medial view of the model. The TM was modeled with two parts: pars flaccida and pars tensa as shown in Figure 3b. The diameter of the TM was 9.76 and 9.01 mm along the manubrium and perpendicular to the manubrium, respectively. The total surface area of the TM was 83.73 mm². The thickness of the TM was not evenly distributed and was between 50–100 μm. It was thicker near the edge and manubrium and thinner in the middle region. Figure 3c shows the posterior view of the TM model with an obvious cone shape. The height of the cone was 2.42 mm. The TM was meshed by 1,151 hexahedral solid element (Solid 185 in ANSYS). Detailed information about the middle ear of this FE model can be found in an earlier published paper by Gan and Wang (2007).

FIG. 3.

A An anterior-medial view of an FE model of a human ear including the ear canal, middle ear cavity, and coiled cochlear. B A lateral view of the FE model of TM including the pars flaccida and pars tensa. C A posterior view of the FE model of TM showing the cone shape of the TM.

The soft tissues, including the TM pars flaccida, TM pars tensa, TM annulus, incudomallear joint, incudostapedial joint, stapedial annular ligament, and round window membrane, were assumed as viscoelastic materials in this study. The standard linear viscoelastic model was used as the constitutive law for these tissues. The mechanical parameters used for these tissues are listed in Table 1 of Zhang and Gan’s paper (2011). The material properties of other middle ear tissues and bones are listed in Tables 2 and 3 of Gan and Wang’s paper (2007).

To simulate the effect of middle ear liquid on TM motion, the middle ear cavity was divided into subdivisions as shown in Figure 3 of Gan and Wang’s paper (2007). The liquid in the cavity was meshed with the eight-node hexahedral fluid elements (Fluid 80 in ANSYS). In this study, two liquid levels were created in the model: 0.3 (up to the umbo of the TM) and 0.6 ml (almost filled the middle ear cavity). The bulk modulus of saline was set as 2.2 GPa, and the viscosity was set as 1 cp. In the FE model with liquid in the middle ear cavity, the mechanical properties of the middle ear tissues remained the same as those of the normal ear without liquid. The TM static deformation induced by the liquid in the middle ear was not considered in the FE model.

At an ideal surface 2 mm away from the TM in the ear canal, 80 dB SPL was applied. Multi-physics (acoustic-fluid-solid) coupled harmonic analysis was conducted in the FE model across the frequency range from 0.2 to 8 kHz using ANSYS (ANSYS Inc., Canonsburg, PA). The TM vibration deflections were obtained as the results and presented as the normalized displacement, which was divided by the sound pressure. Note that in the experiment, the external ear canal was surgically removed to expose the TM. By contrast, the ear canal was constructed in the FE model. This difference may cause the discrepancy between the modeling results and the experimental data.

RESULTS

TM Motion Measured by SLDV

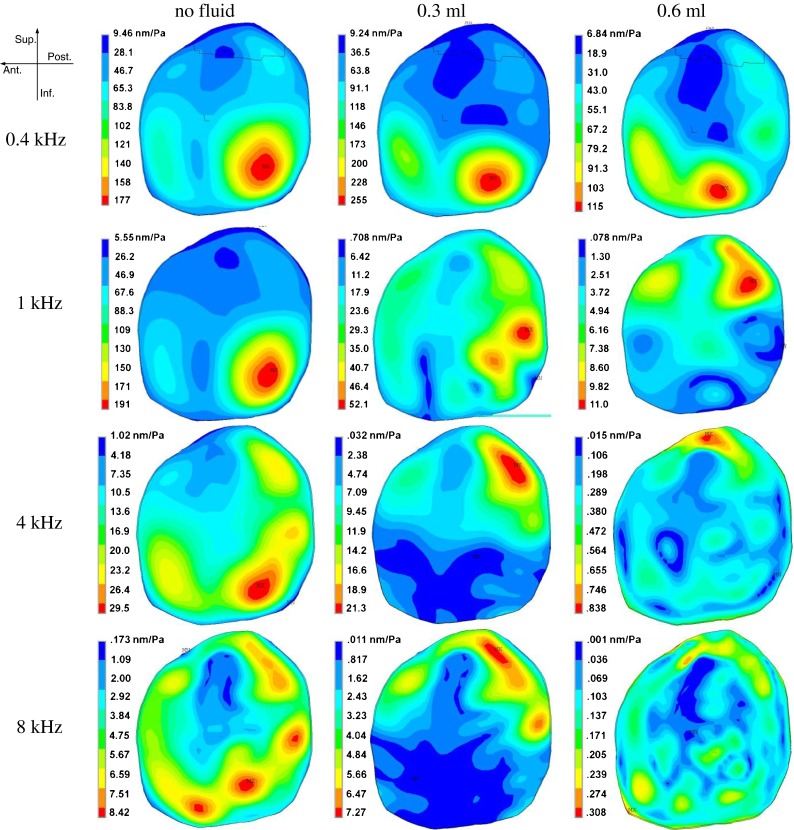
Figure 4 shows the typical deflection shapes of the TM measured by the SLDV on one TB (TB-2, right ear) at three middle ear liquid levels (no liquid, 0.3 ml, and 0.6 ml liquid) and four frequencies: low frequency of 0.4 kHz, medium-low frequency of 1 kHz, medium-high frequency of 4 kHz, and high frequency of 8 kHz. The color bar on the right side of each image represents the displacement amplitude normalized by the input sound pressure in nm/Pa. The orientation of the right ear TM is shown in the upper left-hand corner of the figure.

FIG. 4.

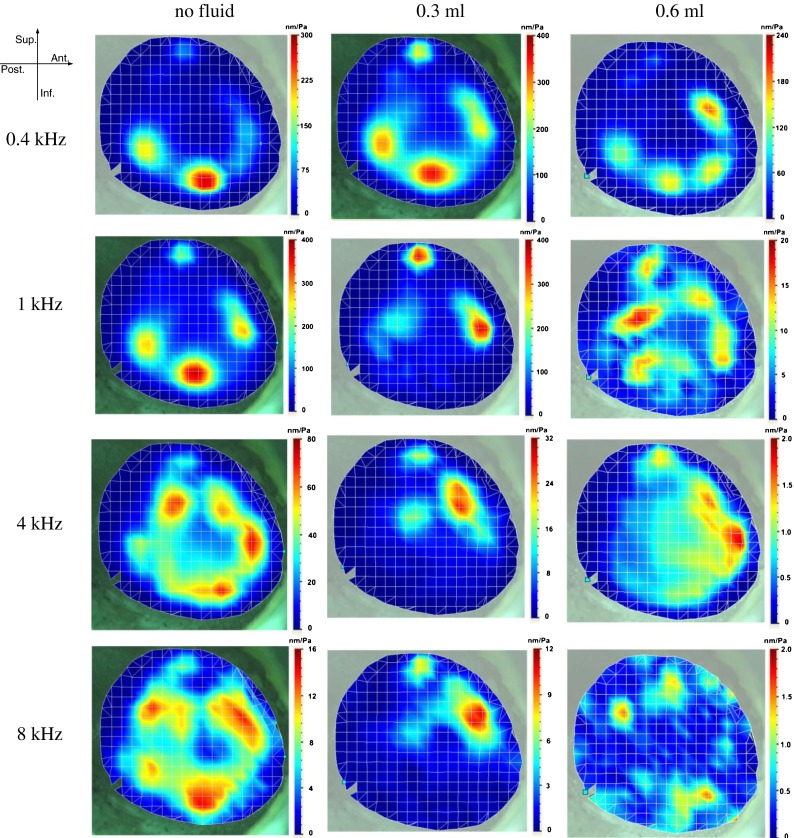
Typical deflection shapes of TM motion measured by SLDV on one temporal bone (TB-2, right ear) under different conditions (no liquid, 0.3 ml middle ear liquid, and 0.6 ml middle ear liquid) and four frequencies (0.4, 1, 4, and 8 kHz).

For the ear without middle ear liquid, at the 0.4 kHz frequency, the deflection shape of the TM motion looks relatively simple with two major vibration peak regions located at the inferior-posterior quadrant of the TM. The maximal displacement amplitude was close to 300 nm/Pa, while the displacement near the umbo was about 50 nm/Pa. When frequency increased to the medium-low range at 1 kHz, the general deflection shape did not change much. However, the maximal normalized displacement level increased slightly to about 400 nm/Pa and two more small displacement peak regions emerged at the anterior and superior portions of the TM. At the medium-high frequency level (4 kHz), there were more than six separate displacement peak regions located along the middle area between the TM annulus and the manubrium, forming a ring-like pattern. At 4 kHz, the vibration at the anterior and superior portions of the TM increased, unlike those in the posterior portion. However, the absolute displacement of the entire TM decreased with a maximal value of 80 nm/Pa. At a higher frequency (8 kHz), the overall displacements decreased further. The deflection shape of the TM became more complicated and formed a thicker peak-ring compared with that at 4 kHz.

For the ear with 0.3 ml saline in the middle ear cavity, at 0.4 kHz, the vibration deflection shape of the TM did not change much compared with the ear without middle ear liquid. However, some slight changes were observed, including a small increase in the overall displacement, particularly in the anterior and superior portions of the TM. This increase may have been caused by the reduction of the middle ear resonance frequency by the liquid. From 1 to 8 kHz, the vibration at the inferior portion of the TM was reduced by the middle ear liquid. The maximal displacement decreased to around 30 nm/Pa at 4 kHz, and about 10 nm/Pa at 8 kHz. The displacement peak regions moved to the superior portion of the TM. No ring-like pattern was observed at high frequencies. The displacement at the umbo decreased slightly compared with that in the ear without middle ear liquid.

For the ear with 0.6 ml saline in the middle ear cavity, at 0.4 kHz, the overall displacement level was slightly reduced by the liquid behind the TM, and the peak regions moved toward the anterior-superior direction. At 1 kHz and above, the displacement of the entire TM decreased tremendously (by a factor of 10 to 40 compared with the ear without middle ear liquid). The deflection shape of the TM became very complicated at high frequencies, with multiple peak regions scattered on the entire TM surface.

Figure 5 shows the instantaneous displacement pattern of the three groups (no liquid, 0.3 ml, and 0.6 ml) of TM surfaces at two different phases (0 and 1/2 cycles) in one complete cycle measured by SLDV in the temporal bone TB-2 (right ear). In the ears without liquid, the entire TM surface generally moved in phase at low frequencies (0.4 and 1 kHz). The major displacement peaks occurred at almost the same time. The phase difference across the entire TM surface was very small. When the frequency increased to 4 kHz, multiple displacement peaks were observed. The peaks did not vibrate in phase anymore. Some small regions in posterior portion of the TM vibrated at the opposite phase to other major peaks. This was possibly induced by the higher modal shape for the larger surface area in the posterior portion. At the even higher frequency of 8 kHz, the TM surface vibration pattern became much more complicated with multiple displacement peaks and phase variations. Different regions were vibrating in opposite directions to one another.

FIG. 5.

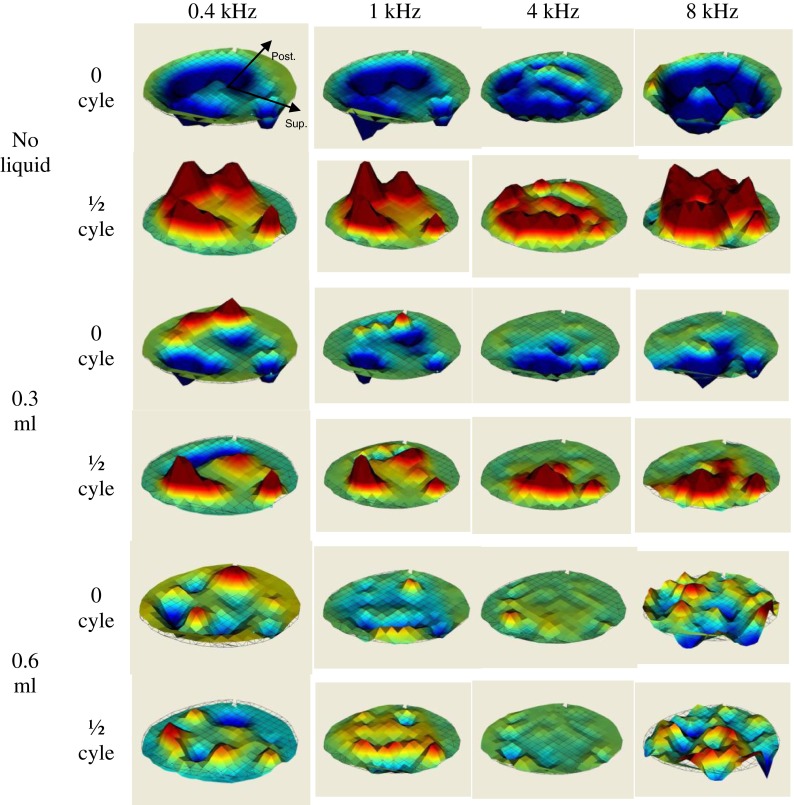
The displacement pattern of three groups (no liquid, 0.3 ml, and 0.6 ml) of TM surfaces at two different phases in one entire cycle measured by SLDV on one temporal bone (TB-2, right ear) at 0.4, 1, 4, and 8 kHz.

When liquid in the middle ear reached 0.3 ml, the vibration phase of the inferior portion covered by liquid was delayed and the TM surface was not vibrating in phase anymore, even at the low frequencies of 0.4 and 1 kHz. The phases of the superior portion not covered by liquid were not affected much and were similar to those of ears without liquid. When the middle ear liquid reached 0.6 ml and the entire TM was covered by liquid, both displacement amplitude and phase distribution became very complicated and there was no clear pattern observed at this stage.

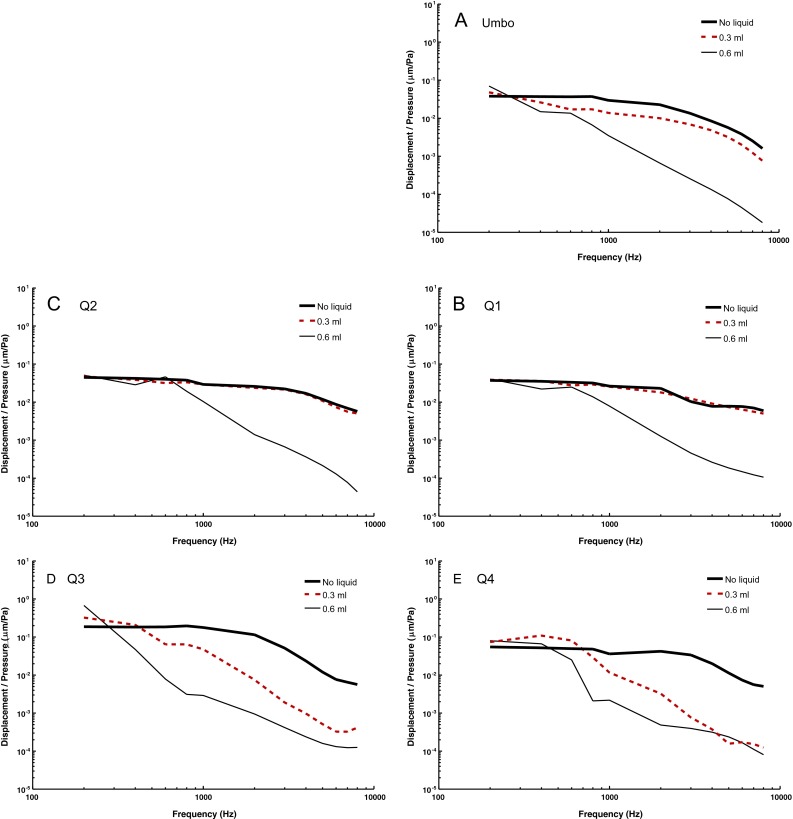
Figure 6 shows the sound-induced nodal motions at the umbo and four different quadrants of the TM. Figure 6a is a schematic of selected nodal locations on the TM: the umbo was selected at the end of the TM-manubrium connection. Q1 is the location selected at the center of the anterior-superior quadrant. The angle between the umbo-Q1 line and horizontal chord is about 45°. Similarly, Q2, Q3, and Q4 were selected at the angular central position of the posterior-superior quadrant, posterior-inferior quadrant, and anterior-inferior quadrant, respectively. Figures 6b–f show the mean normalized displacement-frequency curves with the standard deviation (S.D.) at the umbo, Q1, Q2, Q3, and Q4 locations, respectively, from the four TM samples. Each panel includes the curves measured for the TM of ears without liquid and the TMs with 0.3 and 0.6 ml of middle ear liquid.

FIG. 6.

A The umbo and four quadrants locations on the TM sample. B–F The normalized displacement-frequency curves of the umbo and four quadrants under different conditions (no liquid, 0.3 ml middle ear liquid, and 0.6 ml middle ear liquid) measured by SLDV.

As shown in Figure 6, the displacements in ear without middle ear liquid were similar to those in the ears with liquid at low frequencies (below 1 kHz). However, it is generally known that 226-Hz tympanograms measured in patients with otitis media with effusion usually have much lower compliance than that measured in normal ears. The inconsistency between the two measurements (SLDV and 226-Hz tympanometry) in this case may be due to the absence of middle ear static pressure in this study. A large negative static pressure is very common in otitis media with effusion and can reduce the compliance of middle ear. If there is no middle ear pressure, the low frequency tympanogram is insensitive to middle ear liquid (Dai et al. 2007).

Generally, for no liquid, the TM displacement in the posterior quadrants was larger than that in the anterior quadrants, and the inferior displacement was larger than that occurring superiorly. Q3 had the largest displacement among the five locations. The displacement-frequency curves from the umbo, Q2, Q3, and Q4 had two obvious regimes: slightly increasing below 1 kHz and decreasing above 1 kHz. The curve from Q1 was more flat between 0.2 and 4 kHz. The flatness was induced by the maximal displacement regions moving toward anterior and superior portions at high frequencies. When the middle ear liquid volume was 0.3 ml, close to reaching the umbo, the TM vibration of the superior quadrants (Q1 and Q2) was not affected significantly (P > 0.05). However, the displacement of the inferior quadrants (Q3 and Q4) and the umbo was slightly reduced at frequencies above 1 kHz. When the middle ear liquid volume was 0.6 ml, nearly filling up the middle ear cavity, the vibration amplitudes of the entire TM significantly (P < 0.05) decreased over a broad frequency range from 0.6 to 8 kHz. The liquid-induced displacement reduction was larger in the posterior quadrants (Q2 and Q3) than in the anterior quadrants (Q1 and Q4).

Tympanic Membrane Motion Predicted by the FE Model

Figure 7 shows the deflection shapes of the TM at four selected frequencies (0.4, 1, 4, and 8 kHz) derived from the FE model of the left ear. Just as with the experimental measurements, three conditions were simulated by the FE model: no liquid, 0.3 ml, and 0.6 ml liquid in the middle ear cavity. The FE model-derived TM vibration deflection shapes were generally consistent with those from the SLDV measurements (Fig. 4). Note that the orientation of the left ear is shown in the left upper hand corner, a mirror reflection of Figure 4.

FIG. 7.

The deflection shapes of TM motion simulated by the FE model of a human ear under different conditions (no liquid, 0.3 ml middle ear liquid, and 0.6 ml middle ear liquid) and four frequencies (0.4, 1, 4, and 8 kHz).

For no liquid, the model-derived images show the two-peak pattern at lower frequencies (1 kHz and below) and the ring-like pattern at higher frequencies (4 kHz and above). For the middle ear with liquid, the TM motion pattern at 0.4 kHz shows some changes. The major displacement peak region was moved slightly toward the anterior portion of the TM. When the frequency increased to 1 kHz and above, the mobility of the liquid-covered TM portion was constricted and the major displacement peaks were moved to the superior portion of the TM. For the images at high frequency (8 kHz) with 0.6 ml liquid, the TM motion was complicated with many displacement peaks with an apparent random distribution on the entire TM surface. There are some differences existing between the TM vibration patterns with 0.6 ml obtained from the FE model and experiments. However, a similar trend in both cases is that the displacement level of the whole TM surface decreased substantially.

Figure 8 shows the instantaneous displacement pattern of the three groups (no liquid, 0.3 ml, and 0.6 ml) of TM surfaces at two different phases (0 and 1/2 cycles) obtained from the FE model of a left ear. At the lower frequencies of 0.4 and 1 kHz, the FE model-derived phase images were generally consistent with those obtained from experiments. However, at frequencies above 4 kHz, the phase images from the FE model had some noticeable difference from the experimental images. The sound source location difference between the FE model and the experiment may be one of the contributors. The variations of the distance between the TM surface and the sound source caused an uneven phase distribution at high frequencies. Another factor which contributes to the difference is that the phase data obtained from the current FE model at frequencies above 4 kHz may not be very accurate and still need to be improved. This issue has been discussed in our previous study (Zhang and Gan 2013). The improvement will include the viscoelastic properties of the middle ear soft tissues and the coupling between the air, fluid, and structures.

FIG. 8.

The displacement pattern of three groups (no liquid, 0.3 ml, and 0.6 ml) of TM surfaces at two different phases in one entire cycle obtained from the FE model at 0.4, 1, 4, and 8 kHz.

Figure 9 shows the FE model-derived nodal grid point displacements at the umbo and four quadrants of the TM. The selection of these locations follows the same method described in the previous section outlining experimental measurements. For no liquid, the model-derived results at the umbo, Q1, Q2, Q3, and Q4 were consistent with those measured by SLDV (Fig. 6). The 0.3 ml middle ear liquid mainly affected the mobility of the TM at the inferior regions at frequencies above 0.6 kHz. The liquid had no obvious effect on the nodal location displacements of Q1 and Q2 while it had a detectable effect on the umbo displacement across the entire frequency range. The 0.6 ml middle ear liquid significantly reduces the displacement of the entire TM at frequencies above 0.6 kHz. The reduction in the displacement is as much as 100 times less compared to the normal ear.

FIG. 9.

The normalized displacement-frequency curves of the umbo and four quadrants under different conditions (no liquid, 0.3 ml middle ear liquid, and 0.6 ml middle ear liquid) derived from the FE model.

DISCUSSION

Comparison with Published Measurements

In this study, the full-field sound-induced human TM motion including the umbo displacement was measured by SLDV. In the literature, the middle ear transfer function is generally measured at the umbo, and has been studied using a single beam LDV (Gan et al. 2004a; 2006a, b; Dai et al. 2007, 2008). Gan et al. (2006a, b) studied the umbo vibration in the normal ear and the ear with various liquid levels from 0.1 to 0.6 ml. The umbo displacements shown in Figure 5b are generally consistent with those in Figure 9 of Gan et al.’s paper. Note that their results were presented as the peak-to-peak displacement induced by 90 dB SPL and need to be normalized by sound pressure for a comparison. The displacement at 0.3 ml middle ear liquid in this study was slightly higher than that of Gan et al.’s at high frequencies (above 2 kHz). This could have been caused by temporal bone sample variations and/or different measurement tools. The consistency validated our measurement from the aspect of the umbo motion. However, unlike with the single beam LDV, the SLDV was able to measure the full-field TM surface motion.

Recently, the entire TM surface motion was studied by the personal computer-assisted opto-electronic holographic interferometer in both time-average mode and stroboscopic mode (Furlong et al. 2009; Rosowski et al. 2009, 2011; Aarnisalo et al. 2010; Cheng et al. 2010). The displacement amplitudes (and corresponding deflection shapes) and the phase of the TM motion can be measured using that technology. The experimental measurement and FE modeling results obtained from the ear without middle ear liquid in this study show similar TM motion patterns to those reported by Cheng et al. (2010) and Rosowski et al. (2011). In brief, at low frequencies (1 kHz and below), a simple motion pattern with one or two major displacement peak regions in the posterior quadrants of the TM surface was observed, while at high frequencies (4 kHz and above) a complicated motion pattern with multiple displacement peak regions along the middle area between the TM annulus and manubrium was usually seen.

Compared with SLDV, the holographic interferometer is able to measure at more locations on the TM (more than 10,000 versus 300) in a shorter period of time (a few seconds versus a few minutes). However, this is at the expense of measuring at a single frequency without collecting information related to the damping or other related modal information for each location. The higher spatial resolution results in more measurement points that can describe complex deflection shapes at high frequencies. SLDV can easily sweep the entire frequency range and automatically record phase information of each location on the sample. The frequency response data around the frequencies of interest can also be obtained, thus ensuring modal parameters can be gathered and later analyzed in post-processing. Additionally, it should be noted that the number of measurement points chosen was sufficient to resolve motion at the highest measured frequency (8 kHz), given the corresponding wavelength of the deflection shape, making it possible to avoid spatial aliasing.

Comparison Between SLDV Measurement and FE Model Prediction

In this study, the TM motion was measured by SLDV and predicted by the FE model. The comparison between Figures 4 and 7 indicates a consistency between the experiment and the FE model analysis. In this study, the TM motion was measured by SLDV and predicted by the FE model. In both experimental and modeling results for the no liquid case: the entire surface of the TM generally moves in phase and two local maxima are observed on the posterior-inferior side at low frequencies (0.4 and 1 kHz); multiple-peaks can be seen at high frequencies (4 and 8 kHz); and the direction of motion of the marginal area of the membrane seems to be opposite to that of the central area of the membrane. In summary, for the ear without middle ear liquid, three basic trends can be concluded for the TM motion from low to high frequencies: (1) the deflection shapes become more complicated with more peak regions and an increase in spatial wave numbers per TM diameter when the frequency increases; (2) new displacement peak regions emerge at the anterior and superior portions of the TM when frequency increases; and (3) the overall displacement amplitude decreases and the displacement distribution becomes more dense when the frequency increases.

For the ears with middle ear liquid, the liquid mainly affected TM deflection shape at frequencies higher than 1 kHz. The liquid moved the displacement peaks to the superior portion of the TM, where the vibrations were less reduced. For the ear with liquid filling the middle ear cavity, the membrane does not move in phase at all the frequencies in both experimental and modeling results. There was no clear deflection shape at frequencies of 4 kHz or above. We also found that slight differences existed between the deflection shape obtained from the SLDV measurement and from the FE model for higher frequencies. The maximal displacement value measured by SLDV was about double the model-derived result, and the displacement peak area shown in the images from the experiments was smaller than that from the model. It is particularly remarkable that the measurements and the FE modeling of TM without liquid have such similar mode shapes for selected frequencies given the ear variations already mentioned.

The differences in results between the experimental measurements on temporal bones and the FE modeling might be explained by the variations of individual TB anatomy, and by the material properties of ear tissues in human TBs and those used for the FE model, or by the variations in boundary conditions due to the temporal bone preparation. In the current stage of research, it is a challenge to create a specific FE model for each individual ear. The anatomy of the present FE model was built based on histological section images of a TB (male, age 52, left ear) and the material properties were obtained either from experimental measurements on ear tissues of various TBs in our lab or from the data published in the literature (Gan and Wang 2007; Zhang and Gan 2011; Gan et al. 2011). The variations in anatomy and material properties among different ears may affect the TM vibration shapes either measured from TBs or predicted by the FE model. At this stage of research, even the most comprehensive model of the human ear is not able to replicate the experimental measurements on each individual ear, and particularly diseased ears, with high accuracy.

Contribution of this Study and Future Work

This is the first study on TM surface motion that combines SLDV measurements and FE modeling analysis. The two different approaches provided more insight into sound-induced TM vibration.

SLDV and stroboscopic holography help with understanding TM dynamics more comprehensively. The results reported in this study support the case for using non-intrusive single-point HLV as a clinical tool. The SLDV also has potential for clinical applications. However, it should be noted that it is more complex to set up as compared to a single-point HLV. The complexity comes with a lot more meaningful data, but also adds to the overall acquisition times. The data reported in this study provide some diagnostic clues about the measurement locations and expected displacement ranges using HLVs to distinguish diseased ears (middle ear liquid in this case) from normal ones.

Standard low frequency (226 Hz) tympanometry may not be sensitive to the middle ear-liquid only case without noticeable middle ear pressure in experiments on TBs (Dai et al. 2007). The experiments and FE modeling in this study did not include the middle ear pressure or tissue morphological changes. These changes are common in otitis media with effusion and may cause low compliance in 226 Hz tympanograms. In our previous study on otitis media using the FE model, the changes of ear tissues and middle ear static pressure were considered (Fig. 3 in Gan et al. 2011). The TM displacement at low frequencies in the disease-mimicking ear decreased compared to the normal ear. Compared to tympanometry, the SLDV can provide more comprehensive information from low to high frequencies and the entire TM surface motion, which will be a more precise tool for diagnosing the presence of middle ear liquid.

Future studies on TM motion may consider the relationship between TM motion and clinical tests, such as wideband energy reflectance or absorbance. Recently, an FE model of the human ear was used for analysis of energy absorbance in normal and disordered ears (Zhang and Gan 2013). Compared with single-point displacement of the TM, full-field TM motion should have closer relations to acoustic energy absorbance. The TM motion under the conditions of other middle ear diseases such as otitis media, ossicular chain disarticulation, and otosclerosis will also be studied in the future. It is also noticed that the external ear canal was removed to expose the TM in this study, which is not the case in clinical practice when the TM motion is measured. The effect of the ear canal on surface motion of the TM detected by SLDV needs further studies.