The Effect of Stimulus Bandwidth on the Nonlinear-Derived Tone-Burst-Evoked Otoacoustic Emission

Abstract

Intermodulation distortion has been hypothesized as a mechanism contributing to the generation of short-latency (SL) components in the transient-evoked otoacoustic emission (TEOAE). Presumably, nonlinear interactions between the frequency components within the evoking stimulus induce cochlear distortion products, which mix in the cochlea and ear canal with reflected energy from each stimulus-frequency’s tonotopic place. The mixing of these different components is evidenced in the bandpass-filtered emission waveform as a series of different latency peaks. The current study tested the hypothesis that intermodulation distortion, induced within the spectral bandwidth of the evoking stimulus, is the primary mechanism through which the SL components are generated. The nonlinear-derived tone-burst-evoked OAE (TBOAE_nl) was evoked using 2-kHz tone bursts with durations of 3, 6, 12, and 24 cycles. As tone burst duration doubled, the spectral bandwidth was halved. It was hypothesized that contributions to the TBOAE_nl from SL components would decrease as tone burst duration increased and spectral bandwidth decreased, if the SL components were generated through intermodulation distortion. Despite differences in spectral bandwidth between the evoking stimuli, the latencies and magnitudes of the different latency components between the 3- and 6-cycle TBOAE_nl were comparable. The 12- and 24-cycle TBOAE_nl envelopes were characteristic of destructive phase interactions between different latency components overlapping in time. The different latency components in the 3- and 6-cycle TBOAE_nl introduced a characteristic level dependency to TBOAE_nl magnitude and latency when analyzed across a broad time window spanning the different components. A similar dependency described the 12- and 24-cycle TBOAE_nl input/output and latency-intensity functions, suggesting that the SL components evident in the shorter-duration TBOAE_nl equally contributed to the longer-duration TBOAE_nl, despite reductions in spectral bandwidth. The similarity between the different TBOAE_nl suggests that they share a common generation mechanism and casts doubt on intermodulation distortion as the generation mechanism of SL TEOAE components in humans.

INTRODUCTION

The generation of transient-evoked otoacoustic emissions (TEOAEs) has been and continues to be a subject of debate. The broad bandwidth of the stimuli used to evoke these emissions (e.g., acoustic clicks) seemingly necessitates at least some contribution from intermodulation distortion (IMD). When presented to the cochlea, these stimuli cause broad excitation across the basilar membrane (BM; Don and Eggermont 1978; Recio et al. 1998). If nearby areas were excited simultaneously, they would be expected to induce distortion since the cochlea is a nonlinear system. However, the spatial time filtering imposed by the impedance gradient of the cochlea may limit such interactions.

In the guinea pig, IMD is thought to play a primary role in TEOAE generation (Avan et al. 1995; Withnell and Yates 1998; Yates and Withnell 1999; Withnell et al. 2000). Most recently, Withnell and McKinley (2005) reported that the nonlinear-derived TEOAE (TEOAE_nl) includes both a short-latency (SL) portion with shallow phase gradient and a long-latency (LL) portion with steep phase gradient. The contribution of each portion to the total TEOAE_nl changes with stimulus level, shifting primarily from the LL portion at low levels to the SL portion at higher levels. These observations led Withnell and McKinley to hypothesize that the dominant mechanism underlying TEOAE_nl generation depended on stimulus level, with a place-fixed mechanism at low levels (i.e., linear coherent reflection, LCR; Zweig and Shera 1995; Shera and Guinan 1999) and a wave-fixed mechanism at higher levels (i.e., IMD).

In humans, multiple studies have demonstrated that the TEOAE (both linear- and nonlinear-derived) also includes SL and LL portions (or components), seemingly analogous to those in the guinea pig (Withnell et al. 2008; Goodman et al. 2009; Goodman et al. 2011; Moleti et al. 2012a). As such, IMD has been hypothesized as the underlying generation mechanism. However, SL components have also been observed in the stimulus-frequency (SF) OAE, with latencies and growth rates that approximate the SL TEOAE components (Sisto et al. 2013). The presence of these components in the SFOAE suggests that SL generation depends primarily on the stimulus energy at the frequency of the emission itself and not on interactions between stimulus frequencies remote from that of the emission. Thus, if the SL SFOAE and TEOAE components are analogous, generation through IMD due to nonlinear interactions between different frequencies within the transient stimulus’ bandwidth seems unlikely.

The current study examined the effect of tone burst duration and, therefore, spectral bandwidth on the nonlinear-derived 2-kHz band tone-burst-evoked OAE (TBOAE_nl) to test the hypothesis that IMD is a primary contributor to SL OAE_nl components evoked by stimuli with broad spectral bandwidths. The TBOAE_nl was evoked by 2-kHz tone bursts with durations of 3, 6, 12, and 24 cycles (1.5, 3, 6, and 12 ms, respectively). Each doubling of tone burst duration resulted in a halving of spectral bandwidth, such that the tone burst changed from resembling a band-limited acoustic click at 3 cycles to a pure tone by 24 cycles. Each tone burst was presented across a range of levels. To facilitate comparison between the different TBOAE_nl, tone burst stimuli were calibrated to account for level differences resulting from their different spectral bandwidths (Prieve et al. 1996; Kalluri and Shera 2007a). SL components were hypothesized to contribute to the 3-cycle TBOAE_nl, possibly due to IMD resulting from the broad bandwidth of the 3-cycle tone burst. As tone burst duration increased and spectral bandwidth decreased, the contribution of SL components to the TBOAE_nl was expected to decrease, if IMD was the primary generator.

METHODS

Subjects

Thirteen subjects (8 female, 5 male) between the ages of 18–29 years old participated in the study. All subjects had normal hearing thresholds (≤20 dB HL) at the octave frequencies between 0.25 and 8 kHz in the test ear (8 right ears, 5 left ears) and normal middle ear function (assessed through 226-Hz tympanometry). Data collection was completed over the course of a single 2-h visit. The University of Iowa Institutional Review Board approved the research protocol.

Signal Generation and Data Acquisition

Two-channel stimuli were digitally created at a 44.1-kHz sampling rate using custom-written MATLAB (The Mathworks, Inc.) software and a personal computer (PC) running the Windows (Microsoft, Inc.) operating system. Stimuli were routed from the PC to an external 24-bit soundcard (UltraLite-mk3 Hybrid, Mark of the Unicorn) through a USB 2.0 interface. The resulting two-channel electrical signal was directed through a pair of earphones (Sennheiser IE8) attached by silicone tubing to the receiver ports of an ER10B+ probe assembly (Etymotic Research, Inc.). The ER10B+ probe assembly was coupled to the ear canal by an ER10-14 foam eartip. The ear canal pressure responses were transduced into an electrical signal by a miniature microphone housed in the ER10B+ probe assembly. The microphone voltage was amplified 20 dB by the ER10B+ preamplifier, routed to the external soundcard, and digitized at a sampling rate of 44.1 kHz. The digital signal was stored on the PC hard drive for offline analysis. Signal presentation and data acquisition were controlled by MATLAB using custom-written software.

Measurement and Analysis of TBOAE_nl

Stimuli

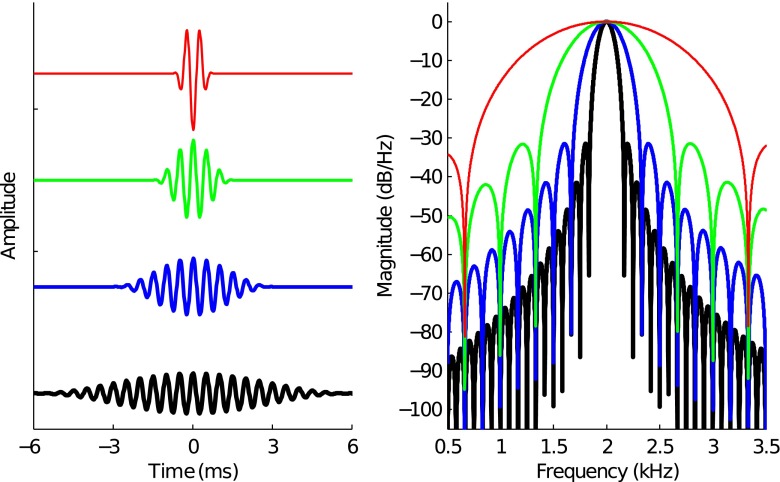
TBOAE was evoked using 2-kHz tone bursts with durations of 3, 6, 12, and 24 cycles (see Fig. 1). Tone bursts were generated in cosine phase and hann-windowed. Each doubling of duration resulted in a halving of the tone burst bandwidth. The bandwidths (defined by the low- and high-cut frequencies at −3 dB re 2 kHz) of the 3-, 6-, 12-, and 24-cycle tone bursts were 1.52–2.48 kHz (2 kHz ± 1/3 octave), 1.76–2.24 kHz (2 kHz ± 1/6 octave), 1.88–2.12 kHz (2 kHz ± 1/12 octave), and 1.94–2.06 kHz (2 kHz ± 1/24 octave), respectively.

FIG. 1.

Time- and frequency-domain representations of the 2-kHz tone burst stimuli. The left panel shows the waveforms for the 3-, 6-, 12-, and 24-cycle tone bursts. The right panel shows the corresponding spectra. Line thickness is used to show increasing number of cycles in the tone burst.

Calibration

Tone bursts were presented at eight levels (6-dB steps). To equate the stimulus levels across the different duration tone bursts (Prieve et al. 1996; Kalluri and Shera 2007a), stimulus levels were specified in terms of the level-per-cycle magnitude (dB re 1-Hz bandwidth or dB/Hz) at 2 kHz. The different duration tone bursts were first designed to have peak amplitudes of 1 (electrical units). Tone bursts were then transformed to the frequency domain via the fast Fourier transform (FFT). The size of the FFT depended on the length of the tone burst; therefore, the number and width of the frequency bins were different for each tone burst stimulus. For a given tone burst duration, the magnitude within each frequency bin was divided by the bandwidth of the bin. The magnitude spectra of the different tone bursts were compared, and scaling factors were derived relating the 2-kHz magnitude (dB/Hz) of the 3-, 6-, and 12-cycle tone bursts to that of the 24-cycle tone burst. When this was done, the scaled tone bursts had peak sound pressure levels (pSPL) of 44–86 dB pSPL (3 cycles; 6-dB steps), 41–83 dB pSPL (6 cycles), 38–80 dB pSPL (12 cycles), and 35–77 dB pSPL (24 cycles), in a calibration cavity (see below). When expressed in terms of 2-kHz level-per-cycle, these dB pSPL levels corresponded to 7–49 dB/Hz (6-dB steps).

The amplitudes of the tone bursts were calibrated in terms of the pressure generated in a long, plastic tube (2-m length, 7-mm inner diameter) terminated by a steel bearing. The long-tube calibration technique was chosen because it is insensitive to standing wave effects that are present in traditional in situ dB SPL ear canal calibrations (Sachs and Burkhard 1972; Stinson et al. 1982; Gilman and Dirks 1986). Additionally, the maximum voltage drive to the transducer is strictly controlled, and the possibility of inadvertently overdriving the transducers is eliminated. This technique has been described previously (Goodman et al. 2009). Briefly, the probe tip is placed into the long tube, and stimuli are presented and recorded repeatedly. The pressure recorded for each stimulus presentation includes the incident pressure delivered by the probe and multiple reflections resulting from the stimulus pressure traveling back and forth between the two ends of the tube. With each round trip, the amplitude of the reflected stimulus pressure is attenuated and eventually falls into the noise floor. In order to isolate the incident pressure delivered by the probe to the tube, it is necessary to use a short-duration stimulus and a slow stimulus repetition rate.

Sixty-four repetitions of a 10-ms, hann-windowed 2-kHz tone burst were delivered to the calibration tube at a rate of 1 per second and recorded. Recordings were highpass filtered using a finite impulse response (FIR) digital filter (250 Hz cut, 256 order). Only the initial 10 ms of each filtered recording was retained. The pressure measured in this time window described the incident pressure delivered by the transducer to the tube and was thus free from internal reflections occurring at the distal end of the tube and propagating back toward the microphone. The amplitudes of the electrical tone burst stimuli were adjusted to yield output levels (as measured in the long tube) at the levels described above.

Presentation

Stimuli were presented using an equal-level, double-evoked, double-source paradigm (Keefe 1998; Keefe and Ling 1998; Schairer et al. 2003). A stimulus buffer was composed of three consecutive stimulus intervals (s₁, s₂, and s_1,2). Each interval was 40 ms long resulting in a total buffer duration of 120 ms. Stimulus interval s₁ contained the tone burst (of level L₁ where L₁ = 7–49 dB/Hz SPL; 6-dB steps) and was routed through channel 1 of the transducer. Stimulus interval s₂ contained the same tone burst as s₁ (L₂ = L₁), but routed through channel 2 of the transducer. Tone bursts were presented simultaneously through channels 1 and 2 of the transducer for s_1,2. The number of stimulus buffers presented depended on the tone burst level, with more presentations for lower level tone bursts to improve the signal-to-noise ratio (SNR) of the evoked emission upon averaging. Two thousand buffers were presented for levels between 7 and 19 dB/Hz SPL, 1,600 were presented for levels between 25 and 37 dB/Hz SPL, and 1,200 were presented for levels between 43 and 49 dB/Hz SPL.

Analysis

Ear canal pressure recordings for each stimulus buffer were divided into three time segments (p₁, p₂, and p_1,2) corresponding to the three stimulus intervals (s₁, s₂, and s_1,2). Each recording was the sum of pressure waves associated with the stimulus, physiological and environmental noise, and the OAE. The nonlinear differential pressure (p_D) was subsequently calculated

$$p_D=p_1+p_2-p_{1,2}\text{.}$$ 1

The primary advantage of the double-evoked extraction is that p_D is free from stimulus contamination, assuming transducer linearity. Stimulus contamination is especially problematic in OAE measurements where (1) the frequency of the stimulus and emission is identical and (2) the duration of the stimulus is sufficiently long (whether by design or due to artifact) that the stimulus and emission overlap in time. Both of these conditions applied to the current study since (1) the evoking stimuli were 2-kHz tone bursts and the 2-kHz band of the emission was analyzed and (2) the durations of the tone bursts extended from 1.5 to 12 ms and overlapped with the expected latency range of the 2-kHz band TBOAE (approximately 3–12 ms, depending on stimulus level; Tognola et al. 1997; Sisto and Moleti 2007; Rasetshwane et al. 2013).

A consequence of the double-evoked extraction is that the extracted OAE pressure will not always accurately describe the total OAE pressure evoked by the s₁ stimulus ($p_{1_{\mathit{OAE}}}$). In other words, only a portion of the evoked OAE is extracted (Schairer et al. 2003; Kalluri and Shera 2007b). Theoretically, specifying the level of the s₂ stimulus (L₂) so that it corresponds to the saturating portion of the OAE input-output (I/O) function will minimize inaccuracy in the extraction. However, specifying L₂ to correspond to the saturating portion of the I/O function is not always feasible as a high L₂ may result in excessive nonlinear transducer distortion and/or high physiological noise levels relative to the noise levels associated with the lower L₁ (Schairer et al. 2003). Additionally, it is typically not immediately obvious as to the L₂ associated with saturation of the I/O function. This is especially true for the different latency components in TEOAEs, as they exhibit different growth rates and level dependencies such that the L₂ associated with saturation for an LL component may not necessarily result in saturation for an SL component (Moleti et al. 2012a).

Preliminary data for the study was collected with L₂ set 12 dB higher than L₁. However, this paradigm precluded measurement of the early time portion of 3-cycle TBOAE at high stimulus levels as noncanceling stimulus artifact generated by the s₂ tone burst contaminated this part of the recording. Since IMD is thought to contribute to the early time portion of the emission at high stimulus levels, it was important to retain as much of this portion of the emission at the highest possible stimulus levels. Subsequent data collected using an equal-level paradigm (i.e., L₂ = L₁) permitted measurement of earliest portions of the TBOAE_nl across a wider range of L₁ that extended to higher stimulus levels. Therefore, the equal-level paradigm was used for the current study.

To reduce filter artifact, the initial and final 5 ms of p_D were ramped on and off, respectively, using a 1/2-cycle Hann function. The windowed responses were then highpass filtered using an FIR digital filter (250 Hz cut, 128 order). The root-mean-square (RMS) levels of the filtered responses were calculated and subjected to an artifact rejection algorithm (Goodman et al. 2009; see Hoaglin et al. 1983) in order to identify recordings contaminated by high levels of intermittent noise. Briefly, the first and third quartiles of the RMS levels were calculated, and the interquartile range was derived. Recordings with an RMS exceeding the third quartile by more than 1.5 times the interquartile range were excluded from further analysis.

Retained responses were filtered using a 1/3 octave bandpass FIR digital filter (2-kHz center frequency, 512 order). The K filtered responses were synchronously averaged in the time domain to yield an estimate of the nonlinear (nl)-derived 2-kHz band TBOAE (${\overline{p}}_{\mathit{OA}{E}_{\mathit{nl}}}\left[n\right]$, n indicates the sample number),

$${\overline{p}}_{\mathit{OA}{E}_{\mathit{nl}}}\left[n\right]=\frac{1}{K}{\displaystyle \sum _{k=1}^K}{p}_D\left[n,k\right]\text{.}$$ 2

The analytic expression of ${\overline{p}}_{\mathit{OA}{E}_{\mathit{nl}}}$ (${\widehat{\overline{p}}}_{\mathit{OA}{E}_{\mathit{nl}}}$) was calculated using the discrete Hilbert transform (denoted by ℋ),

$${\widehat{\overline{p}}}_{\mathit{OA}{E}_{\mathit{nl}}}\left[n\right]={\overline{p}}_{\mathit{OA}{E}_{\mathit{nl}}}\left[n\right]+j\mathit{H}\left({\overline{p}}_{\mathit{OA}{E}_{\mathit{nl}}}\left[n\right]\right)\text{.}$$ 3

From the analytic signal, the instantaneous magnitude ($\left|{\widehat{\overline{p}}}_{\mathit{OA}{E}_{\mathit{nl}}}\right|$), or envelope, was calculated as

$$\left|{\widehat{\overline{p}}}_{\mathit{OA}{E}_{\mathit{nl}}}\left[n\right]\right|=\sqrt{\mathit{Re}{\left({\widehat{\overline{p}}}_{\mathit{OA}{E}_{\mathit{nl}}}\left[n\right]\right)}^2+\mathit{Im}{\left({\widehat{\overline{p}}}_{\mathit{OA}{E}_{\mathit{nl}}}\left[n\right]\right)}^2}\text{.}$$ 4

An estimate of the time-domain noise was calculated as the standard error of the mean of the instantaneous magnitude. First, the analytic signal of each individual nonlinear differential response was computed,

$${\widehat{p}}_D\left[n,k\right]=p_D\left[n,k\right]+\mathit{jH}\left(p_D\left[n,k\right]\right)\text{.}$$ 5

The mean instantaneous magnitude ($\left|{\widehat{\overline{p}}}_D\right|$) was subsequently calculated,

$$\left|{\widehat{\overline{p}}}_D\left[n\right]\right|=\frac{1}{K}{\displaystyle \sum _{k=1}^K}\left|{\widehat{p}}_D\left[n,k\right]\right|\text{.}$$ 6

and the noise was computed as the standard error of the mean (SEM),

$$\mathit{SEM}\left[n\right]=\frac{1}{\sqrt{K}}\sqrt{\frac{1}{K-1}{\displaystyle \sum _{k=1}^K}{\left(\left|{\widehat{p}}_D\left[n,k\right]\right|-\left|{\overline{\widehat{p}}}_D\left[n\right]\right|\right)}^2}$$ 7

The TBOAE_nl signal and noise estimates were constrained to an analysis window extending from stimulus onset to stimulus offset, plus an additional 10 ms. This resulted in different duration analysis windows for each tone burst stimulus (3 cycles: 11.5 ms, 6 cycles: 13 ms, 12 cycles: 16 ms, 24 cycles: 22 ms). The 10-ms post-stimulus offset was chosen as it approximates the longest expected latency for a low-level 2-kHz reflection source OAE (Neely et al. 1988; Tognola et al. 1997; Shera and Guinan 2003; Sisto et al. 2007). A time vector was mapped to each analysis window with time 0 corresponding to the peak of the tone burst stimulus.

TBOAE_nl magnitude ($L_{\mathit{OA}{E}_{\mathit{nl}}}$) was calculated as the RMS of the weighted TBOAE envelope within the analysis window,

$$L_{\mathit{OA}{E}_{\mathit{nl}}}=20\mathit{lo}{g}_{10}\left(\frac{1}{N}\sqrt{{\displaystyle \sum _{n=0}^{N-1}}\left(w\left[n\right]{\left|{\widehat{\overline{p}}}_{\mathit{OA}{E}_{\mathit{nl}}}\left[n\right]\right|}^2\right)}/0.00002\right)\text{.}$$ 8

The weighting function (w) applied a binary weight to each sample (n) of the windowed TBOAE_nl and depended on the instantaneous SNR,

$$\mathit{SNR}\left[n\right]=20{log}_{10}\left(\frac{\left|{\widehat{\overline{p}}}_{\mathit{OA}{E}_{\mathit{nl}}}\left[n\right]\right|}{\mathit{SEM}\left[n\right]}/0.00002\right)\text{,}$$ 9

according to

$$w\left[n\right]=\left\{\begin{array}{c}\hfill 1\mathit{for}\mathit{SNR}\left[n\right]\ge 11\hfill \\ \hfill 0\mathit{for}\mathit{SNR}\left[n\right]<11\hfill \end{array}\right.\text{.}$$ 10

Additionally, in order for a sample with an SNR >11 to receive a weighting of 1, the adjacent 21 samples (corresponding to a full cycle of a 2-kHz wave) also had to have an SNR >11. This constraint minimized contributions from samples that were more likely noise than OAE energy. The 11-dB SNR criterion was established by calculating the SNR at which the probability of a false positive (classifying noise as signal) was less than 5 %. Criteria were initially established for each stimulus level as the number of averages (K) across levels were not constant (K = 1,200, 1,600, or 2,000). K, 1-s long, randomly generated number sequences were created using MATLAB’s normally distributed pseudorandom number generator function. Sequences were filtered using the same highpass and bandpass filters that were applied to the ear canal pressure recordings. The mean instantaneous magnitude and standard error of the mean were calculated (see Eqs. 4 and 7). The former represented an estimate of the signal and the later represented an estimate of the noise. The empirical distribution function (EDF) for each value of K was determined and fit using a cubic spline interpolant. The SNR corresponding to a false-positive rate of 5 % was similar across all values of K and occurred between 10.8 and 11.06 dB SNR. Consequently, a criterion of 11 dB SNR was chosen and used for all stimulus levels.

Compared to calculating TBOAE_nl magnitude from the time-domain waveform (as is traditionally done), magnitude defined from the envelope is 3 dB larger. The origin of this difference is the inclusion of the imaginary part of the analytic signal when calculating the TBOAE_nl envelope (see Eq. 4). Compared to the real part of the analytic signal, the imaginary part has the same amplitude but differs in phase by π/2 radians. Summing the squared real and imaginary parts of the analytic signal results in a doubling of intensity and, therefore, a 3-dB increase in the RMS of the TBOAE_nl envelope compared to that of the TBOAE_nl waveform.

TBOAE_nl latency (${\tau }_{\mathit{OA}{E}_{\mathit{nl}}}$) was also defined using the TBOAE_nl envelope and weighting function,

$${\tau }_{\mathit{OA}{E}_{\mathit{nl}}}=\frac{{\displaystyle {\sum }_{n=0}^{N-1}}\left(w\left[n\right]{\left|{\widehat{\overline{p}}}_{\mathit{OA}{E}_{\mathit{nl}}}\left[n\right]\right|}^{2}t\left[n\right]\right)}{{\displaystyle {\sum }_{n=0}^{N-1}}\left(w\left[n\right]{\left|{\widehat{\overline{p}}}_{\mathit{OA}{E}_{\mathit{nl}}}\left[n\right]\right|}^2\right)}\text{,}$$ 11

where t was the time vector for the analysis window (ms). This definition quantifies latency as the energy-weighted mean of the time vector and gives greatest weight to time indices corresponding to peaks in the TBOAE_nl envelope, where the SNR is the largest. Attributing greatest weight to high-SNR regions of TBOAE_nl reduces the variability of the OAE latency measure (Shera and Bergevin 2012).

RESULTS

TBOAE_nl Envelopes

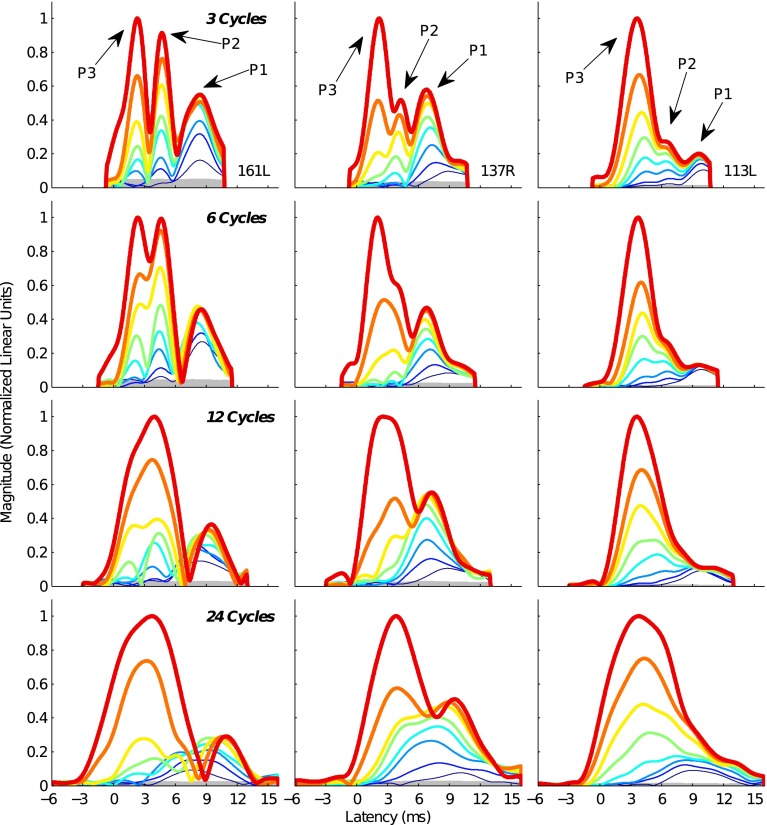
Figure 2 shows the TBOAE_nl envelopes evoked by each tone burst stimulus for three representative subjects (arranged in columns). In each plot, the magnitudes of the envelopes have been normalized relative to the peak magnitude of the envelope evoked by the highest-level tone burst (49 dB/Hz SPL). Similarly, time has been specified relative to the peak of the evoking tone burst (resulting in negative time values). The TBOAE_nl envelopes for the 3-cycle tone bursts (top row) typically exhibited three different latency peaks (P1, P2, and P3). At the lowest stimulus levels, only the longest-latency peak (P1) was present above the noise floor. As stimulus level increased, several earlier, less-compressive growing magnitude peaks emerged (e.g., P2 and P3). The differential growth rates between the peaks often resulted in the largest magnitude peak shifting from the longest-latency peak at low stimulus levels to the shorter-latency peaks at high stimulus levels. The temporal location of each magnitude peak remained nearly constant with stimulus level.

FIG. 2.

TBOAE_nl envelopes from 3 representative subjects. Columns show envelopes for an individual subject, and rows show envelopes for a given tone burst duration (row 1/top row—3 cycles, row 2–6 cycles, row 3–12 cycles; row 4/bottom row—24 cycles). Increasing line thickness shows increasing tone burst level. Arrows indicate the different latency peaks identified in the 3-cycle TBOAE_nl. The shaded gray region indicates the noise floor.

The 6-cycle TBOAE_nl envelopes (second row) resembled those for the 3-cycle tone burst, although they spanned a wider time range as a consequence of the increased duration of the evoking stimulus. These envelopes were also characterized by a series of different latency magnitude peaks. Three peaks were generally apparent in the 6-cycle TBOAE_nl envelopes, with only the longest-latency peak present at low stimulus levels and less-compressive growing shorter-latency peaks emerging at higher stimulus levels. The less-compressive growth of the earlier peaks resulted in their magnitudes exceeding that of the longest-latency peak at the highest stimulus levels. The temporal locations of the peaks were similar to the peaks in the 3-cycle TBOAE_nl envelopes. The 6-cycle TBOAE_nl peaks were generally more poorly resolved in time than those of the 3-cycle tone burst. For instance, in subject 137R (middle column), the P2 and P3 peaks that were evident for the 3-cycle TBOAE_nl merged into a single peak in the 6-cycle TBOAE_nl. The envelopes for the other subjects showed a similar decrease in the resolution of the shorter-latency peaks.

Compared to the shorter-duration tone bursts, the 12-cycle TBOAE_nl envelopes (third row) were more dispersed across time, consistent with the longer duration of the evoking stimulus. Despite the narrower bandwidth of the 12-cycle tone burst, the TBOAE_nl exhibited characteristics similar to the 3- and 6-cycle TBOAE_nl. First, only a longer-latency peak was observed at the lowest stimulus levels. Second, at least one shorter-latency peak emerged as stimulus level increased. Third, the shorter-latency peak(s) grew less compressively than the longer-latency peak. And fourth, the largest magnitude peak shifted from the longer-latency peak at low stimulus levels to the shorter-latency peak(s) at high stimulus levels. Multiple peaks occurring earlier in time than the longest-latency peak were not typically evident in the 12-cycle TBOAE_nl envelopes. Rather, a single peak was observed across the same latency range where two seemingly distinct peaks were present in the 3- and 6-cycle TBOAE_nl envelopes (e.g., subjects 161L and 137R).

When the tone burst duration was increased to 24 cycles (fourth row), the TBOAE_nl still exhibited characteristics consistent with contributions from earlier- and later-occurring TBOAE_nl energy. As was observed in the TBOAE_nl envelopes evoked by the shorter-duration stimuli, the peak with the largest magnitude shifted to a shorter latency as stimulus level increased. Moreover, these envelopes were characteristic of destructive phase interactions between at least two components that partially overlapped in time (Talmadge et al. 1999). For instance, the envelopes for subject 161L exhibited a sharp magnitude null between 6 and 10 ms (depending on stimulus level).

Different Latency TBOAE_nl Components

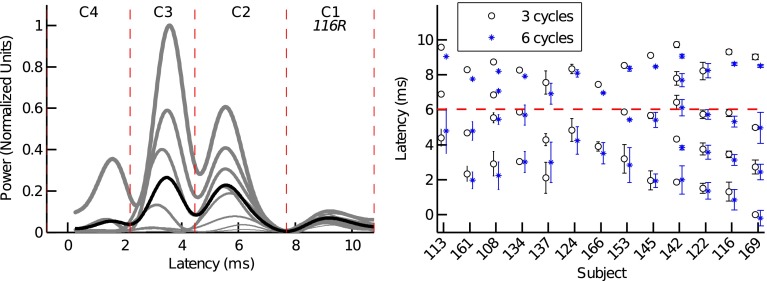
The temporal resolution of the different latency magnitude peaks in the 3- and 6-cycle TBOAE_nl envelopes allowed for these TBOAE_nl to be divided into different latency components. First, the 3- and 6-cycle TBOAE_nl instantaneous magnitudes (i.e., envelopes) were transformed to instantaneous power (by squaring the envelopes) and the mean power envelopes (averaged across stimulus levels) were calculated for each subject. Second, a peak-picking algorithm was used to identify the time indices of magnitude peaks and nulls from the mean envelopes. A “component” was defined as the portion of the TBOAE_nl within a time window that spanned adjacent magnitude nulls. The magnitude and latency of each component were calculated according to Eqs. 8 and 11, respectively. However, for each component, the weighting function (i.e., w[n], Eq. 10) was adjusted such that all samples of the envelope falling outside of the temporal window of the component were set to 0. The left panel of Figure 3 provides an illustration of the different latency components identified from the 3-cycle TBOAE_nl for subject 116R. Four components were identified for this subject (C1, C2, C3, and C4).

FIG. 3.

Different latency components in the 3- and 6-cycle TBOAE_nl. The left panel illustrates how different latency components (i.e., C1, C2, C3, and C4) were defined (data is shown for the 3-cycle TBOAE_nl from subject 116R). Gray lines are the TBOAE_nl envelopes evoked for different stimulus levels (denoted by line thickness). The black line is the mean envelope from which the time boundaries of the different latency components were defined (indicated by the dashed lines). The right panel plots the mean latencies (±1 standard deviation) of the different latency components identified in the 3- (circles) and 6-cycle (asterisks) TBOAE_nl, for all subjects. In some cases, the standard deviations were sufficiently small that error bars are not apparent. The horizontal dashed line is at a latency of 6.03 ms and was the latency boundary chosen for separating SL from LL components.

The right panel of Figure 3 shows the mean latencies (and standard deviations) of all components identified for each subject, for the 3- (circles) and 6-cycle (asterisks) TBOAE_nl. Between 2 and 5 components were identified across subjects for both the 3- and 6-cycle TBOAE_nl. Most of the components had latency falling within a range from 1 to 10 ms. The latency of each component exhibited only small changes with stimulus level, as indicated by the width of the error bars. The approximate level invariance of different latency components has previously been observed in the TE and SFOAE (e.g., Goodman et al. 2011; Sisto et al. 2013). On average, a factor of 1.76 (standard deviation = 0.42) and 1.86 (0.56) separated the latencies of adjacent components in the 3- and 6-cycle TBOAE_nl, respectively. This is similar to the factor of approximately 1.6 observed by Goodman et al. (2009) and Moleti et al. (2012a) between the SL and LL component in the TEOAE. Within each subject, both the number of components and each component’s latency for the 6-cycle TBOAE_nl were similar to those for the 3-cycle TBOAE_nl. For instance, 4 components were identified in both the 3- and 6-cycle TBOAE_nl for subject 122R; the 3-cycle TBOAE_nl latencies were 1.51, 3.76, 5.73, and 8.22 compared to the 6-cycle TBOAE_nl latencies of 1.36, 3.57, 5.73, and 8.24, respectively. In two subjects (113L and 137R), 3 components were identified in the 3-cycle TBOAE_nl, but only 2 components were identified in the 6-cycle TBOAE_nl. For these subjects, the two earliest-occurring components in the 3-cycle TBOAE_nl have merged into a single component in the 6-cycle TBOAE_nl (consistent with observations from Figure 2), as evidenced by the standard deviation of the 6-cycle component spanning the latencies of the two 3-cycle components.

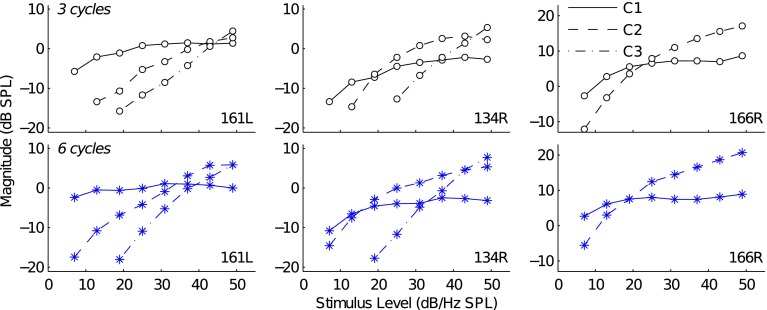
For each subject, components with similar latencies between the 3- and 6-cycle TBOAE_nl also exhibited similar I/O functions. Figure 4 plots the I/O functions of the different latency components in the 3- (top row of panels) and 6-cycle (bottom row of panels) TBOAE_nl, measured in 3 representative subjects. Components are identified based on their relative latencies with C1 indicating the longest-latency component, C2 indicating the component earlier-in-time and adjacent to C1, and C3 indicating the component earlier-in-time and adjacent to C2. In all cases, the component with the largest magnitude shifted from C1 at low-to-moderate stimulus levels to C2 at higher levels and, in certain cases (subject 134R), to C3 at the highest levels. This observed shift was a consequence of the less-compressive growth of the earlier-occurring components.

FIG. 4.

3- and 6-cycle TBOAE_nl component I/O functions for three representative subjects (161L, 134R, and 166R). The top and bottom row of panels show I/O functions for the 3- and 6-cycle TBOAE_nl, respectively. Each column shows data for a single subject. Line style denotes the component where C1 corresponds to the longest-latency component, C2 corresponds to the component earlier-in-time and adjacent to C1, and C3 (when present) corresponds to the component earlier-in-time and adjacent to C2.

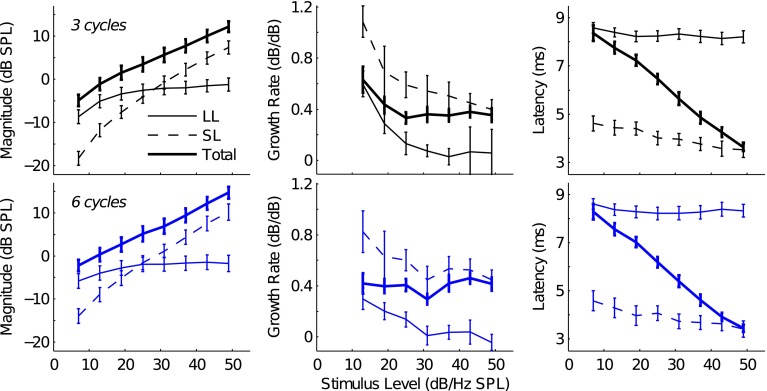
To avoid a somewhat arbitrary grouping and across-subject analysis of the different latency components based on their label (i.e., C1 and C2), components were instead grouped according to their latency relative to that expected for a 2 kHz OAE generated through LCR near the tonotopic place. From low-level SFOAE latency data reported in Shera and Guinan (2003; Table 1), a 2-kHz emission latency of less than 6.03 ms is expected only 5 % of the time. This criterion was adopted to separate the different latency components into either SL or LL categories (indicated by the horizontal broken line in the right panel of Fig. 3). The magnitudes (μPa) and latencies of all components categorized as SL components were averaged across subjects at each stimulus level to quantify the level dependence of SL TBOAE_nl magnitude and latency. The same was done with all components categorized as LL components to quantify the level dependence of the LL TBOAE_nl. Group data (I/O, growth rate, and latency-intensity functions) for the 3- and 6-cycle SL and LL TBOAE_nl are presented in the top and bottom rows of panels, respectively, in Figure 5.

FIG. 5.

Mean 3- and 6-cycle SL, LL, and total TBOAE_nl I/O, growth rate, and latency-intensity functions. The top and bottom row of panels show data for the 3- and 6-cycle TBOAE_nl, respectively. I/O functions are plotted in the left column, growth rate functions are plotted in the middle column, and latency-intensity functions are plotted in the right column. Error bars indicate the standard error. Line style denotes the SL, LL, and total TBOAE_nl.

The top left panel of Figure 5 plots the mean I/O functions (across subjects; error bars indicate the standard error) for the 3-cycle SL and LL TBOAE_nl. At low stimulus levels, the LL TBOAE_nl had the largest magnitude; however, as stimulus level increased, the magnitude of the SL TBOAE_nl eventually exceeded that of the LL TBOAE_nl. The top middle panel of Figure 5 plots the mean 3-cycle SL and LL TBOAE_nl growth rates as a function of stimulus level. Growth rates were calculated by differentiating the I/O functions. Both the LL and SL magnitudes grew increasingly compressively as stimulus level increased: The growth rate of the LL TBOAE_nl decreased from 0.60 to 0.06 dB/dB while the growth rate of the SL TBOAE_nl decreased from 1.09 to 0.40 dB/dB.

The mean latencies of the 3-cycle SL and LL TBOAE_nl are plotted as a function of stimulus level in the top right panel of Figure 5. The latency of the LL TBOAE_nl was approximately independent of stimulus level. In contrast, the latency of the SL TBOAE_nl decreased from 4.62 to 3.52 ms as stimulus level increased from 7 dB/Hz SPL to 49 dB/Hz SPL. The near level invariance of LL TBOAE_nl latency mimics that observed in the individual components from Figure 3 and was presumably due to the fact that the LL TBOAE_nl generally included only a single LL component for each subject (subject 16R is one exception to this as this subject had 3 LL components). On the other hand, 2–3 SL components were typically included in the calculation of SL TBOAE_nl latency such that latency decreased as the distribution of TBOAE_nl energy shifted to progressively earlier-occurring components with increasing stimulus level. The mean latency of the LL TBOAE_nl across stimulus levels was 8.65 ms (standard deviation = 0.16) compared to 4.03 ms (±0.41) for the SL TBOAE_nl.

The bottom row of panels in Figure 5 plots analogous data to those data plotted in the top row, but for the 6-cycle TBOAE_nl. The I/O, growth rate, and latency-intensity functions for the 6-cycle SL and LL components resembled those for the 3-cycle SL and LL components. Growth rates for the 6-cycle LL TBOAE_nl decreased from 0.30 to −0.04 dB/dB across stimulus levels while growth rates for the SL TBOAE_nl decreased from 0.82 to 0.45 dB/dB. The mean latencies across stimulus levels of the LL and SL TBOAE_nl were 8.34 (±0.13) and 3.92 ms (±0.39), respectively.

Total TBOAE_nl I/O and Latency-Intensity Functions

Overlaid on the component-specific data in Figure 5 are the mean data for the 3- and 6-cycle TBOAE_nl analyzed across a time window spanning both the SL and LL components (thick solid lines). The TBOAE_nl analyzed across this time window is hereafter referred to as the total TBOAE_nl (or simply the TBOAE_nl). Comparing the level dependence of the magnitude and latency of the total TBOAE_nl to the SL and LL TBOAE_nl illustrates how the latter influences the former. Compared to the SL and LL TBOAE_nl (whether 3 or 6 cycles), the magnitude of the total TBOAE_nl was larger (left panels), which was to be expected since the total TBOAE_nl included the contributions from both SL and LL components. Similar to the magnitudes of the SL and LL TBOAE_nl, the magnitude of the total TBOAE_nl increased with stimulus level. Reflecting the changing contributions from the SL and LL portions, the growth rate of the total TBOAE_nl (middle panels) approximated that of the LL TBOAE_nl at the lowest stimulus levels (where this portion of the TBOAE_nl was dominant) but was closer to the growth rate of the SL TBOAE_nl at the highest stimulus levels (where this portion of the TBOAE_nl was dominant).

In contrast to the latencies of the SL and LL TBOAE_nl, which were roughly constant, the latency of the total TBOAE_nl depended on stimulus level (right panels of Fig. 5). Latency decreased from 8.35 to 3.63 ms for the 3-cycle TBOAE_nl and from 8.29 to 3.44 ms for the 6-cycle TBOAE_nl as stimulus level increased from 7 to 49 dB/Hz. The observed decrease in total TBOAE_nl latency was expected, given the I/O functions and latencies of the SL and LL TBOAE_nl. Specifically, the long latency of the total TBOAE_nl at low stimulus levels was consistent with the LL TBOAE_nl being the primary contributor to the TBOAE_nl. As stimulus level increased and the contribution from the SL TBOAE_nl increased, total TBOAE_nl latency decreased to approximate the latency of the SL TBOAE_nl. Stover et al. (1996) demonstrated a similar phenomenon underlying the level dependency of DPOAE latency.

The poorer temporal resolution of the 12- and 24-cycle TBOAE_nl envelopes precluded examination of potential contributions from SL and LL components and direct comparison with those in the 3- and 6-cycle TBOAE_nl. However, the data from Figure 5 suggested that contributions from SL and LL components to the TBOAE_nl might be deduced by analyzing the total TBOAE_nl. Specifically, if different latency components contributed to the 12- and 24-cycle TBOAE_nl to the same extent that they contributed to the 3- and 6-cycle TBOAE_nl, then, the magnitudes, growth rates, and latencies of the 12- and 24-cycle total TBOAE_nl should approximate those of the 3- and 6-cycle total TBOAE_nl.

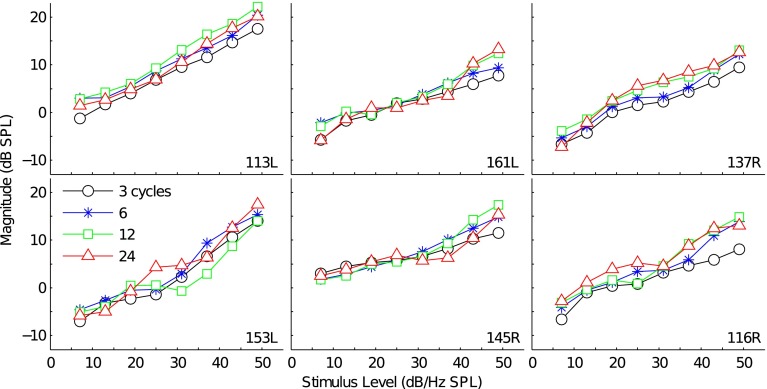
Figure 6 plots the 3-, 6-, 12-, and 24-cycle total TBOAE_nl I/O functions for 6 representative subjects. TBOAE_nl magnitudes of 3 and 6 cycles increased monotonically with stimulus level. For some subjects, the increase in TBOAE_nl magnitude for a given increase in stimulus level varied across the I/O function. For instance, both 3- and 6-cycle TBOAE_nl magnitudes for subjects 137R and 153L exhibited increasingly compressive growth through 25 dB/Hz SPL but grew less compressively at higher stimulus levels. In contrast to the 3- and 6-cycle TBOAE_nl I/O functions, the I/O functions for the 12- and 24-cycle TBOAE_nl occasionally exhibited nonmonotonic growth across certain stimulus levels. For instance, magnitude notches occur in the 12- and 24-cycle TBOAE_nl I/O functions for subject 116R at 25 dB/Hz SPL and 31 dB/Hz SPL, respectively. Magnitude notches have previously been observed in measured SFOAE_nl I/O functions (Schairer et al. 2003) and have been hypothesized as being indicative of destructive phase interactions between different components overlapping in time and/or shifts in the fine structure. Verhulst et al. (2012) similarly noted notches in the modeled, linear-extracted SFOAE; however, differences in the extraction paradigms may preclude direct comparisons between the notches reported here and in Schairer et al. to those in Verhulst et al. Aside from the notches, 12- and 24-cycle TBOAE_nl magnitudes generally increased with stimulus level, and the 3-, 6-, 12-, and 24-cycle TBOAE_nl I/O functions were similar within each subject.

FIG. 6.

I/O functions for the 3-, 6-, 12-, and 24-cycle total TBOAE_nl for 6 representative subjects. Each panel shows the functions for a single subject. Marker style denotes tone burst duration.

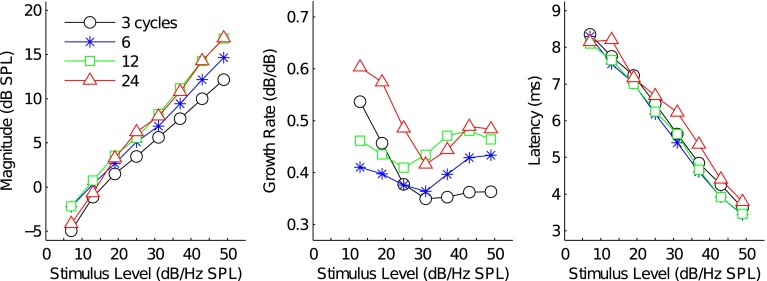
Figure 7 plots the mean I/O (left panel) and growth rate functions (middle panel) across subjects for the different TBOAE_nl. TBOAE_nl magnitudes were similar at each stimulus level. The largest difference was approximately 5 dB and occurred at 49 dB/Hz SPL between the 3-cycle and 24-cycle TBOAE_nl. Growth rate functions are shown in the middle panel and were derived by calculating the derivative of the I/O functions after first smoothing the I/O functions with a spline interpolant. The growth functions for the different TBOAE_nl all exhibited a region of increasingly compressive growth with increasing stimulus level that extended to between 25 and 31 dB/Hz SPL. At higher stimulus levels, the trajectory of the growth rate functions changed, and growth rates either remained nearly constant with increasing stimulus level (e.g., 3-cycle TBOAE_nl) or became less compressive. Recall that the increasing contribution from the SL component associated with increasing stimulus level was responsible for the change in the trajectory of the growth rate function for both the 3- and 6-cycle TBOAE_nl (see Fig. 5). Both the change in growth rates and similar magnitudes between the 12-/24-cycle TBOAE_nl and the 3-/6-cycle TBOAE_nl suggests that SL and LL components analogous to those in the TBOAE_nl evoked by the shorter-duration tone bursts also contributed to the TBOAE_nl evoked by the longer-duration tone bursts.

FIG. 7.

Mean I/O, growth rate, and latency-intensity functions for the 3-, 6-, 12-, and 24-cycle total TBOAE_nl. The left panel plots the I/O functions, the middle panel plots the growth rate functions, and the right panel plots the latency-intensity functions. Marker style denotes tone burst duration.

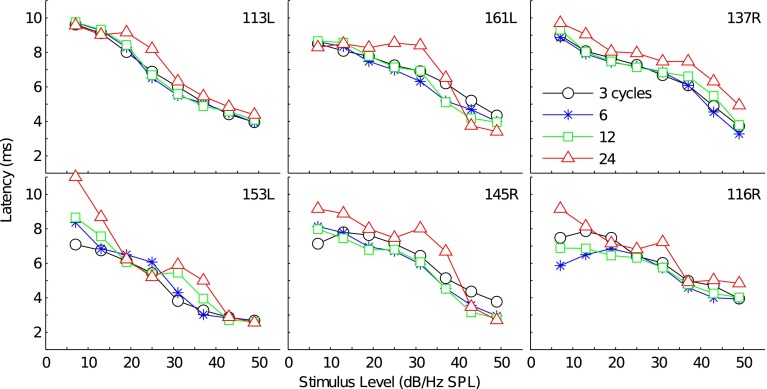
Figure 8 plots the total TBOAE_nl latency-intensity functions for the same subjects’ whose I/O functions were plotted in Figure 6. In most subjects and for the 3-, 6-, and 12-cycle tone bursts, total TBOAE_nl latency decreased monotonically with stimulus level. Additionally, the latencies for the 3-, 6-, and 12-cycle TBOAE_nl were comparable at each stimulus level. Similar to the latencies for the TBOAE_nl evoked by the shorter-duration tone bursts, latency for the 24-cycle TBOAE_nl generally decreased as stimulus level increased. However, in several subjects and across a portion of the latency-intensity function, latency either remained nearly constant or increased as stimulus level increased (e.g., subjects 161L and 145R, respectively), thereby causing these latencies to deviate from those for the TBOAE_nl evoked by the shorter-duration tone bursts. Within these same subjects’ functions, latencies often exhibited a rapid decrease as stimulus level continued to increase and eventually approximated the latencies for the shorter-duration tone bursts at the highest stimulus levels.

FIG. 8.

Latency-intensity functions for the 3-, 6-, 12-, and 24-cycle total TBOAE_nl for 6 representative subjects. Subjects are the same as those presented in Figure 6. Each panel shows the functions for a single subject. Marker style denotes tone burst duration.

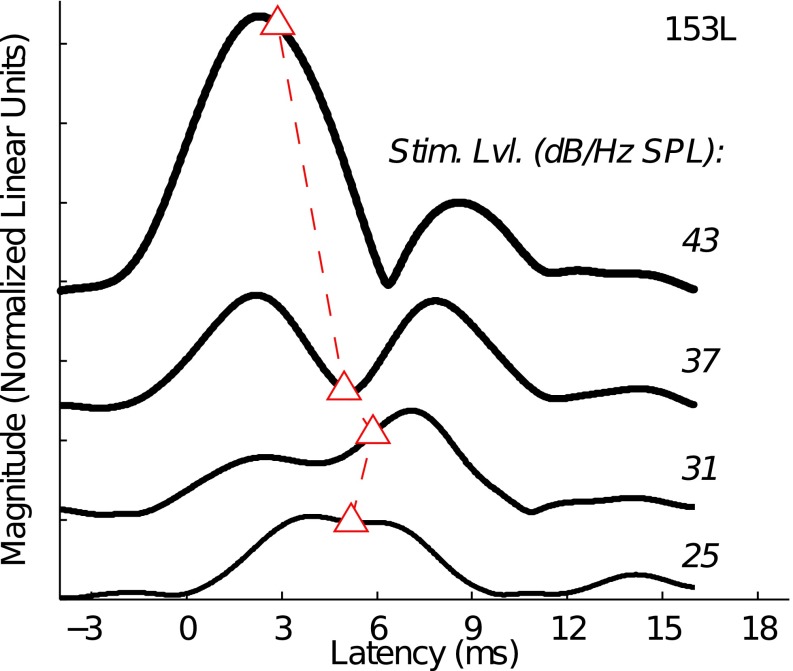
The irregular changes in 24-cycle TBOAE_nl latency across certain stimulus levels were typically associated with the emergence of a shorter-latency magnitude peak in the TBOAE_nl envelope. Figure 9 plots the 24-cycle TBOAE_nl envelopes for subject 153L at stimulus levels from 25 to 43 dB/Hz SPL, where the latency-intensity function for the 24-cycle TBOAE_nl deviated from those for the 3-cycle TBOAE_nl. Overlaid on each envelope is the latency calculated from Eq. 11. As stimulus level increased from 25 to 31 dB/Hz, the dominant magnitude peak that was initially centered around 5 ms split into two peaks, which had the effect of slightly increasing TBOAE_nl latency. It was this increase in latency that caused the latency-intensity function to deviate from those for the shortest-duration tone bursts. As stimulus level continued to increase, TBOAE_nl latency approximated the time index of the shorter-latency peak and the latency-intensity function approached those for the TBOAE_nl evoked by the shorter-duration tone bursts.

FIG. 9.

Illustration of the association between an emerging SL peak and an increase in 24-cycle TBOAE_nl latency (subject 153L). TBOAE_nl envelopes are shown for stimulus levels between 25 and 43 dB/Hz SPL. Triangles correspond to the calculated latency of each envelope. As stimulus level increased, a SL peak emerged at 31 dB/Hz SPL. The emergence of this peak was associated with a slight increase in TBOAE_nl latency.

The right panel of Figure 7 plots the mean latency-intensity functions for each tone burst stimulus. Latencies were similar between the different TBOAE_nl at each stimulus level. As stimulus level increased, latencies decreased from 8.35 to 3.63, 8.29 to 3.44, 8.10 to 3.47, and 8.15 to 3.80 ms for the 3-, 6-, 12-, and 24-cycle TBOAE_nl, respectively. To quantify the level dependency of TBOAE_nl latency, each function was fit by a first-order polynomial. Latencies decreased with increasing stimulus levels at rates of 0.116 ms/dB (5th–95th % confidence bounds ± 0.0123), 0.119 ms/dB (±0.0116), 0.116 ms/dB (±0.013), and 0.11 ms/dB (±0.0195). These rates correspond to approximately 0.2 cycles/dB when expressed relative to the period of a 2-kHz wave. Similar rates are observed in TEOAE_nl data from Sisto and Moleti (2007), TBOAE_nl data from Rasetshwane et al. (2013), and cochlear reflectance data from Rasetshwane and Neely (2012). In the SFOAE_nl, Schairer et al. (2006) reported approximately a 50 % decrease in latency across a 30-dB increase in stimulus level, which is similar to that observed in the TBOAE_nl (e.g., the median 24-cycle TBOAE_nl latency decreased from 7.16 to 3.80 ms—a 53 % decrease—between 19 dB/Hz SPL and 49 dB/Hz SPL). Recall that the level dependency of the 3- and 6-cycle total TBOAE_nl was due to the largest contribution to the TBOAE_nl shifting from the LL component at low stimulus levels to the SL component at higher stimulus levels. The similarity between the TBOAE_nl evoked by the longer-duration tone bursts and the 3- and 6-cycle TBOAE_nl thus suggests that all TBOAE_nl included comparable contributions from SL and LL components.

The latency-intensity functions plotted in Figure 7 exhibited relatively little dependency on tone burst duration. This result is seemingly at odds with findings from Rasetshwane et al. (2013). Similar to the current study, these investigators measured TBOAE latency as a function of stimulus level for different duration 2-kHz tone bursts; however, their tone bursts spanned a much narrower time frame (2–4 ms) compared to the current study (1.5–12 ms). Their findings demonstrated that the latency of the TBOAE systematically increased as tone burst duration increased. It is hypothesized that the origin of Rasetshwane et al. findings was due to referencing latency to tone burst onset as opposed to the peak of the tone burst. As the rise time of the tone burst increases, the peak occurs at a later moment in time relative to stimulus onset, thereby causing the peak of the TBOAE to be increasingly delayed relative to stimulus onset. By referencing latency to the peaks of the tone bursts, as done in the current study, the influence of differences in rise times is reduced.

DISCUSSION

The Effect of Stimulus Bandwidth on the TBOAE_nl

Previous studies have reported the presence of different latency components within the TEOAE (Withnell and McKinley 2005; Goodman et al. 2009, 2011; Moleti et al. 2012a). Common findings across these studies were the following: (1) Shorter-latency components grew less compressively than longer-latency components, (2) the dominant component contributing to the TEOAE shifted to shorter-latency components as stimulus level increased, and (3) the latency of each component was nearly level invariant (Carvalho et al. 2003). It is notable that these studies all used acoustic clicks to evoke the OAE, with spectral bandwidths wider than those for the tone bursts used in the current study. The broad bandwidth of click stimuli has previously been hypothesized to result in IMD and the generation of SL TEOAE components (Withnell and McKinley 2005; Withnell et al. 2008; Goodman et al. 2009; Moleti et al. 2012a).

In the current study, different latency components were measurable in both the 3- and 6-cycle TBOAE_nl envelopes, despite their relatively narrow bandwidths compared to clicks. For most subjects, three or four components were evident, several of which (i.e., the SL components) had latency earlier than expected for generation through LCR at the tonotopic place (Shera and Guinan 2003). As with the different latency components in the aforementioned TEOAE studies, shorter-latency components grew less compressively than longer-latency components, and the latencies of all components were approximately level invariant. The I/O functions and latencies of the different components in the 6-cycle TBOAE_nl approximated those in the 3-cycle TBOAE_nl, demonstrating that the generation of these components was relatively independent of the stimulus energy at frequencies beyond ±1/6 octaves re: 2 kHz (i.e., the bandwidth of the 6-cycle tone burst). Therefore, any contribution to the TBOAE_nl resulting from IMD would necessitate nonlinear interactions between stimulus frequencies within a narrow range of the TBOAE_nl frequency.

The 2f₁ − f₂ distortion product (f₂/f₁ ≈ 1.2) has recently been implicated as the potential source of at least one of the SL components (Moleti et al. 2012a) as the latency factor separating LL and SL components in the TEOAE (∼1.6; Goodman et al. 2009; Moleti et al. 2012a) approximates that expected between an emission generated at the tonotopic place through LCR and an emission generation through low-side cubic distortion (f₂/f₁ ≈ 1.2) at the f₂ place (Moleti et al. 2012a; see Konrad-Martin and Keefe 2003 for DPOAE vs SFOAE latency comparisons). The reduction in spectral bandwidth between the 3- and 6-cycle 2-kHz tone bursts does not support this hypothesis, however. In order to generate a 2-kHz-band 2f₁ − f₂ distortion source OAE (f₂/f₁ ≈ 1.2), stimulus energy around 2.5 kHz (f₁) and 3.1 kHz (f₂) is required, but the 6-cycle tone burst’s energy at and around these frequencies relative to that for the 3-cycle tone burst was attenuated by approximately 20 dB. Despite this attenuation, 6-cycle TBOAE_nl SL components at comparable latencies and magnitudes to 3-cycle TBOAE_nl SL components were observed. As such, 2f₁ − f₂ distortion (f₂/f₁ ≈ 1.2) is not supported as the likely source of SL components, although this does not preclude potential contributions from other distortion products or from 2f₁ − f₂ at f₂ / f₁ other than 1.2. Indeed, if IMD does contribute to the SL components, it likely does so through complex stimulus frequency interactions that cannot be reduced to a single distortion product.

The method used to unmix the different latency components from the 3- and 6-cycle TBOAE_nl (i.e., time windowing) was not suitable for the 12- and 24-cycle TBOAE_nl due to the poorer temporal resolution of these responses. However, the morphologies of these envelopes were consistent with contributions from different latency components. Specifically, at moderate-to-high stimulus levels, the 12- and 24-cycle TBOAE_nl envelopes often exhibited a shorter- and longer-latency magnitude peak, separated by a magnitude null. Talmadge et al. (1999) demonstrated that magnitude nulls in the DPOAE envelope are associated with the offset and onset of the SL distortion and LL reflection source components, respectively, when the two components are in antiphase. In the case of the TBOAE_nl envelopes for the longer-duration tone bursts, magnitude nulls are hypothesized to correspond to the offset of a shorter-latency component and onset of a longer-latency component in antiphase (or nearly antiphase). This is not to say that the shorter-latency component is a distortion source component but, rather, that the 12- and 24-cycle TBOAE_nl envelopes are characteristic of wave interference between overlapping components with different latencies and phases.

Assuming that the same SL components contributed to the 3-, 6-, 12-, and 24-cycle 2 kHz TBOAE_nl, their generation would depend primarily on stimulus energy across a frequency region constrained to ±1/24 octave re: 2 kHz (i.e., the bandwidth of the 24-cycle tone burst). Findings from Sisto et al. (2013) using time-frequency analysis to unmix the SFOAE_nl into LL and SL components support this hypothesis. The latencies of these SFOAE_nl components approximated those of TEOAE_nl components and exhibited qualitatively similar magnitudes and growth rates. As mentioned by Sisto et al., closer agreement between the SF and TEOAE_nl components may have been evidenced if the stimuli used to evoke the SF and TEOAE were calibrated to account for the effect of stimulus bandwidth, as was done in the current study (see Prieve et al. 1996; Kalluri and Shera 2007a).

To infer SL and LL contributions to the 12- and 24-cycle TBOAE_nl, comparable to those for the 3- and 6-cycle TBOAE_nl, the I/O and latency-intensity functions of the total TBOAE_nl were compared across tone burst durations. Recall that the I/O and latency-intensity functions for the 3- and 6-cycle TBOAE_nl were shaped by the relative contributions of the different latency components (see Fig. 5). The agreement between the 3-, 6-, 12-, and 24-cycle TBOAE_nl magnitudes and latencies across stimulus levels is interpreted as evidence that the same LL and SL components contributed to the 3- and 6-cycle TBOAE_nl as well as the 12- and 24-cycle TBOAE_nl. Admittedly, comparing the level dependence of the 12- and 24-cycle TBOAE_nl to that of the 3- and 6-cycle TBOAE_nl provides only an indirect test of whether the same components contributed to the TBOAE_nl, regardless of bandwidth. A more direct test would require unmixing the 12- and 24-cycle TBOAE_nl into different latency components (e.g., evoking the TBOAE_nl with additional tone bursts with center frequencies around 2 kHz and using time-frequency analysis; Moleti et al. 2012b; Sisto et al. 2013).

The similarity between the TBOAE_nl evoked by tone bursts from 3- to 24-cycles demonstrates that the generation of each frequency band within the TBOAE_nl depends primarily on stimulus energy within the same frequency band (Xu et al. 1994; Prieve et al. 1996). In other words, the generation of the TBOAE_nl—regardless of the evoking stimulus’ bandwidth—occurs through relatively independent cochlear channels. This finding contrasts with the hypothesis that SL components in the TEOAE are primarily generated through IMD (Withnell et al. 2008; Goodman et al. 2009; Moleti et al. 2012a). It is important to remember that the data from the current study were obtained from humans. Interspecies differences in cochlear mechanics may preclude a generalization of the current findings. For instance, TEOAE measurements in guinea pigs implicate an IMD mechanism (Withnell and Yates 1998; Yates and Withnell 1999; Withnell and McKinley 2005). Even in humans, the cochlear channels through which the TEOAE is generated may not be entirely independent of one another. Konrad-Martin and Keefe (2003, 2005) observed that when a transient stimulus is used to evoke the OAE (e.g., a short tone burst), the spectrum of the OAE exhibits asymmetry with the magnitudes of higher-frequency OAE components being larger than lower-frequency components. They hypothesized that this asymmetry is a by-product of two-tone suppression where the higher-frequency components suppress the slightly lower-frequency components. In the current study, two-tone suppression between the different frequency components in the TBOAE_nl may explain the more compressive growth of the 3- and 6-cycle TBOAE_nl compared to the 12- and 24-cycle TBOAE_nl, given the broader bandwidths of the tone bursts used to evoke the former. If two-tone suppression does influence the TEOAE, then IMD may as well; however, any such contributions appear to be small (e.g., Moleti et al. 2013).

Influence of TBOAE_nl Extraction Paradigm

A known consequence of the double-evoked technique (or any nonlinear-derived technique, e.g., Kemp et al. 1990) that is the extracted OAE may include only a portion of the total OAE evoked by the s₁ stimulus (Tognola et al. 2001; Schairer et al. 2003; Kalluri and Shera 2007b; Moleti et al. 2012a). Compared to nonequal-level variants of the double-evoked paradigm, an even greater portion of the OAE is lost in the extraction when using the equal-level variant. It is therefore important to consider whether the phenomenon described in the current study, observed using an equal-level, double-evoked extraction, also generalizes to the TBOAE_nl evoked using other nonlinear paradigms and the TBOAE evoked using linear paradigms.

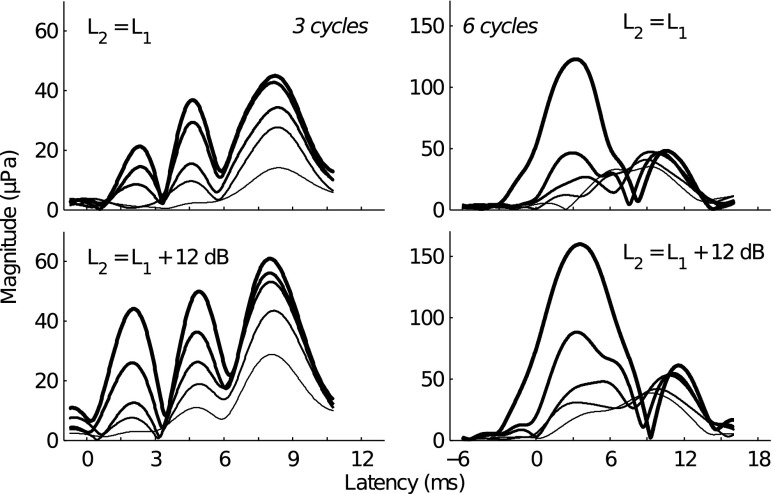
The first column of panels in Figure 10 compares the 3-cycle TBOAE_nl envelopes evoked using equal-level (L₂ = L₁) and nonequal-level (L₂ = L₁ + 12 dB) double-evoked paradigms within the same subject (161L), at identical stimulus levels (7–31 dB/Hz SPL). Recall from the “METHODS” section that a nonequal-level paradigm was initially used for data collection but was abandoned in favor of the equal-level paradigm as the latter afforded extraction of the SL components at higher stimulus levels (note that these levels are not shown in Fig. 10). Subject 161L was one of three who participated in both data collection efforts. Different latency components characterized both data sets and components for L₂ = L₁ were smaller in magnitude than those for L₂ = L₁ + 12 dB (as expected, see “METHODS”). As such, the SL components were measureable at lower stimulus levels for L₂ = L₁ + 12 dB. Thus, although the 3-cycle TBOAE_nl components are attenuated for L₂ = L₁, the presence of analogous components in the L₂ = L₁ + 12 dB data set implies that the same phenomenon underlies both (see Goodman et al. 2009; Moleti et al. 2012b for L₂ = L₁ + 15 dB). Unfortunately, emission data for the longer-duration tone bursts using L₂ = L₁ + 12 dB were not collected at the same L₁ as were used for L₂ = L₁. However, as shown in the second column of panels in Figure 10, the 24-cycle TBOAE_nl envelopes between the two data sets resembled each other and were characteristic of wave interference between different latency components.

FIG. 10.

Comparison of 3- and 24-cycle TBOAE_nl envelopes between equal- (L ₂ = L ₁) and nonequal-level (L ₂ = L ₁ + 12 dB) double-evoked paradigms (subject 161L). The left column shows data for the 3-cycle TBOAE_nl (top row L ₂ = L ₁, bottom row L ₂ = L ₁ + 12 dB). The right column shows data for the 6-cycle TBOAE_nl. The 3-cycle TBOAE_nl envelopes were evoked at equal L ₁ for both paradigms. L ₁ for the 24-cycle TBOAE_nl envelopes using the equal-level paradigm was 3 dB higher than L ₁ using the nonequal-level paradigm. Line thickness increases with increasing stimulus level (i.e., L ₁).

It remains possible that the TBOAE evoked using a linear paradigm depends more strongly on stimulus bandwidth than does that evoked using nonlinear paradigms. Unfortunately, temporal and spectral overlap between the OAE and stimuli precluded the use of a linear extraction paradigm and, therefore, comparisons with the nonlinear-evoked data. However, Goodman et al. (2011) and Moleti et al. (2012a) both presented evidence demonstrating that the different latency components in the TEOAE_nl were also evident in the TEOAE extracted using a linear paradigm. Compared to the TEOAE_nl, TEOAE components were larger in magnitude (see Fig. 13 in Moleti et al. 2012a) and had slightly more compressive growth rates (see Fig. 4 in Goodman et al.). Thus, while there are differences in the OAE measured across linear and nonlinear paradigms, the common finding that different latency components contribute to the evoked OAE demonstrates that the findings from the current study are not unique to the equal-level, double-evoked extraction paradigm.

Generation Mechanisms of SL Components

The conclusion that IMD in humans is not a primary contributor to TBOAE_nl SL component generation does not preclude generation of these components at off-frequency places in the cochlea (i.e., frequency places away from the characteristic frequency place). Indeed, the different latencies of these components seem to necessitate generation at different cochlear locations. One hypothesis is that the SL components are generated basal to the tonotopic place through LCR (Goodman et al. 2011; Moleti et al. 2013). Using a nonlinear cochlear model simulation of TEOAE_nl generation, Moleti et al. (2013) implicated SL component generation resulting from reflection of the traveling wave off impedance discontinuities approximately 0.3 octave basal to the tonotopic place. Even more recently, Moleti et al. (2014) provided experimental evidence implicating generation of the SL components between 0.5 and 1 mm basal to the TEOAE_nl frequency’s tonotopic place (0.11–0.21 octave basal; Greenwood 1961, 1990), on average.

Other potential generation mechanisms of SL components (whether TE, TB, or SFOAE for linear or nonlinear evoking paradigms) include nonlinear coherent reflection (Talmadge et al. 2000), distributed sources of nonlinear distortion (Siegel et al. 2005), and reflection from the tail portion of the traveling wave (Guinan 1990; Siegel et al. 2004; Choi et al. 2008). SL components may also potentially arise through fast backward propagation of the emission through cochlear fluid compression waves (Ren 2004). Regardless of the exact mechanism, the similarity observed in the current study between the different TBOAE_nl argues for a common generation mechanism underlying click-evoked OAE (approximated by the 3-cycle TBOAE_nl) and SFOAE (approximated by the 24-cycle TBOAE_nl) generation across a wide range of stimulus levels (Kalluri and Shera 2007a; Sisto et al. 2013).