Estimating Cochlear Frequency Selectivity with Stimulus-frequency Otoacoustic Emissions in Chinchillas

Abstract

It has been suggested that the tuning of the cochlear filters can be derived from measures of otoacoustic emissions (OAEs). Two approaches have been proposed to estimate cochlear frequency selectivity using OAEs evoked with a single tone (stimulus-frequency (SF)) OAEs: based on SFOAE group delays (SF-GDs) and on SFOAE suppression tuning curves (SF-STCs). The aim of this study was to evaluate whether either SF-GDs or SF-STCs obtained with low probe levels (30 dB SPL) correlate with more direct measures of cochlear tuning (compound action potential suppression tuning curves (CAP-STCs)) in chinchillas. The SFOAE-based estimates of tuning covaried with CAP-STCs tuning for >3 kHz probe frequencies, indicating that these measures are related to cochlear frequency selectivity. However, the relationship may be too weak to predict tuning with either SFOAE method in an individual. The SF-GD prediction of tuning was sharper than CAP-STC tuning. On the other hand, SF-STCs were consistently broader than CAP-STCs implying that SFOAEs may have less restricted region of generation in the cochlea than CAPs. Inclusion of <3 kHz data in a statistical model resulted in no significant or borderline significant covariation among the three methods: neither SFOAE test appears to reliably estimate an individual’s CAP-STC tuning at low-frequencies. At the group level, SF-GDs and CAP-STCs showed similar tuning at low frequencies, while SF-STCs were over five times broader than the CAP-STCs indicating that low-frequency SFOAE may originate over a very broad region of the cochlea extending ≥5 mm basal to the tonotopic place of the probe.

INTRODUCTION

Otoacoustic emissions (OAEs) may provide a window on cochlear processes such as frequency selective filtering (for review see Kemp 2007). Two approaches have been proposed to estimate frequency selectivity with stimulus-frequency (SF) OAEs: based on the SFOAE phase vs frequency gradient (i.e. group delay) and based on SFOAE suppression patterns (e.g. Kemp and Chum 1980; Schairer et al. 2006; Keefe et al. 2008; Lineton and Wildgoose 2009; Shera et al. 2010; Bentsen et al. 2011; Joris et al. 2011; Charaziak et al. 2013). Although these approaches could be applied to other types of emission (e.g. Zurek 1981; Zwicker and Wesel 1990; Harris et al. 1992; Abdala et al. 2014), SFOAEs seem most suitable for two reasons. First, SFOAEs are evoked with a single tone which minimizes the intricacies of interaction between responses to complex stimuli (e.g. mutual suppression, see Kemp et al. 1990; Rhode and Recio 2001; Jedrzejczak et al. 2008). Second, because SFOAEs have been hypothesized to originate near the tonotopic cochlear place of the evoking tone, they could provide a localized picture of cochlear processes at least at low-stimulus levels (Zweig and Shera 1995; Shera and Guinan 1999).

The use of SFOAE group delays (SF-GDs) to derive frequency selectivity is based on the postulated proportionality between basilar membrane (BM) GD and emission GD (Zweig and Shera 1995; Shera et al. 2008). If BM vibrations have the minimum-phase property, there should be a covariance between GD and the sharpness of tuning, with sharper tuning requiring proportionally longer delays (Bode 1945). Based on these assumptions, a proportionality factor, or so-called a “tuning ratio”, has been empirically derived to link cochlear filter quality factor (Q) obtained from auditory nerve fiber (ANF) recordings and SF-GDs for several laboratory species (Shera et al. 2002, 2008; Joris et al. 2011). Assuming that tuning ratios are independent of species, it has been argued that humans have better frequency selectivity as compared to common laboratory species because they have exceptionally long SF-GDs (Shera et al. 2002; Joris et al. 2011).

As with other cochlear measures (e.g. ANF, BM, or hair cell responses), OAEs exhibit two-tone suppression (e.g. Sachs and Kiang 1968; Sellick and Russell 1979; Kemp and Chum 1980; Cooper 1996; Rhode 2007). A suppression tuning curve (STC) can be measured by varying the frequency and level of a suppressor until a predefined change (i.e. criterion) in the response to a fixed probe tone is obtained. Multiple studies indicate that OAE-STCs qualitatively resemble behavioral tuning curves and ANF/BM single-tone frequency tuning curves (FTCs) for both spontaneous emissions and those evoked by various types of stimuli (e.g. Kemp and Chum 1980; Zurek 1981; Zwicker and Wesel 1990; Harris et al. 1992). In humans, SF-STCs mimic the major characteristics of behavioral tuning curves and have similar Qs at least at the group level (Kemp and Chum 1980; Long 1984; Keefe et al. 2008; Charaziak et al. 2013). Although SFOAE suppression patterns have been measured in some laboratory species (Guinan 1990; Souter 1995), to the best to our knowledge, only one study described SF-STCs and these were as sharply tuned as ANF-FTCs in wild-type mice (Cheatham et al. 2011b). Although in general, STCs may underestimate cochlear tuning, they should nevertheless consistently reflect the frequency selective properties of the cochlea (e.g. appendix in Lineton and Wildgoose 2009).

Even though both SF-GDs and SF-STCs reflect some aspects of frequency selective filtering of the auditory system at the population level, their accuracy in evaluating cochlear frequency selectivity in individuals is uncertain (Shera et al. 2002, 2010; Shera and Guinan 2003; Keefe et al. 2008; Joris et al. 2011; Charaziak et al. 2013). For instance, Charaziak et al. have shown that SF-STCs have limited utility for estimating behavioral tuning, an indirect measure of cochlear tuning, in individuals. The goal of this study was to evaluate whether either SF-GDs or SF-STCs obtained at low probe levels (30 dB sound pressure level (SPL)) showed tuning that correlates with more direct (and invasive) measures of cochlear tuning (compound action potential suppression tuning curves, (CAP-STCs)) in an animal model (chinchilla). Given that the use of SFOAEs to derive tuning in chinchillas has not been explored thoroughly, we obtained SF-STCs and SF-GDs for several conditions (varying suppression criteria and/or probe levels) to assess if methodological differences could contribute to any discrepancies in SFOAE-derived tuning as compared to CAP-STCs.

METHODS

Animal preparation

Fifteen adult male chinchillas served as experimental subjects. The anesthesia was induced with ketamine hydrochloride (20 mg/kg, injected subcutaneously) followed by an initial dose of Dial (diallyl-barbituric acid or allobarbital, 50 mg/kg) in urethane (200 mg/kg) that eliminated limb withdrawal reflexes. Supplementary doses of dial in urethane (20 % of the initial dose) were administered as needed to maintain the depth of anesthesia. The rectal temperature was kept near 38 °C with a self-regulating electric heating pad. The animals were tracheotomized, the head was immobilized in a head holder, and the pinna, the cartilaginous part of the ear canal, and the lateral portion of the bony meatus were removed to visualize the tympanic membrane. The tip of an OAE probe was placed close to the tympanic membrane (2–3 mm), and the probe was sealed with ear impression compound to the bony rim of the ear canal. The ipsilateral bulla was opened posteriorly to place a silver ball electrode near the round window for CAP recordings. An electrode placed in the skin of contralateral ear served as a reference with the ground electrode attached to the head holder. In 11 animals, the tendon of the tensor tympani muscle was severed (note: because we did not observe any sizable changes in either CAP thresholds or OAE levels after cutting the muscle, the data from all 15 animals were grouped together). All recordings were made in a sound attenuated booth. The state of the preparation was monitored via recordings of CAP thresholds (see CAP measurements) as well as via recordings of low-resolution SFOAE (see SFOAE measurements) and/or distortion product (DP) OAEs (L₁/L₂: 35/50 dB SPL, f₂/f₁ = 1.2, f₂ varied from 0.5 to 20 kHz, 10 points/octave). The data collection was terminated if the CAP thresholds shifted on average by more than 10 dB and/or OAE levels showed low signal-to-noise ratio (i.e. ~<10 dB). At the end of the experiment, the animal was euthanized via decapitation while still deeply anesthetized. All animal procedures were approved by the Animal Care and Use Committee of Northwestern University.

Instrumentation

Acoustic stimulation was delivered via tubes connected to the transducer (modified Radio Shack RS-1377 Super Tweeters) housed in separate steel boxes. The earphone assembly contained also an Etymōtic ER-10S OAE probe (a customized version of the four-microphone ER-10A with an additional stainless steel tube for sound delivery, endoscope, etc., blocked for this study). The whole assembly was heated to prevent fluid condensation. The differential outputs of both D/A channels of a 24-bit sound card (Card Deluxe-Digital Audio Labs) were routed through a custom-built power amplifier (Texas Instruments, TPA6120A2 head-phone driver IC). The output of the OAE probe microphone preamplifier was connected to one of the differential inputs of the sound card via a differential driver (6 dB gain) and a high-pass filter (with a corner frequency of 155 Hz and slope of 18 dB/octave). The transfer function of the microphone (magnitude and phase) was measured as described by Siegel (2007) and used to compensate the measured stimulus and emission signals. Sound delivery and data acquisition were controlled with either-custom made software (Visual Basic 6.0, Microsoft Corp.) or EMAV ver. 3.24 (Neely and Liu 2011). Tones were generated digitally using the sound card with a sample rate of 44.1 kHz (buffer size 8,192 points) in EMAV and with a sample rate of 88.2 kHz (buffer size 4,096 points) in the custom software. The biological origin of OAEs was confirmed by running the acquisition protocols in a test cavity and sometimes in the ear following euthanasia.

SFOAE measurements

The SFOAEs were measured with a suppression method (e.g. Brass and Kemp 1993; Kalluri and Shera 2007). For all measurements, the SFOAE was calculated as the difference between the averaged responses to the probe tone (f_probe) alone and to the probe tone in the presence of a suppressor tone (f_sup); the SFOAE residual was picked from the magnitude and phase component of the fast Fourier transform of the resulting waveform at the frequency of the probe tone. The residual measures the amount of SFOAE suppression by another tone, and in cases of complete suppression, the SFOAE residual should be a good estimate of the total SFOAE evoked by the probe tone (Brass and Kemp 1993). Two repetitions of the f_probe and f_probe + f_sup time domain averages were stored in separate buffers. The noise floor was estimated at the probe frequency from the spectrum of the difference between time domain responses stored in the two buffers. Trials demonstrating high noise levels were automatically repeated. The phase of the f_probe stimulus was measured and subsequently subtracted from the phases of the SFOAE residuals to compensate for the stimulus delay. Compensating all measured responses by the transfer function of the probe’s microphone thus assures accurate measurement of the phase of the stimulus and emission pressures at the inlet of the microphone. The SFOAE were expressed as the equivalent magnitude and phase of a tone that would have produced the measured change in the probe response (Guinan 1990).

Low-resolution SFOAE measurements (f_probe varied 0.5–16 kHz in 215 Hz steps at 30 dB SPL, f_sup = f_probe − 43 Hz at 60 dB SPL, EMAV) were collected in all animals to monitor the stability of the preparation and are not reported here. The SF-GDs were extracted from high-resolution SFOAE recordings (f_probe varied 0.28–12 kHz in 86 Hz steps at 30 dB SPL, f_sup = f_probe − 43 Hz at 65 dB SPL, EMAV; the procedures for calculating SF-GDs are detailed in Data analysis). Additional high-resolution SFOAE measurements were collected in five animals (two of which were part of another study) at probe levels of 20–50 dB SPL varied in 10 dB steps (note: for one animal, only 20 and 30 dB SPL data were obtained). These additional measurements were used to evaluate the effect of probe level on the SF-GD-derived estimates of frequency selectivity.

The high-resolution SFOAE measurements were also used to identify the f_probe evoking the largest SFOAE levels (≥0 dB SPL with SNR ≥ 6 dB) near the 1, 4, 8, and 12 kHz nominal frequencies. These probe frequencies (i.e. optimized in regards to each animal’s SFOAE fine structure) were further used for SF-STC and CAP-STC recordings. The individual values of f_probe varied within 0.97–1.2 kHz (median (Mdn) = 1.1 kHz), 3.5–4.8 kHz (Mdn = 4.1 kHz), 7.4–8.8 kHz (Mdn = 8.0 kHz), and 10.4–12.3 kHz (Mdn = 12.0 kHz). For simplicity, we ignored the individual differences in f_probe and refer to the nominal probe frequencies when reporting the data. The effect of varying f_probe over a larger frequency range was evaluated in more detail in three animals, where SF-STCs were collected at up to five more values of f_probe (0.3–16 kHz range) in addition to the STCs collected at the four nominal frequencies (1, 4, 8, and 12 kHz).

The SF-STCs were measured as iso-residual curves as a function of f_sup for a fixed f_probe at a probe level of 30 dB SPL. For each f_sup, the suppressor level was varied automatically using a tracking procedure until the SFOAE residual was within ±1 dB of the residual criterion (0 dB SPL). The f_sup was varied from 0.4f_probe to 2.1f_probe with a resolution of 5 points/octave and with increased resolution to 15 points/octave in the range from 0.7f_probe to 1.4f_probe. The f_sup was never allowed to be either a harmonic or a subharmonic of f_probe. For f_probe near and below 1 kHz, the range of suppressor frequencies was extended up to 6f_probe (5 points/octave). For each SF-STC, the phase of SFOAE residual at the criterion threshold was measured across f_sup to form an iso-response phase curve. Data collection was automatically terminated when the suppressor level reached 85 dB SPL, when no response meeting the threshold criterion was found in 15–20 attempts or when the noise level exceeded a predefined noise rejection criterion (typically −10 dB SPL) in 10 consecutive attempts. Measuring a single SF-STC usually took 10–15 min.

Additional SF-STCs were collected in a subset of 12 animals to evaluate the effects of the probe level (range from 10 to 50 dB SPL, at integer multiples of 10 dB; criterion fixed at 0 dB SPL) and of the residual criteria (range from −6 to 18 dB SPL at integer multiples of 6 dB; probe level fixed at 30 dB SPL) on SF-STC tuning.

It was not possible to obtain SF-STCs for all animals at all four nominal probe frequencies when the SFOAE residual levels were too low (<criterion) or due to time limits. Before measuring a SF-STC, the SFOAE residual levels at f_probe were always evaluated by measuring SFOAE input–output functions (probe level varied from 0 to 60 dB SPL, f_sup = f_probe − 43 Hz at 65 dB SPL, custom software).

CAP measurements

The CAP amplitude was measured as the peak-to-peak amplitude of N1 (averaged over 64 presentations of 10 ms tone-burst stimuli including 1 ms rise-fall times, ~100 Hz 3-dB bandwidth, alternating polarity, repetition frequency of 21 Hz). The CAP thresholds were measured automatically with a tracking procedure (custom software) as the lowest SPL that evoked a response of 10 μV for probe frequencies 0.5–20 kHz (2 points/octave). The tracking procedure adjusted the level of the tone burst until the CAP response was equal to the criterion (±1 dB). The level of the tone burst was then increased in 2 dB steps to generate a 4-point input–output function that crossed the criterion. The final value of CAP threshold was obtained by solving a linear regression fit to the input–output function for the criterion of 10 μV.

The CAP-STCs were collected as iso-response curves for a fixed tone-burst probe as a function of the tonal f_sup (custom software). For a fixed f_sup, the suppressor level was varied in an automatic search protocol until the peak-to-peak magnitude of N1 was reduced by 3 dB (±1 dB). The tone burst center frequency was always equal to the f_probe used for SF-STC recordings. The probe level was adjusted to produce a CAP amplitude exceeding the threshold (typically ~20 μV), based on a CAP input–output function measured briefly before CAP-STC recordings. The chosen probe levels ranged from 15 to 60 dB SPL in integer multiples of 5 dB (Mdn = 30 dB SPL). The f_sup was varied from 0.5f_probe to 2f_probe with resolution of 5 points/octave, with the maximum suppressor level limited to 90 dB SPL. A single CAP-STC was collected usually in 20–25 min.

Data analysis

A commonly used metric of frequency selectivity (quality factor, Q₁₀) was used to compare the SF-GD, SF-STC, and CAP-STC results. For SF-STC and CAP-STC, Q₁₀ was calculated as the ratio of f_probe to the width of the tuning curve 10 dB above its lowest point (the tip). The width of the tuning curve was calculated across the widest part of the curve (e.g. ignoring double tips or other irregularities). In three cases, the high/low-frequency side of the SF-STCs did not reach the level of 10 dB above the tip, so the highest/lowest f_sup available was taken as the boundary of the curve width resulting in overestimation of Q₁₀.

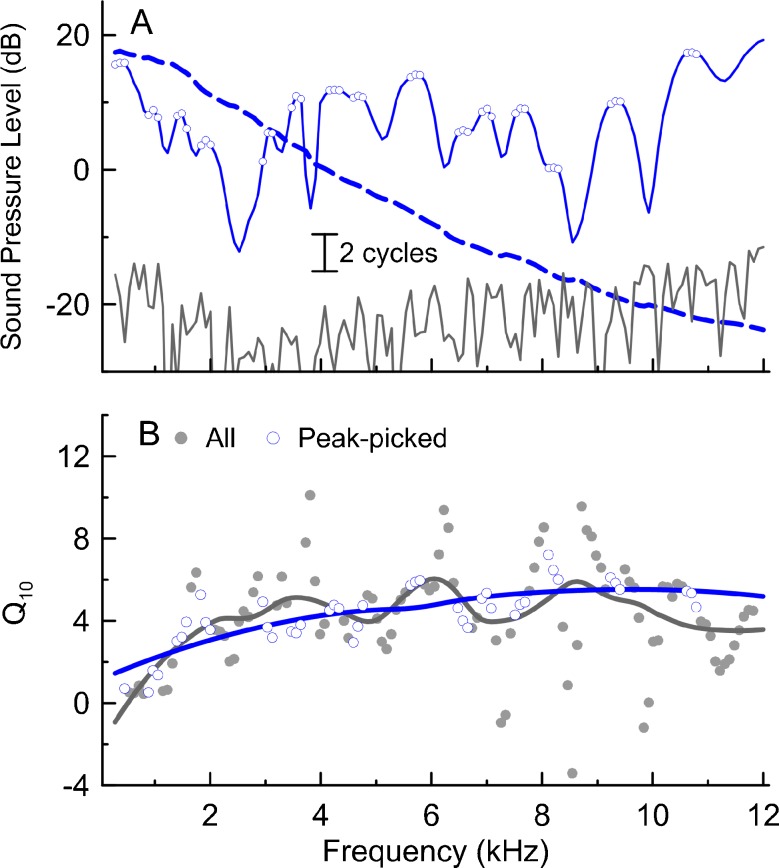
The procedure to extract Q₁₀ from SF-GD involved several steps. First, the SF-GDs (expressed in stimulus periods) were computed as the negative slope (linear fit to three data points) of the unwrapped phase vs frequency curve (Fig. 1A, dashed blue line) obtained from high-resolution SFOAE measurements. To find a reliable estimate of the SF-GD trend, we included only the SF-GDs calculated for values of f_probe corresponding to the SFOAE level peaks (plus one point above and below the peak frequency, see Fig. 1A open blue circles; so-called “peak-picking” method, see Shera and Bergevin 2012 for more details). Identifying the peaks in the SFOAE level vs frequency curve was facilitated by gentle smoothing with a Savitzky-Golay filter (third order with a frame of five; Fig. 1A, blue line). The “peak-picked” SF-GDs were then converted to Q_ERB values using empirically derived “tuning ratio” (r) for chinchilla (extracted for 0.4–11.8 kHz frequency range from Fig. 9 in Shera et al. 2010) where Q_ERB = r × SF-GD and subsequently converted to Q₁₀ (Q₁₀ = 0.56 × Q_ERB; Fig. 1B, blue open circles), assuming frequency independence of the Q₁₀/Q_ERB ratio (see footnote 6 in Shera and Guinan 2003; ratio derived from Fig. 6 in Temchin et al. 2008; also see Fig. 16 in Verschooten et al. 2012). The SF-GD-derived estimates of Q₁₀ were then smoothed with a LOESS fit (local regression, Cleveland 1979; see Fig. 1B blue line) to find the Q₁₀ values corresponding to each f_probe used in the STCs measurements. As shown in an example in Figure 1B, the peak-picking method tends to exclude the most extreme values (compare open blue vs closed gray circles) resulting in smoother LOESS fits (blue vs gray solid lines).

FIG. 1.

A method for deriving Q ₁₀ from SF-GDs. A High-resolution SFOAE levels (blue line, smoothed with a Savitzky-Golay filter) with the level peaks (±1 point around) marked with open blue symbols and the corresponding unwrapped SFOAE phase (dashed line). The noise level is shown in gray. B Q ₁₀ (circles) derived from SF-GDs (calculated from the slope of phase vs frequency curve shown as the dashed blue line in A) together with LOESS fits (unprocessed data in gray and data selected with the peak-picking strategy in blue, see Data analysis).

The data analysis was carried out in MATLAB (ver. R2010b, MathWorks) or in SPSS (ver. 22, IBM). The statistical significance of the results was tested with a linear regression model accounting for within-subject variability (Bland and Altman 1995; Seltman 2013). To meet the assumptions of the regression model, the values of Q₁₀ and f_probe were transformed logarithmically [${log}_{10}\left(Q_{10}\right)=\alpha \times {log}_{10}\left(f_{probe}\right)+\beta$, where α is the slope and β is the intercept of the model] because a linear relationship is assumed between these two variables on a log-log scale (Oxenham and Shera 2003; Shera and Guinan 2003; Shera et al. 2010). Additional explanatory variables were included in the model depending on the purpose of the analysis (e.g. test type, probe level, criterion). The interaction terms were included in the model only if significant (p < 0.05).

RESULTS

General observations

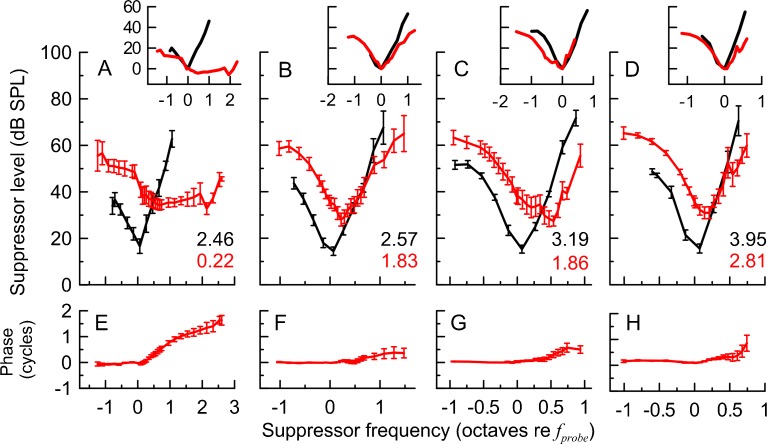
We collected 50 SF-STCs (30 dB SPL probe; criterion 0 dB SPL) and 53 CAP-STCs at f_probe of 1, 4, 8, and 12 kHz from 15 animals. The average SF-STCs (red) and CAP-STCs (black) are shown in (Fig. 2A–D). The CAP-STCs were band-pass shaped with the tips tuned to the frequency of the probe (Dallos and Cheatham 1976). The SF-STCs had also band-pass shapes at 4, 8, and 12 kHz but were consistently tuned to a frequency above f_probe. A shift in the tips of tuning curves toward higher frequencies is often observed for OAE-STCs (e.g. Wilson 1980; Brass and Kemp 1993; Tavartkiladze et al. 1994). At 4–12 kHz frequencies, the iso-response SFOAE phase curves tended to be relatively flat with small leads for f_sup > f_probe (panels F–H). At 1 kHz, SF-STCs had high-pass characteristics (Fig. 2A) associated with a large accumulation of phase in the iso-response SFOAE residual with increasing f_sup above f_probe (Fig. 2E). To facilitate comparison between the overall shapes of STCs, we normalized them to their tips (insets in Fig. 2A–D, see the figure caption for details). For the 4, 8, and 12 kHz probes, the SF-STCs replicated well the shapes of CAP-STCs, although the former demonstrated broader tuning (see Q₁₀ listed in each panel). At 1 kHz, the flanks of SF-STCs and CAP-STCs could be aligned on the low-frequency sides but not on the high-frequency sides, due to the high-pass properties of SF-STC.

FIG. 2.

Average SF-STCs (red) and CAP-STCs (black) calculated only for animals with data for both measurement types at 1 kHz (A, n = 13), 4 kHz (B, n = 14), 8 kHz (C, n = 13), and 12 kHz (D, n = 10). The Q ₁₀ values for the average STCs are shown in each panel. The error bars denote ±1 standard error. The insets in A–D show average STCs normalized to the suppressor level and frequency at their minima, with the exception of the average 1-kHz SF-STC that was arbitrary shifted so that its low-frequency side best matches the low-frequency side of the CAP-STC. Scaling of the y-axes (suppressor level in dB re tuning curve minimum) is identical for all the insets. The x-axes of the insets denote the suppressor frequency in octaves re f _sup at the tuning curve minima. The bottom panels (E–H) show average SFOAE residual iso-response phase curves paired with the average SF-STCs in the upper panels. Prior to averaging the SFOAE, residual phase curves were unwrapped and normalized to the phase value at the f _sup just below f _probe to avoid effects of intersubject differences in absolute phase.

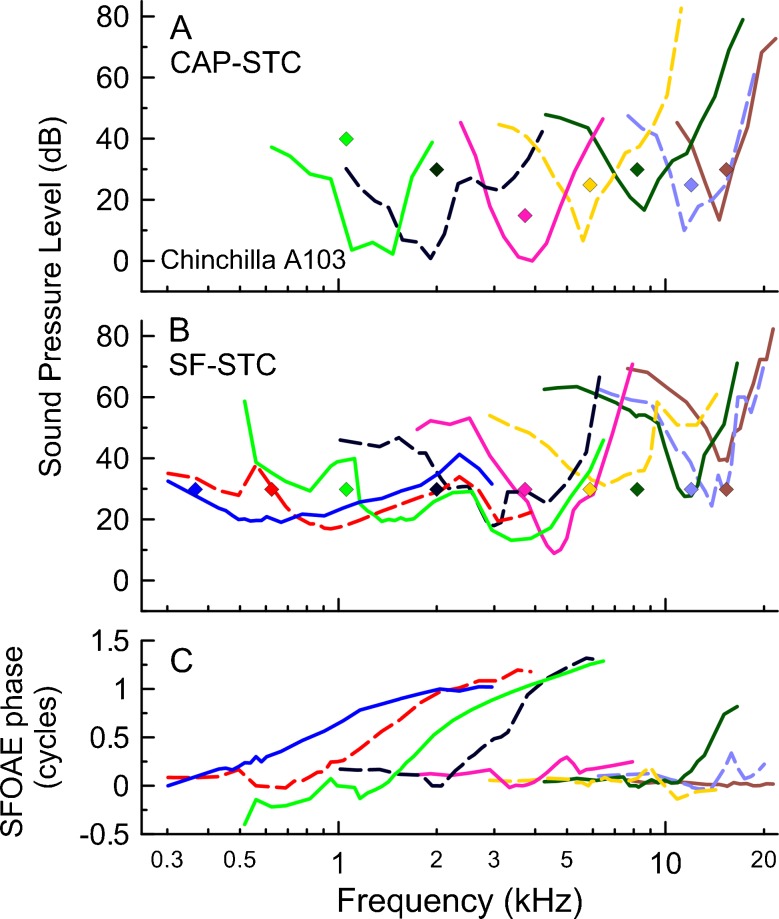
The reasonable agreement between SF-STCs and CAP-STCs at frequencies between 4 and 12 kHz paired with the contrast between the two 1-kHz curves poses the question of whether SF-STCs for f_probe below some border frequency between 1 and 4 kHz are always broad and not tuned, or alternatively, that there is a continuous change in SF-STCs tuning properties along the frequency axis. To answer that question, we measured additional SF-STCs (n = 12) and CAP-STCs (n = 7) in three animals at f_probe covering the range 0.3–16 kHz. As shown in a representative example in Figure 3, the CAP-STCs (A) had band-pass characteristics down to the lowest f_probe tested (1.1 kHz). In contrast, SF-STCs were broader than corresponding CAP-STCs at probe frequencies <3 kHz (Fig. 3B). Although for the two lowest values of f_probe (0.37 and 0.62 kHz), there are no CAP-STC data available for control, the broad widths of the SF-STCs (Fig. 3B, blue and red) are unlikely to reflect cochlear frequency selectivity as the ANF-FTC remain tuned at these frequencies in chinchillas (e.g. Ruggero and Temchin 2005). Data from Figure 3 suggest that there was a gradual change in SF-STCs tuning properties along the frequency axis, from broad to narrow tuning with increasing f_probe. The iso-response SFOAE residual phase tended to be more flat at higher than lower values of f_probe (Fig. 3C).

FIG. 3.

The CAP-STCs (A) and SF-STCs (B) with their corresponding SFOAE residual iso-response phase curves (C) for chinchilla A103. The diamonds mark the probe frequency and level. The curves collected at the same probe frequency are plotted in identical colors across the three panels. The CAP-STCs were typically not measured for f _probe < 700 Hz due to technical difficulties (e.g. energy splatter of the tone burst, poorer CAP synchronization).

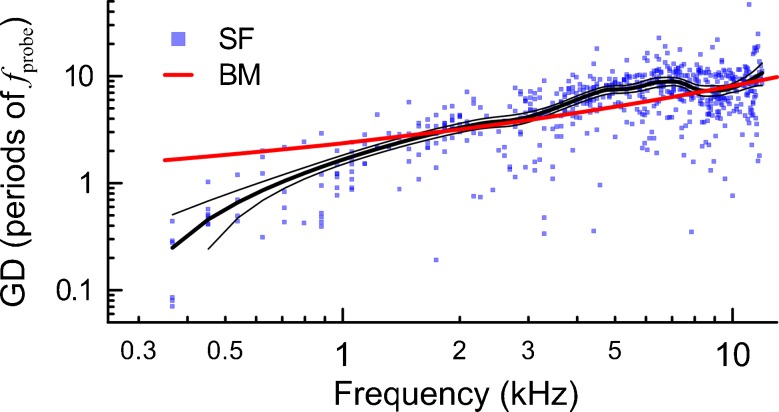
The high-resolution SFOAE measurements with 30 dB probes used to derive SF-GDs had good signal-to-noise ratios (e.g. Fig. 1A, blue vs gray lines), with median of 26 dB (25th and 75th % tiles of 18.3 and 33.5 dB, respectively). Although the SFOAE levels had highly individualized pattern of peaks and valleys along the frequency axis (i.e. fine-structure; Fig. 1A, blue), in most cases, there was a consistent notch in the 2–3 kHz frequency region (Mdn = −13 dB SPL at 2.4 kHz as compared to median amplitudes of 5–10 dB SPL at other frequencies, also see Fig. 5 in Siegel et al. 2005). The SF-GDs derived from 13 animals are shown in Figure 4 (blue squares). The SF-GDs tended to increase with increasing probe frequency (black trend line) as also observed for BM-GDs (red line). However, SF-GDs were considerably shorter than BM-GDs below 2 kHz (black vs red, Fig. 4). Some possible sources of this discrepancy are discussed elsewhere (Siegel et al. 2005; Shera et al. 2010).

FIG. 4.

The SF-GDs were calculated with a peak-peaking strategy for measurements obtained with 30 dB SPL probe levels in 13 chinchillas (blue squares). The LOESS trend line (black thick line) with a 95 % confidence interval (calculated via bootstrapping; black thin lines) is shown to guide the eye. The average BM group delays for chinchillas is shown in red (as in Siegel et al. 2005).

Measurements of frequency selectivity

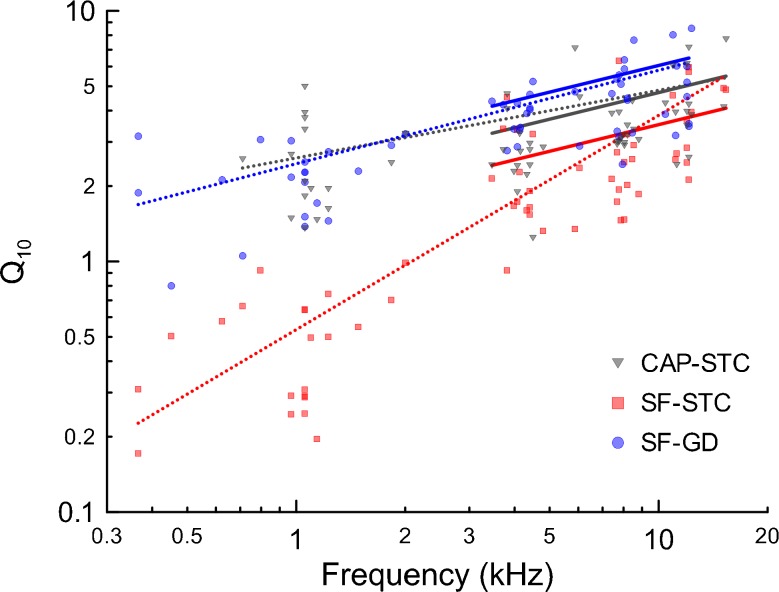
Figure 5 shows estimates of frequency selectivity (expressed as Q₁₀) derived from CAP-STCs, SF-GDs, and SF-STCs. As the sharpness of tuning of CAP-STCs was our control measure of frequency selectivity, we referenced the Q₁₀ derived from the two SFOAE measures to corresponding Q₁₀ values of CAP-STCs by including in the linear regression model (see Data analysis) an indicator variable “test type” with the CAP-STC data serving as the baseline (Seltman 2013). The model parameters are given in Table 1 (left column). The model indicated a significant increase in the sharpness of tuning of CAP-STCs with increasing f_probe (Fig. 5, gray dotted line). While the sharpness of tuning of SF-STCs had a significantly stronger dependence on frequency than CAP-STCs (Fig. 5, red dotted line; p < 0.001), the difference in slope estimates between tuning derived from SF-GDs and CAP-STCs was only borderline significant (blue dotted line; p = 0.066). We interpret these results as indicating a general lack of strong covariance between estimates of tuning based on SFOAEs and CAPs.

FIG. 5.

Sharpness of tuning expressed as Q ₁₀ derived from CAP-STCs (gray triangles), SF-GDs (blue circles) and SF-STCs (red squares) as a function of probe frequency. The linear regression model fits (see Table 1) are shown as color-coded lines for the three methods (dotted line, regression model including all frequencies; solid lines, regression model for f _probe >3 kHz).

TABLE 1.

The parameters of the linear regression model fit to the data in Figure 5 (on a log-log scale, see Data analysis).

		Linear regression model
		0.3 < f probe < 16 kHz		3 < f probe < 16 kHz
	CAP-STC slope	0.27	(p < 0.001)	0.35	(p < 0.001)
Slope difference	SF-GD vs CAP-STC	0.11	(p = 0.066)	–	n.s.
	SF-STC vs CAP-STC	0.59	(p < 0.001)	–	n.s.
	CAP-STC intercept	−0.40	(p = 0.007)	−0.74	(p = 0.009)
Intercept difference	SF-GD vs CAP-STC	−0.33	(p = 0.12)	0.11	(p = 0.001)
	SF-STC vs CAP-STC	–	–	−0.13	(p < 0.001)

The model was fit to data over either the full range of probe frequencies or to data obtained only for high frequencies (>3 kHz). Both models were significant (p < 0.001) and explained 82.7 and 44.0 % of variability in sharpness of tuning, respectively (based on the adjusted R ²). In the first “full” model, most of the variance was predicted by the probe frequency (R ² = 0.42) while in the other “restricted” model by the variables coding the test type (R ² = 0.26). The intercept estimate for SF-STC in the first model was omitted due to significant change in slope (i.e. significant interaction between test type and frequency).

The strong frequency dependence of the sharpness of SF-STCs tuning was due to the unusually broad tuning of low-frequency SF-STCs (Figs. 2 and 3) that may be indicative of broad SFOAE generation region (see Discussion). Similarly, at low frequencies, chinchilla SF-GDs are considerably shorter than expected based on BM-GDs [Fig. 4; note: short SF-GD do not produce small Q₁₀ at low frequencies as the tuning ratio used to calculate Qs “accounts” for that difference (Siegel et al. 2005; Shera et al. 2010)]. It seems reasonable to assess the parameters of the regression model after excluding the low-frequency data (Table 1, right column). The “frequency-reduced” regression model indicated that SFOAE-derived Q₁₀ increased with frequency with the same rate as CAP-STCs Q₁₀ (Fig. 5 solid lines) meaning there were no significant interactions between the test types and probe frequency (p > 0.3; Table 1, right column). However, even though the sharpness of tuning derived from either SFOAE measure covaried with CAP-STC tuning, the SF-GD consistently overestimated the sharpness of the CAP-STC tuning while the opposite was true for SF-STCs (Table 1, see the differences in the intercepts).

The effect of measurement conditions on Q₁₀

Dependence of tuning of SF-STCs on the residual criterion

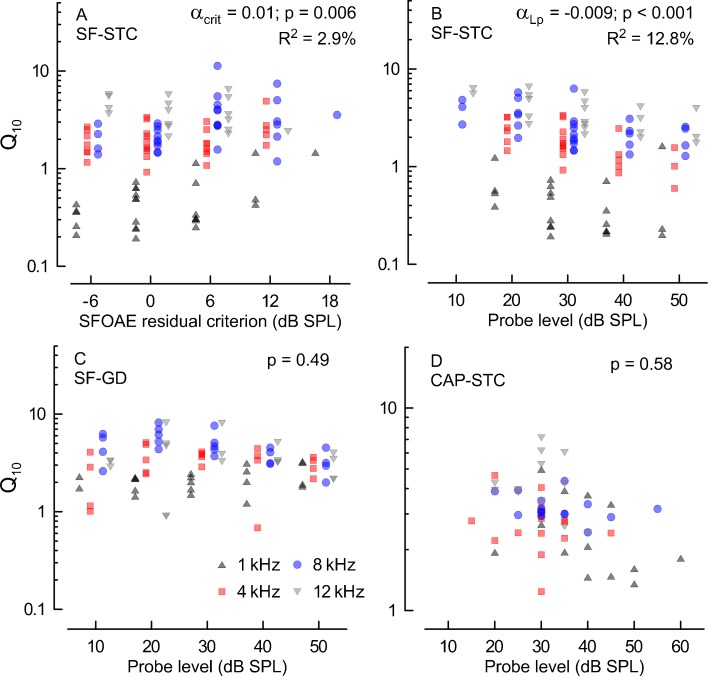
The SF-STCs were constructed as iso-response curves with a nonstandard approach in which a constant change in the ear canal pressure (a criterion residual amplitude) is detected instead of tracking a constant drop in the response amplitude (a decrement criterion) for a given suppressor condition. The residual criterion approach is easier to apply in instances when the response to the probe alone condition cannot be directly measured as in case of SFOAEs. To assess how the change in residual criterion affected the sharpness of SF-STCs, we collected additional tuning curves at varying residual criteria but fixed probe level (30 dB SPL). We obtained 24 SF-STCs at 1 kHz, 30 at 4 kHz, 29 at 8 kHz, and 17 at 12 kHz. All of the conditions were not tested in all animals, but each animal contributed SF-STCs collected with at least two criteria at a given f_probe. The linear regression model indicated that sharpness of tuning was positively albeit weakly associated with the criterion (p = 0.006, see the estimate of the slope in Fig. 6A) and the majority of the variance in the model was explained by the probe frequency (R² = 0.77). This change in sharpness of tuning appears to be mainly an effect at 1 kHz (Fig. 6A, black triangles) and less so at 4, 8, and 12 kHz.

FIG. 6.

The effects of measurement conditions on Q ₁₀ for probe frequencies of 1 kHz (black triangles), 4 kHz (red squares), 8 kHz (blue circles) and 12 kHz (gray triangles). A Q ₁₀ for SF-STCs collected at varying SFOAE residual criteria (x-axis) with probe level fixed at 30 dB SPL. B, C Q ₁₀ derived from SF-STCs (criterion of 0 dB SPL) and from SF-GDs for probe levels ranging from 10 to 50 dB SPL (in 10 dB steps; x-axis). D the subset of CAP-STCs Q ₁₀ reproduced from Fig. 5 as a function of the probe level. The symbol shape and color denotes the probe frequency (see the legend in C). The data for different frequencies in A–C are plotted slightly offset along the x-axis to reduce overlap. The Q ₁₀ (on a log scale) data were fitted with a linear regression model that included frequency and either residual criterion (A) or probe level (B–D) as explanatory variables (note: interaction terms were not significant in any case). The estimates of slopes (α) and their contribution to R ² (if significant) for the x-axis variable are shown on each panel.

The effect of probe level

The CAP-STCs were collected at varying probe levels across animals that produced N1 amplitudes clearly above threshold (~20 μV). On the other hand, when estimating frequency selectivity with SF-GDs, a constant low-level probe has been used (Shera et al. 2002, 2008; Schairer et al. 2006; Lineton and Wildgoose 2009; Bentsen et al. 2011; Joris et al. 2011). Because there is no data available in the literature indicating whether a fixed low-level probe or probe level fixed relative to threshold would be a better approach for estimating frequency selectivity with SF-STCs, we decided to employ the former strategy for consistency with measurements of SF-GDs. To assure that these methodological differences in CAP and SFOAE measurements had little influence on our conclusions, we collected additional SFOAE data at varying probe levels to assess its effects on derived values of Q₁₀.

We obtained 20 SF-STCs at 1 kHz, 24 at 4 kHz, 28 at 8 kHz, and 21 at 12 kHz for probe levels varying from 10 to 50 dB SPL. All animals were not tested with all the conditions, but SF-STCs were always tested for at least two probe levels at fixed f_probe in a single animal. There was a significant decrease in Q₁₀ with increasing the probe level at all frequencies (p < 0.001, Fig. 6B), although the frequency had a stronger effect on Q₁₀ in a regression model (R² = 0.65) than the probe level (R² listed in Fig. 6B).

The Q₁₀ values derived from SF-GDs from five chinchillas at varying probe levels are shown in Figure 6C. Negative Q₁₀ values were excluded from the plot and analysis (2 out of 88). We did not find a significant dependence of Q₁₀ on the probe level (p = 0.49) which contrasts with data obtained in humans where shorter SF-GDs (i.e. broader tuning) are observed at higher vs lower probe levels (Schairer et al. 2006).

Although we did not evaluate the effects of changing the probe level on the sharpness of tuning of CAP-STC within a given animal as for the SFOAE measurements, it is informative to reproduce data from Figure 5 for the 1, 4, 8, and 12 kHz probe frequencies as a function of the probe level used to measure the CAP-STCs (Fig. 6C). As we did not find any statistically significant changes in Q₁₀ with the probe level, we conclude that the fact that we obtained our CAP-STCs at variable probe levels had a negligible effect on estimating frequency selectivity.

In summary, we find that Q₁₀ derived from different methods was rather robust to changes in measurement conditions. The only significant changes were observed for tuning of SF-STCs, but these were relatively small compared to effects of the probe frequency and thus were unlikely to have greatly affected comparisons to the tuning of CAP-STCs shown in Figure 5.

DISCUSSION

Covariation of Different Measures of Sharpness of Tuning

The aim of this study was to evaluate whether SFOAEs can serve as a suitable measure of frequency selectivity as compared to CAP-STCs in chinchillas. We used two methods to estimate frequency selectivity based on OAEs: SF-GDs and SF-STCs (e.g. Kemp and Chum 1980; Shera et al. 2002). For all three methods (SF-GDs, SF-STCs, and CAP-STCs), there was a significant increase in sharpness of tuning with increasing probe frequency (Fig. 5). Although we found a significant covariation between Q₁₀ derived from either SFOAE method and from CAP-STCs for the >3 kHz probe frequencies (Table 1), the adapted regression model explained only 26 % of the variability in sharpness of tuning due to the test type, after accounting for the frequency effects and individual differences. Thus, even though both SFOAE methods seem to be good predictors of frequency selectivity after accounting for the differences in mean Q₁₀ (see the next section), the relationship appears too weak to accurately predict frequency selectivity in an individual with either SFOAE method. The regression model fitted to the Q₁₀ values obtained over the whole tested frequency range (Fig. 5, dotted lines) indicated either no significant or borderline significant covariation between SF-STC or SF-GD and CAP-STC tuning (Table 1), suggesting that at low frequencies, neither SFOAE method is a good predictor of CAP-STC tuning in an individual.

The quantitative differences in Q₁₀ derived from the three methods

At high-frequencies, SF-GDs overestimated the sharpness of CAP-STCs (e.g. Fig. 5). This discrepancy between Q₁₀ derived from SF-GDs vs CAP-STCs is partially due to the fact that the latter measure is not an ideal test of cochlear frequency selectivity. Specifically, CAP-STCs underestimate the tuning of ANF-FTCs and BM-FTCs, where a threshold response from an ANF or BM place to a single tone of varying frequency is established. This is not the same as measuring a change in response of a population of ANFs (i.e. CAP) to a fixed probe caused by suppressors of varying frequencies (STC; see next section). On the other hand, the tuning ratios used to transform SF-GDs into Q₁₀ were empirically derived based on the tuning of ANF-FTCs. Thus, it is not unexpected that there was good agreement between Q₁₀ derived from SF-GDs and ANF-FTCs on a group level (Shera et al. 2010). The fact that the tuning ratio was empirically derived based on averaged data may have introduced some error when calculating individual values of Q₁₀ and thus resulted in low covariation between Q₁₀ derived from SF-GDs and CAP-STCs. Specifically, the ratio of Q₁₀ derived from SF-GD and ANF-FTC is expected to vary from animal to animal due to factors influencing one but not the other measure of frequency selectivity. For instance, SF-GD-based estimates of tuning may depend on intricacies of OAE generation process (e.g. different patterns of impedance inhomogeneities along the cochlear partition across animals) which would have no effect on tuning of ANF-FTC (see appendix in Lineton and Wildgoose 2009 for a modeling example). Lastly, even though we did not find significant changes in Q₁₀ derived from SF-GDs with probe level (Fig. 6C) or analysis strategy (Fig. 1B), it is possible that these factors contributed to discrepancies with tuning of CAP-STCs.

The SF-STCs tended to underestimate the sharpness of CAP-STCs across the tested frequency range (e.g. Fig. 5) which would be expected if SFOAEs are generated over a less restricted region of the cochlea than CAPs (see Extended region of SFOAE generation at low-frequencies section). Some differences in the tuning of CAP-STCs and SF-STCs may relate to methodological discrepancies such as the differences in probe level, criteria, or stimulus type (tone vs tone burst). Even if these methodological differences contribute to slightly broader tuning of SF-STCs for f_probe > 3 kHz, it is highly unlikely these factors alone could explain the extremely broad tuning of curves measured with low-frequency probes.

CAP-STCs as a measure of cochlear frequency selectivity

The CAP elicited at low to moderate stimulus levels reflects responses from spatially localized ANFs innervating frequency-tuned regions along the cochlear partition (Teas et al. 1962; Özdamar and Dallos 1978). Not surprisingly, frequency selectivity derived from CAP measures seems to be a reasonably good approximation of ANF-FTCs (Ruggero and Temchin 2005; Cheatham et al. 2011a; Verschooten et al. 2012), which besides the recordings from the BM are the most direct way of measuring cochlear frequency selectivity (Narayan et al. 1998). While a few CAP-STCs were obtained at moderate to high probe levels (50–60 dB SPL), which would be expected to result in broader tuning due to spread of excitation of the probe response along the BM, the Q₁₀ values were not greatly different from those measured with lower-level probes (Fig. 6D).

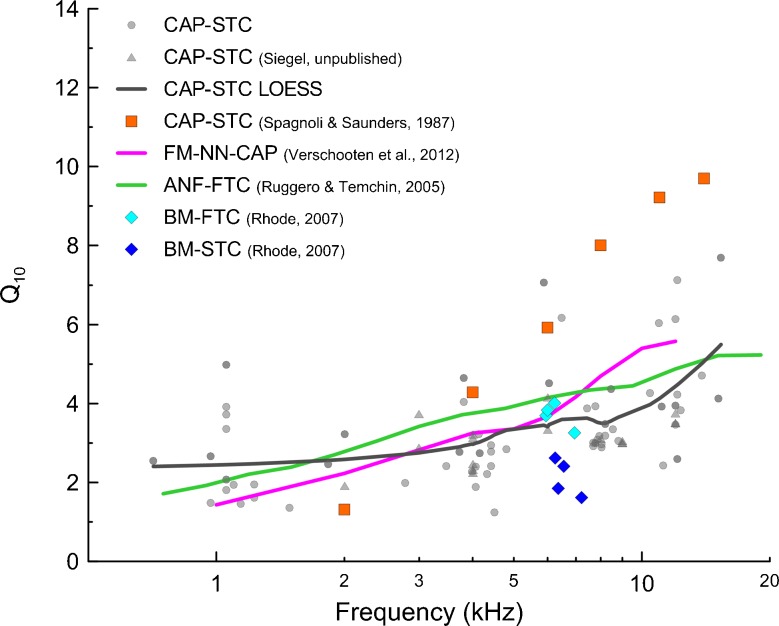
A simple relationship appears to exist between Q₁₀ derived from CAP-STCs and ANF-FTCs (close to one to one) in gerbils, mice, rats, and guinea pigs (reviewed in Ruggero and Temchin 2005). The relationship appeared to be more complex for chinchillas, where the Q₁₀ of CAP-STCs obtained by Spagnoli and Saunders (1987) grew more steeply with frequency than the neural data (Fig. 7, orange squares vs solid green line). However, the sharpness of tuning of CAP-STCs obtained in our laboratory showed frequency dependence similar to ANF-FTCs (Fig. 7, gray vs green solid lines). Possible sources of discrepancies between the CAP-STCs reported here and those reported by Spagnoli and Saunders (1987) include differences in the number of subjects (17 here vs 4), differences in stimulus presentation, and different methods for constructing STCs (automated tracking procedure here vs visual detection of threshold). Nevertheless, our data indicate that the relationship between the sharpness of tuning of CAP-STCs and ANF-FTCs in chinchillas is similar to that observed in other laboratory species.

FIG. 7.

Sharpness of tuning (Q ₁₀) derived from simultaneous masked CAP tuning curves [gray circles: data from this study, gray triangles: unpublished data of Siegel from two chinchillas collected with the same methods as described here, gray solid line: LOESS trend, span 0.7; orange squares: data from (Spagnoli and Saunders 1987) as shown in (Ruggero and Temchin 2005)]. Forward-masked CAP curves obtained with a notched-noise paradigm for a low-level fixed probe using a 33 % (3.5 dB) N1-P1 amplitude decrement criterion are shown in magenta (Verschooten et al. 2012). The Q ₁₀ values for auditory nerve fiber frequency threshold tuning curves are shown in green (Ruggero and Temchin 2005). FTCs represent the level of tone needed to increase the response of a nerve fiber by some criterion amount (e.g. by 20 spikes/s above the spontaneous rate) as a function of frequency. The diamonds represent Q ₁₀ extracted from basilar membrane tuning curves (from Fig. 15 in Rhode 2007): frequency threshold tuning curves for 1 nm displacement criterion in cyan and suppression tuning curves for 1 dB decrement criterion for probe level fixed at 30 dB SPL in blue. All data were obtained in chinchillas.

The simultaneous masking paradigm has been criticized as being inappropriate for frequency selectivity measurements due to the contribution of suppressive effects (e.g. Houtgast 1972; Oxenham and Shera 2003) that may result in underestimating cochlear frequency selectivity measured directly with ANF-FTCs or BM-FTCs (Sachs and Kiang 1968; Sellick and Russell 1979; Harrison et al. 1981; Rhode 2007). In the simultaneous masking paradigm, both the probe and the masker are presented at the same time and may produce mutual suppression of their intracochlear responses. For instance, Rhode (2007) showed that BM-STCs (measured with an approach analogous to CAP-STCs) can be twice as broad as single-tone BM-FTCs (Fig. 7, blue and cyan diamonds). Indeed, we observed that Q₁₀ derived from CAP-STCs tends to cluster just below the Q₁₀ values obtained for ANF-FTCs (in the mid-frequency range Q₁₀ of CAP-STCs = ~0.8 Q₁₀ of ANF-FTCs), plausibly reflecting suppressive effects. As Rhode’s BM-FTCs appear to be as sharply tuned as ANF-FTCs (Fig. 7, cyan diamonds vs green line; also see Narayan et al. 1998), the BM-STCs appear to be broader than CAP-STCs (blue diamonds vs gray line). We have no explanation for this result.

Contrary to Rhode’s results, there are reports showing good agreement between suppression and single-tone tuning curves obtained from ANF and BM recordings (Pickles 1984; Cooper 1996). These data suggest that CAP-STCs may also underestimate the single-tone tuning of ANF-FTCs due to factors other than suppression. In particular, the CAP is a population response of ANF to the onset of a tone-burst stimulus that is less localized than the response to stimulation with a pure tone and is thus expected to show broader tuning than an ANF-FTC.

The nonsimultaneous masking (e.g. forward masking) paradigm has been favored over the simultaneous masking paradigm to assess frequency selectivity, because it does not allow for suppressive interaction between the probe and the masker (e.g. Harris and Dallos 1979; Oxenham and Shera 2003). Surprisingly, recently reported CAP tuning derived from the forward-masked notched-noise paradigm (FM-NN) in chinchillas by Verschooten et al. (2012) is not very different from our simultaneous masked CAP-STCs, at least in the mid-frequency range (Fig. 7, magenta vs gray lines). The FM-NN paradigm has been developed to deal not only with suppression effects but also with the so-called “off-frequency” listening effect by using a masker with a spectral notch surrounding the probe instead of a tonal masker. Both of these effects may lead to underestimation of frequency selectivity as reported in behavioral studies in humans (e.g., Oxenham and Shera 2003). However, contrary to these expectations, there seems to be no clear advantage of using the forward-masked paradigm to estimate frequency selectivity, at least with CAP recordings at the group level.

Extended region of SFOAE generation at low frequencies

For probe frequencies of 3 kHz and above, the SF-STCs demonstrated tuning similar to CAP-STCs, which agrees with the view that SFOAEs originate primarily within a restricted region of the basilar membrane (Zweig and Shera 1995; Shera and Guinan 1999; Talmadge et al. 2000; Lichtenhan 2012). However, the tendency for broader tuning than CAP-STCs may indicate that the region of SFOAE generation extends basal to the probe’s characteristic place, indicated by the hint of a small SFOAE residual phase accumulation at f_sup > f_probe (Fig. 2, panels F–H) and tuning of the tips of SF-STCs to f_sup > f_probe (Fig. 2, panels B–D). At frequencies below 3 kHz, the SF-STCs were considerably broader than the corresponding CAP-STCs, as would be expected if SFOAEs originated over a considerably larger region of the cochlea (Guinan 1990; Siegel et al. 2005; Choi et al. 2008). For these tuning curves, the residual criterion could be reached with f_sup as much as 2.5 or more octaves above the f_probe at relatively low suppressor levels (~40 dB SPL, e.g. Figs. 2A and 3B). Although in BM responses from the apical region (0.5–0.7 kHz), suppression could be observed with suppressors ~2 octaves above the probe frequency, the suppression thresholds were higher in level (~60 dB SPL) than observed here for SFOAEs (Cooper 1996). Thus, the broad tuning of low-frequency SF-STCs is not related to either neural or basilar membrane suppression tuning and most probably indicates a broad region of SFOAE generation plausibly extending as much as 5 mm or more basal to the characteristic place of the probe. The observed pattern of SFOAE residual phase accumulation (e.g. Fig. 2E) is expected if the phase of SFOAE revealed by the suppressor is determined by the phase of the probe tone near the place of the suppressor.

If some part of the SFOAE originates at locations basal to the characteristic place of the probe, then it is expected that these emissions should have shorter group delays than predicted from BM travel times, as reported previously, especially for low frequencies in chinchillas (Fig. 4; Siegel et al. 2005). Shera et al. (2008) suggested that the SFOAEs in chinchillas constitute a mixture of short- and long-latency components. While the long-latency component seems to originate near the tonotopic place of the probe, the source of the short-latency components is uncertain but possibly at locations basal to the peak (Siegel et al. 2005; Shera et al. 2008, 2010). In chinchillas, the short-latency components are particularly strong at frequencies below 3 kHz (Shera et al. 2008) which coincides with the frequency range where we observed unusually broad SF-STCs. Curiously, all these transitions in SFOAE features appear to correspond in frequency to a so-called apical-basal transition in chinchillas (Temchin et al. 2012). Temchin and colleagues suggested that low-frequency traveling waves may be reflected in the transition region giving arise to “basal” emission sources with short-latencies. It is possible that the notch in SFOAE level vs frequency curves observed near 2–3 kHz (Fig. 1A) is another manifestation of this transition (e.g. interference of SFOAE components with short and long latencies), although it may also in part be related to a small dip in the magnitude of the middle ear gain function at ~2.5 kHz observed in open bulla preparations (e.g. Songer and Rosowski 2006; Ravicz and Rosowski 2013). Noteworthy, the short-latency component has been also present even at the highest probe frequencies, although smaller in magnitude than the long-latency ones (Shera et al. 2008). This supports our hypothesis that SF-STCs for higher f_probe (>3 kHz) underestimate the tuning of CAP-STCs in part due to a broader generation region. It must be emphasized though that the decomposition to short- vs long-latency components is arbitrary, and as suggested by gradual transition in SF-STC shapes with frequency (Fig. 3B), the SFOAE likely represent a continuum of generators with varying delay rather than a separate distributions of short- and long-latency generators.

The idea of emissions being generated over a broad region of the basilar membrane is neither new nor unique for SFOAEs and chinchillas. Suppression patterns, noise-exposure experiments, component decomposition analysis and correlations between OAEs and hearing threshold suggest that SFOAEs, transient-evoked (TE) OAEs, and distortion-product (DP) OAEs in humans and several laboratory species may have an extended generation region (e.g. Sutton 1985; Guinan 1990; Avan et al. 1993, 1995, 1997; Withnell et al. 2000; Harding et al. 2002; Ellison and Keefe 2005; Dreisbach et al. 2008; Martin et al. 2009, 2010; Charaziak et al. 2013; Sisto et al. 2013).

An alternative explanation for broad tuning of SF-STCs comes from a modeling study, where it has been shown that suppressors for f_sup > f_probe induce an emission by inducing mechanical perturbations and/or sources of nonlinear distortion acting near the suppressor tonotopic place that can dominate the extracted SFOAE residual (Shera et al. 2004). As our data cannot rule out that possibility, it is important to address why this mechanism would contribute primarily to the SFOAEs evoked only with low-frequency probes but not high-frequency probes for which we observed band-pass SF-STC tuning.

CONCLUSIONS

The SFOAEs carry information about frequency selective processing when evaluated at higher probe frequencies (>3 kHz). Whether the (weak) relationship between SFOAE-derived tuning and CAP-STCs would improve/hold for individuals demonstrating larger ranges of Q₁₀ remains an open question. At lower frequencies, both SF-GDs and SF-STCs indicated tuning that did not covary strongly with that of CAP-STCs, plausibly due to a broad generation region of SFOAEs.