Evaluation and management implications of uncertainty in a multispecies size-structured model of population and community responses to fishing

Abstract

1. Implementation of an ecosystem approach to fisheries requires advice on trade-offs among fished species and between fisheries yields and biodiversity or food web properties. However, the lack of explicit representation, analysis and consideration of uncertainty in most multispecies models has limited their application in analyses that could support management advice.

2. We assessed the consequences of parameter uncertainty by developing 78 125 multispecies size-structured fish community models, with all combinations of parameters drawn from ranges that spanned parameter values estimated from data and literature. This unfiltered ensemble was reduced to 188 plausible models, the filtered ensemble (FE), by screening outputs against fish abundance data and ecological principles such as requiring species' persistence.

3. Effects of parameter uncertainty on estimates of single-species management reference points for fishing mortality (F_MSY, fishing mortality rate providing MSY, the maximum sustainable yield) and biomass (B_MSY, biomass at MSY) were evaluated by calculating probability distributions of estimated reference points with the FE. There was a 50% probability that multispecies F_MSY could be estimated to within ±25% of its actual value, and a 50% probability that B_MSY could be estimated to within ±40% of its actual value.

4. Signal-to-noise ratio was assessed for four community indicators when mortality rates were reduced from current rates to F_MSY. The slope of the community size spectrum showed the greatest signal-to-noise ratio, indicating that it would be the most responsive indicator to the change in fishing mortality F. Further, the power of an ongoing international monitoring survey to detect predicted responses of size spectrum slope was higher than for other size-based metrics.

5. Synthesis and applications: Application of the ensemble model approach allows explicit representation of parameter uncertainty and supports advice and management by (i) providing uncertainty intervals for management reference points, (ii) estimating working values of reference points that achieve a defined reduction in risk of not breaching the true reference point, (iii) estimating the responsiveness of population, community, food web and biodiversity indicators to changes in F, (iv) assessing the performance of indicators and monitoring programmes and (v) identifying priorities for data collection and changes to model structure to reduce uncertainty.

Introduction

One facet of the adoption of an ecosystem approach to fisheries is the need to specify and meet objectives for ecosystem components and attributes as well as target species (Garcia & Cochrane ²⁰⁰⁵; Rice ²⁰¹¹). This requires that objectives can be defined and advice provided on management actions to meet them. In practice, both agreeing on objectives and advising how to meet them have been challenging, in part because advice on consequences of adopting alternate objectives and the probability of meeting them is uncertain and this uncertainty is not quantified.

Several models have been developed to assess fishing effects on community or ecosystem properties (e.g. Plagányi ²⁰⁰⁷). They have improved understanding of fisheries interactions with ecosystems and are often used to underpin state assessments, but relatively few are used operationally; the main exceptions being those that consider interactions among small groups of species (e.g. Gjosaeter, Bogstad & Tjelmeland ²⁰⁰²). One reason for limited uptake is that model outputs are assumed to be highly uncertain, and yet there have been few attempts to express uncertainty and its implications (e.g. Hill et al. ²⁰⁰⁷; Espinoza-Tenorio et al. ²⁰¹²; Gaichas et al. ²⁰¹²; Link et al. ²⁰¹²). This contrasts with analysis and advice on single-species exploitation, for which advisers and managers have longstanding experience presenting and addressing uncertainty (e.g. Francis & Shotton ¹⁹⁹⁷).

Effects of parameter uncertainty on complex ecosystem models are poorly understood and may be challenging to address owing to practical constraints such as long run-times and few data for parameterization or validation. However, the complexity of these models is not a prerequisite for addressing many operational management questions (e.g. Fulton, Smith & Johnson ²⁰⁰³; Butterworth & Plaganyi ²⁰⁰⁴), and a range of less complex models that further simplify ecosystems and/or deal with subsets of ecosystems can be adopted. One class of these models includes size-based multispecies models. These focus on groups of interacting fish species in an otherwise generalized food web and seek to predict changes in species' abundance at size as a function of fishing mortality F (e.g. Hall et al. ²⁰⁰⁶; Rochet et al. ²⁰¹¹; Blanchard et al. ²⁰¹⁴). These models are practical to apply as they are based on measurable properties of species' life histories and dynamics, are relatively straightforward to parameterize with empirical data and have short run-times. They are also suitable for supporting management advice as they predict the effects of changes in F on both size and abundance of species in the modelled community and can therefore be used to estimate single-species fisheries and conservation reference points in a multispecies context as well as a range of community metrics proposed or specified as indicators for evaluating the fishing effects (e.g. Shin et al. ²⁰⁰⁵; EU ^{2008, 2010}; Greenstreet et al. ²⁰¹¹; Shephard, Reid & Greenstreet ²⁰¹¹).

To support development of operational management advice on the effects of fishing, we develop and apply a method to assess and describe parameter uncertainty and its consequences in a size-based multispecies model. Parameter uncertainty is explicitly incorporated into the analysis by developing multiple models based on the full range of possible parameter values, rather than applying a single model based on a best estimate of each individual parameter. Emergent population dynamics predicted by each model are then screened against data to generate a reduced set of models displaying credible dynamics. The approach is used to describe uncertainty in single species and community reference points and single species and community responses to alternate management actions. Predicted uncertainties are used to assess the power of monitoring surveys to detect responses in community metrics and to identify where investment in future data collection should be targeted to reduce uncertainty.

Materials and methods

Analyses were performed using a modified version of the length-based multispecies model initially developed by Hall et al. (2006) to represent the Georges Bank fish community and subsequently applied to the North Sea community (Rochet et al. ²⁰¹¹). The model represents 21 fish species in 32 equal length classes (each c. 5 cm), spanning the full size range of species represented in the model (Table 1). Progression of individuals through length classes is represented using the deterministic von Bertalanffy growth equation (VBGE). Individuals mature when they reach a threshold size defined by a logistic model, with 50% of individuals mature at the length of maturity (L_mat) defined in Table 1. Reproduction is described with a spawner–recruit relationship, which determines the numbers of recruits entering the smallest size class from the biomass of mature individuals. Species' dynamics are linked via predation mortality (M2), which varies with predator abundance, and size and species preference. Size preference is described with a preference function based on a log-normal distribution and species preference with a diet matrix indicating who eats whom (Hall et al. ²⁰⁰⁶). In each length class, individuals are also susceptible to residual natural mortality (M1) and fishing mortality (F). Other details of model structure and implementation are provided in Hall et al. (2006) and Rochet et al. (2011).

Table 1.

Default parameter values and species' abundances for modelled species. Spawning stock biomass (SSB) was obtained from survey data or ICES stock assessments, minimum and maximum estimates of SSB from ICES stock assessments were used to filter model variants. F_MSY and F_HIST were used in simulations. Lifetype indicates if the species is pelagic (P), semi-pelagic and demersal (D1) or strictly demersal (D2), and a and b are the species-specific ‘shape’ parameters, enabling conversion from length (L, cm) to weight (W, g) via the relation W = aL^b, L_∞ is the asymptotic length, L_mat is the length at 50% maturity and ĸ is the von Bertalanffy growth parameter. Maximum SSB was estimated with ICES stock assessment data if these were available; otherwise, estimates were based on ICES North Sea International Bottom Trawl Survey data

Common name	Species	Lifetype	L∞ (cm)	K (year−1)	Lmat (cm)	a (×1000)	b	Maximum SSB (t)	Minimum SSB (t)	Maximum SSB (t)	FMSY (year−1)	FHIST (year−1)
Sprat	Sprattus sprattus	P	17	0·681	12	5·9	3·109	380 236	78 083	380 236	1·30	1·06
Norway Pout	Trisopterus esmarkii	D1	24	0·849	14	7·5	3·024	462 487	63 034	462 487	0·35	0·48
Sandeel	Ammodytes spp.	P	24	1·000	12	4·9	2·783	1 243 757	148 723	1 243 757	0·35	0·57
Poor Cod	Trisopterus minutus	D1	23	0·520	15	8·2	3·087	786 976	–	–	0·72	0·55
Long Rough Dab	Hippoglossoides platessoides	D2	25	0·340	15	5·3	3·143	46 140	–	–	0·60	0·55
Dab	Limanda limanda	D2	32	0·536	13	15·9	2·864	276 779	–	–	0·41	0·55
Herring	Clupea harengus	P	33	0·606	23	4·8	3·198	2 857 134	691 752	2 857 134	0·25	0·25
Horse Mackerel	Trachurus trachurus	P	28	0·380	19	31·6	2·652	193 771	–	–	0·50	0·63
Lemon Sole	Microstomus kitt	D2	37	0·420	27	12·3	2·971	24 915	–	–	0·33	0·55
Sole	Solea solea	D2	47	0·284	21	8·9	3·017	90 300	17 600	90 300	0·22	0·53
Mackerel	Scomber scombrus	P	38	0·510	26	5·2	3·167	248 438	–	–	0·32	0·63
Whiting	Merlangius merlangus	D2	52	0·323	21	9·9	2·943	527 871	181 713	527 871	0·21	0·37
Witch	Glyptocephalus cynoglossus	D2	44	0·200	29	1·7	3·389	38 129	–	–	0·27	0·55
Gurnard	Eutriglia gurnardus	D2	43	0·266	18	16·0	2·815	166 957	–	–	0·27	0·55
Plaice	Pleuronectes platessa	D2	65	0·122	22	12·5	2·943	500 800	182 000	500 800	0·25	0·55
Starry Ray	Amblyraja radiata	D2	66	0·230	46	10·7	2·940	74 341	–	–	0·15	0·55
Haddock	Melanogrammus aeglefinus	D2	71	0·271	27	9·2	3·013	524 367	63 074	524 367	0·30	0·58
Cuckoo Ray	Leucoraja naevus	D2	92	0·110	59	2·6	3·217	7809	–	–	0·11	0·55
Monkfish	Lophius piscatorius	D2	106	0·180	61	29·7	2·841	15 000	–	–	0·10	0·55
Cod	Gadus morhua	D2	150	0·216	54	8·1	3·050	86 562	24 534	86 562	0·19	0·88
Saithe	Pollachius virens	D1	119	0·175	49	8·5	3·024	327 700	105 400	327 700	0·30	0·38

Expected ranges of parameter uncertainty were expressed for seven key parameters with a default estimate and four alternate values that spanned the range of uncertainty reported in published literature or estimated from data (Table S1). Model variants were established for all combinations of parameter values, generating an initial set of 5⁷ (78 125) variants. Each variant was run under ‘no-fishing’ and ‘historic fishing’ scenarios, and outputs were screened to establish whether all species persisted (with no-fishing) and species' biomass was consistent with independent estimates (with ‘historic fishing’, details below). Model variants that produced outputs that did not meet these criteria were excluded. The remaining model variants were treated as equally plausible and dubbed the filtered ensemble (FE). Evaluations of fishing scenarios were conducted using the FE and thus generated probability distributions of outputs.

Eleven species in the model are assessed by ICES with age-based single-species models; Norway pout Trisopterus esmarkii (Nilsson), sandeel Ammodytes spp., herring Clupea harengus Linnaeus, horse mackerel Trachurus trachurus (Linnaeus), sole Solea solea (Linnaeus), mackerel Scomber scombrus Linnaeus, whiting Merlangius merlangus (Linnaeus), plaice Pleuronectes platessa Linnaeus, haddock Melanogrammus aeglefinus (Linnaeus), cod Gadus morhua Linnaeus and saithe Pollachius virens (Linnaeus). For these species, default VBGE parameters were calculated by fitting the VBGE to ICES weight-at-age data. For remaining species, VBGE parameter estimates were taken from Rochet et al. (2011) and Blanchard et al. (2014). Prey species that were not individually modelled were represented as a constant resource of 10¹⁰ g of ‘other food’ available to all predator length classes at each time step. This equates to a total of 2·5 × 10⁶ tonnes of other food available to the whole community at each time step. Preliminary sensitivity tests involving 10-fold changes in other food, and varying its size profile, confirmed that while some outputs from the FE were sensitive to the quantity and representation of other food, these choices led to unreasonable M2 values (Figs S1–S3, Sparholt ¹⁹⁹⁰). The modelling approach assumes that the modelled community is closed (dynamics determined solely by internal processes), an assumption that is necessarily violated to some extent in a continuous marine environment.

Recruitment was assumed to be deterministic, with individuals recruiting at the mid-point of the smallest length class. The Ricker spawner–recruit relationship used by Hall et al. (2006) was replaced with a hockey-stick spawner–recruit relationship (HS-SRR, Barrowman & Myers ²⁰⁰⁰). This was changed because the Ricker relationship led to a steeper size spectrum slope (SSS) when unfished than at modest fishing pressures, in contrast with theory and observation (e.g. Rice & Gislason ¹⁹⁹⁶; Bianchi et al. ²⁰⁰⁰; Andersen & Beyer ²⁰⁰⁶) and because the HS-SRR provided a better fit to ICES data which included few recruitment estimates at relatively high spawner biomass. For the default model parameterization, α (the initial slope of the HS-SRR) was estimated as a function of L_∞ from data (Denney, Jennings & Reynolds ²⁰⁰²), and an upper limit for β, the fraction of maximum spawning stock biomass (SSB_max) above which recruitment is assumed constant, was estimated by fitting the HS-SRR to ICES spawner and recruit abundance data from single-species stock assessments (ICES ²⁰¹³). Lower values of β were selected from a linear series of successive 20% reductions in β (Table S1). For each species, we then estimated α from L_∞ and the inflection point in the segmented regression as a fraction of maximum spawner biomass (SSB_max). SSB_max for assessed species was defined as the highest species' SSB reported in ICES stock assessments from 1990 to 2010. For non-assessed species, SSB_max was each species' highest SSB as estimated from swept area in the North Sea Quarter 1 International Bottom Trawl Survey (IBTS) from 1990 to 2010 (ICES ^2012a). Swept area abundance estimates were corrected for selectivity and availability by species, following the method of Fraser, Greenstreet & Piet (2009).

Natural mortality was divided into non-predation (M1) and predation (M2) mortality, where M2 varied with predator abundance. Total predation mortality imposed by each predator was calculated based on the food requirements needed to support growth, taking account of growth efficiency. Predators consumed prey species defined as suitable in a diet interaction matrix that specifies possible interactions among all species. A predator of a given size could consume individuals of an available prey species within a defined predator: prey size ratio (Hall et al. ²⁰⁰⁶; Table S1). All modelled species also consume individuals of a suitable size in ‘other food’. Mortality imposed by predators was partitioned among available prey according to relative prey abundance at size. The default diet interaction matrix from Rochet et al. (2011) was supplemented with two variants based on empirical diet data, where predators were allowed to consume prey species if the frequency of occurrence of the prey in diet data was greater than a specified threshold (Tables S1–S4). For two remaining variants of the diet matrix, we assumed that all species ate all other species or that pelagic species only ate pelagic species, and demersal species only ate demersal species.

Fishing mortality was applied assuming species-specific relative size selectivity established from fits to ICES (2012b) F at length data. Model scenarios were fishing at MSY (F_MSY, the fishing mortality that produced the maximum sustainable yield, Table 1, Fig. S4) and fishing with ‘historic’ fishing patterns (F_HIST, Table 1, Fig. S4). For the F_HIST scenario, the F applied to each of the 11 modelled and assessed species was mean F for 1990–2010 (ICES ^2012b). Non-assessed species were grouped with assessed species of similar morphology and behaviour and were assumed to be fished at the same F (Pope et al. ²⁰⁰⁰). Poor cod, gurnard Eutriglia gurnardus (Linnaeus) and monkfish Lophius piscatorius Linnaeus were grouped with haddock, cod and whiting. Long rough dab Hippoglossoides platessoides (Fabricius), dab Limanda limanda (Linnaeus), lemon sole Microstomus kitt (Walbaum), witch Glyptocephalus cynoglossus (Linnaeus), starry ray Amblyraja radiata (Donovan) and cuckoo ray Leucoraja naevus (Müller & Henle) were grouped with plaice. For the F_MSY scenario, F_MSY values for assessed species were obtained from ICES (2012b). For the non-assessed species, the F leading to 40% spawner-per-recruit (F₄₀) was assumed to be a proxy for F_MSY, and F₄₀ values were estimated following Le Quesne & Jennings (2012).

Output from each of the 78 125 model variants was tested against two test criteria to filter out variants with parameter sets leading to unrealistic community properties. Each model variant was run for 45 years with F = 0 to predict an unfished equilibrium community state, followed by 30 years fishing at F_HIST. The first test criterion was that all species should persist in the unfished model system, with biomass exceeding 1% of current biomass estimates from ICES assessments or survey data analyses. The second test criterion was applied after 30 years fishing at F_HIST. It specified that mean predicted biomass of assessed species during the last 15 years of the F_HIST simulation should be more than half the lowest, but less than twice the highest, biomass estimate from 1990 to 2010 (assessment data from ICES ^2012b). We used a factor of two because biomass estimates from the single-species assessments are uncertain, and because we adopted a deterministic spawner–recruit relationship when environmental trends and stochastic processes influence recruitment dynamics in the real world. Using the screening criteria, each of the 78 125 model variants was classified as plausible or rejected. Consequences of modifying the factor, dubbed the tolerance factor, from 1·5 to 3·0 were examined (Figs S5, S6 and S7). Selected parameter options in the FE were examined to identify which parameters introduced most uncertainty in model outputs, and to assess whether model dynamics were independent of any given parameter choice.

Accepted model variants, referred to as the FE, were run for 30 years into the future under given fishing scenarios to generate ensemble predictions of the potential response of individual species and community metrics to F. For the F_MSY scenario, all species were fished at their predicted F_MSY, and at F = 0 to F = 5F_MSY, in 0·1 steps. This set of F_MSY scenarios did not allow for examination of yield trade-offs among species, as all F were scaled equally (same proportional change in F applied to each modelled species), but was used to provide a measure of the relative magnitude of uncertainty in predictions of the single-species reference points F_MSY, B_MSY (the SSB at F_MSY) and Y_MSY (yield at F_MSY) derived in a multispecies context.

During simulations, biomass and yield of each species and the value of each community metric were calculated annually. Community metrics calculated were as follows: mean length (ML), biomass fraction >40 cm (dubbed the large fish indicator, LFI), slope of the size spectrum (slope of relationship between log numbers in each log size class and log size, SSS) and mean maximum weight by biomass (biomass-weighted mean of species' W_∞; a measure of the life-history composition of the community (mean maximum weight, MMW, Shin et al. ²⁰⁰⁵). Metrics were calculated using abundance estimates for individuals >15 cm, approximating sizes adequately selected in trawl surveys in the North Sea (Fraser, Greenstreet & Piet ²⁰⁰⁹). When assessing fishing effects on individual species, we referred to species as collapsed when SSB fell below 10% of unexploited SSB. Outputs of simulations are presented as frequency distributions, treating all variants in the FE as equally plausible. Uncertainty was expressed as 50th and 90th percentile intervals within the FE. The 50% and 90% intervals spanned the 25th to 75th and 5th to 95th percentiles of the frequency distribution of output values generated by the FE, respectively.

We calculated the statistical power of the North Sea IBTS Quarter 1 survey to detect predicted changes in community metrics during a transition from fishing at F_HIST to F_MSY. Statistical power was defined as the probability that the predicted change in metric value achieves a statistical significance (here set at 0·10) over a 5- or 15-year period. As well as the statistical significance and sampling period, power depends on the magnitude of the residual variance, which was estimated by taking residuals from a loess smoother (Fryer & Nicholson ¹⁹⁹³, span = 1) fitted to a time series (1990–2011) of metrics calculated from North Sea IBTS Quarter 1 survey data. Metrics were calculated from survey data using only the species and size classes included in the multispecies model. Power to detect the predicted change in each metric during the transition from fishing at F_HIST to F_MSY was estimated for each model variant in the FE based on 10 000 random draws from a normal distribution fitted to residuals of the empirical time series.

Results

Individual species' biomass predictions from the models in the unfiltered ensemble (UE), when fishing according to the F_MSY scenario, tended to span 2 or more orders of magnitude (Fig. 1), indicating that initial spread of parameter choices provided little constraint on predictions. Uncertainty in predicted biomass is greatly reduced for the FE where uncertainty is reduced to between one-half and one order of magnitude (Fig. 1). Only 188 of 78 125 possible model variants passed the screening criteria. The default model did not pass the screening criteria. Changing the screening criteria for biomass at F_HIST to allow a tolerance factor of 1·5× to 3× for the relationship between ICES single-species biomass estimates and model outputs increased the size of the FE (Fig. S5), but had a small effect on outputs and uncertainty and did not change qualitative behaviour and relative performance of species and community metrics (Figs S6 and S7).

Fig 1.

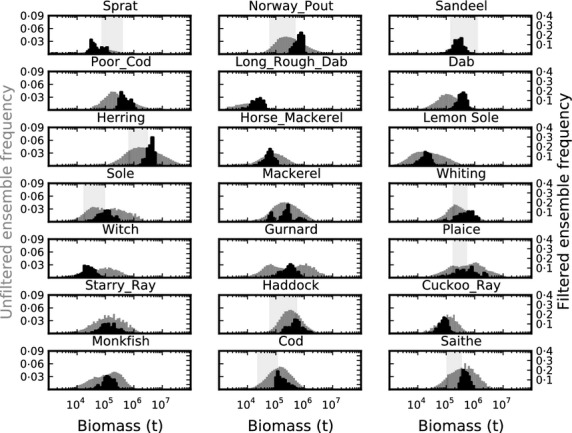
Frequency distribution of estimated biomass of modelled species at F_MSY. Grey histograms denote the frequency distribution of biomass estimates from models in the unfiltered ensemble (UE), black histograms the biomass estimates from models in the filtered ensemble (FE). The vertical shaded band represents the biomass range reported by ICES for assessed species for years 1990–2010.

To evaluate impacts of parameter uncertainty on estimates of management reference points for each individual species in the multispecies model, the spread of F_MSY and B_MSY estimates for all models in the FE was compared with mean F_MSY calculated across all models in the FE. For F_MSY, there was 50% probability that a given value was within ±25% of the mean and 90% probability that it was within ±50% of the mean (Table 2), for all species except plaice. For B_MSY, there was a 50% probability of predicting single-species values to within ±40%; 90% intervals were much wider, typically spanning a factor of 5–10. Probability distributions of outputs from the FE provided information on uncertainty that could inform decisions such as how to set F_MSY to achieve a defined reduction in the risk that true F exceeds F_MSY. For example, if F_MSY for cod was 0·23, there would be 50% confidence that the actual F_MSY limit was not breached. However, if the F_MSY limit was set to increase confidence to 75%, or 95%, F_MSY would need to be reduced to 0·21 or 0·17, respectively (Table 2).

Table 2.

Estimates of single-species fisheries reference points with the filtered ensemble (FE). Mean estimates for F_MSY and B_MSY are presented as uncertainty intervals (UI) spanning 50% and 90% of the members of the FE. F_MSY ratio is the ratio of the F_MSY predicted by the multispecies model to estimates of F_MSY from ICES single-species stock assessment models

Common name	FMSY (year−1)	50% UI FMSY (year−1)	90% UI FMSY (year−1)	FMSY ratio	BMSY (×105 t)	50% UI BMSY (proportion)	90% UI BMSY (proportion)
Sprat	0·78	0·65–0·91	0·52–1·04	0·60	1·26	0·64–1·32	0·46–1·95
Norway Pout	0·82	0·67–0·98	0·52–1·16	2·35	5·07	0·76–1·24	0·50–1·45
Sandeel	1·11	0·84–1·36	0·67–1·57	3·18	2·13	0·69–1·24	0·46–1·69
Poor Cod	0·77	0·65–0·86	0·50–1·08	1·07	6·88	0·69–1·25	0·54–1·66
Long Rough Dab	0·84	0·72–1·02	0·54–1·14	1·39	0·32	0·67–1·25	0·41–1·69
Dab	0·85	0·70–0·98	0·57–1·15	2·07	3·19	0·79–1·19	0·53–1·55
Herring	0·54	0·45–0·62	0·35–0·73	2·17	28·3	0·82–1·20	0·52–1·48
Horse Mackerel	0·54	0·45–0·60	0·35–0·80	1·07	0·80	0·64–1·24	0·33–1·96
Lemon Sole	0·48	0·36–0·56	0·33–0·69	1·45	0·20	0·68–1·29	0·40–1·80
Sole	0·68	0·55–0·77	0·44–0·99	3·08	0·90	0·62–1·23	0·41–2·16
Mackerel	0·49	0·42–0·58	0·32–0·67	1·55	2·59	0·47–1·04	0·17–3·20
Whiting	0·75	0·59–0·90	0·46–1·03	3·55	4·26	0·62–1·23	0·39–2·15
Witch	0·34	0·27–0·41	0·24–0·49	1·27	0·28	0·57–1·27	0·33–2·04
Gurnard	0·84	0·70–0·97	0·54–1·19	3·12	2·81	0·65–1·20	0·41–1·96
Plaice	0·31	0·23–0·38	0·15–0·50	1·24	8·64	0·26–1·06	0·13–3·89
Starry Ray	0·21	0·17–0·24	0·14–0·26	1·38	1·49	0·42–1·19	0·23–2·49
Haddock	0·48	0·36–0·57	0·30–0·72	1·61	4·70	0·52–1·19	0·26–2·61
Cuckoo Ray	0·11	0·10–0·12	0·09–0·13	1·02	0·86	0·70–1·18	0·49–1·82
Monkfish	0·20	0·17–0·23	0·15–0·25	2·01	0·90	0·65–1·31	0·32–1·88
Cod	0·23	0·21–0·27	0·17–0·27	1·21	1·72	0·55–1·25	0·45–2·44
Saithe	0·34	0·24–0·42	0·21–0·45	1·13	5·54	0·69–1·21	0·51–1·99

Model F_MSY predictions were consistent with single-species estimates for 12 species, higher for eight and lower for sprat (Fig. 2). F_MSY estimates were higher for mid-sized species, the likely explanation being predation release as large fish were depleted at high F. Relationships between B_MSY and B₀ followed theoretical expectations of B_MSY ≈ B₀/2 (e.g. Punt et al. ²⁰¹⁴).

Fig 2.

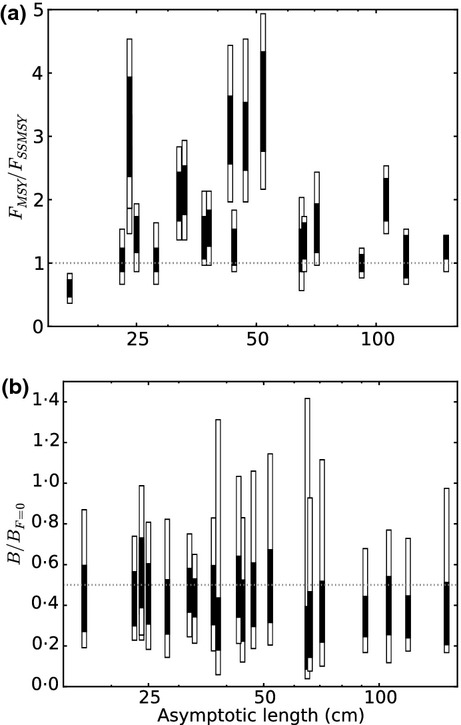
Relationship (a) between F_MSY predicted with model variants in the filtered ensemble (FE) as a proportion of F_MSY from ICES single-species stock assessment models (F_SSMSY) and asymptotic length, and (b) between B_MSY as a proportion of B₀ predicted with model variants in the FE and asymptotic length. Black bars and open bars denote 50% and 90% uncertainty intervals, respectively.

Community metrics showed qualitatively similar responses to changes in F (Fig. 3), although the SSS showed a near linear decline in response to increasing F, while the LFI, ML and MMW displayed a nonlinear relationship with F. There was considerable uncertainty in predicted values of the community metrics at F_MSY and across the full range of F (Fig. 3).

Fig 3.

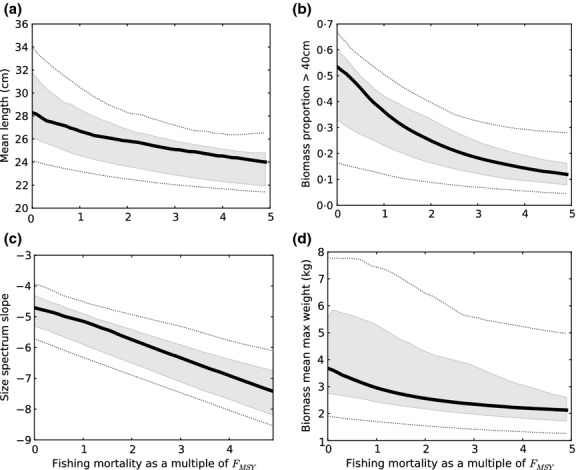
Relationship between the community metrics and fishing mortality predicted by the model variants in the filtered ensemble (FE). Black line is the mean value, and the grey and broken lines denote uncertainty intervals including 50% and 90% of FE members, respectively. Metrics are (a) mean length, (b) proportion of large fish, (c) size spectrum slope and (d) mean maximum weight.

If a community metric is to provide feedback on effects of management action, then it should show a response to these effects and this should be detectable in monitoring data. This requires that the change in metric value following a defined management action should be greater than uncertainty in prediction, and the predicted change in the metric value should be detectable given interannual variation in data. To compare theoretically expected change in community metrics with uncertainty in prediction, the ratio of the metric at F_HIST:F_MSY, for each FE variant, was compared with the 50% and 90% uncertainty intervals for the prediction at F_HIST, where the 50% and 90% uncertainty intervals were expressed as a proportion of the mean metric value (Fig. 4). The mean change in the values of the metrics fell outside the 50% uncertainty interval for MMW, LFI and SSS, but not for ML. For MMW, LFI and SSS, the predicted change in indicator values for the entire FE lay outside the 50% uncertainty interval, and for SSS, predicted change also lay outside the 90% interval. Thus, SSS is expected to be the most responsive community indicator.

Fig 4.

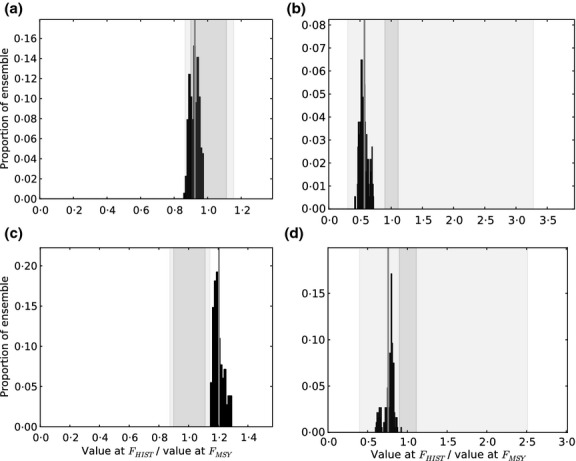
Frequency distribution of community metrics predicted with models in the filtered ensemble (FE) and expressed as the ratio of values of each metric at F_HIST and F_MSY (black histogram). The vertical grey line is the mean ratio of values of each metric at F_HIST and F_MSY. Vertical shaded bands indicate 50% (dark) and 90% (light) uncertainty intervals for the prediction at F_HIST, with intervals presented as a proportion of the mean metric value. Metrics are (a) mean length, (b) proportion of large fish, (c) size spectrum slope and (d) mean maximum weight.

Power of the North Sea IBTS to detect changes in community metrics was assessed by comparing the magnitude of change in mean metric values when model F transitioned from F_HIST to F_MSY with the magnitude of interannual variation in metric values from IBTS data. For community metrics applied to all demersal species (Table 1, see Lifetype D1), there was a 0·6 to 0·8 mean power of detecting a change in ML, MMW or LFI that occurred over 5 years and a mean power of >0·9 of detecting a change in SSS (Fig. 5). After 15 years simulated monitoring, mean power was still <0·8 for ML, ≈0·9 for MMW, ≈0·95 for the LFI and 1·0 for SSS. For all community metrics except SSS, there was significant variation in power among FE variants after 15 years. For example, for LFI, power ranged from 0·7 to 1·0. Power to predict changes in community metrics for all demersal species was generally a little lower than for strictly demersal species (Table 1, see Lifetype D2), but SSS still provided greatest power after 5 and 15 years (Fig. S8).

Fig 5.

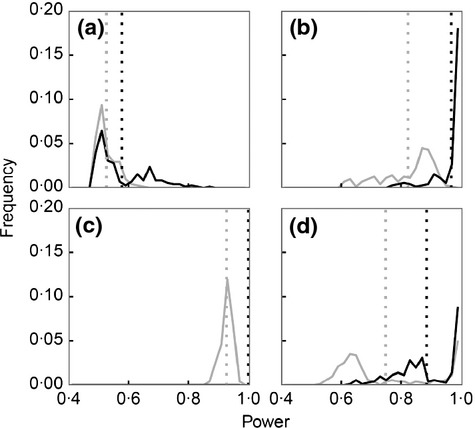
Frequency distributions for the predicted power of the North Sea International Bottom Trawl Survey (IBTS) to detect modelled changes in the values of community metrics for all demersal fishes (Lifetype D1, Table 1) when fishing mortality is reduced from F_HIST to F_MSY over 5-year (grey) and 15-year (black) periods. Metrics are (a) mean length, (b) proportion of large fish, (c) size spectrum slope and (d) mean maximum weight. Vertical lines denote mean power for all model variants in the filtered ensemble (FE).

Total community yield was maximized when F ≈ 1·6 × F_MSY (Fig. 6). Fishing mortality had to be reduced to F_MSY or below to avoid all possibility of species' collapse. At 3 × F_MSY, an approximation of maximum ‘historic’ F for North Sea target species, mean total yield was predicted to be similar to yield at F_MSY, or around 85% of the maximum, but two species were expected to collapse, and probability of collapse was >0·1 for another five species. In these fishing simulations, F across all species was increased and decreased evenly, with F ratios among species defined from single-species estimates of F_MSY. This fishing strategy tends to predict relatively high yields for all species in the community at F_MSY (Fig. S9) and few trade-offs that result from more uneven distributions of F in relation to F_MSY. The sensitivity of sprat to collapse may be an indication of the differing age at selection applied in our model and the ICES assessment models and/or may reflect relatively high estimates of F_MSY in the ICES assessment.

Fig 6.

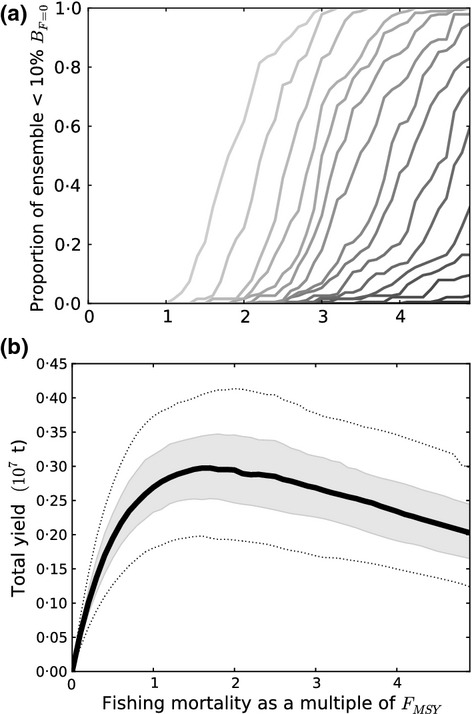
(a) Probability of species' collapse as a function of fishing mortality, with probability expressed as the proportion of variants in the filtered ensemble (FE) which result in collapses (B < 10% B₀). The lightest grey tone indicates probability for the most sensitive species and successively darker tones the probabilities for two or more (up to 14) species. (b) Relationship between mean total yield from the community and fishing mortality. Grey shading and broken lines denote 50% and 90% uncertainty intervals, respectively.

We assessed contributions of each parameter to uncertainty in model outputs (Table 3). Parameters contributing most to overall uncertainty in the UE were L_∞ followed by the diet matrix, where only one option gave successful outcomes. The choices of M1, predator–prey size ratio, growth efficiency and HS-SRR parameters all made similar contributions to overall variance in model outputs; in each case, these parameter choices only accounted for about 60% of the variance generated by choice of L_∞. Only the diet matrix of Rochet et al. (2011) was incorporated in FE model variants. A single parameter choice was responsible for >50% of successful outcomes for predator–prey size ratio and growth efficiency, while the distribution was more even for M1, HS-SRR α and L_∞.

Table 3.

Proportion of accepted model variants in the filtered ensemble (FE) that incorporated each parameter option, and the relative variance in biomass projections related to each parameter in the unfiltered ensemble (UE). The relative variance describes the variance in biomass projections related to each parameter as a proportion of the variance in biomass projections related to asymptotic length. For parameter choices, see Table S1

	Parameter choice (FE)					Relative variance (UE)
	1	2	3	4	5
Diet matrix	1·00	0·00	0·00	0·00	0·00	0·83
Predation size selection	0·60	0·20	0·06	0·06	0·08	0·58
Natural mortality (M1)	0·25	0·17	0·36	0·19	0·03	0·60
Spawner–recruit (β)	0·04	0·09	0·22	0·45	0·20	0·59
Growth efficiency (Ge)	0·07	0·62	0·10	0·03	0·18	0·61
Asymptotic length (L∞)	0·15	0·08	0·16	0·23	0·38	1·00
Spawner–recruit (α)	0·21	0·09	0·31	0·19	0·20	0·65

Discussion

Incorporating plausible parameter uncertainty in model inputs led to many implausible outputs, and screening against data removed >99% of variants. The resulting FE was used to assess uncertainty in single species and community reference points and single species and community responses to alternate management actions. Probability distributions of outputs from the FE provided information on uncertainty. This can inform decisions on the values of reference points to achieve a defined reduction in risk that reference points are not exceeded. Some management frameworks are already designed to take account of information on uncertainty. For example, in the United States, the ‘Overfishing Limit’ (OL) corresponds to our central estimate of B_MSY while the ‘Acceptable Biological Catch’ (ABC) is set lower than the OL, with the difference between OL and ABC determined by the uncertainty in the OL prediction and the risk that the manager accepts (National Marine Fisheries Service ²⁰⁰⁹). Outputs from our FE can also be used to assess power of monitoring surveys to detect responses in different community metrics and to identify parameters where investment in future data collection or changes to model structure may be targeted to reduce uncertainty.

Results are clearly contingent on assumptions. In particular, assumed selectivity patterns and relative F among species have a significant influence on estimates of species' abundance, size composition and yield. For simplicity, we scaled F to all species uniformly in relation to F_MSY. This does not provide an accurate representation of the way F is applied to North Sea stocks, nor did it attempt to reflect a realistic alteration in F in response to management measures, although both issues could be addressed in future. Our preferred emphasis was on evaluating the extent and implications of uncertainty associated with multispecies and community predictions, rather than re-evaluating reference points for North Sea stocks.

Our main measure of indicator performance was sensitivity; the capacity to differentiate responses to changes in F. Another relevant measure is the specificity of response to fishing, the extent to which changes in the indicator are driven by fishing as opposed to other causes (e.g. Houle et al. ²⁰¹²). To evaluate specificity would require a model that sought to describe environmental and other influences on the fish community. Our evaluation of the capacity of four community indicators to describe change in state when transiting from historic North Sea F to the current management target of fishing at, or below, F_MSY (EU ²⁰¹³) demonstrated that SSS tracked change with lowest uncertainty. If model predictions of change were realistic then power analysis demonstrated that the NS-IBTS was more likely to detect trends in SSS, as defined here, than any other indicator. Power to detect changes in community indicators for strictly demersal species was better than for all demersal species, likely because the former are more effectively sampled by survey gear (Fraser, Greenstreet & Piet ²⁰⁰⁹) resulting in lower interannual variation. The more consistent and detectable response of SSS to changes in F compared with other community indicators, including the LFI, was consistent with results in Blanchard et al. (2014) based on a single parameterization of an alternate multispecies size-structured model that accounted for food-dependent growth and incorporated stochastic recruitment variation. Our power calculations assume that community changes associated with moving from F_HIST to F_MSY take 5 or 15 years. This allowed relative performance of indicators to be compared. We did not attempt to predict absolute rates of change in community indicators because they are highly dependent on stochastic processes, especially recruitment.

The frequency with which different parameter choices appear in the FE, coupled with relative variance in outputs associated with different parameters, helps identify when investment in refining parameter values may be desirable. Results suggested that the diet matrix was especially influential with neither empirically based diet matrix leading to accepted models. This may be due to limitations of diet studies that may not provide evidence of consumption when some prey species are small, relatively delicate and/or highly digestible, because they quickly become unidentifiable in stomach contents. This could apply to sprat consumption for example. Developing diet matrices likely requires consideration of other evidence for feeding interactions, as attempted by Rochet et al. (2011). Further, in models with no explicit representation of spatial structure, the diet matrix also identifies feeding interactions that are not feasible owing to species' spatial separation. The simple assumption that everything eats everything was not supported in our size- and species-based model. Some species require a refuge from predators in the modelled community for their dynamics to mimic those observed in data.

Our conclusions about the effects of parameter uncertainty may not hold for other models with more tightly coupled species dynamics or including food-dependent growth (e.g. Blanchard et al. ²⁰¹⁴). Further, much density dependence in our model is generated by the HS-SRR which fits quite poorly to data that are already expensive to generate. It is unlikely that more data would reduce our uncertainty about a relationship that has to be used in population models to capture a number of unspecified density-dependent processes that may be impossible to characterize given other sources of variation (e.g. Szuwalski et al. ²⁰¹⁴). Consequently, the advantages of a model structure that is robust to parameter uncertainty are balanced by disadvantages when model structure omits potentially important processes.

In summary, there have been few attempts to explore effects of uncertainty in multispecies models, which limits interpretation of outputs and their use in management advice. This study has demonstrated one practical method for explicitly introducing parameter uncertainty in model outputs and describing uncertainty in single species and community reference points and responses to fishing mortality. The research also demonstrates the level of caution that needs to be applied in interpretation of outputs from community models based on single parameter sets.

Data accessibility

The data used in this article are publicly available via the International Council for the Exploration of the Sea (ICES) Data Portal and from the Centre for Environment, Fisheries and Aquaculture Science (CEFAS) Integrated Database and Portal for Fish Stomach Records (DAPSTOM). More detailed descriptions of data sources are provided in the ‘Materials and methods’ section of this article.

Supporting Information

Additional Supporting Information may be found in the online version of this article.

Table S1

Parameter values in the unfiltered ensemble.

Table S2. Diet matrix option 1 (Rochet et al. ²⁰¹¹).

Table S3. Diet matrix option 3 with a cut-off diet fraction by numbers of 0·001 (Pinnegar & Platts, 2011).

Table S4. Diet matrix option 4 with a cut-off diet fraction by numbers of 0·01 (Pinnegar & Platts, 2011).

Table S5. Diet matrix option 5.

Fig. S1. Estimated predation mortality rates (M2) in the unfished system based on outputs from model variants in the filtered ensemble (FE) with 10¹⁰ g ‘other food’.

Fig. S2. Estimated predation mortality rates (M2) in the unfished system based on outputs from model variants in the filtered ensemble (FE) with 10⁹ g ‘other food’.

Fig. S3. Estimated predation mortality rates (M2) in the unfished system based on model variants in the filtered ensemble (FE) with 10¹¹ g ‘other food’.

Fig. S4. Fishing mortality as a function of length for the F_HIST (historic average 1990–2010, red line) and F_MSY (single species MSY estimates, blue line) scenarios.

Fig. S5. The number of models in the filtered ensemble (FE) as a function of the tolerance factor accepted when screening model outputs against ICES stock assessment data.

Fig. S6. The effects of changes to the tolerance factor on mean F_MSY (red) and associated uncertainty (50% uncertainty intervals: black bars; 90% uncertainty intervals: open bars).

Fig. S7. The effects of changes to the tolerance factor on values of four indicators and the associated uncertainty (50% uncertainty intervals: black bars; 90% uncertainty intervals: open bars).

Fig. S8. Frequency distributions for the predicted power of the North Sea International Bottom Trawl Survey (IBTS) to detect modelled changes in the values of community metrics for strictly demersal fishes (Lifetype D2, Table 1, accompanying paper) when fishing mortality is reduced from F_HIST to F_MSY over 5 year (grey) and 15 year (black) periods.

Fig. S9. Species' yields as a function of fishing mortality, as predicted with model variants in the filtered ensemble.