Bounds for Pure Direct Effect

To the Editor

The pure or natural direct effect quantifies the effect of an exposure on an outcome that is not mediated by an intermediate variable.^1–5 For exposure A, mediator M, and outcome Y, let M(a) and Y (a) = Y(a, M(a)) define the counterfactual mediator and outcome had exposure taken value a. Likewise, let Y(a,m) define the counterfactual outcome had exposure and mediator taken the values a and m; respectively. Finally let Y(a, M(a*)) denotes the counterfactual outcome had exposure taken value a and the mediator taken the value it would have under treatment a*. the average pure direct effect on the additive scale is then defined for a ≠ a *:

$$\mathit{PDE}(a,a^{\ast })=E\{Y(a,M(a^{\ast }))-Y(a^{\ast })\}$$

Throughout, assume that, as encoded in the diagram given in Figure 1A, treatment is randomized,

$$A\perp \perp \{Y(a,m),M(a)\}$$ (1)

and also, M is randomized within levels of A,

$$Y(a,m)\perp \perp M(a)|A=a$$ (2)

Figure 1.

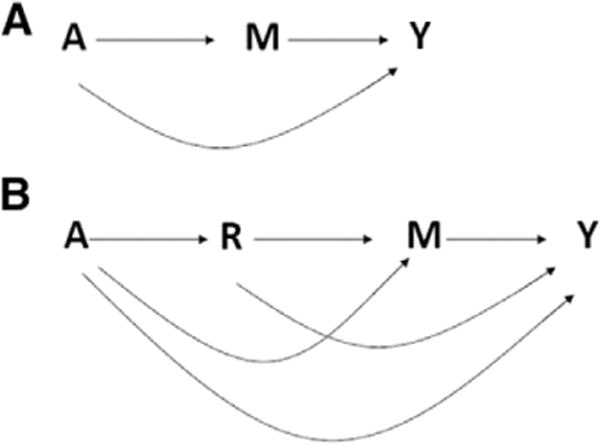
Assumptions (1) and (2) are sufficient under the 3-node diagram to identify the total average causal effect E {Y (a, m) − Y(a*, m)} and the controlled direct effect E{Y (a, m)−Y(a*, m)}. However, assumptions (1) and (2) taken to be the only counterfactual independencies for each value of a encoded in the 3-node mediator graph of Figure 1A do not suffice to identify counterfactual averages of the form E{Y (a, M(a*))}, and therefore, these assumptions alone cannot identify PDE(a, a*).

Identification of PDE(a, a*) has been controversial even in this simple setting, as it requires interpreting Figure 1A to encode additional counter-factual independencies, such that in addition to (1) and (2); we also have for all a; a* the following²:

$$Y(a,m)\perp \perp M(a^{\ast })|A=a$$ (3)

This latter assumption is sometimes described as simply requiring that, conditional on exposure, there is no unobserved confounding between the mediator and the outcome, as depicted in Figure 1A.^2–4 However, the assumption is much stronger, because it implies independencies about counterfactuals indexed by distinct treatment interventions (ie, cross-world counterfactual independencies), whereas, the traditional statement of no unobserved confounding (1) and (2) ensures that all counterfactuals involved in the independence statements are defined for a single treatment value a.^6,7 In principle, assumptions (1) and (2) can be made to hold experimentally, say by randomizing A and subsequently randomizing M conditional on A, whereas assumption (3) is more audacious and should be made with caution in practice, as it cannot be experimentally enforced and, therefore, it is not strictly subject to scientific scrutiny.⁶ robins and Richardson⁶ recommend altogether abandoning the cross-world independence assumption, therefore failing to identify PDE(a, a*), and propose reporting nonparametric bounds for PDE(a, a*) that rely only on assumptions (1) and (2). For binary Y, A, and M, the Robins–Richardson bounds⁶ are given for PDE(1, 0):

$$L\le \mathit{PDE}(1,0)\le U$$ (4)

$$\begin{array}{l}L=\max \left\{\begin{array}{l}0,\mathrm{Pr}(M=0|A=0)\\ +E[Y|A=1,M|=0]-1\end{array}\right\}\\ +\max \left\{\begin{array}{l}0,\mathrm{Pr}(M=1|A=0)\\ +E[Y|A=1;M=1]-1\end{array}\right\}\\ -E[Y|A=0]\\ U=\min \left\{\begin{array}{l}\mathrm{Pr}(M=0|A=0),\\ E\left(Y|A=1,M=0\right)\end{array}\right\}\\ +\min \left\{\begin{array}{l}\mathrm{Pr}(M=1|A=0),\\ E[Y|A=1,M=1]-E[Y|A=0]\end{array}\right\}\end{array}$$

Tchetgen Tchetgen and VanderWeele consider identification of PDE(a, a*) under the 4-node mediation graph with exposure-induced confounder R as depicted in Figure 1B.⁷ the mediator in this diagram is subject to exposureinduced confounding, which by the recanting witness criterion, renders PDE(a, a*) nonidentified from the observed data, even if instead of (3); one were to assume the nonparametric structural equations model with independent errors (NPSEM-IE) representation of the diagram in Figure 1B.⁷ Under these assumptions, we have that conditioning on A and R recovers cross-world counterfactual independencies for the mediator and outcome,⁷ that is for all a and a*

$$Y(a,m)\perp \perp M(a^{\ast })|A=a,R(a)=r$$ (5)

Tchetgen Tchetgen and VanderWeele⁷ establish that PDE(a, a*) becomes identified in the NPSEM-IE for Figure 1B provided an additional assumption also holds, either

1. the treatment and confounder R are binary and the effect of treatment on R is monotone at the individual level, that is, R(a*) ≤ R(a) for a* < a, or,

2. there is no average additive interaction between R and M in their joint effects on Y, that is,

   $$\begin{array}{l}E\left(Y|a,m,r\right)-E\left(Y|a,m^{\ast },r\right)\\ -E\left(Y|a,m^{\ast },r\right)+E\left(Y|a,m^{\ast },r^{\ast }\right)=0\end{array}$$

Alternative identifying assumptions under the NPSEM-IE were also considered by Robins and Richardson.⁶ Note that Tchetgen Tchetgen and VanderWeele⁷ thus continue to make a cross-world counterfactual independence assumption now given by (5). Here, we extend the Robins–Richardson bounds for PDE(a, a*) so that they may be used in the presence of exposure-induced confounding as depicted in Figure 1B upon interpreting the causal diagram strictly as encoding assumptions (1) and

$$Y(a,m)\perp \perp M(a)|A=a,R=r$$ (6)

In the eAppendix, we establish that for binary A and M, and a = 1, a* = 0, under assumptions (1) and (6),

$$L^{\ast }\le \mathit{PDE}\left(1,0\right)\le U^{\ast }$$ (7)

$$\begin{array}{l}{L}^{\ast }=\max \{0,\mathrm{Pr}(M(0)=0)+E[Y(1,0)]-1\}\\ +\max \{0,\mathrm{Pr}(M(0)=1)+E[Y(1,1)]-1\}\\ -E[Y(a=0)]\\ U^{\ast }=\min \{\mathrm{Pr}(M(0)=0),E[Y(1,0)]\}\\ +\min \left\{\begin{array}{l}\mathrm{Pr}(M(0)=0),E[Y(1,1)]\\ -E[Y(a=0)]\end{array}\right\}\end{array}$$

Therefore, the bounds L* and U* are identified provided E [Y (a,m)], E [Y (a)], and E [M(a)] are themselves identified. Under the usual no unobserved confounding assumptions (1) and (6), we indeed have

$$\begin{array}{c}E[Y(a,m)]={\displaystyle \sum _{r}E[Y|a,m,r]}f(r|a),\\ E[Y(a)]=E[Y|a],\\ E[M(a)]=E[M|a]\end{array}$$