A Combined Covalent-Electrostatic Model of Hydrogen Bonding Improves Structure Prediction with Rosetta

Abstract

Interactions between polar atoms are challenging to model because at very short ranges they form hydrogen bonds (H-bonds) that are partially covalent in character and exhibit strong orientation preferences; at longer ranges the orientation preferences are lost, but significant electrostatic interactions between charged and partially charged atoms remain. To simultaneously model these two types of behavior, we refined an orientation dependent model of hydrogen bonds [Kortemme et al. 2003] used by the molecular modeling program Rosetta and then combined it with a distance-dependent Coulomb model of electrostatics. The functional form of the H-bond potential is physically motivated and parameters are fit so that H-bond geometries that Rosetta generates closely resemble H-bond geometries in high-resolution crystal structures. The combined potentials improve performance in a variety of scientific benchmarks including decoy discrimination, side chain prediction, and native sequence recovery in protein design simulations, and establishes a new standard energy function for Rosetta.

1 INTRODUCTION

The accurate modeling of interactions between polar atoms remains an important problem that impacts efforts to predict and design macromolecular structure. Hydrogen bonds (H-bonds) and H-bond networks play a central role in stabilizing polar interactions, and considerable effort has been put into building and testing computational procedures for modeling them.^1–6 The properties that make H-bonds essential for biological function also make them challenging to model. H-bonds, like covalent bonds, form geometrically specific interactions that help biomolecules adopt conformations necessary for binding and catalysis. However, the orientation preferences of H-bonds are weaker than those of covalent bonds, allowing a diversity of interaction geometries, and unlike covalent bonds, H-bonds are weak enough that they can easily break and form during a folding or binding event. The distance and orientation of a specific H-bond in a well-folded protein depends not only on the energetic preferences of that bond, but on all the covalent and non-covalent forces that determine the low free energy conformation of the protein. These challenges mean existing forcefields often under- or double-count the forces contributing to H-bond formation. Recent progress in computational methods now allow us to empirically evaluate the performance of existing H-bond models and adjust them to improve recapitulation of local geometries as well as overall structure prediction accuracy, which we undertake here for the H-bond model in the Rosetta forcefield.

Three primary strategies have been developed for modeling H-bonds. First, quantum mechanics (QM) calculations can capture the partial covalent bond character of H-bonds, but are generally too computationally intensive to use when scoring large numbers of alternative conformations of a macromolecule.^7–9 Second, many programs for macromolecular simulations use an electrostatic model to evaluate H-bonds.^10–16 These models typically fix isotropic partial charges to atoms and evaluate Coulomb’s law over all pairs of charges. In this strategy a H-bond is rewarded because the hydrogen has a partial positive charge that interacts favorably with the negatively charged acceptor. This strategy is powerful because it applies to a diverse array of chemical types and captures some of the known geometric preferences of H-bonds, such as the preference to place the positively charged hydrogen directly between the negatively charged acceptor and donor (i.e. AHD = 180°, in Fig. 1). Such atom-centered electrostatic models, however, cannot capture geometric preferences that arise from a non-uniform distribution of electrons on the acceptor. A clear example of this occurs with sp²-hybridized oxygens, where an atom-centered electrostatic model prefers to align the donor, hydrogen, acceptor, and carbon bound to the acceptor (labeled BB, in Fig. 1) for a favorable interaction between the donor-hydrogen dipole and the acceptor-acceptor base dipole. QM calculations and examinations of H-bonds in high-resolution crystal structures indicate that the most favorable H-bonds instead align the donor-hydrogen dipole with a vector defined by the acceptor and its lone pair electrons.^17,18 One could capture these preferences in an electrostatic model by placing partial charges on the lone pair positions¹⁹ or using multipole expansion about the atomic centers,^20–22 but these are not standard approaches.

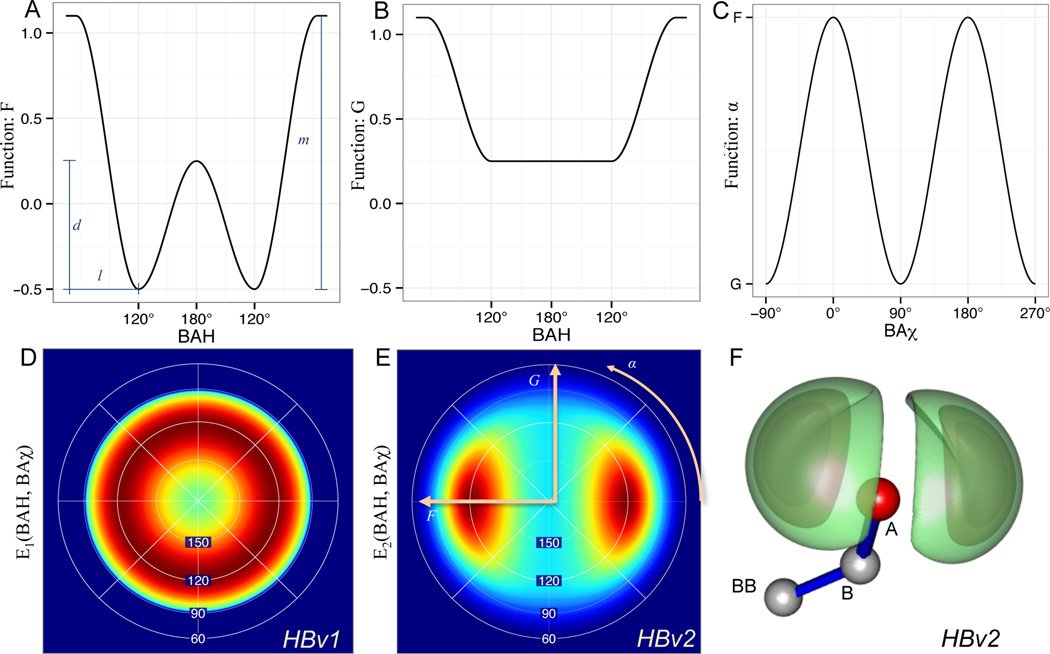
Figure 1.

H-bond degrees of freedom in HBv2 are defined on the Acceptor BBase, Base, and Acceptor atoms and the Donor Hydrogen and Donor atoms, depending on the chemical types (S.4.1).

The third strategy for modeling H-bonds includes explicit terms in the energy function that depend on the distance and relative orientation of the atoms forming the H-bond, for example in classic forcefields such as Lippincott and Schroeder²³, structure evaluation programs such as DSSP²⁴ and WHAT-IF²⁵, in structure prediction programs such as Rosetta¹⁷, SMoG²⁶, YETI²⁷, Xplor-NIH²⁸, ligand docking programs such as Hammerhead/Surflex²⁹, and semi-empirical forcefields such as ABEEMσπ/MM¹⁵, MM3^30–32, and PM6³³, each of which were designed to capture the partial covalent character of H-bonds. These and other terms in molecular energy functions are called knowledge-based if they are non-parametrically derived from the observed frequencies of local geometric features (e.g. H-bond distances and angles) in high-resolution crystal structures, or called empirical if a parametric functional form is fit so structure predictions recapitulate experimental data. Prior to this work, the modeling program Rosetta used knowledge-based energy terms to evaluate hydrogen-acceptor distances, donor-hydrogen-acceptor angles, and hydrogen-acceptor-acceptor base angles in H-bonds¹⁷. These terms recapitulate distance and orientation preferences of H-bonds from QM simulations, and improve Rosetta’s performance in a variety of scientific benchmarks. With this H-bond model, Rosetta has been used to predict and design a variety of macromolecular structures, including novel protein folds and assemblies.^34–39 However, many modeling problems, especially those involving polar interactions, remain challenging. For example, for Rosetta-designed protein-protein interactions, the more extensive the H-bond network, the more likely they were to fail in the laboratory.⁴⁰ For these reasons, we revisited the H-bond model in Rosetta to see if we could improve its ability to create native-like H-bond geometries and improve performance in large-scale benchmarks that depend on energy function accuracy.

Two observations suggest that it should be possible to improve the current knowledge-based H-bond model in Rosetta, here denoted as HBv1 (H-Bond potential, version 1). First, some orientation preferences noticed in the original H-bond study by Kortemme and Morozov were not encoded in Rosetta, most notably, the preference for H-bonds to align with the lone pair electrons on the oxygen. This preference is seen in the distribution of the BA_χ dihedral angle (Fig. 1) defined by the hydrogen atom, the acceptor atom, the acceptor base, and an atom covalently bound to the acceptor base; for angles of 0° or 180°, the hydrogen is co-planar with the lone pair electrons. Kortemme and Morozov found more H-bonds with BA_χ near 0° and 180°, than with BA_χ near 90°. This preference, however, was not implemented in the Rosetta energy function.

Second, we hypothesized that since HBv1 is a knowledge-based potential derived solely from native H-bond geometries, combining it with the rest of the energy function leads to double counting that may produce non-physical H-bond geometries. For instance, in Rosetta simulations, both the HBv1 and the van der Waals terms influence the distribution of H-bond distances. Correcting model interaction by reducing the dissimilarity between local Rosetta and native H-bond distribution—to create empirical potentials—has recently become possible for two reasons: We have developed sophisticated sampling protocols, incorporating stochastic sampling and gradient-based minimization of both backbone and side chain torsion angles, enabling efficient sampling of the intrinsic preferences of the energy function,⁴¹ and we have developed a computational framework for rapidly exploring and comparing distributions of local geometric features, facilitating evaluating the physical realism of Rosetta generated H-bonds.⁴²

In this study, we not only reevaluate the distance and angle dependent functions used within HBv1, but also reexamine the decision to use an explicit H-bond term rather than an atom-centered electrostatic model. As mentioned above, an explicit H-bond term can capture orientation preferences at close range, but an electrostatic model can provide other advantages, including favorable interactions at longer ranges, potentially allowing H-bond donors and acceptors to more easily find each other during conformational sampling, and providing repulsive forces between atoms of like charge, where HBv1 provides only attractive forces. For example, in previous studies with Rosetta, HBv1 produced non-native oxygen-oxygen contacts that would be destabilized under an electrostatic model.⁴³ Other work with Rosetta suggests that adding electrostatics to HBv1 can improve performance in large-scale scientific tests, such as decoy discrimination.¹⁸ Thus, we also explore combining the explicit H-bond model in Rosetta with an electrostatics model. Other laboratories, however, have reported mixed results when combining explicit H-bond terms with an electrostatic model.^{11,27,44–48} Integrating these closely related models to produce native-like H-bond geometries is a significant challenge, but gives an opportunity to capture the dual nature of H-bonds: allowing covalent-bond-like orientation preferences while adopting a wide array of nearly isoenergetic configurations.

To evaluate H-bond and electrostatic models we used two types of computational tests. First, we examined how well low energy structures generated by Rosetta under various energy functions recapitulated properties of native H-bonds; we call these feature recovery tests.⁴² Feature recovery tests not only report the intrinsic orientation preferences of a particular H-bond model, but also probe if the model is appropriately balanced with other terms in the energy function. Second we evaluated large-scale scientific benchmarks for structure prediction and design, including discriminating native from non-native protein conformations, predicting free energies of mutation, predicting protein side chain and loop conformations, and recovery of native-like sequences when performing protein design simulations on native protein backbones.

Using the feature recovery tests and scientific benchmarks we evaluated various functional forms for the explicit H-bond model and tested this model in conjunction with a distance-dependent Coulomb model of electrostatics. We show improved feature recovery test results for an H-bond model that includes additional orientation constraints for sp² and sp³ acceptors. Using an electrostatics model alone generates H-bonds with non-native geometries, but combining explicit H-bond potentials with an electrostatics model can produce native-like geometries if the H-bond model is reparameterized to account for the new forces generated by the electrostatic potential. The final combined covalent-electrostatic model of H-bonding improved performance in all of the scientific benchmarks.

2 RESULTS

2.1 Measuring recapitulation of native feature distributions

To characterize H-bonding preferences of native conformations we used the Top8000 chains set^49,50 curated from X-ray crystal structures deposited in the Protein Databank.⁵¹ We placed H-atoms with Reduce⁵² and filtered at the 70% homology level and by the availability of electron density maps, yielding ~1.3 million intra-protein H-bonds which we call the Native set. Then, using Rosetta’s Feature Analysis framework,⁴² we used the ReportToDB RosettaScripts Mover to extract geometric observables (features) including H-bond degrees of freedom (Fig. 1), donor and acceptor chemical types (S.4.1), and primary sequence separation (SeqSep) into a relational database. Finally, using feature analysis R scripts, we sampled feature instances from the feature database, derived feature distributions using kernel density estimation, and visualized them using grammar of graphics.^53,54

To characterize H-bonding preferences of candidate energy functions we optimized each native conformation with Rosetta’s FastRelax protocol,⁴¹ which iterates between discrete sidechain optimization and quasi-Newton minimization while ramping up Lennard-Jones repulsion. FastRelax typically displaces a native structure ~1.5 Å all-atom RMSD from its starting coordinates (Tbl. 1). Assuming the experimentally observed crystal structure is at a minimum in nature’s energy function, systematic discrepancies between Rosetta-relaxed the Native feature distributions reveal problems with the energy function.

Table 1.

Scientific Benchmark Results¹

Energy Function	Rlx. Native		Rotamer Recovery						Sequence Recovery				Loop Rec.		Decoy		ΔΔG
	RMSD		One		Cluster		All		Monomer		Interface		Med. Top5		Discrim.		Point Mut.
	(Å)	SEM	(%)	SEM	(%)	SEM	(%)	SEM	(%)	SEM	(%)	SEM	(Å)	SEM	Score	SEM	(R)	SEM
Score12	1.86	0.014	81.54	0.009	65.91	0.17	76.69	0.16	37.0	0.27	37.6	0.29	0.82	0.24	−2.89	0.12	0.67	0.021
Elec	1.96	0.014	83.29	0.017	69.59	0.17	79.19	0.16	38.5	0.38	38.3	0.28	0.67	0.18	−6.02	0.13	0.66	0.022
HBv1	1.85	0.014	82.98	0.014	70.20	0.17	78.81	0.16	36.1	0.38	39.2	0.32	0.94	0.19	−3.56	0.19	0.66	0.022
HBv2	1.88	0.014	83.13	0.007	70.84	0.16	78.85	0.16	36.8	0.21	38.7	0.36	0.88	0.22	−3.99	0.17	0.65	0.022
ElecHBv1	1.75	0.013	83.58	0.017	70.66	0.16	79.50	0.16	38.4	0.38	40.4	0.28	0.67	0.18	−5.77	0.13	0.67	0.021
ElecHBv2	1.76	0.013	84.50	0.015	71.65	0.16	80.30	0.15	39.8	0.30	40.3	0.29	0.64	0.18	−6.85	0.12	0.68	0.021

¹The top performer for each benchmark is bold. Standard errors of the mean (SEM) are computed as follows: RlxNat, LoopRec: $\frac{\sigma }{\sqrt{n}}$, (RotOne, SeqMon, SeqIFace, DecoyDis): Residual SE from loess fit to H-bond weight sweep (Fig. 8), (RotClust, RotAll): $\sqrt{\frac{pq}{n}}$ where $p=1-q=\frac{\%\text{Rec}}{100},\mathrm{\Delta }\mathrm{\Delta }\mathrm{G};\sqrt{\frac{1-R^2}{n-2}}$.

Sections (2.3–8) describe H-bond feature discrepancies identified in HBv1, and corrected in a new model, HBv2.

2.2 HBv1 and HBv2 Functional Forms

Given donor and acceptor, the HBv1 model is the sum of 3 terms of the AH_dis, BAH, and AHD degrees of freedom, clipped at 0 and down weighted by solvent exposure of the sites (w_env ∈ [0.2, 1]),

$$E_{\mathrm{H}\mathrm{B}\mathrm{v}1}=w_{\text{env}}\text{min}(0,f_{A{H}_{\mathit{\text{dis}}}}^1+g_{AHD}^1+h_{BAH}^1)$$ (1)

The model parameters depend on the hybridization of the acceptor (sp², sp³, or ring), whether the sites are backbone or sidechain, and the sites’ sequence separation. BAH and AHD functions switch between a “long” range and “short” range form depending on the length of the H-bond (AH_dis). Further details about HBv1, including cross-term fade functions (2.8, S.3.22) and the backbone/sidechain-exclusion rule (2.6) are discussed below.

To more explicitly capture the preference of H-bonds to align with the lone pair electrons on acceptors, the HBv2 model replaces $h_{BAH}^1$ with a term $h_{BAH,B{A}_{\chi }}^2$ (Fig. 2) that evaluates both BAH and BA_χ and replaces the hard min with a smooth min, s(x) = {x, −2.5x² + 0.5x − 0.025, 0} with breaks at −0.1 and 0.1,

$$E_{\mathrm{H}\mathrm{B}\mathrm{v}2}=w_{\text{env}}s(f_{A{H}_{\mathit{\text{dis}}}}^2+g_{AHD}^2+h_{BAH,B{A}_{\chi }}^2)$$ (2)

Figure 2.

The $h_{BAH,B{A}_{\chi }}^2$ functional form for sp² acceptors avoids a numeric instability in BA_χ at BAH angle 180°, by smoothly interpolating between in-plane (A) and out-of-plane (B) BAH potentials as a function of BA_χ (C): $h_{BAH,B{A}_{\chi }}^2$. The Lambert-azimuthal projection of $h_{BAH}^1$ (from HBv1) (D), $h_{BAH,B{A}_{\chi }}^2$ (from HBv2) (E) and 3d rendering of E_HBv2 (F) with a linear AHD and contoured at [−1.2,−1.0, and − .78] shows that HBv2 describes two symmetric lobes corresponding to the ideal sp² orbitals, while HBv1 does not.

HBv2 expands the chemical types based on chemical groups (S.4.2). It eliminates dependence on sequence separation and the separate AHD and BAH functions for short and long values for AH_dis

2.3 Modeling sp^>2 hybridized acceptors

To investigate sp² acceptor H-bond angle preferences, we compared the joint (BAH, BA_χ) distribution for Native against HBv1, which does not model the BA_χ angle, visualized by the density-preserving Lambert-azimuthal projection (Fig. 2D, S.3.2).

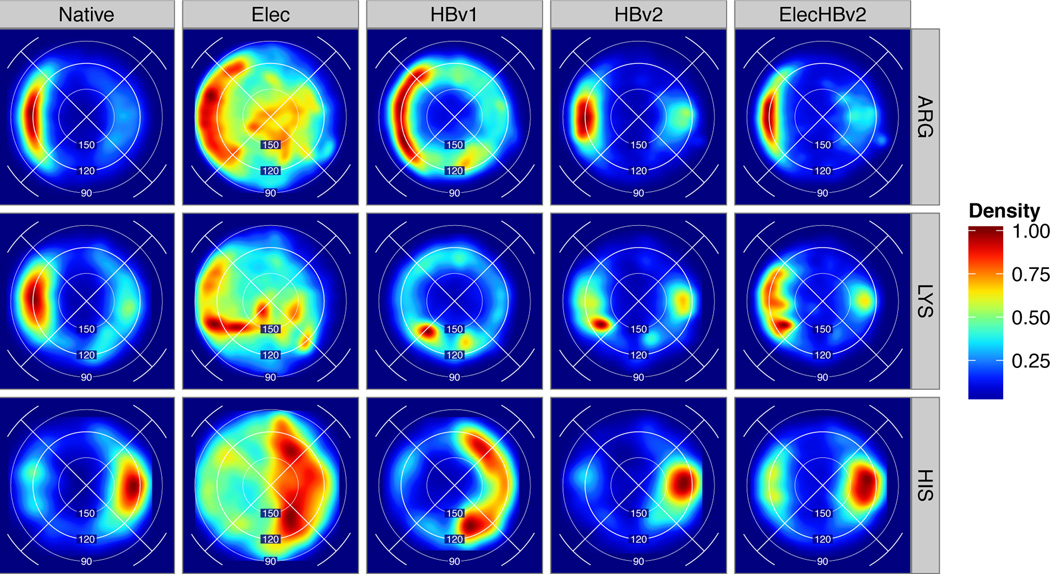
Overall, the Native distribution (Figs. 3,4,5B, S.3.1, S.3.3) concentrates density in two lobes in the sp² plane consistent with the planar orientation of the lone-pair orbitals. For some chemical types, such as carboxylate-hydroxyl (D/E to S/T) and carboxamide-hydroxyl (N/Q to S/T), we observe equal density for the trans and cis orbitals, while for others, such as carboxyl-guanidino (D/E to R) and backbone-backbone with SeqSeq > 5, the trans orbital receives more density (Fig. 3,4). It was not immediately obvious whether the observed differences between the two orbitals would require that the energy function assign different energies to them; perhaps other factors could explain the differences. For example, bidentate salt-bridges (D/E to R)⁵⁵ may explain carboxyl-guanidino’s trans orbital preference and the predominance of anti-parallel β-sheets may explain backbone/backbone’s cis orbital preference.

Figure 3.

H-bond geometries for Asp and Glu acceptors paired with charged donors from native protein structures and models created with different energy functions: Elec, HBv1, HBv2 and ElecHBv2. For each cell, the Lambert-azimuthal projection of the conditional (BAH, BA_χ) feature density is estimated and scaled to the range [0,1].

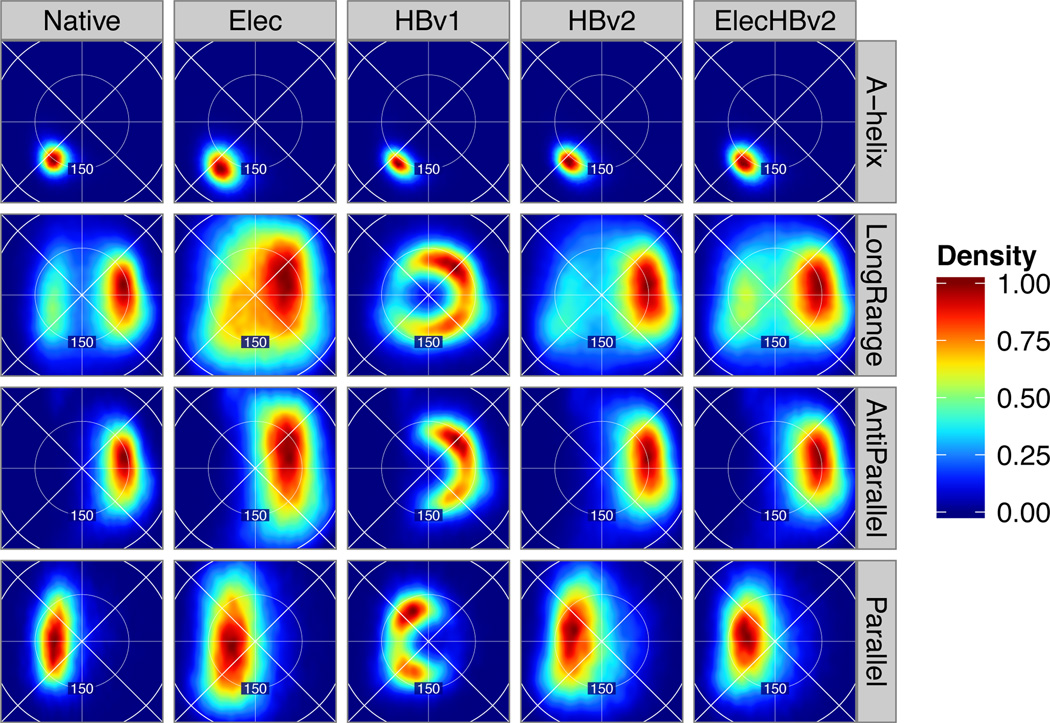
Figure 4.

Geometries of backbone-backbone H-bonds. Lambert azimuthal projection of BAH, BA_χ feature density for α-helices, residue pairs with sequence separation greater than 5 (LongRange), anti-parallel and parallel β-sheets by sample source (columns). The Native-LongRange interactions show a distinctive “beetle” shape that we sought to recapitulate with HBv2.

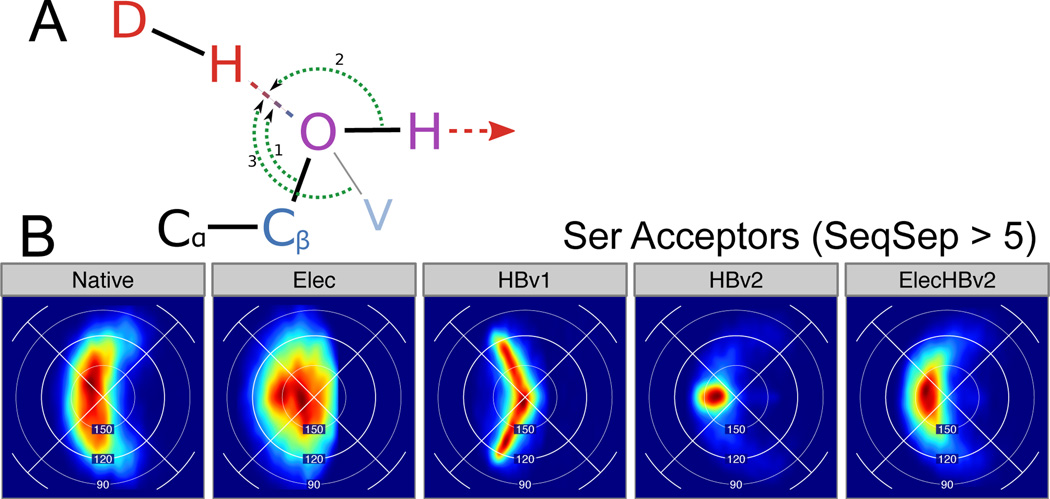
Figure 5.

Serine hydrogen bonds. (A) Schematic of a serine hydroxyl group accepting an H-bond. Choices of the Base atom define the BAH angle; HBv2 uses C_β (1), HBv1 uses H (2), and the visualization use V (3). (B) Lambert azimuthal projection of (BAH, BA_χ) feature density for H-bonds with serine Acceptors, with SeqSep > 5.

HBv1 recapitulates BAH angle preferences, but the BA_χ distribution bears very little resemblance to the Native distribution: The carboxylate-hydroxyl BA_χ distribution is flat, giving a “donut” shape plot (S.3.3). The carboxylate-amino (D/E to K) distribution is out-of-phase, peaking at 90° and 270° with troughs at 0° and 180°. The backbone-backbone distribution is similarly distorted. The fact that the Native BA_χ distribution does not emerge from the HBv1 energy function suggests the combination of the $f_{A{H}_{\mathit{\text{dis}}}}^1,g_{AHD}^1$, and $h_{BAH}^1$ functions and sterics is insufficient. Surprisingly, we found for HBv2 that a simple, symmetric potential (Fig. 2) reproduced not only the in-plane preference, but also interesting features of the Native sp² distributions in a range of contexts. It reproduced the relative in-plane preferences for carboxylate-hydroxyl versus carboxamide-hydroxyl H-bonds; the “beetle” shape in the Lambert-azimuthal projection for long-range backbone-backbone H-bonds (Fig. 4); and the strong preference for a BA_χ dihedral of 180° that carboxyl-guanidino H-bonds show (S.3.1). That is, sterics (broadly construed as “the shape of chemical groups”) explains a significant fraction of the differences between the distributions of different acceptor/donor chemical types. We parameterize HBv2 consistently across all sp² hybrized acceptors, allowing steric interactions between them and their donors to form (with some exceptions) native-like H-bond distributions.

Consider backbone-backbone H-bonds. HBv1, which was formulated as a knowledge-based potential, uses different $h_{BAH}^1$ terms for backbone-backbone contacts with a sequence separation > 4, = 4, and < 4. The terms have minima at 158°, 150°, and 123°, and score term weights 1, 0.5, and 0.5, respectively. In contrast, HBv2 uses the same $h_{BAH,B{A}_{\chi }}^2$ term (Eq. 2) for all sp² acceptor H-bonds yet, to a high degree, recapitulates the BAH distributions conditional on sequence separation (Fig. 4, S.3.8). Since comparing conditional feature distributions for near-native conformations does not reveal inter-class energetic preferences (e.g. should helical H-bonds be “worth” more than β-sheet H-bonds?), we make HBv2 assign equal minimum energy to each H-bond (S.3.9) and assess this decision through structure prediction scientific benchmarks discussed below.

HBv2 offers a cautionary example about double counting in knowledge-based potentials. If we had set out to fit non-parametric BA_χ potentials for each chemical context we would have encoded steric effects. The dynamic range for carboxyl-hydroxyl BA_χ energies would have been higher than those for carboxamide-hydroxyl contacts and the trans orbital would have been preferred over the cis orbital in carboxyl-guanidino contacts. When combined with sterics already present in our sidechain geometries, this would have “double counted” the trans orbital preference and produced the wrong distributions. Additionally, to be computationally feasible, macromolecular prediction protocols typically introduce bias relative to the canonical ensemble for the energy function, for example, by including coordinate minimization, or terminating sampling before proper mixing has been achieved. Therefore using empirical methods to test the energy function in the context of relevant prediction protocols ensures the energy function is useful in practice.

Surprisingly, use of the HBv2 model improves the close H_α-O distance distribution across β-strands (S.3.26), which some have attributed to weak carbon H-bonding.^56–59 This suggests that the sp² character of β-sheet H-bonds may contribute to β-strand shearing and shorten H_α-O distances.

A further benefit of a simple model, such as the $h_{BAH,B{A}_{\chi }}^2$ term, is that identifying contexts with poor recapitulation can suggest further energy function refinements. For example, native H-bonds with sidechain donors and backbone acceptors have less sp² character than those to sidechain sp² acceptors (S.3.1). This may result from averaging over constrained secondary-structure-dependent motifs such as ST-turns. HBv2 should show these motif effects as it consists of relaxed-natives; however, it over-accentuates the BA_χ angular dependence. Intriguingly, backbone-lysine contacts, which illustrate this failure (S.3.4), should be mediated by electrostatics due to the formal charge and relative flexibility of lysine sidechains, which HBv1 and HBv2 model only at the residue level. When combined with the Elec model (Sec 2.10–11), the sp² character is reduced across the board, making the ElecHBv2 more close to the Native distribution.

2.5 Modeling sp³ hybridized acceptors

In both HBv1 and HBv2, the acceptor type determines how BAH is measured. In HBv1, the BAH for hydroxyl (sp³) acceptors is measured as the angle between the donor hydrogen, the heavy-atom acceptor (e.g. OG on serine) and the hydroxyl hydrogen (e.g. HG on serine) attached to the acceptor (Fig. 5A); the “base” is taken as the hydrogen instead of the carbon to which the hydroxyl oxygen was bound (e.g. CB on serine). The rationale for this decision was to avoid hydroxyl/hydroxyl H-bonds where the two hydrogens would both donate and the two oxygens would both accept.

We compared the distributions of BAH and HAH angles (measured from CB and HG, respectively) from Native and HBv1. Surprisingly, HBv1’s BAH distribution matched the Native distribution better than the HAH distribution, despite HAH being explicitly modeled (S.3.10 and S.3.11). We were also curious whether we could see a preference for sp³-hybridized acceptors to accept at the lone-pair positions in a way analogous to what we observed for sp²-hybridized acceptors. Since hydrogen atoms are invisible in crystal structures and their locations have to be inferred, we examined H-bonds only where the hydroxyl acted as an acceptor and where the location of a second nearby acceptor could unambiguously locate the hydroxyl hydrogen. We again relied on the Lambert-azimuthal projection, this time placing the hydroxyl hydrogen along the positive x-axis. Instead of observing two peaks in the distribution above and below the x-axis where the two sp³ lobes would be found, we found a single, broad distribution (Fig. 5B). In contrast to the Native distribution, the HBv1 distribution was too narrow and curved in the wrong direction.

We fit a new polynomial for the $h_{BAH,B{A}_{\chi }}^2$ function in E_HBv2 for sp³ hybridized acceptors, again as a polynomial of cos(BAH). We also included a sinusoidal penalty term for locating the hydroxyl hydrogen near the donor hydrogen. For sp³ hybridized acceptors, the $h_{BAH,B{A}_{\chi }}^2$ function uses the BA_χ dihedral (e.g. defined by [H_γ, C_β, O_γ, H_don] for serine acceptors, Fig. 5A):

$$h_{BAH,B{A}_{\chi }}^2=\text{poly}(\text{cos}(BAH))+\frac{1}{4}(1+\text{cos}(B{A}_{\chi }))$$ (3)

The coefficients for the polynomial were fit while enforcing a derivative of 0° at BAH=180° (unlike the BAH polynomials used in HBv1), although the cos (BA_χ) term adds a derivative discontinuity/numerical instability of its own. Our choice is for computational efficiency, and could be replaced with a term that examined the [H_OH, O, H_don] angle (Angle (2) in Fig. 5A). The effects of this discontinuity seem mild, however, and are not discernable in the distributions produced by HBv2. The BAH, HA, and Lambert-azimuthal BAH/BA_χ distributions for HBv2 match the Native distribution well (Fig. 5B, S.3.10, S.3.11).

2.6 Modeling hydroxyl donor behavior

We were surprised that the Native distributions of the χ₂ dihedral angles for donor serines and threonines (controlling the placement of the hydroxyl hydrogen atom) did not cluster at the staggered dihedral angles of 60°, − 60°, and 180°. Instead, they were non-uniformly distributed (S.3.12), generally with a broad depression at χ₂ = 0°, often with a peak at χ₂~ ± 90° and broad density between 90° and 270°. In HBv1, SER/THR χ₂ was sampled only at the staggered values, missing many H-bonds that could have been formed to nearby acceptors. We expanded χ₂ sampling, taking samples at 20° intervals starting from 0°.⁶⁰ The resulting distribution for χ₂ matched the Native distribution from structures generated in the AbRelax protocol in spite of having no explicit penalty for χ₂ near 0°; sterics again seems the most likely source of the nonrandom shape of the χ₂ distribution. This indicated that a special potential on χ₂ to recover the observed distribution was not needed.

In contrast to serine and threonine, tyrosine shows a striking preference to donate in the plane, as has been previously observed.^61,62 In HBv1, TYR χ₂ was sampled at 0° and 180° when building rotamers during packing, yielding the correct distribution, and we preserved that behavior in HBv2. We nevertheless added a term to the score function, yhh_planarity, which puts a sinusoidal penalty on χ₂ to prevent H-bonds formed in the phenol plane from minimizing out of it.

In studying the way we modeled sp³ donors, we reevaluated HBv1’s rule that excludes sidechain/backbone H-bonds if the backbone group is already participating in a backbone/− backbone H-bond. The aim of this rule is to avoid forming H-bonds in α-helices where a serine on residue i donates to a backbone carbonyl on residue i − 3, or where a threonine on residue i donates to a backbone carbonyl on residue i − 4. Such intra-helical H-bonds are rarely observed in real proteins, but are commonly found in Rosetta designs made without this rule. We hoped HBv2’s more stringent geometric requirements would allow us to disable this rule, but these intra-helix H-bonds form with quite good H-bond geometries (S.3.13–16). We therefore preserved this rule in HBv2.

2.7 Improving AHD distributions

In HBv1, the polynomial $g_{AHD}^1=\text{poly}(\text{cos}(AHD))$ defined the dependence on the AHD angle. The cosine transformation is the appropriate volumetric normalization for the AHD angle, and is more rapidly computed than the angle itself. The HBv1 polynomials, however, were fit with no restriction that their derivatives should be 0° at an AHD angle of 180°. This left a derivative discontinuity at 180°, the energy minimum, accumulating density at the pole when structures were minimized. Our attempts to constrain HBv2 polynomials to have a derivative of zero at AHD = 180° produced AHD distributions that insufficiently favored H-bonds with AHD near 180° until we fit polynomials to AHD itself, $g_{AHD}^2=\text{poly}(AHD)$, which produced native-like distributions (S.3.18 and S.3.19).

2.8 Improving AH_dis distributions

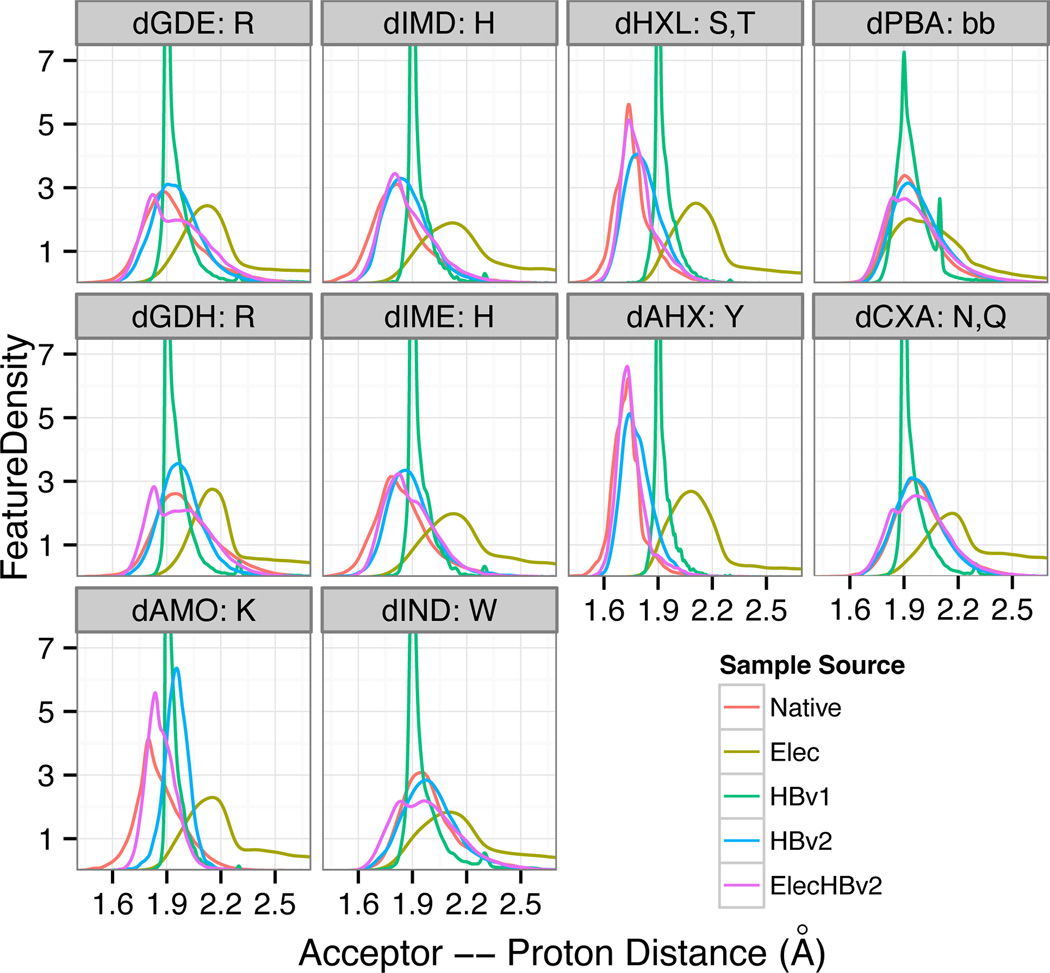
The AH_dis distance distributions generated by HBv1 differ from Native in both the location and shape of the peaks. In most cases, the peak locations matched those of the Native, with notable exceptions for hydroxyl donors, while the HBv1 distributions were consistently sharper (Fig. 6).

Figure 6.

H-bond distances (sequence separation greater than 5) as a function of donor type from native protein structures and models created with different energy functions.

The HBv1 distributions also showed consistent artifacts with small, sharp peaks occurring at 1.9 and 2.1 Å (S.3.20). We have previous encountered this type of artifact at the locations of derivative discontinuities; discontinuities frustrate gradient-based minimization, producing pileups.⁴² Now, HBv1 employed piecewise linear functions of the cross terms that range between zero and one (fade functions) to disable the interaction when any one dimension becomes too extreme and also to interpolate between the short- and long-range angle polynomials. The terms from (Eq. 1) have the following functional form,

$$f_{A{H}_{\mathit{\text{dis}}}}^1=\text{poly}(A{H}_{\mathit{\text{dis}}})I_{AHD}{I}_{BAH}$$

$$g_{AHD}^1={\text{poly}}_s(AHD)I_{A{H}_{\mathit{\text{dis}}}}^s{I}_{BAH}+{\text{poly}}_l(AHD)I_{A{H}_{\mathit{\text{dis}}}}^l{I}_{BAH}$$ (4)

$$h_{BAH}^1={\text{poly}}_s(AHD)I_{A{H}_{\mathit{\text{dis}}}}^s{I}_{AHD}+{\text{poly}}_l(AHD)l_{A{H}_{\mathit{\text{dis}}}}^l{I}_{AHD}$$

which is visually depicted in (S.3.22). Notably, the spline knots of $I_{A{H}_{\mathit{\text{dis}}}}^s$ and $I_{A{H}_{\mathit{\text{dis}}}}^l$ coincided with the artifacts at 1.9, 2.1, and 2.3 Å and, indeed, using smooth polynomial fade functions partially reduced the artificial accumulation at these distances. Use of the fade functions, however, also increased the complexity of the H-bond functional form. For example, the H-bond energy depends on AH_dis not only through $f_{\mathrm{A}{\mathrm{H}}_{\mathit{\text{dis}}}}^1$ via poly(AH_dis) but also through $g_{\mathrm{A}\mathrm{H}\mathrm{D}}^1$ via $I_{\mathrm{A}{\mathrm{H}}_{\mathit{\text{dis}}}}^s$ and $h_{\mathrm{B}\mathrm{A}\mathrm{H}}^1$ via $I_{\mathrm{A}{\mathrm{H}}_{\mathit{\text{dis}}}}^l$.

To mitigate the derivative discontinuities for HBv2, rather than simply smoothing the fade functions (through e.g. splines), we removed them, simplifying the functional form. Instead, for each term, at the boundary of acceptable geometry, we raised the energy sufficiently to overcome the contributions from the other terms and disable the interaction.

Kortemme (2003) introduced fading to switch between short and long range polynomials, based on their observation that the native AHD distribution is more concentrated at 180° for shorter H-bonds than longer H-bonds. They interpreted this to mean that in nature increasing H-bond length increases the tolerance for AHD angle deviations, which they encoded into the HBv1 H-bond functional form. To test this interpretation, we compared the cumulative distribution function (CDF) of the AHD angle conditional on AH_dis for Native and natives relaxed with and without the fade functions (HBv1 and HBv2) (S.3.21). Surprisingly, HBv2 was able to recapitulate the dependence of AHD on AH_dis. We hypothesized that the dependence observed in Native could instead be caused by other terms in the energy function such as steric and electrostatic repulsion that exclude wide angles at short H-bonds.

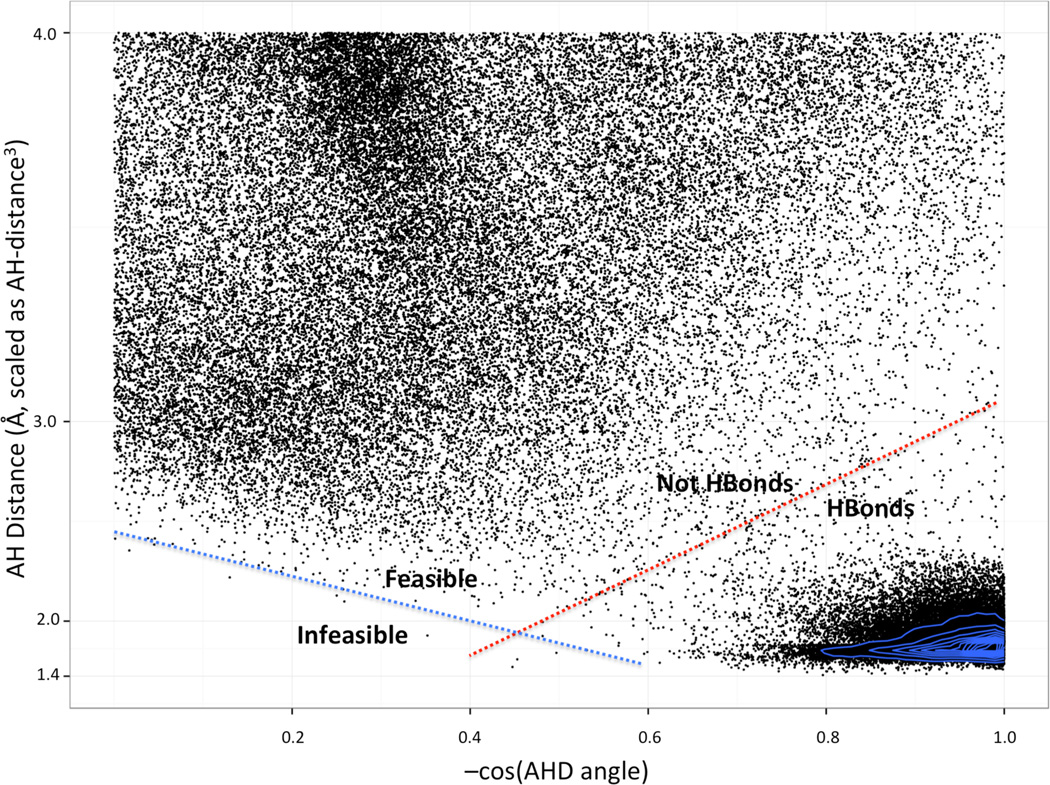
To further investigate the origin of the distance dependence, we plotted the Native joint AHD × AH_dis distribution. This distribution, when normalized so random interactions have a flat distribution, shows a low-density boundary separating H-bonds with short distances and linear angles from random contacts with greater distances and more bent angles (Fig. 7, red line). The slope of this trough suggests there is a trade off between good distances and good angles, so that for long H-bonds, to form an interaction requires a more linear AHD angle—opposite the intuition used for HBv1. However, there is an excluded region covering very short and very bent contacts. The complete absence of interactions is consistent with stiff steric or electrostatic repulsion, perhaps between atoms covalently bonded to the atoms participating in the H-bond. The slope of the feasible boundary (Fig. 7, blue line) explains the observed angular dependence on AH_dis. Since the AHD CDF could be reproduced in the absence of the face functions, we did not include them in HBv2, simplifying the functional form.

Figure 7.

AH_dis vs AHD scatter plot for Native hydroxyl-donor to backbone-acceptor polar contacts. The thin blue lines contour a kernel density estimation (KDE) of the points to show density otherwise obscured by overplotting. Note, due to boundary effects, the KDE underestimates the density at − cos(AHD) = 1.0. The dimensions are scaled so randomly placed contacts will have a uniform distribution.

With these structural changes to the HBv2 functional form, we manually fit the coefficients for the $f_{A{H}_{\mathit{\text{dis}}}}^2$ polynomials for each of the donor/acceptor types. We iteratively modified the potential, generated relaxed native structures, and compared the resulting H-bond distributions against those of native structures (S.3.23, S.3.24). This allowed us to recapitulate the remarkable variation in distance distributions observed in native structures. For hydroxyl donors, we first had to extend the Rosetta atom typing because HBv1 treated hydroxyl donors as equivalent to amide donors. We also had to adjust the Lennard-Jones parameters to allow for the extremely close contacts (1.7 Å) that are preferred by hydroxyl donors. Though hydroxyl hydrogens are not visible in crystal structures and their locations must be inferred, the very-close contacts that they prefer are also visible in the shortened acceptor-heavyatom-donor distances (S.3.25); hydroxyl/− carboxylate heavyatom-acceptor distances are 0.2 Å closer than backbone-nitrogen/carboxylate heavyatom-acceptor distances, which matches the gap between the peaks at 1.7 Å vs 1.9 Å for hydrogen-acceptor distances.

2.9 Scientific benchmarks with the HBv2 model

Our aim in developing HBv2 was to improve the physical realism of Rosetta-generated H-bonds, with a broader goal of improving protein structure prediction and design. To test the impact of HBv2 on the predictive capacity of Rosetta we performed 8 large-scale scientific benchmarks. The Decoy Discrimination test examined the ability of the energy function to discriminate near-native conformations from non-native conformations for a given sequence. This protocol differs from many standard decoy discrimination benchmarks in that it refines the starting decoys with the given energy function.⁶³ This is a more rigorous approach that prevents an energy function from taking advantage of idiosyncrasies in the original models, however it does require a large amount of computer time (~200,000 CPU hours to test a single variation of an energy function). In the Rotamer Recovery benchmarks (One, Cluster, and All) the side chains were removed from native backbones and the side chain packing protocol in Rosetta was used to rebuild them. Performance was quantified by recording the fraction of rebuilt side chains that adopt the native rotamer. This was performed in three separate ways: rebuilding all the side chains at once (All), rebuilding small clusters of residues while holding neighbors in their native conformations (Cluster), or rebuilding only a single residue in the context of the native protein (One). In the Monomer and Interface Sequence Recovery benchmarks the sequence optimization protocol in Rosetta was used to design new sequences for a set of proteins or protein-protein interfaces and the designed sequences were compared to the native sequences. In the ddG benchmark we compared single residue mutation ΔΔG predictions against experimentally measured values.^42,60 In the Relax Native benchmark we refined native structures with the FastRelax protocol and examined how far the structures moved from the crystal structure. To test how sensitive the scientific benchmarks were to the overall weight placed on the H-bond energy term, we performed many of the benchmarks with a range of weights for the H-bond term.

“Score12” has been the standard full atom score function in Rosetta for several years. During this period improvements to the energy function have not been made to the default version of Score12, but rather have been accessible through command line flags that indicate the user wants to use a given change to the energy function. Here, we group these changes into the HBv1 energy function. These modifications include updated idealized coordinates for the amino acid side chains, switching to a new rotamer library compiled by Dunbrack and colleagues,⁶⁴ adjustments to the knowledge-based torsion potential that remove derivative discontinuities,⁴² and reversion of EEF1 solvation parameters to their original values (S.5). As expected, HBv1 either outperformed Score12 or performed equally well in the scientific benchmarks, and served as the baseline for the changes described here.

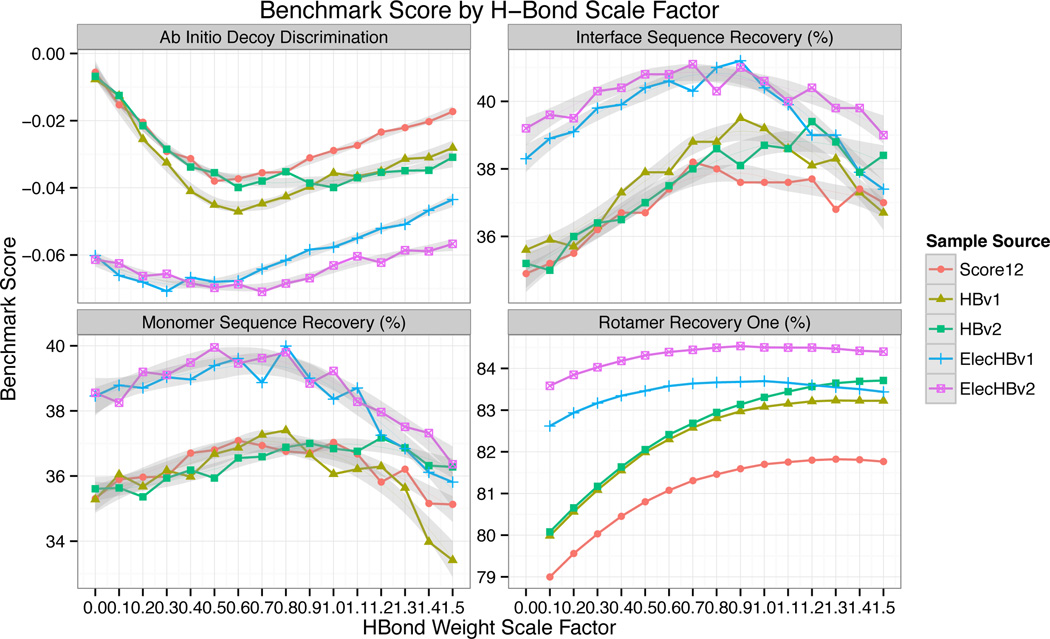
Switching from HBv1 to HBv2 resulted in only modest changes to the scientific benchmarks (Tbl. 1). There were small improvements in all three of the side chain recovery benchmarks, while the decoy discrimination score was slightly better for HBv1 at H-bond weights below 0.8 while there was a slight preference for HBv2 at an H-bond weight of 1 (Fig. 8). Overall, these results suggest that the benchmarks are not very sensitive to the fine details of H-bond geometries that are being considered here. Since the geometric features of H-bonds are more native-like using HBv2, and the benchmark results were largely unchanged, we consider HBv2 an improvement over HBv1.

Figure 8.

Scientific benchmarks as a function of H-bond weight. Lower values indicate improved performance for the decoy discrimination test, while higher values indicate improved performance for the sequence recovery and rotamer recovery tests. Grey regions indicate 90% confidence interval for locally-weighted, degree-2 polynomial regression (loess).⁶⁸ Based on these results ElecHBv2 with a weight of 0.8 was chosen as the preferred energy function.

2.10 Benchmarking an electrostatics potential in the absence of explicit H-bond potentials

As discussed in the introduction, an alternative approach for modeling H-bonds is to use Coulomb’s law to calculate electrostatic forces between atoms. This approach was not adopted in previous versions of Rosetta because there was evidence that it would not favor H-bonds with native-like geometries. To directly test this assumption, we introduced a Coulomb potential into Rosetta. To focus on short-range interactions like H-bonds and to retain the computational efficiency of the Rosetta energy function, we implemented a distance dependent dielectric model of electrostatics, where the dielectric constant is proportional to 1/r.^65,66 We used partial charges from CHARMM 19.⁶⁷ Additionally, we removed the low-resolution, knowledge-based “fa_pair” term from Rosetta that favored placing amino acids with opposite charges near each other. We call this model Elec; its implementation details are given in (S.4.3.2).

Given its simplicity and lack of orientation dependence, we were not surprised to see that the H-bond feature distributions for structures refined with the Elec energy function did not closely resemble the distributions from native structures. H-bond distances (AH_dis) were longer and showed higher variance (Fig. 6). For sp² acceptor H-bonds, the BAH, BA_χ feature distributions lack the clean bimodal character observed in natives, though some motif specific effects that reflect steric constraints were recapitulated, for instance the preferred geometries of H-bonds in helices and sheets. For sp³ acceptor groups the BAH and BA_χ distributions were broader than the Native feature distributions (Fig. 5B).

Despite the non-native geometries of H-bonds generated with the Elec potential, it performed well in many of the scientific benchmarks. Decoy discrimination, monomer sequence recovery, and rotamer recovery of whole proteins (All) were all better with Elec than with either HBv1 or HBv2. The repulsive forces between like-charged atoms and the attractive forces between atoms of unlike charge that are not forming H-bonds must be helping distinguish native from nonnative conformations. These favorable results encouraged us to develop an electrostatics potential that preserved native-like H-bond geometries.

2.11 Combining the electrostatic model with the explicit H-bond potentials

Morozov previously showed that combining an electrostatics model with the explicit H-bond model in Rosetta could lead to better decoy discrimination, but no effort was made at that time to combine the potentials in a way that favored H-bonds with native-like geometries.¹⁸ We sought to combine Coulomb electrostatics with the HBv2 potential in a way that preserved the shape of the energy landscape as a function of AH_dis, i.e. the first derivatives of the HBv2 and the new combined potential and were parameterized to be similar. It is the first derivative of the potentials that determine the local distributions; the combined potential ought to balance against the rest of the Rosetta force field in a similar manner to HBv2. Thus, we formed ideal H-bonds from pairs of amino acids evaluating the Coulomb potential over the AH_dis dimension. We then we refit the $f_{A{H}_{\mathit{\text{dis}}}}^2$ polynomials for each pair by subtracting the electrostatic contribution at each distance and shifting the whole potential to set the minimum value to −0.5, to be consistent with HBv1 and HBv2 (in both HBv1 and HBv2, each of the f, g, and h functions have a minimum value of −0.5). We refer to this new combined potential as ElecHBv2. We also tested another potential, ElecHBv1, which is purely the addition of the electrostatics term to the HBv1 potential.

To determine the overall weight to place on the H-bond potential when combining it with the Coulomb potential we tested several benchmarks (decoy discrimination, sequence recovery, rotamer recovery) with varying weights assigned to the H-bond term (Fig. 8). All of the benchmarks had maximum values near a weight of 0.8, and so this was chosen as the final weight in ElecHBv2. Using ElecHBv2, all of the benchmarks show improved performance over HBv2 and Elec. Interestingly, in some cases the feature distributions for ElecHBv2 were also improved over HBv2. This was most striking for hydroxyl acceptors (Fig. 5B). The HBv2 distributions are much narrower than the Native distribution and the Elec distributions are broader; the combined potential is a closer match than either. In general, many of the feature distributions for HBv2 were tighter than for Native, and adding the Coulomb term broadened the potentials to be more native-like (Figs. 3,4,5B).

Including an explicit Coulomb potential in the Rosetta force field does require considering more atom pairs when calculating energies and affects the smoothness of the energy function, which influences convergence rates during optimization. To evaluate the computational cost, 35 proteins of varying size were optimized with the FastRelax protocol using the various energy functions. The average run time differed by less than 15% when comparing Score12, Elec, HBv1, and ElecHBv2 (S.6.1).

3 DISCUSSION

HBv1 was developed using the traditional paradigm for knowledge-based potentials: fit the functional form to the Native feature distribution. A danger of this approach is that observed complexity in the Native distribution may not require a complex potential, but may result from the interaction between a simple potential and other components of the energy function such as sterics or electrostatics. In the latter case, then directly encoding the Native distribution as a potential can lead to unnecessary complexity and “double count” the other potentials. In contrast, we developed the HBv2 model using an empirical paradigm: fit the functional form so feature distributions in simulated structures match the Native feature distributions. Through iterative exploration of aspects of the model we discovered that a simple, physically-motivated functional form was able to recapitulate a range of subtle details of H-bonding. We developed a single potential for all sp² acceptors (all backbone secondary structure types and all sidechain types) having two symmetric minima corresponding to the donated hydrogen pointing at the acceptor lone pair electrons. Even with this uniformity, when combined with the full energy function (HBv2 or ElecHBv2), it was able to recapitulate the varied geometries of H-bonds in α-helices, tight turns and β-sheets (Fig. 4) as well as H-bonds to charged (Fig. 3) and uncharged sidechains (S.3.1). Further, the uniformity facilitates generalizing the potential to new contexts, such as noncanonical amino acids and small molecule ligands.

In this study we used both local feature analysis and large-scale scientific benchmarks to guide and evaluate our changes to the energy function. In many cases, we found that the two approaches were complementary. Feature analysis was particularly useful at identifying specific components of the energy function that could be improved. For instance, atom-atom distance distributions revealed sharp peaks due to discontinuities in the first derivatives of the potentials, and Lambert-azimuthal projections made it clear that HBv1 was not producing native-like geometries for H-bonds with sp²-hybridized acceptors. Large-scale benchmarks such as decoy discrimination are not always well suited to finding mistakes of this type, and indeed in many cases fixing small deficiencies in the potential did not lead to large changes in the scientific benchmarks. However, the scientific benchmarks were useful in evaluating large changes to the potential that went beyond fixing a particular problem. The best example of this was the boost in performance gained from adding a Coulomb potential to the Rosetta force field. A further advantage of training our energy function using the same protocols that we use for protein structure prediction and design is that the biases these protocols introduce (e.g. through minimization) are learned by the energy function; when we later go to predict new protein structures, the energy function will give us the right distribution of conformations. The upshot is that when we develop new sampling protocols, we might need to retrain our energy function.

Rosetta has been used successfully for a wide variety of structure prediction and design applications that require high-resolution modeling. Outside of nucleic acid modeling, the energy function has generally not included a Coulomb potential. How has Rosetta been so successful without an energy term that is standard in most molecular mechanics forcefields? With this question in mind, it is interesting to compare the relative performance of the explicit H-bond and Coulomb potentials in the various scientific benchmarks (Tbl. 1). In ΔΔG prediction, rotamer recovery and sequence recovery the two approaches perform similarly. This similarity is not because H-bonding is unimportant—removing both the Coulomb potential and the explicit H-bond term leads to a large drop in performance (Fig. 8, HBv2, H-bond weight = 0). These results suggest that for many applications using either an explicit H-bond term or a Coulomb potential to model H-bonds may give similar results. However, other benchmarks and feature analyses suggest that there are important differences between the two approaches. Using the Coulomb potential alone resulted in H-bond geometries that are not commonly observed in native proteins, and HBv2 produced overly sharp feature distributions. In decoy discrimination the Coulomb potential outperformed HBv2, perhaps because it accounts for repulsion forces absent from HBv2. Strikingly, the combined potential, ElecHBv2, outperformed the other potentials in all of the scientific benchmarks, and the feature distributions for ElecHBv2 were more native-like than HBv2 in many cases. The strong performance of ElecHBv2 may reflect the dual nature of H-bonds: partially as electrostatic phenomena that arise from uneven distributions of charge, and partially covalent bonds with distinct geometrical preferences.

The results from both feature analyses and scientific benchmarks have led the Rosetta community to adopt ElecHBv2 (now known as Talaris2014) as the default full atom energy function, in place of Score12. There are many aspects of ElecHBv2 that may be amenable to further improvement. Currently, the HBv2 potential assigns the same energy to all H-bonds with ideal geometries, regardless of the atom types that are involved. Adding the Coulomb potential modulates H-bond strength to some degree—e.g., H-bonds with charged groups are now stronger—but further perturbations that depend on atom types or environment may be better. The preference of a polar group to be buried or exposed is a fine balance determined by H-bonding, van der Waals interactions, electrostatics and desolvation effects; efforts to tune H-bonding strength should be coupled with an evaluation of the calculated desolvation free energies. Rosetta uses an implicit solvation model that is pairwise additive and does not account for orientation effects, i.e. desolvating a polar atom “from the side” in a way that does not disturb its ability to H-bond with water may be more favorable than desolvating it in a way that blocks H-bonding with water. The scientific benchmarks and feature analysis that we have employed here should provide an excellent framework for evaluating future changes to the H-bond, electrostatics and solvation potentials.

4 METHODS

4.1 Features analysis

To compare the properties of H-bonds we use the Features Analysis Tool described in Leaver-Fay et al.,⁴² which takes in batches of structures, each representing either native or Rosetta predictions (produces using a specific protocol and energy function), generates a database of elementary features, and then applies R-based features analysis scripts that estimate and plot feature distributions. The technical workflow is detailed in S.1, and a compendium of the generated plots is available in S.2.

We used kernel density estimation (KDE) to estimate smooth density distributions from feature instances. When the features are derived from geometric transformations or change of variables, it is essential that the estimated density be normalized correctly. For instance, in figure 2, we normalize by weighting each point by $1/A{H}_{\mathit{\text{dis}}}^2$ so that the if the acceptor atom (A) is fixed at the origin and the donor (H) atoms are distributed uniformly in space, the resulting feature distribution would be flat.

A limitation of KDE is that domain boundaries require special consideration. For example, in estimating the density over the AHD angle feature, a standard Gaussian kernel for a bond whose atoms are nearly linear will have density that will substantially spill over the 0° boundary. Our approach for comparing distributions at boundaries and in general was to recognize that often no single plot will reveal all details of a feature and considering multiple visual summaries can be useful. So, for the AHD angle we estimated densities where the domain is reflected across the boundary, empirical cumulative distribution functions, and Lambert-azimuthal projections of the (AH_χ, AHD) angles. The challenge of visualizing distributions at boundaries obscured a derivative discontinuity in HBv1 at AHD = 0° that was corrected in HBv2. As another example, the BA_χ torsion feature has a periodic boundary condition.

4.2 Polynomial fitting

We developed a small Python program using the Tkinter and numpy modules to manually fit polynomials. This program allows the user to lay down control points on the x/y plane with the mouse and then fit polynomials using least-squares regression with Lagrange multipliers to constrain our polynomials to pass through certain points with a derivative of 0.⁶⁹ The program is available in version Rosetta3.5. in Rosetta/main/tests/features/scripts/parameter_analysis-/hbonds/poly_fit.py.

4.3 Relax Native Recovery

The FastRelax protocol was performed with 6656 high-resolution crystal structures (Sec. 2.1, S.5.3) and the all-atom RMSD between the resulting models and the native structure was calculated.

4.4 Monomer Sequence Recovery

The monomer sequence recovery benchmark tests an energy function’s ability to recover in a complete-protein redesign simulation the native amino acid identities for a protein given its (fixed) native backbone. The test set consisted of 38 large proteins.⁷⁰ Sequence recovery was performed with the discrete, full-protein rotamer-and-sequence optimization protocol, PackRotamers (S.6.2). Before running PackRotamers for a given energy function, we refit structure-independent reference energies (conditional only on the residue type) using the OptE protocol⁴² and an independent set of protein structures, which maximized sequence recovery while favoring native-like amino acid composition.

4.5 Interface Sequence Recovery

We used the Rosetta protocol PackRotamers to redesign the interface residues of 96 transient protein-protein heterodimeric complexes from crystal structures with resolution less than 2 Å no missing density for interface residues, and no small molecules at the interface. The sequence recovery rate was computed as the average recovery rate over ten independent runs.

4.6 Rotamer Recovery

The rotamer recovery One benchmark optimizes residues one-at-a-time with the backbone and remaining sidechains fixed in their native conformation. To accurately model crystal contacts, we built in the symmetry mates. The benchmark runs on 9,452 non-alanine, non-glycine residues from the Top8000 that have a B-factor < 30 Ų, and coming from structures where the total number of residues in the complex containing the symmetry mates is less than 5,000. To predict the side-chain conformation, we use the RTMin protocol,⁷¹ which optimizes each discrete rotamer in turn using quasi-Newton minimization, selecting the resulting conformation with the lowest energy. A rotamer is considered recovered if all side chain χ angles are within 20° of their native angle.

The rotamer recovery Cluster benchmark optimizes four residues at a time, where each pair of residues has at least one pair of atoms within 4.5 Å of each other. Residues within 8 Å of the cluster are optimized alongside the cluster residues; all the remaining residues are held fixed in their native conformation. This benchmark uses the PackRotamers protocol to optimize the sidechains. For the Cluster benchmark we considered 76,811 clusters from the Top8000 where each residue has B-factor < 30 Ų. A cluster is considered recovered if at least two of its residues have all of their χ angles within 10° of the their native angles.

The rotamer recovery All benchmark optimizes all residues at once, with the backbone conformation fixed. We considered 466,797 positions in the Top8000 set with B-factor < 30 Ų. To predict the conformations, we used the MinPack protocol, which is an extension of the PackRotamers protocol. At each rotamer substitution, the MinPack protocol runs a short minimization on the rotamer’s χ dihedrals before deciding whether to accept or reject the substitution. Recovery is measured on a per residue basis, where a rotamer is recovered if all of its χ angles are within 20° of their native angles.

4.7 Loop Benchmark

The loop-prediction benchmark tests de novo protein loop prediction using the loop-prediction benchmark established in Leaver-Fay.⁴² Briefly, the benchmark considers 45 12-residue loops and uses 8,000 kinematic closure trajectories for each target.⁷² Accuracy is measured by the minimum C_α-RMSD over the five lowest scoring conformations.

4.8 ab initio Conformation Recovery

This benchmark measures a score function’s ability to discriminate low-scoring, high-RMSD decoys from near-native conformations. It relies upon a set of 87 small (between 57 and 260 residues) mostly monomeric (3 are homodimers, 1 is a heterodimer), ligand free proteins (Tbl. 1). The benchmark uses Cartesian minimization, so the energy functions tested by this benchmark were first altered to turn on the bond-angle and bond-length term (cart_bonded) and, to avoid double counting, to turn off the proline ring closure term (pro_close).⁶³

The benchmark takes as input 1,000 low-energy conformations for each protein that were selected from a large pool of structures generated by the Score12 energy function using Rosetta’s AbRelax protocol followed by loophash diversification.⁷³ The lowest energy structures for each in a range of RMSD bins were selected and serve as the starting conformations for this benchmark. To assess the discrimination ability of the candidate score function, the benchmark optimizes each of the 1,000 starting conformations 5 times using the FastRelax protocol, for a total of 425k optimization trajectories, and records the resulting energy and RMSD to the native. This process requires 30k − 140k cpu hours depending on the size of the protein and the computational complexity of the score function.

The resulting energies for each sequence are normalized by mapping the energies of the inner 90% quantile to the range [0, 100]. The discrimination score is computed as the average normalized energy gap between the lowest-energy structure under 1 Å RMSD from the native, and the lowest-energy structure over 1 Å and less range of upper bound RMSD values. In analyzing the results, five proteins were found to be particularly noisy and were excluded (Tbl. 1).