Abstract
Multibody software designed for mechanical engineering has been successfully employed in biomedical research for many years. For real time operation some biomedical researchers have also adapted game physics engines. However, these tools were built for other purposes and do not fully address the needs of biomedical researchers using them to analyze the dynamics of biological structures and make clinically meaningful recommendations. We are addressing this problem through the development of an open source, extensible, high performance toolkit including a multibody mechanics library aimed at the needs of biomedical researchers. The resulting code, Simbody, supports research in a variety of fields including neuromuscular, prosthetic, and biomolecular simulation, and related research such as biologically-inspired design and control of humanoid robots and avatars. Simbody is the dynamics engine behind OpenSim, a widely used biomechanics simulation application. This article reviews issues that arise uniquely in biomedical research, and reports on the architecture, theory, and computational methods Simbody uses to address them. By addressing these needs explicitly Simbody provides a better match to the needs of researchers than can be obtained by adaptation of mechanical engineering or gaming codes. Simbody is a community resource, free for any purpose. We encourage wide adoption and invite contributions to the code base at https://simtk.org/home/simbody.
Keywords: biomedical simulation, biological joints, minimal coordinates, coupled motion, compliant contact, real time simulation, neuromuscular simulation, biomolecular simulation, open source
1. Introduction
Multibody dynamics methods and software were developed in a mechanical and aerospace engineering context and have become indispensable in these application areas [1–5]. When studying the mechanical aspects of biological systems it is natural to employ the same tools, and much has been learned as a result (e.g., [6–11]). However, the analogy between engineered mechanical systems and evolved biomechanical systems is imprecise, and multibody mechanics tools designed for engineered systems can be difficult to apply to study the dynamics of complex biological structures. For example, biomechanical joints typically do not perform simple rotations about fixed axes and may comprise several moving parts; contact between soft biomaterials may involve significant deformation; redundant actuation of joints is common; data needed for parameterization are not directly measurable; and available measurements tend to contain large errors and inconsistencies. In the context of whole-body musculoskeletal mechanics, segment mass properties and muscle path geometry, for example, are hard to measure, while body segment kinematics (i.e., joint angles) estimated from surface markers are inconsistent with accelerations determined from external force measurements (i.e., ground reaction forces). As a result of issues like these, concepts that are simple to apply to engineered systems, such as “generalized coordinate” or “moment arm”, become difficult to define precisely in a biomechanical context. A further difficulty is that while the culture and economics of mechanical engineering make the use of commercial multibody codes practical and cost effective, in research or teaching the costs and lack of transparency of commercial codes can be problematic.
Game physics engines like ODE [12] have been developed for gaming and virtual worlds with an emphasis on real time performance and efficient handling of contact. Although biomechanical researchers have used game engines in their work [13], these codes were not designed for predictive simulation and attain performance by using simplified theory that may not converge to correct results. Developers of game engines understand that; for example the ODE manual [12], states in section 3.3 “ODE should not be used for quantitative engineering.” Real time performance can be important in quantitative research, but it is necessary to have a way to quantify the tradeoff between accuracy and performance. Methods built on sound theory that provide selectable accuracy can provide high speed, and can also be made to converge to high fidelity when necessary.
These and similar issues across many aspects of biomedical computation led the NIH to include in its Roadmap for Medical Research support for several national centers for building reusable biomedical computational infrastructure. Simbios is the national center for physics-based simulation of biological structures at Stanford University [14]. Simbios is charged with defining and developing an open source biosimulation toolkit, called SimTK, which provides computational libraries that enable development and sharing of a wide variety of domain-specific biomedical simulation software built on a common core. A major component of SimTK is the multibody dynamics code Simbody, which is the topic of this report.
In this paper we will discuss how Simbody addresses the biosimulation issues listed above. We introduce some of Simbody’s novel architectural features in section 2, and then present the methods Simbody uses to advance time in a dynamic simulation in section 3. Section 4 details Simbody’s formulation of multibody systems, and section 5 and an appendix cover methods to simulate collisions and contact. We will conclude with a discussion of Simbody’s current state, the next steps in its development, and an invitation for community participation.
2. Simbody overview
Simbody is an Application Programming Interface (API). The Simbody programming library is intended as a community resource that can be used to incorporate robust, high performance, minimal-coordinate O(n) multibody dynamics into a broad range of domain-specific end-user applications. Applications using Simbody have been implemented in areas of biomedical research across a wide range of scales and purposes. These range from studying the motion of biomolecular machines built from amino and nucleic acid components [15], to studying pathological gait in musculoskeletal models of humans [16], to design of biologically inspired robots and avatars [17]. Desired accuracy is user-controllable to cover needs from interactive real time simulation to detailed, high fidelity simulation.
Simbody is a tool for programmers, but these programmers do not need to be expert dynamicists. Rather, they are expected to be application developers who have expertise in the needs of biomedical researchers in particular areas of study, such as causes of pathological gait or structural basis of RNA function. Although Simbody contains some novel developments, it is conceived primarily as a reliable tool for use in biomedical research, rather than as a vehicle for multibody dynamics research. Consequently Simbody’s development is managed by professional software engineering staff at Simbios, with emphasis placed on testing, documentation, packaging, distribution, and support. Simbody is written in C++ and presents an object-oriented API to the application programmer. It is distributed in binary form for multiple platforms, or can be built easily from source. Details provided below apply to the Simbody 2.2 release [18]. Simbody is licensed under permissive open source terms [19] for any academic, commercial, government, or personal use to encourage wide adoption and broad community support that will maximize its ongoing impact on biomedical research and ultimately patient care.
2.1. Simbody scope
Simbody provides the biomedical application programmer with a diverse set of tools to handle the modeling and computational aspects of multibody dynamics, to ensure correct and efficient deployment without requiring specialized knowledge of multibody dynamics. In practice that means we must address more than just the formulation of multibody equations of motion. Thus, Simbody also includes contact modeling, numerical integration and differentiation, constraint stabilization and redundancy handling, assembly analysis, optimization and root finding, vector and matrix manipulation, numerical linear algebra, event isolation and event handling, accuracy control, threading, debugging, visualization, and real time interaction. Customizable user-written extensions are supported for force and constraint elements, as well as for novel internal coordinate joints [20] whose kinematics can be based on empirical measurements.
For scientific and engineering use, it is critical to allow user-specifiable accuracy in simulations. To do this efficiently requires variable-step integration methods that estimate errors and can adapt to the changing computational demands needed to maintain accuracy and stability during a simulation. In turn that means trial evaluations are performed, requiring strict management of the system state to avoid referencing out-of-date computations after step rejection. Out-of-date computations are qualitatively similar to the correct values, so they can easily remain unnoticed, especially by users who are not expert dynamicists. Simbody’s architecture prevents these errors.
2.2. Top-level architecture
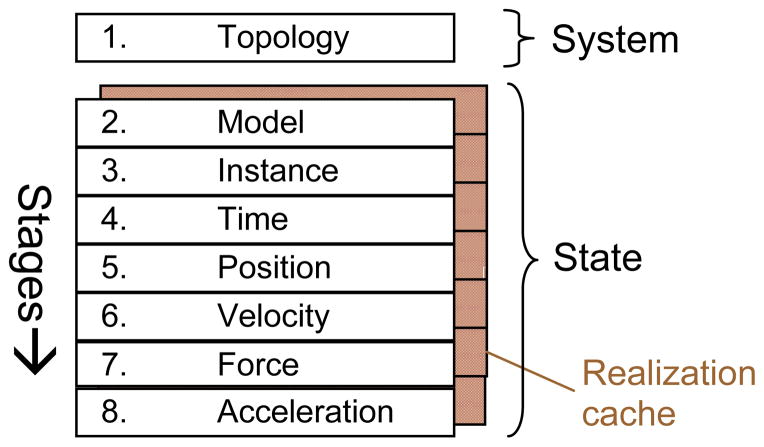
The three primary objects in the Simbody architecture are the System, State, and Study (Fig. 1). A System object encapsulates the components of a model (e.g. bodies, joints, force elements) and the code necessary to perform computations with that model. A System defines a model’s parameterization, but is itself stateless and remains unchanged during a study. A complete set of values for each of the System’s parameters is called a “state” for that System, and such sets are maintained in separate State objects constructed to be compatible with that System. (Here uppercase “State” refers specifically to the software object of that name in the Simbody API; lowercase “state” refers to a set of numerical values.) The response of a System is completely determined by the state values presented to it. A Study couples a System and one or more States, and represents a computational experiment intended to reveal something about the System. By design, the results of any Study can be expressed as a state or series of states that satisfies some pre-specified criteria, along with results that the System can calculate from those values. Such a series of states is called a trajectory.
Fig. 1.
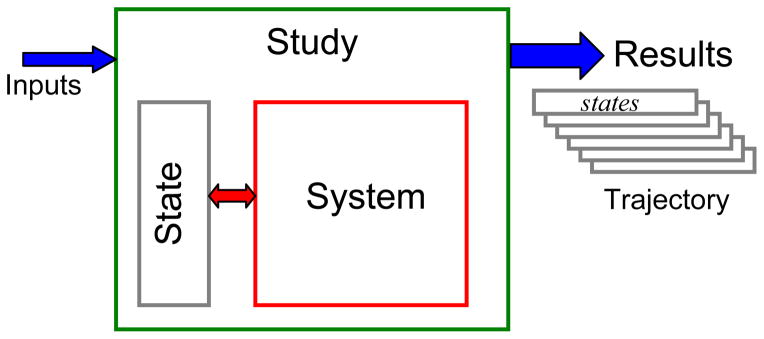
Top-level Simbody architecture. A read-only System object contains the model components and defines the parameterization. Values of those parameters are stored separately in State objects. A Study generates a series of states (State values) representing a desired solution such as a physical time history.
Simbody’s notion of “state” is more general than the common use of the term. By state, we mean everything variable about a System. That includes not only the traditional continuous time, position and velocity variables, but also discrete variables, memory of past events, modeling choices, and a wide variety of parameters that we call instance variables (e.g. masses and lengths). A System’s compatible State objects have entries for the values of each of these variables.
This design allows the conceptually simple model depicted in Fig. 1 to express every kind of investigation one may wish to perform. Here are some examples. A simple evaluation Study merely asks the System to evaluate specific quantities, such as the position of an end effector or the reaction force in a joint, using values taken from a particular State (which remains unchanged). An assembly Study returns a new state whose generalized coordinate values satisfy a set of position constraints, such as loop closures or couplers. An inverse kinematic Study returns a series of states whose generalized coordinates generate virtual marker positions that best match a series of marker observations. A dynamic Study produces a series of time, position, and velocity values that satisfy Newton’s laws of motion. An energy minimization is a Study that seeks values for the State’s position coordinates at which an energy calculation yields its minimum value. A Monte Carlo simulation is a Study yielding a trajectory that satisfies an appropriate probability distribution, such as a Boltzmann distribution. Design studies, also used for parameter fitting, find values for instance variables such as lengths, masses, attachment points, material properties, or coefficients which meet specified criteria. Modeling Studies select among models or algorithmic choices to improve defined measures of behavior, such as accuracy, stability, or execution speed. Since by definition all System variability is contained in the State, we can guarantee that any desired results regarding the System can be expressed in terms of State values, provided that a corresponding System is available to interpret them.
There are other significant advantages to having separate State objects. Trajectories may be saved and restored simply by copying State objects, with no danger that “hidden” states may be missed. Examples include enable/disable flags for model components, “previous solution” values for continuity and acceleration of nonlinear model calculations such as wrapping geometry, and controller or muscle dynamics states. Trial states may be generated and discarded easily, and states may be sampled or compared with no overhead associated with switching from one state to the next.
2.3. Handling of state
Careful handling of state is required for correctness and efficiency of a simulation. Given values for state variables, there are many useful quantities that can be calculated (reaction forces, say). These calculations can be very expensive so we only want to calculate them once for a given state and save the result. But, if the state changes these must be recalculated so we do not accidentally reference “stale” (out-of-date) computations. This must be dealt with automatically to prevent mistakes, which can be very difficult to detect. Simbody addresses this by including carefully-managed storage for state-dependent computations within the State object. This storage space is called the realization cache, and the process of calculating the values stored in it is known as realizing the state. By realizing we mean presenting a State to a System and asking the System object to compute the physical consequences of the values in that State. As a concrete example, a finger tip location is a consequence of the state’s generalized coordinate values.
In practice, evaluation of a multibody system proceeds in distinctly ordered steps. Positions must be known before velocities can be calculated. Velocities must be known before forces can be calculated. Applied force calculations must precede accelerations. At the same time, for a given state variable we can say which of those steps are invalidated by changes to that variable’s value. For example, a generalized speed (velocity variable) invalidates velocity, force, and acceleration calculations but has no effect on already-calculated positions. Simbody’s State architecture exploits this structure by dividing the state variables and the realization cache into stages as shown in Fig. 2.
Fig. 2.
Organization of the state variables and realization cache into ordered stages. A change to a state variable at stage s invalidates all cache entries at levels s and above. Construction of the System may be viewed as the first stage of computation (topology).
Although cached results are stored in the State object, those results are not logically part of the system state. They are simply intermediate calculations that have been derived from the state, and can easily be discarded and re-created when necessary. They are needed only for efficient computation using the System-State-Study architecture. Further, we can automatically invalidate cache entries whenever a state variable at that stage or earlier is changed. Any attempt to access an invalid value will either initiate recomputation or raise an error message as appropriate. Simulation programmers will recognize this as an architectural substitute for error-prone ad hoc “isValid” flags that otherwise proliferate to avoid expensive recalculation.
To summarize briefly: a System by itself is stateless once constructed. The values of state variables stored in a particular State object completely determine the response of the System. That response is produced by realizing the State, which is done in sequential stages. The results of realization are stored in a hidden cache that is physically contained in the State object, but is not logically part of the state in the sense that, except for computation speed, cache values do not alter the behavior of the System. Cache values are automatically invalidated when state variables they depend on are changed, and access to invalid values is detected and prevented.
3. Time stepping
Simbody-based simulations are classified as hybrid simulations [21], meaning they consist of both continuous evolution in time and discrete events. Advancing such a system through time is handled by an algorithm called a time stepper, consisting of a numerical integrator for advancing through smooth parts of the simulation and detecting pending events, and an event handler for dealing with those events.
3.1. Formulation of dynamic equations as seen by the time stepper
A time stepper does not need to know much about the internal workings of the model it is advancing through time. Consequently the formulation that Simbody presents to the time stepper is simpler than the multibody formulation we will describe subsequently. Fundamentally, these are the equations as seen by the time stepper:
| (1) |
| (2) |
| (3) |
Here t is the independent variable (time), y is a vector of continuous state variables, and d is an arbitrary set of discrete state variables. The first equation is a set of ordinary differential equations (ODE) in y. The second is a set of algebraic equations (constraints), such as loop closure conditions, coordinate couplers, prescribed motion, or contact conditions. Together, equations (1) and (2) constitute the continuous portion of the system as a set of differential-algebraic equations (DAE) [22] that can be used to advance states y through time smoothly while d remains fixed. Equation (3) represents a set of event trigger functions that are constructed to change sign (pass through zero) when an event occurs, for example a signed distance between objects or the difference between a reaction force and a maximum limit at which a model change is required.
More precisely, our continuous system (1), (2) is formulated as a differential equation on a manifold (DEM) [23–25]. Such a system additionally guarantees that when constraint equations (2) are satisfied their time derivatives are satisfied automatically. Therefore, the differential equations (1) must be formulated to satisfy the constraint derivatives. That is, we require that
| (4) |
Simbody produces differential equations that assure condition (4) is met, as discussed in section 4. A DEM is considerably easier to solve than a general DAE and permits us to use conventional numerical integration methods designed for ODEs, augmented as described below.
3.2. Advancing the continuous system
Simbody offers a variety of numerical integrators with differing properties. These consist of conventional error controlled, variable step integrators suitable for advancing ODE Eqn. (1) through time with a specified accuracy and include a variety of explicit Runge-Kutta methods well-suited for biomechanical and real time applications [26], a velocity Verlet method for biomolecular systems [27], and, for stiff systems [28], a unique variable-order backwards difference formula (BDF) implicit integrator CPODES developed in collaboration with Lawrence Livermore National Laboratory’s Center for Applied Scientific Computing. CPODES is a modification of CVODE [29] to add coordinate projection in the manner described by Dehombreaux et al. [30] and justified theoretically in [31].
All Simbody integrators are capable of continuous (dense) output [26, 32], meaning that they can efficiently and accurately interpolate state values at any time within a step. This important capability allows step size choice to be decoupled from the desired reporting interval. Thus a Simbody step can be much larger than a reporting interval yet deliver accurate results for each report. In addition all Simbody integrators are capable of monitoring Eqn. (3) for sign transitions and using their interpolation capability to efficiently isolate the time at which a transition occurs, to facilitate event handling by the time stepper.
Note that, because of the DEM condition in Eqn. (4), if given initial conditions that are on the manifold of Eqn. (2) then perfect integration of Eqn. (1) would result in a trajectory that remained on the manifold. However, truncation error inherent in methods for approximate numerical integration allows the solution to drift away from the manifold. Eqn. (2) can be used directly to eliminate this drift, and improve the solution overall, using the method of coordinate projection [31, 33–34]. Coordinate projection is superior to the more commonly-used Baumgarte stabilization method [35] for several significant reasons. See Ascher et al. [34] for a detailed discussion. Briefly, Baumgarte stabilization requires a difficult choice of feedback gains: too small and the constraints drift unacceptably; too large and the problem becomes numerically stiff. The optimal gains depend on both the step size and integration method in use. Coordinate projection has no constants to choose and guarantees that the solution lies on the manifold at every step. Taking an ODE step and then removing constraint errors with coordinate projection also improves the ODE solution [25, 31], provided the projection is normal to the constraint manifold in a suitable norm [36], reducing the error estimate and permitting larger time steps.
Coordinate projection is particularly attractive computationally when there are few constraint equations, yielding small projection matrices. Simbody’s biological internal coordinate joints eliminate most constraints otherwise needed for biomechanics [20]. Details of Simbody’s implementation of coordinate projection and event isolation can be found in the Simbody documentation [37].
3.3. Controlling accuracy
Simbody is intended to be useful to people who are not expert in numerical simulation. The collection of accuracy controls offered by some numerical methods can be bewildering. Our goal is to offer instead a single scalar accuracy parameter α, which corresponds roughly to the “% relative error” or “number of significant digits” desired in the results. This is necessarily a qualitative description but in our experience it comes closest to what biomedical researchers (and most other scientists and engineers) mean when they discuss “accuracy.” A fully quantitative understanding of error in variable step, variable order, event-isolating numerical methods applied to the propagation of a chaotic hybrid DAE system requires specialized training in numerical analysis that is rare even among numerical simulation experts. Instead we ask our users to provide only information they understand such as how many digits they want, or even just “more accuracy” or “less accuracy.” We use that information as follows to influence our quantitative numerical treatment to attempt to satisfy the user’s qualitative request.
Accuracy request α is related to the desired number of digits n as follows:
| (5) |
Thus four digits of accuracy is requested by setting α=0.0001, roughly corresponding to a “relative error” of 0.01%. Real time simulation with Simbody generally involves accuracy requests of 1–10%. Accuracy α is thus similar to the “relative tolerance” (rtol) parameter provided by most numerical integrator implementations [38]. However, there is no equivalent to the common “absolute tolerance” (atol) parameter. Instead, Simbody combines α with internally-calculated scaling factors for estimated state variable errors and actual constraint violations to define two equations that must be satisfied before an integration step can be accepted:
| (6) |
| (7) |
where εy is a vector of the integrator-provided estimates of absolute error in each element of y, and c is the constraint error function from Eqn. (2) returning a vector of absolute errors. εy and c contain a mix of potentially incompatible error units such as lengths, angles, and velocities. Diagonal weighting matrices W and T map each error to a “unit” error in the represented quantity, and then finally we interpret α as the acceptable fraction of unit error in the chosen norm, typically root mean square. Simbody can estimate values for W and T using knowledge of coordinate types, an overall length and time scale, and other internally-available information. Expert users may alter these calculations.
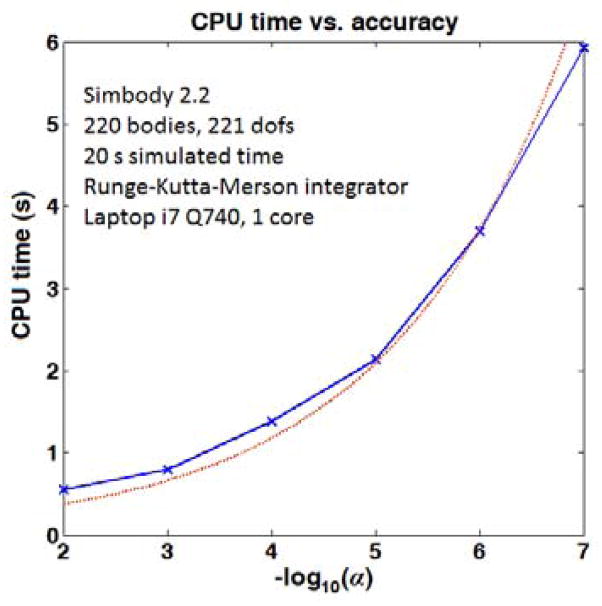
In practice this procedure results in rational control over accuracy for non-expert users via a single “knob” that can be turned to increase or decrease the level of accuracy with predictable results. It is our assessment that few users are better served by exposing more knobs. Fig. 3 shows one numerical example. More information about accuracy in Simbody can be found in [37].
Fig. 3.
CPU time vs. accuracy example. We ran six identical 20s simulations at accuracies α=10−2 to 10−7, recording the amount of CPU time required. The system comprised 11 20-body chains using randomly oriented revolute joints, attached to a common oscillating base, with gravity and light damping. All dofs had random initial velocities assigned, with speeds low enough to avoid chaotic motion so that all simulations approximated identical trajectories. The number of steps (and thus CPU time) required by a 4th-order integrator should be proportional to α−1/4. The plotted red line is 0.118 α−1/4. Note that absolute CPU times can vary substantially for similar-sized systems with different characteristics; this is intended only as an example of relative performance vs. accuracy.
3.4. Real time interaction
A simulation suitable for real time interaction with a human must match simulated time to clock time, deliver simulation frames for screen update at a steady pace, and be responsive to user input. Typically this is achieved by using a fixed-step numerical integrator so that every unit of simulated time has the same computational cost. But for most dynamic systems, step size requirements to achieve accuracy and stability vary substantially during a simulation. For a fixed-step simulation, the step size must be chosen to achieve adequate performance during the worst-case interval (e.g., ground impact during running), which may be only a very small fraction of the total time. This causes many unnecessary steps to be taken during the easier parts of the simulation, increasing the total amount of computation required for the full simulation. That limits the maximum complexity of systems that can run in real time to those that can achieve real time rates even during their most computationally demanding intervals. Using variable step sizes, substantially more complex systems could achieve real time performance on average but might have intervals where they fall behind. For “hard” real time systems (e.g. controllers for antilock brakes or spacecraft attitude), where a missed frame can be literally fatal, it is difficult to exploit this fact. However, for the “soft” real time requirement of interacting with humans it is practical to exploit variable step integration to permit more complex models to run in real time while maintaining stability and accuracy.
For soft real time applications, Simbody includes support for a method adapted from the “local lag” approach [39] used to manage network latency for networked games and distributed virtual environments. The idea is to exploit slow human reaction time to smooth out simulation variability. Delays of up to 100ms are typically imperceptible [40–42] and longer delays can be nearly unnoticeable and tolerable in many applications. A first-in-first-out delay buffer of selectable length tdelay is used to collect frames that are regularly-spaced in simulated time but arrive at a variable rate in real time. At the other end of the buffer, frames are extracted at a fixed real time rate, but delayed slightly behind real time. For example, if the frame rate is 50/s (20ms/frame) and tdelay=120ms, then there is room for six frames in the buffer. In this case frames are removed regularly from the buffer every 20ms but their times lag real time by 120ms.
This approach is able to eliminate variability produced by occasional difficult intervals during a simulation and by discrete event handling, provided that the resulting delays do not exceed tdelay and that the average performance is real time or faster. The use of variable-step methods with interpolation capability substantially improves average speed since steps of length up to tdelay can be taken while delivering regularly-spaced frames at the required rate. Each step, regardless of length, has the same computational cost; interpolated frames usually have negligible cost. The architectural separation of System from State (see section 2.2) facilitates the real time implementation since it is only necessary to copy whole State objects into the delay buffer and retrieve them later.
4. Formulation of the multibody system
Simbody uses a generalized coordinate formulation with the goal of having the fewest possible coordinates to represent the pose and motion of a multibody system. However, it does not attempt to reduce the system to an ODE; instead we choose coordinates to form a basis in which to express the motion and then require that motion be restricted to a constraint manifold. This formulation provides a compact representation of motion with a small number of coordinates and small number of constraints, and allows for robust treatment of important numerical issues such as constraint stabilization, poor conditioning, and redundant constraints.
The solution method for the unconstrained system is a recursive O(n) method following the spatial operator approach of Rodriguez and Jain [3, 43–45] and extending the templatized C++ implementation of Schwieters [46]. The m constraint equations are adjoined in the manner described below. As discussed in ref. [47], this introduces an O(m3) term in the computational complexity. However, because Simbody supports biologically-realistic internal coordinate joints capturing coupled rotation and translation [20], the need for most constraints is eliminated and we typically have n≫m. Further, only blocks of coupled constraints need be solved simultaneously, so the cubic term applies only to the maximum number of coupled constraints which is typically much lower than the total number of constraints, and in many systems can be viewed as a constant since the amount of coupling does not necessarily grow with problem size. In practice we have not yet found constraint coupling to be a bottleneck and Simbody does not currently exploit decoupling. Jain [48] presents a method for efficiently eliminating locally-coupled constraints in the spatial algebra framework that we intend to incorporate in a future release.
4.1. Equations of motion
A Simbody multibody system is constructed via the API as a tree-structured system of “mobilized bodies” each consisting of a body and its unique inboard internal coordinate joint (hinge) which we call a mobilizer. This avoids confusion with the biologically-meaningful term “joint” which may be modeled as a mobilizer, or with constraints, or with force elements, or some combination. Simbody mobilizers and their capabilities are discussed extensively in Seth et al. [20]. To the tree of mobilized bodies is added a set of holonomic (position) and nonholonomic (velocity) constraints restricting the motion of bodies or directly affecting generalized coordinates.
Mobilizers are not constraints. Instead, the ith mobilizer provides its body with 0 ≤ ni ≤ 6 degrees of freedom with respect to its parent body. These are parameterized with ni generalized speeds ui which collectively form the basis for our equations of motion. The mobilizer also introduces a set of nqi ≥ ni generalized coordinates qi to represent the pose (relative position and orientation) of the body with respect to its parent. The time derivatives of generalized coordinates are related to the generalized speeds by the kinematic differential equation:
| (8) |
where Ni is an nqi × ni invertible matrix. When nqi > ni there are nqi − ni local constraints that the qi must satisfy; in practice these are almost always quaternion normalization constraints. These constraints are introduced only for numerical stability and have no physical significance; they do not produce forces, have little computational cost and will not be discussed further here. u = {ui} and q = {qi} are the generalized speeds and coordinates for the system as a whole, giving
| (9) |
where N is block diagonal.
Simbody constraints may be specified in terms of geometry (e.g. distance between points, non-penetration, non-slip) as well as directly on generalized speeds or coordinates (e.g. prescribed motion, couplers), and linear acceleration-only constraints may also be specified. However, Simbody automatically reduces these to algebraic relationships among the coordinates and speeds which is how we will present them here. The first set of equations arises from constraints that are explicitly specified during modeling:
| (10) |
| (11) |
| (12) |
Here t is time, q and u are defined above. In addition to the above equations, the time derivatives of the holonomic and nonholonomic constraints must also be satisfied, adding three more equations:
| (13) |
| (14) |
| (15) |
From differentiation of Eqns. (10) and (11) it can be seen that P = (∂p/∂q)N and V = ∂v/∂u. bp and bv collect terms that do not depend on u̇. Eqn. (10) defines the position constraint manifold that restricts q, Eqns. (11) and (13) together define the velocity constraint manifold that restricts u, and Eqns. (12), (14) and (15) generate unknown constraint forces λ that appear in the equations of motion and affect u̇. For exposition of the equations of motion, the acceleration constraints are assembled together:
| (16) |
where and . Matrix G(q) is the acceleration constraint Jacobian which in general is poorly conditioned or singular due to redundant constraints; b(t,q,u) is the acceleration constraint residual. The remaining dynamic equations are:
| (17) |
| (18) |
where z is a set of auxiliary continuous variables defined by first order differential equations (e.g. for muscle dynamics or controllers), λ is the vector of m Lagrange multipliers representing the constraint forces, and M(q) is the n×n symmetric, positive definite internal coordinate mass matrix. finertial(q,u) are the velocity-dependent Coriolis and gyroscopic forces, converted to generalized forces. fapplied(t,q,u,z) collects all explicitly applied body forces and torques including gravitational forces (converted to generalized forces), plus any directly applied generalized forces (e.g. motor torques).
Equations (9) through (18) are propagated through time by Simbody’s numerical integrators during continuous intervals, giving trajectories q(t), u(t), and z(t). For comparison with section 3 note that y = {q,u, z} and function c comprises functions p, ṗ, and v.
4.2. Solving for accelerations
For forward dynamics, Eqns. (16) and (17) are solved simultaneously for the unknowns u̇ and λ. When G has full row rank (i.e., rank(G)=m), the solution is unique. In general rank(G)<m due to redundant constraints, leaving λ underdetermined although u̇ is still unique. Commonly, multibody codes that are able to handle this situation (e.g. SD/FAST [49]) do so by dropping some of the constraints, so that only a subset of constraints generates forces. This can lead to absurd results that we consider unacceptable since they can undermine a non-expert user’s confidence in the tool. While the “right” answer can only be obtained by replacing redundant constraints with more detailed compliant elements, one can do much better than delete constraints altogether. Simbody instead determines a least-squares solution for underdetermined λ which in many cases returns the limiting value of compliant elements as their stiffness goes to infinity; in any case we produce a plausible solution in which redundant constraints each carry part of the load rather than having any of them zero.
Recall that Simbody is a recursive O(n) multibody code. Despite the form of the equations written above, Simbody does not normally calculate the n×n mass matrix, since that would be O(n2) and inverting it would be O(n3). (M and other system matrices can be obtained when needed.) Here we will show what is being calculated and comment on the computational complexity; space does not permit showing how this is performed using recursive spatial operators. The interested reader may consult refs. [43, 46, 50] for details.
Using the fact that M is invertible, Eqns. (16) and (17) can be combined to eliminate u̇:
| (19) |
where u̇0 = M−1(fapplied − finertial) is the generalized acceleration vector of the unconstrained system, and the right hand side is g0 = g (t, q, u;u̇0) in Eqn. (16), that is, the acceleration constraint errors that result from the unconstrained accelerations. The operator M−1v for any column vector v is available in O(n) time, so u̇0 is calculated in O(n). g() is the vector of acceleration errors for each of m constraint equations, given the generalized accelerations; each error is available in constant time from the definition of its constraint element, so g() is O(m). Thus the right hand side of (19) is available in O(n+m) time.
Let Ym×m = GM−1GT. This matrix is formed as follows: a (generalized force-like) column of GT is formed explicitly in O(n) time from the constraint element definition. The O(n) M−1v operator is applied. The resulting acceleration is supplied to g() in Eqn. (16), yielding a column of Y in O(n+m) time. This is done for m columns, so the total cost of forming Y is O(mn+m2). We can now rewrite Eqn. (19) as:
| (20) |
If Y has full rank m this equation may be solved by any suitable method such as LU with pivoting. If it is acceptable simply to drop some of the equations in the singular case, we may obtain the non-zero subset of λ using a QR method. For a least squares solution, we would like the solution
| (21) |
where Y+ is the pseudoinverse of Y. Pseudoinverse is commonly calculated with an SVD decomposition, but Simbody uses the complete orthogonal factorization (QTZ) instead, which is approximately 5X faster than SVD. See ref. [51] for information on any of these methods; Simbody uses the implementation provided by LAPACK [52]. All of these factorizations have complexity O(m3) so the total cost of determining λ is O(m3+mn+m2). As discussed above, we expect m to be very small due to our extensive use of internal coordinate joints [20]. And if the problem were to be solved in uncoupled blocks (not yet done), m and n represent only those constraints and generalized coordinates that are coupled.
Once we have obtained the multipliers λ, we calculate fconstraint = GT λ in a single O(n) evaluation, then Eqn. (17) gives us u̇ = M−1(fapplied − finertial − fconstraint) which is a final O(n) application of the M−1v operator.
5. Contact modeling
Biomechanical models often involve contact among components of the model. In many cases the contacts can be idealized into joints or constraints. However, real contact forces arise from deformations of the compliant materials from which biological systems are composed. Simbody provides two compliant contact models that take deformations into account to generate contact forces. One is based on Hertz contact theory [53–54] which analytically generates accurate forces and deformations based on linear elasticity theory, but limited to simple geometric objects. The second is the Elastic Foundation Model [54–55], which uses meshes to represent arbitrarily complicated geometric surfaces in contact, but calculates deformations and forces using a simplified elastic model. These models are augmented with a dissipation model described by Hunt and Crossley [56] and a model of Stribek friction [57]. For each contact element, we produce a force composed of three effects: stiffness, dissipation, and friction:
| (22) |
Calculation of fstiffness differs between the two compliant contact models but we use the same method for the dissipation and friction terms once the stiffness force has been determined.
5.1. Hertz stiffness, Hunt and Crossley dissipation, Stribek friction
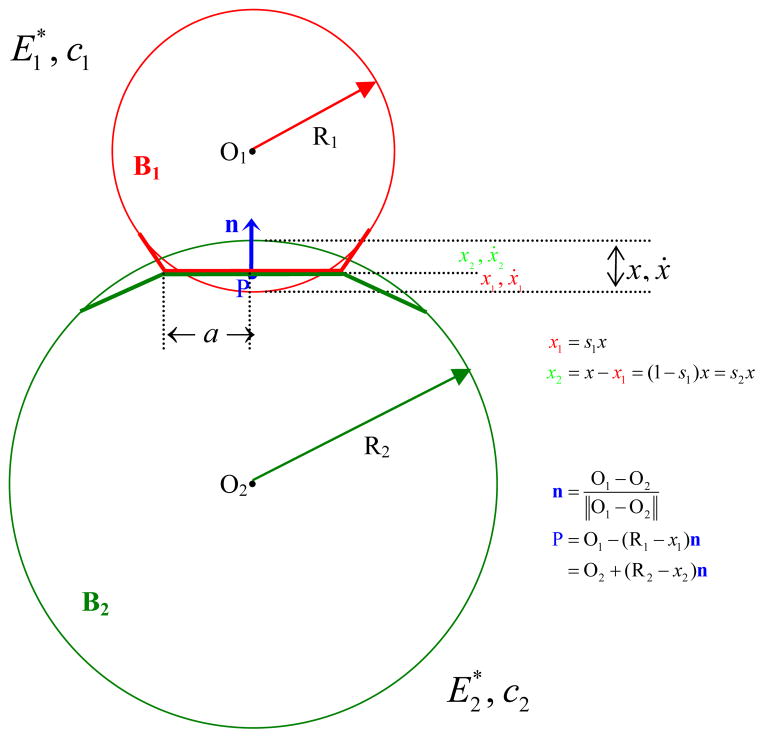
To apply Hertz theory rigorously, we need two linearly elastic materials in non-conforming contact, where the dimensions of the contact patch are small compared to the curvatures, and small compared to the overall dimensions of the object [54]. Contact must initiate at a common point at which the two surface normals are opposed. Each of the contacting surfaces must be well-approximated by a paraboloid at the contact point. Brought into a common frame, these may be added together to characterize the separation between the two surfaces. That sum will also be a paraboloid, so it can be expressed using just two principal curvatures to represent the relative contact curvatures. See ref. [54], section 4.1 for a discussion. Thus the undeformed geometry of contact can be represented by a contact point and normal, and the two principal curvatures of the separation paraboloid. Any sufficiently smooth nonconforming surfaces can be described this way [58], and Hertz theory can also be applied to cylindrical contact that initiates in a line rather than a point. Currently Simbody provides Hertz contact for planes, spheres, and ellipsoids. Fig. 4 illustrates the geometry of contact for the case of two spheres.
Fig. 4.
Contact geometry for the Hertz/Hunt and Crossley model.
Deformation is characterized by a scalar displacement x that is the total deformation of the two surfaces along the contact normal, with x>0 when the surfaces are contacting. Displacement x may also be viewed as the minimum distance by which one of the surfaces would have to be translated along the contact normal so that no deformation of either surface would be required to prevent overlap.
Under the above restrictions, Hertz theory assumes that the deformation of the two surfaces produces an elliptical contact patch, in a contact plane perpendicular to the contact normal. The resulting normal force, contact patch dimensions, and pressure distribution can then be determined just from material properties, undeformed contact geometry, and deformation x. The force magnitude is
| (23) |
Here R is a composite relative radius of curvature, E* is a composite elastic modulus, and σ≥1 is an eccentricity factor with σ=1 for circular contact, slowly growing as a function of elliptic integrals of the ratio of the two relative curvatures [54]. R and σ depend only on the curvatures of the separation paraboloid, so the parenthesized quantity above is independent of x. Note that although the materials are assumed linear elastic, the force-displacement relationship is nonlinear because of the changing geometry during contact. Appendix A gives details for calculating R, σ and E* from undeformed contact geometry and material properties.
To apply this force, Simbody calculates an instantaneous contact point P, located along the line separating the initiation points on each surface, with the exact location dependent on the relative stiffnesses of the two contacting materials. If the materials are the same, P will be located midway between the two surfaces. If one surface is much stiffer than the other then P will be located much closer to the undeformed surface of the stiff (non-deforming) body than to the undeformed surface of the soft body. P determines the height of the contact patch ellipse along the contact normal and is the center point of the contact patch ellipse. The contact force is applied to each body at P along the contact normal in opposite directions, such that the force is always pushing on each surface, never pulling.
For Hunt and Crossley dissipation to apply rigorously, the impact velocities should be small enough not to cause permanent yielding of the materials [56, 59]. Once the magnitude of the stiffness force has been determined as above, the Hunt and Crossley dissipation force may be calculated as
| (24) |
where c* is an effective dissipation coefficient combining the individual dissipation properties of the two contacting materials. The material property c may be determined from impact experiments as the negated slope of the coefficient of restitution vs. impact velocity curve at low velocities, using the relationship e = 1−cv where e is the measured coefficient of restitution and v is the impact speed [60]. (Coefficient of restitution is not a material property.) See Appendix A for details on computing c* from individual material properties.
Note that fHC is a signed quantity; this creates an empirically observed hysteresis. Hunt and Crossley [56] show that the total force fHz + fHC ≥ 0 under typical conditions; negative total forces are due to unmodeled losses (such as “ringing”) so we do not allow the total to become negative:
| (25) |
This accounts for all contact forces in the normal direction, that is
| (26) |
Finally, the friction force is calculated as follows. Find the body stations (points) coincident with the contact point P and calculate their relative velocity v in the contact plane. With slip rate v = |v| we calculate the magnitude of the friction force as follows
| (27) |
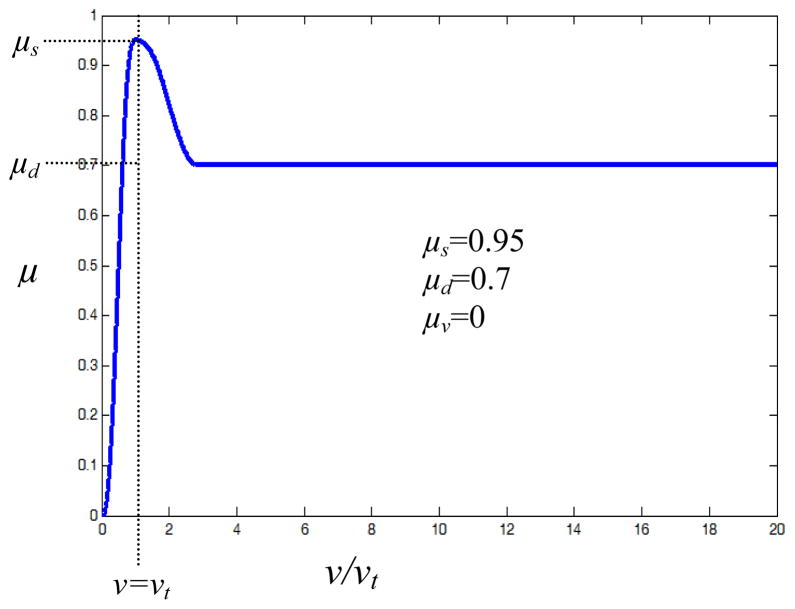
The function μ calculates an effective coefficient of friction that is dependent only on the slip velocity, but is parameterized by given surface properties of the materials in contact: static, dynamic, and viscous coefficients of friction, and a transition speed at which static friction reaches its peak value. Fig. 5 shows the shape of this curve in the absence of viscous friction. With viscous friction the final segment would have a positive slope rather than zero. Simbody implements this function using a three-segment spline with the first two segments quintic polynomials to ensure C2-smooth transitions between static friction, the Stribeck transition region, and the final sliding region. The transition velocity is set to a tiny value that is negligible for the problem at hand. One may also use intermittent no-slip constraints to enforce stiction with exactly zero slip, but in practice the above continuous method produces robust behavior without detecting and handling stiction transition events explicitly.
Fig. 5.
Stribeck friction curve showing effective coefficient of friction as a function of slip velocity. Transition velocity vt is set to a negligible value.
A drawback of this method is that the system may become stiff in the stiction region if transition velocity is set very small, reducing the efficiency of explicit integration [28]. Some choices of material and properties can also make the problem stiff. However, as discussed in section 3.2, Simbody provides an implicit integrator CPODES that performs well on stiff problems, provided they are not too large. The size limitation is due to the necessity for CPODES to periodically calculate numerically, and factor, the matrix of partial derivatives of Eqn. (1). Whether the much-increased step size compensates for the additional costs is highly problem dependent, and we have not yet adequately characterized the tradeoffs. We have seen a number of human-sized models for which CPODES has been highly effective, and it is easy to try a variety of integration methods in the Simbody framework.
5.2. Elastic foundation model
The Elastic Foundation Model (EFM) [54–55] assumes that contacting solids may be considered rigid bodies but for a thin layer of elastic material of thickness h at the surfaces. Linear elastic properties are determined for the material properties in contact and combined into a composite stiffness modulus E* as for Hertz contact, though with a different combining formula; see Appendix A. The geometry of each surface, which can be arbitrarily complicated, is approximated with a triangular mesh of suitable density. At the centroid of each triangle on each surface is placed a spring whose stiffness k can be determined from the area of its triangle, the composite material property E* and thickness h. This forms a “bed of springs” on the surface of each body that can be used to generate forces during contact.
At run time when an EFM body A contacts another body B, Simbody determines all the triangles of A whose centroids are inside body B, considering only undeformed geometry. For each of these triangles, the point S on body B’s surface closest to the centroid is determined. A displacement x is determined as the distance from the centroid to S. Then a force kx is applied to both bodies using a contact point P along the line segment between the centroid and S. P’s placement accounts for the relative stiffness of the two bodies as described for Hertz contact above. A Hunt and Crossley-like dissipation term kx(c* ẋ) is added to complete the normal force, and relative velocities are calculated at P and used to generate friction forces in the plane of the triangle using Eqn. (27). This is repeated independently for each overlapping triangle. If B is also an EFM body, then the same calculation is performed for each of B’s triangles whose centroids are inside A. All force contributions from each triangle are summed up and used to calculate the net force and moment applied to the two rigid bodies. The distribution of normal forces is also used to calculate the center of pressure for the irregular contact patch.
EFM produces results that are inferior to the finite element method (FEM) but take much less time to compute. In contrast to Hertz and FEM, EFM does not account for coupling between elements and hence does not converge to the result predicted by linear elastic material theory even at very fine mesh resolutions. As shown in Fig. 6, EFM can be viewed as a discretization of a Winkler foundation [61], commonly used to represent particulate materials like soil.
Fig. 6.

Continuum bases for contact models. EFM discretizes a Winkler foundation, while Hertz and FEM are based on linear theory of elasticity.
Despite this limitation, EFM can give very good agreement with FEM for total force even though patch geometry may not agree as well [62]. Simbody does not provide a built-in FEM contact method although one could be supplied as a user force element. For most uses of Simbody FEM would be prohibitively expensive; EFM can be a useful alternative but should be used cautiously.
5.3. Rigid contact
An alternative approach to collision and contact problems is to treat the contact objects as rigid and to use unilateral constraints to prevent interpenetration and sliding [63–64]. Collisions are handled impulsively with a coefficient of restitution supplied to emulate dissipative collisions. These are essentially non-physical assumptions but can be useful in practice and have been used successfully for some biomechanical research, e.g. [65]. Simbody’s constraints, operators, and event handling mechanism can be employed currently to use this contact method, and automated support is planned in a near future Simbody release.
Temporary replacement of compliant elements with rigid ones is especially useful in biomechanics for muscle induced acceleration analysis [66–67], since reaction forces are generated instantaneously with constraints. In this case compliant element deformations and patch calculations can be used to guide placement of the rigid constraints. Hamner, et al. [68] uses Simbody constraints to implement induced acceleration analysis in OpenSim [16].
6. Future directions
Simbody is used heavily in biomechanics through the OpenSim application and in other research areas, where it has proven fast and reliable. (See companion paper [69] in this volume for more information about OpenSim.) However, we hope to improve it in a number of ways over the next few years. In particular, we plan to add to our collision/contact system an option for treating some or all contacts using rigid contacts and impulsive collisions as discussed above, with automated handling of unilateral constraints. We also plan to extend the set of analytical surfaces that can be used with the Hertz compliant contact method. Jain and Rodriguez [44] provide a method for significant speed improvements for systems with prescribed motion that we intend to incorporate. Jain [48] describes a promising method for eliminating locally-coupled constraints which we will also explore.
We also hope to grow our library of predefined forces, constraints, and mobilizers and invite community contributions. We are continuously improving our documentation and encourage contributions of examples, and to the Simbody Wiki. Feature requests and bug reports are tracked and support forums available. All source code is available and submissions of patches, enhancements, and new features are welcome. For more information about obtaining and/or contributing to Simbody, visit the Simbody home page https://simtk.org/home/simbody.
Acknowledgments
The authors thank the many contributors to Simbody’s development, including Peter Eastman, Radu Serban, Paul Mitiguy, Jack Middleton, Christopher Bruns, and Charles Schwieters. Samuel Hamner provided many helpful comments on an earlier draft of this paper. This work was supported by the National Institutes of Health through grants U54 GM072970 and R24 HD065690.
Appendix A. Contact model details
This appendix gives details of the calculation of terms that appear in section 5.
A.1. Material properties combining rules; location of contact point
We are given Young’s modulus Ei and Poisson’s ratio νi, i=1,2 for a pair of contacting objects. These are first combined into the plane strain modulus for each material: . To use Hertz theory, we need a single equivalent modulus combining both materials. The literature (e.g. [54]) seems to suggest but this would be inconsistent with the nonlinear Hertz relationship, by the following reasoning. First, the relative curvature is a geometric property and is straightforward to calculate: R = R1 R2 (R1 + R2). Looking at Fig. 4, note that the contact situation depicted should be indistinguishable from one in which B1 (the top, red body) had met an infinitely rigid halfspace, with a displacement of x1 instead of x, provided that B1’s radius were R instead of R1. The effective modulus would be just of B1. Hertz theory would then give . By the same reasoning, we can view B1 as a rigid half space and see that the force on B2 (with radius changed to R) would be unchanged at . But the forces must be the same on both bodies and the same as . Recalling that x = x1 + x2, we now have enough information to write E* in terms of and :
This combining formula is similar, but not identical, to . We can now rearrange this to determine how x is split into x1 and x2 given the stiffnesses of the materials, the result we need to determine the contact point location P:
By inspection, the time derivatives ẋ1 and ẋ2 are split in the same ratios, which gives us a way to define an equivalent dissipation coefficient for ẋ: c* = c1s1+c2(1−s1), where . To summarize, here are the combining rules we use for Hertz:
Note that the EFM method uses linear elements, and thus the standard combining rule is the correct one to use for calculating E* and s1, s2.
A.2. Elliptical contact
We presented the Hertz contact force calculation in Eqn. (23) with a correction factor σ to deal with the eccentricity of the contact ellipse. The correction factor is
| (28) |
where k = a/b, m = 1−(1/k)2, E and K are complete elliptic integrals of the first and second kinds, resp., a, b the semi-major and semi-minor axes of the contact ellipse, resp. so k ≥ 1. The ratio a/b of the contact ellipse dimensions in turn depends only on the principal semi-curvatures A, B, B ≥ A of the (undeformed) separation paraboloid that describes the relative contact geometry:
| (29) |
The above expressions may be derived from references [54] and [70–71]. Eqn.(29) can be solved numerically to machine precision for k, or by approximation. Simbody uses the approximations from [70] which provide smooth, high-accuracy approximations for k and the elliptic integrals, giving σ accurate to five decimal places. Ref. [71] provides a method for calculating this to machine precision, which Simbody includes for testing purposes but does not use during simulation.
References
- 1.Hooker WW, Margulies G. The dynamical attitude equations for an n-body satellite. J Astronautical Sciences. 1965;12:123–128. [Google Scholar]
- 2.Featherstone R. Robot dynamics algorithms. Boston: Kluwer; 1987. [Google Scholar]
- 3.Rodriguez G, Jain A, Kreutz-Delgado K. A spatial operator algebra for manipulator modeling and control. The International Journal of Robotics Research. 1991 Aug 1;10(4):371–381. [Google Scholar]
- 4.Rosenthal DE, Sherman MA. High performance multibody simulations via symbolic equation manipulation and Kane’s method. J Astronautical Sciences. 1986;34:223–239. [Google Scholar]
- 5.Ryan RR. ADAMS multibody systems analysis software. In: Schielen W, editor. Multibody Systems Handbook. New York: Springer-Verlag; 1990. pp. 361–402. [Google Scholar]
- 6.Zajac FE, Neptune RR, Kautz SA. Biomechanics and muscle coordination of human walking: Part I: Introduction to concepts, power transfer, dynamics and simulations. Gait & Posture. 2002;16(3):215–232. doi: 10.1016/s0966-6362(02)00068-1. [DOI] [PubMed] [Google Scholar]
- 7.Piazza SJ. Muscle-driven forward dynamic simulations for the study of normal and pathological gait. Journal of NeuroEngineering and Rehabilitation. 2006;3(5) doi: 10.1186/1743-0003-3-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Delp SL, Loan JP. A computational framework for simulating and analyzing human and animal movement. Computing in Science & Engineering. 2000;2(5):46–55. [Google Scholar]
- 9.Pandy MG. Computer modeling and simulation of human movement. Annual Review of Biomedical Engineering. 2001;3(1):245–273. doi: 10.1146/annurev.bioeng.3.1.245. [DOI] [PubMed] [Google Scholar]
- 10.de Jongh CU, Basson AH, Scheffer C. Predictive modelling of cervical disc implant wear. Journal of Biomechanics. 2008;41(15):3177–3183. doi: 10.1016/j.jbiomech.2008.08.025. [DOI] [PubMed] [Google Scholar]
- 11.Riley PO, Croce UD, Casey Kerrigan D. Propulsive adaptation to changing gait speed. Journal of Biomechanics. 2001;34(2):197–202. doi: 10.1016/s0021-9290(00)00174-3. [DOI] [PubMed] [Google Scholar]
- 12.Smith RL. Open Dynamics Engine (ODE) Manual. 2004 http://opende.sourceforge.net/wiki/index.php/Manual_(All.
- 13.Sellers WI. GaitSym. 2011 Mar 20;2011 http://www.animalsimulation.org. [Google Scholar]
- 14.Schmidt JP, Delp SL, Sherman MA, et al. The Simbios National Center: Systems biology in motion. Proceedings of the Ieee. 2008 Aug;96(8):1266–1280. doi: 10.1109/JPROC.2008.925454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Flores SC. Fast flexible modeling of RNA structure using internal coordinates. IEEE/ACM Transactions on Computational Biology and Bioinformatics. 2010;99 doi: 10.1109/TCBB.2010.104. no. PrePrints. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Delp SL, Anderson FC, Arnold AS, et al. OpenSim: open-source software to create and analyze dynamic simulations of movement. Biomedical Engineering, IEEE Transactions on. 2007;54(11):1940–1950. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
- 17.Pronost N, Sandholm A, Thalmann D. Correlative joint definition for motion analysis and animation. Computer Animation and Virtual Worlds. 2010;21(3–4):183–192. [Google Scholar]
- 18.Sherman MA. Simbody home page. 2011 https://simtk.org/home/simbody.
- 19.X. Consortium. The MIT License. 2011 http://opensource.org/licenses/mit-license.
- 20.Seth A, Sherman M, Eastman P, et al. Minimal formulation of joint motion for biomechanisms. Nonlinear Dynamics. 2010;62(1):291–303. doi: 10.1007/s11071-010-9717-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zeigler BP, Praehofer H, Kim TG. Theory of Modeling and Simulation. 2. Academic Press; 2000. [Google Scholar]
- 22.Brenan KE, Campbell SL, Petzold LR. Numerical solution of initial-value problems in differential-algebraic equations. New York: North-Holland; 1989. [Google Scholar]
- 23.Ascher U. Stabilization of invariants of discretized differential systems. Numerical Algorithms. 1997;14(1):1–24. [Google Scholar]
- 24.Hairer E, Lubich C, Wanner G. Geometric numerical integration : structure-preserving algorithms for ordinary differential equations. 2. Berlin; New York: Springer; 2006. [Google Scholar]
- 25.Shampine LF. Conservation laws and the numerical solution of ODEs. Computers & Mathematics with Applications. 12(5–6 Part 2):1287–1296. [Google Scholar]
- 26.Hairer E, Nørsett SP, Wanner G. Solving ordinary differential equations I: nonstiff problems. 2. Berlin; New York: Springer-Verlag; 1993. rev. ed. [Google Scholar]
- 27.Verlet L. Computer experiments on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Physical Review. 1967;159(1):98–103. [Google Scholar]
- 28.Hairer E, Wanner G. Solving ordinary differential equations II: stiff and differential-algebraic problems. 2. Berlin; New York: Springer-Verlag; 1993. rev. ed. [Google Scholar]
- 29.Cohen SD, Hindmarsh AC. CVODE, a stiff/nostiff ODE solver in C. Computers in Physics. 1996;10(2):138–143. [Google Scholar]
- 30.Dehombreux P, Verlinden O, Conti C. An Implicit Multistage Integration Method Including Projection for the Numerical Simulation of Constrained Multibody Systems. Multibody System Dynamics. 1997;1(4):405–424. [Google Scholar]
- 31.Eich E. Convergence Results for a Coordinate Projection Method Applied to Mechanical Systems with Algebraic Constraints. Siam Journal on Numerical Analysis. 1993 Oct;30(5):1467–1482. [Google Scholar]
- 32.Hairer E, Ostermann A. Dense output for extrapolation methods. Numerische Mathematik. 1990;58(1):419–439. [Google Scholar]
- 33.Vlasenko D, Kasper R. A New Software Approach for the Simulation of Multibody Dynamics. Journal of Computational and Nonlinear Dynamics. 2007;2(3):274–278. [Google Scholar]
- 34.Ascher UM, Chin H, Petzold LR, et al. Stabilization of Constrained Mechanical Systems with DAEs and Invariant Manifolds. Mechanics of Structures and Machines. 1995;23(2):135–157. [Google Scholar]
- 35.Baumgarte J. Stabilization of constraints and integrals of motion in dynamical systems. Computer Methods In Applied Mechanics And Engineering. 1972;1:1–16. [Google Scholar]
- 36.von Schwerin R. Multibody system simulation : numerical methods, algorithms, and software. Berlin; New York: Springer-Verlag; 1999. [Google Scholar]
- 37.Sherman M. Simbody Theory Manual. Simbios Center at Stanford University; 2011. https://simtk.org/docman/view.php/47/231/SimbodyTheoryManual.pdf. [Google Scholar]
- 38.W. H. Press. Numerical recipes in C++ : the art of scientific computing. 2. Cambridge, UK; New York: Cambridge University Press; 2002. [Google Scholar]
- 39.Mauve M, Vogel J, Hilt V, et al. Local-lag and timewarp: providing consistency for replicated continuous applications. Multimedia, IEEE Transactions on. 2004;6(1):47–57. [Google Scholar]
- 40.Teal SL, Rudnicky AI. A performance model of system delay and user strategy selection. Proceedings of the SIGCHI conference on Human factors in computing systems; Monterey, California, United States. 1992. pp. 295–305. [Google Scholar]
- 41.Shneiderman B. Response time and display rate in human performance with computers. ACM Comput Surv. 1984;16(3):265–285. [Google Scholar]
- 42.Card SK, Moran TP, Newell A. The psychology of human-computer interaction. Hillsdale, N.J: L. Erlbaum Associates; 1983. [Google Scholar]
- 43.Rodriguez G, Jain A, Kreutz-Delgado K. Spatial operator algebra for multibody system dynamics. J Astronautical Sciences. 1992;40(1):27–50. [Google Scholar]
- 44.Jain A, Rodriguez G. Recursive dynamics algorithm for multibody systems with prescribed motion. Journal of Guidance, Control, and Dynamics. 1993;16(5):830–837. [Google Scholar]
- 45.Jain A, Vaidehi N, Rodriguez G. A fast recursive algorithm for molecular dynamics simulation. Journal of Computational Physics. 1993;106(2):258–268. [Google Scholar]
- 46.Schwieters CD, Clore GM. Internal coordinates for molecular dynamics and minimization in structure determination and refinement. Journal of Magnetic Resonance. 2001 Oct;152(2):288–302. doi: 10.1006/jmre.2001.2413. [DOI] [PubMed] [Google Scholar]
- 47.Anderson KS, Critchley JH. Improved ‘Order-N’ Performance Algorithm for the Simulation of Constrained Multi-Rigid-Body Dynamic Systems. Multibody System Dynamics. 2003;9(2):185–212. [Google Scholar]
- 48.Jain A. Recursive algorithms using local constraint embedding for multibody system dynamics. ASME Conference Proceedings. 2009;2009(49019):139–147. [Google Scholar]
- 49.Hollars MG, Rosenthal DE, Sherman MA. SD/FAST User’s Guide B.2. Symbolic Dynamics, Inc; 1994. [Google Scholar]
- 50.Featherstone R. Rigid body dynamics algorithms. 1. New York, NY: Springer; 2007. [Google Scholar]
- 51.Golub GH, Van Loan CF. Matrix computations. 3. Baltimore: Johns Hopkins University Press; 1996. [Google Scholar]
- 52.Anderson E. LAPACK users’ guide. 3. Philadelphia: Society for Industrial and Applied Mathematics; 1999. [Google Scholar]
- 53.Hertz H. On the contact of elastic solids. J Reine Angew Math. 1882;92:156–171. [Google Scholar]
- 54.Johnson KL. Contact mechanics. Cambridge Cambridgeshire; New York: Cambridge University Press; 1985. [Google Scholar]
- 55.Blankevoort L, Kuiper JH, Huiskes R, et al. Articular contact in a three-dimensional model of the knee. Journal of Biomechanics. 1991;24(11):1019–1031. doi: 10.1016/0021-9290(91)90019-j. [DOI] [PubMed] [Google Scholar]
- 56.Hunt KH, Crossley FRE. Coefficient of restitution interpreted as damping in vibroimpact. ASME Journal of Applied Mechanics. 1975;42:440–445. [Google Scholar]
- 57.Armstrong-Hélouvry B. Control of machines with friction. Boston: Kluwer Academic Publishers; 1991. [Google Scholar]
- 58.Struik DJ. Lectures on classical differential geometry. 2. New York: Dover Publications; 1988. [Google Scholar]
- 59.Marhefka DW, Orin DE. Simulation of contact using a nonlinear damping model. International Conference on Robotics and Automation; Minneapolis, Minnesota, USA. 1996. pp. 1662–1668. [Google Scholar]
- 60.Goldsmith W. Impact : the theory and physical behaviour of colliding solids. Mineola, N.Y: Dover Publications; 2002. [Google Scholar]
- 61.Winkler E. Theory of elasticity and strength. Czechoslovakia: Dominicus Prague; 1867. [Google Scholar]
- 62.Pérez-González A, Fenollosa-Esteve C, Sancho-Bru JL, et al. A modified elastic foundation contact model for application in 3D models of the prosthetic knee. Medical Engineering & Physics. 2008;30(3):387–398. doi: 10.1016/j.medengphy.2007.04.001. [DOI] [PubMed] [Google Scholar]
- 63.Pfeiffer F, Glocker C. Multibody dynamics with unilateral contacts. New York: Wiley; 1996. [Google Scholar]
- 64.Baraff D. Fast contact force computation for nonpenetrating rigid bodies. Proceedings of the 21st annual conference on Computer graphics and interactive techniques; 1994. pp. 23–34. [Google Scholar]
- 65.Piazza SJ, Delp SL. Three-Dimensional Dynamic Simulation of Total Knee Replacement Motion During a Step-Up Task. Journal of Biomechanical Engineering. 2001;123(6):599–606. doi: 10.1115/1.1406950. [DOI] [PubMed] [Google Scholar]
- 66.Zajac FE, Gordon ME. Determining muscle’s force and action in multi-articular movement. Exercise and Sport Sciences Reviews. 1989;17(1):187–230. [PubMed] [Google Scholar]
- 67.Riley PO, Kerrigan DC. Kinetics of stiff-legged gait: induced acceleration analysis. Rehabilitation Engineering, IEEE Transactions on. 1999;7(4):420–426. doi: 10.1109/86.808945. [DOI] [PubMed] [Google Scholar]
- 68.Hamner SR, Seth A, Delp SL. Muscle contributions to propulsion and support during running. Journal of Biomechanics. 2010;43(14):2709–2716. doi: 10.1016/j.jbiomech.2010.06.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Seth A, Sherman MA, Reinbolt JA, et al. OpenSim: A musculoskeletal modeling and simulation framework for in silico investigations and exchange. IUTAM Symposium on Human Body Dynamics; Waterloo, Canada. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Antoine J-F, Visa C, Sauvey C, et al. Approximate Analytical Model for Hertzian Elliptical Contact Problems. Journal of Tribology. 2006;128(3):660–664. [Google Scholar]
- 71.Dyson A, Evans HP, Snidle RW. A simple, accurate method for calculation of stresses and deformations in elliptical hertzian contacts. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 1989–1996 (vols 203–210) 1992;206(23):139–141. [Google Scholar]