Abstract
Despite current knowledge of tendon structure, the fundamental deformation mechanisms underlying tendon mechanics and failure are unknown. We recently showed that a shear lag model, which explicitly assumed plastic interfibrillar load transfer between discontinuous fibrils, could explain the multiscale fascicle mechanics, suggesting that fascicle yielding is due to plastic deformation of the interfibrillar matrix. However, it is unclear whether alternative physical mechanisms, such as elastic interfibrillar deformation or fibril yielding, also contribute to fascicle mechanical behavior. The objective of the current work was to determine if plasticity of the interfibrillar matrix is uniquely capable of explaining the multiscale mechanics of tendon fascicles including the tissue post-yield behavior. This was examined by comparing the predictions of a continuous fibril model and three separate shear lag models incorporating an elastic, plastic, or elastoplastic interfibrillar matrix with multiscale experimental data. The predicted effects of fibril yielding on each of these models were also considered. The results demonstrated that neither the continuous fibril model nor the elastic shear lag model can successfully predict the experimental data, even if fibril yielding is included. Only the plastic or elastoplastic shear lag models were capable of reproducing the multiscale tendon fascicle mechanics. Differences between these two models were small, although the elastoplastic model did improve the fit of the experimental data at low applied tissue strains. These findings suggest that while interfibrillar elasticity contributes to the initial stress response, plastic deformation of the interfibrillar matrix is responsible for tendon fascicle post-yield behavior. This information sheds light on the physical processes underlying tendon failure, which is essential to improve our understanding of tissue pathology and guide the development of successful repair.
1. Introduction
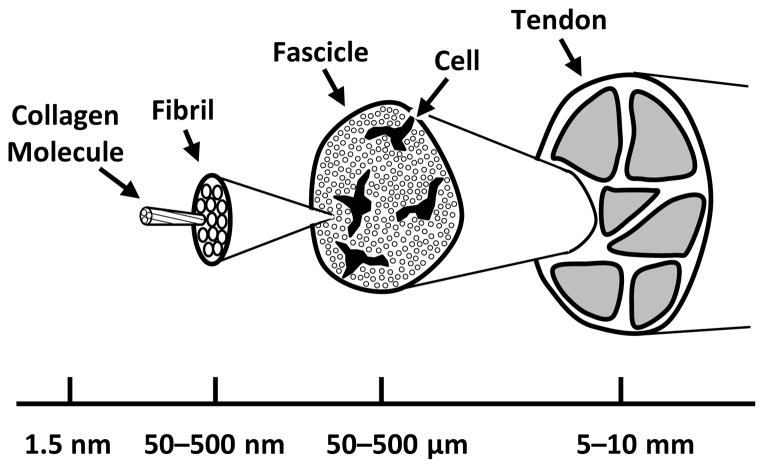
From an engineering perspective, tendons are hydrated composite biomaterials with a complicated hierarchical structure spanning multiple length scales (Fig. 1) (Kastelic et al., 1978). At the macroscopic level, tendons are separated into subunits called fascicles, which are dense collections of highly aligned collagen fibrils interspersed with cells (Rowe, 1985). The fibrils are separated by an interfibrillar matrix composed of proteoglycans, elastin, collagen VI, and other macromolecules (Thorpe et al., 2013a). However, the primary components of tendon are collagen I molecules, which are contained within the fibrils in a semi-crystalline organization and connected through naturally occurring inter-molecular crosslinks (Bailey et al., 1998; Hulmes et al., 1995; Orgel et al., 2006). Despite the detailed understanding of tendon hierarchical structure, it is unknown how each of the tissue components across the various length scales contributes to the macroscale tissue response. Identifying these structure-function relationships is crucial for understanding tendon pathology leading to tissue failure and for developing repair strategies using either cell-mediated regeneration or tissue engineered replacements.
Figure 1.
Tendon hierarchical structure (adapted from Kastelic et al. (1978)). Collagen molecules are organized into extracellular structures called fibrils, which are the primary tensile load bearing elements in tendon. The fibrils are highly aligned and tightly packed into fascicles, which are the final macroscopic subunits in tendon. Within each fascicle are cells and an interfibrillar matrix surrounding the fibrils containing proteoglycans, elastin, and other macromolecules.
A central question is whether collagen fibrils are continuous structures that extend across the entire tendon length. Despite difficulties finding fibril ends in tendon and the observation of fibril branching (Kadler et al., 2000; Provenzano and Vanderby, 2006), multiscale experimental testing of tendon fascicles suggests that fibrils are discontinuous and transmit load through shearing of the interfibrillar matrix (Bruehlmann et al., 2004; Gupta et al., 2010; Puxkandl et al., 2002; Rigozzi et al., 2011; Szczesny and Elliott, 2014). We recently showed that a shear lag model, which explicitly assumes interfibrillar load transfer between discontinuous fibrils, can explain the multiscale fascicle mechanics, strongly suggesting that fibrils are indeed discontinuous (Szczesny and Elliott, 2014). Furthermore, that study proposed that the fascicle post-yield behavior is produced by plastic deformation of the interfibrillar matrix. However, it is unclear whether alternative physical mechanisms, including elastic interfibrillar deformation and fibril yielding, also contribute to fascicle mechanical behavior.
Shear lag models have been widely used to represent several biological tissues composed of discontinuous reinforcing elements embedded in a softer matrix (Ahmadzadeh et al., 2014; Buehler, 2008, 2006; Gao et al., 2003; Jäger and Fratzl, 2000; Zhang et al., 2010). The fundamental assumption of all shear lag models is that the externally applied load is transferred to the reinforcing elements through shear stresses acting at the interface with the surrounding matrix. The classic shear lag model first proposed by Cox (1952) has been applied to tendon (Torp et al., 1975). However, this formulation assumed that the matrix is isotropic linear elastic and that the shear forces generated in the matrix are not directly coupled to the relative sliding between fibrils (Hull and Clyne, 1996). More recent models have relaxed these restrictions and coupled interfibrillar shear stresses to specific tissue components, but they still assume elasticity of the interfibrillar matrix (Ahmadzadeh et al., 2013; Bar-On and Wagner, 2013; Fessel and Snedeker, 2011). Alternative formulations have been developed incorporating a plastic, elastoplastic, and viscous interfibrillar matrix (Ahmadzadeh et al., 2014; Ciarletta and Ben Amar, 2009; Gao et al., 2008; Goh et al., 2007; Mijailovich et al., 1993; Szczesny and Elliott, 2014). However, there has not been an evaluation of how well the various forms of shear lag models predict the multiscale mechanical behavior of tendon fascicles.
The objective of the current work was to determine if plasticity of the interfibrillar matrix is uniquely capable of explaining the multiscale mechanics of tendon fascicles including the tissue post-yield behavior. This was examined by comparing the predictions of a continuous fibril model and three separate shear lag models incorporating an elastic, plastic, or elastoplastic interfibrillar matrix with published multiscale experimental data (Szczesny et al., 2014). The potential effects of fibril yielding on each of these models were also considered. The results demonstrated that only the plastic or elastoplastic shear lag models were capable of reproducing the experimental data and the post-yield behavior in particular, which suggests that plastic deformation of the interfibrillar matrix is responsible for yielding of tendon fascicles. This information sheds light on the physical processes underlying tendon failure, which is essential to improve our understanding of tissue pathology and guide the development of successful repair.
The general principles of the shear lag models as well as the specific formulations for the elastic and plastic models are presented in Section 2. In order to compare the shear lag models to experimental data, the derived equations were modified to account for fibril crimping (Section 2.4), which is responsible for the initial “toe-region” in the stress-strain behavior of tendon fascicles (Diamant et al., 1972). In Section 3, the multiscale behavior of both the elastic and plastic models are compared along with their predictions of the experimental data and the potential effects of fibril yielding. Finally, Section 4 presents the derivation and performance of the elastoplastic shear lag model.
2. Shear Lag Model Formulations
2.1. General Features
For the current study of tendon fascicles, the fascicle structure is simplified as a staggered array of discontinuous fibrils embedded in an extrafibrillar matrix (Szczesny and Elliott, 2014; Ahmadzadeh et al., 2013; Goh et al., 2007), which is represented by a periodic unit cell that is half the fibril length (L) (Fig. 2). At any point x where there is relative sliding between the fibrils, an interfibrillar shear stress (τ(x)) acts equally over the entire fibril circumference, leading to the following equilibrium equation:
| (1) |
where σi(x) is the stress in the i-th fibril and r is the fibril radius. Note that the ends of the fibrils are unloaded, P is the stress at fibril midpoint, and, based on symmetry, σ2(x) = σ1(L/2 − x). It is assumed that the fibrils are linear elastic with a modulus Ef and that the axial displacements of the fibrils are uniform throughout their cross-section (i.e., no intra-fibrillar shear). The only difference between the shear lag models presented in this paper is the form taken by the interfibrillar shear stress (τ(x)). Once this is specified, expressions for the fibril stress and displacements (ui(x)) are determined using the boundary condition u1(L/2) = −u2(0) = U/2 with the strain applied to the unit cell (εuc) equal to 2U/L.
Figure 2.
The construction of the shear lag models consists of a periodic array of discontinuous and staggered fibrils. Tensile load was transferred between fibrils through an interfibrillar shear stress (τ(x)).
2.2. Elastic Interfibrillar Matrix
The classic shear lag model first proposed by Cox (1952) assumes that the interfibrillar matrix is isotropic linear elastic and that the matrix strain far from the fibrils is equal to the macroscale strain applied to the tissue composite (Hull and Clyne, 1996). This second assumption may not be valid given the high density and close packing of fibrils in tendon (Parry and Craig, 1984). Therefore, recent applications of shear lag models to tendon have described the interfibrillar shear stress as a function of the relative sliding between adjacent fibrils (Ahmadzadeh et al., 2013; Mijailovich et al., 1993), which can be expressed as
| (2) |
where G is the shear modulus of the interfibrillar matrix and h is the distance between the fibril surfaces. Although more complicated formulations have been developed based on assumptions for the organization and behavior of specific tissue components (Ahmadzadeh et al., 2013; Ciarletta and Ben Amar, 2009; Fessel and Snedeker, 2011; Goh et al., 2007; Zhang et al., 2010), Eq. (2) captures the fundamental mechanisms underlying elastic shear lag models. Assuming hexagonal lateral fibril packing, the interfibrillar distance can be related to the fibril volume fraction (ϕ) and radius (Hull and Clyne, 1996):
| (3) |
Solving the governing equilibrium equation (Eq. (1)) using the boundary conditions described in Section 2.1 produces the following expressions for the fibril stress, interfibrillar shear stress, and fibril displacements:
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
where Lc is the characteristic length over which load is transferred between fibrils. The average stress in the unit cell (σuc) is given by the stress averaged over the two fibrils, which, due to symmetry, reduces to
| (10) |
Note that the expression for σuc is equal to the fibril stress at the midpoint of the unit cell (σ1(L/4) = σ2(L/4)).
2.3. Plastic Interfibrillar Matrix
Various shear lag models have incorporated plasticity of the interfibrillar matrix (Ciarletta and Ben Amar, 2009; Gao et al., 2008; Goh et al., 2007; Mijailovich et al., 1993). Here we used a simple perfectly plastic constitutive behavior to represent the fundamental features of plasticity of the interfibrillar matrix (Szczesny and Elliott, 2014). Specifically, relative sliding between fibrils was assumed to produce a constant interfibrillar shear stress:
| (11) |
By enforcing compatibility along the fibril length, direct integration leads to the following piecewise solutions for the fibril stress and displacements:
| (12) |
| (13) |
| (14) |
| (15) |
where Ls is the length from the fibril ends over which there is relative sliding between fibrils. As in Eq. (10), due to symmetry, the stress averaged over the two fibrils is equal to the fibril stress at the midpoint of the unit cell (σuc = σ1(L/4) = P/2). Therefore, the average stress in the unit cell is
| (16) |
2.4. Fibril Uncrimping
In order to compare the shear lag models to experimental data, the equations described above were modified to account for fibril crimping, which is responsible for the initial non-linearity (i.e., toe-region) in the macroscale tissue behavior (Diamant et al., 1972). The fibrils, and hence each unit cell, were assumed to be initially crimped and bear load only after the applied tissue stretch (λ) reaches a specific uncrimping stretch (λc). Since fibrils are not uniformly crimped within a fascicle (Kastelic et al., 1978; Rowe, 1985), a gamma probability distribution was used to represent the spread of tissue stretches required to uncrimp the unit cells (γ(λc − 1)) (Sacks, 2003; Szczesny et al., 2012), which was parameterized by the mean uncrimping stretch ( ) and standard deviation of uncrimping ( ). The macroscale tissue stress (σT) was then calculated through the weighted integral of the expressions for σuc (Eq. (10,16)) multiplied by the fibril volume fraction
| (17) |
where εuc in Eq. (10,16) is substituted with λ/λc − 1, which is the expression for the strain of the unit cell after uncrimping normalized by its uncrimping stretch.
A similar correction for uncrimping must be made in order to compare the fibril strains predicted by the model to the strains measured experimentally. Since the fibril strains were measured using optical microscopy (Szczesny et al., 2014), the apparent (experimentally observed) fibril strains are not simply the strains for which the fibrils bear load, but are the cumulative elongation of the fibrils normalized by their original crimped length. Therefore, the equivalent apparent strain (εapp) of the uncrimped fibrils predicted by the shear lag models is
| (18) |
Note that the term σuc/Ef represents the true fibril strain (averaged over the fibril length) due to the application of load following uncrimping. Prior to uncrimping (i.e., λ < λc), the apparent fibril strain is equal to the tissue strain (λ − 1). Again using a gamma distribution for uncrimping stretches, the apparent fibril:tissue strain ratio (ηapp) predicted by the models is
| (19) |
where Γ(λ − 1) is the gamma cumulative distribution function. Note that the first term in brackets represents the fibrils that are still crimped and, therefore, have the same apparent strain as the tissue. These techniques have previously been validated to accurately represent fibril uncrimping in tendon fascicles (Szczesny and Elliott, 2014). For the comparison of the model predictions with experimental data, the fibril radius and volume fraction were assumed to be 85 nm and 0.7, respectively (Parry and Craig, 1984; Screen et al., 2005), and the remaining model parameters (Ef, τp, L, ) were based on a previous fit of the plastic model using Eq. (17) to average macroscale fascicle mechanics (Szczesny et al., 2014) (Table 2). The same parameter values were used for the elastic model (Table 2), with the value of G (~1 Pa) chosen to give a linear-region tissue response that was similar to the prediction of the plastic model.
Table 2.
Model Parameter Values
| Ef | 700 MPa |
| L | 10 mm |
| r | 85 nm |
| 0.7 | |
| G | 0.5 – 1 Pa |
| τp | 0.275 kPa |
| 1.003 | |
| 0.0017 |
3. Comparison of Elastic and Plastic Models
3.1. General Behavior
Before investigating how well the elastic and plastic models replicate fascicle multiscale mechanics, it is instructive to compare their general behavior. In particular, consider the length over which load is transferred between fibrils through interfibrillar shear. For the elastic model, this is described by Lc, which, according to Eq. (9), is a fixed value determined by material and geometric constants. This means that the amount of interfibrillar sliding in the elastic model is the same regardless of the strain applied to the tissue. Furthermore, while the magnitudes of the fibril stress, interfibrillar shear stress, and fibril displacements scale with εuc (Eq. 4–7), their distributions are independent of the applied tissue strain since Lc remains constant (Fig. 3). In contrast, the expression for the load transfer length in the plastic model (Ls) is dependent on the unit cell strain and, therefore, the applied tissue strain (Eq. (15)). This indicates that in the plastic model the amount of interfibrillar sliding, and hence the behavior of the model, changes with the applied tissue strain. At low strains, Ls is less than Lc, which means that there is less interfibrillar sliding (i.e., smaller region where u1 ≠ u2) in the plastic model than in the elastic model (Fig. 3C–D). This is because the interfibrillar shear stress in the plastic model is greater than the maximum interfibrillar shear stress in the elastic model (Fig. 3B). Furthermore, less interfibrillar sliding means that more strain is transmitted to the fibrils, resulting in a higher average fibril stress in the plastic model compared to the elastic model (Fig. 3A).
Figure 3.
Comparison of the fibril stress (σ), interfibrillar shear stress (τ), and fibril displacements (u) along the unit cell length in the elastic and plastic shear lag models with increasing applied tissue strain (from row 1 to 3). (Row 1: A–D) Initially, when Ls is less than Lc, there is less interfibrillar sliding (i.e., smaller region where u1 ≠ u2) in the plastic model compared to the elastic model (εuc = 0.5%). (Row 2: E–H) As the applied tissue strain increases, Ls becomes similar to Lc and the amount of interfibrillar sliding is approximately the same between the two models. The fibril stress distribution and point at which the interfibrillar shear stress approaches zero are also very similar between the two models (εuc = 1.4%). (Row 3: I–L) At higher applied strains, Ls continues to increase until Ls = L/4, where the interfibrillar sliding and shear stress occur across the entire fibril length, maximally loading the fibrils. In contrast, the elastic model produces identical distributions of stresses and displacements since the characteristic length over which loads are transmitted between fibrils (Lc) remains constant. Model parameters: Ef = 700 MPa, r = 85 nm, ϕ = 0.7, τp = 0.275 kPa, G = 1 Pa, L = 10 mm.
As more strain is applied to the tissue, the interfibrillar sliding in the plastic model increases but remains constant in the elastic model. When Ls and Lc are comparable in magnitude, the amount of interfibrillar sliding and point at which the interfibrillar shear approaches zero is approximately the same in both models (Fig. 3F–H). At this point, the fibril stress distribution over the unit cell is also very similar between the elastic and plastic models (Fig. 3E). However, if the applied strain continues to increase, then ultimately the interfibrillar shear stress will act over the entire fibril length in the plastic model (Ls = L/4). At this point (εuc = 3τpL/4rEf = εp) the fibrils are fully loaded with interfibrillar shear and sliding occurring at all points along the fibril length (Fig. 3I–L). Any tissue strain beyond this point will simply cause the fibrils to slide without further elongation. In contrast, as expected from Eq. (4–7) for the elastic model, the distributions of the fibril stress, interfibrillar shear stress, and fibril displacements are simply scaled by the applied strain, with no change in the distribution shape.
3.2. Consequences on Multiscale Behavior
The difference in load transfer lengths between the plastic and elastic shear lag models has important consequences on the resulting macroscale tissue behavior. Ignoring any uncrimping nonlinearities in the tissue stress response (these are included in Section 3.3), the macroscale tissue modulus predicted by each model can be determined by differentiating the expressions for σuc (Eq. (10,16)) with respect to εuc and multiplying by the fibril volume fraction:
| (20) |
| (21) |
where Ee and Ep are the tissue moduli for the elastic and plastic models, respectively. Similar to the load transfer lengths, the tissue modulus for the elastic model is constant and independent of the applied tissue strain. In contrast, the tissue modulus for the plastic model is a function of εuc, which is equal to the applied tissue strain in the case of no fibril crimping. Initially, when εuc is zero, the modulus is equal to Ef, which is equivalent to the case where the fibrils are continuous and extend across the entire tissue length. As the applied tissue strain increases, the modulus continuously decreases until εuc = εp. At this point, the tissue stress (i.e., σuc) ultimately reaches a maximum value of τpL/2r and, as described earlier, any increase in the tissue strain beyond this point simply causes the fibrils to slide without increasing the fibril stress, which produces a perfectly plastic response at the macroscale tissue level.
Similar differences between the plastic and elastic shear lag models are also observed at the fibrillar length scale. Dividing the expressions for σuc for each model (Eq. (10,16)) by Ef produces the average fibril strain and further dividing by εuc results in the fibril:tissue strain ratios:
| (22) |
| (23) |
where ηe and ηp are the fibril:tissue strain ratios for the elastic and plastic shear lag models, respectively. Similar to the macroscale tissue modulus, for the elastic model, the fibril:tissue strain ratio is constant while, for the plastic model, the strain ratio decreases with applied tissue strain. In fact, it is exactly this behavior at the fibrillar level that produces the drop in the tissue modulus with applied strain and ultimately leads to perfectly plastic macroscale behavior. The significance of the decreasing fibril:tissue strain ratio inherent in the plastic shear lag model will be evident when both models are applied to multiscale fascicle experimental data in the next section.
3.3. Prediction of Tendon Fascicle Multiscale Mechanics
In this section the multiscale behavior predicted by the elastic and plastic shear lag models (Eq. (17,19)) are compared to published experimental data of tendon fascicles (Szczesny et al., 2014). A model with continuous fibrils that span the entire fascicle length is used as a reference, where σuc = Ef · εuc. The plots of the tissue behavior demonstrate that the continuous model cannot reproduce the macroscale stress response (Fig. 4A) or the fibril:tissue strain ratio (Fig. 4B). In particular, since the fibrils in this model are continuous, then, by definition, the fibril:tissue strain ratio is fixed at one, which does not agree with the experimental observations. This suggests that the fibrils are discontinuous and that a shear lag model is more appropriate. However, the elastic shear lag model does not perform substantially better. As expected from Eq. (10) and (20), the elastic model produces a linear macroscale tissue response after initial fibril uncrimping, which cannot replicate the observed strain-softening of the tendon fascicle (Fig. 4A). In addition, after the initial drop due to fibril uncrimping, the elastic model predicts a constant fibril:tissue strain ratio (Eq. (22)), which does not match the experimentally measured decrease in the fibril:tissue strain ratio with increased tissue strain (Fig. 4B). In contrast, the plastic shear lag model can reproduce the macroscale tissue behavior including the post-yield response (Fig. 4A). Furthermore, this model successfully predicts the general relationship between the fibril and tissue strains (Fig. 4B). This suggests not only that the fibrils are discontinuous but that plastic deformation of the interfibrillar matrix is responsible for the fascicle multiscale mechanics.
Figure 4.
Model predictions of tendon fascicle multiscale mechanics (mean ± standard deviation) (Szczesny et al., 2014). (A,B) The poor performance of a continuous fibril model (dashed line) in reproducing (A) the tissue stress response and (B) the fibril:tissue strain ratio suggests that fibrils are indeed discontinuous. The elastic shear lag model (dotted line) provides only marginally improved results since, after the fibrils are uncrimped, it predicts a constant tissue modulus and a constant fibril:tissue strain ratio. However, the plastic shear lag model (solid line) can accurately replicate the macroscale strain-softening as well as the continuous drop in the fibril:tissue strain ratio, suggesting that plasticity of the interfibrillar matrix explains tendon fascicle mechanics. Model parameters: Ef = 700 MPa, r = 85 nm, ϕ = 0.7, τp = 0.275 kPa, G = 0.5 Pa, L = 10 mm, , and . (C,D) The effects of fibril yielding were approximated by a 30% reduction in the fibril modulus (red lines). (C) While fibril yielding may enable the continuous and elastic models to replicate the macroscale strain-softening, (D) it does not improve the prediction of the fibril:tissue strain ratio. However, for the plastic model, fibril yielding may improve the agreement with the experimental fibril:tissue strain ratios at higher applied tissue strains.
It is possible that alternative processes other than interfibrillar plasticity (e.g. fibril yielding) could explain the tissue strain-softening behavior and potentially improve the performance of the continuous model or the elastic shear lag model. To investigate this possibility, the fibril modulus was reduced by 30% and the model simulations were repeated. Although this does not strictly represent a progressive drop in fibril modulus, in the absence of clear experimental data for fibril yielding, it does provide an estimate of how each model would be affected by such behavior. As expected, for the continuous model and both shear lag models, the tissue stress is lower with the reduced fibril modulus (Fig. 4C). Therefore, it is conceivable that a progressive drop in the fibril modulus could improve the fit of the tissue post-yield behavior for the continuous and elastic models. However, the reduced fibril modulus increases the fibril:tissue strain ratio for the elastic shear lag model, while the fibril:tissue strain ratio for the continuous model remains at one (Fig. 4D). This demonstrates that fibril yielding does not improve the prediction of the fibril strains for either the continuous model or the elastic shear lag model. For the plastic model, the increased fibril strains due to fibril yielding possibly improves the prediction of the fibril:tissue strain ratio at higher tissue strains. This suggests that while plasticity of the interfibrillar matrix is necessary to explain the fascicle post-yield behavior, fibril yielding may contribute as well.
4. Combined Elastoplastic Shear Lag Model
4.1. Model Formulation
Although the plastic shear lag model described above can reproduce the general fascicle multiscale behavior (Fig. 4), it is likely that the interfibrillar matrix does have an elastic response at low stress values. Additionally, it is more likely that the interfibrillar shear stress gradually increases with interfibrillar sliding up to a maximum value before becoming plastic instead of the binary response described in Eq. (11). Therefore, in this section, an elastoplastic shear lag model is presented with an interfibrillar matrix that is initially elastic and then behaves perfectly plastically upon reaching a shear stress τp.
The constitutive behavior of the elastoplastic interfibrillar matrix can be described by bounding the elastic expression in Eq. (2), such that |τ(x)| ≤ τp. Alternatively, if we define Lp as the length from the fibril ends where the interfibrillar shear stress has become perfectly plastic, then we can use the following spatial definition for elastoplastic constitutive behavior:
| (24) |
By enforcing compatibility along the fibril length, applying the boundary conditions described in Section 2.1, and ensuring the interfibrillar shear stress is continuous (i.e., u1(Lp) − u2(Lp) = τph/G), direct integration of Eq. (1) leads to the following piecewise solutions for the fibril stress, interfibrillar shear stress, and fibril displacements:
| (25) |
| (26) |
| (27) |
| (28) |
where Lc is given by Eq. (9) and
| (29) |
| (30) |
| (31) |
| (32) |
| (33) |
| (34) |
For an applied unit cell strain of εuc, Lp is determined by solving the equation
| (35) |
Again, based on symmetry, the stress applied to the unit cell averaged over the two fibrils is σuc = P/2, which can be determined from Eq. (29).
4.2. General Behavior
Initially, the elastoplastic model behavior matches the elastic shear lag model since the interfibrillar matrix has an elastic response while τ(x) ≤ τp (Fig. 5A–C). The unit cell strain at which the interfibrillar shear stress initially becomes plastic at the fibril ends (i.e., τ(0) = τ(L/2) = τp) is determined from Eq. (35) with Lp = 0 and is given by
Figure 5.
Distributions of the fibril stress (σ), interfibrillar shear stress (τ), and fibril displacements (u) along the unit cell length for the elastoplastic shear lag model. (A–C) At strains below εp,i, the model behaves identically to the elastic shear lag model since τ(x) ≤ τp. (D–F) As the applied strain increases, the interfibrillar shear stress becomes plastic at the fibril ends (Lp) and the region of interfibrillar sliding (i.e., u1 ≠ u2) enlarges towards the center of the unit cell. (G–I) Ultimately, at a strain of εp,f the interfibrillar shear stress has become plastic along the full fibril length (Lp = L/4). Model parameters: Ef= 700 MPa, r = 85 nm, ϕ = 0.7, τp = 0.275 kPa, G = 0.5 Pa, L = 10 mm.
| (36) |
As the applied strain increases, the region of plastic interfibrillar shear stress and interfibrillar sliding enlarges towards the center of the unit cell (Fig. 5D–F). Ultimately, at a unit cell strain of εp,f the interfibrillar shear stress has become plastic along the full fibril length (i.e., Lp = L/4; Fig. 5G–I):
| (37) |
Note that the second term is the expression for εp in the plastic shear lag model (Section 3.1). Since all the terms in Eq. (37) are positive values, this means that the initial elasticity of the interfibrillar matrix increases the tissue strain at which the fibrils are maximally loaded and the macroscale tissue response becomes perfectly plastic.
4.3. Prediction of Tendon Fascicle Multiscale Mechanics
The combined elastoplastic shear lag model was compared to the plastic model described above (using the same model parameters as in Table 2 and Section 3.3) in order to evaluate the importance of adding elasticity within the interfibrillar matrix to the plastic shear lag model. At the macroscopic level, the elastoplastic model produced a tissue response that was very similar to the plastic model (Fig. 6A). However, the effect of the interfibrillar matrix elasticity was more pronounced on the fibril:tissue strain ratio, producing a small improvement in the model predictions at low tissue strains (Fig. 6B). At strains above εp,f, the two models converged since the response of the interfibrillar matrix in the elastoplastic model has become fully plastic at this point. These simulations demonstrate that, while the initial elasticity of the interfibrillar matrix may contribute to the tissue response at low strains, matrix plasticity is responsible for the post-yield behavior.
Figure 6.

Effect of initial elasticity of the interfibrillar matrix on model predictions of tendon fascicle multi-scale mechanics (mean ± standard deviation) (Szczesny et al., 2014). (A) At the macroscopic level, the elastoplastic model produced a tissue response that was very similar to the plastic model. (B) While the elastoplastic model improves the prediction of the fibril:tissue strain ratio at low applied tissue strains, the post-yield behavior is still dominated by plasticity of the interfibrillar matrix. Model parameters: Ef = 700 MPa, r = 85 nm, ϕ = 0.7, τp = 0.275 kPa, G = 0.5 Pa, L = 10 mm, , and .
5. Discussion
Recently we proposed that the multiscale mechanics of tendon fascicles can be explained by a shear lag model incorporating a perfectly plastic interfibrillar matrix that transmits load between discontinuous fibrils (Szczesny and Elliott, 2014). The objective of this study was to evaluate whether alternative models based on an elastic interfibrillar matrix could provide equally successful explanations of the fascicle mechanics. Comparing the predictions of these models with the plastic shear lag model demonstrated that the plastic model has a unique ability to reproduce the tissue behavior at multiple length scales. A key feature of the plastic shear lag model is that interfibrillar sliding increases with greater applied tissue strain (Eq. 15), which is consistent with previous microscale measurements (Screen et al., 2004; Szczesny and Elliott, 2014; Szczesny et al., 2014; Thorpe et al., 2013b). This increased interfibrillar sliding reduces the amount of strain that is transmitted to the fibrils during testing and results in a decrease in the tissue modulus, which is consistent with the observed multiscale experimental data of tendon fascicles (Fig. 4A–B). In contrast, none of these behaviors are replicated by the elastic shear lag model. An elastoplastic shear lag model, in which the interfibrillar matrix is initially elastic before becoming plastic, does improve the prediction of the fibril:tissue strain ratio at low applied tissue strains (Fig. 6B); however, the improvement is small despite the addition of an extra model parameter. Therefore, these data suggest that, while elasticity of the interfibrillar matrix contributes to the initial tissue response to loading, interfibrillar plasticity is indeed the dominant deformation mechanism underlying fascicle post-yield behavior.
The unique ability of the plastic shear lag model to replicate tendon fascicle mechanics is consistent with previous suggestions that fascicle failure is due to plasticity within the interfibrillar matrix rather than fibril rupture. Tensile testing of individual fibrils produces failure strains and stresses that are substantially higher than the values obtained from tendon fascicles, even after accounting for the fibril volume fraction (Hansen et al., 2009; Shen et al., 2010; Svensson et al., 2013), which suggests that fascicle failure is not due to fibril rupture. In addition, tendon fascicles stretched beyond their yield point contain fibrils with localized plastic deformation that do not show signs of rupture until after a substantial amount of fatigue loading (>800 cycles) (Fung et al., 2009; Veres et al., 2013). Fascicle behavior during long-term creep and notch tension testing suggests that damage processes are localized to the interfibrillar matrix (Ker, 2007; Wang and Ker, 1995). This agrees with findings suggesting dissipative deformation mechanisms within the interfibrillar matrix (Gupta et al., 2007, 2005; Gutsmann et al., 2005; Svensson et al., 2010), possibly due to the breakage and reformation of weak non-covalent bonds (Liu et al., 2005). Such energy dissipation through plastic deformation of the interfibrillar matrix would serve as a toughening mechanism for tendon and help prevent complete rupture due to localized tissue defects.
While fibrils may not rupture, it is possible that fibril yielding also contributes to the strain-softening behavior observed in the post-yield behavior of tendon fascicles. Fascicles subjected to sub-rupture tensile testing contain kinked fibrils, which may indicate some form of fibril yielding (Fung et al., 2009; Thorpe et al., 2014; Veres et al., 2013). However, despite numerous experimental studies of the tensile properties of individual fibrils, little data exists concerning fibril yielding and post-yield behavior (Hansen et al., 2009; Shen et al., 2010; Svensson et al., 2013; van der Rijt et al., 2006; Yang et al., 2012). Furthermore, molecular dynamics simulations predict fibril yielding due to molecular sliding within fibrils but only at large fibril strains (>25%) (Buehler, 2008, 2006). Therefore, we simulated the effects of fibril yielding by evaluating the model performance with a reduced (but still constant) fibril modulus. Although this does not simulate true fibril yielding, it does provide an upper bound estimate for the effects since the fibril modulus is reduced throughout testing rather than after reaching some particular yield strain.
We found that fibril yielding, while potentially explaining the macroscale strain-softening, does not improve the prediction of the fibril:tissue strain ratio for the continuous fibril model or the elastic shear lag model (Fig. 4C–D). It is possible that fibril yielding could bring the fibril:tissue strain ratio predicted by the plastic model closer to the experimental values at high tissue strains, but it is unclear if the fibrils would reach their yield point in this model. At a tissue strain of 8%, the maximum fibril strain averaged over the fibril length is only 2.31% in the plastic model, which demonstrates how interfibrillar sliding can protect fibrils from yielding and complete rupture. This agrees with X-ray diffraction studies of fascicles from 6–12 month-old rats (which were also used for the experimental data in Fig. 4 and 6 (Szczesny et al., 2014)) that found that sliding between fibrils preceded molecular slippage within fibrils, and likely, fibril yielding (Folkhard et al., 1987). Hence, plastic interfibrillar sliding is a more likely explanation of the multiscale data than fibril yielding.
The use of relatively simple shear lag models in this study provided a clear comparison of how the capabilities and limitations of each model were dictated by the choice of the constitutive behavior for the interfibrillar matrix. Other shear lag models have been developed that assume more complex properties or organization of specific tissue components (e.g. proteoglycans) to generate elastic, plastic, and viscous behaviors of the interfibrillar matrix (Ahmadzadeh et al., 2013; Ciarletta and Ben Amar, 2009; Fessel and Snedeker, 2011; Gao et al., 2008; Goh et al., 2007; Mijailovich et al., 1993; Zhang et al., 2010). These models offer interesting explanations for tissue behavior, although the experimental data necessary to qualify their underlying assumptions are limited (Fessel and Snedeker, 2011; Lujan et al., 2007; Rigozzi et al., 2013; Svensson et al., 2011). We attempted to avoid this issue and clarify interpretations of the models’ capabilities by using formulations based on fundamental principles common to nearly all shear lag models. For example, despite its simplicity, the elastic shear lag model presented in this study captures the basic features of other elastic models, including the constant values for Lc, the tissue modulus, and the fibril:tissue strain ratio (Ahmadzadeh et al., 2013; Bar-On and Wagner, 2013; Gao et al., 2003; Hull and Clyne, 1996; Jäger and Fratzl, 2000). The conclusions of this study can guide the future development and application of multiscale models that encapsulate multiple phenomena across the full tendon hierarchical structure, including nonlinear strain-stiffening fibril behavior as well as viscous and poroelastic effects (Gautieri et al., 2011; Reese, 2013; Shen et al., 2011; Yang et al., 2012; Yin and Elliott, 2004).
Since the main purpose of this study was to compare the general ability of various shear lag models to reproduce the multiscale mechanics of tendon fascicles, an optimization and sensitivity analysis of the model parameters were not performed. Still, it is worth considering the effects and physiological significance of the chosen values for the model parameters, especially the fibril length. A length of 10 mm was chosen in this study since it is the approximate midpoint between the lower bound of 1 mm, suggested by previous measurements of fibril lengths in fetal tendon (Birk et al., 1995), and the upper bound of 25 mm, based on the initial grip-to-grip distance used in the experimental testing (Szczesny et al., 2014). While fibril lengths may not be the same in different tendons or different animals, 10 mm is not an unreasonable assumption for the fibril length in rat tail tendon fascicles, which are over 100 mm long (Legerlotz et al., 2010). Furthermore, while different fibril lengths change the values of the interfibrillar shear properties (i.e., τp for the plastic model and G for the elastic model ), the qualitative behavior of the models themselves is unaltered (Szczesny and Elliott, 2014). Regarding the interfibrillar shear properties, there are limited data in the literature to compare with the model parameters. Nevertheless, macroscale testing of human ligament produced a shear modulus of less than 1 kPa (Bonifasi-Lista et al., 2005), which is comparable to the plastic interfibrillar shear stress (τp). Finally, while ~1 Pa is a relatively low modulus value, the large shear strains that occur in the interfibrillar matrix during fibril sliding produce high shear stresses, causing the interfibrillar matrix in the elastoplastic model to reach the plastic limit (εp,i) at approximately 1% tissue strain. Therefore, while these parameter values may vary across tendons, tissues, and species, the representative values used here are reasonable for rat tail tendon fascicles and for the study objective of comparing various model formulations against multiscale fascicle mechanics.
One limitation of this study is that only a single experimental dataset of rat tail tendon fascicles was used to evaluate the performance of the models. While rat tail tendon fascicles are a widely used tissue model for tendon (Folkhard et al., 1987; Hansen et al., 2009; Kastelic et al., 1978; Li et al., 2013; Reese, 2013; Screen et al., 2004; Svensson et al., 2013; Torp et al., 1975), fascicles from other tendons may behave differently. For example, the plateau in the macroscale stress observed in rat tail fascicles (Fig. 4A and (Szczesny and Elliott, 2014)) also occurs in the common digital extensor tendon (Screen et al., 2013) but not in the Achilles tendon or superficial digital flexor tendon, at least up to 10% strain (Kahn et al., 2010; Screen et al., 2013). Furthermore, multiscale tissue mechanics are known to vary with tissue type, age, and cross-linking (Folkhard et al., 1987; Han et al., 2013; Li et al., 2013; Puxkandl et al., 2002; Svensson et al., 2013; Thorpe et al., 2013b; Torp et al., 1975). Nevertheless, fibril:tissue strain ratios less than one have also been observed in several tendons and tissues (Han et al., 2013; Liao et al., 2005; Rigozzi et al., 2011; Thorpe et al., 2013b), which suggests that discontinuous fibrils are not unique to rat tail tendon. Future investigations can apply the modeling principles presented in this study to other collagenous tissues in order to compare the microscale deformation mechanisms and determine whether the interfibrillar matrix in these tissues also behaves plastically.
6. Conclusions
This study demonstrated that incorporating plasticity of the interfibrillar matrix in shear lag models is necessary to reproduce the multiscale tendon fascicle mechanics. While elasticity of the interfibrillar matrix may contribute to the initial tissue behavior, only plastic interfibrillar deformation could replicate the macroscale strain-softening as well as the increasing interfibrillar sliding and decreasing fibril:tissue strain ratio observed at microscopic length scales. This suggests that plastic deformation of the interfibrillar matrix is responsible for the post-yield behavior of tendon fascicles. Identifying the mechanisms that reduce the tissue’s ability to bear load is necessary to understand the initiation and progression of tendon pathology ultimately leading to complete rupture. This knowledge can then be used to restore proper tendon function by repairing the underlying structural defects through tissue regeneration. Finally, determining the fundamental structure-function relationships in tendon is essential for designing tissue engineered replacements that effectively reproduce native tissue behavior.
Table 1.
Nomenclature
| General Terms | |
| Ef | Fibril modulus |
| L | Fibril length |
| P | Fibril stress at fibril midpoint |
| r | Fibril radius |
| U | Total elongation of unit cell |
| ui | Displacement of i-th fibril |
| x | Position along unit cell |
| Γ | Gamma cumulative distribution function |
| γ | Gamma probability distribution function |
| εuc | Unit cell strain |
| εapp | Apparent fibril strain |
| ηapp | Apparent fibril:tissue strain ratio |
| λ | Tissue stretch |
| λc | Tissue stretch required to uncrimp unit cell |
| Mean uncrimping stretch | |
| Standard deviation of uncrimping stretches | |
| σi | Fibril stress of i-th fibril |
| σuc | Average stress in unit cell |
| σT | Macroscale tissue stress |
| τ | Interfibrillar shear stress |
| Fibril volume fraction | |
| Elastic Model | |
| Ee | Macroscale tissue modulus |
| G | Shear modulus of interfibrillar matrix |
| h | Surface-to-surface distance between fibrils |
| Lc | Characteristic load transfer length |
| ηe | Fibril:tissue strain ratio |
| Plastic Model | |
| Ep | Macroscale tissue modulus |
| Ls | Length over which interfibrillar sliding occurs |
| εp | Unit cell strain where interfibrillar sliding occurs over entire fibril length |
| ηp | Fibril:tissue strain ratio |
| τp | Interfibrillar shear stress due to interfibrillar sliding |
| Elastoplastic Model | |
| Lp | Length over which interfibrillar shear stress is plastic |
| εp,i | Unit cell strain at which interfibrillar shear first becomes plastic |
| εp,f | Unit cell strain where interfibrillar shear is plastic over entire fibril length |
| τp | Plastic limit for interfibrillar shear stress |
Various models were applied to tendon fascicle multiscale mechanics.
Fibril yielding could not explain microscale post-yield behavior.
Only shear lag models assuming plasticity of interfibrillar matrix were successful.
Suggests fascicle yielding is due to plastic deformation of interfibrillar matrix.
Acknowledgments
This research was supported by an NIH COBRE grant (NIH/NCRR P20 RR016458).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Spencer E. Szczesny, Email: esy@seas.upenn.edu.
Dawn M. Elliott, Email: delliott@udel.edu.
References
- Ahmadzadeh H, Connizzo BK, Freedman BR, Soslowsky LJ, Shenoy VB. Determining the contribution of glycosaminoglycans to tendon mechanical properties with a modified shear-lag model. J Biomech. 2013;46:2497–2503. doi: 10.1016/j.jbiomech.2013.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahmadzadeh H, Smith DH, Shenoy VB. Viscoelasticity of Tau Proteins Leads to Strain Rate-Dependent Breaking of Microtubules during Axonal Stretch Injury: Predictions from a Mathematical Model. Biophys J. 2014;106:1123–1133. doi: 10.1016/j.bpj.2014.01.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey AJ, Paul RG, Knott L. Mechanisms of maturation and ageing of collagen. Mech Ageing Dev. 1998;106:1–56. doi: 10.1016/s0047-6374(98)00119-5. [DOI] [PubMed] [Google Scholar]
- Bar-On B, Wagner HD. Structural motifs and elastic properties of hierarchical biological tissues – A review. J Struct Biol. 2013;183:149–164. doi: 10.1016/j.jsb.2013.05.012. [DOI] [PubMed] [Google Scholar]
- Birk DE, Nurminskaya MV, Zycband EI. Collagen fibrillogenesis in situ: fibril segments undergo post-depositional modifications resulting in linear and lateral growth during matrix development. Dev Dyn. 1995;202:229–243. doi: 10.1002/aja.1002020303. [DOI] [PubMed] [Google Scholar]
- Bonifasi-Lista C, Lake SP, Small MS, Weiss JA. Viscoelastic properties of the human medial collateral ligament under longitudinal, transverse and shear loading. J Orthop Res. 2005;23:67–76. doi: 10.1016/j.orthres.2004.06.002. [DOI] [PubMed] [Google Scholar]
- Bruehlmann SB, Matyas JR, Duncan NA. ISSLS prize winner: Collagen fibril sliding governs cell mechanics in the anulus fibrosus: an in situ confocal microscopy study of bovine discs. Spine. 2004;29:2612–2620. doi: 10.1097/01.brs.0000146465.05972.56. [DOI] [PubMed] [Google Scholar]
- Buehler MJ. Nature designs tough collagen: explaining the nanostructure of collagen fibrils. Proc Natl Acad Sci U S A. 2006;103:12285–12290. doi: 10.1073/pnas.0603216103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buehler MJ. Nanomechanics of collagen fibrils under varying cross-link densities: atomistic and continuum studies. J Mech Behav Biomed Mater. 2008;1:59–67. doi: 10.1016/j.jmbbm.2007.04.001. [DOI] [PubMed] [Google Scholar]
- Ciarletta P, Ben Amar M. A finite dissipative theory of temporary interfibrillar bridges in the extracellular matrix of ligaments and tendons. J R Soc Interface. 2009;6:909–924. doi: 10.1098/rsif.2008.0487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diamant J, Keller A, Baer E, Litt M, Arridge RG. Collagen; ultrastructure and its relation to mechanical properties as a function of ageing. Proc R Soc B. 1972;180:293–315. doi: 10.1098/rspb.1972.0019. [DOI] [PubMed] [Google Scholar]
- Fessel G, Snedeker JG. Equivalent stiffness after glycosaminoglycan depletion in tendon--an ultra-structural finite element model and corresponding experiments. J Theor Biol. 2011;268:77–83. doi: 10.1016/j.jtbi.2010.10.007. [DOI] [PubMed] [Google Scholar]
- Folkhard W, Mosler E, Geercken W, Knörzer E, Nemetschek-Gansler H, Nemetschek T, Koch MHJ. Quantitative analysis of the molecular sliding mechanisms in native tendon collagen — time-resolved dynamic studies using synchrotron radiation. Int J Biol Macromol. 1987;9:169–175. doi: 10.1016/0141-8130(87)90047-X. [DOI] [Google Scholar]
- Fung DT, Wang VM, Laudier DM, Shine JH, Basta-Pljakic J, Jepsen KJ, Schaffler MB, Flatow EL. Subrupture tendon fatigue damage. J Orthop Res. 2009;27:264–273. doi: 10.1002/jor.20722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao H, Ji B, Jäger IL, Arzt E, Fratzl P. Materials become insensitive to flaws at nanoscale: Lessons from nature. Proc Natl Acad Sci USA. 2003;100:5597–5600. doi: 10.1073/pnas.0631609100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao Y, Wineman AS, Waas AM. Mechanics of muscle injury induced by lengthening contraction. Ann Biomed Eng. 2008;36:1615–1623. doi: 10.1007/s10439-008-9547-3. [DOI] [PubMed] [Google Scholar]
- Gautieri A, Vesentini S, Redaelli A, Buehler MJ. Hierarchical structure and nanomechanics of collagen microfibrils from the atomistic scale up. Nano Lett. 2011;11:757–766. doi: 10.1021/nl103943u. [DOI] [PubMed] [Google Scholar]
- Goh KL, Meakin JR, Aspden RM, Hukins DWL. Stress transfer in collagen fibrils reinforcing connective tissues: effects of collagen fibril slenderness and relative stiffness. J Theor Biol. 2007;245:305–311. doi: 10.1016/j.jtbi.2006.10.008. [DOI] [PubMed] [Google Scholar]
- Gupta HS, Fratzl P, Kerschnitzki M, Benecke G, Wagermaier W, Kirchner HOK. Evidence for an elementary process in bone plasticity with an activation enthalpy of 1 eV. J R Soc Interface. 2007;4:277–282. doi: 10.1098/rsif.2006.0172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta HS, Seto J, Krauss S, Boesecke P, Screen HRC. In situ multi-level analysis of viscoelastic deformation mechanisms in tendon collagen. J Struct Biol. 2010;169:183–191. doi: 10.1016/j.jsb.2009.10.002. [DOI] [PubMed] [Google Scholar]
- Gupta HS, Wagermaier W, Zickler GA, Raz-Ben Aroush D, Funari SS, Roschger P, Wagner HD, Fratzl P. Nanoscale deformation mechanisms in bone. Nano Lett. 2005;5:2108–2111. doi: 10.1021/nl051584b. [DOI] [PubMed] [Google Scholar]
- Gutsmann T, Hassenkam T, Cutroni JA, Hansma PK. Sacrificial bonds in polymer brushes from rat tail tendon functioning as nanoscale velcro. Biophys J. 2005;89:536–542. doi: 10.1529/biophysj.104.056747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han WM, Heo SJ, Driscoll TP, Smith LJ, Mauck RL, Elliott DM. Macro- to microscale strain transfer in fibrous tissues is heterogeneous and tissue-specific. Biophys J. 2013;105:807–817. doi: 10.1016/j.bpj.2013.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen P, Hassenkam T, Svensson RB, Aagaard P, Trappe T, Haraldsson BT, Kjaer M, Magnusson P. Glutaraldehyde cross-linking of tendon--mechanical effects at the level of the tendon fascicle and fibril. Connect Tissue Res. 2009;50:211–222. doi: 10.1080/03008200802610040. [DOI] [PubMed] [Google Scholar]
- Hull D, Clyne TW. An introduction to composite materials. Cambridge University Press; Cambridge; New York: 1996. [Google Scholar]
- Hulmes DJ, Wess TJ, Prockop DJ, Fratzl P. Radial packing, order, and disorder in collagen fibrils. Biophys J. 1995;68:1661–1670. doi: 10.1016/S0006-3495(95)80391-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jäger I, Fratzl P. Mineralized collagen fibrils: a mechanical model with a staggered arrangement of mineral particles. Biophys J. 2000;79:1737–1746. doi: 10.1016/S0006-3495(00)76426-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadler KE, Holmes DF, Graham H, Starborg T. Tip-mediated fusion involving unipolar collagen fibrils accounts for rapid fibril elongation, the occurrence of fibrillar branched networks in skin and the paucity of collagen fibril ends in vertebrates. Matrix Biol. 2000;19:359–365. doi: 10.1016/s0945-053x(00)00082-2. [DOI] [PubMed] [Google Scholar]
- Kahn CJF, Wang X, Rahouadj R. Nonlinear Model for Viscoelastic Behavior of Achilles Tendon. J Biomech Eng. 2010;132:111002. doi: 10.1115/1.4002552. [DOI] [PubMed] [Google Scholar]
- Kastelic J, Galeski A, Baer E. The multicomposite structure of tendon. Connect Tissue Res. 1978;6:11–23. doi: 10.3109/03008207809152283. [DOI] [PubMed] [Google Scholar]
- Ker RF. Mechanics of tendon, from an engineering perspective. Int J Fatigue. 2007;29:1001–1009. doi: 10.1016/j.ijfatigue.2006.09.020. [DOI] [Google Scholar]
- Legerlotz K, Riley GP, Screen HRC. Specimen dimensions influence the measurement of material properties in tendon fascicles. J Biomech. 2010;43:2274–2280. doi: 10.1016/j.jbiomech.2010.04.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Fessel G, Georgiadis M, Snedeker JG. Advanced glycation end-products diminish tendon collagen fiber sliding. Matrix Biol. 2013;32:169–177. doi: 10.1016/j.matbio.2013.01.003. [DOI] [PubMed] [Google Scholar]
- Liao J, Yang L, Grashow J, Sacks MS. Molecular orientation of collagen in intact planar connective tissues under biaxial stretch. Acta Biomater. 2005;1:45–54. doi: 10.1016/j.actbio.2004.09.007. [DOI] [PubMed] [Google Scholar]
- Liu X, Yeh ML, Lewis JL, Luo ZP. Direct measurement of the rupture force of single pair of decorin interactions. Biochem Biophys Res Commun. 2005;338:1342–1345. doi: 10.1016/j.bbrc.2005.10.096. [DOI] [PubMed] [Google Scholar]
- Lujan TJ, Underwood CJ, Henninger HB, Thompson BM, Weiss JA. Effect of dermatan sulfate glycosaminoglycans on the quasi-static material properties of the human medial collateral ligament. J Orthop Res. 2007;25:894–903. doi: 10.1002/jor.20351. [DOI] [PubMed] [Google Scholar]
- Mijailovich SM, Stamenović D, Fredberg JJ. Toward a kinetic theory of connective tissue micromechanics. J Appl Physiol. 1993;74:665–681. doi: 10.1152/jappl.1993.74.2.665. [DOI] [PubMed] [Google Scholar]
- Orgel JPRO, Irving TC, Miller A, Wess TJ. Microfibrillar structure of type I collagen in situ. Proc Natl Acad Sci U S A. 2006;103:9001–9005. doi: 10.1073/pnas.0502718103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parry DA, Craig AS. Growth and development of collagen fibrils in connective tissue. In: Ruggeri A, Motta PM, editors. Ultrastructure of the Connective Tissue Matrix. Martinus Nijhoff; Boston: 1984. pp. 34–64. [Google Scholar]
- Provenzano PP, Vanderby R., Jr Collagen fibril morphology and organization: implications for force transmission in ligament and tendon. Matrix Biol. 2006;25:71–84. doi: 10.1016/j.matbio.2005.09.005. [DOI] [PubMed] [Google Scholar]
- Puxkandl R, Zizak I, Paris O, Keckes J, Tesch W, Bernstorff S, Purslow P, Fratzl P. Viscoelastic properties of collagen: synchrotron radiation investigations and structural model. Proc R Soc B. 2002;357:191–197. doi: 10.1098/rstb.2001.1033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reese SP. Tendon Fascicles Exhibit a Linear Correlation Between Poisson’s Ratio and Force During Uniaxial Stress Relaxation. J Biomech Eng. 2013;135:034501. doi: 10.1115/1.4023134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rigozzi S, Müller R, Stemmer A, Snedeker JG. Tendon glycosaminoglycan proteoglycan sidechains promote collagen fibril sliding-AFM observations at the nanoscale. J Biomech. 2013;46:813–818. doi: 10.1016/j.jbiomech.2012.11.017. [DOI] [PubMed] [Google Scholar]
- Rigozzi S, Stemmer A, Müller R, Snedeker JG. Mechanical response of individual collagen fibrils in loaded tendon as measured by atomic force microscopy. J Struct Biol. 2011;176:9–15. doi: 10.1016/j.jsb.2011.07.002. [DOI] [PubMed] [Google Scholar]
- Rowe RW. The structure of rat tail tendon. Connect Tissue Res. 1985;14:9–20. doi: 10.3109/03008208509089839. [DOI] [PubMed] [Google Scholar]
- Sacks MS. Incorporation of experimentally-derived fiber orientation into a structural constitutive model for planar collagenous tissues. J Biomech Eng. 2003;125:280–287. doi: 10.1115/1.1544508. [DOI] [PubMed] [Google Scholar]
- Screen HRC, Lee DA, Bader DL, Shelton JC. An investigation into the effects of the hierarchical structure of tendon fascicles on micromechanical properties. Proc Inst Mech Eng [H] 2004;218:109–119. doi: 10.1243/095441104322984004. [DOI] [PubMed] [Google Scholar]
- Screen HRC, Shelton JC, Chhaya VH, Kayser MV, Bader DL, Lee DA. The influence of noncollagenous matrix components on the micromechanical environment of tendon fascicles. Ann Biomed Eng. 2005;33:1090–1099. doi: 10.1007/s10439-005-5777-9. [DOI] [PubMed] [Google Scholar]
- Screen HRC, Toorani S, Shelton JC. Microstructural stress relaxation mechanics in functionally different tendons. Med Eng Phys. 2013;35:96–102. doi: 10.1016/j.medengphy.2012.04.004. [DOI] [PubMed] [Google Scholar]
- Shen ZL, Dodge MR, Kahn H, Ballarini R, Eppell SJ. In vitro fracture testing of submicron diameter collagen fibril specimens. Biophys J. 2010;99:1986–1995. doi: 10.1016/j.bpj.2010.07.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen ZL, Kahn H, Ballarini R, Eppell SJ. Viscoelastic properties of isolated collagen fibrils. Biophys J. 2011;100:3008–3015. doi: 10.1016/j.bpj.2011.04.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svensson RB, Hassenkam T, Grant CA, Magnusson SP. Tensile properties of human collagen fibrils and fascicles are insensitive to environmental salts. Biophys J. 2010;99:4020–4027. doi: 10.1016/j.bpj.2010.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svensson RB, Hassenkam T, Hansen P, Kjaer M, Magnusson SP. Tensile force transmission in human patellar tendon fascicles is not mediated by glycosaminoglycans. Connect Tissue Res. 2011;52:415–421. doi: 10.3109/03008207.2010.551569. [DOI] [PubMed] [Google Scholar]
- Svensson RB, Mulder H, Kovanen V, Magnusson SP. Fracture mechanics of collagen fibrils: influence of natural cross-links. Biophys J. 2013;104:2476–2484. doi: 10.1016/j.bpj.2013.04.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczesny SE, Edelstein RS, Elliott DM. DTAF dye concentrations commonly used to measure microscale deformations in biological tissues alter tissue mechanics. PloS One. 2014;9:e99588. doi: 10.1371/journal.pone.0099588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczesny SE, Elliott DM. Interfibrillar shear stress is the loading mechanism of collagen fibrils in tendon. Acta Biomater. 2014;10:2582–2590. doi: 10.1016/j.actbio.2014.01.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczesny SE, Peloquin JM, Cortes DH, Kadlowec JA, Soslowsky LJ, Elliott DM. Biaxial tensile testing and constitutive modeling of human supraspinatus tendon. J Biomech Eng. 2012;134:021004. doi: 10.1115/1.4005852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorpe CT, Birch HL, Clegg PD, Screen HRC. The role of the non-collagenous matrix in tendon function. Int J Exp Pathol. 2013a;94:248–259. doi: 10.1111/iep.12027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorpe CT, Klemt C, Riley GP, Birch HL, Clegg PD, Screen HRC. Helical sub-structures in energy-storing tendons provide a possible mechanism for efficient energy storage and return. Acta Biomater. 2013b;9:7948–7956. doi: 10.1016/j.actbio.2013.05.004. [DOI] [PubMed] [Google Scholar]
- Thorpe CT, Riley GP, Birch HL, Clegg PD, Screen HRC. Fascicles from energy-storing tendons show an age-specific response to cyclic fatigue loading. J R Soc Interface. 2014;11:20131058. doi: 10.1098/rsif.2013.1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torp S, Arridge RG, Armeniades CD, Baer E. Structure-property relationships in tendon as a function of age. In: Atkins ED, Keller A, editors. Structure of Fibrous Biopolymers; Proceedings of the 26th Symposium of the Colston Research Society. Colston Research Society; London. 1975. pp. 197–221. [Google Scholar]
- Van der Rijt JAJ, van der Werf KO, Bennink ML, Dijkstra PJ, Feijen J. Micromechanical testing of individual collagen fibrils. Macromol Biosci. 2006;6:697–702. doi: 10.1002/mabi.200600063. [DOI] [PubMed] [Google Scholar]
- Veres SP, Harrison JM, Lee JM. Repeated subrupture overload causes progression of nanoscaled discrete plasticity damage in tendon collagen fibrils. J Orthop Res. 2013;31:731–737. doi: 10.1002/jor.22292. [DOI] [PubMed] [Google Scholar]
- Wang XT, Ker RF. Creep rupture of wallaby tail tendons. J Exp Biol. 1995;198:831–845. doi: 10.1242/jeb.198.3.831. [DOI] [PubMed] [Google Scholar]
- Yang L, van der Werf KO, Dijkstra PJ, Feijen J, Bennink ML. Micromechanical analysis of native and cross-linked collagen type I fibrils supports the existence of microfibrils. J Mech Behav Biomed Mater. 2012;6:148–158. doi: 10.1016/j.jmbbm.2011.11.008. [DOI] [PubMed] [Google Scholar]
- Yin L, Elliott DM. A biphasic and transversely isotropic mechanical model for tendon: application to mouse tail fascicles in uniaxial tension. J Biomech. 2004;37:907–916. doi: 10.1016/j.jbiomech.2003.10.007. [DOI] [PubMed] [Google Scholar]
- Zhang ZQ, Liu B, Huang Y, Hwang KC, Gao H. Mechanical properties of unidirectional nanocomposites with non-uniformly or randomly staggered platelet distribution. J Mech Phys Solids. 2010;58:1646–1660. doi: 10.1016/j.jmps.2010.07.004. [DOI] [Google Scholar]