A model-informed rank test for right-censored data with intermediate states

Abstract

The generalized Wilcoxon and log-rank tests are commonly used for testing differences between two survival distributions. We modify the Wilcoxon test to account for auxiliary information on intermediate disease states that subjects may pass through before failure. For a disease with multiple states where patients are monitored periodically but exact transition times are unknown (e.g. staging in cancer), we first fit a multi-state Markov model to the full data set; when censoring precludes the comparison of survival times between two subjects, we use the model to estimate the probability that one subject will have survived longer than the other given their censoring times and last observed status, and use these probabilities to compute an expected rank for each subject. These expected ranks form the basis of our test statistic. Simulations demonstrate that the proposed test can improve power over the log-rank and generalized Wilcoxon tests in some settings, while maintaining the nominal type 1 error rate. The method is illustrated on an ALS data set.

1. Introduction

In clinical trials that compare treatments on overall survival, some patients are censored due to drop-out or the administrative completion of the study. In analyses of survival of patients, under the usual independent censoring assumption, patients who are censored at a specific time are treated as having the same prognosis as those who are alive and continue in follow-up. However, there is often information on each patient’s clinical status at the time they are censored that could be used to refine these analyses. Many chronic diseases involve a complex process by which individuals move through different disease states (progress), and by including this “auxiliary” information on censored patients in the analysis of survival, we can hope to obtain a more precise treatment comparison. For example, in clinical trials of Amyotrophic Lateral Sclerosis (ALS), we obtain intermediate information on neurological function via ALSFRS-R scores, which may be predictive of survival. The goal of this paper is to develop a new test to improve power and accuracy in treatment comparisons based on a survival endpoint.

There have been several methods developed that utilize auxiliary information in survival analysis. In many of these papers, the authors reconstruct overall survival estimates with the additional information, and compute test statistics that are based on the new survival estimates. Finkelstein and Schoenfeld [1], and Gray [2] propose methods based on a 3-stage model with progression as an intermediate stage. Malani [3] incorporates biomarkers into the survival estimate by redistributing the weight of censored observations to individuals with similar biomarker values at the time of censoring. Murray and Tsiatis [4, 5 ] propose weighted Kaplan-Meier estimators to account for fixed or time-dependent covariates and propose a test statistic based on that of Pepe and Fleming [6, 7] for comparing the two samples. They indicated that their estimate was equivalent to Malani’s for categorical markers and that it is also related to the inverse probability of censoring weighted (IPCW) survival curve estimate of Robins and Rotnitzky [8]. Mackenzie and Abrahamowicz [9] proposed tests based on functionals of any type of Kaplan-Meier estimators, including ones that account for longitudinal markers such as the Murray-Tsiatis estimator. Under certain conditions their adjusted hazard ratio and log-rank test are equivalent to the IPCW versions proposed by Robins and Finkelstein [10]. Hsu et al. [11, 12 , 13 ] use auxiliary variables and a multiple imputation approach to estimate the marginal survival function and adjust for dependent censoring, and apply the conventional nonparametric two-sample tests to the augmented data sets. This method involves reducing the auxiliary variables into two sets of risk scores via proportional hazards models, one for event times and one for censored times, and utilizing these scores in the imputation scheme. Conlon et al. [14] use time to recurrence as an auxiliary variable for survival, and impute missing values due to censoring. Song [15] developed a covariate adjusted log-rank test in the recurrent events setting.

While each of these approaches rely on tests constructed from auxiliary variable refined estimates of the survival curve, the approach we propose is to develop an extension of Efron’s modification for the Gehan-Wilcoxon test [16]. Our test is based on scores for each patient, derived from the probabilities that they survived longer than other subjects in the study. We use these probabilities to construct what are essentially expected ranks for each subject given their observed states and censoring times, and then make inference on the ranks. To estimate the probabilities, we propose using a multi-state Markov model. The Markov model is chosen for its simplicity and flexibility in modeling different disease processes. With it, we can accommodate forward and backward transitions between states and estimate transition probabilities even when the exact transition times in to and out of each state are unknown (resulting in interval censored data), which is often the case in clinical studies as patients are monitored over periodic visits.

We first present our modification of the Gehan-Wilcoxon test, some basic notation, and concepts for multi-state models, including how to estimate the probabilities that we need. Next, simulation results are presented, illustrating in which settings the method is valid and works best. Then we demonstrate the method on an ALS (Lou Gehrig’s disease) data set. Finally, in the discussion we consider the merits and drawbacks of our method, possible variations and extensions on the model, and other considerations to be taken when implementing it.

2. Methods

2.1. Test Statistic

We are interested in using auxiliary information, the disease state at the censoring time for each subject, to improve the efficiency of the Gehan rank statistic used to test for equality of two survival distributions [17]. For the Gehan test, if we have two groups of subjects, then for every pair of individuals i and j, the test assigns a score u_ij, where u_ij = 1 if i clearly survived longer than j, u_ij = 0 if it is unclear who survived longer, and u_ij = −1 if j outlived i. Let Z_i be the indicator that subject i is in group 1. The “rank” for individual i is given by U_i = Σ_j u_ij, and the numerator of this test statistic is Σ_i Z_iU_i.

Efron proposed a modification of the Gehan-Wilcoxon test, assigning to pairs of subjects a value equal to the probabaility that i outlives j given the follow-up times and censoring indicators for both [16]. We note that this modification assigns the same score of +1 or −1 when survival times can be compared, but for subjects for whom u_ij = 0 in Gehan’s test, Efron’s test could give a non-zero value to the comparison. Efron suggested using Kaplan-Meier type estimates for the probabilities above, conditional on the censoring times but not disease states [16].

We now suggest a further modification of Efron’s test by including auxiliary information available at the censoring times. Let T_i and C_i be the survival and censoring times for individual i, respectively, let δ_i = I(T_i < C_i), and Z_i the indicator that subject i is in group 1. Suppose individuals independently move move among d possible states 1,…,d, where d is an absorbing state (e.g. death). Let S_i(t) denote the state occupied at time t for subject i. Further, suppose we observe the state of individual i at m_i times {t_i1,…,t_imi}. For the pair of subjects i and j, the statistic we propose assigns the score:

$$u_{ij}^p=P(T_i>T_j\mid S_i(t_{{im}_i}),S_j(t_{{jm}_j}),C_i,C_j)-P(T_i<T_j\mid S_i(t_{{im}_i}),S_j(t_{{jm}_j}),C_i,C_j),$$ (1)

where P(T_i > T_j|S_i(t_imi), S_j(t_jmj),C_i,C_j) denotes the probability of subject i surviving beyond subject j conditional on each of their last observed disease states and censoring times. If it is known that j fails before i, or i before j, the score u_ij would be 1 or −1 respectively, as in the Gehan test. If it is not known who of i or j lived longer, we must calculate the probability given in (1). This is described in the next section. The basis for using probabilities is that they give us the expected Wilcoxon scores when we do not have full data (i.e. when there is censoring). The expected rank score for individual i is given by $U_i={\sum }_j{u}_{ij}^p$, and as in the Gehan test the numerator of the statistic is W = Σ_i Z_iU_i.

Under the null hypothesis that the treatment has no effect on the transitions between states, and the censoring distributions in both groups are equal, the permutation distribution of W has mean 0 and variance [18]:

$$\mathit{var}(W)=\frac{n_1{n}_2{\sum }_{i=1}^{n_1+n_2}{U}_i^2}{(n_1+n_2)(n_1+n_2-1)}$$ (2)

2.2. Multi-State Models

Multi-state Markov models give us a simple and flexible way to model the disease state process, and estimate the probabilities we need to compute our test statistic. These models are well-established and have been used in a variety of medical and epidemiological applications, including modeling hospital length of stay [19, 20 ], competing risks of bone marrow transplantation [21], estimating risk of death after an intermediate event [22] and modeling an epidemic in populations susceptible to an infectious disease [23, 24 , 25 ]. Our use of the multi-state Markov model differs from other work in that it is auxiliary; we are simply using the model as a flexible tool to unify the measurement of patient disease states and mortality in order to estimate the desired probabilities described in the previous section. With continuing research on multi-state models in general, the models used for this method may become more and more sophisticated, as long as the probabilities can still be estimated. For example, Naranjo et al. recently developed a method that allows multi-state models to accommodate missing response and covariate data [26].

A formulation of these models can also take into account the interval-censored nature of data on time to intermediate states (and if necessary, the absorbing state), as those times typically will not be oberved exactly. For a thorough treatment of estimation for multi-state Markov models with panel or interval-censored data, see Kalbfleisch and Lawless [27], Gentleman et al. [28], and Commenges [29]. We will briefly cover the notation and concepts here. The notation will follow that of Kalbfleisch and Lawless [27], and Jackson [30]. An important issue is that the model should be fit under the null hypothesis, that is, it is fit on the pooled data set. This way when two subjects are censored at the same time and in the same state, there will be no difference in their expected rank. In this paper, we will use the time-homogeneous Markov model to illustrate the method, though some extensions on the model are possible and will be discussed later.

Suppose we have d states, 1,…,d, where d represents the absorbing state, and S(t) is the state occupied by a randomly chosen individual at time t. The continuous-time Markov process can be specified in terms of transition intensities,

$$q_{rs}(t)=\underset{\delta t\to 0}{lim}\frac{Pr(S(t+\delta t)=s\mid S(t)=r)}{\delta t}$$

This is the rs^th entry of the d x d transition intensity matrix Q, and represents the instantaneous risk of moving from state r to state s at time t. The rows of Q sum to zero, with the diagonal entries defined to be q_rr(t) = −Σ_{s≠ r} q_rs(t). For time-homogeneous models, where the intensities are independent of t, this is related to the sojourn time spent in state r, which has an exponential distribution with mean $-q_{rr}^{-1}$. The pattern of zeros in the intensity matrix determines which states individuals can move to and from, and this is be specified by the investigator. For example, if the last state is absorbing, the bottom row of the matrix will be 0 because subjects cannot move out of the absorbing state.

Now define:

$$p_{rs}(u,t+u)=Pr(S(t+u)=s\mid S(u)=r).$$

This is the rs^th entry of the d x d transition probability matrix P(u,t + u), and represents the probability of moving from state r to state s in the interval (u,t + u). If we have a time-homogeneous model, then the transition intensities are constant over the interval (u,t +u), and P(u,t +u) reduces to P(t). The models can be fit and transition probabilities can be calculated with the msm package for R. [30, 31]; other packages for this exist as well. For details on the likelihood and computation of transition probabilities, see Appendix.

2.3. Estimating the Probabilities

After we fit the model, we can estimate the transition probabilities needed to compute our test statistic. There are three scenarios under which we need to calculate an estimate for the probability of subject i surviving beyond j: 1) when j fails after i is censored; 2) i fails after j is censored; 3) or when both subjects are censored.

1. Suppose i is observed to be in state k at t_imi, i.e. S_i(t_imi) = r, is censored at c_i ≥ t_imi, and j fails at t_j > c_i. Then the probability that subject i survives longer than subject j is given by:

   $$Pr(T_i>t_j\mid S_i(t_{{im}_i})=r,T_i>c_i)=\frac{1-p_{r,d}(t_{{im}_i},t_j)}{1-p_{r,d}(t_{{im}_i},c_i)}$$

2. This is the same as the case above, with i and j switched. The probability that i would have survived longer than j is 1 − Pr(T_j > t_i|S_j(t_jmj) = r, T_j > c_j)

3. Without loss of generality, suppose subject i is observed in state r_i at t_imi, censored at c_i, and subject j is observed in state r_j at t_jmj, and censored at c_j > c_i. Then the probability of i surviving longer than j is estimated by:

   $$\begin{array}{l}Pr(T_i>T_j\mid S_i(t_{{im}_i})=r_i,S_j(t_{{jm}_i})=r_j,T_i>c_i,T_j>c_j)=\\ \sum _{k=1}^{d-1}\sum _{l=1}^{d-1}\frac{p_{r_{i}k}(t_{{im}_i},c_j)}{1-p_{r_{i}d}(t_{{im}_i},c_i)}\frac{p_{r_{j}l}(t_{{jm}_j},c_j)}{1-p_{r_{j}d}(t_{{jm}_j},c_j)}{\int }_0^{\infty }[1-p_{k,d}(c_j,c_j+t)]p_{l,d}^{\prime }(c_j,c_j+t)dt\end{array}$$ (3)

   where $p_{l,d}^{\prime }(t)$ represents the l,d^th entry of $\frac{dP(t)}{dt}=Q\text{Exp}(\text{Qt})$. We can see how to arrive at 3 by first assuming that both subjects are censored at the same time c_j. Then we get the integral above by the law of total probability, integrating the survival function for subject i weighted by the density function for the event time for subject j conditional on each of their disease states. However, we have to weight the integral by the probability that subject i is in state k and subject j is in state l at time c_j, where k and l are any of the non-absorbing disease states.

For some models, analytic forms for the function p_rs(t) are complicated functions of the intensities, so in general we will estimate this function locally for each t over a fine grid of values, and use numerical integration to compute the integral above. However, for simpler models, analytic expressions for the functions are tractable (though the integral above may still need to be computed numerically). For example, for a three-state unidirectional model with transition intensity matrix:

$$Q=\left(\begin{array}{ccc}-q_{12}& q_{12}& 0\\ 0& -q_{23}& q_{23}\\ 0& 0& 0\end{array}\right)$$

the transition probability functions to state 3 (death) would be:

$$\begin{array}{l}{p}_{13}(t)=\frac{q_{23}{e}^{-q_{12}t}-q_{12}{e}^{-q_{23}t}+q_{12}-q_{23}}{q_{12}-q_{23}},q_{12}\ne q_{13}\\ p_{13}(t)=e^{-qt}(e^{qt}-qt-1),q_{12}=q_{23}\\ p_{23}(t)=1-e^{-q_{23}t}\\ p_{33}(t)=1\end{array}$$

Symbolic algebra software such as Mathematica [32] can be used to obtain these expressions. Note that the multi-state Markov model is just one possible choice of probability model. A different class of models, including semi-Markov, could be used provided that we can estimate the necessary probabilities.

A quantity that may also be of interest to investigators is the hazard of transitioning to the absorbing state over time. While the hazard and the limiting hazard rates of absorption can be derived for the multi-state process, this paper focuses on using the state information and transition probabilities to augment a nonparametric comparison of survival. Please see Aalen et al. for details on obtaining the hazard functions [33].

2.4. Remark on Permissible Transitions

The advantage of using a continuous-time Markov model is that it can accommodate transitions between any stages, but the fit will be more complex and convergence of parameters is not guaranteed, particularly if the sample size is insufficient for the number of transition parameters that need to be estimated. The allowed transitions in the model should make sense from a clinical standpoint. For example, Satten and Longini used multi-state models to examine the progression of CD4 cell counts before the onset of AIDS [34]. They discretized CD4 counts into 6 stages, allowing transitions only between adjacent stages. This makes sense clinically, because someone cannot go from stage 2 (700–900 CD4 count) to stage 4 (350–500), without passing through stage 3 (500–700). If CD4 counts are measured at visits that are far apart, then we might observe someone transition from stage 2 to stage 4 between visits. However, even if we never observed them in stage 3, we know that they had to pass through stage 3 on the way to stage 4. That is, they cannot instantaneously transition from stage 2 to stage 4. When using a continuous-time model for a continuously changing outcome, we only need to allow transitions between adjacent stages to specify the model. In some cases, the disease process will allow jumps. In the same example, the authors allow transition to the absorbing stage 7 (AIDS or death) from any of stages 3–6.

The zeroes in the Q matrix are determined by where we do not allow transitions to occur. For example, if we disallow an instantaneous transition from state 2 to state 4, the entry Q_2,4 will be 0. Zeroes will populate much of the Q matrix in many chronic disease settings, and this is ideal for model parsimony and convergence of parameters. If the model is excessively intricate for the number of transitions that we observe in the data, then maximum likelihood estimation may yield non-identifiable parameters. This can be an issue in the common setting of interval-censored transitions, where we only observe patients intermittently and do not know the exact transition time between two states. While we cannot specify an absolute minimum number of transitions that should be observed to ensure stable parameters (of course, at a bare minimum we need to observe at least 1 of each allowed transition), there are prescriptions to check and remedy the problem of non-identifiability. Initial values for Q need to be set before maximum likelihood estimation, so we should check that the parameters converge to the same solution using a variety of different initial values. If we end up with multiple unique solutions, we may need to simplify the model to allow fewer transitions or states. In general, it is good practice to use the simplest model that is consistent with the science of a disease process. Jackson also discusses options pertaining to the maximization algorithm that may help with convergence, including adjusting the tolerance level and rescaling the log-likelihood [30]. As far as the precision of model estimates, that is not a major issue with our method as long as they are identifiable, because we conservatively fit the model under the null hypothesis, on the pooled data.

2.5. Covariates and Piecewise-Constant Transition Intensities

Thus far we have only considered time-homogeneous Markov models. Covariates can be included with a type of proportional hazards model, described by Kalbfleisch and Lawless [27] and Marshall and Jones [35], where $q_{rs}(z(t))=q_{rs}^{(0)}\mathit{exp}({\beta }_{rs}^{T}z(t))$, where $q_{rs}^{(0)}$ is the baseline transition intensity from state r to state s, ${\beta }_{rs}^T$ is a vector of parameters, and z(t) a vector of possibly time-dependent covariates. The parameters are interpreted just as a Cox model for a particular transition intensity. For example, if we had a single covariate z that took values 0 or 1, then β_rs represents the log-hazard ratio of transitioning from state r to state s for a subject with z = 1 vs z = 0. Confidence intervals for β_rs are also available in the msm package in R. For each observation the likelihood contribution p_rs(t_k,t_k+1) is replaced with the conditional probability given the time-dependent covariates at time k, i.e. p_rs(t_k,t_k+1; z(t_k)). Multi-state models can accommodate fixed covariates in this way, and use time-dependent covariates to relax time-homogeneity.

Relaxing the time-homogeneous assumption is straightforward with interval censored transitions through the use of piecewise-constant transition intensities. This can be done by modelling a time-dependent covariate that changes value at each cut point where we want the intensities to change. For example, if we want the q_rs transition to change at time t_c, we could specify z(t) = 0 for t < t_c, and z(t) = 1 for t ≥ t_c in the model above. In general, suppose we allow the transition intensity matrix Q(t) to change at time points t_c1 ,…, t_cm, so that Q(t) = Q₀ over [0,t_c1), and Q(t) = Q_j over [t_cj, t_cj+1), and Q(t) = Q_m over [t_cm, ∞). Now suppose we want to calculate P(t₁,t₂) where t_cj−1 < t₁ < t_cj, and t_ck < t₂ < t_ck+1. Then

$$P(t_1,t_2)=P(t_1,t_{c_j})P(t_{c_{j+1}},t_{c_{j+2}})\cdots P(t_{c_{k-1}},t_{c_k})P(t_{c_k},t_2)$$

[36]. That is, it is just the product of transition probability matrices over the time-homogeneous intervals. Then we can calculate the necessary probabilities for our test statistic as before. If piecewise constant intensities are to be used in the modelling, the cut points should always be specified prior to the study.

2.6. Power and Sample Size

The test statistic is given by $T=\frac{W}{\sqrt{\mathit{var}(W)}}$, where W and var(W) are defined as in section 2.1. Define Q₁ and Q₂ to be the hypothesized transition matrices for groups 1 and 2, respectively. Let T₁, T₂ be the failure time random variables that correspond to Q₁, Q₂, and let C₁, C₂ the censoring random variables. Let t₁, t₂ be the random variables for the final observation times, and S₁(t₁) and S₂(t₂) be the random states at those visit times for each group. Define δ = P(T₁ > T₂|Q₁, Q₂,C₁,C₂, S₁(t₁), S₂(t₂)) − P(T₁ < T₂|Q₁, Q₂,C₁,C₂, S₁(t₁), S₂(t₂)). Without loss of generality, under the alternative that δ > 0, the power of the test is given by:

$$1-\beta \approx 1-\mathrm{\Phi }(z_{1-\frac{\alpha }{2}}-\frac{n_1{n}_2\delta }{\sqrt{\mathit{var}(W)}}),$$

where β is the probability of making a type 2 error, Φ is the cumulative distribution function of the standard normal distribution, n₁ and n₂ are the sample sizes in each group, and z_p is the p^th percentile of the standard normal distribution. Obtaining δ and an estimate for the variance is difficult to do analytically, as they will be complex functions of the transition intensities, censoring distributions, and observation times. However, we can use simulation to obtain an approximate power or sample size for the test. To do so, first we need to specify hypothesized values for Q₀ and Q₁, censoring distributions, and an observation scheme. We can then generate multi-state data for each group, using a very large sample size for each group, and apply the method to this generated data set. Jackson provides a function for this type of data generation in the msm package in R [30]. Let $n_1^S$ be the simulation sample size for group 1 and $n_2^S={kn}_1^S$ where 0 < k ≤ 1. After generating the data, we can estimate δ with $\widehat{\delta }=\frac{1}{n_1^S{n}_2^S}\widehat{W}$, and var(W) with $\widehat{\mathit{var}(W)}$ using formula 2 in section 2.1. Let $\widehat{\sigma }=\frac{1}{n_1^S{n}_2^S}\sqrt{\widehat{\mathit{var}(W)}}$. Then for given type 1 and type 2 errors α and β, we can estimate the necessary sample size per group with

$$n_1=n_1^S{\left[\frac{(z_{1-\alpha /2}-z_{\beta })\widehat{\sigma }}{\widehat{\delta }}\right]}^2\text{and}{n}_2={kn}_1.$$

3. Simulations

We performed several simulations to assess power and type 1 error of the test statistic when the data were generated under a multi-state Markov model, when the model was misspecified, and under both equal and unequal censoring distributions. We compared the results of our test with the Wilcoxon rank-sum test on the unobserved exact death times, the Gehan-Wilcoxon test [17], and the G^ρ family of tests of Harrington and Fleming [37], with ρ = 0 (log-rank test) [38, 39 ], and ρ = 1 (Peto & Peto Wilcoxon test) [40]. With our proposed test and the Gehan test, we computed the test statistic using the permutation variance, and compared it to a standard normal distribution. For each set of simuations, censoring distributions were uniformly distributed, each subject’s state was observed at the same fixed set of times, {1,2,3,…}, until failure or censoring, and transitions into the absorbing state are assumed to be observed exactly while all other transitions are interval censored. For each scenario, 1000 repetitions were performed for type 1 error, and 500 repetitions for power.

3.1. Model Correctly Specified

First we generated the data from a 3-state progressive multi-state Markov model under H₀ (Table 1). One can think of the 3 states as initial diagnosis (1), progression (2), and death (3). Under this model, the size of our proposed test was around the nominal level of 0.05 and comparable to that of the other tests considered. This held for each of the sample sizes considered, and under both equal and unequal censoring distributions. This also held for unequal sample sizes (results omitted) in the two groups.

Table 1.

Type 1 error (%): 3-state progressive multi-state Markov model (correctly specified).

Censoring	n1 = n2	Wilcoxon*	Gehan	Peto-Peto	Log-rank	Proposed
Equal, 50 %	30	4.5	4.4	4.3	5.1	4.3
	50	5.0	5.6	4.9	5.4	5.2
	100	3.1	4.7	4.4	4.9	4.2
Equal, 70 %	30	4.7	5.7	5.2	5.3	5.4
	50	6.0	5.4	5.6	5.9	5.9
	100	5.5	4.4	4.6	4.4	4.6
Unequal, 50, 68%	30	4.5	4.2	4.9	5.2	4.0
	50	5.0	6.3	6.4	5.9	5.7
	100	3.1	5.0	5.5	5.1	4.9
Unequal, 70, 81 %	30	4.5	4.2	4.9	5.6	4.9
	50	4.1	4.4	6.3	6.5	5.2
	100	6.6	5.5	7.0	7.7	6.9

^*Wilcoxon rank-sum test performed on (unobserved) exact death times, in all simulation tables.

For power, there were three types of alternative distributions considered (Table 3). For group 1, denote the transition intensities from state 1 to 2 and state 2 to 3 by λ₁ = 0.2 and λ₂ = 0.1, respectively. Let c₁λ₁ and c₂λ₂ be the transition intensities for group 2. The alternatives considered were: (1) c₁ = c₂ = 1.5; (2) c₁ = 2, c₂ = 1; and (3) c₁ = 1, c₂ = 2. In the first case, the hazard ratio of transitioning to the next state for group 2 versus group 1 was 1.5 for each transition. In the second alternative, the hazard from state 1 to state 2 is twice as high for group 2, but the hazard from state 2 to 3 is the same. This corresponds to group differences in only the intermediate transition. And in the third case, the hazard from state 2 to 3 is twice as high in group 2, but the same for state 1 to 2 (group differences in last transition, but not the intermediate one). Under alternative 1, of the four tests, the proposed test and the log-rank test performed best and were comparable to each other. Under the second alternative, the proposed test was far superior to the others under both equal and unequal censoring, with a relative increase of more than 20% power over the next best test in each simulation. Under alternative 3, the proposed test was inferior to the log-rank and the Peto-Peto test, but comparable to Gehan’s test.

Table 3.

Power(%): 3-state progressive multi-state Markov model (correctly specified)

Scenario	Censoring	n1 = n2	Wilcoxon*	Gehan	Peto-Peto	Log-rank	Proposed
1	Equal, 50, 35 %	50	74.8	55.4	60.4	63.0	64.0
		100	95.4	84.6	87.6	88.6	89.4
	Equal, 70, 55 %	50	71.6	41.2	45.4	44.8	48.6
		100	94.4	71.0	74.2	76.4	80.6
	Unequal, 50, 52 %	50	72.6	49.6	53.4	55.0	56.6
		100	93.0	76.4	81.4	84.4	84.8
	Unequal, 70, 69 %	50	70	41.6	47.4	50.4	52.0
		100	93.8	62.4	69.6	73.6	76.0
2	Equal, 50, 42 %	50	27.4	23.8	23.2	18.0	28.8
		100	47.2	40.8	41.4	36.6	49.8
	Equal, 70, 61 %	50	25.0	21.2	21.4	20.2	31.6
		100	46.8	36.0	34.8	32.0	49.6
	Unequal, 51, 59 %	50	26.0	20.6	22.6	21.8	28.2
		100	47.4	43.2	46.2	45.4	59.2
	Unequal, 70, 73 %	50	30.4	21.0	23.6	24.6	37.4
		100	47.8	35.4	41.6	43.0	63.2
3	Equal, 50, 35 %	50	63.8	45.0	49.6	53.5	45.4
		100	93.8	78.3	82.2	85.4	77.6
	Unequal, 50, 52 %	50	70.2	45.6	51.2	52.7	43.7
		100	94.8	73.4	79.4	82.4	73.2

With the same models and heavier censoring, the percentage gain in power for our proposed test versus the others was more substantial under the first two alternatives.

3.2. Model Misspecified

When the model was misspecified with a 3-state process generated by Weibull sojourn times in each state (table 2), the size of the test was correct under equal censoring distributions, but was inflated for some parameter levels under unequal censoring distributions. This was most severe with heavy censoring (50+% in each group) and when the shape parameter (k) for each transition time was equal to 0.5, which indicates a transition rate that decreases over time. With k = 1.5 for each state transiiton time, the type 1 error was also inflated for larger sample sizes, and was exacerbated by heavy censoring. With k = 0.5 for the state 1 sojourn time, and k = 1.5 for the state 2 sojourn time, the size of the test was accurate under equal and unequal censoring and all sample sizes. This may be because the probabilities were getting underestimated for one of the transitions, and overestimated for the other. Under unequal sample sizes (results omitted), the type 1 error was controlled under equal censoring, but in some cases inflated under unequal censoring as before.

Table 2.

Type 1 error(%): 3-state progressive model with Weibull distributed sojourn times, with varying shape paramaters for state-to-state transitions

shape(k1, k2)	Censoring	n1 = n2	Wilcoxon*	Gehan	Peto-Peto	Log-rank	Proposed
(0.5,0.5)	Equal, 50 %	30	4.0	4.1	4.3	4.5	3.7
		50	6.0	4.4	4.9	5.4	5.5
		100	4.7	4.0	4.1	4.3	4.8
	Unequal, 50, 68%	30	4.7	5.2	5.3	5.8	7.8
		50	4.7	6.0	6.1	6.8	9.4
		100	5.6	5.3	5.2	5.7	14.5
(1.5,1.5)	Equal, 50 %	30	5.6	5.3	4.5	5.6	5
		50	3.9	5.0	5.4	5.2	5.2
		100	4.9	5.3	5.4	5.4	4.9
	Unequal, 50, 68%	30	5.4	4.6	4.6	4.6	4.8
		50	5.3	5.6	5.2	5.2	5.2
		100	5.5	6.0	6.4	5.6	6.1
(0.5,1.5)	Equal, 50 %	30	5.2	5.7	5.8	5.4	5.4
		50	5.1	4.7	4.7	5.0	4.9
		100	6.0	5.7	4.9	4.8	5.1
	Unequal, 50, 68%	30	4.5	4.6	3.9	4.5	3.9
		50	4.4	4.3	4.0	4.1	3.7
		100	4.6	4.7	4.1	4.2	4.9

Under the alternative with weibull-distributed sojourn times (table 4), the results were similar to those under the correctly specified model (with equal censoring). As before, say for group 1 we have scale parameters λ₁ and λ₂ for transitions from state 1 to 2 and 2 to 3, respectively. Then for group 2 we used c₁λ₁ and c₂λ₂ as scale parameters. We set the shape parameters k₁ = k₂ = 0.5 (decreasing hazard rate over time), and k₁ = k₂ = 1.5 (increasing hazard rate). The alternatives here correspond to the same used with the model correctly-specified. If the shape parameters were set to 1, this would correspond to the same data-generation process given under the multi-state Markov model. Unsurprisingly, the results for each alternative were similar to those obtained with data generated by the Markov model under equal censoring (see Table 1–2). Results for unequal censoring were biased when the shape parameters were less than 1, and are not presented.

Table 4.

Power(%): 3-state progressive model with Weibull distributed sojourn times, with varying shape paramaters for state-to-state transitions

Scenario	shape(k1, k2)	Censoring	n1 = n2	Wilcoxon*	Gehan	Peto-Peto	Log-rank	Proposed
1	(0.5,0.5)	Equal, 60, 50 %	50	24.5	17.2	18.2	18.1	19.6
			100	44.6	31.2	31.7	31.5	32.5
	(1.5, 1.5)	Equal, 51, 33 %	30	80.0	62.9	67.5	70.0	69.3
			50	96.7	84.5	87.4	90.5	89.7
2	(0.5,0.5)	Equal, 58, 50 %	50	19.4	12.2	14.6	14.6	16.2
			100	28.4	21.0	18.8	18.8	25.6
	(1.5,1.5)	Equal, 51, 42 %	30	26.7	21.9	22.6	20.9	27.6
			50	41.4	31.5	32.1	28.2	39.8
3	(0.5,0.5)	Equal, 60, 50 %	50	24.1	15.1	16.7	17.2	15.6
			100	45.2	27.0	28.7	29.8	25.1
	(1.5,1.5)	Equal, 51, 34 %	30	78.4	55.7	60.9	68.3	57.3
			50	95.6	80.8	84.7	89.9	82.3

4. Example Analysis

We will illustrate the proposed method on data from a clinical trial of patients with amyotrophic lateral sclerosis (ALS) [41]. Subjects in the trial were monitored for two endpoints: survival, and rate of decline in neurological function as measured by their ALSFRS-R scores. The ALSFRS-R is a functional rating scale by which physicians estimate the degree of functional impairment in ALS patients [42]. The scale ranges from 0–48, with a higher score indicating better function. ALSFRS-R was measured periodically in patients until death, drop-out, or the end of the study. We discretized this score into 4 states: 37–48 (state 1), 25–36 (2), 13–24 (3), 0–12 (4). Subjects could go back and forth between states, and die from any state. The model is displayed graphically in Figure 1.

Figure 1.

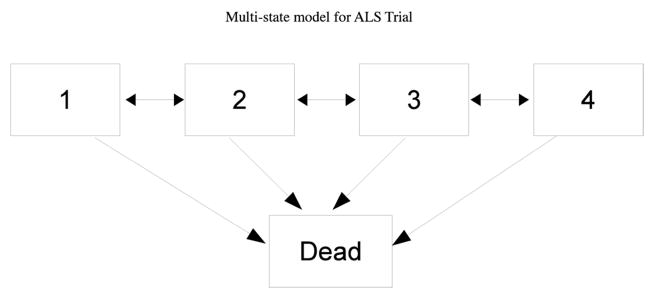
Multi-state model for ALS Trial, where states represent categories of ALSFRS-R scores. 1: 37–48; 2: 25–36; 3: 13–24, 4: 1–12.

We fit the model to the longitudinal data using the msm package for R [30], and obtained the following transition intensity matrix:

$$Q=\left(\begin{array}{ccccc}-.00591& .00587& 0& 0& .00004\\ .000764& -.00458& .00364& 0& .00017\\ 0& .000861& -.00505& .00239& .0018\\ 0& 0& .00228& -.00882& .00654\\ 0& 0& 0& 0& 0\end{array}\right)$$

From this, we can get the transition probability matrix, P(t), at any time t. For example, for this model, P(365) is given by:

$$P(365)=\left(\begin{array}{cccccc}& \mathit{State}1& \mathit{State}2& \mathit{State}3& \mathit{State}4& \mathit{State}5\\ \mathit{State}1& 0.160205349& 0.37811134& 0.2464864& 0.05075964& 0.1644373\\ \mathit{State}2& 0.049180104& 0.28219468& 0.2905536& 0.07527923& 0.3027923\\ \mathit{State}3& 0.007575872& 0.06865881& 0.2401140& 0.09250760& 0.5911437\\ \mathit{State}4& 0.001489027& 0.01697812& 0.0882921& 0.06732805& 0.8259127\\ \mathit{State}5& 0.000000000& 0.00000000& 0.0000000& 0.00000000& 1.0000000\end{array}\right)$$

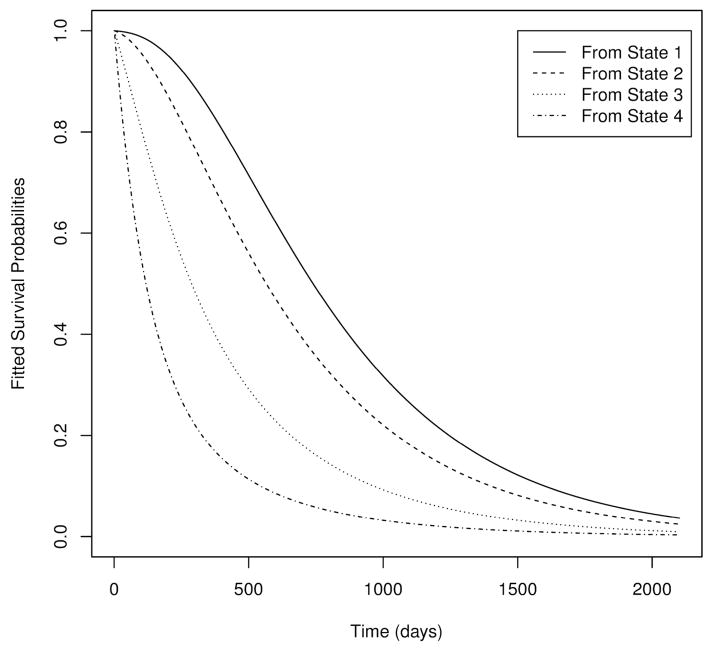
This gives us the probability of a subject being in a particular state after 1 year (365 days), given their current state (in the matrix, current state is indexed by rows). For example, the probability of a subject dying within a year given that they are currently in state 1 is estimated to be 0.164. A plot of the fitted survival probabilities from each state is given in Figure 2. We can see that estimated survival is worse for subjects with lower ALSFRS-R scores, so we hope to recover some information on survival that is lost due to censoring by accounting for the subjects state. We examined survival with respect to the variable site of onset, which is the type of diesease. The log-rank test gave a z-statistic of −2.249, with two-sided p-value .0245. For the Peto-Peto Wilcoxon test, Z = −2.296, with a p-value of .0217. After applying our method, we obtained a Z-statistic of −2.39 and p-value .0166.

Figure 2.

Plot of survival probabilities from each state based on fitted multi-state model.

5. Discussion

The proposed test aims to use auxiliary information to test for group differences in survival when there are a general number of intermediate states and possible transitions between those states. It should be noted that with censoring, we are under a somewhat more restrictive null hypothesis of equality of transition intensities for each group. The reason for this is because we chose to fit the model on the pooled data. The advantages of doing so are that we will get less variable model estimates under the null, we can use a permutation variance when we have equal censoring or when the model is correctly specified, and subjects who are censored at the same time and in the same state will have the same score. The drawback is that we may not be gaining much, if any, power under certain types of alternatives (see Simulations). Another option is to fit separate models for each group, and get a bootstrap estimate of the standard error. We did not assess how this would perform relative to fitting under the null.

There are a few advantages and disadvantages to using the multi-state Markov model for auxiliary information. A major advantage is that we can estimate the model parameters even when we do not know the exact transition times between states, and get survival probabilities conditional on observed disease status. It is also flexible and can accommodate a number of disease states, forward and backward transitions, and different observation times between subjects. The main limitation is that it is a parametric model, and if it is incorrect, the test can behave poorly when censoring distributions differ substantially between groups. Semi-Markov models may be more appropriate and can also be used to estimate transition probabilities in some settings, but this will likely require knowing the exact transition times, and disallow backward transitions in the model.

We can also incorporate covariates into the model using a type of proportional hazards model. The transition matrices for a particular set of covariates can be calculated, and the transition probabilities obtained from there. Adding too many covariates, however, can yield poor model estimates because the number of parameters increases by the number of possible transitions for each additional covariate. To limit this, covariates can be constrained to only affect specific transitions. One important application of this is using time-dependent covariates to allow the transition intensities to change at specific time points. This allows us to relax the strict assumption of time-homogeneity.

Assessing the fit of the model should be of interest to investigators who decide to use this method. While diagnostics are limited for models with panel-observed or interval-censored data, some methods are available. See Titman and Sharples for a review [36].

Limitations of this method include that it will not be valid under informative censoring or informative sampling times, i.e., when the censoring times or observation times depend on the current disease state of the individual. Sweeting et al. developed a model that incorporated informative observations times into the likelihood, which would be applicable with our method [43]. Additionally, a calculation for desired sample size may be difficult to obtain analytically, but we have provided a procedure to approximate it via simulation.

We have shown through simulations that in some settings, use of this method can improve power over the traditional tests. The most substantial improvement occurred with a progressive disease where the mechanism of treatment mainly delays transition to the intermediate states, which is often the case for targeted cancer treatments. The reason for this is that censored individuals in the non-treatment group will, on average, be in later disease stages and thus less likely to survive than those on treatment. In general, the utility we get from this method versus others will depend on the amount of censoring, the data-generation process, and the treatment mechanism. While the proposed method performed increasingly better than others under heavier censoring, we need to observe at least a few transitions into the absorbing state in order to get reliable parameter estimates. Thus, the amount of censoring may not be excessively high, particularly in relatively small samples.

We also determined that the method yields a valid test under equal censoring distributions, even when the model does not match the data-generating process. Thus, it will be most appropriate to use in settings with roughly equal follow up, such as clinical trials. The ill effects of model misspecification with unequal censoring can possibly be mitigated by using piecewise constant transition intensities with a sufficient number of cut points.

6. Appendix

The Kolmogorov forward differential equations relate the transition probability matrix P(t) and the transition intensity matrix Q:

$$\frac{dP(t)}{dt}=P(t)Q$$

The solution to this gives us P(t) = exp(Qt), where exp denotes the matrix exponential. This is defined as the power series: ${\sum }_{k=0}^{\infty }\frac{1}{k}{X}^k$, where X is an n x n matrix. This can be difficult to compute, but in most cases, it can be computed via an eigensystem decomposition of Q. That is, if Q has k distinct eigenvalues, d₁,…, d_k, then Q = UDU⁻¹, where D is the diagonal matrix with entries d₁,…d_k, and U is the matrix whose columns are the eigenvectors of Q. Then P(t) = Ue^DtU⁻¹.

The full likelihood for the model is given by the product of the transition probabilities between states over all individuals and observation times:

$$L(Q)=\prod _{i=1}^N\prod _{k=1}^{m_i}{p}_{S_i(t_{ik}),S_i(t_{i,k+1})}(t_{ik},t_{i,k+1})$$

Maximum likelihood estimates for the transition intensities can be computed by numerical optimization of the likelihood, via derivative-free algorithms such as Nelder-Mead [44], or through quasi-Newton methods [45]. Jackson notes that this likelihood is only valid when the sampling times t_ik are non-informative, that is, the current observation does not depend on the current state. For more on this, see Jackson [30] and Gruger [46]. For details on modelling informative sampling times as part of the likelihood, see Sweeting et al. [43].