Design and Inference for the Intent to Treat Principle using Adaptive Treatment Strategies and Sequential Randomization

Abstract

Nonadherence to assigned treatment jeopardizes the power and interpretability of intent-to-treat comparisons from clinical trial data and continues to be an issue for effectiveness studies, despite their pragmatic emphasis. We posit that new approaches to design need to complement developments in methods for causal inference to address nonadherence, in both experimental and practice settings. This paper considers the conventional study design for psychiatric research and other medical contexts, in which subjects are randomized to treatments that are fixed throughout the trial and presents an alternative that converts the fixed treatments into an adaptive intervention that reflects best practice. The key element is the introduction of an adaptive decision point midway into the study to address a patient's reluctance to remain on treatment before completing a full-length trial of medication. The clinical uncertainty about the appropriate adaptation prompts a second randomization at the new decision point to evaluate relevant options. Additionally, the standard ‘all-or-none’ principal stratification (PS) framework is applied to the first stage of the design to address treatment discontinuation that occurs too early for a mid-trial adaptation. Drawing upon the adaptive intervention features, we develop assumptions to identify the PS causal estimand and introduce restrictions on outcome distributions to simplify Expectation-Maximization calculations. We evaluate the performance of the PS setup, with particular attention to the role played by a binary covariate. The results emphasize the importance of collecting covariate data for use in design and analysis. We consider the generality of our approach beyond the setting of psychiatric research.

1. Introduction

Large scale comparative effectiveness trials are conducted in real world settings to provide an evidence base directly relevant to clinical practice. Despite the emphasis on practical intervention options, often a substantial percentage of subjects do not complete the effectiveness study protocol. This may have as much to do with the treatments being evaluated, as with the introduction of a controlled environment. This is especially true in psychiatry, in which both practice and trial settings are plagued by high rates of nonadherence and discontinuation. Two landmark studies exemplify the challenge for psychiatric treatment research. The Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE) Schizophrenia Study reported a 74% discontinuation rate, despite optimizing treatment to forestall medication failures and allowing (randomized) medication changes [1]. About 40% of subjects dropped out of the Sequenced Treatment Alternatives to Relieve Depression (STAR*D) Study during early phases of the trial [2,3]. In this trial, randomization to each successive 12-week stage of treatment took into account the preferences of patients and their treating clinicians [4]. Such high rates of nonadherence and dropout jeopardize the power and interpretability of intent-to-treat (ITT) comparisons. However, this is not a failure of the ITT principle, but rather a reflection of the studies themselves. A similar view has been expressed in a National Research Council report on how to prevent missing data in clinical trials [5].

To help fix ideas, consider the design that is ubiquitous in mental health and many medical contexts: randomization to parallel groups in which assigned treatment is fixed for the duration of the trial. The simplicity of this design is undercut by the complexity of the patient's response to the unrealistic attempt to rigidly control treatment, and the results are often dissatisfying on all counts, with artificially fixed treatments and critically incomplete data. Because the study protocol fails to accurately reflect the realities of clinical practice, the pragmatic argument for ITT inference can fail to convince the intended audience. Causal methods have been developed to tease out scientifically relevant results from fixed-treatment trial data with non-negligible nonadherence. These methods, however, attempt to fix the consequences of the design's weakness, rather than the design itself. Design alternatives are crucial to a comprehensive solution to nonadherence, for both experimental and real world settings. The approach we take in this paper rests on the observation that the principle of analysis by ITT should also inform design [6]. The intent is to ensure clinically relevant ITT comparisons that preserve the initial head-to-head comparison of scientific interest.

The key modification we make to the standard design is to convert each fixed treatment option to an ‘adaptive treatment strategy’ (ATS) [7], which allows more flexible management of each subject's treatment and adherence to it. The ATS includes a decision point midway into the trial that addresses the critical question faced by clinicians: What to do when the patient wants to give up on treatment before completing a full-length trial of medication or therapy. Resolving the clinical uncertainty as to how to proceed prompts the introduction of a second (mid-trial) randomization to evaluate relevant ATS options, such as changing the treatment that was assigned at baseline, or attempting to enhance adherence to it. That design is a Sequential Multiple Assignment Randomization Trial (SMART) [8]. Both the ATS (applied in practice by the clinician) and the randomization (applied in the SMART by the trialist) are adaptive, taking into account the patient preferences at that point, to maximize continued adherence. Similar SMART designs have been proposed for evaluating adherence enhancement strategies for patients with type II diabetes, although they do not incorporate individual preferences [9]. The SMART design is also similar to those for STAR*D and CATIE, except for the timing of the new randomization. It occurs earlier in the course of treatment because both studies showed that adaptively changing treatment at the end of the standard medication or therapy trial is not sufficient to prevent nonadherence.

In some contexts, design alone cannot address nonadherence because a substantial number of subjects may discontinue treatment too early for a clinically reasonable mid-trial adaptation. To address such premature discontinuation when it may occur, we extend the principal stratification (PS) framework for all-or-none nonadherence [10] to the first stage of the proposed SMART design. The idea is to restrict causal inference to the subset of subjects who would persist at least to a therapeutic dose of therapy or medication on either baseline option. This restriction further strengthens the connection to the scientific goals of the standard design.

In Section 2, we develop the design framework and the principal stratification setup for causal estimands. Sections 3 and 4 present our approach to identification and inference for the causal estimands. In Section 5 we evaluate the role played by different design parameters on the performance of the principal stratification set up. Section 6 concludes with discussion. Throughout, the exposition is grounded in mental health treatment research. We briefly discuss the generality of our approach to addressing nonadherence as part of Section 6.

2. Design and Inference for Intent to Treat

2.1 Design: SMART counterpart to fixed-treatment trial

Our conversion of the standard fixed-treatment protocol into an adaptive intervention centers on critical decisional uncertainty intrinsic to treatment nonadherence: In response to patient dissatisfaction to a medication or therapy that is not yet fully evaluable, is it optimal to change treatment or should efforts be made to enhance adherence to the current treatment? Given the patient would have limited exposure to treatment (perhaps only long enough to achieve a therapeutic dose), there may be clinical uncertainty about the appropriate adaptation if the patient expresses reluctance to remain on treatment. Uncertainty about the possible consequences if the patient can be convinced to continue treatment raises the question of whether to try to enhance adherence or change to another treatment. Moreover, the decision leading to optimal long-term benefit may depend on the treatment itself, given different modes of action and effectiveness across distinct drug classes and therapy modalities. This is the scientific rationale for adding another stage of randomization to the original design (with alternatives ‘enhance adherence’ vs. ‘change treatment’).

The simplest form of the conversion to a SMART design presupposes that early discontinuation is not a significant risk, as can be the case for psychotherapy treatment of certain anxiety and depressive disorders [11]. To be concrete, suppose that one of the treatments, labeled T₀ is an established cognitive therapy for panic disorder, while the alternative T₁, is a more intensive behavioral intervention. Further assume that after reaching therapeutic dose (a certain number of sessions), the subject's preferences about treatment to that point are measured as ‘stay’ or ‘switch’. We specify four possible ATS options that use individual preferences to operationalize the critical decision underlying the new design:

• Strategy 1: Start on T₀. Rule 1: Once the patient achieves a therapeutic dose of T₀, obtain and act upon preferences: if ‘stay’, keep on current treatment; if ‘switch’, change to T₂. Continue to follow.

• Strategy 2: Start on T₀. Rule 2: Once the patient achieves a therapeutic dose of T₀, obtain and act upon preferences: if ‘stay’, keep on current treatment; if ‘switch’, add adherence enhancement. Continue to follow.

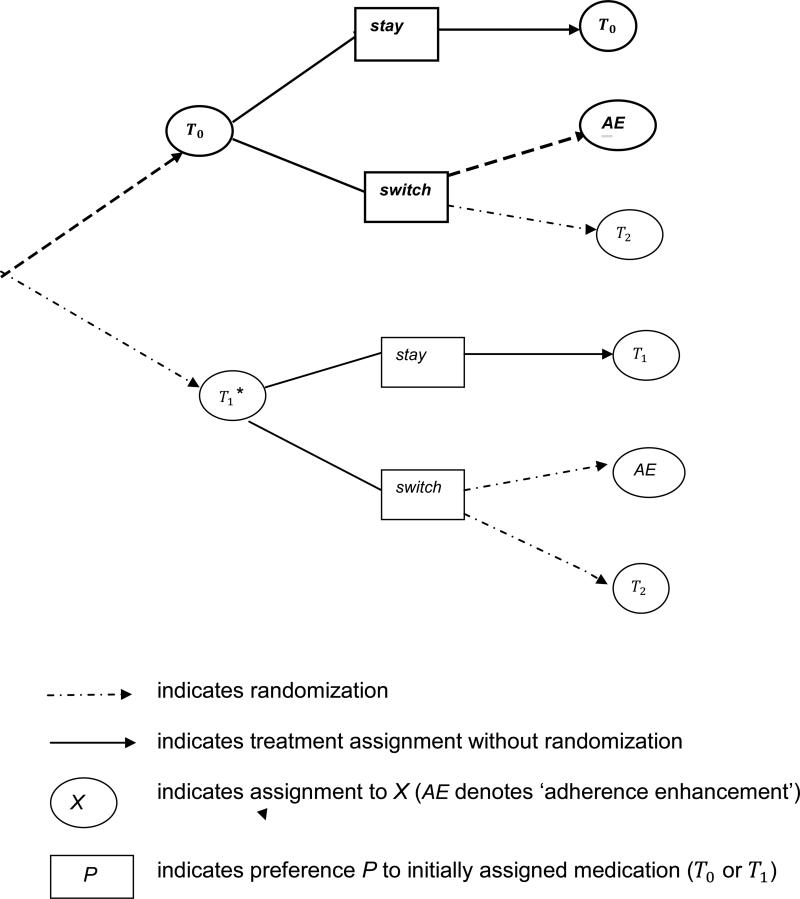
• Strategies 3 and 4 are similarly defined in terms of T₁. As in the standard design, randomization at baseline is to either T₀ or T₁; randomization upon reaching therapeutic dose on assigned treatment is (adaptively) to the two options specified by Rules 1 and 2 for subjects who prefer to switch treatment: ‘change treatment’ or ‘enhance adherence’ (see Figure 1). Note that each ATS is comprised of two of the six possible branches in the two-stage design. For example, the second strategy includes the first two branches in the design tree (bolded in Figure 1). Also, the second randomization inherits the treatment adaptation of the ATS: whether a subject is re-randomized and to what is determined by individual preferences and the possible options specified by the competing ATS.

Figure 1.

Two-stage SMART-ES design for evaluating four strategies (strategy 2 is bolded). There are two options for initial medication, T₀ and T₁. The ATS alternatives for mid-course treatment changes are adaptively randomized to individuals preferences.

We refer to the design in Figure 1 as SMART-ES, where SMART designates (as above) that this is a Sequential Multiple Adaptive Randomization Trial [8] and Equipoise-Stratification (ES) formalizes preference-based randomization [4]. The SMART-ES design resembles those developed for improving adherence to diabetes treatment [9], but is distinguished notably by the inclusion of individual preferences in the ATS (and in the randomization). The consideration of clinically-driven preferences during the course of treatment approximates shared decision-making that occurs in practice, thereby reducing the possibility of nonadherence specific to the experimental context. More generally, we conceptualize preferences obtained through clinician-patient discussion as a broad indicator that encompasses emerging response to the current treatment, which is pivotal to mid-course treatment decisions.

For general applicability, the ATS in the design must explicitly specify how to treat individuals who fail to persist to a minimal therapeutic dose of therapy or medication. The strategies must also contend with the potential for treatment with medication to introduce sufficient side effects to preclude further use by some patients. Assume now that the treatments of interest are two medications and that T₀ is an established, generally tolerated active control (e.g., a well-studied selective serotonin reuptake inhibitor antidepressant), while the alternative T₁ is a more aggressive medication that may have intolerable effects in some patients. To allow for the possibility of early discontinuation and intolerance, the first ATS becomes:

• Strategy 1 (revised): Start on T₀. Rule 1: If the patient tolerates and persists to a therapeutic dose of T₀, obtain and act upon preferences: if ‘stay’, keep on current treatment; if ‘switch’, change to T₂. Continue to follow. If the patient fails to persist before reaching a (tolerated) therapeutic dose, switch to T₁, and proceed as in Rule 1.

The remaining strategies are revised in the same way, e.g., specifying a switch to T₀ if the patient fails to persist after starting on T₁. The intentional crossover derives from the original equipoise concerning the effects of T₀ and T₁, given lack of sufficient clinical indication to rule out either alternative. Note that the revised first and second strategies are stated generally, even though intolerance (as distinct from persistence) is not expected under T₀. Also, fully operational strategies for the clinician would require options beyond T₀ and T₁ to handle patients who fail to persist to a tolerated dose under either.

2.2 Inference: Principal stratification setup for persistence

We apply the principal stratification (PS) framework [10] to the initial stage of the (second) SMART-ES design to account for the inability or failure of some subjects to persist on assigned medication until a therapeutic dose is reached. The usual stability assumption ‘SUTVA’ is assumed so that individual potential outcomes under either baseline treatment are well defined [12]. The goal is to obtain approximately valid inferences for the latent subset of subjects who would persist at least to a therapeutic dose and exposure duration under either initial assignment.

Let Z indicate randomization to the aggressive treatment (Z = 1) or the active control (Z = 0), and D be a trinary indicator: persist through a minimal therapeutic medication trial (D = P), tolerate but fail to persist (D= A), intolerant (D = I), with A standing for abandonment of assigned treatment. We adopt the standard potential outcomes notation, e.g., D₀ is the indication D that would occur under Z = 0. Note that the observed outcome D ≡ D_Z. Nine possible latent types are determined by (D₀, D₁): G = PP, AP, PA, AA, PI, IP, AI, IA, or II, where PP is interpreted as ‘persist, persist’, etc. and G indicates latent type. When evaluating medications for which intolerance is not be an issue, D becomes binary and G = PP, AP, PA, or AA. The binary case would also be applied to psychotherapy treatments, when early discontinuation occurs with some frequency.

The causal estimand of interest is the average treatment effect for the principal stratum G = PP, which we refer to as the ‘persister’ average causal effect (PACE). PACE is the similar to the ‘survivor’ average causal effect (SACE) defined for the dichotomy of survive or not (‘persist’ = ‘survive’) [13,14]. For SMART-ES, there are two versions, PACE(W) and PACE(Y), where W is measured after observing D, and Y is measured at the end of the study. Note that W is an intermediate outcome along the way to Y, the primary outcome and object of study. This allows flexibility in choosing W so as to maximize the validity of any assumptions needed for PS inference.

Formally, PACE(W) = E(W₁|G = PP) - E(W₀|G = PP). The causal estimand PACE(Y) is similarly defined but must take into account mid-trial treatment adaptation. To do so, we use the comparison of (revised) strategies 2 and 4 to define PACE(Y) as E(Y_(1,AE)|G = PP) - E(Y_(0,AE)|G = PP), where (z,AE) corresponds to the ATS that calls for starting with T_z, z = 0 or 1, and adaptively adding adherence enhancement (if a switch is preferred). The causal effect from the fixed-treatment trial closely resembles PACE(Y), in that all subjects participating in the PS estimand are assigned to initial treatment throughout the study, possibly in combination with adherence enhancement. Oetting et al. [15] present additional comparisons specific to a two-stage SMART design that could also serve to define PACE(Y). For example, the initial treatment effect is defined as the marginal or main effect of Z on Y, which pools over possible treatment adaptations (switch medication vs. add adherence enhancement) for Z = 0,1. The main effects comparison may be useful when most subjects prefer to change assigned treatment (and are hence re-randomized [16]), thereby ensuring maximal sample size for the PS estimand. All derivations we develop would apply directly to this alternative.

As defined, PACE(W) and PACE(Y) are the ITT effects (effects of treatment assignment) for subjects who would persist under either initial treatment. In particular, PACE(Y) takes into account any deviations from protocol after persistence. By intent, the SMART-ES design is meant to forestall such deviations to ensure that the ITT comparisons that develop over time will closely resemble the adaptive interventions that would occur in clinical practice. The overall ITT effect may be written as the weighted average of the stratum-specific estimands for different latent types (effects for II and AA are zero [14]). For the remainder of this article, our focus is on PACE(W) and PACE(Y) because they preserve the scientific goal of the original fixed-treatment trial.

3. Identification of the ‘persistence’ PS Estimand

The latent nature of principal strata makes identifiability of causal effects a primary challenge. This is particularly so when the number of latent types increases, as it does by additionally modeling the potential for intolerance. A naive approach to identifying PACE(W) or PACE(Y) in this case would be to exclude subjects who are unable to tolerate assigned treatment. Doing so would seemingly simplify latent structure by allowing D to be binary, while shifting focus to a more clinically relevant population of subjects who are able to persist to therapeutic doses. However, exclusion of observed intolerance does not completely exclude latent intolerance. In particular, a subject who persists under Z = 0 would be kept in the smaller reference population but may not tolerate Z = 1 (type PI). Nonetheless, we show below that plausible assumptions can be made that effectively reduce trinary D to the binary case. To do so, we consider PACE(W) because W is measured proximally to D, and prior to any treatment adaptation that is intrinsic to the ATS under evaluation.

As before, let PACE(W) = E(W₁|G = PP) - E(W₀|G = PP). Consider the quantities that are often used to point identify the PS estimand: (1) the relative sizes of each latent type: Pr(D₀ = t, D₁ = t’) = π_tt′, t, t’ = A,P,I, and (2) the mixture distributions of latent types determined by Z and D (see Table 1). We appeal to the features of the treatments and the conceptualization of the PS setup to allow reduction to binary D. First, as previously described, intolerance is assumed to not occur under the active control:

Table 1.

Latent type membership in cells determined by Z, D (D trinary)

	D = P	D = A	D= I
Z = 0	PP, PA, PI	AA, AP,AI	II, IP,IA
Z = 1	PP,AP, IP	AA, PA,IA	II, PI, AI

A1. π_IP = π_IA = π_II = 0

Second, the effort or persistence required to stay on a treatment long enough to experience intolerance is similar to that required to reach (minimal) therapeutic dose. For our context, this suggests that a subject who is unwilling to make the effort to persist under Z = 0 will abandon the more aggressive treatment before reaching intolerance:

A2. π_AI= 0

It also supports:

A3. E(W₀|G = PI) = E(W₀|G = PP)

The clinical rationale is that subjects of type PP and PI are persistent under either treatment, but one is stymied by the side effects of the aggressive treatment. Assumption A3 ensures that the PACE(W) estimand coincides for binary and trinary D, allowing subjects of latent type PI to be pooled with subjects of type PP (see Z = 0, D = P in Table 1). Taken together, A1-A3 allow reduction to the binary case, noting that the first two assumptions imply that subjects observed to have D = I are of latent type PI, a subset which is extraneous to our purposes (see D = I in Table 1). In an abuse of notation, we use D hereafter to indicate persistence or not (see Table 2).

Table 2.

Latent type membership in cells determined by Z, D (D trinary)

	D = P	D = A
Z = 0	PP, PA	AA, AP
Z = 1	PP,AP	AA, PA

Under the supposition that (reduced) D is binary, we make the following identifying assumption commonly used for ‘all or none’ non-compliance in a trial of two treatments:

A4. Monotonicity: π_AP = 0

The proportion π_AP is assumed to be zero because of the nature of the treatments. For example, sicker patients may be motivated to persist under medication T₁ despite possible side effects because of greater illness burden, but would also do so under T₀. Later we discuss relaxation of this assumption.

The exclusion restriction assumption is often used with monotonicity to fullyidentify the PS estimand but does not hold here, analogous to its failure for the SACE estimand [13]. Failure of exclusion precludes identifying Table 2 in the standard way, although the population proportions remain identified given A4. Specifically, it is not possible to disentangle the mixture distribution that occurs when Z= 0, D =P. One way to address this is to exploit the ‘crossover’ feature of SMART-ES, and impose (structural) stochastic restrictions on data observed when subjects who fail to persist under assigned treatment (Z = 0 or 1) are switched to the other treatment (Z=1 or 0). Another is to impose parametric, rather than structural assumptions. We find greater generality in the parametric approach, which we pursue here in detail.

4. Inference for the ‘persistence’ PS estimand

Table 2 shows that inference for PACE(W) and PACE(Y) can be carried out using the subset of subjects observed to persist under assigned treatment. Given Assumption A4 (there are no subjects of type AP), the latent type indicator G can be replaced by a binary one, defined as C = 1 if of type PP, and 0 if of type PA; C indexes the mixture of subjects assigned to active control. Inference from the data in the Z = 1, D = P cell can be obtained by standard methods. Inference from the data in the Z = 0, D = P cell is suitably addressed by algorithms such as expectation-maximization (EM) that convert the mixture structure into a missing data problem, which we adopt.

For illustration, we consider the simplest design that contains the key elements of our setup for mixture distribution calculations: a single randomization Z (at baseline), W and D measured midway into the trial, Y measured at the end of the trial. We suppress the second randomization during exposition, noting that PACE(Y) is essentially a function of the values of Z, because treatment adaptation is fixed at a specific option. For notational convenience, we also suppress the conditioning on Z = 0, D =P, which holds throughout Section 4; for example, Pr(W|Z = 0, D = P) is written as Pr*(W). We use the subscript i to denote quantities associated with a specific individual and let θ be the vector of parameters for the mixture distribution of subjects of type PP and PA.

To simplify EM or similar calculations, we make two conditional independence assumptions:

A5. Pr* (C | W, Y) = Pr* (C|W);

A6. Pr* (W, Y| C) = Pr* (W|C)Pr(Y|C).

The corresponding joint distribution Pr*(W,Y|C) = Pr*(W|C)Pr(Y|C) is specified as:

$$P{r}^{\ast }(W,Y,C)=\int \prod _{i\in S(0,P)}{f}^{\ast }(W_i,Y_i,C_i\mid \theta )P\left(\theta \right)d\theta$$ (4.1)

with probability or density function f*(W_i, Y_i, C_i|θ) and prior distribution P(θ); S(0, P) is the subset of subjects with observed values Z = 0, D = P. For suitable priors, (4.1) often provides a basis for maximum likelihood (ML) inference. Alternatively, both assumptions can be stated in terms of f*(·|·), noting that the likelihood function is proportional to it. For example, f*(C |W, θ) = f*(C |W, θ).

The SMART-ES design provides general support for A5 and A6 because of the second intervention (add adherence enhancement), which is introduced adaptively by each of the ATS. The non-random treatment changes for selected subjects dilute the relationship between W (response to an incomplete trial of initial treatment) and Y (response to the entire strategy). This is particularly so because adaptation depends intrinsically on emerging response via individual preferences to switch treatment obtained at the same time as W. Furthermore, if the’ main effects’ definition of PACE(Y) is used, there is additional dilution due to pooling over which treatment change to make (add adherence enhancement vs. switch medication). The overall effect is to weaken any relationship between early response and final outcome that may sometimes be anticipated in a fixed-treatment study. Setting W to some measure of early response and Y to a (distal) clinical state such as recovery may specifically support the assumptions when early response is strongly related to C and therefore W mediates the relationship of C to Y.

The application of A5 and A6 is straightforward with the EM algorithm. Given W,Y, and a current estimate of θ, denoted θ_c, the E-step in EM replaces each (unobserved) C_i with its conditional expectation, Pr*(C_i = 1 |W_i, Y_i, θ_c). The calculation, which is derived using Bayes Rule as:

$$\frac{P{r}^{\ast }(C_i=1\mid {\theta }_c)f^{\ast }(W_i,Y_i\mid C_i=1,{\theta }_c)}{P{r}^{\ast }(C_i=1\mid {\theta }_c)f^{\ast }(W_i,Y_i\mid C_i=1,{\theta }_c)+P{r}^{\ast }(C_i=0\mid {\theta }_c)f^{\ast }({\mathrm{W}}_i,{\mathrm{Y}}_i\mid {\mathrm{C}}_i=0,{\theta }_c)}$$ (4.2)

shows that A5 eliminates the need to specify joint density functions for the E-step, with (4.2) simplifying to:

$$\frac{P{r}^{\ast }(C_i=1\mid {\theta }_c)f^{\ast }(W_i\mid C_i=1,{\theta }_c)}{P{r}^{\ast }(C_i=1\mid {\theta }_c)f^{\ast }(W_i\mid C_i=1,{\theta }_c)+P{r}^{\ast }(C_i=0\mid {\theta }_c)f^{\ast }(W_i\mid {\mathrm{C}}_i=0,{\theta }_c)}$$ (4.3)

The second step, the M-step, uses the expected complete-data likelihood from the E-step based on (4.3) to obtain the next estimate of θ. Assumption A6 further allows the ‘maximization’ calculation to be factored into separate models for W and Y, while applying (4.3) to each. For example, it may be plausible to specify separate (marginal) Gaussian mixture models for W and Y, reducing the M-step to two standard calculations. In this case, the M-step for E*(Y |C = 1) ≡ E(Y|C = 1, Z = 0, D = P) is:

$$\frac{\sum _i{w}_{i,{\theta }_c}{Y}_i}{\sum _i{w}_{i,{\theta }_c}}$$ (4.4)

where i ∈ S(0, P) and w_{i θc} = Pr*(C_i = 1 |W_i, θ_c) ≡ Pr*(C_i = 1 |W_i, Y_i, θ_c). The calculation shows that inference for PACE(Y) is linked to that for PACE(W) via the use of the individual estimates of latent type membership that are (posterior) functions of W. The result is intuitive given the intervening adaptive intervention introduced by the SMART-ES design between the measurement of (W,D) and Y.

4.1 Bayesian model for mixture distribution

We assume both initial treatments have been previously studied in standard (fixed-treatment) trials. In particular, a good estimate of the rate of persistence under Z = 1 should be available. This provides an a priori value for π_PP, given monotonicity. We also assume that covariate data have been collected to help aid parametric identification of the mixture distribution [14, 17] and consider the case of a single binary X. The conditional versions of the assumptions for EM calculations become:

A7. Pr*(C |W, Y, X) = Pr*(C|W, X)

A8. Pr*(W, Y|C, X) = Pr*(W|C, X)Pr*(Y|C, X).

Let θ be the vector of parameters for the mixture distribution of subjects of type PP and PA, assumed to be Gaussian. The (complete-data) model for W and the model for C used in the EM calculations are specified as regressions:

$$\begin{array}{cc}\hfill & f^{\ast }(W\mid C=j,\mathit{X},\theta )\sim Normal({\beta }_j\mathit{X},{\sigma }_j^2),j=0,1\hfill \\ \hfill & P{r}^{\ast }(c\mid \mathit{X},\theta )\sim exp\left(w\mathit{X}\right)∕(1+exp\left(w\mathit{X}\right))\hfill \end{array}$$ (4.5)

where X is X augmented with a column for the intercept. A diffuse conjugate prior distribution similar to the one used by Hirano et al. [18] takes the form of adding extra observations to the likelihood function. There are 5 observations for each value of X, scaled by 0.01 (g = 0.01⁻² in Zellner's g prior for β_j[19]; their W values are set to the overall sample mean of W, and their Z values are set to π₀*5 for X = 1/0, where π₀ is the a priori value for π_PP. All parameters are functions of θ, e.g., β_j ≡ β_j(θ), and are a priori independent. As above, conditioning on Z = 0, D = P has been suppressed.

5. Evaluation of PS setup for SMART-ES

A central issue underlying the approach to inference for PACE(Y) described in Section 4 is how well given choices for W and X can be used to disentangle the mixture distribution of subjects of type PP and PA, as exemplified by how well the individual estimates of latent type membership predict mixture membership. To a large extent, this will be governed by the distance between latent type components [20] and the inclusion of (predictive) covariates in the modeling [17]. For evaluation of the PS setup, we simulate data using different values for π_PP drawn from the range of clinically relevant ones. We consider the sample size and mixture structure thought to be ‘minimally’ necessary, in the sense that smaller sample or (between-type) effect sizes may not allow feasible inference via principal stratification. We presume that both π_PP and the effect sizes implicit in the mixture structure are governed (to some extent) by design through inclusion, exclusion and other criteria, thereby making the simulation study pertinent to design. We also extend our evaluation to Y to understand overall performance.

5.1 Simulation study for intermediate outcome W

The simulations varied according to: (a) π_PP = 0.6, 0.7, 0.8 (early discontinuation under the aggressive treatment at most 40%); and (b) whether or not Pr(C|X) = Pr(C) (X may or may not be related to C). Otherwise, simulated design scenarios were fixed at (c) n = 200 is the number of subjects observed to persist after randomization to Z = 0; (d) μ₀ = 3, μ₁ = 2 are the means of W for subjects of types PA and PP, (e) ${\sigma }_0^2={\sigma }_1^2={\sigma }^2=1$; β₀ - β₁ = 1 = σ; (g) when X is related C the odds ratio is 2; (h) Pr(X = 1) = 0.6. For (a), values of π_PP less than 0.60 were excluded because larger rates of failure to even persist on Z = 1 threaten the clinical relevance of ITT comparisons, including the PACE estimand. Also, we did not consider π_PP = 0.9, even if achievable by design, as any adjustment due to mixture modeling would likely be dominated by the additional uncertainty it introduces. For (d), the between-type distance of one standard deviation is realistic for our context.

A motivating clinical example for the simulation setup distinguishes latent types PP and PA in terms of severity of illness (PP subjects may pursue aggressive treatment despite possible side effects because they experience a greater burden of illness) and speed of response thought to typify those less sick (PA subjects tend to abandon aggressive treatment with its side effects because they experience early relief and no longer believe it is necessary to continue in the face of the side effects). We set X to be an indicator of symptom severity at baseline and W to be an index of symptom severity (or change in severity) measured after persistence under Z = 0. This scenario sets up large between-type differences in the marginal distribution of symptoms (condition d) and in changes from baseline (condition f). Moreover, assumptions A7 and A8 required for EM calculations should be satisfied if we set Y to be recovery, a qualitative clinical milestone quite distinct from early response, especially given the treatment changes adaptively introduced after W. Conditioning on X should improve their plausibility.

Each simulation scenario was replicated 50 times. In all cases, the true model was fit according to Section 4. Starting values for the EM calculations were set using the method of Finch et al. [21] for two-component normal mixtures, which uses a starting value for π_PP, denoted π_S, to estimate starting values for the other parameters. Specifically, the sample is ordered and split into [nπ_S] and n-[nπ_S] observations, where [ ] stands for the integer part of x; the regression estimates and the pooled variance of the split sample are used as the starting values for β₀, β₁, w (logistic parameter in 4.5) and σ² respectively. This method performs well, with respect to locating the global maximum [22]. For any given scenario, π_S was set to π₀, the a priori value for π_PP.

5.2 Simulation results

Table 3 reports the estimates of μ_j, j = 0,1, (in terms of absolute relative bias and π_PP obtained from the different scenarios. However, as described in Section 4, the estimated probabilities that an individual is of latent type PP are more germane to inference for PACE(Y). To this end, we calculated the allocation rate (AR) using the indicator C (PP or not) and the estimated discriminant rule: $w_{i\widehat{\theta }}\ge .5$ implies PP, where $w_{i\widehat{\theta }}\equiv Pr(C_i=PP\mid W_i,\widehat{\theta })$ and $\widehat{\theta }$ is the (converged) estimate of θ. AR is an estimate of the proportion of subjects with correctly identified latent type, which is maximized when the true discriminant rule is used [23]. Larger values of AR indicate better mixture disentanglement and improved inference for the mixture model [20], quantifying the degree to which modeling W provides reasonable inference for PACE(Y). To more fully evaluate how performance depends on the two design scenarios for X, Table 3 also includes the case of no covariate relationships.

Table 3.

The impact of the binary covariate X as it relates to (C,W)

Regression scenarioa	π PP	${\widehat{\pi }}_{\mathrm{pp}}$	AR	Relativeb bias of ${\widehat{\mu }}_1$	Relative bias of ${\widehat{\mu }}_0$
X not related to W or C	0.6	0.57	0.64	0.19	0.16
X related to W	0.6	0.58	0.67	0.08	0.08
X related to W and C	0.6	0.62	0.65	0.08	0.09
X not related to W or C	0.7	0.65	0.68	0.15	0.18
X related to W	0.7	0.69	0.72	0.07	0.09
X related to W and C	0.7	0.73	0.73	0.08	0.10
X not related to W or C	0.8	0.75	0.77	0.11	0.21
X related to W	0.8	0.79	0.81	0.04	0.10
X related to W and C	0.8	0.72	0.76	0.09	0.17

^aIndicates which regression relationships were simulated and fit to the data

^bRelative bias of ${\widehat{\mu }}_j=\mid ({\mu }_j-{\widehat{\mu }}_j)∕{\mu }_j\mid ,j=0,1$

The simulation results show that the use of X led to better estimates of μ₀ and μ₁. For example, the relative bias in ${\widehat{\mu }}_1$ ranged from 19% = 0.38 σ (no X) to 8% = 0.16 σ (X related to C and W) when π_PP= 0.6. The scenario when X is related to W, but not C, helps to discern the role played by covariate data. In this case, the difference in slopes (condition f in the simulations) can be represented as an interaction term for C and X in the regression model for W corresponding to (4.5), thereby aiding parametric identification of the mixture distribution. When β₀ = μ₁ there will still be some benefit due to X. Specifically, the conditional or adjusted means (associated with the main effect of X) will be equal to the unadjusted means ((β₀ and β₁), but reduced conditional (population) variances help to disentangle the mixture distribution. In this sense, increased precision due to covariate adjustment not only provides improved efficiency but also improved identification, even in the absence of an interaction of X and C.

Table 3 also shows a pronounced effect of changes to (π_PP on the allocation rate, which ranged from 0.64 (π_PP= 0.6, no X) to 0.81 (π_PP = 0.8, X relates only to W). Larger values of π_PP also led to reduced bias in ${\widehat{\mu }}_1$ but increased bias in ${\widehat{\mu }}_0$. The simple model of no covariate data makes explicit the tradeoff expressed by the directional differences in bias. For example, the overall AR of 0.77 (row 7) decomposes into the conditional allocation rates among subjects of type PP and PA, equal to 0.88 and 0.31, respectively. Thus, misclassification errors are concentrated in the mixture component with substantially fewer data. Note that AR remained fairly stable across scenarios for a given value of π_PP. This suggests that the estimated probabilities are more difficult to improve solely through the addition of covariate data. Rather, it may be necessary to include a disproportionate number of subjects of type PP (via π_PP) to ensure sufficient information for their distribution when PACE(W) and PACE(Y) are the target estimands.

To supplement the results in Table 3, we carried out simulations for the case of no covariate data, with n as large as 500 and π_PP = 0.7, 0.8. Table 4 shows that increasing the (standardized) difference between π₀ and π₁ improves estimates at the population (reduced bias) and subject (reduced misclassification) levels. In particular, comparison to Table 3 shows AR to benefit as much or even more from a larger mean difference as from inclusion of X (n = 200). Note that there is modest impact due to even substantial increases to the sample size.

Table 4.

The impact of sample and effect sizes when there are no covariate data

Sample size	Effect sizea	π PP	${\widehat{\pi }}_{\mathrm{pp}}$	AR	Relativeb bias of ${\widehat{\mu }}_1$	Relative bias of ${\widehat{\mu }}_0$
200	1	0.8	0.75	0.77	0.11	0.21
500	1	0.8	0.77	0.77	0.10	0.19
200	1.5	0.8	0.77	0.81	0.10	0.20
300	1.5	0.8	0.78	0.82	0.08	0.23
400	1.5	0.8	0.79	0.82	0.08	0.22
500	1.5	0.8	0.79	0.82	0.07	0.21
200	1	0.7	0.65	0.68	0.15	0.18
500	1	0.7	0.67	0. 69	0.12	0.14
200	1.5	0.7	0.68	0.76	0.11	0.23
300	1.5	0.7	0.70	0.77	0.09	0.22
400	1.5	0.7	0.70	0.78	0.08	0.21
500	1.5	0.7	0.70	0.78	0.08	0.20

^aEffect size = μ₀-μ₁

^bRelative bias of ${\widehat{\mu }}_j=\mid ({\mu }_j-{\widehat{\mu }}_j)∕{\mu }_j\mid ,j=0,1$

To summarize the main findings: (1) the impact of covariate data can be considerable but is largely limited to population estimates; (2) the overall allocation rate can be substantially improved at the expense of heavily misclassifying subjects of type PA; (3) even large increases to sample size are less important than the choice of W and the effect size it imposes on the mixture structure.

5.3 Extension to final outcome Y

The ability to improve the allocation rate by including a greater number of subjects of type PP is specifically pertinent to inference for PACE(Y) because the estimators for the two PACE estimands are connected solely through the individual estimates of latent type membership (see expression 4.4). For the simulation setup for W, the negative impact of titling the study sample in this way is to degrade inference for subjects of latent type PA. However, it is necessary to further consider Y to evaluate the impact on overall performance.

For simplicity, we return to the design setup in Section 4. Let Y|(C = PA) ~ N(m, 1) and Y|(C = PP) ~ N(0, 1). (To be consistent with simulation notation, we suppress the conditioning on Z = 0, D = P.) Two extreme cases are instructive. First, suppose that m is much larger than E(W|C = PA) – E(W|C = PP) > 0. In this case, the penalty paid for misclassifying a subject of type PA will larger when considering the outcome Y than for W, given greater for separation of the mixture components comprising the distribution of Y; accordingly, we would expect greater bias Ê(Y|C = PP) because subjects of type PA are from the same distribution as for subjects of type PP. When differences between PP and PA means are similar for W and Y, the bias in the two estimates would be similar. We expect the patient's underlying clinical process to moderate differences in mixture structure over time, making the last case generally most likely.

A more tractable evaluation of overall performance is possible when Y is discrete, as in the clinical example in Section 5.1. Assume now that Y| (C = PA) ~ Bernoulli(p₀) and Y| (C = PP) ~ Bernoulli(p₁). Recall from Table 3 that the relative bias in ${\widehat{\mu }}_1\equiv \widehat{E}(W\mid C=PP)$ is at most 9% when X is related to W or (W, C), or equivalently at most 0.18 of a standard deviation. If we assume p₀ = 0.7, p₁ = 0.3, the between-type effect size is approximately 0.80, which is less than the one standard deviation (ES) difference for E(W| C = PA) – (W|C = PP). In this case, we would expect that the penalty paid for overweighting subjects of type PA will not differ too much for the two estimators, say perhaps at most 10% relative bias in Ê(Y|C = PP) or equivalently 0.065 of a say perhaps at most 10% relative bias in Ê(Y|C = PP) or equivalently 0.065 of a standard deviation (much less than the 0.18σ for W). Similarly, if p₁ were instead equal to 0.5 (p₀ = 0.7), then a relative bias of 10% would translate to 0.1 of a standard deviation. If the between were larger, e.g., 1.3 ES, as would occur when p₀ = 0.85, p₁ = 0.25, the relative bias would likely not exceed that Ê(W|C = PP) when expressed in standard deviations units. These calculations suggest that the overall performance of the PS setup for the SMART-ES design largely inherits that obtained for the intermediate outcome W.

6. Discussion

Underlying our approach to addressing nonadherence in randomized trials is the premise that if the trial design anticipates and adapts to nonadherence then it is possible to conduct an analysis that respects the ITT principle while yielding conclusions that are clinically interpretable and useful. We have used the ITT principle to motivate conversion of the fixed treatments offered in the conventional treatment trial design into an adaptive intervention that reflects best clinical practice. The key element is the introduction of an adaptive decision point midway into the trial to address a patient's reluctance to remain on a medication or therapy that is not yet fully evaluable. The resulting SMART-ES structure importantly isolates by design one patient's ‘mid-course’ dissatisfaction with a substantial exposure to current treatment from another patient's highly premature discontinuation from treatment (when it may occur). This has allowed us to define relevant ITT causal effects by applying the standard ‘all-or-none’ Principal Stratification to the first stage of the design to address early discontinuation. Restricting the PS setup in this way helps to represent nonadherence as a binary indicator (persist or not), which is often unrealistic when treatment is considered across the entire study protocol (see Stuart et al. [24] for discussion). The clinical underpinnings of the timing of the adaptive decision point and corresponding definition of persistence played a role as well, by providing a scientific basis for needed assumptions.

The ‘persistence’ PS estimand referred to as PACE in this paper is new but similar in latent type structure to the previously studied ‘survivor average causal effect’ (SACE). As for SACE, the failure of the usual exclusion restriction creates the need to strengthen identification of PS causal effects in other ways. One approach has been to use a form of latent independence as an identifying assumption [17,25], which is a version of assumption A6 in Section 4 used to simplify EM calculations. Instead, we have explored how covariate data could aid parametric identification, particularly with the goal to effectively link inference for PACE(W) to that for PACE(Y) via individual estimates of latent type membership. For this reason, the allocation rate was used as a primary measure in the evaluation of the performance of the PS setup.

The simulation study highlights the importance of collecting data on covariates and intermediate outcomes so that appropriate X and W can be used to maximize covariate associations and between-type separation in the PS mixture structure. Since primary interest is in PACE(Y), there is greater flexibility in selecting W than in typical PS analyses. The potentially wider set of outcomes also provides more opportunity to expand to a bivariate PS mixture model. Choosing W = (W₁,W₂) that are either highly correlated or close in expected value should improve the predictive accuracy of estimates of latent type [20, 26]. We have shown that better individual estimates can also be achieved when the proportion of type PP in the study population is high (π_PP = 70%, 80%). In this case, inference for subjects of type PA degrades, but this seems to be a good tradeoff, particularly for the SMART-ES context. Specifying design criteria such as inclusion and exclusion of subjects so as to increase π_PP may take better advantage of covariates deemed related to latent type than (only) including them in the analysis.

To fully evaluate the PS setup, we considered the impact on inference for PACE(Y) of tilting the study sample to favor PP subjects and conclude that the overall performance largely inherits that obtained for PACE(W). We expect this pattern to hold generally for other PS models (e.g., expansion to bivariate W) because the estimators for PACE(Y) and PACE(W) are connected solely through the individual estimates of latent type membership. This property of our approach allows the details of the PS modeling for W (or W) to be carried out flexibly according to the application, choosing methods for good subject-level estimates. This would be particularly important when the monotonicity assumption (A4) is in doubt and better parametric identification is needed (e.g., through more elaborate Bayesian models [26, 27]). This may be the case, for example, when the trial compares a new treatment to a placebo control.

The focus on psychiatric treatment trials in this paper was motivated by the high rates of nonadherence that occurred in two innovative large-scale effectiveness trials for depression and schizophrenia. The problems of nonadherence and early discontinuation are also widespread for treatment of medical disorders, making the SMART-ES design and the ‘persistence’ PS setup more broadly of interest. Such applications may more commonly entail consideration of placebo-controlled studies. The case of a placebo control in comparison to a treatment for psychiatric or medical illness maps directly into the one considered in detail in previous sections (a generally tolerated active control). In particular, any occurrence of intolerance while taking placebo may usually be deemed a failure to persist, given the absence of any adverse effects due to treatment or sufficient duration during the early phase of the trial for intolerable symptoms to develop under placebo. Hence, the identifying assumptions introduced in Section 4 apply immediately, thereby giving our approach greater generality. We note that when early discontinuation from the treatments or therapies of interest is modest or negligible, the simplest version of the SMART-ES design can be applied with little assumption. In particular, there are no restrictions on the nature of the control or experimental treatments and their effects, as there is no need to apply Principal Stratification.

Finally, as noted by others, the reliance on latent mixtures to define ITT effects taxes feasibility of their inference in the absence of structural restrictions to fully identify the causal estimand. Successful SMART-ES implementation may require tuning basic design elements (who gets into the study, what is the nature of the treatments) in order to maximize between-type effect sizes and minimize the proportion of study subjects that are extraneous to the ITT effect.