On Model Selections for Repeated Measurement Data in Clinical Studies

Abstract

Repeated measurement designs have been widely used in various randomized controlled trials for evaluating long term intervention efficacies. For some clinical trials, the primary research question is to compare two treatments at a fixed time, using a t-test. Though simple, robust, and convenient, this type of analysis fails to utilize a large amount of collected information. Alternatively, the mixed effects model is commonly used for repeated measurement data. It models all available data jointly and allows explicit assessment of the overall treatment effects across the entire time spectrum. In this paper, we propose an analytic strategy for longitudinal clinical trial data where the mixed effects model is coupled with a model selection scheme. The proposed test statistics not only make full use of all available data but also utilize the information from the optimal model deemed for the data. The performance of the proposed method under various setups, including different data missing mechanisms, is evaluated via extensive Monte Carlo simulations. Our numerical results demonstrate that the proposed analytic procedure is more powerful than the t-test when the primary interest is to test for the treatment effect at the last time point. Simulations also reveal that the proposed method outperforms the usual mixed effects model for testing the overall treatment effects across time. In addition, the proposed framework is more robust and flexible in dealing with missing data compared to several competing methods. The utility of the proposed method is demonstrated by analyzing a clinical trial on the cognitive effect of testosterone in geriatric men with low baseline testosterone levels.

1. Introduction

In many clinical trials, multiple responses (or longitudinal measurements) at various time points including baseline and after a randomized treatment assignment are often collected for each subject. The repeated measurement design is useful in investigating intervention efficacies, risk factors of chronic diseases, long term treatment effects, etc. For some studies, researchers are interested in intervention efficacy at a fixed point in time and thus restrict their analysis to the response differences from the last time point to baseline via a t-test. For properly randomized trials, the systematic differences in baseline covariates are eliminated. Thus, this t-test is valid for evaluating the last time point intervention efficacy even under a repeated measurement design. Another commonly used analysis strategy is analysis of covariance (ANCOVA) [1] in which the baseline values are included as covariates. For instance, for a longitudinal clinical trial study in evaluating the effect of intracoronary transfer of autologous bone-marrow cells on improving the global left-ventricular ejection fraction [2], ANCOVA was applied for comparing the response differences from the last follow up time to baseline between the two treatment groups, i.e. optimum postinfarction medical treatment versus bone-marrow-cell. It has been shown that the ANCOVA model can reduce potential bias in the treatment effect estimate due to randomly imbalanced baseline covariates [3].

Though simple and convenient, these approaches only make use of the information at baseline and the last time point and ignore a large amount of potentially valuable information. To utilize complete data, the mixed effects model [4] is often used to simultaneously model the longitudinal responses and the covariance structure of repeated measurements flexibly. In addition to assessing the last time point treatment effect, the mixed effects model allows one to evaluate and test the overall effects across every time point. Furthermore, the mixed effects model, if correctly specified, can provide more accurate and efficient treatment effect estimates. Another advantage of mixed effects model is its flexibility in dealing with missing data, which occur frequently in clinical trials. As an example, in the DURATION-2 trial [5], each patient with type 2 diabetes was randomly assigned to one of three intervention groups, i.e. exenatide, sitagliptin, or pioglitazone. The efficacy of exenatide was compared to that of sitagliptin or pioglitazone in terms of glycosylated haemoglobin (HbA(1c)) changes from baseline to week 26 post treatment start. In this study, the discontinuation rates at the final time point were 20.6%, 13.3% and 20.6% for the three treatment arms respectively. By taking the longitudinal information and correlations among the repeated measurements into account using mixed effects model, the information from the non-missing observations can help partially recover the lost information in the missing data. However, in practice, the optimal mixed effects model and the valid covariance structure deemed for the data are unknown. For well designed randomized trials, it is common to employ the grand full model by including all possible fixed effect terms along with an unstructured covariance matrix. This strategy is valid in general, but not necessarily efficient. The full model can be very conservative under certain situations (see Section 3 for simulation results). In searching for an efficient analysis strategy, researchers may first identify the optimal model deemed for the data via a given model selection procedure, and then perform statistical analysis on the selected model. Model selection criteria, AIC [6], BIC [7], corrected AIC [8] and others are available and often used in practice. However, the stochastic nature associated with the model selection procedure [9] makes the post-model selection statistical inference challenging.

In this paper, we propose an analytic procedure for longitudinal randomized controlled trial data. We first select the optimal model over a set of mixed effects models based on BIC criteria. BIC has been shown to be consistent and asymptotically selects the correct model if the correct model is among the candidate model set [10–12]. Based on the selected optimal model, we propose two test statistics, one for testing the overall treatment effects across time and the other for testing the treatment effect at the last time point. The proposed statistics not only make full use of the available data but also utilize the information from the optimal model deemed for the data. Further, we develop a restricted cluster bootstrap resampling scheme to take the stochastic variation associated with the model selection procedure into account in the proposed test statistics. The organization of the paper is as follows: In Section 2, the details of the proposed method are illustrated; In Section 3, simulation studies under different settings and missing data scenarios are conducted to investigate the performance of the proposed method; The practical usage of the proposed method is demonstrated in Section 4 with a real clinical trial; Final remarks and a discussion are given in Section 5.

2. Methods

To fix the notation, we first define x_ijk as the (continuous) response variable of j^th subject (j = 1, · · · , n_i) from the i^th treatment group (where i = 1 & 0 refers the treated and untreated group, respectively) measured at the k^th time point (k = 0, · · · , T) with x_ij0 being the baseline measurement. Further, let y_ijk ≡ x_ijk − x_ij0 (k = 1, · · · , T) represent the response difference at time point k from baseline.

For well designed longitudinal clinical trials, the following mixed effects model is commonly used to analyze all available observations jointly, allowing one to test for overall treatment effects and for effects at any single time point, including the last time point, T.

$$FullModel:y_{ijk}={\alpha }_0+{\alpha }_{Trt}I(i=1)+\sum _{k=1}^{T-1}{\alpha }_{k}I(time=k)+\sum _{k=1}^{T-1}{\alpha }_{k+T-1}I(i=1)I(time=k)+r_{ijk}+{∊}_{ijk}$$ (1)

where I is the indicator function (1 if true, 0 otherwise); α₀ is the intercept and α_Trt is the treatment effect corresponding to the last measurement time point; the α_ks^′ (k = 1, · · · , T − 1) are the main time effects and the α_k+T−1 s^′ (k = 1, · · · , T − 1) are the corresponding time × treatment interactions; the r_ijks′ are the subject specific random effects and r_ij ~ N(0, Ω) where r_ij = (r_ij1, · · · , r_ijT) and the covariance matrix Ωdescribes the correlation structure among the repeated measurements; the random measurement error ${∊}_{ijk}\sim N(0,{\sigma }_{∊}^2)$. The hypothesis corresponding to the overall treatment effects is thus

$$H_0:{\alpha }_{Trt}={\alpha }_T={\alpha }_{T+1}=\cdots ={\alpha }_{2T-2}=0vs{H}_a:\text{Otherwise}.$$ (2)

To test the hypothesis, we employ the likelihood ratio statistics for testing between the full model (1) and the following null model:

$$NullModel:y_{ijk}={\alpha }_0+\sum _{k=1}^{T-1}{\alpha }_{k}I(time=k)+r_{ijk}+{∊}_{ijk}$$ (3)

with an unstructured covariance matrix Ω. We denote this likelihood ratio test statistics as ζ_MBP, with MBP referring to the mixed effects model based power analysis. In addition, we may similarly test the last time point treatment effect by simply testing the hypothesis H₀ : α_Trt = 0 vs H_a : α_Trt ≠ 0.

The full mixed effects model is valid but not necessarily efficient when there exists no time × treatment interaction. When no such interaction exists, a more efficient main effect only model is the following:

$$MainEffectsModel:y_{ijk}={\alpha }_0+{\alpha }_{Trt}I(i=1)+\sum _{k=1}^{T-1}{\alpha }_{k}I(time=k)+r_{ijk}+{∊}_{ijk}$$ (4)

and the hypothesis for testing the overall treatment effects now becomes H₀ : α_Trt = 0 vs H_a : α_Trt ≠ 0.

However, for a given dataset, it is not known a priori if time × treatment interaction exists. A common practice is to first identify an optimal model deemed for the data via either a model selection procedure or testing procedure. Based on the selected model, a formal statistical analysis follows. One issue with the two-step approach is that due to the stochastic nature associated with the selected model, the post-model selection inference without adjusting for the selection variation will no longer be valid. Below we describe a valid post-model selection testing procedure under the mixed effects model framework.

Post-Model Selection Statistical Inference:

We first select the optimal model using the BIC criteria from a set of J candidate models including the full model (1) and the main effects model (4) with different covariance structures. In particular, the covariance structures that we consider include compound symmetry (CS), autoregressive (AR), and unstructured (UN) covariance matrices that are commonly used in practice. However, it is straightforward to include other candidate covariance structures. Let M̂ be the selected optimal model, based on which we obtain the maximum likelihood estimates (MLE) of the parameters and make the statistical inference.

Overall Treatment Effects Testing:

To test the overall treatment effects, we propose the following test statistics where MSA stands for model selection test of overall treatment effects:

$${\zeta }_{MSA}=\{\begin{array}{cc}{\tilde{\tilde{\alpha }}}^{\prime }{\widehat{\Sigma }}^{-1}\tilde{\alpha }\hfill & \text{if}\widehat{M}\in \text{full model set}\left(1\right)\hfill \\ {({\tilde{\alpha }}_{Trt}∕SE\left({\tilde{\alpha }}_{Trt}\right))}^2\hfill & \text{if}\widehat{M}\in \text{main effects model set}\left(4\right)\hfill \end{array}\phantom{\}}$$

where ${\tilde{\alpha }}^{\prime }=({\tilde{\alpha }}_{Trt},{\tilde{\alpha }}_T,\cdots ,{\tilde{\alpha }}_{2T-2})$ is the MLE of α^′ = (α_Trt, α_T , · · · , α_2T−2) from the optimal model M̂ if it happens to be the full model (1), while ${\tilde{\alpha }}_{Trt}$ is the MLE of α_Trt from the optimal model M̂ when it happens to be the main effects model (4). The $\widehat{\Sigma }$ and $SE\left({\tilde{\alpha }}_{Trt}\right)$ are the corresponding estimated covariance matrix and standard error of $\tilde{\alpha }$ and ${\tilde{\alpha }}_{Trt}$, respectively. Details on obtaining $\widehat{\Sigma }$ and $SE\left({\tilde{\alpha }}_{Trt}\right)$ will be discussed in the next subsection. Under H₀, if the selected optimal model M̂ belongs to the full model set (1), ζ_MSA ~ χ² (T). Otherwise, ζ_MSA ~ χ² (1). Note that, with the built in model selection procedure, testing the overall treatment effects reduces to testing the last time point effect when the optimal model belongs to the main effects model set, leading to improved power, as will be shown by simulation studies in Section 3.

Last Time Point Treatment Effect Testing

In practice, it is common to test the last time point treatment effect by the following simple t-test:

$${\zeta }_t=\frac{{\widehat{\alpha }}_{Trt,t}}{SE\left({\widehat{\alpha }}_{Trt,t}\right)}$$

where ${\widehat{\alpha }}_{Trt}={\stackrel{‒}{y}}_{1.T}-{\stackrel{‒}{y}}_{0.T}$ is the sample mean difference between the two treatment groups. $SE\left({\widehat{\alpha }}_{Trt}\right)=\sqrt{\frac{{\sum }_{j=1}^{n_0}{\left(y_{0jT-{\stackrel{‒}{y}}_{0.T}}\right)}^2+{\sum }_{j=1}^{n_1}{\left(y_{1jT-{\stackrel{‒}{y}}_{1.T}}\right)}^2}{n_0+n_1-2}}$, ${\stackrel{‒}{y}}_{1.T}=\frac{1}{n_1}{\sum }_{j=1}^{n_1}{y}_{1jT}$, ${\stackrel{‒}{y}}_{0.T}=\frac{1}{n_0}{\sum }_{j=1}^{n_0}{y}_{0jT}$ and n₁ & n₀ are the number of subjects in the treated and untreated groups, respectively. A well randomized procedure guarantees that there exists no systematic difference for baseline covariates between the two comparison groups, which in turn ensures the validity of the t-test above.

In addition to the t-test, the full mixed effects model (1) along with an unstructured covariance matrix can be used to fit repeated measurement data and the following test statistics ζ_FUN (referring full mixed effects model with unstructured covariance) can be constructed for testing the last time point treatment effect:

$${\zeta }_{FUN}=\frac{{\widehat{\alpha }}_{Trt,FUN}}{SE\left({\widehat{\alpha }}_{Trt,FUN}\right)}$$

where ${\widehat{\alpha }}_{Trt,FUN}$ and $SE\left({\widehat{\alpha }}_{Trt,FUN}\right)$ are the last time point treatment effect maximum likelihood estimate from the full mixed effects model (1) using unstructured covariance matrix and its standard error, respectively.

Post-model selection analysis can be similarly restricted to test for the last time point treatment effect α_Trt in model (1) or (4) with the following statistics

$${\zeta }_{MSL}=\frac{{\tilde{\alpha }}_{Trt,\widehat{M}}}{SE\left({\tilde{\alpha }}_{Trt,\widehat{M}}\right)}$$

where ${\tilde{\alpha }}_{Trt,\widehat{M}}$ is the MLE of α_Trt from the optimal model M̂ and $SE\left({\tilde{\alpha }}_{Trt,\widehat{M}}\right)$ is the post-model selection standard error of ${\tilde{\alpha }}_{Trt,\widehat{M}}$. Under H₀, ζ_MSL ~ N(0, 1).

Restricted Cluster Bootstrapping Covariance Estimations

The covariance and variance estimation post-model selection is rather complex owing to the stochastic nature associated with the selected optimal model. Shao [9] proposed a bootstrapping procedure for simple linear regression models which we adopt here for mixed effects models. However, the empirical procedure of Shao [9] cannot be applied directly here, since observations within each subject are correlated and hence treating each observation as a resampling unit is no longer applicable. Instead, the cluster (or block) bootstrapping scheme [13, 14] can be used to preserve the correlation structure within each subject. For simplicity of presentation, we describe the estimation procedure for $\widehat{\Sigma }$, given the fact that the optimal model is from the full model set (1). The variance estimation of ${\tilde{\alpha }}_{Trt,\widehat{M}}$ can be similarly constructed. The process is defined as follows:

For a given dataset D, conduct model selection using the BIC criteria and denote the selected optimal model as M̂. Let B be the total number of bootstrapping iterations. For the b^th bootstrapped dataset, D^b (b = 1, · · · ,B), let M̂^b be the optimal model selected. If M̂^b = M̂ , let ${\tilde{\alpha }}^b$ be the MLE of α from M̂^b. The bootstrapping covariance estimate, ${\widehat{\Sigma }}_B$ of $\tilde{\alpha }$ is then calculated as:

$${\widehat{\Sigma }}_B=\frac{1}{B^{\ast }-1}\sum _{b=1}^B({\tilde{\alpha }}^b-{\stackrel{‒}{\alpha }}^b)\otimes {({\tilde{\alpha }}^b-{\stackrel{‒}{\alpha }}^b)}^{\prime }I({\widehat{M}}^b=\widehat{M})$$

where ${\stackrel{‒}{\alpha }}^b=\frac{1}{B^{\ast }}{\sum }_{b=1}^B{\tilde{\alpha }}^{b}I({\widehat{M}}^b=\widehat{M})$, $B^{\ast }={\sum }_{b=1}^{B}I({\widehat{M}}^b=\widehat{M})$ and ⨂ represents the outer product. In summary, the restricted cluster bootstrapping procedure works as follows:

• Step 1: Perform model selection on the observed dataset, D, to get the optimal model M̂.

• Step 2: Conduct cluster level resampling with replacement to get a resampled dataset and perform model selection on the resampled dataset D^b. Obtain the selected optimal model M̂_b. If M̂_b = M̂, i.e. the same model is chosen in the original model selection and the resampling, then the MLE of α, i.e. ${\tilde{\alpha }}^b$, is used for the calculation of ${\widehat{\Sigma }}_B$.

• Step 3: Repeat Step 2 B times and calculate ${\widehat{\Sigma }}_B$, i.e. the post-model selection covariance matrix estimate of $\tilde{\alpha }$.

3. Simulation Studies

To evaluate the performance of the proposed model selection test statistics ζ_MSL and ζ_MSA, we compared them with ζ_t, ζ_FUN and ζ_MBP via extensive simulations which are also used to evaluate the proposed restricted cluster bootstrapping procedure. Specifically, for testing the last time point treatment effect, we compare the proposed model selection test statistics ζ_MSL with the t-test ζ_t and full mixed effects model with unstructured covariance test statistics ζ_FUN . For overall treatment effects testing, we compare the proposed model selection test statistics ζ_MSA with the mixed effects model based likelihood ratio test statistics ζ_MBP. Numerical studies are conducted under two categories:

Case I (No Missing): Outcomes are generated according to the following mixed effects model with different time × treatment interactions to mimic real world clinical trial data:

$$y_{ijk}=-70+0.3\ast I(i=)+4\ast I(k=1)+3\ast I(k=2)+2\ast I(k=3)+I(k=4)+{\alpha }_1\ast I(i=1)I(k=1)+{\alpha }_2\ast I(i=1)I(k=2)+{\alpha }_3\ast I(i=1)I(k=3)+{\alpha }_4\ast I(i=1)I(k=4)+r_{ijk}+{∊}_{ijk}$$ (5)

Specifically, 4 sets of data are generated with 1) strong interaction (α₁ = 0.45, α₂ = 0.42, α₃ = 0.39, α₄ = 0.36); 2) moderate interaction (α₁ = 0.24, α₂ = 0.27, α₃ = 0.33, α₄ = 0.36); 3) weak interaction (α₁ = 0.1, α₂ = 0.075, α₃ = 0.05, α₄ = 0.025); and 4) no interaction where all the interaction terms are set to 0. The last time point treatment effect is set to 0.3 with total 5 post randomization repeated measurements. The random measurement error ε_ijk ~ N(0, 1) and the random cluster effect r_ij ~ N(0, ). We simulated data with various forms of Ω, including CS, AR, and UN. Simulations were also conducted for different sample sizes and correlation strength scenarios. However, similar conclusions are obtained and for ease of presentation, only the results based on the simulated data with the following compound symmetry covariance structure Ω are presented:

$$\Omega ={\left(\begin{array}{ccccc}\hfill 1\hfill & \hfill 0.4\hfill & \hfill \cdots \hfill & \hfill 0.4\hfill & \hfill 0.4\hfill \\ \hfill \hfill & \hfill 1\hfill & \hfill 0.4\hfill & \hfill \cdots \hfill & \hfill 0.4\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill 0.4\hfill & \hfill ⋮\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill & \hfill 0.4\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1\hfill \end{array}\right)}_{5\times 5}$$

For each setting, the total number of simulations is set to 1000. Results for the last time point treatment effect and the overall treatment effects testing with 100 subjects in each treatment arm are given in Tables 1 and 2, respectively.

Table 1.

Last Time Point Treatment Effect Testing without Missing^a

Data Model	Interaction	Statisticsb	Power	Type I Error
Full (CS)	Strong	ζ t	0.336	0.044
		ζ FUN	0.343	0.046
		ζ MSL	0.981	0.048
	Moderate	ζ t	0.336	0.044
		ζ FUN	0.343	0.046
		ζ MSL	0.987	0.048
	Weak	ζ t	0.336	0.044
		ζ FUN	0.343	0.046
		ζ MSL	0.834	0.048
Main Effects (CS)	None	ζ t	0.336	0.044
		ζ FUN	0.343	0.046
		ζ MSL	0.710	0.048

^aresults based on 1000 simulations with 100 subjects at each treatment arm

^bmodel selection via BIC with 200 bootstrap resampling

ζ_t: t-test for last time point effect

ζ_FUN: test last time point effect via full mixed effect model with UN covariance

ζ_MSL: model selection test statistics for testing last time point effect

Table 2.

Overall Treatment Effects Testing without Missing^a

Data Model	Interaction	Statisticsb	Power	Type I Error
Full (CS)	Strong	ζ MBP	0.996	0.044
		ζ MSA	1.000	0.048
	Moderate	ζ MBP	0.967	0.044
		ζ MSA	0.995	0.048
	Weak	ζ MBP	0.621	0.044
		ζ MSA	0.834	0.048
Main Effects (CS)	None	ζ MBP	0.479	0.044
		ζ MSA	0.710	0.048

^aresults based on 1000 simulations with 100 subjects at each treatment arm

^bmodel selection via BIC with 200 bootstrap resampling

ζ_MBP: mixed effects model based likelihood ratio test for overall effects

ζ_MBP: model selection statistics for testing overall treatment effects

From the “Type I Error” column of Table 1, it is clear that the type I errors of the three tests (i.e. ζ_t, ζ_FUN , and ζ_MSL) are well controlled near the nominal level 0.05. Examining the column of “Power” reveals that the proposed model selection test statistics ζ_MSL is consistently more powerful than the t-test ζ_t or the full mixed effects model test statistic ζ_FUN. This observation holds whether the data are generated from the full model or main effects model, or when time × treatment interaction is strong or weak. For example, for data generated from the main effects model, the power of ζ_t is 0.336 and 0.343 for ζ_FUN while the power of ζ_MSL is 0.71, more than doubled. Similarly, for data generated from the full model (5) with weak time × treatment interaction, the power gain of ζ_MSL is even more evident: 0.834 for ζ_MSL versus 0.336 for ζ_t and 0.343 for ζ_FUN . This simulation result also demonstrates that there is almost no gain for using ζ_FUN over ζ_t to test the last time point treatment effect. Note, the term of “strong”, “moderate”, and “weak” that describe the interaction are all in a relative sense. Even for the “strong” interaction setting, we purposely set the interaction to be strong but not in an overwhelming way such that the full mixed effects model is not uniformly selected. Otherwise, ζ_MSL and ζ_FUN will end up with the same or similar power.

Examining Table 2 for the overall treatment effects testing, the type I error rates for both test statistics, i.e. ζ_MBP and ζ_MSA, are controlled near the nominal level 0.05. Checking the “Power” column in Table 2 again further reveals that the proposed test statistics ζ_MSA is much more powerful than ζ_MBP when the data are generated from the main effects model. A clear pattern is that the weaker time × treatment interaction is, the more power ζ_MSA gains over ζ_MBP is. For instance, the power of ζ_MBP is 0.479 and 0.71 for ζ_MSA when data are from the main effects model. When time × treatment interactions are relatively strong, the two tests are comparable.

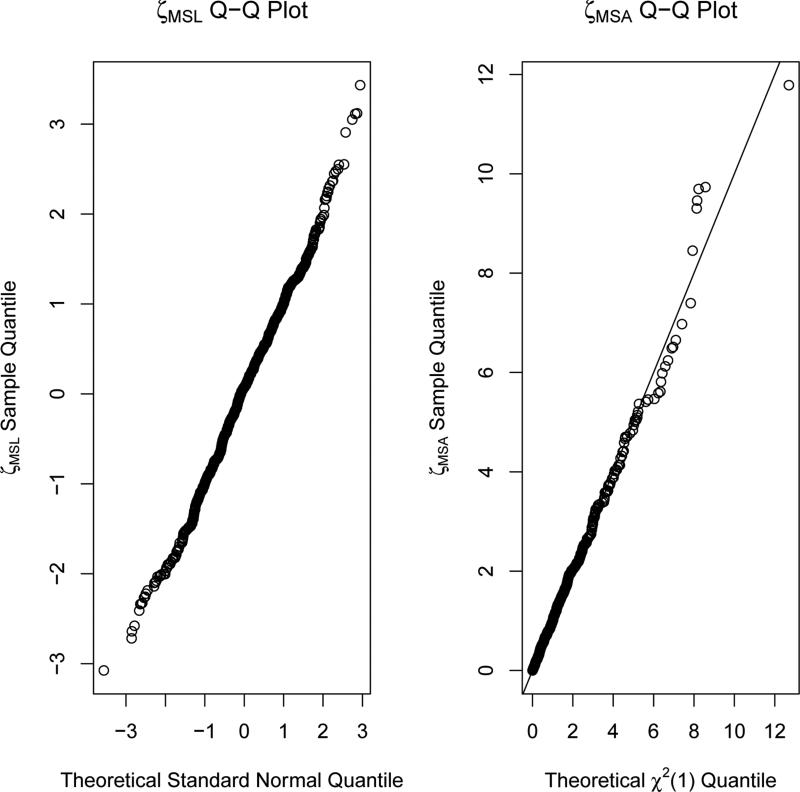
To investigate the performance in controlling the type I error rate for the proposed test statistics, we generated Q-Q plots of the proposed test statistics ζ_MSL and ζ_MSA under the null. These plots are presented in Figure 1 and they follow the theoretical distributions quite well, demonstrating their good performance for controlling the type I error rate in testing the last time point and overall treatment effects.

Figure 1.

Model Selection Test Statistics Distributions Under the Null

In practice, researchers could test for interaction first. If the interaction term comes out non-significant, the reduced main effects model is then used for assessing the treatment effect. However, this two-stage procedure is essentially another variable/model selection-based procedure and again has the stochastic nature associated with the selected model. Due to the stochastic nature of determining whether the full or main effects model is used, this procedure could fail to control the type I error rate. In the above simulation settings for Table 1 and 2, the type I error rate of this two-stage procedure is 0.085 while it is 0.048 for our proposed test statistics.

To further compare the proposed strategy with the ANCOVA method for testing the treatment effect at the last time point as suggested by one of the reviewers, we design the following simulation setting with the baseline measurement as a covariate and the response as the raw measurement at each post-baseline time point, instead of the change from the baseline.

$$x_{ijk}=-70+0.5\ast x_{ij0}+0.3\ast I(i=1)+4\ast I(k=1)+3\ast I(k=2)+2\ast I(k=3)+I(k=4)+{\alpha }_1\ast I(i=1)I(k=1)+{\alpha }_2\ast I(i=1)I(k=2)+{\alpha }_3\ast I(i=1)I(k=3)+{\alpha }_4\ast I(i=1)I(k=4)+r_{ijk}+{∊}_{ijk}$$

where x_ij0 ~ N(0, 1). All other specifications are the same as that in model (5). When testing the last time point effect, we consider the ANCOVA model test statistics ${\zeta }_{ANCOVA}=\frac{{\widehat{\alpha }}_{Trt}}{SE\left({\widehat{\alpha }}_{Trt}\right)}$ where ${\widehat{\alpha }}_{Trt}$ is the MLE from the following ANCOVA model: x_ijT = α₀ + α_TrtI(i = 1) + α_xx_ij0 + ε_ij. Correspondingly, for all mixed effects models, the baseline response measurement x_ij0 is included as a fixed effect covariate. The model selection procedures proceed exactly the same as mentioned previously. Simulation results are presented in Tables 3 and 4 for testing the last time point and overall treatment effects.

Table 3.

Last Time Point Treatment Effect Testing with Baseline as a Covariate^a

Data Model	Interaction	Statisticsb	Power	Type I Error
Full (CS)	Strong	ζ t	0.531	0.059
		ζ ANCOVA	0.573	0.053
		ζ FUN	0.579	0.053
		ζ MSL	0.951	0.042
	Moderate	ζ t	0.531	0.059
		ζ ANCOVA	0.573	0.053
		ζ FUN	0.579	0.053
		ζ MSL	0.988	0.042
	Weak	ζ t	0.531	0.059
		ζ ANCOVA	0.573	0.053
		ζ FUN	0.579	0.053
		ζ MSL	0.988	0.042
Main Effects (CS)	None	ζ t	0.531	0.059
		ζ ANCOVA	0.573	0.053
		ζ FUN	0.579	0.053
		ζ MSL	0.942	0.042

^aresults based on 1000 simulations with 100 subjects at each treatment arm

^bmodel selection via BIC with 200 bootstrap resampling

ζ_t: t-test for last time point effect

ζ_ANCOVA: test last time point effect via ANCOVA model

ζ_FUN: test last time point effect via full mixed effect model with UN covariance

ζ_MSL: model selection test statistics for testing last time point effect

Table 4.

Overall Treatment Effects Testing with Baseline as a Covariate^a

Data Model	Interaction	Statisticsb	Power	Type I Error
Full (CS)	Strong	ζ MBP	1.000	0.047
		ζ MSA	1.000	0.042
	Moderate	ζ MBP	1.000	0.047
		ζ MSA	1.000	0.042
	Weak	ζ MBP	0.917	0.047
		ζ MSA	0.988	0.042
Main Effects (CS)	None	ζ MBP	0.775	0.047
		ζ MSA	0.842	0.042

^aresults based on 1000 simulations with 100 subjects at each treatment arm

^bmodel selection via BIC with 200 bootstrap resampling

ζ_MBP: mixed effects model based likelihood ratio test for overall effects

ζ_MBP: model selection statistics for testing overall treatment effects

Inspecting Table 3, we see that the ANCOVA model is more powerful than the t-test method. The proposed test statistic, ζ_MSL, still has the best performance among the four test statistics while controlling the type I error rate at the same level. Results in Table 4 show that the proposed test statistic ζ_MSA outperforms ζ_MBP for testing the overall treatment effects when the raw score is used as the outcome instead of the change from the baseline while the baseline measurement is treated as a fixed effects covariate.

Case II (Missing Data Scenarios): Under the repeated measurement design, missing data are frequently observed due to, for example, patient withdrawal related or unrelated to their treatment or response sequence. Statistical analysis with missing data becomes more complicated and challenging. We next investigate the impact of missing data on the proposed tests. The first scenario is missing completely at random (MCAR) where the numbers of missing observations per treatment arm are (5, 5, 5, 5, 20) for the five measurement time points, respectively, and missing data are randomly selected across all samples. Thus the missing probability does not depend on any observed or unobserved variables. In this simulation, data are generated in the same manner as those in Tables 1 and 2 except that we randomly mark some observations as missing. The results for data with moderate time × treatment interaction or no interaction are presented in Table 5.

Table 5.

Missing Completely At Random (MCAR)^a

Data Model	Interaction	Statisticsb	Hypothesis Test	Powerc	Type I Errorc
Full (CS)	Moderate	ζ t	Last Time Point	0.267(0.336)	0.042(0.044)
		ζ FUN		0.288(0.343)	0.046(0.046)
		ζ MSL		0.989(0.987)	0.050(0.048)
		ζ MBP	Overall Effect	0.961(0.967)	0.038(0.044)
		ζ MSA		0.995(0.995)	0.050(0.048)
Main Effects (CS)	None	ζ t	Last Time Point	0.267(0.336)	0.042(0.044)
		ζ FUN		0.288(0.343)	0.046(0.046)
		ζ MSL		0.699(0.710)	0.050(0.048)
		ζ MBP	Overall Effect	0.459(0.479)	0.038(0.044)
		ζ MSA		0.699(0.710)	0.050(0.048)

^aresults based on 1000 simulations with 100 subjects at each treatment arm

^bmodel selection via BIC with 200 bootstrap resampling

^cvalues inside parentheses are based on no missing scenario

ζ_t: t-test for last time point effect

ζ_FUN: test last time point effect via full mixed effect model with UN covariance

ζ_MSL: model selection test statistics for testing last time point effect

ζ_MBP: mixed effects model based likelihood ratio test for overall effects

ζ_MSA: model selection statistics for testing overall effects

Comparing the numbers in Table 5 outside and inside the parentheses, which correspond to the analysis results from data with and without missing observations, it shows that MCAR had minimal impact on either type I error or power for both the mixed effects model based and the proposed model selection based test statistics. This is probably due to the relatively small proportion of missing observations. However, the changes in type I error and power are noticeable for the simple t-test, i.e. type I error is slightly inflated and power drops noticeably with missing data. The power of ζ_FUN in testing the last time point effect suffers noticeably when there exist data missing completely at random. This demonstrates the robustness of the proposed methods in dealing with MCAR. Furthermore, the power gains as we observed previously for ζ_MSA over ζ_MBP and ζ_MSL over ζ_t & ζ_FUN still hold which further reveal the efficiency and robustness of the proposed methods.

For many clinical studies, missing mechanisms may not be completely at random and depend on some observed baseline covariates, or missing at random (MAR). Next we investigate the performance of the proposed framework under MAR. In this simulation, data are generated similarly to those in Table 5 except that an additional covariate u_ij, associated with the response variable, is introduced and used for inducing missing data:

$$y_{ijk}=-70+0.3\ast I(i=1)+0.3\ast u_{ij}+4\ast I(k=1)+3\ast I(k=2)+2\ast I(k=3)+I(k=4)+{\alpha }_1\ast I(i=1)I(k=1)+{\alpha }_2\ast I(i=1)I(k=2)+{\alpha }_3\ast I(i=1)I(k=3)+{\alpha }_4\ast I(i=1)I(k=4)+r_{ijk}+{∊}_{ijk}$$ (6)

where u_ij ~ Unif(−1, 1). The missing data are generated as: for the treatment arm 0 and one of the 1^st four time points k (k = 1, 2, 3, 4), five subjects with u_ij > 0 are randomly selected to have their observations set to missing, while for the treatment arm 1, 5 subjects with u_ij < 0 are randomly selected to create missing observations. For the last time point, we randomly select 20 subjects in the treatment arm 0 with u_ij > 0.5 and another 20 subjects from the treatment arm 1 with u_ij < −0.5 and set their observations to missing. We set α₁, · · · , α₄ to be moderate or 0.

Instead of imputing missing data, we analyze the simulated data with models (1), (3) and (4) except that we add baseline u_ij as a covariate into these models. Under this setting, the baseline covariate u_ij is imbalanced and becomes a confounding variable. As a further comparison, when testing the last time point effect, we include the ANCOVA model test statistics ${\zeta }_{ANCOVA}=\frac{{\widehat{\alpha }}_{Trt}}{SE\left({\widehat{\alpha }}_{Trt}\right)}$ where ${\widehat{\alpha }}_{Trt}$ is the MLE from the following ANCOVA model: y_ijT = α₀ + α_TrtI(i = 1) + α_uu_ij + ε_ij. The simulation results are presented in Table 6.

Table 6.

Missing At Random (MAR)^a

Data Model	Interaction	Statisticsb	Hypothesis Test	Powerc	Type I Errorc
Full (CS)	Moderate	ζ t	Last Time Point	0.193(0.328)	0.060(0.047)
		ζ ANCOVA		0.285(0.327)	0.064(0.044)
		ζ FUN		0.310(0.343)	0.049(0.049)
		ζ MSL		0.989(0.987)	0.054(0.046)
		ζ MBP	Overall Effect	0.968(0.965)	0.054(0.044)
		ζ MSA		0.995(0.995)	0.054(0.046)
Main Effects (CS)	None	ζ t	Last Time Point	0.176(0.325)	0.060(0.047)
		ζ ANCOVA		0.265(0.331)	0.064(0.044)
		ζ FUN		0.303(0.338)	0.049(0.049)
		ζ MSL		0.689(0.710)	0.054(0.046)
		ζ MBP	Overall Effect	0.463(0.486)	0.054(0.044)
		ζ MSA		0.689(0.710)	0.054(0.046)

^aresults based on 1000 simulations with 100 subjects at each treatment arm

^bmodel selection via BIC with 200 bootstrap resampling

^cvalues inside parentheses are based on no missing scenario

ζ_t: t-test for last time point effect

ζ_ANCOVA: test last time point effect via ANCOVA model

ζ_FUN: test last time point effect via full mixed effect model with UN covariance

ζ_MSL: model selection test statistics for testing last time point effect

ζ_MBP: mixed effects model based likelihood ratio test for overall effects

ζ_MSA: model selection statistics for testing overall effects

Comparing the numbers in Table 6 outside and inside the parentheses which correspond to the analysis results from the data with and without missing observations, it demonstrates that MAR appears to have an effect on the type I error rate for the t-test. For example, for the full data without missing observations, the type I error is 0.047 but this number is inflated to 0.06 with missing data for the situation with moderate interaction. By contrast, the type I errors for the proposed methods are well controlled. Further, the impact of missing data on the power is larger for the t-test and ζ_FUN than that for the proposed methods. For instance, the power, 0.325 for the data without missing, is sharply reduced to 0.176 with missing data for the scenario of no interaction. In this scenario, the power change using ζ_FUN for testing the last time point effect is minor, i.e. from 0.338 to 0.303. Also the power gain of ζ_MSA over ζ_MBP is consistent with the results reported in the previous tables. The power gain of ζ_MSL over t-test and ζ_FUN is even more dramatic, further indicating the efficiency and robustness of the proposed methods. Due to the missing data, the baseline covariates become imbalanced and confounded with the response values. Compared with the t-test, ANCOVA statistics are more robust to missing data by adjusting for imbalanced baseline covariates as confounding factors [3]. Clearly, the t-test is invalid under this scenario since it violates the randomized controlled trial assumption that there exists no systematic differences for the baseline covariates.

In practice, missing mechanisms can be more complicated than MAR for repeated measurement studies where missing mechanism depends on unobserved variables, resulting in the so called missing not at random (MNAR) data. Our next simulation considers MNAR data. Specifically, we analyze the same data as simulated under MAR, except that the baseline covariate u_ij is now assumed to be unobserved, but instead we have another covariate v_ij which is observed and correlated with u_ij as follows:

$$v_{ij}\sim \{\begin{array}{cc}N(1,1)\hfill & \text{if}{u}_{ij}>0\hfill \\ N(-1,1)\hfill & \text{if}{u}_{ij}\le 0\hfill \end{array}\phantom{\}}$$

Similar to the analysis of MAR data, we analyze the simulated data with models (1), (3) and (4) but we add the observed baseline v_ij instead of u_ij as a covariate into these models. The simulation results are presented in Table 7.

Table 7.

Missing Not At Random (MNAR)^a

Data Model	Interaction	Statisticsb	Hypothesis Test	Powerc	Type I Errorc
Full (CS)	Moderate	ζ t	Last Time Point	0.171(0.327)	0.061(0.043)
		ζ FUN		0.251(0.342)	0.062(0.051)
		ζ MSL		0.989(0.985)	0.051(0.050)
		ζ MBP	Overall Effect	0.955(0.963)	0.052(0.048)
		ζ MSA		0.994(0.994)	0.051(0.050)
Main Effects (CS)	None	ζ t	Last Time Point	0.168(0.338)	0.061(0.043)
		ζ FUN		0.262(0.347)	0.062(0.051)
		ζ MSL		0.671(0.690)	0.051(0.050)
		ζ MBP	Overall Effect	0.430(0.476)	0.052(0.048)
		ζ MSA		0.671(0.690)	0.051(0.050)

^aresults based on 1000 simulations with 100 subjects at each treatment arm

^bmodel selection via BIC with 200 bootstrap resampling

^cvalues inside parentheses are based on no missing scenario

ζ_t: t-test for last time point effect

ζ_FUN: test last time point effect via full mixed effect model with UN covariance

ζ_MSL: model selection test statistics for testing last time point effect

ζ_MBP: mixed effects model based likelihood ratio test for overall effects

ζ_MSA: model selection statistics for testing overall effects

From Table 7, it is evident that similar conclusions hold here. The t-test is sensitive to MNAR data for both the type I error and power. However, the proposed methods are robust to missing data and have well controlled type I error. Again, the power gain for ζ_MSA over ζ_MBP and ζ_MSL over t-test and ζ_FUN under MNAR persists as seen previously. In practice, we can adjust for these baseline values by including them as covariates in the proposed analysis procedures. Provided they are good surrogate variables of the unobserved covariates related to the missing data, they can help to reduce potential bias in the treatment effect analysis and boost the testing power.

4. Real Data Analysis

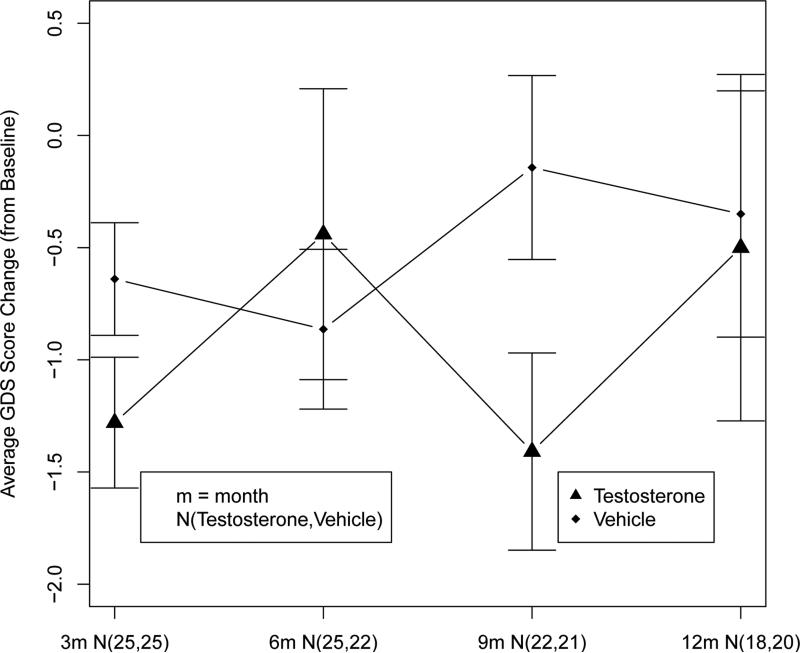
To illustrate a practical application of the proposed methods, we apply them to a clinical trial [15] regarding the cognitive effect of testosterone on geriatric men (age ≥ 65). In this study, 60 subjects were recruited and randomly assigned to two treatment groups, testosterone (Trt = 1) and vehicle (Trt = 0). The primary outcome of the study is the geriatric depression scale (GDS) which is continuous and ranges from 0 to 30. Higher GDS scores indicate more severe depression. GDSs for the subjects were repeatedly measured at baseline, 3, 6, 9, and 12 months. Our primary interest is to compare the overall treatment effects between the two treatment groups across time.

The summary of the data is depicted in Figure 2 where the average GDS scores change from baseline for each of the time by treatment group is presented. It seems that there exists some time by treatment interactions although the interaction terms are not significantly strong enough to be detected by the BIC model selection procedure or the likelihood ratio test statistics (p-value=0.10).

Figure 2.

Average GDS Score Change (from Baseline) Comparison

Based on BIC model selection criteria, the main effects only model with unstructured covariance structure best fits this dataset. Therefore, the overall treatment effects testing reduces to testing the hypothesis H₀ : α_Trt = 0 vs H_a : α_Trt ≠ 0 by using the proposed test statistic ${\zeta }_{MAS}={({\tilde{\alpha }}_{Trt}∕SE\left({\tilde{\alpha }}_{Trt}\right))}^2$. With 200 rounds restricted cluster bootstrapping for variance estimates, we conclude that there exists an overall significant (p-value=0.04) difference between the two treatment groups. For a further comparison, we also tested the overall treatment effects using ζ_MBP with the grand full mixed effects model, and the p-value is 0.04. This result is consistent with what we observed in the simulation study, i.e. the performance of ζ_MBP is comparable to that of ζ_MSA in testing the overall treatment effects when the time by treatment interaction is not weak. However, if the t-test was used to evaluate the treatment effect with only the last time point data, we would obtain an insignificant treatment effect (p-value=0.87).

5. Discussion

In this paper, we proposed a new analytic framework for repeated measurement randomized trial data based on the mixed effects model. The proposed analysis scheme combines a model selection procedure with a testing procedure. The model selection procedure makes use of the information from the optimal model deemed for the data for testing treatment effect(s) to increase power. To ensure the validity of the post-model selection inference, we further developed a restricted cluster bootstrapping variance estimation strategy to estimate the (co)variance of the treatment effect estimate(s). Our proposed test statistics take into account the stochastic nature of the model selection process such that the proposed test statistics asymptotically follow χ² distributions under the null. This provides us the validity to control the type I error rate. As shown by our simulations, the proposed method outperforms the simple t-test, the grand full mixed effects model and the likelihood ratio test (LRT) between the grand full model and null model. The power gain for our proposed method over the t-test and the grand full mixed effects model for testing the last time point effect is substantial across all of our simulation scenarios. Compared to the LRT from the full mixed effects model, our method is superior under most of the simulation scenarios, except that the two methods are comparable when the data are generated from the full model with strong time by treatment interaction. In practice, sometimes the clinical trial protocol may specify the use of the full mixed effects model to test the last time point treatment effect regardless of whether the full mixed effects model best fits the data or not. For protocol integrity purposes, the proposed methodologies no longer apply. It is worth mentioning that in the repeated measurement clinical trial setting, an alternative to the mixed effects model approach considered in this paper, is a (weighted) summary measures method, which uses the (weighted) post-baseline measurements mean difference as the estimator of the treatment effects, and it can be efficient under some scenarios. In this regard, more details about these schemes could be found in [16, 17]. Furthermore, the performance of ANCOVA model on the mean of all post-baseline treatment values for evaluating the overall treatment effects deserves further investigation.

The simulations also reveal that the substantial power gain of the proposed methods over the t-test and the LRT from the mixed effects model remains for data simulated under various missing mechanisms. The proposed analytic procedure is more robust to missing data than the simple t-test because of its flexibility in adding covariates related to missing data directly or indirectly (i.e. surrogate variables) to reduce the bias due to missing data. However, this paper does not intend to comprehensively resolve the missing data problem and our simulations on missing data are simple and used strictly to demonstrate the performance of the proposed method over the other existing methods. How the proposed methods behave for data under more complicated missing mechanisms deserves further attention and is beyond the scope of this paper. Note, the proposed analysis framework is based on continuous data. Extending the proposed framework to other response data types, such as binary responses or censored survival data should be investigated.