Change Point Testing in Logistic Regression Models with Interaction Term

Abstract

A threshold effect takes place in situations where the relationship between an outcome variable and a predictor variable changes as the predictor value crosses a certain threshold/change point. Threshold effects are often plausible in a complex biological system, especially in defining immune responses that are protective against infections such as HIV-1, which motivates the current work. We study two hypothesis testing problems in change point models. We first compare three different approaches to obtaining a p-value for the maximum of scores test in a logistic regression model with change point variable as a main effect. Next, we study the testing problem in a logistic regression model with the change point variable both as a main effect and as part of an interaction term. We propose a test based on the maximum of likelihood ratios test statistic and obtain its reference distribution through a Monte Carlo method. We also propose a maximum of weighted scores test that can be more powerful than the maximum of likelihood ratios test when we know the direction of the interaction effect. In simulation studies, we show that the proposed tests have correct type I error and higher power than several existing methods. We illustrate the application of change point model-based testing methods in a recent study of immune responses that are associated with the risk of mother to child transmission (MTCT) of HIV-1.

1. Background

In this paper we study a change point model, also known as a threshold model, in which a covariate has no effect before reaching an unknown threshold and has a constant effect thereafter. This type of change point model is a popular approach for handling nonlinearity in the relationship between two variables without over-parameterization, and has been widely used in econometrics, quality control, human genetics, and many more fields of study. Our interests in change point models arise from efforts to find immune response biomarkers that associate with HIV-1 infection in the vaccinated subjects [1] or mother-to-child transmission (MTCT) [2]. Several factors motivate us to consider change point models. First, it is often unclear how to properly transform a continuous immune response variable to be used in the regression. Second, we often create score variables that are combinations of individual immune response measurements. The relationship between the outcome variable and a score is more likely to be nonlinear than individual components of the score. Third, our current understanding of how immune systems operate is consistent with the existence of a threshold effect, i.e. only an immune response above a certain quality and quantity threshold can result in protection from HIV-1 infection or transmission.

A particular focus of this paper is change point models in which the thresholded covariate appears both in a main effect term and an interaction term. Interaction models have received a lot of attention lately in human genetics research as a tool to study gene × environment interaction. In the HIV-1 vaccine research field, studying interaction is important because each immune response variable measures one aspect of the immune responses, and different aspects of the multifaceted immune responses may need to work together synergistically to offer protection [2]. Alternatively, one aspect of the immune responses may prevent other aspects of the immune responses from working effectively against the virus [1].

One challenge in hypothesis testing for change point models is that under the null hypothesis, the threshold parameter becomes unidentifiable. This type of problem, highlighted by Davies [3, 4, 5], has motivated much previous works in the biostatistical literature on change point testing [3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14]. However, some methods, e.g. [4], don’t apply to the model we study in this paper, which is discontinuous in the change point variable. Furthermore, some of the proposed methods, e.g. [11], have not had type I error evaluated by simulation studies in finite samples. In Section 2, we compare three approaches to performing a maximum of scores test in the relatively simple setting of a logistic regression model with change point in the main effect only.

In Section 3, we propose a maximum of weighted scores test and a maximum of likelihood ratios test for a change point model with interaction term. Of particular relevance to Section 3 is the work by Koziol and Wu [7], which was concerned with identifying a change point in a predictor that modifies the effect of treatment in a randomized two-arm clinical trial. In addition, Pastor-Barriuso, Guallar and Coresh (2003) [10] proposed a general, maximum of likelihood ratios test for change point models that can also be applied with an interaction term.

In Section 4, we conduct simulation studies to study the type I error of the proposed tests, and compare their power with some commonly used non-change point model methods in data analysis. In Section 5, we illustrate the proposed methods in a study of humoral immune responses that are associated with the risk of HIV-1 MTCT. We end with a discussion in Section 6.

2. Maximum of Scores Test for Models with Main Effect Only

We start our investigation with a simple logistic model with a change point in a main effect, and compare three approaches to performing a maximum of scores test. Consider the following model

$$\text{logit}\{\text{Pr}(Y=1)\}={\alpha }^{T}z+\beta I(x>e),$$ (1)

where Y is a binary variable, z is a vector of covariates, x is the change point variable. α is the vector of coefficients associated with z, β is the effect size associated with the change point variable, and e is the threshold parameter. We are interested in testing the null hypothesis β = 0. The score test, which is based on the behavior of the test statistic under the null, is a natural choice here because the score statistics are asymptotically normally distributed. Let L_i denote the log likelihood for the i^th observation. For each e, the score with respect to β evaluated at β = 0 is

$${\frac{\partial L_i}{\partial \beta }|}_{\beta =0}=I(x_i>e)\{y_i-\frac{1}{1+\text{exp}(-{\alpha }^T{z}_i)}\}=I(x_i>e)(y_i-{\mu }_i),$$

where μ_i = expit (α^T z_i). For a given e, let k = #{x_i > e}. Denote w_i (e) = 1/k if x_i > e and 0 otherwise. Let w (e) = [w₁ (e), …, w_n (e)]^T. Plug in the maximum likelihood estimate for α under the null model and we have the score statistics, as a function of e,

$$S_1(e)=w{(e)}^T(Y-\hat{\mu })=\frac{1}{k}\sum _{i:x_i>e}(y_i-{\hat{\mu }}_i).$$ (2)

The score statistics is simply the sum of residuals for all observations with x greater than the threshold. This makes intuitive sense because when the data are from a model with β > 0, the residuals are likely to be greater than 0 for observations with x greater than the true threshold and less than 0 for observations with x less than the true threshold.

The score statistics depends on the threshold parameter which cannot be estimated under the null because it is not part of the null model. If there is knowledge about the plausible value for e in a specific application, we will wish to use that knowledge. More often we have no idea where the threshold may be, and a common strategy is to take the maximum of the score statistics evaluated at a sequence of thresholds e₁, …, e_M chosen to be evenly spaced on the scale of sample quantiles. To avoid edge effects, we set e₁ and e_M to be 10% and 90% quantiles, respectively. The asymptotic joint distribution of [S₁ (e₁) ⋯ S₁ (e_M)]^T under the null model is given by the following theorem. The proof is straightforward using standard generalized linear model theory.

Theorem 1

Denote W₁ = [w (e₁) ⋯ w (e_M)] Under the null,

$$\sqrt{n}{[S_1(e_1)\cdots S_1(e_M)]}^T=\sqrt{n}{W}_1^T(Y-\hat{\mu })\Rightarrow N(0,V_1)$$

where $V_1=W_1^{T}AD{A}^T{W}_1$,D = diag {μ(1 − μ)} and A = I − DZ (Z^TDZ)⁻¹ Z^T.

Let μ̂ = expit (α̂^T z) and D̂ = diag {μ̂ (1 − μ̂)}, where α̂ is the estimate under the null. For any given threshold e, define V̂₁ (e) = w (e)^T ÂD̂Âw (e) and $T(e)=\sqrt{n}|S_1(e)|/\sqrt{{\hat{V}}_1(e)}$. The distribution of T (e) can be approximated by a normal distribution with mean 0 and variance 1.

The first approach to testing is based on a maximum of scores statistic defined as

$$T_{\text{max}}=\text{max}\{T(e_1),\cdots ,T(e_M)\}.$$ (3)

The distribution of T_max can be approximated by the maximum of a multivariate normal distribution with mean 0, variance 1 and a correlation matrix derived from V̂₁, and the p-value can be obtained by comparing T_max with random samples from this multivariate normal distribution. The power of this test statistic improves with the density of the chosen thresholds; the greater M is, the greater the opportunity to maximize power. However, as M increases, the correlation between neighboring T (e)’s increases and the incremental gain in the power of T_max attenuates. Tests based on T_max require the simulation of a multivariate normal distribution with an estimated correlation matrix.

In the second approach, we explore the use of asymptotic theory that passes the need to perform random sampling for testing. If we let M go to infinity, under suitable regularity conditions, the distribution of T (·) converges to a mean 0 Gaussian random process and the finite dimensional distribution of {T (e₁), …, T (e_M)} is the same as given in Theorem 1. One potential method is to estimate an upper bound for the tail probability Pr (T_max > c). Davies [4] (Section 2) recommends using the inequality

$$\text{Pr}(\text{sup}T(e)>c:ℒ\le e\le 𝒰)\le \mathrm{\Phi }(-c)+\text{exp}(-c^2/2){\int }_{ℒ}^{𝒰}\frac{1}{\sqrt{8\pi }}\mathrm{E}\left|\frac{\partial T}{\partial e}\right|de,$$

where Φ is the normal cumulative distribution function. This approach does not work however, because it requires taking the derivative of T (e) with respect to e and the upper bound explodes. Instead we apply results from Antoch et al. [11], which provides an analytical approximation of the tail probability of the supremum of normalized scores. Let $T_{\text{sup}}^T={\text{sup}}_e\{|S_1(e)|/\sqrt{1^T\hat{D}1k(e)\{n-k(e)\}/n}\}$ where we write k as k (e) to make its dependence on e explicit. Adapting Theorem 3.1 and Remark 3.2 of Antoch et al. [11], we have

$$\text{Pr}(T_{\text{sup}}^A<\sqrt{2\text{log log}n}+\frac{\text{log log log}n}{2\sqrt{2\text{log log}n}}+\frac{t-\frac{1}{2}\text{log}\pi }{\sqrt{2\text{log log}n}})\to \text{exp}\{-2\text{exp}(-t)\}$$

as n → ∞. Let $t=\sqrt{2\text{log log}n}{T}_{\text{max}}^A-2\text{log log}n-\frac{1}{2}\text{log log log}n+\frac{1}{2}\text{log}\pi$. The p-value associated with an observed $T_{\text{sup}}^A$ is then 1 − exp {−2 exp (−t)}.

The third approach we explore is also asymptotic and does not require Monte Carlo sampling. Let $U={\hat{V}}_1^{-1/2}\sqrt{n}{[S_1(e_1)\cdots S_1(e_M)]}^T$. The distribution of U can be approximated by a multivariate standard normal distribution, and we obtain a p value by comparing U^TU with a chi-squared distribution of degree M.

Simulation study results from Section 4 indicate that the first of these approaches, the Monte Carlo-based methods for obtaining p-values, has the right type I error rate, and a modestly large M is sufficient to achieve high statistical power. The second and third approaches, on the other hand, have unacceptably conservative type I error in the simulation studies of the model with main effects only.

3. Hypothesis Testing for Change Point Models with Interaction Term

We now study hypothesis testing for a logistic regression model with the change point variable appearing both as a main effect and as part of an interaction term

$$\text{logit}\{\text{Pr}(Y=1)\}={\alpha }^{T}z+{\beta }_{1}I(x>e)+{\beta }_2{z}_{1}I(x>e),$$ (4)

where z₁ is a component of the covariate vector z, β₁ is the effect size associated with the main effect of the change point variable, and β₂ is the effect size associated with the interaction term involving the change point variable. Also denote β = [β₁ β₂]^T. We are interested in testing β₁ = β₂ = 0. Although the null model is the same as the null model in testing β = 0 in model (1), the test here can potentially be a more powerful test against the null because sometimes we may fail to detect a weak main effect, but succeed in detecting a weak main effect and a weak interaction effect together.

The score vector with respect to β₁ and β₂ evaluated at β₁ = β₂ = 0 is

$${\left[\begin{array}{c}\hfill \partial L_i/\partial {\beta }_1\hfill \\ \hfill \partial L_i/\partial {\beta }_2\hfill \end{array}\right]|}_{{\beta }_1={\beta }_2=0}=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill z_{i,1}\hfill \end{array}\right]I(x_i>e)(y_i-{\mu }_i).$$

Plug in the estimate for μ_i in the null model and we have a vector of score statistics [S₁ (e) S₂ (e)], where S₁ (e) is as defined in (2) and S₂ (e) is defined as follows:

$$S_2(e)={(w*z_1)}^T(Y-\hat{\mu })=\frac{1}{k}\sum _{i:x_i>e}{z}_{1,i}(y_i-{\hat{\mu }}_i),$$ (5)

where w * z₁ is element-wise multiplication of two vectors w and z₁. For a sequence of M potential thresholds, we can form a score statistics vector of length 2M. Its asymptotic joint distribution under the composite null β₁ = β₂ = 0 is given by the following theorem. The proof is similar to the proof of theorem 1 and follows from generalized linear model theory.

Theorem 2

Under the null β₁ = β₂ = 0,

$$\sqrt{n}{[S_1(e_1)S_2(e_1)\cdots S_1(e_M)S_2(e_M)]}^T=\sqrt{n}{W}_2^T(Y-\hat{\mu })\Rightarrow N(0,V_2),$$

where W₂ = [w (e₁) w (e₁) * z₁ ⋯ w (e_M) w (e_M) * z₁] is a n × 2M matrix, D = diag {μ (1 − μ)}, A = I − DZ (Z^TDZ)⁻¹ Z^T, ADA^T is a n × n matrix, and $V_2=W_2^T(AD{A}^T)W_2$

We propose two approaches to test the null hypothesis β₁ = β₂ = 0. First, we take a maximum of likelihood ratios approach. Under a fixed threshold e*, model (4) becomes

$$\text{logit}\{\text{Pr}(Y=1)\}={\alpha }^{T}z+{\beta }_{1}I(x>e^{*})+{\beta }_2{z}_{1}I(x>e^{*}).$$ (6)

Let the likelihood ratio statistic for comparing model (6) and the null model be Q(e*). For fixed e*, the standard regularity conditions hold and thus Q(e*) converges to a chi-squared distribution with two degrees of freedom under the null hypothesis. To account for unknown threshold location, we propose the maximum of likelihood ratios statistic

$$L{R}_{\text{max}}=\text{max}\{Q(e_1),\cdots ,Q(e_M)\}.$$

This type of approach has been used in other settings. For example, Pastor-Barriuso, Guallar and Coresh (2003) [10] used it to make inference for change point models that allow a variable to have different linear effects before and after the change point. To obtain p values, Pastor-Barriuso et al. applied an improved, second-order Bonferroni inequality to find an upper bound of the tail probability of the maximum of multivariate Chi-squared distribution. Their results indicated that the bound was sharp for moderate to large sample sizes in the model they studied. We will denote this method of making inference as $L{R}_{\text{max}}^{\mathrm{P}\mathrm{G}\mathrm{C}}$ in the simulation studies. For the interaction model and the sample sizes under consideration in this paper, we find this procedure to be on the conservative side.

To have a method that has similar performance as the maximum of weighted scores test and is computationally more efficient, we propose a new method to obtain the p-value for the maximum of likelihood ratios test. Our method is based on the fact that under the null, the likelihood ratio statistic Q(e*) for a given threshold can be asymptotically expressed as

$$𝒬(e^{*})=[S_1(e^{*})S_2(e^{*})]{Î}_{\beta \beta .\alpha }^{-1}(e^{*})\left[\begin{array}{c}\hfill S_1(e^{*})\hfill \\ \hfill S_2(e^{*})\hfill \end{array}\right]+o_p(1),$$

where ${Î}_{\beta \beta ·\alpha }^1(e^{*})$ is the estimated information for β in model (6) by plugging in parameters estimated under the null. Specifically, the p-value for the test based on LR_max can be obtained as follows:

• Draw B independent random samples of size 2M from a multivariate normal distribution with mean 0, variance 1 and correlation matrix derived from JV₂J, where J is a 2M × 2M block diagonal matrix with ${Î}_{\beta \beta ·\alpha }^{1/2}(e^{*})$ on the diagonal.

• Each of the B samples can be viewed as a sequence of M pairs of random variables. For the b^th sample, compute the M sums of squares of pairs of random variables, and denote their maximum value by $L{R}_{\text{max}}^b$

• Obtain the p-value as # $\{L{R}_{\text{max}}>L{R}_{\text{max}}^b\}/B$.

In the simulation studies, we will refer to this approach to obtaining the significance level as $L{R}_{\text{max}}^{MC}$.

The second approach we take is based on a maximum of weighted scores test statistic. Let z̃₁ denote the affine transformation of z₁ with mean 0 and scale 1, and let S̃₂ (e) denote the corresponding score statistics. S₂ (e) can be expressed as a linear combination of S₁ (e) and S̃₂ (e) that is related to the affine transformation of z₁ leading to z̃₁. This motivates us to examine a range of combinations in the form of S_w (e) = S₁ (e) + wS̃₂ (e). Let T_w (e) denote S_w (e) divided by its standard deviation estimated under the null. We propose a maximum of weighted scores test based on

$$T_{\text{max}}^w=\underset{e}{\text{max}}\{\text{max}\{T_1(e),T_2(e),T_{w_1}(e),\cdots ,T_{w_N}(e)\}\}.$$

Here {w₁, ⋯, w_N} are a series of N weights. The p-value can be obtained by comparing $T_{\text{max}}^w$ with random samples of maximum of a multivariate normal distribution with mean 0, variance 1 and an estimated correlation matrix of {T₁ (e), T₂ (e), T_w1 (e), ⋯ T_wN (e)}.

Different choices of weights result in different test statistics. Among the many choices of weights are two basic options: 1) two-sided weights, e.g. w ∈ {±1/4, ±1/3, ±1/2, ±1, ±2, ±3, ±4} and 2) one-sided weights, e.g. w ∈ {1/4, 1/3, 1/2, 1, 2, 3, 4} or w ∈ {−1/4, −1/3, −1/2, −1, −2, −3, −4}. The one-sided weights can be more powerful than the two-sided weights if we are sure about the direction of the interaction effect, but less so if we are wrong in our conviction.

4. Simulation Studies

4.1. Main effect only

We first check the sizes of the three testing approached discussed in Section 2.We simulate two covariates, Z and X, from a bivariate normal distribution: Z ~ N (0, 1), X ~ N (4.7, sd = 1.6) and the correlation ρ between Z and X is either 0 or 0.3. The binary outcome is simulated from a Bernoulli with mean

$$\text{logit}\{\text{Pr}(Y=1)\}=\alpha +\text{log}(1.4)Z.$$

α is chosen so that the proportion of cases in the dataset is 1/3. The sample size is 250.We test whether there is a threshold effect in x.

The estimated Type 1 error rates from 10,000 replicates are shown in Table 1. The standard deviation of the estimate at the nominal rate is 0.22%. The results show that approximating the distribution of T_max using the estimated covariance matrix gives type I error rates that are close to the nominal level. However, approximating the distribution of $T_{\text{sup}}^A$ with the asymptotic expression from [11] leads to a conservative test. An additional experiment shows that increasing the sample size to 500 leads to a small improvement. For example, the rejection rate increases from 0.007 to 0.010 at alpha level 0.05 when ρ = 0. These results suggest that for the asymptotic approach to work, rather high sample sizes are required. Testing with U^TU is also conservative, presumably due to the difficulty in inverting a high-dimensional variance-covariance matrix. Additional simulation results (not shown) show that the test becomes more conservative as M, the number of thresholds examined, increases.

Table 1.

Type I error rates of hypothesis testing procedures for logistic regression models with change point variable as a main effect, based on 10,000 simulation replicates.

ρ Significance level	0			0.3
	0.010	0.050	0.100	0.010	0.050	0.100
Tmax (M = 10)	0.008	0.050	0.098	0.010	0.049	0.102
Tmax (M = 50)	0.010	0.050	0.100	0.011	0.051	0.100
Tmax (M = 100)	0.009	0.051	0.103	0.011	0.050	0.100
Antoch	0.000	0.007	0.028	0.001	0.020	0.056
UTU	0.001	0.016	0.051	0.001	0.013	0.047

ρ: correlation of predictor Z and X.

In a data analysis, along with change point model-based testing methods, we may also consider discretization of covariates. For example, we may encode a covariate x as a binary variable dichotomized at median, and use a Wald test to test the coefficient associated with the variable. Alternatively, we may encode the covariate x as a trichotomous variable with cut points chosen as the 33% and 67% percentiles, and use a generalized Wald test to test the overall hypothesis that there is no association between the outcome and x. We now conduct a simulation study to compare the statistical power of these two methods with change point method-based testing methods based on T_max. In addition, we will also investigate the impact of the choice of M, the number of change points to consider, on the power of T_max-based methods.

We simulate data from

$$\text{logit}\{\text{Pr}(Y=1)\}=\alpha +\text{log}(1.4)Z+\beta I(X>e).$$

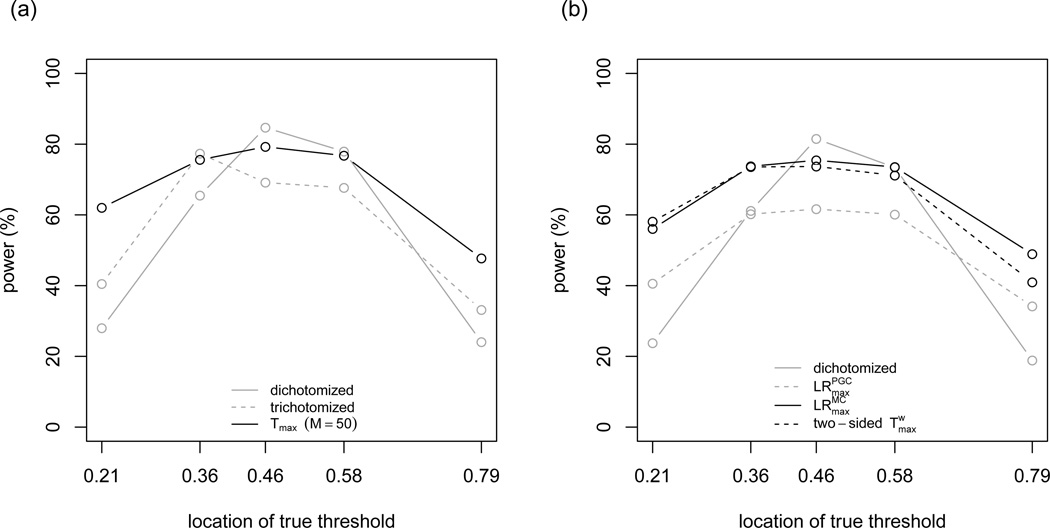
The covariates are simulated as above. We let e range from 3.4 to 6 to cover a representative set of quantiles of the distribution of X. We examine three values of β: log (0.8), log (0.6) and log (0.4); α is chosen so that the proportion of cases in each dataset is 1/3 on average. The estimated power from 2,000 replicates for all methods is shown in Table 2 and Figure 1(a).

Table 2.

Powers of hypothesis testing procedures for logistic regression models with change point variable as a main effect, based on 2,000 simulation replicates..

ρ Threshold	0					0.3
	0.21	0.36	0.46	0.58	0.79	0.21	0.43	0.53	0.65	0.82
OR=0.8
trichotomized	7.0	9.5	9.0	7.5	9.5	6.5	9.0	9.0	9.5	8.0
dichotomized	7.0	9.0	14.0	13.5	8.0	7.0	9.5	12.0	11.5	6.5
Tmax (M = 10)	9.0	8.0	10.0	10.5	9.5	9.0	8.5	10.0	12.5	9.5
Tmax (M = 50)	11.5	12.0	13.5	11.0	12.0	10.0	11.0	11.5	12.0	13.0
Tmax (M = 100)	11.0	10.5	12.5	10.5	12.5	10.0	10.0	11.0	11.5	13.0
OR=0.6
trichotomized	14.5	33.5	26.0	28.5	13.0	15.0	33.5	24.0	27.0	14.5
dichotomized	11.0	26.0	42.5	37.0	14.5	10.5	24.0	38.5	33.5	11.5
Tmax (M = 10)	21.0	32.5	32.5	30.5	20.0	23.0	29.5	32.5	35.0	21.5
Tmax (M = 50)	25.0	32.5	36.5	31.5	21.5	21.5	31.0	32.0	32.5	25.0
Tmax (M = 100)	26.0	34.0	38.5	33.5	23.0	22.0	31.0	32.5	31.5	25.0
OR=0.4
trichotomized	46.0	82.0	71.5	71.5	37.5	40.0	78.0	69.5	69.0	35.0
dichotomized	36.5	70.5	87.0	81.0	27.0	27.5	68.0	87.0	77.5	21.5
Tmax (M = 10)	62.0	75.5	83.5	80.5	46.5	56.5	75.0	81.5	73.0	47.0
Tmax (M = 50)	64.5	77.5	84.0	80.5	47.5	60.5	77.0	82.5	76.5	47.0
Tmax (M = 100)	61.5	77.5	84.0	79.0	46.5	61.5	77.0	81.0	76.0	47.5

ρ: correlation of predictor Z and X. The threshold values are given in the quantiles of the distribution of X. OR: odds ratio of the main effect.

Figure 1.

Powers of hypothesis testing procedures for logistic regression models. (a) A model with change point parameter in the main effect only, β = log(0.4), ρ = 0; (b) a model with change point parameter in both the main and interaction effect, β₁ = log(0.67), β₂ = log(0.4), ρ = 0. The locations of true threshold are given in terms of the quantiles of the distribution of X.

These results suggest that the choice of M does not greatly impact the power of T_max-based tests; as M increases from 10 to 50, the power increases slightly, and as M increases from 50 to 100, the power sees no changes in most scenarios.

The performance of the tests based on binary encoding depends greatly on how close the true threshold is to the median of the covariate distribution. For example, when the true odds ratio is 0.4 and ρ = 0, the power of the tests based on binary encoding ranges from 27% to 87%. On the other hand, under the same setting, the power of the tests based on change point models varies much less, ranging from 47% to 84%. In other words, the change point method trades a small loss in power when the true threshold is close to the median for a relatively large gain in power when the true threshold is away from the median of the covariate. Thus, the maximum of score test based on the change point model is an omnibus procedure that is powerful against alternatives under a wide range of threshold values. Trichotomizing the covariate x is more powerful than dichotomization when the true threshold is away from the median, but almost always inferior to the change point method. Results from other β’s and ρ = 0.3 are similar.

4.2. Main effect plus interaction

To study the performance of the proposed tests for interaction model, we simulate data from

$$\text{logit}\{\text{Pr}(Y=1)\}=\alpha +\text{log}(1.4)Z+{\beta }_{1}I(X>e)+{\beta }_2\times Z\times I(X>e).$$

We simulate (Z, X) from a bivariate normal distribution as described in Section 4.1; additional results for covariates simulated from Gamma distributions are collected in the Web Supporting Materials. α is chosen so that the proportion of cases in the dataset is 1/3. The sample size is 250. We test the null hypothesis that β₁ = β₂ = 0 at 5% alpha level. For change point model-based methods, M is chosen to be 50.

We compare the proposed approaches, $L{R}_{\text{max}}^{MC}$ and $T_{\text{max}}^w$ (one-sided and two-sided), with three others tests: (1) As in the previous simulation, we consider a common practice of encoding x as a binary variable dichotomized at median and performing a likelihood ratio test based on the discrete covariate. (2) We consider an inference procedure based on the maximum of likelihood ratios proposed by Pastor-Barriuso, Guallar and Coresh (2003) [10], which applied an improved, second-order Bonferroni inequality to find an upper bound of the p-value. The test will be denoted by $L{R}_{\text{max}}^{PGC}$. (3) We consider a test based on T_max, which ignores any potential effect modification.

Based on 10,000 replicates, the test based on dichotomizing covariates at median and the test based on T_max have close to nominal type 1 error rates. The tests based on $L{R}_{\text{max}}^{MC}$ and $T_{\text{max}}^w$ have slightly elevated type I error rates at around 6%. The test based on $L{R}_{\text{max}}^{PGC}$ appears to be conservative with a type I error rate of 3.2%, which is probably due to the upper bound being not tight enough under the current simulation scenario with a moderate sample size of 250.

For power, we consider 12 simulation scenarios formed by the interaction of two β₁: {log (0.67), −log (0.67)}, three β₂: {log (0.8), log (0.6), log (0.4)}, and two ρ: {0, 0.3}. Results from 2,000 replicates are shown in Table 3 and Figure 1(b), and several conclusions can be drawn: (i) The order of performance is roughly $L{R}_{\text{max}}^{MC}\approx \text{two}-\text{sided}{T}_{\text{max}}^w>L{R}_{\text{max}}^{PGC}>T_{\text{max}}$. (ii) The one-sided $T_{\text{max}}^w$ performs better/worse than the two-sided $T_{\text{max}}^w$ when β₁ and β₂ have the same/opposite sign. This is clear from, for example, contrasting the results from β₁ = log (0.67), β₂ = log(0.4), ρ = 0 and β₁ = log (0.67), β₂ = log(−0.4), ρ = 0. In practice, if we do not have a strong belief about the directions of the effects, it is advisable to choose the two-sided $T_{\text{max}}^w$ test over the one-side one. (iii) The advantage of $L{R}_{\text{max}}^{MC}$ over T_max decreases as the odds ratio for the interaction term approaches 1, and when β₂ = log (0.8), the two methods have similar performance. This demonstrates that it is worth testing an alternative hypothesis containing interaction term even if the interaction effect is fairly modest. (iv) Compared to dichotomizing x at the median, $L{R}_{\text{max}}^{MC}$ slightly underperforms when the true threshold is near the median of x, but has substantial advantages otherwise. The level of trade-off is similar to the level seen in the simulation studies for main effect only.

Table 3.

Powers of hypothesis testing procedures for logistic regression models with change point variable both as a main effect and as part of an interaction term, based on 10,000 simulation replicates..

ρ Threshold	0					0.3
	0.21	0.36	0.46	0.58	0.79	0.21	0.43	0.53	0.65	0.82
OR=(0.67, 0.8)
dichotomized	7.2	14.9	23.2	19.8	7.4	6.4	13.1	19.9	18.7	7.8
Tmax	13.6	17.9	19.2	18.4	10.6	10.0	15.0	15.6	15.7	11.9
$L{R}_{\text{max}}^{PGC}$	5.4	8.7	9.5	9.7	5.5	4.1	7.8	8.4	8.7	6.5
$L{R}_{\text{max}}^{MC}$	12.3	17.4	19.2	18.6	11.0	10.2	15.3	16.1	16.1	13.2
two-sided $T_{\text{max}}^w$	12.2	16.6	16.8	16.1	8.3	9.8	13.9	15.3	15.2	10.0
one-sided $T_{\text{max}}^w$	13.9	17.8	18.9	18.2	9.4	10.4	16.0	17.1	17.2	11.6
OR=(0.67, 0.6)
dichotomized	10.8	27.7	43.0	36.7	9.9	8.8	22.6	38.9	37.6	14.1
Tmax	13.6	18.1	18.2	18.3	11.2	7.3	12.4	16.4	19.4	18.4
$L{R}_{\text{max}}^{PGC}$	13.4	21.4	23.2	22.1	10.9	8.8	15.5	19.6	22.3	17.0
$L{R}_{\text{max}}^{MC}$	24.7	34.8	36.4	34.6	21.5	18.0	26.6	31.5	35.3	27.4
two-sided $T_{\text{max}}^w$	22.2	32.2	33.7	30.8	16.2	16.8	27.2	30.9	32.8	23.4
one-sided $T_{\text{max}}^w$	25.8	36.2	36.9	34.3	19.3	18.9	29.9	34.0	36.1	26.7
OR=(0.67, 0.4)
dichotomized	23.8	61.2	81.5	73.4	18.9	19.7	52.8	76.9	74.1	23.5
Tmax	12.3	17.2	16.0	15.7	8.6	5.8	10.3	15.2	21.2	22.8
$L{R}_{\text{max}}^{PGC}$	40.6	60.2	61.6	60.1	34.2	30.6	50.8	55.4	59.6	41.2
$L{R}_{\text{max}}^{MC}$	56.1	73.7	75.4	73.5	48.9	46.5	65.4	70.5	72.5	58.3
two-sided $T_{\text{max}}^w$	58.1	73.6	73.7	71.2	40.9	47.1	65.6	69.9	71.2	50.0
one-sided $T_{\text{max}}^w$	61.4	76.8	76.5	75.0	44.9	49.5	68.3	73.3	74.6	54.1
OR=(1.5, 0.8)
dichotomized	7.4	14.1	22.6	20.1	7.0	8.6	16.4	22.2	18.5	6.8
Tmax	11.6	16.2	17.2	17.9	12.4	13.7	16.7	16.8	16.6	9.8
$L{R}_{\text{max}}^{PGC}$	6.1	8.4	8.7	9.3	5.3	6.5	9.7	9.7	9.1	4.8
$L{R}_{\text{max}}^{MC}$	12.1	17.1	18.1	17.7	12.0	14.1	17.2	17.8	16.9	10.6
two-sided $T_{\text{max}}^w$	9.8	14.8	17.1	17.4	12.0	10.9	15.6	16.6	16.0	10.2
one-sided $T_{\text{max}}^w$	8.1	11.6	13.8	14.4	9.8	10.0	12.5	12.4	11.6	6.8
OR=(1.5, 0.6)
dichotomized	11.4	29.5	47.2	41.8	11.5	14.4	30.2	42.6	35.2	9.3
Tmax	11.6	17.3	18.0	18.1	13.6	19.6	21.3	18.8	14.2	6.2
$L{R}_{\text{max}}^{PGC}$	13.4	22.1	24.5	22.3	12.4	19.0	24.4	23.8	19.8	7.9
$L{R}_{\text{max}}^{MC}$	23.6	34.3	38.1	36.9	22.3	30.7	36.7	36.7	31.5	18.2
two-sided $T_{\text{max}}^w$	20.8	34.0	37.5	36.1	24.4	28.1	34.0	33.6	30.5	17.0
one-sided $T_{\text{max}}^w$	15.4	23.6	25.9	24.9	16.1	24.6	26.4	24.0	20.0	9.0
OR=(1.5, 0.4)
dichotomized	24.6	63.5	83.9	78.8	23.4	31.2	65.4	82.2	73.3	18.9
Tmax	12.4	16.2	16.4	18.1	14.2	29.8	25.8	21.1	12.8	4.7
$L{R}_{\text{max}}^{PGC}$	43.4	61.0	66.6	65.0	40.4	54.3	63.4	64.9	58.6	28.7
$L{R}_{\text{max}}^{MC}$	58.2	74.6	78.1	76.8	55.3	67.0	76.6	76.7	71.4	42.1
two-sided $T_{\text{max}}^w$	58.6	74.0	77.2	76.2	54.8	67.6	75.4	75.8	69.4	40.0
one-sided $T_{\text{max}}^w$	47.8	64.6	68.3	66.8	43.1	63.1	68.7	68.9	60.0	29.1

ρ: correlation of predictor Z and X. The threshold values are given in the quantiles of the distribution of X. OR: odds ratios for the main and interaction effect.

5. Application in HIV-1 Transmission

The risk of mother to child transmission (MTCT) is less than 1% in the setting of optimal antiretroviral prophylaxis. Yet, more than 250,000 infants still acquire HIV-1 annually due to lack of access or adherence to ARVs or acute infection during pregnancy or breast-feeding. Development of a maternal or infant HIV-1 vaccine will undoubtedly hasten the elimination of pediatric HIV-1. To further our understanding of effective human immune responses that will prevent HIV-1 infection, a study was carried out to identify maternal HIV-1 specific immunologic biomarkers that are associated with the risk of HIV-1 MTCT [2].The study used samples from the historical Women and Infants Transmission Study cohort of U.S. HIV-infected mother-infant pairs enrolled prior to the availability of antiretroviral drugs in an observational study of vertical HIV-1 transmission and pathogenesis [15]. Eight-three HIV-transmitting mothers and 165 nontransmitting mothers with available plasma samples were selected for the study. None of the mothers breast-fed or received any antiretroviral prophylaxis.

One immune response variable of particular interest is V3_score. This variable is a linear combination of several variables measuring the strength of IgG antibody binding to the variable loop (V3) region [16] of several variants of HIV-1 Envelope proteins (Env). We examined the association between HIV-1 transmission and V3_score via three models. All models include several clinical factors known to be associated with the risk of vertical transmission including viral load, gestational age, etc. and do not contain interaction terms. The three models differ in how V3_score is encoded. In the first model, V3_score is treated as a continuous variable; in the second, it is treated as a binary variable dichotomized at median; and in the third, it is modeled as a change point variable. The p-values from Wald tests in the first two models are 0.04 and 0.35, respectively. The discrepancy of the two results can be explained by the result from the third model, where the maximum of scores test p value is 0.04 and the threshold that yields the maximum score statistics is at 10% of the V3_score distribution, far from the median.

Different immune biomarkers measure distinct aspects of the immune response to HIV-1. To have an effective defense against HIV-1, these different aspects of the immune response may have to work together synergistically. This suggests that it is important to study the interaction between immune biomarkers. In the MTCT correlates study, the analysis plan identifies nine immune response biomarkers as ‘primary variables’ based on the RV144 immune correlates study [1] and previous studies on immune responses implicated to be important in MTCT. To study potential threshold effects in interaction, we fit logistic models of the form

$$\text{logit}\{\text{Pr}(\mathrm{M}\mathrm{T}\mathrm{C}\mathrm{T})\}={\alpha }_{1}Z+{\alpha }_2\times {\mathrm{V}}_1+{\beta }_1\times I({\mathrm{V}}_2>e)+{\beta }_2\times {\mathrm{V}}_1\times I({\mathrm{V}}_2>e),$$ (7)

where Z is a the clinical covariates vector, and V₁ and V₂ are a pair of continuous immune response biomarkers. This model treats V₁ as a continuous variable, and studies the threshold effect of V₂; and we fit a total of 72 models. The p-values for testing β₁ = β₂ = 0 using $L{R}_{\text{max}}^{MC}$ are < 0.05 in 13 models. To adjust for multiple testing, we compute false discovery rates [17] and apply a threshold of 0.20 to optimize the hypothesis-generating discovery of immune correlates. There are 9 p-values that pass this cutoff. For comparison, we also fit models in which V₂ is dichotomized at median. The numbers of models with p-values less than 0.05 and false discovery rates less than 0.20 drop to 7 and 6, respectively.

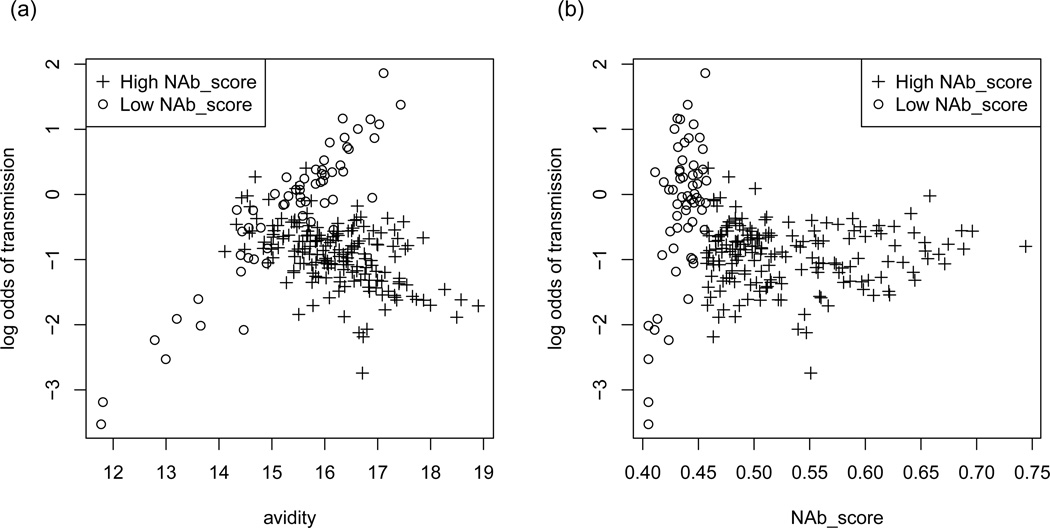
Two of the interactions identified by the change point models but not the dichotomized models contain NAb_score as the change point variable. NAb_score measures the amount and breadth of neutralizing antibodies [18]. By itself, NAb_score does not have a significant association with transmission risk whether it is studied as a continuous, median-dichotomized or change point variable. When NAb_score is dichotomized at median in the interaction model, likelihood ratio tests reject β₁ = β₂ = 0 only when V₁ measures IgG antibody binding to Env gp41 subunit. However, when NAb_score is encoded as a change point variable, the null is also rejected when V₁ measures antibody avidity or IgA antibody binding to Env gp41 subunit, neither of which shows significant association with transmission risk on their own. To further illustrate the threshold effect, we estimate the regression coefficients in model (7) for V₁ = avidity and V₂ = NAb_score by maximum likelihood method. With the avidity covariate standardized to have empirical mean 0 and standard deviation 1, the point estimates are α̂₂ = 0.84, β̂₁ = −1.22, and β̂₂ = −1.17. Standard errors are not reported here because variance estimates that assume a true underlying change point model can be too optimistic, and robust variance estimates are an active research topic [19, 20]. Figure 2 shows the log odds of MTCT predicted by the model versus avidity and NAb_score. Figure 2(a) shows that the slope for avidity is different among the two NAb_score subgroups, demonstrating the interaction effect. Figure 2(b) shows that subjects with low NAb_score generally have higher log odds of transmission than those with high NAb_score, but some subjects with low NAb_score and low avidity (lower left quadrant) have lower odds of transmission.

Figure 2.

Predicted log odds of MTCT as a function of (a) avidity and (b) NAb_score.

6. Discussion

This paper is motivated by the need to detect threshold effects in the study of synergistic human immune responses to HIV-1 virus. The main contribution of the paper is the proposal of a maximum of likelihood ratios test and a maximum of weighted scores test for a change point logistic model with interaction term. These methods are implemented in a R package chngpt, and can be downloaded from the Comprehensive R Archive Network (CRAN). The broad pattern of interaction uncovered by the change point method in the HIV-1 MTCT immune correlates study suggests it is important to elicit multiple immune responses for any successful HIV-1 vaccine.

The maximum of likelihood ratios test we propose for change point models with interaction differs from existing works, the closest among which is a maximum of likelihood ratios type test from [10]. Our approach differs from theirs in the following ways. First, we consider a threshold model with interaction, while they consider a different change point model without interaction. Second, while the two test statistics appear similar in spirit (both first fixing the threshold and then maximizing the likelihood ratio statistic over all thresholds), the methods for obtaining p-values are different. Pastor-Barriuso et al. applied an improved, second-order Bonferroni inequality to find an upper bound of the tail probability of the maximum of multivariate Chi-squared distribution. Their results indicated that the bound was sharp for moderate to large sample sizes in the model they studied. For the interaction model and the sample sizes under consideration in this manuscript, we find the procedure to be on the conservative side. Our proposed method for making inference has close to nominal alpha level, and is more powerful in our simulation studies.

The maximum of weighted scores test can be applied using different weights. When we are comfortable making assumption about the direction of the interaction effect, we can apply one-sided weights, which leads to a slightly more powerful test than the maximum of likelihood ratios test; when we do not want to make any assumption, we can apply two-sided weights, which is almost as powerful as the maximum of likelihood ratios test, but has a higher computational cost.

The change point model with interaction we focus on essentially treats the change point variable as a binary variable. Such a model is useful when the scientific thought process calls for studying a dichotomized version of a continuous covariate, but there is little evidence to suggest the location of the cutoff. Besides this model, there are many other types of change point models with interaction. A common variant allows differing linear effects before and after the change point [10]. The testing approach based on $L{R}_{\text{max}}^{MC}$ that we have developed is also applicable there. Another useful model allows the threshold parameter to depend on a binary covariate, e.g.

$$\text{logit}\{\text{Pr}(Y=1)\}=\alpha +{\gamma }^{T}Z+({\beta }_1+{\beta }_{2}G)\times I(X>e+G\delta ),$$

where G is a binary covariate encoded as a 0/1 variable. Testing β₁ = β₂ = 0 can in principle be carried out using $L{R}_{\text{max}}^{MC}$, but other hypothesis testing problems, such as δ = 0 or β₂ = 0, are different in nature, and deserve further study.

In many biomedical studies, two-phase sampling [21, 22, 23] is used to improve design efficiency. For example, in the study of HIV-1 vaccine immune responses that might confer protection, many immune biomarkers are too expensive to measure for all study subjects [1]. A subset of study subjects is typically chosen by dividing the cohort into strata and sampling without replacement within each stratum. Often one stratum corresponds to the cases and other strata are formed using select phase I covariates. It is important to develop change point model testing methods suitable for two-phase sampling. Inverse probability weighting (IPW) is an oft-used approach to handle differing sampling probabilities and the tests we have developed can be extended in a straightforward fashion through IPW. A common criticism of IPW is lack of power, and studies of testing methods based on maximum likelihood treatment [24] are warranted.