Abstract
Phase I/II trials utilize both toxicity and efficacy data to achieve efficient dose finding. However, due to the requirement of assessing efficacy outcome, which often takes a long period of time to be evaluated, the duration of phase I/II trials is often longer than that of the conventional dose-finding trials. As a result, phase I/II trials are susceptible to the missing data problem caused by patient dropout, and the missing efficacy outcomes are often non-ignorable in the sense that patients who do not experience treatment efficacy are more likely to drop out of the trial. We propose a Bayesian phase I/II trial design to accommodate non-ignorable dropouts. We treat toxicity as a binary outcome and efficacy as a time-to-event outcome. We model the marginal distribution of toxicity using a logistic regression and jointly model the times to efficacy and dropout using proportional hazard models to adjust for non-ignorable dropouts. The correlation between times to efficacy and dropout is modeled using a shared frailty. We propose a two-stage dose-finding algorithm to adaptively assign patients to desirable doses. Simulation studies show that the proposed design has desirable operating characteristics. Our design selects the target dose with a high probability and assigns most patients to the target dose.
Keywords: Adaptive design, Phase I/II trial, Dose finding, Non-ignorable missing data, Dropout
1. Introduction
Traditionally, phase I and phase II trials are performed separately. Phase I trials are designed to determine the maximum tolerated dose (MTD) of a new agent, and subsequent phase II trials are conducted to evaluate the potential efficacy of the new drug at the MTD. Clinical trial designs that integrate phases I and II have also been proposed, with the aim of enhancing the efficiency of the design. Gooley et al. [1] proposed a phase I/II clinical trial design in the study of bone marrow transplantation to find a dose that balances the risks of two immunologic complications. O’Quigley, Hughes, and Fenton [2] presented a class of designs aiming to identify the dose yielding the highest treatment success rate for HIV studies. Thall and Cook [3] proposed a Bayesian phase I/II trial design based on trade-offs between toxicity and efficacy probabilities. Yin et al [4] proposed a Bayesian design based on the odds ratio of toxicity and efficacy. Yuan and Yin [5] developed a time-to-event phase I/II design to accommodate the case that toxicity or efficacy may not be immediately observable. Mandrekar, Cui, and Sargent [6] proposed a dose-finding design for trials evaluating combinational biological agents based on a continuation ratio model by collapsing binary toxicity and efficacy outcomes into a trinary outcome. Yuan and Yin [7] developed a Bayesian phase I/II design for drug-combination trials. Cai, Yuan, and Ji [8] proposed a phase I/II trial design to find the biologically optimal dose combination for biological agents. O’Quigley and Zohar [9] provided a comprehensive review of earlier phase I/II designs.
By assessing toxicity and efficacy simultaneously, phase I/II clinical trials have advantages over trials using the conventional approach of separating the two phases. For example, phase I/II trials are more efficient in finding the target dose by using both toxicity and efficacy data, and avoid the need to informally adjust the dose when the MTD turns out to be too toxic in phase II trials. However, due to the requirement of assessing the efficacy outcome, the duration of phase I/II trials is often substantially longer than that of the conventional dose-finding trials. In oncology, particularly for cytotoxic agents, toxicity is typically acute and observable shortly after the treatment is administered; whereas efficacy (e.g., complete remission or partial remission) often requires a relatively long time period (e.g., several treatment cycles) to be evaluated. As a result, patient attrition often occurs, that is, patients may prematurely drop out of the study before their efficacy outcomes are evaluated. For example, Cullen et al. [10] described two randomized trials (namely, MIC1 and MIC2 trials), which were designed to determine whether the addition of chemotherapy influenced duration and quality of life in patients with lung cancer. MIC1 trial was for patients with localized, unresectable disease, and MIC2 trial was for patients with extensive disease. In MIC1, patients were randomized to receive either chemotherapy (CT) followed by radical radiotherapy (CT + RT) or radiotherapy (RT) alone. In MIC2, patients were randomized to chemotherapy plus palliative care (CT + PC) or palliative care (PC) alone. The dropout rates were 29% and 20% for CT + RT and RT arms, respectively, in MIC1 trial; and 22% and 24% for CT + PC and PC arms, respectively, in MIC2 trial. Marchetti et al. [11] reported a phase II trial to evaluate the safety and efficacy of thalidomide in patients with myelofibrosis with myeloid metaplasia. In that trial, the dropout rate reached 51% after 6 months of treatment.
These dropouts, and the resulted missing (efficacy) data, are often non-ignorable (or informative) in the sense that the dropout probability of a patient depends on his/her efficacy outcome. For example, patients who do not experience efficacy are often more likely to drop out of the study than patients who experience efficacy. Therefore, the common approach of ignoring the missing data, e.g., regarding the dropouts as “invaluable” patients, results in biased estimates [12]. To the best of our knowledge, this issue of non-ignorable missing data has not been previously addressed in the context of phase I/II clinical trial design. To be consistent with most cases in practice, herein we assume that toxicity is quickly ascertainable and thus always observable, and that only efficacy is subject to missingness due to patient dropout. Note that patients may drop out due to toxicity, but that does not cause missing data for toxicity because toxicity typically is observed before dropout occurs.
Our motivating example is a phase I/II trial to find the optimal dose of plerixafor to treat refractory acute myeloid leukemia, where toxicity may occur at any time during the first 30 days from the start of treatment, while efficacy is evaluated up to 90 days post-treatment. Five dose levels (0.1, 0.3, 0.5, 0.7, 0.9mg/kg) of plerixafor, administered with 10mcg/kg G-CSF (i.e., a cytokine), were investigated. The clinical protocol defined efficacy as the achievement of a morphologic complete remission (CR) or morphologic complete remission with incomplete blood count recovery (CRi). CR was defined as a morphologic leukemia-free state (including <5% blasts in bone marrow aspirate, with marrow spicules and a count of > 200 nucleated cells and no blasts with Auer rods, no persistent extramedullary disease, absolute neutrophil account > 1,000/mm3, and platelet count > 100,000/mm3). CRi was defined as CR with the exception of neutropenia <1,000/mm3 or thrombocytopenia <100,000/mm3. The dose-limiting toxicities (DLTs) included grade 4 or higher adverse events attributable to either leukostasis or tumor lysis, grade 3 toxicities attributable to leukostasis or tumor lysis that did not improve with standard supportive care measures (e.g., intravenous fluids, supplemental oxygen, leukapheresis) within 24 hours to grade 2, and persistent grade 3 or higher neutropenia. The goal of the trial was to find the dose that is safe (i.e., toxicity probability ≤ 30%) and has the highest efficacy. Because the follow-up period for assessing efficacy was long, we expected that a substantial number of patients might prematurely drop out of the study before their efficacy outcomes were scored, inducing missing data for the efficacy outcome.
We propose a Bayesian phase I/II dose-finding design that handles such non-ignorable dropouts. Assuming that toxicity is quickly ascertainable after the initiation of the treatment and thus always observable, we model toxicity as a binary outcome using a logistic regression. We jointly model efficacy and dropout as bivariate time-to-event outcomes using Cox proportional hazards models [13]. A shared frailty term is introduced to induce correlation between time to dropout and time to efficacy, thereby accounting for the non-ignorable dropouts. Conditional on observed data, we continuously update the estimates of toxicity and efficacy and propose a two-stage dose-finding algorithm to adaptively assign patients to the desirable doses.
The remainder of this article is organized as follows. Section 2 presents a joint probability model for binary toxicity, time to efficacy and time to dropout, as well as the estimation procedure. Section 3 describes a two-stage dose-finding algorithm. Section 4 examines the operating characteristics of the proposed design through simulation studies.We provide concluding remarks in Section 5.
2. Method
2.1. Probability Model
Consider a phase I/II clinical trial with J doses, d1 < d2 < … < dJ, under investigation. We assume that toxicity endpoint X is quickly ascertainable after the initiation of the treatment and thus always observable, with X = 1 indicating the occurrence of toxicity, and X = 0 otherwise. This assumption is plausible for most cytotoxic agents, for which toxicity is acute. In addition, as cancer is a life-threatening disease, we do not expect patients to drop out of the study shortly after the initiation of the treatment before their toxicities are assessed. Let πT (Z) ≡ Pr(X = 1|Z) denote the toxicity probability of a given dosage Z ∈ (d1, …, dJ). We assume that πT (Z) follows a logistic model as follows,
| (1) |
where μT and βT are unknown parameters.
Unlike toxicity, the evaluation of efficacy often requires a long follow-up time, say τ. As a result, the efficacy outcome is often subject to missingness due to the possible loss of patient data to follow-up. To account for the potentially non-ignorable dropout, we treat efficacy as a time-to-event outcome and jointly model the efficacy measurement process and dropout process. Note that our primary interest here is efficacy, not the dropout process. The reason for jointly modeling them is to adjust for nonignorable missing data caused by dropout. As we model efficacy and dropout as time-to-event outcomes, the dropout process can be viewed an informative censoring process for the time to efficacy.
Let tEi and tDi denote the time to efficacy and time to dropout, respectively, for the ith patient, and let hE(tEi|Z) and hD(tDi|Z) denote the corresponding hazard functions given a dosage Z ∈ (d1, …, dJ). Let rn denote the total number of dropouts at the moment that the (n + 1)th patient arrives and is ready for dose assignment. We model tEi and tDi using the following shared-frailty proportional hazards model,
| (2) |
| (3) |
where λ and γ are baseline hazards, βE,1, βE,2 and βD are regression parameters characterizing the dose effects, I(·) is an indicator function, and c is a prespecified cutoff. In equation (2), we include a quadratic term to accommodate possibly unimodal or plateaued dose-efficacy curves, e.g., for biological agents. The common frailty θi shared by the two hazard functions is used to account for the potentially informative censoring due to dropout (i.e., the correlation between the times to efficacy and dropout). We assume that θi follows a normal distribution with mean 0 and variance σ2, i.e., f(θi) = N(0, σ2). To allow for the flexibility such that the correlation between the two endpoints can be either positive, negative, or 0, we introduce parameter α in equation (3). A positive (or negative) value of α indicates a positive (or negative) correlation between efficacy and dropout. When α = 0, the two times to the event outcomes are independent. As clinical trial is a sequential process, it is possible that at a moment of model fitting and decision making, no patient has dropped out. In this case, there is no need to model the dropout process, and we can decouple the time to efficacy from the time to dropout by simply removing the shared frailty θi. This is done by the indicator function I(rn > c) with c = 0. In practice, we may prefer ignoring the dropout issue for simplicity when there are only 2 or 3 dropouts, then we should set c = 2 or 3. Because rn depends on n, strictly speaking, models (2) and (3) are not the usual proportional hazard (or Cox) regression models but a group of sequentially conditional proportional hazard models. This makes the interpretation of model parameters less straightforward. However, it does not cause any problem here because our goal is to find the target dose (i.e., dose finding), not to make accurate inference for model parameters. In other words, these models only serve as “working” models in our design to guide dose escalation and deescalation. As long as the models provide reasonable fit to the data, they will lead to appropriate dose escalation and selection. As an example, the well known continual reassessment method often employs a restrictive one-parameter working model, but performs well in finding the target dose [14]. For notational brevity, we suppress subscript n in rn hereafter. As a side note, compared to most existing phase I/II designs which consider bivariate efficacy-toxicity distribution, our model seems more complex because of modeling a trivariate distribution. However, because our design utilizes extra data information (i.e., time to dropout), the model actually is not more complicated than most phase I/II designs with respect to available data. Specifically, our toxicity model is a logistic regression, and efficacy model is a simple parametric survival model with a constant baseline hazard. Such (or more sophisticated) model choices have been previously used in phase I/II designs [3, 5].
Because the sample size of phase I/II trials is typically small, we take a parsimonious approach by assuming constant baseline hazards. For the same reason, we also ignore the correlations between efficacy/dropout and toxicity. Initially, we considered a more elaborate model, which accounts for the correlations between times to efficacy/dropout and toxicity by modeling the conditional distributions of tEi and tDi, given the value of the toxicity outcome Xi = j with j = 0 or 1, as follows,
This model allows different baseline hazards for patients who experience or do not experience toxicity. Numerical study, however, shows this more elaborate model does not improve the performance of the design because there is very limited information to estimate the correlation between toxicity and efficacy/dropout. Hereafter, we focus only on models (2) and (3).
Under the proposed time-to-event model, the efficacy of dose Z (i.e, the response rate at the end of follow-up period τ), say πE(Z), is given by the cumulative distribution function of tEi, i.e., πE(Z) = pr(tEi ≤ τ|Z). The goal of our design is to find the dose Z that is safe and has the largest efficacy probability πE(Z) while satisfying certain minimum efficacy requirements.
For the ith patient, we define the actually observed times YEi = min(tEi, tDi, ci) and YDi = min(tDi, ci), and censoring indicators δEi = I(tEi ≤ min(tDi, ci)) and δDi = I(tDi ≤ ci), where ci is the time to administrative censoring. Note that dropout (i.e., tD) can censor efficacy (i.e., tE), but not vice versa. Letting Θ = (λ, γ, βE,1, βE,2, βD, μT, βT, θi, σ2, α) denote model parameters, the likelihood for the ith patient with data Di = (Xi, YEi, YDi, δEi, δDi) is given by
where
and
Let f(Θ) denote the prior distribution for Θ, the joint posterior distribution of Θ based on n treated patients is
2.2. Prior and posterior Inference
We assume that the components of Θ are mutually independent a priori. We assign baseline hazards λ and γ independent gamma priors with λ ~ Gamma(a1, b1) and γ ~ Gamma(a2, b2), where Gamma(a, b) denotes a Gamma distribution with shape parameter a and inverse scale parameter b. We assign the variance parameter σ2 an inverse gamma prior distribution with shape parameter a3 and scale parameter b3, i.e., σ2 ~ InvGamma(a3, b3). For regression parameters, we assume normal priors and . We set a1 = a2 = a3 = 0.1, b1 = b2 = b3 = 0.1 and such that the resulting priors are vague and the posterior distributions of the parameters will be dominated by the observed data. For the correlation parameter α, we assign a uniform prior distribution with support [−5, 5], which covers the range of correlation that may be encountered in practice.
We sample the posterior distribution of Θ using Gibbs sampler. Let θ generically denote the conditional parameters, and let Dn denote the data for the n patients who are already in the trial, i.e., Dn = {(Xi, YEi, YDi, δEi, δDi), i = 1, ⋯, n}. We sequentially sample the elements of Θ from the following full conditional distributions:
-
If r ≤ c, the following steps (steps 6–10) can be skipped because there is no need to fit the dropout model.
[γ|Dn, θ] ~ Gamma(a2 + ∑i δDi, b2 + ∑i YDi exp(αθi + βDZi))
[α|Dn, θ] ∝ exp {α∑δDiθi − γ∑i (YDi exp(αθi + βDZi)))}I(−5 ≤ α ≤ 5)
3. Dose-finding Algorithm
At the beginning of the trial, little data is available and it is difficult to estimate model parameters reliably and to make correct decisions on dose assignments. To facilitate the trial process, we propose to use the following rule-based start-up procedure to collect some preliminary data before switching to the model-based dose-finding strategy. Given a cohort of size 3, we start the trial by treating the first cohort of patients at the lowest dose d1. At the current dose dj,
If ≥2 out of 3 patients experience toxicity, then the trial moves forward to model-based dose finding, starting at dose dj−1. If dj = d1, i.e., dj is the lowest dose, then the trial is terminated.
If 1 out of 3 patients experiences toxicity, then the trial moves forward to model-based dose finding, starting at dose dj.
If 0 out of 3 patients experiences toxicity, the next dose assignment is escalated to dj+1. However, if dj = dJ, i.e., dj is the highest dose, then the trial moves forward to model-based dose finding, starting at dose dj.
We require that patients accrued during this start-up procedure be completely followed before the model-based dose-finding algorithm is in effect.
Our model-based dose-finding algorithm is described as follows. Let ϕE and ϕT be the respective physician-specified lower efficacy limit and upper toxicity limit. Based on the data from the first n patients who have been enrolled into the trial, we define admissible dose set 𝒜 as a set of doses Z satisfying both the efficacy requirement
| (4) |
and the toxicity requirement
| (5) |
where aE, bE, aT and bT are non-negative tuning parameters that can be calibrated by simulation to achieve good design operating characteristics. Since the estimates of toxicity and efficacy are highly unreliable at the beginning of the trial and become more reliable when more data accumulate, the criteria should depend on the sample size. We choose the posterior probability cutoffs (i.e., aE + bEn/N and aT + bT n/N) depending on the sample size n such that the toxicity and efficacy requirements adaptively become more stringent when more patients are enrolled into the trial.
Let dh be the current highest tried dose, and pc be the dose escalation cutoff. Based on the data from the k cohorts of patients who have been enrolled into the trial, our model-based dose-finding algorithm assigns a dose to the (k + 1)th cohort as follows.
If the posterior probability of toxicity at dh based on the data obtained from the first k cohorts satisfies pr(πT (dh) < ϕT |data) > pc and dh ≠ dJ, we escalate the dose and assign the (k + 1)th cohort to dh+1.
Otherwise, we assign the (k + 1)th cohort to the dose Z in 𝒜 that has the largest probability of efficacy, i.e., πE(Z) = max(πE(d), d ∈ 𝒜). If 𝒜 is an empty set, we terminate the trial.
Once the maximum sample size is exhausted, the dose in 𝒜 with the largest estimate of πE(Z) is selected as the final recommended dose.
4. Simulation Studies
4.1. Operating Characteristics
We investigated the operating characteristics of our proposed design through simulation studies. Taking the setting of the motivating leukemia trial, we considered five doses (0.1, 0.3, 0.5, 0.7, 0.9) and the maximum sample size N of 51. The physician-specified toxicity upper bound and efficacy lower bound were ϕT = 0.3 and ϕE = 0.25, respectively. The follow-up time for evaluating efficacy was 3 months (i.e., τ = 3), and patient accrual followed a Poisson process with a rate of 3 per month. We set α = −1 such that patients who had a lower probability of experiencing efficacy were more likely to drop out of the trial. We used σ2 = 3.5 to induce a moderate correlation with Kendall’s τ of 0.5 between the time-to-event efficacy and dropout. We took the probability cutoffs pc = 0.5, aT = 0.035, bT = 0.095, aE = 0.035, and bE = 0.085. We compared our design to the EffTox design proposed by Thall and Cook [3]. The original EffTox design models efficacy as a binary endpoint and assumes no dropouts. For the purpose of comparison, we examined two variations of the EffTox design with different strategies to deal with dropouts. The first variation of the design, denoted as EffTox 1, took a conservative approach: if a patient has missing efficacy outcome due to dropout, treat that as no efficacy. The second variation of the design, denoted EffTox 2, took a complete-case approach: if a patient has missing efficacy data due to dropout, remove that patient. Despite being ad hoc, these two strategies are commonly used in practice to handle dropouts. For EffTox 1 and EffTox 2 designs, in the case that patients have not dropped out and their efficacy outcomes have not been fully assessed yet, we suspended the accrual to wait for their outcomes to be fully determined before enrolling the next new patient. To make the EffTox designs comparable with our proposed design, we adopted the same target dose definition and dose-finding algorithm in the EffTox designs as in the proposed design.
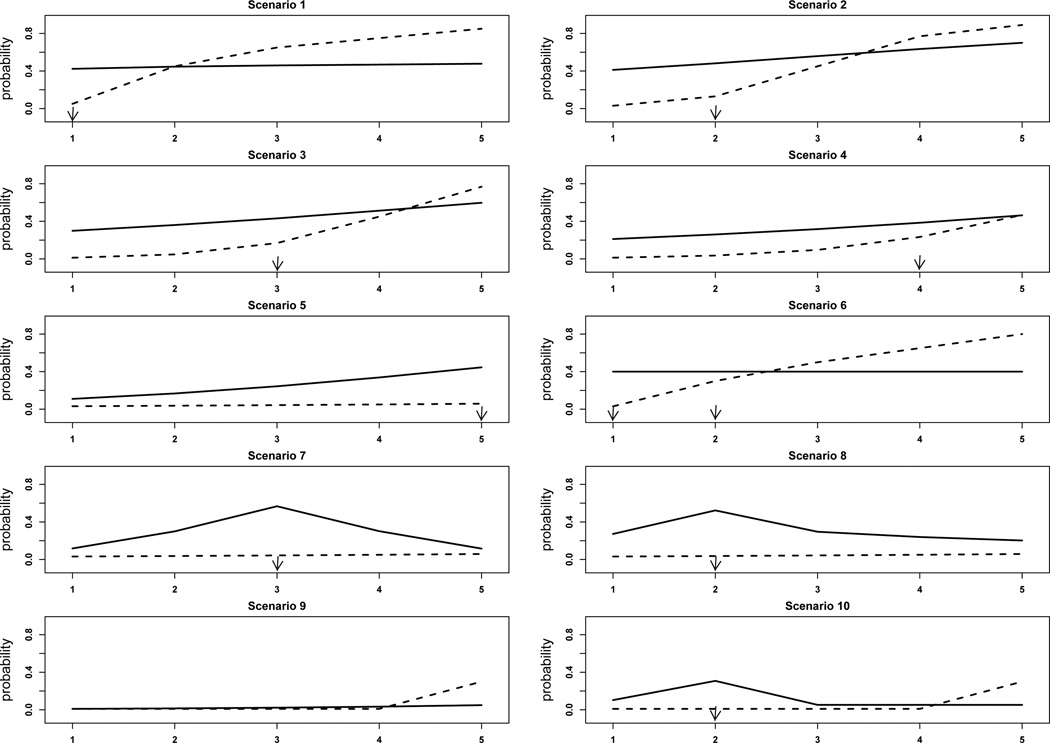
We simulated 10 scenarios with different numbers of target doses, locations of the target doses, and true marginal probabilities of toxicity and efficacy (see Figure 1). Each scenario was determined as follows: the toxicity probabilities at the 5 dose levels were set to the desired probabilities, not necessarily from model (1). Each patient’s efficacy and dropout data were sampled from the following models:
| (6) |
| (7) |
where j = 0, 1, k = 1, ⋯, 5, βE,1, ⋯, βE,5 and βD,1, ⋯, βD,5 were chosen to get desired marginal efficacy and dropout probabilities at the five dose levels, and θi ~ N(0, σ2). By using {βE,k, k = 1, ⋯, 5} and {βD,k, k = 1, ⋯, 5}, instead of and βDZi as in equations (2) and (3), we did not assume a linear or quadratic dose effect. When simulating time to efficacy, we chose the baseline hazards λ0 and λ1 such that the efficacy rates at the end of follow-up, i.e., πE(Z), matched the marginal probabilities of efficacy. Because the marginal probabilities vary across scenarios, the values of λ0 and λ1 must be different in the 10 scenarios. For each scenario, we considered two levels of dropout rates, about 30% and about 50%, by choosing appropriate values of γ0 and γ1. The dropout rate is defined as the number of patients with missing efficacy outcomes divided by the total number of patients. Under each scenario, we simulated 1,000 trials.
Figure 1.
Dose-response curves for the ten scenarios in the simulation study. The solid and dashed lines are the efficacy and toxicity curves, respectively. Target doses are indicated by arrows.
Tables 1 and 2, differentiated by 30% and 50% dropout rates, respectively, summarize the operating characteristics of the three designs (our proposed design and the EffTox 1 and EffTox 2 designs). Under each scenario, the first row shows the true marginal probabilities of efficacy evaluated at three months and the true probabilities of toxicity, and the second to fourth rows show the selection probability and the average number of patients treated (in parentheses) at each dose under the three designs. The right-most column in each table shows the average trial duration. In the first 5 scenarios, efficacy increases with dose and there is only one target dose. The difference between these scenarios is the location of the target dose. In scenario 1, toxicity shows a sudden increase from dose level 1 to dose level 2. The target dose is the first dose as it is the only dose satisfying both physician-specified toxicity and efficacy criteria. Under both levels of dropout rates, the proposed design led to slightly lower selection percentage and patient allocation at the target dose than the EffTox 1 design. However, the trial duration under the proposed design was much shorter than that under the EffTox 1 design, because the proposed design eliminated the need to temporarily suspend patient accrual by modeling efficacy as a time-to-event outcome rather than a binary outcome (as in EffTox1 and EffTox2). The EffTox 2 design was overly aggressive and selected dose level 2 over 50% of the time. In scenario 2, the proposed design resulted in slightly lower and higher target dose selection percentage and patient allocation than EffTox 1 design with 30% and 50% dropout rates, respectively. Again, the EffTox 2 design was overly aggressive; and compared to the EffTox 1 and 2 designs, the proposed design substantially shortened the trial duration. In scenarios 3–5, the target doses are dose levels 3, 4, and 5, respectively. For these three scenarios, the proposed design outperformed the two EffTox designs under both dropout rates, and with 50% dropout, the advantage of the proposed method was even more pronounced. For example, in scenario 4, with 30% dropout, the proposed design had a target dose selection percentage that was 7.1% and 6.8% higher than EffTox 1 and 2 designs, respectively. With 50% dropout, the differences were 18.9% and 19.6%, respectively.
Table 1.
Selection percentage and the average number of patients (shown in parentheses) treated at each dose level under the proposed design and EffTox 1 and 2 designs with dropout rate about 30%. The bolded numbers are target doses.
| Design | Dose level | Duration (months) |
||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Scenario 1 | ||||||
| (πE, πT) | (0.42, 0.05) | (0.45, 0.45) | (0.46, 0.65) | (0.47, 0.75) | (0.48, 0.85) | |
| Proposed | 78.2 (25.4) | 18.3 (22.0) | 0.1 (2.3) | 0.0 (0.1) | 0.0 (0.0) | 22.2 |
| EffTox1 | 81.6 (27.8) | 14.6 (18.8) | 0.0 (2.5) | 0.0 (0.2) | 0.0 (0.0) | 35.7 |
| EffTox2 | 26.8 (10.8) | 54.5 (22.3) | 12.2 (11.3) | 3.9 (4.9) | 1.5 (1.3) | 29.1 |
| Scenario 2 | ||||||
| (πE, πT) | (0.41, 0.03) | (0.48, 0.13) | (0.56, 0.45) | (0.63, 0.77) | (0.7, 0.89) | |
| Proposed | 3.3 (4.8) | 83.1 (28.3) | 13.1 (16.0) | 0.1 (1.8) | 0.0 (0.1) | 23.1 |
| EffTox1 | 5.2 (5.7) | 85.9 (28.9) | 8.7 (14.0) | 0.0 (2.2) | 0.0 (0.1) | 35.1 |
| EffTox2 | 1.4 (3.8) | 57.6 (18.6) | 40.6 (22.9) | 0.2 (5.0) | 0.2 (0.7) | 32.7 |
| Scenario 3 | ||||||
| (πE, πT) | (0.3, 0.01) | (0.36, 0.05) | (0.43, 0.17) | (0.51, 0.45) | (0.6, 0.77) | |
| Proposed | 2.1 (4.0) | 10.8 (7.9) | 74.5 (25.5) | 11.8 (12.2) | 0.1 (1.2) | 25.2 |
| EffTox1 | 2.9 (4.2) | 16.4 (9.7) | 74.3 (24.1) | 5.7 (10.8) | 0.0 (1.9) | 38.4 |
| EffTox2 | 0.2 (3.2) | 2.5 (4.5) | 61.4 (17.6) | 35.4 (19.5) | 0.5 (6.2) | 34.2 |
| Scenario 4 | ||||||
| (πE, πT) | (0.21, 0.01) | (0.26, 0.04) | (0.32, 0.1) | (0.38, 0.23) | (0.46, 0.47) | |
| Proposed | 1.6 (3.8) | 8.2 (6.4) | 18.0 (10.1) | 61.8 (21.2) | 7.9 (8.7) | 26.7 |
| EffTox1 | 1.6 (3.9) | 11.2 (7.4) | 26.9 (12.1) | 54.7 (18.9) | 4.0 (8.2) | 42.3 |
| EffTox2 | 0.4 (3.2) | 3.3 (4.9) | 13.7 (7.6) | 55.0 (17.4) | 27.6 (17.9) | 40.2 |
| Scenario 5 | ||||||
| (πE, πT) | (0.11, 0.03) | (0.17, 0.04) | (0.24, 0.04) | (0.34, 0.05) | (0.45, 0.06) | |
| Proposed | 0.1 (3.5) | 2.4 (4.4) | 6.3 (6.1) | 11.3 (7.2) | 75.2 (28.5) | 27.0 |
| EffTox1 | 0.5 (3.4) | 3.5 (4.7) | 9.9 (6.8) | 16.7 (8.8) | 66.8 (26.3) | 40.2 |
| EffTox2 | 0.3 (3.4) | 2.1 (4.2) | 8.8 (5.7) | 18.5 (6.9) | 69.9 (30.7) | 40.2 |
| Scenario 6 | ||||||
| (πE, πT) | (0.4, 0.03) | (0.4, 0.3) | (0.4, 0.5) | (0.4, 0.65) | (0.4, 0.8) | |
| Proposed | 25.3 (12.2) | 70.0 (30.3) | 2.9 (7.0) | 0.0 (0.9) | 0.0 (0.0) | 23.1 |
| EffTox1 | 31.3 (13.0) | 64.8 (28.3) | 1.4 (7.4) | 0.0 (1.3) | 0.0 (0.1) | 38.4 |
| EffTox2 | 12.4 (7.1) | 69.3 (25.5) | 16.9 (13.6) | 1.1 (3.7) | 0.0 (0.9) | 38.1 |
| Scenario 7 | ||||||
| (πE, πT) | (0.12, 0.03) | (0.3, 0.04) | (0.57, 0.04) | (0.3, 0.05) | (0.12, 0.06) | |
| Proposed | 0.5 (3.8) | 20.4 (11.1) | 66.5 (21.0) | 8.2 (7.8) | 0.8 (6.2) | 26.4 |
| EffTox1 | 0.4 (3.8) | 24.3 (12.3) | 57.2 (19.0) | 11.7 (8.3) | 1.6 (6.2) | 40.5 |
| EffTox2 | 0.9 (3.6) | 19.9 (9.7) | 56.3 (18.4) | 19.6 (10.2) | 3.0 (9.0) | 41.4 |
| Scenario 8 | ||||||
| (πE, πT) | (0.27, 0.02) | (0.52, 0.03) | (0.3, 0.05) | (0.24, 0.06) | (0.2, 0.07) | |
| Proposed | 8.6 (7.2) | 56.5 (19.0) | 18.5 (10.8) | 8.9 (6.7) | 5.1 (6.9) | 26.7 |
| EffTox1 | 7.3 (6.6) | 53.6 (19.2) | 21.3 (10.8) | 8.7 (6.4) | 7.0 (7.3) | 41.7 |
| EffTox2 | 4.4 (5.6) | 48.2 (16.3) | 25.5 (11.3) | 15.6 (8.2) | 6.3 (9.6) | 42.6 |
| Scenario 9 | ||||||
| (πE, πT) | (0.01, 0.01) | (0.02, 0.01) | (0.03, 0.01) | (0.04, 0.01) | (0.05, 0.3) | |
| Proposed | 0.0 (3.4) | 0.0 (3.5) | 0.0 (3.3) | 0.0 (3.8) | 0.3 (7.8) | 19.8 |
| EffTox1 | 1.0 (3.3) | 0.6 (3.4) | 0.1 (3.2) | 0.0 (3.7) | 3.0 (7.5) | 21.3 |
| EffTox2 | 1.8 (3.5) | 3.5 (3.7) | 2.5 (3.9) | 4.0 (4.6) | 16.0 (16.2) | 30.6 |
| Scenario 10 | ||||||
| (πE, πT) | (0.1, 0.01) | (0.3, 0.01) | (0.05, 0.01) | (0.05, 0.01) | (0.05, 0.3) | |
| Proposed | 4.4 (8.9) | 35.3 (13.8) | 0.8 (4.8) | 0.1 (4.3) | 0.5 (6.7) | 25.5 |
| EffTox1 | 6.6 (8.2) | 30.6 (12.2) | 0.6 (4.1) | 0.1 (4.1) | 2.7 (6.4) | 33.9 |
| EffTox2 | 9.6 (8.5) | 53.1 (16.5) | 4.1 (5.4) | 1.5 (4.7) | 3.6 (9.2) | 41.7 |
Table 2.
Selection percentage and the average number of patients (shown in parentheses) treated at each dose level under the proposed design and EffTox 1 and 2 designs with dropout rate about 50%. The bolded numbers are target doses.
| Design | Dose level | Duration (months) |
||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Scenario 1 | ||||||
| (πE, πT) | (0.42, 0.05) | (0.45, 0.45) | (0.46, 0.65) | (0.47, 0.75) | (0.48, 0.85) | |
| Proposed | 75.7 (24.5) | 19.8 (22.3) | 0.0 (2.4) | 0.0 (0.2) | 0.0 (0.0) | 21.0 |
| EffTox1 | 78.9 (27.6) | 16.0 (18.6) | 0.0 (2.7) | 0.0 (0.2) | 0.0 (0.0) | 30.6 |
| EffTox2 | 21.2 (9.5) | 52.3 (20.8) | 17.7 (13.6) | 5.8 (4.9) | 1.2 (1.4) | 23.4 |
| Scenario 2 | ||||||
| (πE, πT) | (0.41, 0.03) | (0.48, 0.13) | (0.56, 0.45) | (0.63, 0.77) | (0.7, 0.89) | |
| Proposed | 3.6 (5.0) | 82.6 (28.3) | 13.1 (15.9) | 0.0 (1.6) | 0.0 (0.0) | 21.9 |
| EffTox1 | 10.2 (7.1) | 81.0 (28.0) | 7.9 (13.4) | 0.2 (2.1) | 0.0 (0.1) | 29.7 |
| EffTox2 | 2.3 (3.6) | 54.8 (17.3) | 41.4 (24.1) | 1.0 (5.0) | 0.0 (0.8) | 26.7 |
| Scenario 3 | ||||||
| (πE, πT) | (0.3, 0.01) | (0.36, 0.05) | (0.43, 0.17) | (0.51, 0.45) | (0.6, 0.77) | |
| Proposed | 2.4 (4.1) | 13.7 (8.8) | 71.7 (24.8) | 11.6 (11.8) | 0.0 (1.2) | 23.4 |
| EffTox1 | 4.7 (5.2) | 27.9 (13.5) | 62.1 (21.5) | 4.0 (8.6) | 0.0 (1.7) | 31.8 |
| EffTox2 | 0.2 (3.1) | 3.9 (3.9) | 50.1 (15.6) | 42.1 (20.7) | 3.6 (7.6) | 25.5 |
| Scenario 4 | ||||||
| (πE, πT) | (0.21, 0.01) | (0.26, 0.04) | (0.32, 0.1) | (0.38, 0.23) | (0.46, 0.47) | |
| Proposed | 1.1 (3.7) | 6.9 (6.1) | 20.2 (10.5) | 62.9 (21.7) | 7.1 (8.5) | 24.9 |
| EffTox1 | 3.0 (4.7) | 15.0 (8.6) | 29.2 (12.7) | 44.0 (17.0) | 5.2 (7.2) | 35.4 |
| EffTox2 | 0.5 (3.3) | 2.9 (3.9) | 14.8 (7.2) | 43.3 (15.9) | 38.5 (20.7) | 30.6 |
| Scenario 5 | ||||||
| (πE, πT) | (0.11, 0.03) | (0.17, 0.04) | (0.24, 0.04) | (0.34, 0.05) | (0.45, 0.06) | |
| Proposed | 0.0 (3.5) | 3.5 (4.6) | 7.5 (6.3) | 14.1 (8.0) | 71.6 (27.7) | 25.5 |
| EffTox1 | 0.5 (3.5) | 3.0 (4.7) | 11.2 (7.3) | 16.8 (8.8) | 64.3 (25.4) | 35.4 |
| EffTox2 | 1.1 (3.5) | 4.0 (4.3) | 7.9 (5.5) | 27.0 (7.8) | 59.5 (29.7) | 35.1 |
| Scenario 6 | ||||||
| (πE, πT) | (0.4, 0.03) | (0.4, 0.3) | (0.4, 0.5) | (0.4, 0.65) | (0.4, 0.8) | |
| Proposed | 23.4 (11.6) | 70.8 (30.4) | 2.9 (7.1) | 0.0 (0.9) | 0.0 (0.1) | 22.2 |
| EffTox1 | 29.5 (12.6) | 64.4 (28.2) | 2.2 (7.3) | 0.0 (1.2) | 0.0 (0.1) | 33.3 |
| EffTox2 | 10.5 (6.8) | 66.5 (24.9) | 20.2 (13.8) | 2.2 (4.3) | 0.2 (1.0) | 33.6 |
| Scenario 7 | ||||||
| (πE, πT) | (0.12, 0.03) | (0.3, 0.04) | (0.57, 0.04) | (0.3, 0.05) | (0.12, 0.06) | |
| Proposed | 0.5 (3.9) | 22.6 (11.5) | 62.4 (19.9) | 8.3 (7.9) | 1.7 (6.7) | 24.3 |
| EffTox1 | 1.9 (4.1) | 26.3 (13.1) | 52.8 (17.7) | 10.3 (7.3) | 1.8 (6.7) | 33.6 |
| EffTox2 | 2.0 (3.6) | 23.3 (7.6) | 48.4 (14.3) | 23.3 (10.7) | 2.5 (14.7) | 35.1 |
| Scenario 8 | ||||||
| (πE, πT) | (0.27, 0.02) | (0.52, 0.03) | (0.3, 0.05) | (0.24, 0.06) | (0.2, 0.07) | |
| Proposed | 8.8 (7.1) | 55.7 (18.7) | 19.6 (11.3) | 8.3 (6.2) | 5.9 (7.4) | 24.9 |
| EffTox1 | 7.7 (6.9) | 50.6 (18.1) | 23.7 (11.2) | 8.0 (6.2) | 6.5 (7.6) | 35.1 |
| EffTox2 | 4.2 (5.0) | 35.7 (11.5) | 35.6 (11.2) | 19.9 (9.4) | 4.1 (13.7) | 36.6 |
| Scenario 9 | ||||||
| (πE, πT) | (0.01, 0.01) | (0.02, 0.01) | (0.03, 0.01) | (0.04, 0.01) | (0.05, 0.3) | |
| Proposed | 0.0 (3.3) | 0.0 (3.5) | 0.0 (3.4) | 0.2 (4.1) | 0.4 (8.0) | 19.5 |
| EffTox1 | 0.7 (3.3) | 0.5 (3.3) | 0.1 (3.2) | 0.0 (3.7) | 2.9 (7.8) | 20.7 |
| EffTox2 | 1.8 (3.4) | 3.6 (3.8) | 6.1 (3.9) | 8.8 (5.4) | 20.1 (19.9) | 33.3 |
| Scenario 10 | ||||||
| (πE, πT) | (0.1, 0.01) | (0.3, 0.01) | (0.05, 0.01) | (0.05, 0.01) | (0.05, 0.3) | |
| Proposed | 5.6 (8.3) | 37.8 (14.4) | 0.5 (5.2) | 0.3 (4.4) | 1.0 (7.0) | 24.9 |
| EffTox1 | 7.2 (8.0) | 25.8 (10.8) | 0.6 (4.2) | 0.1 (4.0) | 1.9 (6.3) | 30.9 |
| EffTox2 | 11.7 (7.5) | 52.3 (15.2) | 7.6 (5.6) | 4.5 (5.2) | 7.1 (13.5) | 42.0 |
Scenario 6 simulated the case in which there were two target doses (i.e., dose levels 1 and 2). Under both levels of dropout rates, the proposed and EffTox 1 designs led to similar selection percentages and patient allocations. The performances of these two designs were fairly robust across the two levels of dropout rates. EffTox 2 selected the overly toxic dose level 3 16.9% and 20.2% of the time. Scenarios 7 and 8 were designed for biological agents with efficacy probabilities first increasing and then decreasing. In scenario 7, the proposed design yielded about 10% higher target dose selection percentage than the two EffTox designs and also allocated more patients to the target dose. In scenario 8, the proposed design resulted in slightly higher target dose selection percentage than the EffTox 1 design, and much higher target dose selection than EffTox 2 design, especially with 50% dropout. In scenario 9, none of the 5 doses is efficacious. The proposed design early terminated the trial 99.7% (or 99.4%) of the time when the dropout rate was 30% (or 50%). Scenario 10 is a difficult case because there is only one admissible dose (i.e., dose level 2; the other doses are inadmissible due to low efficacy) and its efficacy probability (πE = 0.3) is just slightly above the lower bound ϕE = 0.25. As a result, both our design and EffTox design led to high (> 50%) inconclusive trials (i.e., the trial was terminated early because none of the doses was estimated as admissible). Nevertheless, given the simulated trials that were not early terminated, the proposed design was most likely to select the target dose (35% versus < 6% for other doses).
4.2. Sensitivity Analyses
To examine the robustness of our design, we conducted sensitivity analyses by (a) simulating the times to efficacy and dropout from the proportional hazards models with Weibull distribution baselines, and from the accelerated failure time models with a log-logistic error. With Weibull models, we considered two shapes (increasing and decreasing) of hazard for the times to efficacy and dropout, resulting in a total of 4 simulation settings. Using the accelerated failure time model with a log-logistic error, we considered three shapes of hazard for efficacy (increasing, decreasing, and hump-shaped) and an increasing shape of hazard for dropout, resulting in 3 situations. For the sensitivity analyses, we matched the marginal probabilities of efficacy, toxicity and dropout to the scenarios with dropout rate of 30%, as shown in Table 1. (b) evaluating the performance of the proposed design in the case of no dropout. (c) considering interaction between toxicity and dose. In the previous section, by simulating patient’s outcomes from (6) and (7), we assumed that there was no interaction between dose and toxicity. In order to assess the robustness of our proposed design to the situation where the true models involve dose-toxicity interactions, we simulated 2 scenarios from the following models,
| (8) |
| (9) |
where j = 0, 1, k = 1, …, 5. By using the above models, interaction between dose and toxicity exists. We simulated two representative scenarios, one with increasing efficacy probabilities and one with efficacy probabilities first increasing then decreasing.
Table 3 reports the operating characteristics of the proposed design when the times to events were generated from Weibull models or accelerated failure time models. We show two representative scenarios: scenario 1 and scenario 2. Across all simulation settings, the results are similar to the original simulation results provided in Table 1. Our design selected the target dose with the largest probability and assigned the largest number of patients to the target dose. These results suggest that our proposed design is robust to violations of the proportional hazards assumption and is not sensitive to mis-specifications of the baseline hazards. Table 4 shows the operating characteristics of the proposed design, EffTox 1 and 2 designs for scenarios 1, 2, and 3, with no dropout. All three designs gave reasonable performance. Table 5 presents results with dose-toxicity interactions. In scenario 1, the target dose is dose level 4, and the efficacy probabilities increase with dose. In scenario 2, the target dose is dose level 3, and the efficacy probabilities first increase then decrease. In both scenarios, our proposed design selected the target dose with probabilities > 60% and treated the largest number of patients at the target dose.
Table 3.
Sensitivity analysis when baseline hazard follows Weibull distribution and when the times to efficacy and dropout follow an accelerated failure time model with a log-logistic error. The bolded numbers are target doses.
| Weibull distribution | Duration (months) |
||||||
|---|---|---|---|---|---|---|---|
| Efficacy | Dropout | Scenario 1 | |||||
| increasing | decreasing | 77.7 (25.9) | 18.2 (21.4) | 0.0 (2.4) | 0.0 (0.1) | 0.0 (0.0) | 22.1 |
| increasing | increasing | 77.6 (25.8) | 19.4 (21.6) | 0.1 (2.3) | 0.0 (0.2) | 0.0 (0.0) | 22.1 |
| decreasing | increasing | 77.4 (26.3) | 20.1 (21.2) | 0.1 (2.5) | 0.0 (0.2) | 0.0 (0.0) | 22.3 |
| decreasing | decreasing | 78.1 (26.0) | 19.2 (21.6) | 0.0 (2.4) | 0.0 (0.1) | 0.0 (0.0) | 22.0 |
| Scenario 2 | |||||||
| increasing | decreasing | 3.5 (4.9) | 81.0 (28.0) | 14.6 (16.2) | 0.1 (1.6) | 0.0 (0.0) | 23.2 |
| increasing | increasing | 2.6 (4.8) | 82.9 (28.2) | 13.1 (15.8) | 0.0 (1.6) | 0.0 (0.0) | 23.2 |
| decreasing | increasing | 3.2 (4.9) | 83.6 (28.0) | 12.9 (16.3) | 0.0 (1.6) | 0.0 (0.1) | 23.2 |
| decreasing | decreasing | 3.5 (5.0) | 82.6 (28.5) | 12.9 (15.7) | 0.1 (1.5) | 0.1 (0.0) | 22.7 |
| Accelerated failure time model | |||||||
| Efficacy | Dropout | Scenario 1 | |||||
| increasing | increasing | 75.9 (25.7) | 17.3 (20.8) | 0.0 (2.2) | 0.0 (0.1) | 0.1 (0.0) | 22.3 |
| decreasing | increasing | 76.4 (25.4) | 21.4 (22.1) | 0.0 (2.4) | 0.0 (0.2) | 0.0 (0.0) | 22.6 |
| hump shaped | increasing | 78.1 (26.5) | 17.8 (20.4) | 0.0 (2.3) | 0.0 (0.1) | 0.0 (0.0) | 22.4 |
| Scenario 2 | |||||||
| increasing | increasing | 4.3 (5.3) | 80.9 (28.4) | 13.0 (15.1) | 0.2 (1.6) | 0.0 (0.0) | 24.1 |
| decreasing | increasing | 2.4 (4.6) | 85.0 (29.2) | 11.8 (15.3) | 0.1 (1.6) | 0.0 (0.0) | 23.4 |
| hump shaped | increasing | 2.9 (4.9) | 83.6 (27.8) | 12.7 (16.3) | 0.0 (1.6) | 0.0 (0.0) | 23.5 |
Table 4.
Selection percentage and the average number of patients (shown in parentheses) treated at each dose level under the proposed design and EffTox 1 and 2 designs for scenarios 1, 2, and 3, with no dropout. The bolded numbers are target doses.
| Design | Dose level | Duration (months) |
||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Scenario 1 | ||||||
| (πE, πT) | (0.42, 0.05) | (0.45, 0.45) | (0.46, 0.65) | (0.47, 0.75) | (0.48, 0.85) | |
| Proposed | 80.4 (27.3) | 15.9 (20.1) | 0.1 (2.3) | 0.0 (0.2) | 0.0 (0.0) | 24.3 |
| EffTox1 | 77.3 (26.1) | 20.1 (20.7) | 0.1 (3.0) | 0.0 (0.3) | 0.0 (0.0) | 47.7 |
| EffTox2 | 77.3 (26.1) | 20.1 (20.7) | 0.1 (3.0) | 0.0 (0.3) | 0.0 (0.0) | 47.7 |
| Scenario 2 | ||||||
| (πE, πT) | (0.41, 0.03) | (0.48, 0.13) | (0.56, 0.45) | (0.63, 0.77) | (0.7, 0.89) | |
| Proposed | 3.0 (4.9) | 83.7 (28.4) | 12.8 (16.0) | 0.1 (1.5) | 0.0 (0.0) | 25.8 |
| EffTox1 | 2.1 (4.3) | 87.4 (27.7) | 10.4 (16.5) | 0.0 (2.3) | 0.0 (0.1) | 47.1 |
| EffTox2 | 2.1 (4.3) | 87.4 (27.7) | 10.4 (16.5) | 0.0 (2.3) | 0.0 (0.1) | 47.1 |
| Scenario 3 | ||||||
| (πE, πT) | (0.3, 0.01) | (0.36, 0.05) | (0.43, 0.17) | (0.51, 0.45) | (0.6, 0.77) | |
| Proposed | 1.3 (3.9) | 6.6 (6.6) | 80.5 (26.0) | 10.2 (12.9) | 0.0 (1.3) | 27.3 |
| EffTox1 | 0.6 (3.5) | 4.1 (5.6) | 84.8 (26.0) | 9.8 (13.6) | 0.0 (2.0) | 48.0 |
| EffTox2 | 0.6 (3.5) | 4.1 (5.6) | 84.8 (26.0) | 9.8 (13.6) | 0.0 (2.0) | 48.0 |
Table 5.
Selection percentage and the average number of patients (shown in parentheses) treated at each dose level under the proposed design with dose-toxicity interactions, with dropout rate about 30%. The bolded numbers are target doses.
| Design | Dose level | Duration (months) |
||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Scenario 1 | ||||||
| (πE, πT) | (0.24, 0.01) | (0.28, 0.04) | (0.32, 0.1) | (0.43, 0.23) | (0.57, 0.47) | |
| Proposed | 1.3 (3.8) | 8.4 (6.3) | 18.4 (10.3) | 61.8 (21.1) | 9.2 (9.2) | 27.0 |
| Scenario 2 | ||||||
| (πE, πT) | (0.13, 0.02) | (0.32, 0.04) | (0.59, 0.08) | (0.33, 0.13) | (0.15, 0.21) | |
| Proposed | 0.6 (3.6) | 17.3 (9.7) | 66.4 (21.4) | 12.2 (9.9) | 1.7 (5.9) | 26.1 |
5. Conclusions
We have proposed a Bayesian dose-finding design for phase I/II clinical trials with non-ignorable dropouts. We assume that toxicity is quickly ascertainable and always observable, while efficacy takes a relatively long time to be assessed and is subject to missing data due to patient dropout. We treat toxicity as a binary outcome and efficacy as a time-to-event outcome. To account for the non-ignorable dropout, we jointly consider the time-to-dropout process. We model the marginal distribution of toxicity using a logistic regression and jointly model the time to efficacy and time to dropout using proportional hazard models. We use a shared frailty to capture the correlation between the times to efficacy and dropout. We propose a two-stage dose-finding algorithm to assign patients to desirable doses and select the target dose. Simulation studies show that the proposed design is robust and has good operating characteristics.
For some clinical applications, the assumption that toxicity is quickly ascertainable and always observable may be violated. For example, in radiotherapy, toxicity may be of late onset and thus may take a long time to be observed. As a result, both the toxicity and efficacy outcomes may be subject to missingness due to patient dropout. To handle these cases, we can extend the proposed method by modeling toxicity as another time-to-event outcome, and jointly model the trivariate time-to-event outcomes (i.e., times to toxicity, efficacy and dropout), using, for example, a copula method [15].
Acknowledgements
The authors thank the Associate Editor and two reviewers for very insightful and constructive comments that substantially improved the paper. Yuan’s research was partially supported by grants CA154591, CA016672 and 5P50CA098258 from the National Cancer Institute.
References
- 1.Gooley TA, Martin PJ, Fisher LD, Pettinger M. Simulating as a design tool for phase I/II clinical trials: An example from bone marrow transplantation. Controlled Clinical Trials. 1994;15:450–462. doi: 10.1016/0197-2456(94)90003-5. [DOI] [PubMed] [Google Scholar]
- 2.O’Quigley J, Hughes MD, Fenton T. Dose-finding designs for HIV studies. Biometrics. 2001;57:1018–1029. doi: 10.1111/j.0006-341x.2001.01018.x. [DOI] [PubMed] [Google Scholar]
- 3.Thall P, Cook J. Dose-finding based on efficacy-toxicity trade-offs. Biometrics. 2004;60:684–693. doi: 10.1111/j.0006-341X.2004.00218.x. [DOI] [PubMed] [Google Scholar]
- 4.Yin G, Li Y, Ji Y. Bayesian Dose-Finding in Phase I/II Clinical Trials Using Toxicity and Efficacy Odds Ratios. Biometrics. 2006;62:777–784. doi: 10.1111/j.1541-0420.2006.00534.x. [DOI] [PubMed] [Google Scholar]
- 5.Yuan Y, Yin G. Bayesian dose finding by jointly modeling toxicity and efficacy as time-to-event outcomes. Journal of the Royal Statistical Society, Series C. 2009;58:719736. [Google Scholar]
- 6.Mandrekar SJ, Cui Y, Sargent DJ. An adaptive phase I design for identifying a biologically optimal dose for dual agent drug combinations. Statistics in Medicine. 2007;26:2317–2330. doi: 10.1002/sim.2707. [DOI] [PubMed] [Google Scholar]
- 7.Yuan Y, Yin G. Bayesian phase I/II drug-combination trial design in oncology. Annals of Applied Statistics. 2011;5:156–174. doi: 10.1214/10-AOAS433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cai C, Yuan Y, Ji Y. A Bayesian dose finding design for oncology clinical trials of combinational biological agents. Journal of the Royal Statistical Society, Series C. 2014;63:159–173. doi: 10.1111/rssc.12039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.O’Quigley J, Zohar S. Experimental designs for phase I and phase I/II dose-finding studies. British Journal of Cancer. 2006;94:609–613. doi: 10.1038/sj.bjc.6602969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cullen M, Billingham LJ, Woodroffe CM, et al. Mitomycin, ifosfamide, and cisplatin in unresectable nonsmall-cell lung cancer: effects on survival and quality of life. Journal of Clinical Oncology. 1999;17:3188–3194. doi: 10.1200/JCO.1999.17.10.3188. [DOI] [PubMed] [Google Scholar]
- 11.Marchetti M, Barosi G, Balestri F, et al. Low-dose thalidomide ameliorates cytopenias and spenomegaly in myelofibrosis with myeloid metaplasia: a phase II trial. Journal of Clinical Oncology. 2004;22:424–431. doi: 10.1200/JCO.2004.08.160. [DOI] [PubMed] [Google Scholar]
- 12.Little RJA, Rubin DB. Statistical analysis with missing data. New York: Wiley; 2002. [Google Scholar]
- 13.Cox DR. Regression models and life-tables (with discussion) Journal of the Royal Statistical Society, Series B. 1972;34:187–220. [Google Scholar]
- 14.O’Quigley J, Pepe M, Fisher L. Continual reassessment method: a practical design for phase I clinical trials in cancer. Biometrics. 1990;46:33–48. [PubMed] [Google Scholar]
- 15.Nelsen RB. An introduction to copulas. New York: Springer; 2007. [Google Scholar]