Abstract
Cellular differentiation and evolution are stochastic processes that can involve multiple types (or states) of particles moving on a complex, high-dimensional state-space or “fitness” landscape. Cells of each specific type can thus be quantified by their population at a corresponding node within a network of states. Their dynamics across the state-space network involve genotypic or phenotypic transitions that can occur upon cell division, such as during symmetric or asymmetric cell differentiation, or upon spontaneous mutation. Here, we use a general multi-type branching processes to study first passage time statistics for a single cell to appear in a specific state. Our approach readily allows for nonexponentially distributed waiting times between transitions, reflecting, e.g., the cell cycle. For simplicity, we restrict most of our detailed analysis to exponentially distributed waiting times (Poisson processes). We present results for a sequential evolutionary process in which L successive transitions propel a population from a “wild-type” state to a given “terminally differentiated,” “resistant,” or “cancerous” state. Analytic and numeric results are also found for first passage times across an evolutionary chain containing a node with increased death or proliferation rate, representing a desert/bottleneck or an oasis. Processes involving cell proliferation are shown to be “nonlinear” (even though mean-field equations for the expected particle numbers are linear) resulting in first passage time statistics that depend on the position of the bottleneck or oasis. Our results highlight the sensitivity of stochastic measures to cell division fate and quantify the limitations of using certain approximations (such as the fixed-population and mean-field assumptions) in evaluating fixation times.
Keywords: Stochastic evolution, Bellman-Harris branching process, bottleneck, oasis, fixation times
1. Introduction
Stochastic models of populations are commonly applied to biological processes such as stem cell dynamics [1, 2], tumorigenesis [3, 4, 5, 6, 7, 8], cellular aging [9], and organismal evolution [10, 11]. In such applications, one is often interested in the statistics of the time it takes for members of a population to first arrive at a specific “absorbing” state. Such a state may represent, for example, a high fitness phenotype that eventually takes over the entire population.
A classic biomedical application of first passage times of a single conserved entity arises in models of cancer progression that attempt to describe the survival probability of patients as a function of time after initial diagnosis or treatment. In the Knudsen hypothesis of cancer progression (illustrated in Fig. 1) [12, 13], an individual acquires a certain number of sequential mutations or “hits” before acquiring cancer [14, 15, 5]. If multiple rare transitions are required before onset of disease, we can define the probability of transition from state ℓ to state ℓ + 1 in time dt as wℓ(t)dt. The overall waiting-time distribution W(t) to first arrive at the diseased state ℓ = L + 1 is a convolution of all the wℓ(t) and can be easily expressed using Laplace transforms: . Since each mutation is considered rare, the event times of each mutation are exponentially distributed. If all transitions occur at the same rate, k0 = k1 = … = k, wℓ(t) = ke−kt, and W̃(s) = kL/(s + k)L. The inverse Laplace transform then gives [16]
Figure 1.

Multistage model in disease progression. When multiple steps are before the system reaches diseased state L + 1, an L-fold convolution of the state-dependent individual waiting time distributions provides the overall waiting time distribution and the survival probability against disease.
| (1) |
This expression assumes that all the transition rates are equally rate-limiting. If kt ≪ 1, the survival probability against disease onset is approximately
| (2) |
If sufficiently accurate fitting of this expression to measured S(t) can be performed, the number of mutations, or “hits” L before onset of cancer can be inferred. Using this Knudsen hypothesis [14], typical cancers have yielded L ~ 4 – 15 or higher [17, 18].
Such studies implicitly assume a “single-particle” picture of a conserved random walker that eventually reaches a target. On a cellular level this picture is appropriate for a single immortal and nonproliferating cell that successively acquires different mutations. Estimates and scaling relationships of first passage times of conserved particles on complex networks have been developed in more general contexts [19, 20]. Similar results have been developed for a fixed multiple number of noninteracting particles [21]. Inverse problems (similar to the inference of the number of mutations in Knudsen’s hypothesis) have also been recently explored. Li, Kolomeisky, and Valleriani [22] considered how first passage times of a conserved random walker can be used to estimate the shortest paths to the absorbing site, even for nonexponentially distributed waiting times between jumps within the network. First passage times of Brownian motion and random walks have also been used to infer properties of continuous energy landscapes [23, 24].
If a network is finite, and all nodes are connected, conserved particles will always arrive at an absorbing state and the survival probability S(t → ∞) → 0. However, in the presence of other pathways for particle annihilation, the absorbing site may never be reached. Additional particles need to be continuously injected into the network in order for one of them to eventually arrive with certainty at a specific absorbing state [25]. Alternative annihilation pathways and immigration lift the fixed population constraint and is an essential feature in cell and population biology.
Going beyond single-particle picture, the classic Wright-Fisher and Moran models of evolution consider a population of organisms distributed between two states [10]. Evolution across multiple states or fitness levels have also been explored in models of stochastic tunneling [26, 27, 28]. Many of these models impose a fixed mean population and do not resolve the possible microscopic transitions an organism can take during the evolution process. These differences in the “microscopic” mechanisms of evolution are especially distinguishable in cell biology, in which changes in genotype or phenotype can arise spontaneously in an individual cell, or from symmetric or asymmetric replication. Different cell fates are clearly important in the context of stem cell differentiation and cancer [11, 8, 2, 29]. Moreover, due to cell death, cell populations typically have high turnover within the timescale of their evolution. Therefore, the total instantaneous population need not be fixed, even if the ensemble-averaged population remains constant. We shall see that the different transitions inherent in cellular differentiation and evolution, as well as fluctuations in population, can qualitatively affect fixation times.
We begin by considering a whole population of cells or “particles” in a network. Fixation in this context will be defined by a single cell or particle first arriving at an absorbing node. Absorbing nodes can represent, for example, terminally differentiated, fully drug-resistant, or highly fit, fully cancerous states. We first treat only a noninteracting population and temporarily neglect any regulation or population constraint such as carrying capacity. The analysis is simplified when the total population is unconstrained; however, we will extend mathematical framework in order to resolve the effects of different types of allowed transitions. To describe the evolution of a whole population of cells and their arrival times to the absorbing nodes, we exploit a multi-type Bellman-Harris branching process that allows for general distributions of waiting times between transition events [30, 10, 31]. Our approach is related the analysis of Portier, Sherman, and Kopp-Schneider [4] and the simulations of Sherman and Portier [3], but we provide numerical, asymptotic, and exact mean-field results to illustrate the effects of microscopic transformations and the different ordering of their rates. New approximations for analyzing processes constrained by carrying capacity are also developed.
In the next section, for completeness, we present the continuous-time semi-Markov multi-type branching formalism and derive the equations obeyed by the probability generating functions for particle numbers at each node in the network. The corresponding equations for the survival probabilities are then derived. By further assuming exponentially distributed waiting times and a sequential evolution model, we explicitly derive the matrix Riccati equation governing the evolution of survival probabilities in the presence of immigration. In the Results, we present analytic, asymptotic, and numerical results for survival probabilities and mean first passage times. Effects of the probabilities of the different cellular transitions on our results are explored. A breakdown of mean-field theories of survival probabilities (even when particles are noninteracting) is described. Effects of heterogeneity in the transition rates are discussed in the context of evolutionary oases and bottlenecks. The conditions under which the order of the transition rates along the evolutionary chain can affect the survival probabilities and first passage times are investigated. Finally, we summarize our results, discuss related biological applications, and describe extensions and future directions.
2. Mathematical Model
Here, we describe in detail a stochastic multi-type population in the presence of immigration. The general framework is presented before restricting ourselves to exponentially distributed inter-transition times and sequential evolution for a more detailed analysis.
2.1. Multitype Branching Process
Our analysis of the problem is most efficiently performed using an age-dependent multi-type branching process where a parent cell of type k waits a time τ before dividing into a number of cells of possibly different types. Cells with different numbers of mutations, or at different stages of differentiation, can have different distributions of waiting times before proliferation. Moreover, each cell type, upon proliferation, can yield different numbers of new cells. In the analysis of this multi-type branching process, we employ the probability generating function (pgf)
| (3) |
in which z = (z1, z2, …, zL, zL+1) and n = (n1, n2, …, nL, nL+1). Pk(n; t) is the probability at time t the entire population contains nj cells of type j, given that the system started at t = 0 with a single cell of type k. We assume that all daughter cells proliferate independently and that each branching event of a single cell of type k yields m1, m2, …, mL+1 cells of type 1, 2, …, L + 1 with probability a(k)(m1, m2, …, mL+1)≡ a(k)(m).
What equation of evolution does Fk(z; t) obey? For notational simplicity, it is easiest to first consider a single-species branching process described by the simple pgf F (z, t) that corresponds to P(n, t|1, 0), the probability of n particles at time t, given a single parent particle at t = 0. If we now define F(z, t|τ) as the generating function of the process conditioned on the original parent particle having first “branched” between τ and τ + dτ, we write the recursion [10, 30, 32]
| (4) |
where
| (5) |
defines the probability a(m) that a particle splits into m identical particles upon branching. Since this overall process is semi-Markov [33], each daughter behaves as a new parent that issues its own progeny in a statistically equivalent manner to the original parent, giving rise to the compositional form in Eq. 4. We now average Eq. (4) over the distribution of waiting times between branching events, g(τ), to find
| (6) |
This Bellman-Harris branching process [30, 31] is defined by two parameter functions, a(m), the vector of progeny number probabilities, and g(τ), the probability density function (pdf) for waiting times between branching events for each particle. Given a single-particle initial condition, F (z, 0) = z and Eq. 6 can be solved to find a F (z, t), from which P (n, t|1, 0) can be generated.
For our multistate model, we simply generalize Eq. 6 to a multi-type process, where particles at different states constitute different types. The vector of progeny probabilities a(m) now becomes a matrix a(k)(m) coupling the birth of different types of particles from a parent particle of state k. Thus,
| (7) |
is the pgf of the progeny number distribution matrix associated with each branching event. The relationship for the multi-type pgf becomes
| (8) |
where gk(τ)dτ is the probability that a particle of type k branches between time τ and τ + dτ after it was created.
The probability that starting from one parent cell in state k no cell of type L + 1 has formed up to time t is simply . According to the definition of the pgf in Eq. 3, we can extract this survival probability using Sk(t) = Fk(zj≠L+1 = 1, zL+1 → 0+; t). Setting zj≠L+1 = 1 in Eq. 8, we find
| (9) |
where S = {Sj≠L+1} is the vector of survival probabilities initiated by a single cell in state j. Since L + 1 is defined as an absorbing state, we are interested in the first time a particle first arrives at node L + 1. Therefore, by setting AL+1 = 0, we allow particles to only accumulate in state L + 1, and define the survival probability SL+1(t) = FL+1(zi≠ L+1 = 1, zL+1 = 0) = 0. This “boundary condition” in the starting positions, along with the initial conditions Sj≠L+1(t = 0), completely defines the problem for S(t).
Note that our model neglects particle-particle interactions and that the transition probabilities a(k)(m) do not depend on the number of particles in the network. Therefore, all initial particles behave independently and the survival probability associated with a system initiated with N cells at node i = 1 is simply Σ(t) ≡ [S1(t)]N. Provided that no particles leave the network other than through state L + 1, Sk(t → 0) = o(t−1), the mean first arrival time is well-defined. However, if the particle dynamics include death, there can be extinction before node L + 1 is reached, and the mean arrival time T will diverge. In this case, a more useful measure of the speed of evolution would be the mean arrival time conditioned on arrival at L + 1 [25].
A process that ensures arrival to the final state L + 1 is injection of particles from an external source. We can extend the branching process formulation to include immigration of parent particles into the system [34, 35]. Suppose that particles of type i are injected into the system with inter-injection times distributed according to hi(τ). Upon assuming an initially empty network, the pgf for the total particle numbers resulting from independently injecting type i particles is thus [30, 34, 35]
| (10) |
where is the pgf constructed from the probability bi(ni) that ni particles are simultaneously injected into state i during each immigration event. For example, if particles are injected only three-at-a-time into node i, bi(ni) = δni,3. In a cellular biology setting, immigration into the ith state can arise from spontaneous mutation or from mutations acquired during replication of an “external” (not included in the states k) wild-type cell or primordial stem cell. Therefore, , where bi(1) and bi(2) are the probabilities that during each event, one and two cells immigrate into state i, respectively. For example, asymmetric differentiation of a stem cell would produce a single incrementally-differentiated cell (state i) and would be described by the asymmetric differentiation probability bi(1). On the other hand, symmetric differentiation into state i would simultaneously inject two cells into state i and occur at a rate proportional to bi(2). Since these are the only allowed mechanisms of cellular immigration, bi(1)+ bi(2) = 1. In the presence of immigration into all possible stages, the pgf of the total particle number is thus .
Upon using Eqs. 8 and 10 to find Ψ(z; t), one can construct quantities such as the expected number of cells of type k, 〈nk(t)〉 = (∂Ψ(z; t)/∂zk)|z=1, and the probability that no cells have yet reached the fully mutated state i = L + 1: Σ(t) = Ψ(zj≤L = 1, zL+1 → 0; t). Without loss of generality, we henceforth restrict our analysis to immigration only into node i = 1. This limit can be explicitly constructed by letting the times between consecutive immigration into stages i > 1 diverge. For example, if hi≠1(τ) = limTi→∞ δ(τ − Ti), Eq. 10 then yields Φi≠1 → 1 and Ψ(z; t) = Φ1(z; t).
When i = 1, Eq. 10 shows that the overall survival probability Σ(t) in the presence of cell immigration obeys
| (11) |
By solving Eqs. 9 for S1(t) and using the result in Eq. 11, we can find the overall survival probability of an initially empty network after cells begin to immigrate into state i = 1. Since cells are not conserved (in particular, they can die), Sj≠ L+1(t → ∞) need not vanish. However, provided particle injection into state i = 1 persists, the absorbing state will eventually be reached with certainty and Σ(t → ∞) → 0. Depending on the immigration frequency and number of imported particles per injection event, reaching the terminal state may be rate-limited by either the internal dynamics defined by a(k)(m) and g(τ), or by immigration described by bi(ni) and hi(τ). Finally, the mean first passage time (MFPT) can be calculated from [25, 36]
| (12) |
2.2. Exponentially distributed sequential processes
Our results can be simplified if branching and immigration times are exponentially distributed, gj(τ) = λje−λjτ and h1(τ) = β1e−β1τ. After some algebra, Eqs. 9 and 11 become
| (13) |
| (14) |
Thus, the survival probability can be explicitly expressed as
| (15) |
where S1(t) is found from solving Eq. 13.
The analysis can be further simplified by assuming a sequential evolution processes where each division by a cell can yield only daughter cells of the same type or of an incrementally more differentiated (or mutated) type. In other words, when a type k cell attempts to proliferate, either death occurs, or daughters of only type k and/or k + 1 are produced. Consequently, a(k)(m) = 0 for any mj > 0 when j ≠ k, k + 1. Therefore, Fk+1 in Eq. 8 is coupled to Fk through the integrand Ak[F1, F2, …, FL+1], and one must solve for all Fj. To be explicit, if the only possible transitions are those depicted in Fig. 2(a), we find
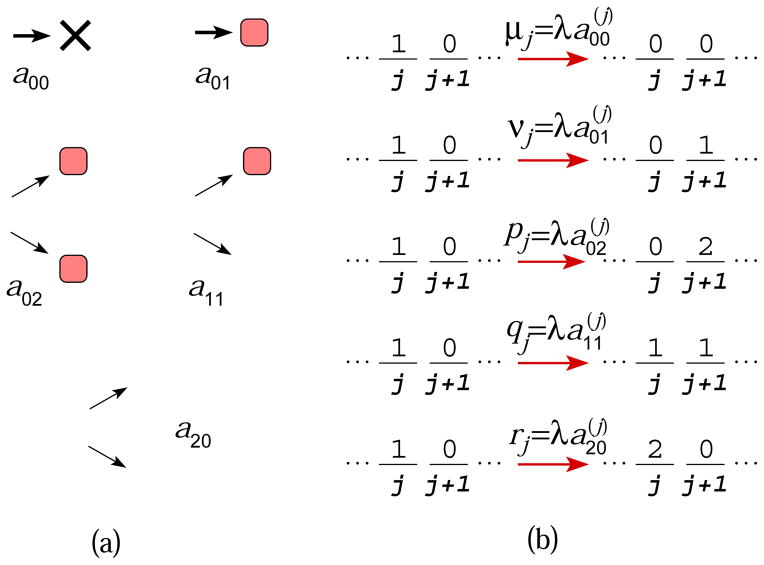
Figure 2.
(a) The five possible transitions of a single cell at an initial stage (white) and their probabilities amn. Dividing cells can produce daughters at a more differentiated or mutated stage (red). Since these are the only possible steps, a00 + a01 + a11 + a20 + a02 = 1. (b) When inter-transition times are exponentially distributed, the rates of each process can be defined in terms of the branching rate and the branching probabilities at each node k.
| (16) |
In the context of cell biology, the probabilities a00, a01, a02, a11 and a20 shown in Fig. 2 represent death, somatic mutation, symmetric differentiation, asymmetric differentiation, and replication after each attempt at cell division. Note that we have not restricted the waiting time distributions for the different transitions. However, for exponentially distributed waiting times, gj(τ) = λje−λjτ, we can define rates for the individual processes by , and , as shown in Fig. 2(b). Similarly, we define α1 = β1b1(1) and α2 = β1b1(2) as the rates of injecting a single particle and double particle into state i = 1, respectively. The values μk, νk, pk, qk, and rk correspond to rates of death, somatic mutation, symmetric differentiation, asymmetric differentiation, and symmetric replication, respectively, of cells in state k.
A sequential evolution model can thus be constructed by assigning a set of transition probabilities at each successive cell state, or node, as shown in Fig. 3. Eq. 13 for Sk(t) and the associated initial condition thus reduces to
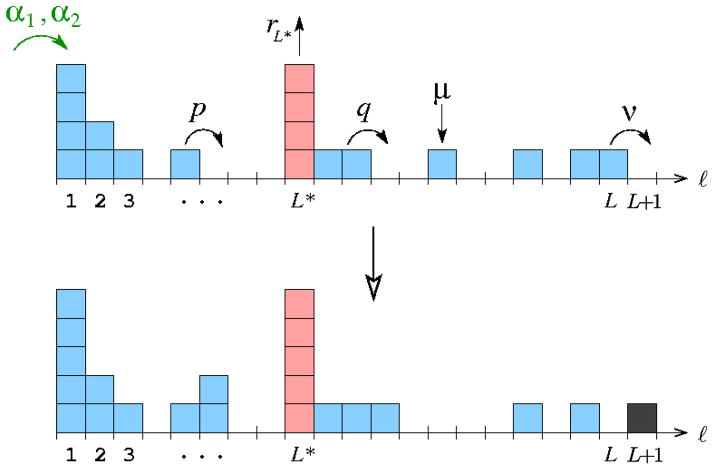
Figure 3.
A sequential evolution model. The possible transitions and their rates are labeled. The rate of single-particle immigration due to e.g., asymmetric differentiation into state k = 1, is defined by α1 = β1b1(1), while the rate of two-particle immigration arising from e.g., symmetric differentiation into state k = 1 is defined by α2 = β1b1(2). Heterogeneities in the transition rates along the sequence can be easily incorporated in our computation. Localized heterogeneities (e.g., at site L*) can be used to model oases or bottlenecks. Our analysis focusses on the first arrival time to state L + 1.
| (17) |
and Sk≤L(0) = 1, SL+1(t) = 0.
3. Results
In this section, we present both analytic and numeric results for Sk(t), Σ(t), and the MFPTs T for sequential, exponentially distributed processes described by Figs. 2 and 3. We discuss their properties as functions of transition rates and system size, and compare these results with those obtained from the simplest mean-field approximations.
3.1. Linear processes
For “linear” dynamics, defined by pk = qk = rk = 0, Eqs. 17 for the survival probability in the absence of immigration and for a single particle initially in state k are linear and can be solved exactly using Laplace transforms:
| (18) |
This result explicitly shows that S̃1(s), and hence Σ(t) is invariant with respect to the order of μi + νi = λi. Therefore, heterogeneity in the transition rates of this linear Poisson process does not influence the first passage times to the absorbing state. Similarly, the survival probability for a sequential process with general waiting time distribution gk(τ) can be found from solving Eq. 9 to find , which is also clearly independent of the order of the transitions.
Eq. 18 can be inverted to obtain explicit expressions for Sk(t). S1(t) can be then used in Eq. 15 to obtain the full survival probability Σ(t), and ultimately the MFPT using Eq. 12. For uniform λk = λ, Eq. 18 simplifies to
| (19) |
which is equivalent to the survival probability of a zero-range process with death [37].
If there is no immigration nor death (μ = 0 and λ = ν), the process is analogous to an irreversible multistep Moran process in which a parent cell immediately dies after producing one mutated/evolved/differentiated daughter cell. The conservation of particles means that eventual arrival to any connected node L + 1 is certain. For an initial condition of N particles in node k = 1, the mean time for a first cell to arrive at the terminal state L + 1 can be constructed from the survival probability S1(t) of a single particle that can only hop forward.
| (20) |
The result S1(t) for a asymmetrically hopping particle on a finite one-dimensional lattice is a special case considered in Pury and Caceres [38].
If there is death (μ > 0) but also immigration (α1 and/or α2 > 0), the explicit expression for the overall survival probability Σ(t) can be found by using Eq. 18 for S1(t) in Eq. 15. In the constant λ = μ + ν case, we find
| (21) |
When α2 = 0 (no double-particle immigration), the integral can be approximated in the small and large limits of Ω ≡ (α1/λ)(ν/λ)L by considering the structure of integrand Σ(t) in Eq. 12[39]:
| (22) |
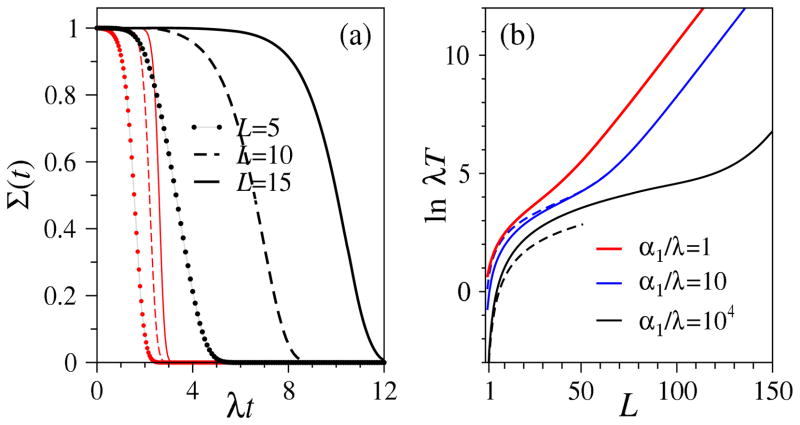
Fig. 4(a) shows exact survival probabilities of the homogeneous sequential linear process for different values of chain length L. For comparison, we plot curves corresponding to different rate parameters μ and ν relative to the total uniform transition rate λ = μ + ν. Fig. 4(b) plots ln λT as a function of chain length L. For large ΩL, the rate limiting step is immigration and the MFPT is approximately the inter-immigration time, normalized by the probability each immigration event eventually leads to fixation (the Ω ≪ 1 limit in Eq. 22).
Figure 4.
(a) Survival probabilities for L = 5, 10, 15 plotted as a function of λt. The set of three thin red curves decaying at short times correspond to α1 = λ, α2 = 0, μ/λ = 0.01, ν/λ = 0.99, while the three black curves decaying at longer times correspond to μ/λ = ν/λ = 0.5. The effects of increased chain length L are more dramatic when particle decay is faster and length-dependent stochastic tunneling becomes rate-limiting. (b) Plots of ln(λT) as a function of L for α1/λ = 1, 10, 104 with fixed α2 = 0, μ/λ = 0.1, and ν/λ = 0.9. The two dashed curves correspond to the asymptotic limits in Eq. 22.
3.2. Nonlinear processes
Now, consider cell replication processes where pk +qk +rk > 0. When these higher order cellular processes arise, Eq. 17 is nonlinear for N > 1, and the evaluation of survival probabilities and first passage times must be approximated or computed numerically. From Eq. 15, we can see that for sufficiently small α1/λ, the survival probability will scale as Σ(t) ~ e−α1(1−S̄1)t. Note that if μk = 0 for all k, the only steady-state solution to Eq. 17 is Sk(t → ∞) ≡ S̄k = 0. Hence, Σ(t) ~ e−α1t, indicating that immigration is the rate limiting step. In the following we we will provide results to a few specific illustrative cases.
3.2.1. Mean field Approximation
The simplest approximation to the survival probability can be obtained without using Eqs. 13 and 15. The time rate of change of survival is simply defined as the total probability flux into absorbing states, conditioned on no particle having yet entered any absorbing state [25]. In our problem, the unconditioned instantaneous particle flux into state L + 1 is Jmf(t) ≡ (pL + qL + νL)〈nL(t)〉, where 〈nL(t)〉 is the expected occupation of state L. If we assume that the mean occupation is uncorrelated with the probability Σ(t) of survival, Σ̇mf ≈ −Jmf(t)Σmf. This approximation is exact when particles are always independent and is widely used. The survival probability under this mean-field assumption is thus
| (23) |
The unconditioned occupation 〈nL(t′)〉 can be found using mass-action equations for the particle density at each site. The Laplace-transformed expected particle number can be written as
| (24) |
where ai ≡ 2pi + qi + νi and bi ≡ μi + νi + pi − ri. Like Eq. 18, this result shows that the mean-field survival probability of a system injected at the first site is independent of the specific order of the rates. Moreover, upon comparing Eq. 24 to Eq. 18, we see that the mean field survival probability Σmf(t) = Σ(t) is exact if α2 = pi = qi = ri = 0.
For general rates but uniform ai = a and bi = b, the general mean-field approximation for the survival probability is
| (25) |
which has a form analogous to Eq. 21. To explicitly see that Σmf(t) is not exact when any α2, p, q, r > 0, consider the single intermediate state case L = 1. In this case, Eq. 17 can be solved exactly to yield explicit expressions for S1(t) and Σ(t):
| (26) |
where
| (27) |
and
| (28) |
Analogous results have been previously considered a general context [28] and in the context of clonal expansion in the two-hit cancer progression model [40].
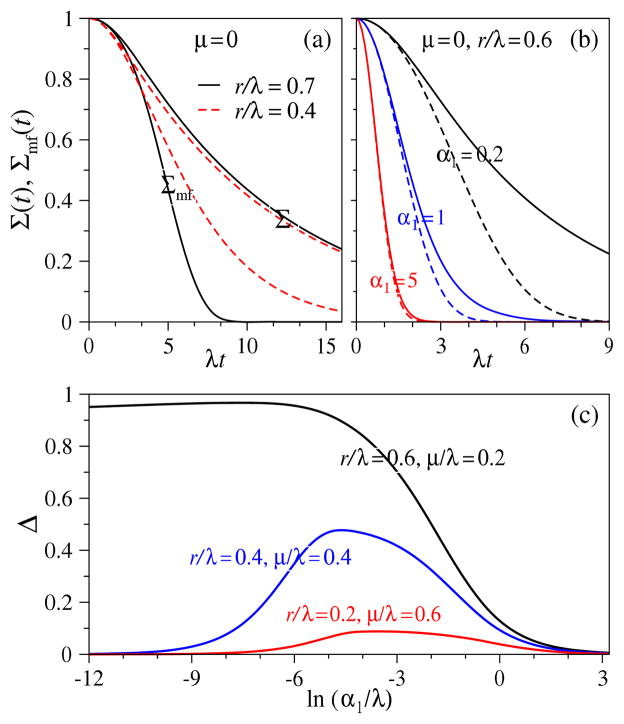
Fig. 5 explicitly shows the difference between Σ(t) and Σmf(t) (Eq. 25) for various values of α2, p, q, r > 0. The discrepancy between the exact and mean-field results vanishes as (α1/b)(a/b)L/L! ≫ 1. In this limit, the numbers of particles derived from independently immigrated lineages are sufficiently large such that the effects of correlations among their branching times are small. The mean-field limit can also be derived by considering the solution to S1 in the short time limit when it deviates only slightly from unity. Linearization of Eq. 17 about Sk = 1 results in a set of equations whose solution also yield the mean-field result of Eq. 25.
Figure 5.
Comparison between exact solutions and mean-field approximations for L = 1. (a) Σ(t) and Σmf (t) for μ = 0 and r/λ = 0.7 (solid) and r/λ = 0.4 (dashed). As expected, differences are larger for larger values of r/λ, where survival probability and the mean occupation 〈n1(t)〉 share more correlations. (b) Σ(t) (solid) and Σmf (t) (dashed) for different values of single-particle immigration α1 and fixed α2 = μ = 0, r/λ = 0.6, and (p + q + ν)/λ = 0.4. The difference is largest for smaller α1 where immigration is rate limiting, and the first arrival at the absorbing state k = 2 is more likely from particles that have replicated at k = 1. (c) Relative errors of MFPTs Δ ≡ (T − Tmf)/T as a function of α1 for the combinations of r/λ, μ/λ indicated. When rates of nonlinear processes (r in this case) are large, the error is large. In the limit of vanishing r/λ, mean-field theory becomes exact and Δ vanishes.
3.2.2. Numerical results
To investigate the effects of nonlinear proliferative processes on evolution and first passage times in larger systems, we solve Eq. 17 numerically and use Eqs. 15 and 12 to find survival probabilities and MFPTs. Since Eq. 17 is nonlinear, we expect the ordering of the rates and positioning of defects along the chain to influence first passage times, in contradistinction to linear processes in which spatial ordering of rates does not play a role.
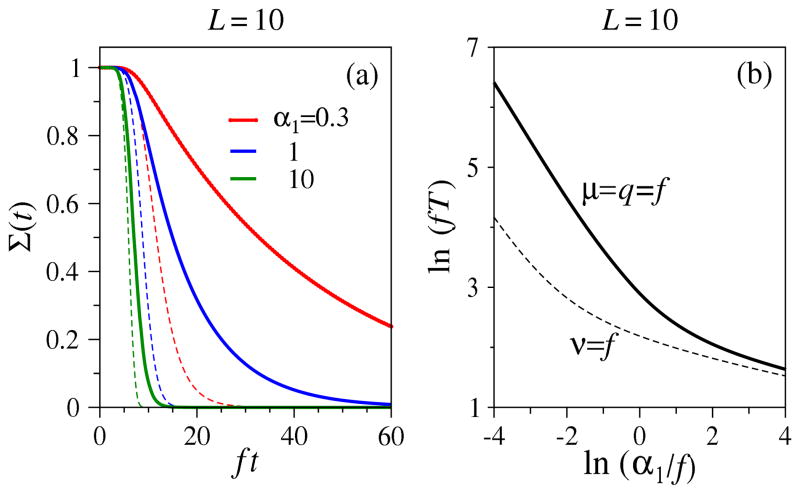
We first compare proliferative processes with an irreversible-mutation linear Moran-type process in which asymmetric differentiation occurs followed immediately by death of the parent cell. This assumption is typically used to enforce fixed population (in the absence of immigration) and in our framework corresponds to νk > 0 and μk = pk = qk = rk = 0. This process is linear and a mean-field assumption yields exact results. A related nonlinear process can be defined by qk = μk > 0 (and νk = pk = rk = 0). This process will give rise to identical expected populations 〈nk(t)〉 if qk are assigned the same values as νk used in the linear Moran-type process. Here, asymmetric differentiation and death are balanced such that the mean occupations are identical to those derived from the linear process μk = pk = qk = rk = 0. However, in the linear process, mutation and death of the parent particle are completely correlated, unlike in the nonlinear process (qk = μk > 0) in which they occur independently. The nonlinear process allows fluctuations in the total population to affect FPT statistics. In Fig. 6, Σ(t) and the MFPTs between two processes with uniform intrinsic rate f, (ν = f, p = q = r = μ = 0) and (q = μ = f, ν = p = r = 0), are contrasted. The results in Fig. 6 can also be qualitatively understood from the likelihood of any particle at site k generating one at site k + 1. If μ = q = f > 0, then any single cell would have a probability of only one half of generating an advancing daughter cell particle. However, in the linear Moran-type process with ν = f, all particles will eventually move forward.
Figure 6.
Comparison of two mean-field-equivalent processes ν = f and μ = q = f along a chain of length L = 10. (a) The dashed curves are Σ(t) for the linear process ν = f and μ = p = q = r = 0, while the thick solid curves correspond to numerical solutions of Eq. 17 for the nonlinear process μ = q = f and ν = p = r = 0. Due to the independent decay processes, the MFPT of the nonlinear process is always greater than that of the linear process. (b) MFPTs as functions of ln(α1/f). Despite the mean-field equivalence, mean-field approximations to the FPTs are qualitatively inaccurate.
In the small α1/f limit, the MFPT of the nonlinear proliferative process scales as T ~ α1(1 − S̄1)−1. For μ = q = f, S̄1 = L/(L + 1), and T ~ (L + 1)/α1 > Tmf, where Tmf is the exact mean-field result for the MFPT of the linear Moran-like process, which can be found from Eq. 22 or by using Eq. 25 in Eq. 12. When α1/f is large, the number of statistically independent particles in the system is large and the survival probability of the proliferative process will approach a common mean-field limit (Eq. 25). Thus, the relative difference between the MFPTs of the linear spontaneous mutation process and the mean-field-equivalent nonlinear process diminishes at large injection rates α1 (and α2). Nonetheless, cells in the proliferative process have a nonzero death rate and the MFPT is bounded above by that of the linear process. Therefore, in terms of reaching the absorbing state, we observe that the linear irreversible Moran-type process is always faster.
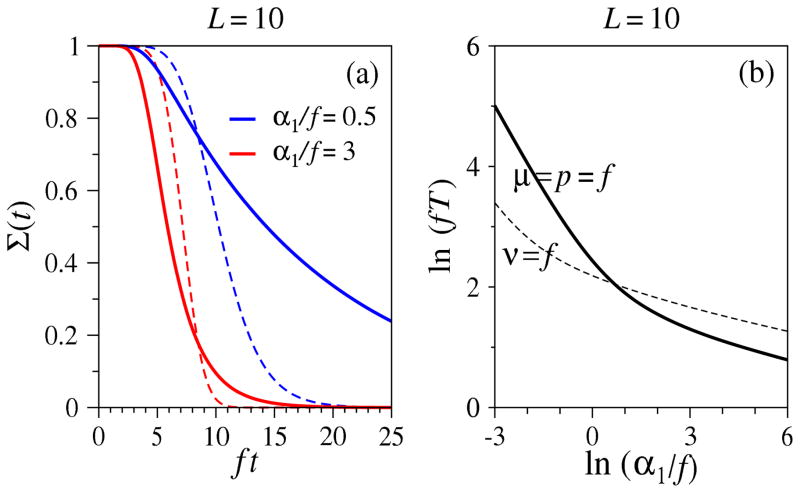
Next, consider another proliferative process that might be expected to yield similar FPTs as the linear Moran-like process. If cells undergo only symmetric differentiation and death with rates p = μ = f and q = r = ν = 0, a parent cell can die or beget two differentiated daughters that each die at the same rate. Even though the expected populations of this process and of the irreversible Moran-type process (ν = f) differ, the mean positions of the lead particle are equal (conditioned on survival). Fig. 7(a) shows the survival probabilities of the two processes for two different values of immigration. For small immigration rates α1/f, the linear (mean-field) process reaches the absorbing state faster, while for high immigration rates, the proliferative process is faster. Fig. 7(b) plots the MFPT of the two processes as a function of injection rate. For small α1/f, the exact MFPT Tmf of the linear process can again be found from the first limit in Eq. 22, while the MFPT of the nonlinear proliferative process scales as T ≈ α1(1 − S̄1)−1. In this case, the lineage associated with each injected cell has a possibility of becoming extinct before fixation, resulting in a MFPT diverging as 1/α1. For L = 10, S̄1 ≈ 0.861 and T ≈ (0.139α1)−1 > Tmf. When α1/f is large, Σ(t) for the nonlinear proliferative process approaches the mean-field result in Eq. 25. Moreover, the associated MFPT can be shown to be less than the MFPT for the linear process. Thus, there is a cross-over at a particular value of immigration below which the linear process becomes evolutionarily faster than the proliferative process. For large α1, immigration is sufficiently fast to allow overall proliferation to push lead particles to overtake those of the corresponding linear Moran-type process, leading to a smaller MFPT.
Figure 7.
Comparison of two processes with similar mean lead-particle positions. (a) This dashed curves are Σ(t) (which is equivalent to Σmf) for the linear process ν = f and μ = p = q = r = 0, while the thick solid curves correspond to numerical solutions of Eqs. 17 and 15 for the nonlinear process μ = q = f and ν = p = r = 0. Due to independent decay process, the MFPT of the nonlinear process is always greater than that of the linear process. (b) The MFPTs as functions of ln(α1/f) for these two processes also dramatically differ, but a cross-over occurs.
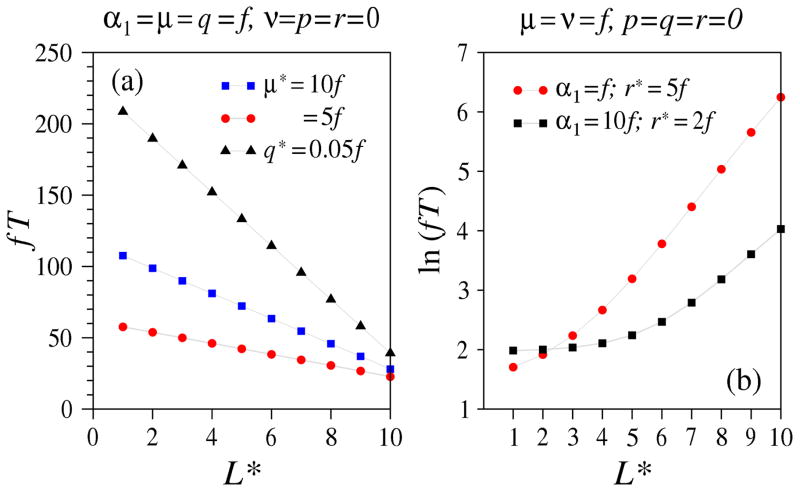
Finally, we illustrate the effects of two types of deserts (or bottlenecks) and two types of oases in an otherwise uniform evolutionary chain. Bottlenecks or deserts at site L* may arise from an enhanced death rate μ*, or from a suppression in ν*, p*, and/or q*. A local oasis can modeled by increased proliferation rates such as r* or p*. For example, Fig. 3 depicts a sequential process with an enhanced growth rate at site L*. Fig. 8 plots the MFPT for a bottleneck (a), and an oasis (b), at different positions along the chain. For the parameters used, bottlenecks are most effective at slowing down fixation when placed near the start the chain; conversely, an oasis is most effective at speeding up fixation when placed near the start of the chain.
Figure 8.
Spatial dependence of bottlenecks and oases. (a) Dependence of the MFPT on the position of a bottleneck. In an otherwise uniform chain with q = μ = f, ν = p = r = 0, cells at site L* die with increased rates μL* ≡ μ* = 5f (red circles) and μ* = 10f (blue squares). Alternatively, this bottleneck site may have a diminished asymmetric division rate qL* = q* = 0.05f (black triangles). (b) The dependence of the MFPT on the position of an oasis at a site with no death (μL* = 0), enhanced growth rates rL* ≡ r* = 2f, 5f, and corresponding immigration rates α1 = f and α1 = 10f, respectively. In the rest of the chain, there are no proliferative processes (p = q = r = 0) and cells both spontaneously mutate and die with rate ν = μ = f.
The linear dependence on bottleneck position shown in Fig. 8(a) can be understood by viewing this scenario as a FPT problem in the second segment of the chain L* < ℓ ≤ L + 1. Related sequential segmentation methods have also been used to self-consistently compute steady-state transport fluxes across excluding 1D lattices [41, 42]. Here, the bottleneck reduces the effective immigration rate into the second segment. If the bottleneck is sufficiently strong (as are the cases shown in Fig. 8(a)), immigration into the second segment is rate-limiting and since ν = 0, we expect the MFPT to scale as 1/(L − L* + 1).
The effect of an oasis site in the presence of an otherwise uniform process involving death and spontaneous mutation is to decrease the MFPT, as shown in Fig. 8(b). If the rates at site L* are such that r* > μ* + ν*, there can be unlimited growth and the rate of immigration into site L* + 1 will exponentially increase time. Thus, an oasis near the beginning of the evolutionary chain will strongly drive immigration into the remaining segment and be more effective at reducing the MFPT to fixation compared to one that is hard to get to near the end of the chain.
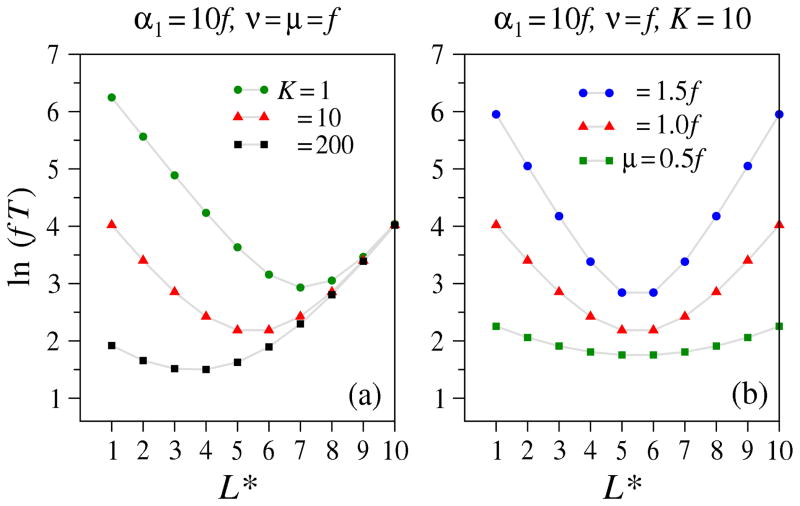
An oasis with a positive net growth rate leads to an unbounded population at long times. However, our approach does not allow for interactions and constraints such as carrying capacity. Nonetheless, if the first arrival times to L + 1 are much smaller than the time it takes for any site to reach carrying capacity (K > exp [(r* − μ*)T]), our unlimited growth model still provides a reasonable approximation to the FPT.
In the opposite limit of small carrying capacity (K ≪ exp [(r* − μ*)T]) another approximation to the MFPT can be obtained. We can model an oasis by assuming that in an otherwise homogeneous chain along which p = q = r = 0, site L* carries a growth process with a carrying capacity K and r* → r*(1 − nL*/K). We also assume that μ* = 0 and that r* is greater than all other rates in the model. Therefore, once the first particle arrives at site L*, its population quickly rises to a level ~ K. These cells then feed into site L* + 1 through mutational processes described by ν, p, or q. By considering two linear processes joined by an oasis at site L*, the MFPT to state L + 1 can be approximated as the mean time to reach L* plus the time to reach state L + 1 given an effective immigration rate Kν into site L* + 1. Not only does the MFPT depend on the spatial structure of the inhomogeneity, but in many cases, there will be an optimal placement of an oasis which most effectively reduces the overall MFPT. Such an optimal placement can be explicitly seen by considering Eq. 22 in the small immigration limit:
| (29) |
where Ω ≡ (α1/λ)(ν/λ)L*−1 and Ω* ≡ (Kν/λ)(ν/λ)L–L*. This approximation clearly shows a position-dependent MFPT provided ν/λ < 1 (μ > 0). The position which yields the smallest MFPT in the ΩL*, Ω*(L – L*) ≪ 1 limit can be approximated by solving ∂T (L, L*)/∂L* = 0:
| (30) |
which shows that when Kν ≈ α1, the oasis lowers the MFPT the most when placed near the midpoint of the chain. Eq. 30 provides good estimates of the optimal oasis position and its dependences on rates.
In Fig. 9(a) we use Eqs. 15 and 12 to compute the MFPT of a two-segment chain. For the segment before the oasis, we use , while for the second segment, . Evaluating the total MFPT T (L* – 1) + T (L – L*) clearly shows that the most effective positioning of an oasis is such that the segment with rate-limiting immigration is shortest. Since changes in μ only affect logarithmically, small changes in the death rate do not affect the optimal oasis position. However, when μ increases, as shown in Fig. 9(b), the MFPTs across each segment increases exponentially with its length, increasing the sensitivity of the overall MFPT to L*.
Figure 9.
MFPT in the presence of an oasis with large growth rate r* → ∞ but a finite carrying capacity K. (a) ln fT for various carrying capacities K at fixed immigration rate α1 = 10f and spontaneous mutation and death rate ν = μ = f. (b) When α1 = Kν = 10f, both effective immigration rates are equal and the MFPT-minimizing position L* ≈ L/2 (Eq. 30).
4. Discussion & Conclusions
We have formulated an efficient way to analyze FPTs on a network containing multiple, mutating, and proliferating particles. Our model allows one to naturally study stochastic evolutionary processes and explicitly include cell fate decisions, fluctuations in total number, and immigration. An analogous generating function approach to multistage mutation of populations has been studied [3, 4]. Here, a number of asymptotic limits are explored and comparisons with mean-field calculations of survival probabilities performed. Kinetic Monte Carlo simulations were also performed and checked against our results. Our main findings illustrate the importance of specific cellular transitions and how mean-field assumptions can be misleading when used to compute first arrival times. Therefore, in evolutionary networks on which cells can stochastically participate in a number of proliferative processes, care must be taken in calculating fixation times. Even though expected particle numbers of a noninteracting particle system can typically be found exactly using mean-field approximations, our results explicitly show how survival probabilities and first passage time statistics cannot be treated using simple mean-field approximations if particles can proliferate. These discrepancies are prominent in conditions of low populations, as encountered in stochastic tunneling.
Furthermore, we find in this work that proliferative processes, including symmetric and asymmetric cell differentiation, render FPTs dependent on the order of the transition rates along a sequential evolutionary chain. A related model of first passage times with immigration into a simple two-path network where each node presents environments with different fitness [43]. For a linear network, in many scenarios, we find that bottlenecks are most effective at increasing the MFPT when placed at the beginning of an evolutionary chain, while an unlimited oasis reduces the MFPT most effectively at the beginning of the chain. If the growth rate of an oasis site is faster than any other time scale, the mean times to the terminal state can be approximated by the mean time for the first cell to arrive at the oasis, plus the time for the progeny of any cell arising from an oasis to arrive at the terminal site. In the presence of regulating interactions that generate e.g., a carrying capacity K, we find intermediate oasis positions that optimally reduce the MFPT to the final L + 1-state. This optimal position is qualitatively determined by the ratio of the effective immigration rates into each of the segments and deviates from the halfway point by the log of the ratio of immigration rates, with the shorter segment associated with the smaller effective immigration rate.
Collectively, our results suggest that fixation times across a number of biological systems may be sensitive to the precise transitions allowed. Examples include stem cell differentiation [2] and mutation [29], where each differentiation or mutational state is represented by distinct nodes. Our approach is also particularly appropriate for modeling progression and drug resistance in cancer. Since mutated or precancerous cells may likely have only a small fitness advantage [18], the numbers of cells in these states may be small, and the effects of proliferative nonlinearity may be important. In such cases, cell states that are drug resistant will do the most harm when occurring at the beginning, or in the interior of the mutational sequence, depending on, respectively, whether a carrying capacity arises or not. We have investigated only simple, irreversible transitions along a 1D sequential chain. Extensions to more complex networks and nonexponentially distributed processes (such as cell-cycle timing) can be readily investigated by numerically solving Eqs. 9 and 11. More complex distributions of different transition rates can also be easily treated numerically.
Finally, note that depending on the specific network structure and transitions, estimates for MFPTs can be achieved by segmenting the chain according to the most rate-limiting stages. However, if waiting time distributions or transition rates vary slowly across nodes in a large network, equations for the survival probability Sk(t) (such as Eq. 17) can be studied in the continuum “hydrodynamic” limit: Sk(t) → S(x, t), x = k/L [44]. Although large system size expansions and continuum limits of a discrete master equation are known to yield inaccurate first passage times [45], continuum limits of Sk(t) and analysis of the resulting PDEs may provide accurate estimates of the discrete system.
Acknowledgments
TC was supported by the NSF through grant DMS-1021818, the Army Research Office through grant 58386MA, and the DoD through grant W911NF-13-1-0117. YW was supported through the Cross-disciplinary Scholars in Science and Technology (CSST) program at UCLA. The authors also wish to acknowledge the support of the KITP at UCSB through NSF PHY11-25915.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Marciniak-Czochra A, Stiehl T, Ho AD, Jager W, Wagner W. Modeling of asymmetric cell division in hematopoietic stem cells-regulation of self-renewal is essential for efficient repopulation. Stem Cells and Development. 2009;18:377–385. doi: 10.1089/scd.2008.0143. [DOI] [PubMed] [Google Scholar]
- 2.Roshan A, Jones PH, Greenman CD. Exact, time-independent estimation of clone size distributions in normal and mutated cells. J Roy Soc Interface. 2014;11:20140654. doi: 10.1098/rsif.2014.0654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sherman CD, Portier CJ. Stochastic simulation of a multistage model of carcinogenesis. Mathematical Biosciences. 1996;134:35–50. doi: 10.1016/0025-5564(95)00105-0. [DOI] [PubMed] [Google Scholar]
- 4.Portier CJ, Sherman CD, Kopp-Schneider A. Multistage, stochastic models of the canser process: A general theory for calculating tumor incidence. Stochastic Environmental Research and Risk Assessment. 2000;14:173–179. [Google Scholar]
- 5.Bellacosa A. Genetic hits and mutation rate in colorectal tumorigenesis: versatility of Knudson’s theory and implications for cancer prevention, Genes. Chromosomes & Cancer. 2003;38:382–388. doi: 10.1002/gcc.10287. [DOI] [PubMed] [Google Scholar]
- 6.Spencer SL, Gerety RA, Pienta KJ, Forrest S. Modeling somatic evolution in tumorigenesis. PLoS Computational Biology. 2006;2:e108. doi: 10.1371/journal.pcbi.0020108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Attolini CSO, Cheng YK, Beroukhim R, Getzand G, Abdel-Wahab O, Levine RL, Mellinghoff IK, Michor F. A mathematical framework to determine the temporal sequence of somatic genetic events in cancer. Proceedings of the National Academy of Sciences USA. 2010;107:17604–17609. doi: 10.1073/pnas.1009117107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Antal T, Krapivsky PL. Exact solution of a two-type branching process: Models of tumor progression. Journal of Statistical Mechanics: Theory and Experiment. 2011;2011:P08018. [Google Scholar]
- 9.Frank SA. Age-specific incidence of inherited versus sporadic cancers: a test of the multistage theory of carcinogenesis. Proc Natl Acad Sci USA. 2005;102:1071–1075. doi: 10.1073/pnas.0407299102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Allen LJS. An Introduction to Stochastic Processes with Applications to Biology. Pearson Prentice Hall; Upper Saddle NJ: 2003. [Google Scholar]
- 11.Antal T, Krapivsky PL. Exact solution of a two-type branching process: Clone size distribution in cell division kinetics. Journal of Statistical Mechanics. 2010:P07028. [Google Scholar]
- 12.Armitage P, Doll R. The age distribution of cancer and a multi-stage theory of carcinogenosis. Int J Epidemiol. 2004;33:1174–1179. doi: 10.1093/ije/dyh216. [DOI] [PubMed] [Google Scholar]
- 13.Moolgavkar SH, Knudsen AG. Mutation and cancer: a model for human carcinogenesis. J Natl Cancer Inst. 1981;66:1037–1052. doi: 10.1093/jnci/66.6.1037. [DOI] [PubMed] [Google Scholar]
- 14.Knudsen AG. Mutation and Cancer: Statistical Study of Retinoblastoma. Proc Natl Acad Sci USA. 1971;68:820–823. doi: 10.1073/pnas.68.4.820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fitzgerald PH, Stewart J, Suckling RD. Retinoblastoma mutation rate in New Zealand and support for the two-hit model. Human Genetics. 1983;64:128–130. doi: 10.1007/BF00327107. [DOI] [PubMed] [Google Scholar]
- 16.Floyd DL, Charris S, van Oijen AM. Analysis of kinetic intermediates in single-particle dwell-time distributions. Biophys J. 2010;99:360–366. doi: 10.1016/j.bpj.2010.04.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rieker RJ, Hoegel J, Kern MA, Steger C, Aulmann S, Mechtersheimer G, Schirmacher P, Blaeker H. A mathematical approach predicting the number of events in different tumors. Pathol Oncol Res. 2000;14:199–204. doi: 10.1007/s12253-008-9050-z. [DOI] [PubMed] [Google Scholar]
- 18.Beerenwinkel N, Antal T, Dingli D, Traulsen A, Kinzler KW, Velculescu VE, Vogelstein B, Nowak MA. Genetic progression and the waiting time to cancer. PLoS Comput Biol. 2007;3:e225. doi: 10.1371/journal.pcbi.0030225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hwang S, Lee DS, Kahng B. First passage time for random walks in heterogeneous networks. Phys Rev Lett. 2012;109:088701. doi: 10.1103/PhysRevLett.109.088701. [DOI] [PubMed] [Google Scholar]
- 20.Agliari E. Exact mean first-passage time on the T-graph. Phys Rev E. 2008;77:011128. doi: 10.1103/PhysRevE.77.011128. [DOI] [PubMed] [Google Scholar]
- 21.Lindenberg K, Seshadri V, Shuler KE, Weiss GH. Lattice random walks for sets of random walkers: First passage times. J Stat Phys. 1980;23:11–25. [Google Scholar]
- 22.Li X, Kolomeisky AB, Valleriani A. Pathway structure determination in complex srochastic networks with non-exponential dwell times. J Chem Phys. 2014;140:184102. doi: 10.1063/1.4874113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bal G, Chou T. On the reconstruction of diffusions using a single first-exit time distribution. Inverse Problems. 2003;20:1053–1065. [Google Scholar]
- 24.Fok PW, Chou T. Reconstruction of bond energy profiles from multiple first passage time distributions. Proc Roy Soc A. 2010;466:3479–3499. [Google Scholar]
- 25.Chou T, D’Orsogna MR. First-Passage Phenomena and Their Applications. World Scientific; 2014. First Passage Problems in Biology. [Google Scholar]
- 26.Isawa Y, Michor F, Nowak M. Stochastic tunnels in evolutionary dynamics. Genetics. 2004;166:1571–1579. doi: 10.1534/genetics.166.3.1571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Weinreich DM, Chao L. Rapid evolutionary escape. Theoretical Population Biology. 2009;75:286–300. [Google Scholar]
- 28.Weissman DB, Desai M, Fisher DS, Feldman MW. The rate at which asexual populations cross fitness valleys. Theoretical Population Biology. 2009;75:286–300. doi: 10.1016/j.tpb.2009.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.McHale PT, Lander A. The Protective Role of Symmetric Stem Cell Division on the Accumulation of Heritable Damage. PLoS Comp Biol. 2014;10:e1003802. doi: 10.1371/journal.pcbi.1003802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Athreya KB, Ney PE. Branching Processes. Springer; New York: 1972. [Google Scholar]
- 31.Fok P, Chou T. Identifiability of age-dependent branching processes from extinction probabilities and number distributions. Journal of Statistical Physics. 2013;152:1–18. [Google Scholar]
- 32.Harris TE. The theory of branching Processes. Dover; New York: 1989. [Google Scholar]
- 33.Wang H, Qian H. On detailed balance and reversibility of semi-Markov processes and single-molecule enzyme kinetics. J Math Phys. 2007;48:013303. [Google Scholar]
- 34.Jagers P. Age-dependent branching processes allowing immigration. Theory of Probability and its Applications. 1968;13:225–236. [Google Scholar]
- 35.Shonkwiler R. On age-dependent branching processes with immigration. Comp & Maths with Appls. 1980;6:289–296. [Google Scholar]
- 36.Redner S. A guide to first-passage processes. Cambridge University Press; 2001. [Google Scholar]
- 37.Shargel BH, D’Orsogna MR, Chou T. Arrival times in a zero-range process with injection and decay. J Phys A. 2010;43:305003. [Google Scholar]
- 38.Pury PA, Caceres MO. Mean first-passage and residence times of random walks on asymmetric disordered chains. Journal of Physics A: Mathematical and General. 2003;36:2695–2706. [Google Scholar]
- 39.Bender CM, Orszag SA. Advanced Mathematical Methods for Scientists and Engineers: Asymptotic Methods and Perturbation Theory. Springer-Verlag; New York: 1999. [Google Scholar]
- 40.Haeno H, Iwasa Y, Michor F. The evolution of two mutations during clonal expansion. Genetics. 2007;177:2209–2221. doi: 10.1534/genetics.107.078915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kolomeisky AB. Asymmetric simple exclusion model with local inhomogeneity. J Phys A: Math Gen. 1998;31:1153–1164. [Google Scholar]
- 42.Chou T, Lakatos G. Clustered bottlenecks in mRNA translation and protein synthesis. Phys Rev Lett. 2004;93:198101. doi: 10.1103/PhysRevLett.93.198101. [DOI] [PubMed] [Google Scholar]
- 43.Hermsen R, Hwa T. Sources and sinks: A stochastic model of evolution in heterogeneous environments. Phys Rev Lett. 2010;105:248104. doi: 10.1103/PhysRevLett.105.248104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lakatos G, O’Brien JD, Chou T. Hydrodynamic solutions of 1D exclusion processes with spatially varying hopping rates. J Phys A. 2006;39:2253–2264. [Google Scholar]
- 45.Doering CR, Sargsyan KV, Sander LM. Extinction times for birth-death processes: Exact results, continuum asymptotics, and the failure of the Fokker–Planck approximation. Multiscale Model Simul. 2005;3:283–299. [Google Scholar]