Abstract
Antiretroviral therapy is able to suppress the viral load to below the detection limit, but it is not able to eradicate HIV reservoirs. Thus, there is a critical need for a novel treatment to eradicate (or reduce) the reservoir in order to eliminate the need for a lifelong adherence to antiretroviral therapy, which is expensive and potentially toxic. In this paper, we investigate the possible pharmacological strategies or combinations of strategies that may be beneficial to reduce or possibly eradicate the latent reservoir. We do this via studies with a validated mathematical model, where the parameter values are obtained with newly acquired clinical data for HIV patients. Our findings indicate that the strategy of reactivating the reservoir combined with enhancement of the killing rate of HIV-specific CD8+ T cells is able to eradicate the reservoir. In addition, our analysis shows that a targeted suppression of the the immune system is also a possible strategy to eradicate the reservoir.
Keywords: HIV, immune response, mathematical model, inverse problem, stability analysis
1 Introduction
Antiretroviral therapy (ART) for HIV infection typically consists of several antiretroviral drugs that each targets a specific stage of the HIV life cycle and is effective in suppressing the viral load to below the detection limit. However, HIV can persist at undetectable levels in the presence of ART and cessation of ART leads to a viral rebound within three to four weeks (e.g., see [35] and references therein). Thus, the majority of HIV patients must adhere to a lifelong ART regimen in order to control the HIV infection.
It has been found that the persistence of HIV is due to several potential viral reservoirs, including resting CD4+ T cells that contain integrated HIV DNA as well as anatomical sanctuaries that are not reached by the antiretroviral drugs (see [35] for details). We remark that resting CD4+ T cells with replication competent HIV DNA integrated into their host genomes, i.e., latently infected CD4+ T cells, refer to those resting CD4+ T cells that contain integrated HIV DNA and are capable of producing virus only upon activation. The size of this latent reservoir is extremely stable. However, the mechanisms for maintaining this stability remain unclear. Several explanations have been proposed and tested through mathematical modeling (see the review in [30]). These include homostatic proliferation of latently infected CD4+ T cells [29] that has been confirmed experimentally [11] and asymmetric cell division [31] wherein it was assumed that latently infected cells generate two daughter cells with one in the latent state and the other in the productive state. Recently, it was shown in [38] that latently infected cells with intermediate transcription activities may maintain their size through a high level of homeostatic proliferation, while the ones with low transcriptional activities are likely to be maintained through the reversion from infected cells with intermediate transcription.
Due to the stability of latent reservoir size, reactivation of latently infected CD4+ T cells serves as a major source of viral rebound upon treatment failure, and hence they are considered to be the most challenging obstacle to HIV eradication (e.g., see [13] and references therein). Thus, there is a critical need for a novel treatment to eradicate this latent reservoir in order to eliminate the need for lifelong adherence to ART, which is not only expensive and toxic [1, 23], but also leaves HIV patients at risk for developing Acquired Immunodeficiency Syndrome (AIDS) [15]. Throughout our discussion we will use the term “eradication” to mean that state where viral load levels are suppressed to very low levels in the absence of continuous therapy. More specifically, we shall mean that state where removal of therapy will result in a low level of viral load which is in the neighborhood of an asymptotically stable set point of viral load.
To have a better understanding of latency, we give a brief introduction to the replication and transcription of HIV and refer the interested reader to [10, 16, 34] and references therein for more information. Following binding to the main receptor of CD4+ T cells, HIV fuses with the cell membrane and releases its contents into the cytoplasm. Once inside the cell, reverse transcriptase converts HIV RNA into a double-stranded DNA molecule (linear cDNA) with long terminal repeats (LTRs), which contain upstream regulatory regions that serve as binding sites for transcription factors which can upregulate virus production. The cDNA is then transported into the nucleus and integrated into the host chromosome with an integrase enzyme. The integrated HIV DNA, i.e., provirus, may then either lie dormant or be transcribed into viral RNA. We remark that if the cDNA fails to integrate, then the cDNA circularizes to form a 2-long terminal repeat (2-LTR) circle. Several mechanisms have been proposed that contribute to the establishment of latently infected CD4+ T cells. Two possible sources of latency are the activated CD4+ T cells that transition to a resting state following infection, and direct infection of a resting CD4+ T cell.
Strategies for eradication of HIV have been proposed in the literature (e.g., see [21, 27, 35, 36] and references therein), including gene therapy to make cells resistant to HIV and pharmacological approaches to eliminate the reservoirs. Specifically, efforts to eradicate the latent reservoir to date have focused on reactivating the latently infected CD4+ T cells in the presence of ART. In theory, this reactivation strategy could induce virus production and subsequent cell death in latently infected CD4+ T cells either from direct cytopathic effects or immune clearance, while, simultaneously, ART could block new infection from the released virus. For example, histone deacetylase (HDAC) inhibitors have emerged as the lead drug candidate for reactivation of the latently infected CD4+ T cells. However, as suggested in [21, 33], simple reactivation of latently infected CD4+ T cells may not be sufficient for eradication of latent reservoir. We propose that a data-driven systems modeling approach can be used to quantitatively estimate the effect of adjuvant therapies, given in addition to ART, on patient viral load and latent reservoir levels. Thereby, the potential for adjuvant drug candidates to eradicate or significantly reduce HIV reservoirs can be evaluated in silico based on previously obtained patient data to inform the design of future clinical trials.
In this paper, we use a mathematical model to elucidate immuno-modulatory strategies that could be used in addition to ART to assist in eradicating the latent reservoir by inducing a stable virus-free or virus-undetectable state. The model we used is adopted from [5], and it includes both previously mentioned sources of establishing latently infected cells. It was found in [5] that this model provides reasonable fits to patients enrolled in a clinical trial that tested the efficacy of ART regimens. The model fit the data for all of the 14 patients considered from that trial, and the clinical data in [5] were from patients that all underwent ART and had at least one treatment interruption. The available clinical data analyzed in [5] included the total number of CD4+ T cells and censored viral load. In addition, the model from [5] was found to have impressive predictive capability when comparing model simulations (with parameters estimated using only half of the longitudinal observations) to the corresponding full longitudinal data sets. Recently, we obtained new clinical data from a study performed at Massachusetts General Hospital in which all patients in the study have never gone off ART after ART was initiated. This newly acquired data includes the amount of integrated HIV DNA, a novel measurement that has not previously been used in mathematical modeling of HIV, in addition to the usual measurements for the total number of CD4+ T cells and the censored viral load. In the following, we use these new data to obtain estimates for the parameters in the model. We then investigate the possible eradication strategies by varying the estimated values of a number of model parameters.
2 Mathematical Model
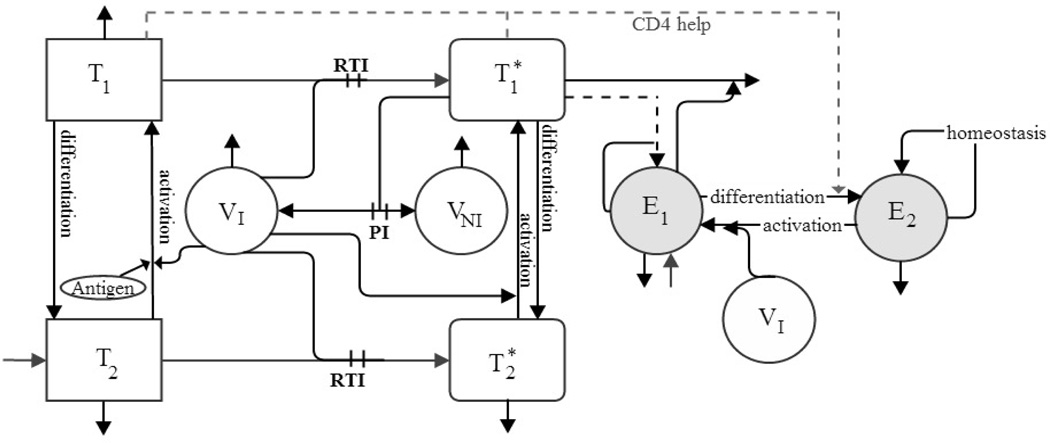
We use the model from [5] to evaluate different strategies that may eradicate the latent reservoir. Descriptions of the state variables are given in Table 1 and the schematic in Figure 1. We allow the differentiation rate from T1 to T2 to be different from the one from to and the activation rate of to be different from that of T2.
Table 1.
Model States.
| states | unit | description | |
|---|---|---|---|
| T1 | cells/µl-blood | uninfected activated CD4+ T cells | |
| cells/µl-blood | infected activated CD4+ T cells | ||
| T2 | cells/µl-blood | uninfected resting CD4+ T cells | |
| cells/µl-blood | infected resting (or latently infected) CD4+ T cells | ||
| VI | RNA copies/ml-plasma | free infectious virus | |
| VNI | RNA copies/ml-plasma | free noninfectious virus | |
| E1 | cells/µl-blood | HIV-specific effector CD8+ T cells | |
| E2 | cells/µl-blood | HIV-specific memory CD8+ T cells |
Figure 1.
Flow chart of model (2.1)–(2.8) with compartments as described in Table 1. PI and RTI denote protease inhibitor and reverse transcriptase inhibitor, respectively.
The corresponding compartmental ordinary differential equation (ODE) model is given by
| (2.1) |
| (2.2) |
| (2.3) |
| (2.4) |
| (2.5) |
| (2.6) |
| (2.7) |
| (2.8) |
with initial condition
In (2.1), d1T1 denotes the natural death of T1, and (1 − ξ1)k1VIT1 is used to represent the infection process that results from encounters between the uninfected activated CD4+ T cells T1 and free virus VI, where ξ1 is the relative efficacy of the reverse transcriptase inhibitor (RTI) with 0 ≤ ξ1 < 1. The term γTT1 is used to account for the phenomenon of differentiation of uninfected activated CD4+ T cells into uninfected resting CD4+ T cells T2. In (2.2), denotes the loss of infected activated CD4+ T cells due to the cytopathic effect of HIV, and the corresponding gain term for VI include a multiplicative factor NT to account for the number of RNA copies produced during this process and a factor (1−ξ2) to account for the protease inhibitor (PI) treatment, where ξ2 denotes the relative efficacy of PI with 0 ≤ ξ2 < 1. The term is used to account for the elimination of the infected activated CD4+ T cells by the HIV-specific effector CD8+ T cells, and is used to account for the phenomenon of differentiation of infected activated CD4+ T cells into latently infected CD4+ T cells at rate γTs.
In (2.3), is used to account for the source rate of naive CD4+ T cells, and d2T2 denotes the natural death of T2. The infection process that results from encounters between the uninfected resting CD4+ T cells T2 and free virus VI is represented by (1 − fξ1)k2VIT2, where the parameter f (0 ≤ f ≤ 1) is used to account for the fact that treatment is potentially less effective in T2 than in T1. The term denotes the activation of the uninfected resting CD4+ T cells, and the corresponding gain term for T1 include a multiplicative factor pT to account for the net proliferation due to clonal expansion and programmed contraction. Similarly, in (2.4) is used to account for the activation of latently infected CD4+ T cells, and the corresponding gain term for also includes a multiplicative factor pT. The natural death of is represented by .
In (2.5) and (2.6), cVI and cVNI respectively denote the clearance of free infectious virus VI and free noninfectious virus VNI, and the factor 103 is introduced to convert between microliter and milliliter scales. The term 103[(1 − ξ1)ρ1k1T1 + (1 − fξ1)ρ2k2T2]VI in (2.5) is used to account for the removal of free virus that takes place when free virus infects T1 and T2.
The first four terms in the right hand side of (2.7) denotes the source, nonlinear infected cell-dependent birth, nonlinear infected cell-dependent death, and constant death, respectively. The term is used to include the essential role that activated CD4+ T cells play in the generation of memory CD8+ T cells, where the parameter Kγ is a half-saturation constant and γE is the maximum rate at which E1 differentiates into E2. In (2.8), is used to denote the homeostatic regulation of E2 with bE2 being the maximum proliferation rate and δE2 being the death rate. The term denotes reactivation of HIV-specific memory CD8+ T cells, and the corresponding gain terms for E1 include a multiplicative factor pE to account for the net proliferation due to clonal expansion and programmed contraction.
3 Inverse Problems
The data for our investigations come from HIV patients who received ART treatment at Massachusetts General Hospital and have not gone off ART once the treatment began. Specifically, there are six patients whose treatment began during the acute phase (the clinicial ID numbers for these patients are prefixed with “AC”), and there are six patients whose treatment began during the chronic phase.
The observables are the total number of CD4+ T cells per µl-blood (where for the model (2.1)–(2.8) this is given by with q being a column vector for those model parameters and initial conditions that need to be estimated), the viral load per ml-plasma (where for the model (2.1)–(2.8) this is represented by VI(t; q) + VNI(t; q)), the integrated HIV-1 DNA per microliter of sample, and the CCR5 per microliter of sample.
To use the measured integrated HIV-1 DNA and CCR5 for our analysis, we first normalize the measured integrated HIV-1 DNA data using the measured CCR5 data to obtain , and then use the following formula
| (3.1) |
to obtain the number of integrated HIV-1 DNA per µl-blood. This is based on the assumption that each cell has two copies of the CCR5 gene. If we further assume that each infected CD4+ T cell contains only one copy of integrated HIV-1 DNA, then (3.1) gives us the measurement of the latently infected CD4+ T cells (for the model (2.1)–(2.8) this is given by ).
Remark: Based on [27] and the references therein, measurements of integrated HIV-1 DNA may be a useful surrogate marker of latently infected cells (even though a large of fraction of integrated HIV-1 DNA are defective). In addition, it was shown in [20] that for infected patients about 85% of infected CD4+ T cells in blood contain only one copy of HIV-1 DNA.
With regard to the viral load measurements, it is worth noting that if the measurements of RNA copies are below the limit of quantification for the assay used (400 copies/ml-plasma, 200 copies/ml-plasma, 80 copies/ml-plasma, 50 copies/ml-plasma, 48 copies/ml-plasma, 25 copies/ml-plasma or 20 copies/ml-plasma), then the observed viral load value is censored to be at its detection limit; that is, in these cases the observed values do not represent the true data values anymore. Furthermore, observations of viral load and CD4+ T cells may not be at the same time points and the observation times and intervals vary substantially among patients. So, in general, for patient number j we have CD4+ T cell data pairs , potentially different time point viral RNA data pairs , and latently infected T cell data pairs . (We remark that is a subset of with far less than for all the patients investigated.) Hence, the clinical data for carrying out the inverse problem involves partial observations, measurements from combined compartments, and highly censored viral load measurements.
3.1 Parameter Estimation
To obtain individual-specific parameter estimates for the model, we carry out an inverse problem for each patient using his/her corresponding clinical data (that is, individuals are fitted individually). We adapt an EM algorithm, which accounts for censored data, from [2, 5]. The variances in CD4+ T cell measurements, in viral load measurements and in latently infected CD4+ T cells measurements, respectively, are likely to be different due to assay differences. Hence, we use the expectation maximization algorithm based on the maximum likelihood estimation technique for (q, ) which, under normality assumptions on the measurement errors, results in a weighted least-squares technique (see [7, 8, 32]) with solution given by
| (3.2) |
for the log10-transformed system of model (2.1)–(2.8) for patient j. In the above equation,
| (3.3) |
where
| (3.4) |
with and , k = 1,2,3. As we noted earlier, is a subset of . Hence, at these time points , we are able to observe , (i.e., total CD4+count− ) but at other time points we can only observe the total number of CD4+ T cells. The number of latently infected CD4+ T cells is negligible compared to the total number of CD4+ T cells (less than one/µl-blood compared to hundreds/µl-blood) and is much smaller than . Hence, for simplicity we use (3.3) as our cost function.
3.2 Numerical Results
For all the simulation results shown below, we fixed the values of the parameters d2, f, δE1, δE2, Ks, Kb1, Kb2, Kd, Kγ, , and as those obtained in [5], and estimated the rest of model parameters and initial conditions (30 out of 42) for each patient. We then fixed another 10 parameters γT, γE, λE, dE, δ, m, KV, c, bE1, bE2, at the population averages across the 12 patients investigated, and re-estimated the remaining 20 parameters for each patient. Table 2 specifies all the fixed parameters (19 model parameters and 3 initial conditions) and their corresponding values.
Table 2.
The values of 12 parameters d2, f, δE1, δE2, Ks, Kb1, Kb2, Kd, Kγ, , and are adopted from Table 5 of [5], and the values of the remaining 10 parameters γT, γE, λE, dE, δ, m, KV, c, bE1, bE2, are fixed as the population averages across the 12 patients investigated.
| parameter | value | parameter | value | parameter | value | ||
|---|---|---|---|---|---|---|---|
| γT | 6.46e−04 | d2 | 3.10e−03 | f | 5.07e−01 | ||
| δ | 1.71e−01 | m | 1.10e+00 | c | 1.27e+01 | ||
| λE | 4.88e−04 | bE1 | 6.93e−02 | Kb1 | 2.49e−02 | ||
| dE | 4.72e−02 | Kd | 1.20e−01 | δE1 | 5.97e−02 | ||
| bE2 | 6.10e−03 | Kb2 | 8.70e+01 | γE | 6.89e−04 | ||
| Kγ | 1.36e+00 | KV | 1.06e+03 | δE2 | 1.45e−03 | ||
| Ks | 2.79e+04 | 3.57e+03 | 6.82e−02 | ||||
| 6.91e−01 | |||||||
The estimated values of the remaining 20 parameters for acutely treated patients (labelled by codes AC161, etc.) are listed in Table 3, and the ones in Table 4 (labelled by individual codes) are for chronically treated patients.
Table 3.
Parameter estimation results for those patients whose treatment started during the acute stage. The labels AC161, AC32, etc., indicate patient numbers for acute stage (AC) enrolled patients.
| params | AC161 | AC32 | AC65 | AC31 | AC34 | AC81 | |
|---|---|---|---|---|---|---|---|
| λT | 8.66e+00 | 2.56e+00 | 2.85e+00 | 2.18e+00 | 1.79e+00 | 2.77e+00 | |
| d1 | 9.12e−02 | 2.88e−02 | 1.82e−01 | 4.69e−02 | 7.43e−02 | 2.74e−02 | |
| ξ1 | 5.24e−01 | 4.93e−01 | 1.46e−01 | 1.93e−01 | 3.63e−01 | 1.88e−01 | |
| k1 | 7.97e−06 | 2.36e−04 | 5.27e−05 | 3.63e−04 | 1.20e−03 | 7.60e−03 | |
| k2 | 1.05e−08 | 2.34e−07 | 3.36e−08 | 6.33e−09 | 1.10e−08 | 1.03e−08 | |
| aT | 9.85e−03 | 1.37e−05 | 7.53e−06 | 1.06e−06 | 2.46e−03 | 2.93e−04 | |
| ξ2 | 1.60e−01 | 4.14e−01 | 2.37e−05 | 2.76e−02 | 5.37e−01 | 2.24e−01 | |
| NT | 1.17e+01 | 3.20e+01 | 6.12e+01 | 1.97e+01 | 2.92e+01 | 1.01e+01 | |
| aE | 1.68e−02 | 1.00e−04 | 2.50e−04 | 8.08e−03 | 3.75e−02 | 1.53e−03 | |
| pE | 3.95e−01 | 1.68e−01 | 3.80e−01 | 1.08e+00 | 1.37e−01 | 6.05e−01 | |
| aA | 4.07e−03 | 5.15e−04 | 9.98e−05 | 5.62e−04 | 1.74e−04 | 4.56e−05 | |
| pT | 9.85e+00 | 5.00e−01 | 9.81e+00 | 7.89e−01 | 1.34e+00 | 5.33e−01 | |
| γTs | 7.98e−06 | 6.08e−05 | 1.65e−05 | 7.98e−05 | 6.14e−05 | 3.35e−04 | |
| aTs | 4.49e−04 | 8.04e−05 | 9.88e−03 | 2.57e−06 | 6.01e−03 | 2.16e−03 | |
| aAs | 9.58e−05 | 1.00e−02 | 7.75e−05 | 1.21e−05 | 2.34e−03 | 6.09e−03 | |
| 1.08e+02 | 7.95e+01 | 4.81e+01 | 3.85e+01 | 4.76e+01 | 4.39e+02 | ||
| 5.98e+01 | 5.82e+01 | 3.93e+01 | 5.33e+01 | 4.85e+01 | 4.43e+02 | ||
| 4.31e+02 | 2.89e+02 | 1.83e+02 | 4.11e+02 | 3.58e+02 | 8.40e+02 | ||
| 2.94e−01 | 6.54e−02 | 9.98e−02 | 9.42e−03 | 9.87e−03 | 1.27e−02 | ||
| 6.93e+04 | 1.50e+05 | 1.58e+05 | 1.16e+05 | 9.54e+03 | 1.43e+03 |
Table 4.
Parameter estimation results for those patients (labels are patient identifiers) whose treatment started during the chronic stage.
| params | CDM | FBO | GMM | SBD | PCJ | SCM | |
|---|---|---|---|---|---|---|---|
| λT | 2.74e+00 | 3.65e+00 | 1.13e+00 | 1.06e+00 | 1.87e+00 | 2.55e+00 | |
| d1 | 2.35e−01 | 1.46e−01 | 9.81e−02 | 2.17e−02 | 1.17e−01 | 1.31e−01 | |
| ξ1 | 1.26e−01 | 9.02e−01 | 1.46e−01 | 3.10e−01 | 4.50e−01 | 5.98e−01 | |
| k1 | 1.95e−03 | 3.72e−04 | 1.38e−04 | 3.50e−03 | 1.14e−03 | 2.82e−04 | |
| k2 | 1.49e−10 | 2.77e−07 | 3.48e−07 | 4.07e−07 | 1.69e−09 | 5.91e−09 | |
| aT | 6.35e−05 | 3.91e−03 | 1.23e−04 | 1.28e−05 | 1.63e−06 | 1.04e−03 | |
| ξ2 | 2.19e−03 | 6.30e−02 | 2.42e−02 | 4.18e−01 | 4.68e−01 | 6.47e−01 | |
| NT | 1.07e+01 | 4.70e+01 | 1.01e+02 | 2.67e+01 | 1.11e+02 | 5.56e+01 | |
| aE | 5.21e−03 | 5.07e−04 | 3.45e−03 | 1.41e−03 | 2.46e−02 | 7.99e−04 | |
| pE | 7.11e−01 | 4.09e−01 | 8.93e−01 | 3.05e−01 | 9.62e−01 | 1.57e+00 | |
| aA | 2.82e−04 | 4.36e−03 | 1.44e−04 | 6.74e−05 | 1.19e−04 | 4.71e−04 | |
| pT | 1.67e+00 | 6.00e−01 | 2.54e+00 | 8.29e−01 | 1.51e+00 | 2.61e+00 | |
| γTs | 2.74e−06 | 7.30e−04 | 6.34e−05 | 1.60e−05 | 2.19e−04 | 1.58e−06 | |
| aTs | 2.36e−03 | 2.96e−04 | 3.85e−03 | 5.54e−04 | 1.07e−03 | 3.17e−03 | |
| aAs | 7.70e−06 | 9.84e−03 | 3.83e−06 | 5.27e−03 | 9.83e−03 | 9.91e−03 | |
| 1.79e+02 | 7.97e+02 | 2.01e+02 | 2.71e+01 | 1.87e+02 | 5.88e+01 | ||
| 1.31e+02 | 3.89e+02 | 4.99e+02 | 2.45e+01 | 2.87e+02 | 7.14e+01 | ||
| 4.75e+02 | 6.76e+02 | 3.99e+02 | 1.60e+01 | 1.72e+02 | 2.12e+02 | ||
| 1.21e−04 | 9.64e−02 | 8.11e−02 | 8.55e−02 | 1.09e−03 | 3.21e−04 | ||
| 1.16e+05 | 3.60e+03 | 6.84e+03 | 2.61e+04 | 3.22e+04 | 1.33e+04 |
3.2.1 Modeling Fitting
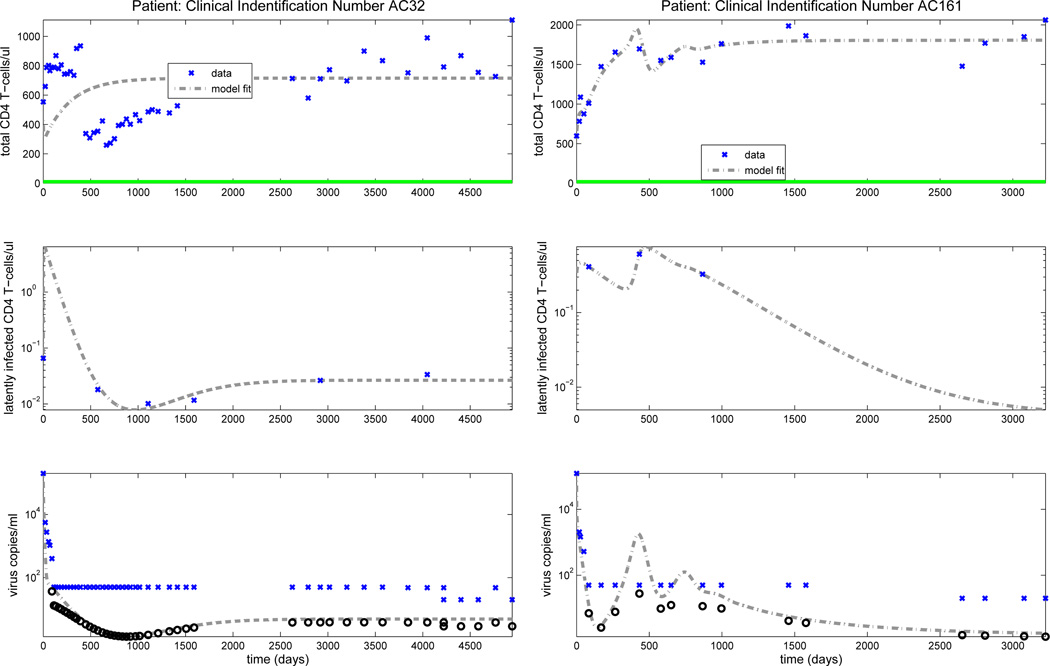
Figure 2 depicts model fitting results for patients AC32 (left column) and AC161 (right column), where time zero is the time point where we have the first observation. From this figure, we see that we obtain reasonable fits in the limits for these two patients. This is also true for the other 10 patients investigated (we refer the interested reader to see Figures 3–8 in [6]). We also note [6] that for some patients our model fits to viral load are much better than those for total CD4+ counts, possibly because the total CD4+ “compartment” is made up of a much more complex sum of components . In addition, we found that the predicted number of HIV-specific CD8+ T cells (E1 + E2) is within the normal range (the maximum value is less than 300 copies/µl).
Figure 2.
Clinical data (‘x’) for the total number of CD4+ T cells, latently infected CD4+ T cells and viral load are shown in the upper, middle and lower rows, respectively. Dark circles denote the predicted censored data values. A solid line along the x-axis in the upper figure indicates periods when the patient is on ART treatment, while a dashed line indicates off-treatment periods.
Figure 3.
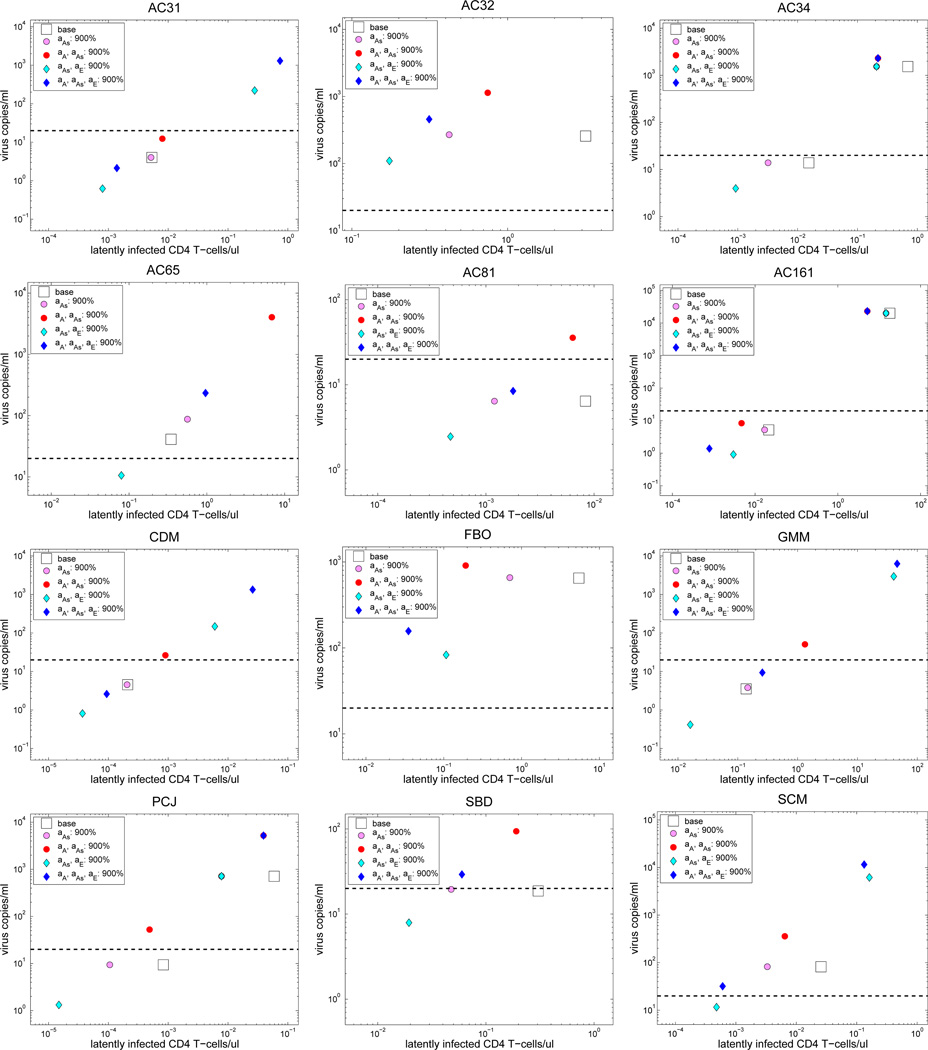
Plots of viral load level versus the concentration of latently infected CD4+ T cells for those locally asymptotically stable equilibrium obtained for the baseline case (shown in the legend by “base”), case (IA1) (shown in the legend by “aAs: 900%”), case (IA2)(shown in the legend by “aA, aAs: 900%”), case (IA3) (shown in the legend by “aAs, aE: 900%”), case (IA4) (shown in the legend by “aA, aAs, aE: 900%”). The dashed black line indicates the detection limit of 20 copies/ml.
3.2.2 Stability Analysis
We obtain the off-treatment (i.e., ξ1 = ξ2 = 0) equilibrium for model (2.1)–(2.8) with parameter values obtained for each patient. Results show that none of these patients has a locally asymptotically stable (a.s.) uninfected equilibrium, which is characterized by zero infected CD4+ T cells and zero viral load level (i.e., , , VI = 0 and VNI = 0). In addition, we found that all the patients have at least one locally a.s. infected equilibrium: patients AC34, AC161 and PCJ have two while all the other patients have only one. We also note that patients AC31, AC34, AC81 AC161, CDM, GMM, PCJ and SBD have a locally a.s. infected equilibrium with viral load level below the detection limit of 20 copies/ml. For these eight patients, we found that it takes 16, 36, 9 and 8 months of treatment to eventually converge to this undetectable steady state for patients AC31, AC34, AC161 and PCJ, respectively. With the estimated initial conditions it will eventually converge to the undetectable steady state for AC81, CDM, GMM and SBD without any treatment. Moreover, we notice that if the concentration of the latently infected CD4+ T cells is greater than 1 cells/µl, then the viral load is above the detection limit of 20 copies/ml. To visually see these findings, we refer the interested reader to Figure 9 of [6].
4 Immuno-modulatory Strategies for Eradication of the Latent Reservoir
We use our validated mathematical model together with patient-specific parameter estimates to investigate which pharmacological strategy or combination of strategies that affect the immune system may help eradicate the latent reservoir. We first present results from an off-treatment stability analysis that was used to investigate the effects of altering (increasing or decreasing) several sets of immune system parameters for each patient. These stability analysis results are then corroborated by a simulation analysis in which we investigated all possible combinations of immune system parameter changes. We observe that the calculation for equilibrium stability for one choice of parameter changes for each patient requires approximately 8 hours on a single core desktop computer. In contrast, simulating the dynamics, e.g., for 6 patient years, for all possible parameter combinations we consider requires approximately 100 hours per patient. Although we did not calculate stability for all possible immune system parameter changes, the changes which we did investigate are among those we feel are clinically relevant.
Specifically, our analyses considered changes to the following parameters:
aA: activation rates of uninfected resting CD4+ T cells,
aAs: activation rates of latently infected CD4+ T cells,
aE: activation rates of HIV-specific memory CD8+ T cells,
pT : proliferation rate of CD4+ T cells,
pE: proliferation rate of HIV-specific CD8+ T cells,
m: elimination rate of infected activated CD4+ T cells by HIV-specific effector CD8+ T cells.
Analysis of these parameters was motivated by existing drugs that might be effective as adjuvant therapies to ART. For example, interferon therapy has several effects, including stimulating CD4+ and CD8+ T cell proliferation and increasing the efficacy of CD8+ T cells (e.g., see [14, 18, 25]). The activation of T cells could be increased with HDAC inhibitor therapy (e.g., see [4, 35, 39]), and could be decreased with immuno-suppression therapy.
4.1 Stability Analysis: Modulation of Immune System Parameters
In our stability analysis, a strategy is deemed to be useful to eradicate the reservoir only if it can make all the patients have a locally a.s. uninfected equilibrium. The rationale is as follows. A given combination of therapies aimed at eradication of the reservoir is given to the patient while he/she remains on ART. When the viral load is close to zero, ART can be withdrawn as the existence of a locally a.s. uninfected equilibrium ensures that the patient’s state will eventually converge to this equilibrium. Once the patient is totally cured, then the given combination of therapies can be withdrawn.
If a strategy is found to be unable to make the patient have a locally a.s. uninfected equilibrium, we compare its results with the ones obtained for the case where the estimated values for all the parameters are not changed, i.e., the baseline, to determine whether or not it is beneficial to the patient. If a proposed strategy and/or the baseline case have more than one locally a.s. equilibrium, then we only compare the results for their corresponding equilibrium with the lowest viral load level. We examined whether any of the following strategies is useful in eradication the reservoir: increasing/decreasing the activation rates, increasing/decreasing the activation and proliferation rates, increasing the activation rates and the efficacy of CD8+ T cells, and, lastly, increasing the activation and proliferation rates and the efficacy of CD8+ T cells.
4.1.1 Stability Analysis: Varying the Activation Rates
We consider the strategies for varying only the activation rates. Specifically, we determine which strategy, activation versus deactivation, is useful in eradicating the reservoir. The deactivation strategy is motivated by the results in [37], where the immunosuppressant therapy “sirolimus” is used to treat HIV-infected kidney transplant recipients and it was found that a longer duration of immunosuppressant therapy was associated with a lower HIV DNA levels.
Results for Increasing the Activation Rates
Since different types of drugs may have different effects on the activation rates of different types of T cells, we investigate four cases: (IA1) increase aAs, (IA2) increase aA and aAs, (IA3) increase aAs and aE, (IA4) increase aA, aAs and aE.
For all the four cases with associated parameters increased by 900% (i.e., increase 10-fold), stability analysis shows that none of these 12 patients has a locally a.s. uninfected equilibrium. To have a clear idea of the effect of each case on these patients, we plotted the viral load level versus the concentration of latently infected CD4+ T cells for those locally a.s. equilibrium obtained for each case, and compare them with the ones obtained for the baseline case. The results are shown in Figure 3. We observe from this figure that for strategy (IA3) all the patients have a lower level of latently infected CD4+ T cells than their corresponding ones obtained for the baseline case. This is also true for most of the patients in the other three cases. Thus, increasing the activation rates in general makes most of the patients have a lower level of latently infected CD4+ T cells. However, each strategy has a different effect on the viral load level. Specifically, the viral load level obtained for case (IA1) is either similar to or larger than that obtained for the baseline case, the one obtained for case (IA2) is bigger than that for the baseline case, and the one obtained for case (IA3) is smaller than the one for the baseline case. The results obtained for case (IA4) are mixed: half of the patients have a lower viral load level than that for the baseline case, and the rest of them have a larger viral load level.
Based on these results, we see that strategy (IA3) is beneficial to the patients while all the other three strategies have a mixed effect on the patients. At this point, a natural question to ask is whether or not one can obtain a locally a.s. uninfected equilibrium for case (IA3) by further increasing the value of aE. To answer this question, we increased aAs by 900% but increased aE by 99900%, and still found that none of the patients has a locally a.s. uninfected equilibrium. In addition, we found that it has detrimental effect on patients AC34 and FBO as for this case both patients have a much higher viral load level than that for the baseline case (we refer the interested reader to [6, Figure 11] for details). However, it is beneficial to all the other 10 patients as for this case they all have a much lower viral load level and concentration of latently infected CD4+ T cells than their corresponding ones obtained for case (IA3). Overall, these results suggest that increasing the activation rate for the HIV-specific CD8+ T cells may not be sufficient to eradicate the reservoir and may have detrimental effects on patients if it is increased too much.
Results for Decreasing the Activation Rates
Here we consider the strategy for decreasing the activation rates of T cells. Specifically, we consider three cases: (DA1) decrease aA, (DA2) decrease aA and aAs, (DA3) decrease aA, aAs and aE.
For case (DA1) with aA decreased by 90%, we found that all of the patients except patient FBO have a locally a.s. uninfected equilibrium. If we further decrease aA by 99%, then patient FBO also has a locally a.s. uninfected equilibrium. We obtained exactly the same results for case (DA2). This suggests that decreasing the activation rates for CD4+ T cells can create stability in the uninfected equilibrium. In addition, decreasing the activation rates for the uninfected resting CD4+ T cells (T2) plays a major role in creating this stability. This is expected as decreasing the activation rates for T2 decreases the number of activated CD4+ T cells, which are the most permissive target for HIV infection.
For case (DA3) with aA, aAs and aE decreased by 90%, we found that all the patients except AC31, AC34, AC81 and FBO have a locally a.s. uninfected equilibrium. Specifically, patients AC31, AC34, AC81 do not have a physical equilibrium in this case, and patient FBO still has one locally a.s. infected equilibrium. If we further decrease aA, aAs and aE by 99%, then all the patients have a locally a.s. uninfected equilibrium. This suggests that global suppression of activation is also possible to create the stability in the uninfected equilibrium.
Summary Remarks on Strategies for Varying Activation Rates
Our analysis suggests that increasing the activation rates in general makes most of the patients have a lower level of latently infected CD4+ T cells. However, it may dramatically increase the viral load level, depending on the intensity and the types of T cells that were activated. This conforms with the results observed in [26], where their results suggest that eradication strategies such as these aimed mainly at the reactivation of latently infected resting CD4+ T cells may face a difficult task because they observed high levels of proliferation in the memory cells and yet they saw no substantial decay in integrated HIV DNA.
Our results also suggest that decreasing the activation rates can create the stability in uninfected equilibrium and thus it can be used as a strategy to eradicate the reservoir. In addition, the intensity of suppression of the activation of uninfected resting CD4+ T cells is essential to the stability of the uninfected equilibrium. This is expected from an intuitive point of view as decreasing the activation rate of uninfected resting CD4+ T cells decreases the number of activated CD4+ T cells (target cells for infection) and hence results in less viral infection and production. Based on the results in [37], this finding is also expected from a clinical point of view.
4.1.2 Stability Analysis: Varying Both Activation and Proliferation Rates
We consider the strategies for varying both the activation rates and the proliferation rates. Specifically, we determine which strategy, increasing versus decreasing of the activation and proliferation rates, is useful in eradicating the reservoir. The strategy for decreasing the activation and proliferation rates (i.e., suppression of the immune response) is again motivated by the study in [37] for using immnosuppressive therapy to treat HIV-infected kidney transplant recipients.
Results for Increasing Both Activation and Proliferation Rates
Here we consider the strategy for increasing both the activation rates and the proliferation rates. Specifically, we consider four cases: (IAP1) increase aAs, aE and pE, (IAP2) increase aAs, aE, pT and pE, (IAP3) increase aA, aAs, aE and pE, (IAP4) increase aA, aAs, aE, pT and pE.
Analysis reveals that none of these patients has a locally a.s. uninfected equilibrium for these four cases with the associated parameters in each case increased by 900%. To have a clear idea of the effect of each case on these patients, we plot the viral load level versus the concentration of latently infected CD4+ T cells for those locally a.s. equilibrium obtained for each case, and compare them with the ones obtained for the baseline case. The results are shown in Figure 12 of [6]. We observed that for the first three cases both the viral load level and the concentration of the latently infected CD4+ T cells are smaller than their corresponding ones obtained for the baseline case. This is also true for most of the patients using the strategy (IAP4). In addition, we fouond that the strategy (IAP1) is the best one in terms of viral load level. This means that increasing the proliferation rates for the CD4+ T cells and increasing the activation rates for the uninfected resting CD4+ T cells both have a negative effect on the patients. Thus, if possible, one should focus on only increasing the activation rates for the latently infected CD4+ T cells and HIV-specific CD8+ T cells and only increasing the proliferation rates for the HIV-specific CD8+ T cells.
At this point, a natural question to ask is whether or not one can obtain a locally a.s. uninfected equilibrium for case (IAP1) by further increasing the value of pE. To answer this question, we increased aAs and aE by 900% but increased pE by 99900%, and still found that none of these patients has a locally a.s. uninfected equilibrium. However, we found that for this case all the patients have a lower viral load level and smaller concentration of latently infected CD4+ T cells than their corresponding ones obtained for case (IAP1) (we refer the interested reader to [6, Figure 13] for details). This results suggest that increasing the proliferation rates for the HIV-specific CD8+ T cells may not be sufficient to eradicate the reservoir but it is beneficial to patients.
Results for Decreasing Both Activation and Proliferation Rates
Now we consider the case for decreasing both the activation rates and the proliferation rates. Specifically, we decreased aA, aAs, aE, pT and pE by 90% and found that all the patients have a locally a.s. uninfected equilibrium. In addition, all these patients only have this one physical equilibrium. This suggests that decreasing both the activation rates and proliferation rates can create the stability in the uninfected equilibrium, and hence a proper suppression of the immune system can be used as a strategy to eradicate the reservoir. Recall that it was found in [37] that a longer duration of immunosuppressant therapy was associated with a lower HIV DNA levels. Hence, our finding is not unexpected from the clinical point of view.
4.1.3 Stability Analysis: Increasing Both Activation Rates and the Efficacy of HIV-Specific Effector CD8+ T Cells
We consider the strategy for increasing both the activation rates and the efficacy of the HIV-specific effector CD8+ T cells. Specifically, we consider two cases: (IAM1) increase aAs, aE and m, (IAM2) increase aA, aAs, aE and m, where the value of m, the efficiency of killing infected cells, is used here to characterize the efficacy of HIV-specific effector CD8+ T cells.
For case (IAM1), we increased aAs and aE by 900% and m by 9900% and found that all the patients except patients FBO, PCJ and SCM have a locally a.s. uninfected equilibrium. However, it does have a beneficial effect on these 3 patients too, as both patients FBO and SCM now have a locally a.s. infected equilibrium with viral load below the detection limit, and patient PCJ now only has an infected equilibrium with viral load 2.997 × 10−3 copies/ml, less than the one obtained for the baseline case. If we further increase m by 49900%, then patients FBO, PCJ and SCM also have a locally a.s. uninfected equilibrium, which is the only physical equilibrium obtained for these patients in this case.
For case (IAM2), we increased aA, aAs and aE by 900% and m by 9900% and found that none of the patients has a locally a.s. uninfected equilibrium. Based on this result and the one obtained for case (IAM1), we see that increasing the activation rate for the uninfected resting CD4+ T cells can destroy the stability of the uninfected equilibrium. If we further increase m by 99900%, then all the patients have a locally a.s. uninfected equilibrium. Thus, if we can only globally activate all the T cells, then we need to increase the efficacy of HIV-specific CD8+ T cells significantly high in order to achieve the stability of the uninfected equilibrium.
Overall, the above results and the ones obtained in Section 4.1.1 for simply increasing the activation rates suggest that the efficacy of HIV-specific CD8+ T cells is essential to the stability of the uninfected equilibrium, and thus it is essential for successful eradication of the reservoir. This is in agreement with the conclusion obtained in [33].
4.1.4 Stability Analysis: Increasing Activation Rates, Proliferation Rates and the Efficacy of HIV-Specific Effector CD8+ T Cells
We consider the strategy for increasing the activation and proliferation rates as well as the efficacy of the HIV-specific effector CD8+ T cells. Specifically, we consider two cases: (IAMP1) increase aAs, aE, pT, pE and m, (IAMP2) increase aA, aAs, pT, pE, aE and m.
For case (IAM1), we increased aAs, aE, pT and pE by 900% and m by 9900% and found that none of these patients has a locally a.s. uninfected equilibrium. Based on this result and the results presented in Section 4.1.3, we again see that increasing the proliferation rates for the CD4+ T cells has a negative effect on the patients as it can destroy the stability of the uninfected equilibrium. If we further increase m by 49900%, then all the patients except patient FBO have a locally a.s. uninfected equilibrium. If we increase m by 99900%, then patient FBO also has a locally a.s. uninfected equilibrium. For case (IAM2), we increased aA, aAs, aE, pT and pE by 900% and m by 99900% and found that all the patients have a locally a.s. uninfected equilibrium. In addition, all these patients only have this one physical equilibrium.
Based on the above results and the ones obtained in Section 4.1.2, we again see that the efficacy of HIV-specific effector CD8+ T cells is essential to the stability of the uninfected equilibrium.
4.1.5 Summary Remarks on Stability Analysis
Overall our results show that reactivation of latently infected CD4+ T cells is not sufficient to eradicate the latent reservoir. In addition, increasing the activation rate for the uninfected resting CD4+ T cells (i.e., aA) has a detrimental effect on patients and so is increasing the proliferation rate pT for the CD4+ T cells. This is expected as increasing either of them would increase the number of activated CD4+ T cells and hence results in more viral infection and production. We found that increasing the proliferation rate and the efficacy of HIV-specific CD8+ T cells are both beneficial to patients and that enhancement of the efficacy of HIV-specific CD8+ T cells is essential to make the reactivation strategy to be successful. Moreover, our results suggest that a proper suppression of immune system is also a possible strategy to eradicate the latent reservoir and that the intensity of suppression of the activation of uninfected resting CD4+ T cells is essential to make this successful.
4.2 Simulation Analysis: Modulation of Immune System Parameters
To verify and extend the stability analysis, we also performed simulations for all possible immune system parameter changes for each patient. The parameter changes we considered were chosen from the set {aA, aAs, aE, pT, pE, m}. Parameters were altered by decreasing 100-fold or 10-fold, left unchanged, or increased by 10-fold or 100-fold, i.e., {−99%, −90%, 0%, 900%, 9900%}, for a total of 56 possible combinations per patient. Estimated values, from clinical data fitting, of the six chosen immune system parameters were altered and the rest of the model parameters were kept the same as their estimated values. We ran simulations for each patient for 3 years on ART, followed by 3 years off ART.
Simulation endpoints, at 6 years, were analyzed to determine which parameter changes could be beneficial towards inducing a stable virus-free or virus-undetectable state while also lowering the concentration of latently infected cells. For our simulation analysis, parameter changes are deemed beneficial if their effect is to lower or keep the viral load below the detection limit after 3 years on ART followed by 3 years off ART. Since simulations can only inform about the short-term dynamics, we also required the viral load and latently infected cell levels to be non-increasing at the 6 year time point (3 years post-ART), e.g., less than or equal to the viral load at 5 years (2 years post-ART). This requirement is used to qualitatively assess the stable convergence of post-ART viral load to levels below the detection limit.
4.2.1 Simulation Analysis: Modulation of Single Immune System Parameters
We first analyzed the effect of changing one of the immune system parameters at a time for each patient, assuming they underwent 3 years of ART. We found (see also Figure 14 of [6]) that lowering the activation rate of non-infected CD4+ T cells, aA, lowered the viral load and latently infected cell count for all patients; increasing aA had the opposite effect¿ In contrast, the majority of patients were insensitive to changes in the activation rate of latently infected cells, aAs. Moreover, some patients showed increases in either the viral load and/or the latently infected cell count when the parameter aAs was increased. Increases in the parameter aE, the CD8+ T cell activation rate, both lowered the viral load and latently infected cell count for most patients. However, we found a non-linear relationship between aE and the viral load and latently infected cell levels for some patients. For example, a 10-fold (900%) increase in aE was beneficial for patient CDM, but a 100-fold (9900%) had the opposite effect and increased the viral load and latently infected cell levels. Similar non-linear effects due to changes in aE were found for both chronically and acutely treated patients (SBD, GMM, FBO, AC81, AC65, and AC31). Decreasing the proliferation rate of CD4+ T cells, pT lowered the viral load and latently infected cell levels to below the detection limit for all patients, whereas increasing pT had the opposite effect. Conversely, increases in the proliferation rate of CD8+ T cells, pE, led to a decrease in viral load and latently infected cell levels, and decreasing pE had the opposite effect.
Lastly, increasing the rate of CD4+ T cell death due to effector CD8+ T cells pushed the viral load to below the detection limit for all patients, while also lowering the latently infected cell levels. For most patients, a 10-fold increase (900%) in m was enough to drive the viral load below the detection limit, however, for patient FBO a 100-fold increase 9900% was necessary. For all patients, a 100-fold increase in m was drastically more beneficial than a 10-fold increase, i.e., the viral load was several orders of magnitude lower. Overall, these results suggest that altering kinetic parameters that effect the host immune system, especially decreasing aA and pT, may have beneficial effects for all patients.
4.2.2 Simulation Analysis: Combinatorial Modulation of Immune System Parameters
Next, we calculated which combination of parameter changes, i.e., immune system modulation strategies, could lower both the viral load and latently infected cell levels for all patients after 3 years of ART. For each set of 56 combinations of parameter changes, we calculated which combinations pushed the viral load below the detection limit after 3 years on ART followed by 3 years off ART. We calculated both patient-specific strategies as well as strategies that were beneficial for all 12 patients considered in this study.
We note that only essential changes were kept, and redundant or ineffective parameter changes were removed. For example, for some patients, lowering aA induced a viral load below the detection limit, whether pE was decreased or increased by 100-fold, and we deduced that aA and not pE was the essential parameter to change. We also removed any strategies that had a non-linear effect on viral load. For example, if increasing aE and decreasing aA, both by 10-fold, decreased the viral load, but increasing aE and decreasing aA, both by 100-fold, increased the viral load, then this strategy was not included. In addition, we also required both 10-fold and 100-fold changes to chosen parameter combinations to reduce the viral load to below the detection limit.
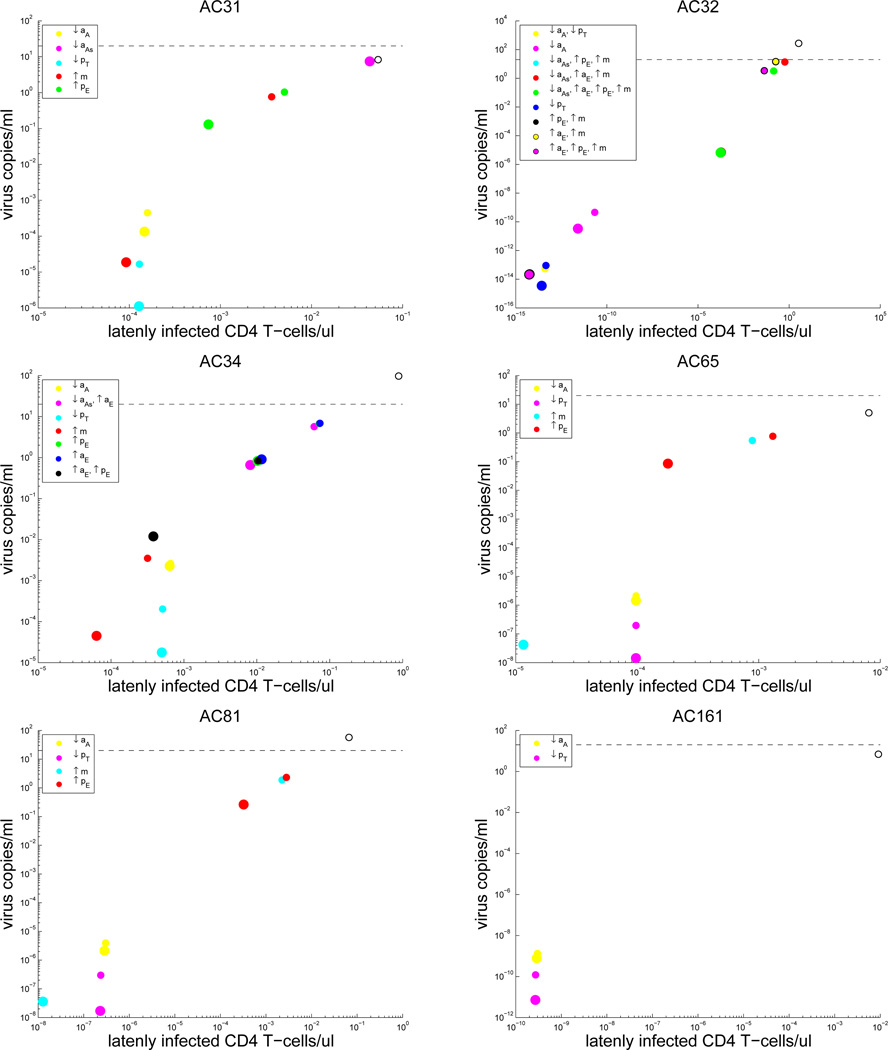
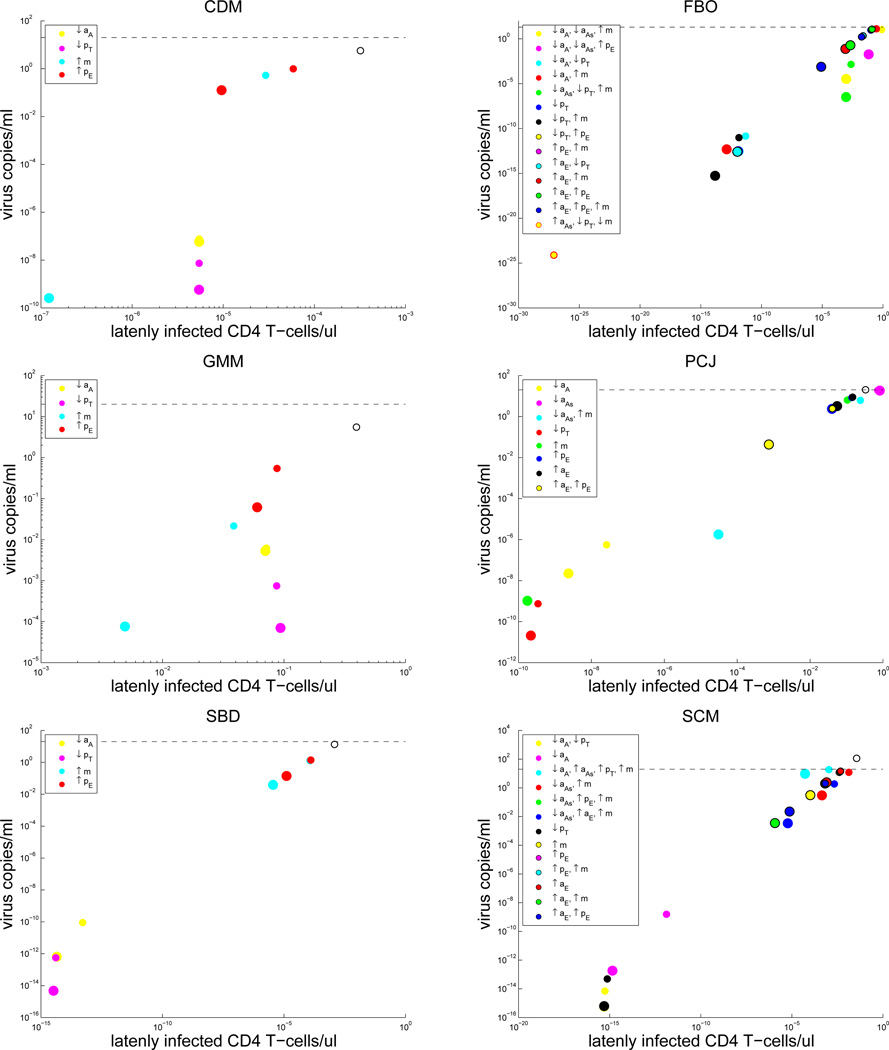
Our patient-specific strategy results highlight the possibility for personalized medicine treatments, where only a small number of parameter changes in immune system kinetics may be necessary for a cure in some patients, whereas other patients may require a diverse set of changes, i.e., combination therapy (Figures 4 and 5). Notably, the only single parameter change strategy that decreases viral load and latently infected cell levels for all 12 patients is decreasing pT.
Figure 4.
Results for those patients whose treatment began during the acute phase: Plots of viral load level versus the concentration of latently infected CD4+ T cells for patient specific treatment strategies. Increases and decreases in kinetic parameters are denoted by up and down arrows, respectively. Large colored circles = 100-fold changes, Small colored circles = 10-fold changes, Baseline levels with no parameter changes = open black/white circles. The dashed black line indicates the detection limit of 20 copies/ml.
Figure 5.
Results for those patients whose treatment began during the chronic phase: Plots of viral load level versus the concentration of latently infected CD4+ T cells for patient specific treatment strategies. Increases and decreases in kinetic parameters are denoted by up and down arrows, respectively. Large colored circles = 100-fold changes, Small colored circles = 10-fold changes, Baseline levels with no parameter changes = open black/white circles. The dashed black line indicates the detection limit of 20 copies/ml. Note: a 100-fold change for the last strategy for patient FBO induced a viral load < 10−200.
In total, we found 21 strategies that were able to induce a viral load below the detection limit for all patients. These strategies are summarized in Table 5, and interested readers are referred to [6, Figures 17 and 18] to visually see the effect of these strategies on viral load and latently infected CD4+ T cell levels for all patients. In theory, combination therapies that correspond to these strategies, i.e., by inducing the respective parameters changes, may lead to a stable virus-free state for all patients who undergo at least 3 years of ART.
Table 5.
Strategies that induce a viral load below the detection limit after 3 years of ART treatment. Increases and decreases in kinetic parameters are denoted by up and down arrows, respectively.
| aA | aAs | aE | pT | pE | m | |
|---|---|---|---|---|---|---|
| Treatment Strategy 1 | ↓ | ↓ | 0 | 0 | 0 | ↑ |
| Treatment Strategy 2 | ↓ | ↓ | 0 | 0 | ↑ | 0 |
| Treatment Strategy 3 | ↓ | ↓ | 0 | 0 | ↑ | ↑ |
| Treatment Strategy 4 | ↓ | ↓ | ↑ | 0 | 0 | ↑ |
| Treatment Strategy 5 | ↓ | 0 | 0 | ↓ | 0 | 0 |
| Treatment Strategy 6 | ↓ | 0 | 0 | 0 | 0 | ↑ |
| Treatment Strategy 7 | ↓ | 0 | 0 | 0 | ↑ | ↑ |
| Treatment Strategy 8 | ↓ | 0 | ↑ | 0 | 0 | ↑ |
| Treatment Strategy 9 | ↓ | 0 | ↑ | 0 | ↑ | 0 |
| Treatment Strategy 10 | 0 | ↓ | 0 | ↓ | 0 | ↑ |
| Treatment Strategy 11 | 0 | ↓ | 0 | 0 | ↑ | ↑ |
| Treatment Strategy 12 | 0 | ↓ | ↑ | 0 | 0 | ↑ |
| Treatment Strategy 13 | 0 | ↓ | ↑ | 0 | ↑ | ↑ |
| Treatment Strategy 14 | 0 | 0 | 0 | ↓ | 0 | 0 |
| Treatment Strategy 15 | 0 | 0 | 0 | ↓ | 0 | ↑ |
| Treatment Strategy 16 | 0 | 0 | 0 | ↓ | ↑ | 0 |
| Treatment Strategy 17 | 0 | 0 | 0 | 0 | ↑ | ↑ |
| Treatment Strategy 18 | 0 | 0 | ↑ | ↓ | 0 | 0 |
| Treatment Strategy 19 | 0 | 0 | ↑ | 0 | 0 | ↑ |
| Treatment Strategy 20 | 0 | 0 | ↑ | 0 | ↑ | ↑ |
| Treatment Strategy 21 | 0 | ↑ | 0 | ↓ | 0 | ↓ |
4.2.3 Summary Remarks on Simulation Analysis
Although there were no significant differences in the immuno-modulatory strategies revealed to be beneficial between acutely treated and chronically treated patients, there were obvious differences in the personalized strategies chosen between patients. For some patients, changes to a single specific CD4+ or CD8+ T cell related parameter were enough to push the viral load to below the detection limit, while other patients required multi-parameter alterations to their immune system kinetics (Figures 4 and 5). A key finding from our simulation results, which is in concordance with our stability analysis, was that the two most beneficial changes for all patients is lowering the activation and proliferation of uninfected CD4+ T cells. This finding was visible in our analysis of single parameter changes (see Figure 14 of [6]) and changes to patient-specific parameter combinations (Figures 4 and 5). Moreover, this strategy was present in the list of treatments that were predicted to be beneficial for all patients (Table 5).
Our simulation results also suggest that increasing the activation, proliferation, and efficacy of CD8+ T cells can increase the effectiveness of ART. In general, we found that the most beneficial immuno-modulatory strategy for all patients is to decrease the activation and proliferation of CD4+ T cells, while simultaneously increasing the activation, proliferation, and efficacy of CD8+ T cells.
5 Discussion
We used a validated mathematical model to evaluate different immuno-modulatory strategies that may reduce or eradicate the latent reservoir. Our analysis suggests that simple reactivation of latently infected CD4+ T cells is not sufficient to eradicate the reservoir and that enhancement of the efficacy of the HIV-specific effector CD8+ T cells is essential to make this strategy to be successful.
Our analysis also suggests that a proper suppression of the immune system may assist to eradicate the reservoir. Specifically, a concordant finding from both our simulation and stability analysis was that decreasing the activation rates of CD4+ T cells, aA, may help lower the viral load and eradicate the reservoir of latently infected cells. We only found one strategy for a single patient, SCM, that included increasing aAs, and that strategy also required a decrease in aA. To confirm this finding, we revisited the patient data set previously analyzed in [5] and found that the two patients with stable virus-free equilibria had significantly lower CD4+ T cell activation rates than the other twelve patients (Mann-Whitney U Test, P = 0.0219, data not shown). Moreover, we found that we could induce stable virus-free equilibria for all fourteen patients from the previous study [5] by decreasing the CD4+ T cell activation rates by 95%, and that this virus-free state could be reached with only 1 year of ART. This finding may be of importance to clinical trials that are currently in progress, e.g., [28], those that treat patients with HDAC inhibitors as an adjuvant therapy to ART. Our model predicts that if HDAC inhibitor therapy increases aA, then it may have the unintended effect of actually increasing the viral load and concentration of latently infected cells when used as the only adjuvant therapy to ART.
We remark that activation and proliferation of CD4+ T cells are controlled by a number of signaling pathways including the mammalian target of rapamycin (mTOR), signal transducer and activator of transcription 5a (STAT5a) and foxhead box O3a (e.g., see [9] and the references therein). Hence, any drug aimed to inhibit these pathways could be potentially used to limit T cell activation and proliferation and might therefore reduce or eradicate the latent reservoir. For example, the aforementioned immunosuppressant therapy “sirolimus” can inhibit mTOR, and the results in [37] suggest mTOR inhibition may prove useful in a combination eradication strategies. Another way to limit the activation of CD4+ T cells is to inhibit the Janus activating kinase-signal transducer and activator of transcription (JAK-STAT) pathway. This pathway is activated early in HIV infection across multiple HIV target cells including macrophages and CD4+ T cells, and it can be inhibited using FDA-approved drugs such as ruxolitinib and tofacitinib (see [17] for details).
Overall, our analysis suggests that a combination of drugs that can target CD4+ and CD8+ T cell phenotypes separately by decreasing CD4+ T cell activation and proliferation rates while also increasing CD8+ T cell activation, proliferation, and efficacy will be of most benefit to the patient. If such drugs can be developed, then it may be possible to eradicate the latent reservoir.
Acknowledgements
This research was supported in part by Grant Number NIAID R01AI071915-10 from the National Institute of Allergy and Infectious Diseases, and in part by the Air Force Office of Scientific Research under grant number AFOSR FA9550-12-1-0188. In addition, the authors are grateful to anonymous referees for their careful reading and helpful comments which led to an improved version of this paper.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
H.T. Banks, Center for Research in Scientific Computation, North Carolina State University, Raleigh, NC 27695-8212 USA
Kevin B. Flores, Center for Research in Scientific Computation, North Carolina State University, Raleigh, NC 27695-8212 USA
Shuhua Hu, Center for Research in Scientific Computation, North Carolina State University, Raleigh, NC 27695-8212 USA.
Eric Rosenberg, Harvard Medical School and Mass General Hospital, Ragon Institute, Boston, MA.
Maria Buzon, Harvard Medical School and Mass General Hospital, Ragon Institute, Boston, MA.
Xu Yu, Harvard Medical School and Mass General Hospital, Ragon Institute, Boston, MA.
Matthias Lichterfeld, Harvard Medical School and Mass General Hospital, Ragon Institute, Boston, MA.
References
- 1.Abdella SH, Wabe NT, Yesuf EA. Management of common adverse effects in the era of highly active antiretroviral therapy in south east Ethiopia. North American Journal of Medical Sciences. 2011;11:499–502. doi: 10.4297/najms.2011.3499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Adams BM, Banks HT, Davidian M, Rosenberg ES. Model fitting and prediction with HIV treatment interruption data, CRSC-TR05-40, NCSU, October, 2005. Bulletin of Mathematical Biology. 2007;69:563–584. doi: 10.1007/s11538-006-9140-6. [DOI] [PubMed] [Google Scholar]
- 3.Archin NM, Vaidya AK, Kuruc JD, Liberty AL, Wiegand A, Kearney MF, Cohen MS, Coffin JM, Bosch RJ, Gay CL, Eron JJ, Margolis DM, Perelson AS. Immediate antiviral therapy appears to restrict resting CD4+ cell HIV-1 infection without accelerating the decay of latent infection. Proc Natl Acad Sci USA. 2012 doi: 10.1073/pnas.1120248109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Archin NM, Liberty AL, Kashuba AD, Choudhary SK, Kuruc JD, et al. Administration of vorinostat disrupts HIV-1 latency in patients on antiretroviral therapy. Nature. 2012;487:482–485. doi: 10.1038/nature11286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Banks HT, Davidian M, Hu S, Kepler GM, Rosenberg ES. Modeling HIV immune response and validation with clinical data. Journal of Biological Dynamics. 2008;2:357–385. doi: 10.1080/17513750701813184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Banks HT, Flores KB, Hu S, Rosenberg E, Buzon M, Yu X, Lichterfeld M. Immuno-modulatory strategies for reduction of HIV reservoir cells, CRSC-TR14-10, Center for Research in Scientific Computation. North Carolina State University; ( http://www.ncsu.edu/crsc/reports/reports14.html) [Google Scholar]
- 7.Banks HT, Hu S, Thompson WC. Modeling and Inverse Problems in the Presence of Uncertainty. Boca Raton, FL: Chapman Hall/CRC Press; 2014. [Google Scholar]
- 8.Banks HT, Tran HT. Mathematical and Experimental Modeling of Physical and Biological Processes. Boca Raton, FL: Chapman Hall/CRC Press; 2009. [Google Scholar]
- 9.Barouch DH, Deeks SG. Immunologic strategies for HIV-1 remission and eradication. Science. 2014;345:169–174. doi: 10.1126/science.1255512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Buzon MJ, Massanella M, Llibre JM, Esteve A, Dahl V, Puertas MC, Gatell JM, Domingo P, Paredes R, Sharkey M, Palmer S, Stevenson M, Clotet B, Blanco J, Martinez-Picado J. HIV-1 replication and immune dynamics are affected by raltegravir intensification of HAART-suppressed subjects. Nature Medicine. 2010;16:460–465. doi: 10.1038/nm.2111. [DOI] [PubMed] [Google Scholar]
- 11.Chomont N, El-Far M, Ancuta P, Trautmann L, Procopio FA, et al. HIV reservoir size and persistence are driven by T cell survival and homeostatic proliferation. Nat. Med. 2009;15:893–900. doi: 10.1038/nm.1972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J. Roy. Stat. Soc., Ser. B. 1977;39:1–38. [Google Scholar]
- 13.Donahue DA, Wainberg MA. Cellular and molecular mechanisms involved in the establishment of HIV-1 latency. Retrovirology. 2013;10 doi: 10.1186/1742-4690-10-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dondi E, Roue G, Yuste VJ, Susin SA, Pellegrini S. A dual role of IFN-α in the balance between proliferation and death of human CD4+ T lymphocytes during primary response. Journal of Immunology. 2004;173:3740–3747. doi: 10.4049/jimmunol.173.6.3740. [DOI] [PubMed] [Google Scholar]
- 15.Egger M, May M, Chene G, Phillips AN, Ledergerber B, Dabis F, Costagliola D, D’Arminio Monforte M, deWolf AF, Reiss P, Lundgren JD, Justice AC, Staszewski S, Leport C, Hogg RS, Sabin CA, Gill MJ, Salzberger B, Sterne JA. ART cohort collaboration, prognosis of HIV-1-infected patients starting highly active antiretroviral therapy: a collaborative analysis of prospective studies. Lancet. 2002;9327:119–129. doi: 10.1016/s0140-6736(02)09411-4. [DOI] [PubMed] [Google Scholar]
- 16.Friedrich B, Li G, Dziuba N, Ferguson MR. Quantitative PCR used to assess HIV-1 integration and 2-LTR circle formation in human macrophages, peripheral blood lymphocytes and a CD4+ cell line. Virology Journal. 2010;7:354–360. doi: 10.1186/1743-422X-7-354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gavegnano C, Detorio M, Montero C, Bosque A, Planelles V, Schinazi RF. Ruxolitinib and Tofacitinib are potent and selective inhibitors of HIV-1 replication and virus reactivation in vitro. Antimicrobial Agents and Chemotherapy. 2014;58:1977–1986. doi: 10.1128/AAC.02496-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Huber JP, Farrar JD. Regulation of effector and memory T-cell functions by type I interferon. Immunology. 2011;132:466–474. doi: 10.1111/j.1365-2567.2011.03412.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Koelsch KK, Liu L, Haubrich R, May S, Havlir D, Günthard HF, Ignacio CC, Campos-Soto P, Little SJ, Shafer R, Robbins GK, D’Aquila RT, Kawano Y, Young K, Dao P, Spina CA, Richman DD, Wong JK. Dynamics of total, linear nonintegrated, and integrated HIV-1 DNA in vivo and in vitro. Journal of Infectious Disease. 2008;197:411–419. doi: 10.1086/525283. [DOI] [PubMed] [Google Scholar]
- 20.Josefsson L, King MS, Makitalo B, Brännström J, Shao W, Maldarelli F, Kearney MF, Hu WS, Chen J, Gaines H, Mellors JW, Albert J, Coffin JM, Palmer SE. Majority of CD4+ T cells from peripheral blood of HIV-1-infected individuals contain only one HIV DNA molecule. Proc Natl Acad Sci USA. 2011;108:11199–11204. doi: 10.1073/pnas.1107729108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Katlama C, Deeks SG, Autran B, Martinez-Picado J, van Lunzen J, Rouzioux C, Miller M, Vella S, Schmitz JE, Ahlers J, Richman DD, Sekaly RP. Barriers to a cure for HIV: new ways to target and eradicate HIV-1 reservoirs. Lancet. 2013;381:2109–2117. doi: 10.1016/S0140-6736(13)60104-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lassen KG, Hebbeler AM, Bhattacharyya D, Lobritz MA, Greene WC. A flexible model of HIV-1 latency permitting evaluation of many primary CD4 T-Cell reservoirs. PLoS ONE. 2012;7:e30176. doi: 10.1371/journal.pone.0030176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Max B, Sherer R. Management of the adverse effects of antiretroviral therapy and medication adherence. Clinical infectious diseases: an official publication of the Infectious Diseases Society of America. 2000;30(Suppl 2):S96–S116. doi: 10.1086/313859. [DOI] [PubMed] [Google Scholar]
- 24.McLachlan GJ, Krishnan T. The EM Algorithm and Extensions. New York: John Wiley; 1997. [Google Scholar]
- 25.McNamara LA, Collins KL. Interferon Alfa therapy: toward an improved treatment for HIV infection. Journal of Infectious Disease. 2013;207:201–203. doi: 10.1093/infdis/jis667. [DOI] [PubMed] [Google Scholar]
- 26.Murray JM, Zaunders JJ, McBride KL, Xu Y, Bailey M, Suzuki K, Cooper DA, Emery S, Kelleher AD, Koelsch KK. HIV DNA subspecies persist in both activated and resting memory CD4+ T cells during antiretroviral therapy. J. Virol. 2014;88:3516–3526. doi: 10.1128/JVI.03331-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pace MJ, Agosto L, Graf EH, O’Doherty U. HIV reserviors and latency models. Virology. 2011;411:344–354. doi: 10.1016/j.virol.2010.12.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rasmussen TA, Søgaard OS, Møller HJ, Brinkmann CR, Olesen R, Laursen AL, Østergaard L, Tolstrup M. HIV Reactivation by the histone deacetylase inhibitor Panobinostat: effects on CNS. Program and abstracts of the Conference on Retroviruses and Opportunistic Infections; Boston, MA. 2014. abstract #482. [Google Scholar]
- 29.Rong L, Perelson AS. Modeling latently infected cell activation: viral and latent reservoir persistence, and viral blips in HIV-infected patients on potent therapy. PLoS Comput. Biol. 2009;5:e1000533. doi: 10.1371/journal.pcbi.1000533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rong L, Perelson AS. Modeling HIV persistence, the latent reservoir, and viral blips. J. Theor. Biol. 2009;260:308–331. doi: 10.1016/j.jtbi.2009.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rong L, Perelson AS. Asymmetric division of activated latently infected cells may explain the decay kinetics of the HIV-1 latent reservoir and intermittent viral blips. Math. Biosci. 2009;217:77–87. doi: 10.1016/j.mbs.2008.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Seber GAF, Wild CJ. Nonlinear Regression. New York: John Wiley & Sons, Inc.; 1989. [Google Scholar]
- 33.Shan L, Deng K, Shroff NS, Durand C, Rabi SA, Yang H, Zhang H, Margolick JB, Blankson JN, Siliciano RF. Stimulation of HIV-1-specific cytolytic T-lymphocytes facilitates elimination of latent viral reservoir after virus reactivation. Immunity. 2012;36:491–501. doi: 10.1016/j.immuni.2012.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sharkey ME, Teo I, Greenough T, Sharova N, Luzuriaga K, Sullivan JL, Bucy RP, Kostrikis LG, Haase A, Veryard C, Davaro RE, Cheeseman SH, Daly JS, Bova C, Ellison RT, Mady B, Lai KK, Moyle G, Nelson M, Gazzard B, Shaunak S, Stevenson M. Persistence of episomal HIV-1 infection intermediates in patients on highly active anti-retroviral therapy. Nature Medicine. 2000;6:76–81. doi: 10.1038/71569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shirakawa1 K, Chavez L, Hakre S, Calvanese V, Verdin E. Reactivation of latent HIV by histone deacetylase inhibitors. Trends in Microbiology. 2013;21:277–285. doi: 10.1016/j.tim.2013.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Smith MZ, Wightman F, Lewin SR. HIV reservoirs and strategies for eradication. Curr HIV/AIDS Rep. 2012;9:5–15. doi: 10.1007/s11904-011-0108-2. [DOI] [PubMed] [Google Scholar]
- 37.Stock PG, Barin B, Hatano H, Rogers RL, Roland ME, Lee T-H, Busch M, Deeks SG. Reduction of HIV persistence following transplantation in HIV-infected kidney transplant recipients. American Journal of Transplantation. 2014;14:1136–1141. doi: 10.1111/ajt.12699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wang S, Rong L. Stochastic population switch may explain the latent reservoir stability and intermittent viral blips in HIV patients on suppressive therapy. J. Theor. Biol. 2014;360:137–148. doi: 10.1016/j.jtbi.2014.06.042. [DOI] [PubMed] [Google Scholar]
- 39.Wei DG, Chiang V, Fyne E, Balakrishnan M, Barnes T, et al. Histone deacetylase inhibitor Romidepsin induces HIV expression in CD4 T Cells from patients on suppressive antiretroviral therapy at concentrations achieved by clinical dosing. PLoS Pathog. 2014;10:e1004071. doi: 10.1371/journal.ppat.1004071. [DOI] [PMC free article] [PubMed] [Google Scholar]