Altered Mechanical Environment of Bone Cells in an Animal Model of Short- and Long-Term Osteoporosis

Abstract

Alterations in bone tissue composition during osteoporosis likely disrupt the mechanical environment of bone cells and may thereby initiate a mechanobiological response. It has proved challenging to characterize the mechanical environment of bone cells in vivo, and the mechanical environment of osteoporotic bone cells is not known. The objective of this research is to characterize the local mechanical environment of osteocytes and osteoblasts from healthy and osteoporotic bone in a rat model of osteoporosis. Using a custom-designed micromechanical loading device, we apply strains representative of a range of physical activity (up to 3000 με) to fluorescently stained femur samples from normal and ovariectomized rats. Confocal imaging was simultaneously performed, and digital image correlation techniques were applied to characterize cellular strains. In healthy bone tissue, osteocytes experience higher maximum strains (31,028 ± 4213 με) than osteoblasts (24,921 ± 3,832 με), whereas a larger proportion of the osteoblast experiences strains >10,000 με. Most interestingly, we show that osteoporotic bone cells experience similar or higher maximum strains than healthy bone cells after short durations of estrogen deficiency (5 weeks), and exceeded the osteogenic strain threshold (10,000 με) in a similar or significantly larger proportion of the cell (osteoblast, 12.68% vs. 13.68%; osteocyte, 15.74% vs. 5.37%). However, in long-term estrogen deficiency (34 weeks), there was no significant difference between bone cells in healthy and osteoporotic bone. These results suggest that the mechanical environment of bone cells is altered during early-stage osteoporosis, and that mechanobiological responses act to restore the mechanical environment of the bone tissue after it has been perturbed by ovariectomy.

Introduction

The interconnected network of osteocytes and osteoblasts in bone tissue is believed to act as the driving force behind bone adaptation, allowing bone tissue to actively remodel its mass and structure in response to the mechanical demands experienced throughout life. Osteocytes and osteoblasts are known to be mechanosensitive, recruiting osteoblasts and osteoclasts to orchestrate an adaptive response when the mechanical environment is not favorable (1–6).

Osteoporosis is a debilitating bone disease, which is characterized by an imbalance in normal bone cell remodeling (7), and results in severe bone loss (8), significantly reduced strength (9,10), and altered bone tissue porosities (11–13). Previous studies have shown altered mechanical properties of trabecular bone in ovariectomized rats compared to sham-operated controls (14,15). Furthermore, tissue-level mineral distribution is altered in a sheep model of osteoporosis (16), and changes in mineralized crystal maturity, mineral-to-matrix ratio, and collagen cross-linking also occur (10). Such changes might occur as a compensatory mechanism triggered by bone loss during osteoporosis. Alternatively, it may be that estrogen deficiency itself leads directly to changes in tissue composition, which consequently alters the local mechanical environment of osteoblasts and osteocytes. This change in mechanical stimuli sensed by bone cells may then initiate a mechanoregulatory response resulting in bone loss. Computational simulations of bone adaptation have predicted osteoporotic-like trabecular architecture (17), and altered bone resorption rates and osteocyte strain levels (18) in response to changes in tissue stiffness. However, it remains that the mechanical stimulation experienced by bone cells within osteoporotic bone in vivo has never been characterized and, as such, these theories remain conjecture.

Because osteocytes are embedded in a mineralized matrix, direct experimental investigation of their mechanical environment is challenging. High-resolution microscopy of exposed two-dimensional bone sections under mechanical loading (19) have predicted perilacunar strains in the range of 7500–35,000 με (20,21). AFM techniques have measured osteoblast strains as high as 40,000 με under an applied load of 20 nN in vitro (22,23). These high strain levels are significant, because previous in vitro cell culture studies have observed an osteogenic response in osteoblastic cells at magnitudes greater than a threshold of ∼10,000 με (6,24). However, the experimental approaches of Nicolella et al. (20,21) involved milled sections of bone tissue and surface polishing to expose embedded osteocytes, and such methods might alter the mechanical environment of the cell (25,26). Furthermore, point loading through AFM techniques is not representative of the substrate strain that osteoblasts on bone surfaces are exposed to in vivo. Computational modeling of the in vivo strain environment of individual osteocytes has predicted strains of 23,000–26,000 με occurring in the osteocyte for an applied load of 3000 με (27), whereas osteoblasts were shown to experience maximum strains of ∼1270 με for applied loading of 1000 με (22,23). While these models provide an insight into bone cell mechanical behavior, an experimental approach, which does not necessitate destruction of or interference with the local mechanical environment, is required to investigate the in situ strain environment of cells in healthy and osteoporotic bone.

Confocal microscopy has been widely applied to visualize the lacunar-canalicular network (28–31), osteocytes (32–36), and microcracking within bone tissue (25,26). Confocal microscopy techniques have been recently combined with in situ mechanical loading to investigate cell mechanics within the intervertebral annulus fibrosus (37) and cartilage under loading (38). However, such methods have never been applied to characterize the local mechanical environment of bone cells in vivo.

The objective of this research is to characterize the local mechanical environment of osteocytes and osteoblasts from normal and osteoporotic bone in a rat model of osteoporosis. We design a purpose-built micromechanical loading rig, and combine this with a confocal microscopy and digital image correlation (DIC) imaging technique, to characterize the mechanical environment of osteoblasts and osteocytes in situ under physiological loading conditions. We investigate the local mechanical environments of osteocytes and osteoblasts after 5- and 34-weeks’ estrogen deficiency, and compare these to cells within the bone tissue of sham-operated controls.

Materials and Methods

Custom-designed loading device

To visualize the local mechanical environment of the cells, a custom loading device was designed that is compatible with a confocal microscope (LSM 51; Carl Zeiss, Oberkochen, Germany). It comprised a specialized loading stage and sample grips to ensure that samples could be held flush with the microscope objective (Fig. 1). A high-torque stepper motor (Model No. ST2818L1006; Nanotec, Munich, Germany) and gearing provided transmission to a precision bidirectional ball power screw (SD0401; ABSSAC, Worcestershire, UK), and thus applied microscale displacements to cortical bone samples (of length 10 mm) during imaging. The applied loading is displacement-controlled, with displacements applied to the whole bone in specified increments, with speeds and magnitudes controlled using commercial software (NANOPRO 1.6; Nanotec). The device is capable of applying bidirectional uniaxial tensile or compressive loading at increments as small as 50 με.

Figure 1.

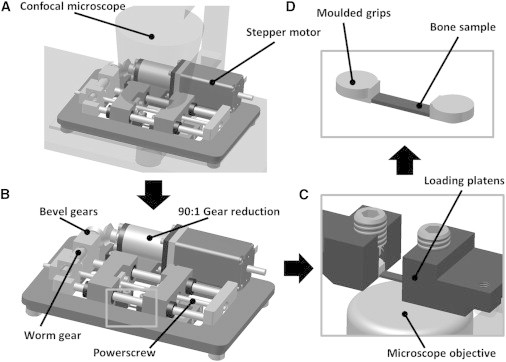
Diagram of custom-designed micro-loading device in position under the confocal microscope (A) and close-up (B). Relationship among bone sample, loading platens, and microscope objective shown in (C) and (D).

Validation of loading device and DIC analysis

The custom-built loading device was validated for the application of bidirectional, uniaxial compression loading on a PMMA (poly(methyl methacrylate)) sample (length 12 mm and radius 3.2 mm) with embedded fluorescent microspheres. Briefly, a PMMA resin (Cat. No. 8510; Akasel, Roskilde, Denmark), was combined with a curing agent (Cat. No. 8562; Akasel) and fluorescent microspheres (10-μm diameter) at a dilution of 1 μL/mL (Fluoresbrite 18140-2; Polysciences, Eppelheim, Germany). A sonicator (2510E-MT; Bransonic Ultrasonics, Danbury, CT) and rotator (Model No. SB3; Stuart Equipment, Bibby Scientific, Stone, Staffordshire, UK) were used to ensure dispersion of the microspheres throughout the sample. The samples were formed by filling 12-mm lengths of 3.2-mm diameter silicone tubing (Cat. No. HV-96410-16; Masterflex, Oldham, UK) with the PMMA resin and allowing this to set overnight. The cylindrical samples were then extracted from the tubing and inserted into the grips for the experimental loading.

A compressive displacement load equivalent to 3000 με was applied to the PMMA/microsphere construct and a series of confocal images were captured for DIC analysis (see Fig. 2 A). The strain distribution within each sphere was determined from a series of images of each loaded sphere using DIC analysis with a previously developed software package (MOIRE) (39–41), which is capable of tracking displacements of pixels in the images (see Fig. 2 B). A correlation coefficient is calculated for each pixel by comparing the deformed image with the reference image. A zero-mean normalized cross-correlation coefficient is then determined for each image pixel. Once the correlation coefficient extremes (maximum and minimum) have been detected, the full-field deformation can be determined, providing a measure of the maximum principal strain. The loading and DIC analysis was repeated for 10 different microspheres and compared to the results of an analytical solution for a homogenous material with spherical inclusions under loading (42).

Figure 2.

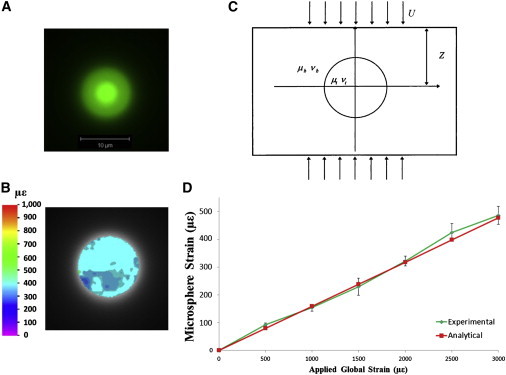
Confocal image of PMMA-embedded fluorescent microsphere (A), with the contour plot of strain within it under 3000 με loading (B). Diagram of analytical solution for spherical inclusion in a homogenous material (C), adapted from Bilgen and Insana (42). Comparison of experimental and analytical results over a range of applied loads is shown in (D). To see this figure in color, go online.

Briefly, the analytical solution allows for calculation of the strain within a spherical object embedded in a homogenous material of different material properties (see Fig. 2 C). The relationship among the strain, material properties, geometry, and displacement is summarized in the equation

$$e=\left(\frac{U}{Z}\right)\left(\frac{2{\mu }_b\left(1+{\nu }_b\right)\left(1-{\nu }_b\right)}{2\left(1+{\nu }_b\right)}\right)\left(-\frac{5\left(1-{\nu }_b\right)}{\left[{\mu }_b\left(7-5{\nu }_b\right)+{\mu }_t\left(8-10{\nu }_b\right)\right]}+\frac{\left(1-2{\nu }_t\right)}{\left[{\mu }_b\left(2-4{\nu }_t\right)+{\mu }_t\left(1+{\nu }_t\right)\right]}\right),$$

where the shear modulus and Poisson’s ratio are denoted by μ_b, ν_b, and μ_t, ν_t for the matrix and microsphere, respectively; strain is denoted by e; displacement by U; and specimen length by 2Z (42). PMMA was assumed to have a shear modulus of 1.7 GPa and Poisson’s ratio of 0.3, while values of 2.1 MPa and 0.3 were assumed for the polystyrene microspheres.

Analysis of the experimental results was compared to the analytical solution at load steps of 500, 1000, 1500, 2000, 2500, and 3000 με. The strain observed experimentally displayed close correlation to the analytical solution over multiple applied loads (Fig. 2 D) The percentage error at each of the 500, 1000, 1500, 2000, 2500, and 3000 με load steps was 9.41, 3.37, 4.13, 1.14, 6.81, and 1.88%, respectively. At 3000 με, an average strain within the microspheres of 486 με (486 ± 32.1 με) was observed by the DIC technique, while the analytical solution predicts a value of 477 με.

Animal model and sample preparation

Ovariectomized rat bone is employed in this study as it has been deemed an appropriate model for postmenopausal osteoporosis in humans (43), with many shared characteristics with human diseased bone (44). Four groups of 8-month old female Wistar (Charles River Laboratories, Willimantic, CT) rats were used in this study: 1) a group in which rats were ovariectomized five weeks before the experiment (n = 4) to induce estrogen deficiency, 2) a control sham-operated group (n = 4), 3) a 34-week postoperative ovariectomized (n = 2) group, and 4) a control sham group (n = 2). Animals were anesthetized using isoflurane gas and then sacrificed by CO₂ inhalation. Upon sacrifice of the animals, checks were performed to confirm the presence or absence of the ovaries for SHAM and OVX animals, respectively. Immediately before sacrifice, rats were injected with FITC (Cat. No. F7250, fluorescein isothiocyanate isomer 1, 30 μL at 10 mg/mL; Sigma-Aldrich, St. Louis, MO) to stain the lacunar-canalicular network, similar to previous methods (28). All procedures were carried out following institutional ethical approval and under an animal license No. B100/4424 granted by the Irish Department of Health.

One femur from each animal was extracted and placed in α-minimum essential medium (α-MEM) supplemented with 10% FBS (fetal bovine serum), 2 mM L-glutamine, 100 U/mL penicillin, and 100 μg/mL streptomycin (all Sigma-Aldrich) at 37°C, to maintain cell viability within the samples. Additionally, the experimental study was performed in <5 h to minimize postextraction time.

Femurs extracted from rats were cut proximally and distally using a diamond blade saw (Isomet; Buehler, Düsseldorf, Germany) to produce 10-mm femoral shaft specimens. These were further cut to produce longitudinal, semicylindrical samples that could be loaded and imaged simultaneously in our custom device (see Fig. 3, A–C). The live samples were kept in media during cutting and preparation, and rinsed with PBS (phosphate-buffered saline) solution immediately before loading to prevent autofluorescence of the media. After cutting and before loading, samples were incubated for 30 min in FITC to enhance staining and a plasma membrane stain (CellMask Orange Plasma Membrane, Cat. No. C10045, 20 μL at 5 mg/mL; Invitrogen, Carlsbad, CA) to visualize the osteoblast and osteocyte cell membranes. All preparation and loading occurred within 5 h after extraction, with samples covered in aluminum foil to prevent photobleaching. PBS was regularly applied to samples during loading and imaging to prevent dehydration. Custom-designed epoxy resin grips were made for each sample, using a mold to prevent bone fracture and edge effects during loading.

Figure 3.

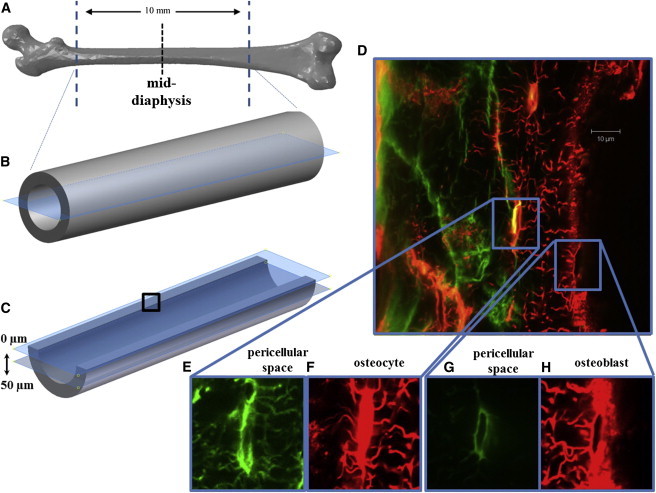
Diagram of removal of proximal and distal ends of femur, followed by longitudinal sectioning of the sample (A–C). Imaging was performed at the middiaphysis, ∼50 μm below the cut surface (dotted line in A and box in (C). Confocal scans were performed from cut face through depth of bone (D), allowing visualization of the lacunar-canalicular network (E) and osteoblast pericellular space (green in G, and the osteocytes (red in F) and osteoblasts (red in H)). To see this figure in color, go online.

Confocal imaging and mechanical loading conditions

Using the custom-built loading device, bidirectional, uniaxial compression loading up to 3000 με, levels at which bone cell stimulation has been predicted experimentally and computationally (27,45,46), was applied longitudinally to the bone samples at a strain rate of 83.3 με/s. Bone cells were imaged in the middiaphysis of the femur to avoid characterizing cells that might experience large displacements occurring near the grips. Confocal scans (LSM 51; Carl Zeiss) were taken with a 63× oil immersion lens, with 0.08-mm-thick glass coverslips (CB00070RA1; Menzel-Gläser, Braunschweig, Germany) separating the moisture in the sample from immersion oil and allowing imaging through the depth of the sample. Wavelength excitations of 488 and 543 nm were applied to scan the pericellular space and the cell membrane, respectively (Fig. 3 D), with an image size of 255 × 255 μm. The image frame size was 1024 × 1024 pixels, which gives a pixel size (resolution) of 0.1 μm. The optical slice thickness was 0.6 μm.

Multitracking was also performed to illuminate both the pericellular spaces in green and the osteocyte and osteoblast cells contained within (see Figs. 3, E and G, and 3, F and H, respectively). Confocal scans of the osteocytes and osteoblasts near the periosteal surface can be seen in red in Fig. 3, F and H, respectively. These scans can be analyzed separately to elucidate the detail of the lacunar-canalicular space in isolation from the cell, and vice versa (visible by comparing Fig. 3, E and F). Only the scans of the individual cells, in red, were investigated in the DIC analysis. Imaging was performed at a depth of at least 50 μm, away from damaged regions that resulted from the cutting process. At this depth, osteocytes are easily discriminated due to their location within the bone. For simplicity we refer to “osteoblasts,” but indeed these observations also apply to the quiescent bone-lining osteoblasts on the surface.

Scans were taken of the cells every 3 s for each 250-με loading step in order to build a series of images to represent cell deformation during loading. This process was repeated for each femur sample loaded, allowing imaging of 10 osteoblasts and 10 osteocytes per specimen. The mechanical behavior of individual cells was consistent over the course of repeated loading cycles (≤10 cycles). This resulted in a total of 240 cells, with 160 and 80 of each cell type for both OVX and SHAM animals, at 5 and 34 weeks postoperation, respectively. Sample images of both an osteoblast and an osteocyte are shown at 0 με in Figs. 4 B and 5 A, respectively.

Figure 4.

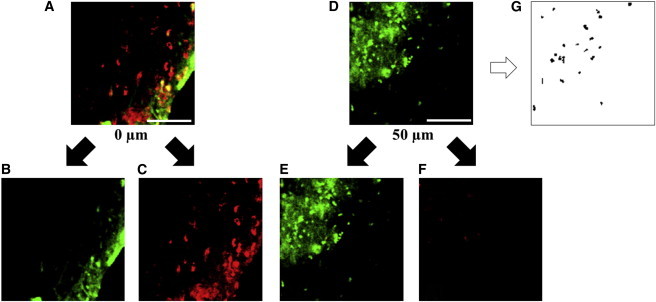
Confocal scans of the same location in a femur sample at (A) 0 μm and (D) 50 μm from the cut surface. (Green staining) Cell viability (B and E); (red staining) cytotoxicity (C and F) (with scale bar, 100 μm). Thresholding of (D) for quantification of cell viability is shown in (G). To see this figure in color, go online.

Figure 5.

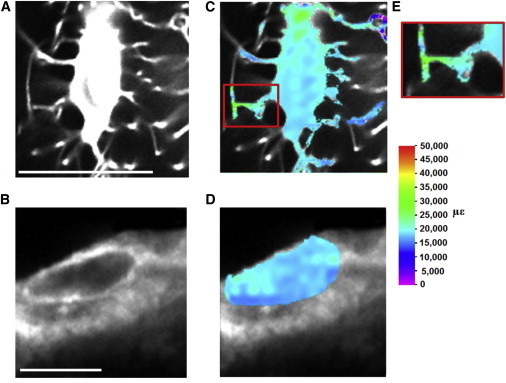
Confocal images of (A) a sample osteocyte and (B) osteoblast at 0 με. Digital image correlation (DIC) is applied to characterize the maximum principal strain distribution in (C) the osteocyte, (D) the osteoblast at 3000 με (scale bar, 10 μm) and (E) strain amplification in an osteocyte cell process. To see this figure in color, go online.

Cell viability

To investigate whether cells at our chosen imaging plane were affected by the cutting process, a cell viability study was performed. A femur was harvested from a 4-month-old female Wistar rat, sectioned, and processed as described above. The sample was then incubated in a Live/Dead Viability/Cytotoxicity assay (Cat. No. L-3224; Invitrogen) for 3 h. Confocal scans of the sample were taken 5 h postextraction at depths of 0 and 50 μm below the cut surface. These scans were performed at 10× magnification using an excitation wavelength of 488 nm. The resulting images are shown in Fig. 4 (green indicating viability and red indicating cytotoxicity due to ruptured cell membranes). Additionally, thresholding was performed in order to use “island counting” techniques in the software IMAGEJ (National Institutes of Health, Bethesda, MD) (Fig. 4 G) to quantify the percentage of live and dead cells at each depth: 34.7% live versus 65.2% dead at 0 μm; 89% live versus 11% dead at 50 μm. This demonstrates that although cell death occurs at the cut surface, at a distance 50 μm from the surface (the location at which the strain analyses are conducted), there is a substantial population of live cells (89%). Because damage to the surrounding matrix would likely have a detrimental effect on cell viability, we can infer that the local mechanical environment of the osteocyte is not substantially damaged during cutting.

DIC analysis

The DIC methods described above were applied to analyze a series of images of the loaded osteocytes and osteoblasts, shown at 0 με in Fig. 5, A and B, respectively. This allowed the strain field in the cells to be calculated, providing contour plots of maximum principal strain distributions within the cells, shown in Fig. 5, C and D. The percentage area of a cell stimulated within a specific range of strain is determined by dividing the number of pixels at strain values within this range by the total number of pixels that represent the cell. This allowed determination of the percentage area of each cell that exceeds the osteogenic strain threshold, which is taken as 10,000 με (6,24). Because this is a two-dimensional DIC analysis, the contour plots represent a section through the cell and the strain results are presented as a percentage area of this section of the cell.

Statistical analysis

Ten of each bone cell type were analyzed from each bone sample, with n = 4 animals per group at 5 weeks postoperation (SHAM-5, OVX-5) and n = 2 animals per group at 34 weeks postoperation (SHAM-34, OVX-34). All data are expressed as a mean ± standard deviation. Statistical differences between groups were determined using the nonparametric Kruskal-Wallis method. Dunn’s test method for comparison between groups was used to determine statistical significance defined as p < 0.05 (MINITAB, Ver. 16; Minitab, Coventry, UK).

Results

Mechanical environment of osteoblasts and osteocytes in healthy bone

The strain distribution experienced by a sample osteoblast and sample osteocyte as a result of the applied loading is shown in Fig. 5, C and D. The strains experienced by these cells, as a proportion of the cell area, are shown in Figs. 6 and 7, respectively. Strains experienced by osteoblasts from healthy bone exceeded the osteogenic strain threshold (10,000 με) in a larger proportion of the cell (13.68 ± 1.31%) than osteocytes (5.37 ± 2.08%), while no significant difference was seen for proportions strained <1000 με. Maximum strains experienced by osteoblasts in healthy bone were 24,921 ± 3832 με, with healthy osteocytes experiencing strains of 31,028 ± 4213 με.

Figure 6.

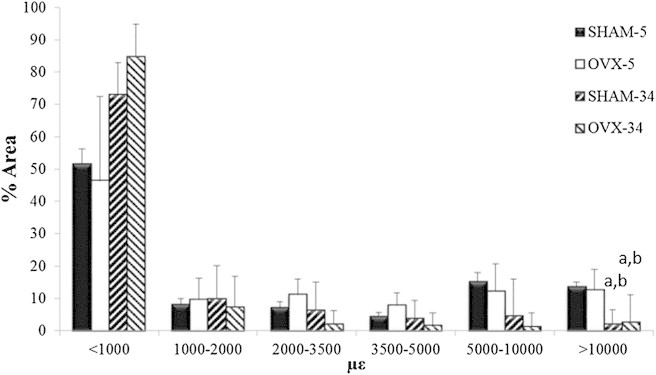
Average maximum principal strain distributions observed after 5 and 34 weeks in osteoporotic (OVX) and healthy (SHAM) osteoblasts as a percentage of cell area. n = 4 for 5-week groups, n = 2 for the 34-week groups, (a) p < 0.05 versus SHAM-5 at corresponding strain level, and (b) p < 0.05 versus OVX-5 at the corresponding strain level.

Figure 7.

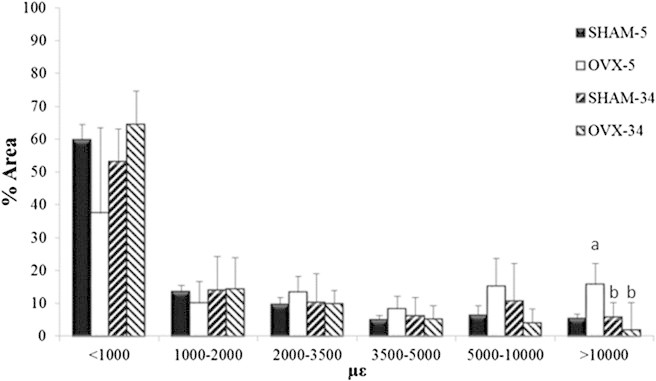
Average maximum principal strain distributions observed after 5 and 34 weeks in osteoporotic (OVX) and healthy (SHAM) osteocytes as a percentage of cell area. n = 2 for 5-week groups, n = 2 for 34-week groups, (a) p < 0.05 versus SHAM-5 at corresponding strain level, and (b) p < 0.05 versus OVX-5 at the corresponding strain level.

A drop in the proportion of the cell exceeding the osteogenic strain threshold (10,000 με) occurs in osteoblasts (2.16 ± 4.39% vs. 13.68 ± 1.31%, p ≤ 0.025) at 34 weeks after the SHAM operation. However, there was no significant change in this value for osteocytes, at (5.77 ± 2.60% vs. 5.37 ± 2.08%). Similarly, there was no significant difference in strains <1000 με between these time points, for either osteoblasts or osteocytes.

Contour plots showed greater variability in strain at the cell membranes than within the cell body for all cell types. This effect was exacerbated in the osteocyte environment, with a more heterogeneous distribution and the highest and lowest strains occurring within the cell processes.

Mechanical environment of osteoblasts and osteocytes during osteoporosis

The effect of osteoporosis on strain within bone cells was examined, with the strain distribution for OVX and SHAM samples compared in Fig. 6 for osteoblasts and Fig. 7 for osteocytes. While it could be seen that strains <1000 με occur in a smaller proportion of osteoporotic osteocytes compared to healthy osteocytes (37.33 ± 14.81% vs. 59.77 ± 10.12%), this difference was not statistically significant (p ≤ 0.095). Strains exceeding the osteogenic strain threshold (10,000 με) in osteoblasts in bones exposed to 5 weeks of estrogen deficiency occur in a similar proportion of the cell to healthy bone at 5 weeks (12.68 ± 6.30% vs. 13.68 ± 1.31%). However, strains exceeding the osteogenic strain threshold occur in a significantly larger proportion of osteocytes at 5 weeks of estrogen deficiency compared to healthy osteocytes (15.74 ± 2.86% vs. 5.37 ± 2.08%, p ≤ 0.048). In addition, osteoporotic osteoblasts exhibited maximum strains of 24,585 ± 3399 με while osteocytes experienced 40,548 ± 6041 με.

After 34 weeks of estrogen deficiency, the proportion of osteoblast and osteocyte cell areas experiencing strains above the osteogenic threshold is significantly lower than osteoblasts (2.71 ± 8.36% vs. 12.68 ± 6.30%, p ≤ 0.025) and osteocytes (1.83 ± 2.24% vs. 15.74 ± 2.86%, p ≤ 0.039) at 5 weeks estrogen deficiency. Furthermore, there was no significant difference between osteoporotic cells and healthy cells after 34 weeks postoperation for either osteoblasts (2.71 ± 8.36% vs. 2.16 ± 4.39%) or osteocytes (2.71 ± 8.36% vs. 5.77 ± 2.60%). Similarly, there was no significant difference between maximum strains in osteoporotic and healthy cells at 34 weeks postoperation for either osteoblasts (14,731 ± 1840 με vs. 16,541 ± 1930 με) or osteocytes (14,474 ± 1446 με vs. 19,195 ± 3,204 με).

Similar to the contour plots of the healthy cells, the highest and lowest strains occurred at the cell membranes of both cell types, particularly in the cell processes of osteocytes. The strain behavior within osteoblasts and osteocytes was not found to vary between osteoporotic or normal bone cells.

Finally, due to the stepped nature of the loading it is possible to capture results for lower levels of applied strain. To determine whether cellular deformation in response to applied loading was nonlinear, strains in osteocytes from the SHAM and OVX groups at 5 weeks were investigated, from 0 to 1500 με. At 1500 με, maximum strains within the osteocytes were approximately half of those observed at 3000 με (SHAM, 14,400 με vs. 31,028 με; OVX, 22,040 με vs. 40,548 με). This indicates that while loading of osteocytes is amplified at the cell level, it increases proportional to the applied macroscopic load.

Discussion

To our knowledge, this study represents the first direct experimental investigation of the changes in the local mechanical environment of osteocytes and osteoblasts in situ during estrogen deficiency. By characterizing the strain distribution within cells using a rat model of osteoporosis, to our knowledge we report for the first time that osteoblasts and osteocytes in both healthy and osteoporotic bone experience strains that are sufficient to stimulate osteogenic responses (>10,000 με) under physiological loading conditions. However, while osteocytes in osteoporotic bone initially (5 weeks postoperation) experience osteogenic strains (>10,000 με) in a greater area of the cell (10%) than those in healthy bone, there is no significant difference for osteoblasts. In contrast, in long-term estrogen deficiency (34 weeks postoperation), there is a significant decrease in the proportion of both osteoblasts and osteocytes exceeding the osteogenic strain threshold (>10,000 με) compared to the respective cells at 5 weeks estrogen deficiency, such that there is no longer a significant difference between either osteoblasts or osteocytes in 34-week osteoporotic and healthy bone.

One limitation of this study is that the confocal microscopy imaging and DIC approach limited the analysis to two-dimensional sections of individual cells, and as such it was assumed that the strains experienced within that cell section are representative of the strains experienced by the whole cell. Immunohistochemistry was not performed to identify the phenotype of the cells. However, their locations were chosen to represent the local mechanical environment of osteoblasts (but also quiescent osteoblasts, the bone-lining cells) and osteocytes. It should be noted that not all animals survived to 34 weeks post-OVX, reducing the number of animals per group at this time point (n = 2 per group). Nonetheless, significant differences were observed in stimulation of cells between animal groups at the 5-week time point, but future studies should investigate the temporal nature of changes in the mechanical environment of bone cells with an animal model that displayed the time-sequence of the complex changes in all of these tissue parameters. Interstitial fluid flow and movement out of plane due to loading cannot be quantified directly using DIC, and, due to the time required to capture the scans between each load step, any time-dependent or flow-induced deformation could not be specifically delineated.

Similarly, it was also not possible to measure the microscale strains in the surrounding bone directly using DIC, because the bone matrix was not fluorescent under confocal laser scanning microscopy. As such the role of specific stimuli, such as fluid flow or matrix strain, cannot be distinguished but likely all contribute to the strains reported here due to the efforts to maintain the in vivo mechanical environment in our experiment. The strain amplification observed at the cell surfaces is unlikely to be an artifact of the DIC approach, because no similar amplification is visible at the surface of the microspheres, despite the clear boundary between it and the surrounding matrix. Moreover, such concentrations of strain along the cell surfaces and cell processes of osteocytes, with lower strains in the cell body, have been predicted by multiple modeling approaches (27,47,48). Therefore, we conclude that the imaging and analysis approaches are robust enough to accurately predict strain in bone cells. To our knowledge, our method represents the first approach to elucidate cellular strains in their local mechanical environment without destructive interference.

It should also be noted that the cutting procedure exposed the bone marrow cavity and the resulting drop in intramedullary pressure may alter interstitial fluid flow within the bone (49,50). However, the samples were kept moist during loading using PBS and the periosteum was maintained intact on the outer surface of the bone. Furthermore, the flow velocities are extremely low within the lacunar-canalicular network (∼60 μm/s) (48,51), and are therefore unlikely to be altered significantly away from the cut surfaces. It is important to note that the type of mechanical stimulation bone cells experience in vivo has been unclear to date, and as such, whether the cells respond to peak strains or overall stimulation of a proportion of the cell body is unknown. For this reason we reported both peak strains and the percentage of cell area experiencing specific strain magnitudes, and compared these to an assumed osteogenic threshold of 10,000 με. This threshold was chosen based on the findings of various experimental, computational and theoretical studies of osteocytes and osteoblasts (19–23), in particular an in vitro cell culture study that reported significant osteogenic responses in osteoblastic cells at magnitudes greater than a threshold of ∼10,000 με (6,24). Future development of confocal laser scanning techniques may be able to better observe the mechanical behavior of the cell during loading, and could be combined with fluorescent studies of calcium and nitric oxide signals in bone cell networks to determine stimulatory strain levels in vivo (52–55).

Previous experimental studies of bone cell mechanobiology have largely involved in vitro cell culture techniques (4–6,22,23). We report maximum strains in healthy osteocytes in situ of ∼31,000 με, far in excess of the applied loading of 3000 με. These results corroborate experimentally observed strain amplification (35,000 με) in the lacunar matrix (20,21) and verify the importance of predicted strain amplification in osteocytes by a glycocalyx or integrin attachments to the matrix (27,56–58). Our results show that osteoblasts in healthy bone are stimulated to a greater extent than osteocytes (based on proportion of the cell >10,000 με). Osteoblasts are exposed to surface bending (59) and marrow shear stress (60,61), and are connected to the bone surface and other cells by discrete attachments (62,63). Indeed, recent computational studies of the bone marrow cavity have predicted that high shear stresses act along bone surfaces, at magnitudes that have been observed to stimulate bone cells in vitro (60). These factors may account for the amplified osteoblast stimulation observed in this study. Despite the greater strain stimulation of osteoblasts observed here, the osteocyte likely experiences both direct strain from the bone matrix as well as an additional stimulus resulting from loading-induced interstitial fluid flow (48), to which osteocytes are highly responsive (3,64). Interestingly, in this study, osteocytes experienced greater maximum strains than osteoblasts, and it is noteworthy that these stimuli occurred along the cell processes, known to be the most mechanosensitive area of the osteocyte (32,65).

Of particular interest in this study are the precise changes that occur during early-stage estrogen deficiency that may alter the mechanical environment of bone cells. At the onset of osteoporosis, microstructural changes in bone strength (9,10), mass (8), mineral density (9,16,66), trabecular architecture (8,10,66), and trabecular mineral and matrix composition (9,10,14,66) occur. Previous studies have observed that changes in the geometry of the osteocyte lacunar-canalicular environment occur during estrogen deficiency (11–13). The image-analysis software IMAGEJ (National Institutes of Health) was used to calculate circularity of each cell body (i.e., the degree of roundness) analyzed in this study, but the results indicated that there was no statistical difference between the circularity of SHAM (0.2779 ± 0.1236) and OVX osteocytes (0.2277 ± 0.1418), p = 0.434. While we have not observed a difference in the dimensions of the cell body during estrogen deficiency, previous studies have observed and quantified changes in the lacunar-canalicular anatomy (11–13,67), and these may play a role in the stimulation changes observed here.

Additionally, a recent computational study by our group demonstrated that mechanical stimulation of osteocytes can differ vastly depending on location within the extracellular matrix, particularly in relation to micropores (47). This may be important during estrogen deficiency, because porosity has been observed to increase significantly in an ovine model of osteoporosis (68). Furthermore, estrogen treatment has recently been observed to cause significant decreases in osteoblast cytoskeletal stiffness (69), and such changes might play a role in the altered mechanical stimulation reported here. Our experimental method maintains all aspects of the local mechanical environment of bone cells, including the composition of the extracellular and pericellular matrix, the geometry of the lacunar-canalicular network, physical connections between the cell and its surroundings, the cell mechanical behavior, and the in vivo mechanical stimuli arising from loading-induced fluid flow and matrix strain. Therefore, any of these complex changes in structure and composition could dictate the changes in cellular strains reported here.

It is intriguing to speculate on the temporal changes in mechanical stimulation of bone cells during osteoporosis observed here. While theories have been proposed as to the mechanisms that cause osteoporosis (70,71), here we delineate the timeline of observed events in order to gain an insight into the development of the disease. In a rat model of osteoporosis, osteoclastogenesis increases significantly as early as 1 week post-OVX (72), resulting in decreased bone volume fraction and trabecular number by 4 weeks post-OVX (73). This initial bone loss likely alters the micromechanical loading of bone cells, but this has never before been demonstrated. To our knowledge, our results show for the first time that osteocytes experience higher strains in osteoporotic bone than in healthy bone by 5 weeks post-OVX, thus verifying that early bone loss increases the stimulation of osteocytes in the remaining bone. Significant increases in trabecular thickness (74,75) and stiffness (14) occur at later time points in rats, at 14 and 34 weeks post-OVX, which might explain our observations of restoration of the strain environment of osteocytes to control levels in late-stage osteoporosis (34 weeks post-OVX). It was also observed that osteoblasts and osteocytes experienced strains <1000 με, levels believed to initiate disuse-related bone resorption (76). This likely occurs due to a strain-shielding effect whereby the pericellular matrix reduces strain transfer to the cell, a phenomenon that has been predicted in computational models of osteocytes and chondrocytes (27,77,78).

Interestingly, it was seen that the percentage area of osteoporotic cells experiencing such strains at 5 weeks post-OVX was lower than controls at the same time point, whereas at 34 weeks post-OVX, such strains were more prevalent in osteoporotic bone cells than control cells. While these observations were not statistically significant, when coupled with those of the osteogenic stimulation they suggest that during the initial stage of osteoporosis, bone cells experience a decreased resorption stimulus and an increased osteogenic stimulus, but that this effect is diminished during late-stage osteoporosis. Furthermore, studies of ovine trabecular and cortical bone reported an initial significant decrease (12 months post-OVX) in mineral content and elastic modulus relative to controls, but that these properties and compressive strength matched control levels in long-term estrogen deficiency (31 months post-OVX) despite continued increases in porosity and turnover (9,79). Therefore, although the timing of changes in tissue properties appears to vary between animal models, there is a clear trend of early bone loss followed by increases in tissue stiffness to return properties to control levels. Taken together with results of this study, these experimental observations of temporal changes in both cortical and trabecular bone support the theory that a compensatory mechanobiological response occurs during later stage osteoporosis to counter altered tissue mechanics due to estrogen deficiency (80).

Finally, it is important to note that the results of the study may differ to the human disease of osteoporosis, since specific differences exist between the rat and human bone biology, including the rare occurrence of basic multicellular unit remodeling in rat bone (81), as well as the apparent absence of classic Haversian systems, or osteons (44). Nonetheless, the ovariectomized rat is an established model of postmenopausal osteoporosis in humans that is commonly used, due to the fact that the model displays many of the same characteristics, such as increased rate of bone turnover with absorption exceeding formation (82,83), greater decrease in trabecular bone compared to cortical bone (82–84), decreased calcium absorption (82,85,86), and similar skeletal responses to drug treatments and exercise (87–90). Therefore the overall remodeling activity of rat bone bears remarkable similarities to that of human bone (91) and, as such, the results of this study provide, to our knowledge, novel information that might inform future study of the human bone disease of osteoporosis.

Conclusions

In summary, we report experimental evidence that osteocytes in healthy bone tissue experience higher maximum strains (31,028 ± 4213 με) than osteoblasts (24,921 ± 3832 με), whereas osteoblasts experience elevated strains (>10,000 με) throughout a greater proportion of their cell body than osteocytes. Most interestingly we show that, in early-stage osteoporosis, osteocytes sense osteogenic strain magnitudes in a greater proportion of the cell (10%), with 23% greater maximum strains, than healthy cells. However, we also observe that, in late-stage osteoporosis, cellular strains in both cell types decrease significantly compared to early-stage osteoporosis, such that there is no significant difference between bone cells in healthy and osteoporotic bone. This suggests that a mechanobiological response may have occurred to alter the mechanical environment, perhaps in an attempt to restore homeostasis. This study provides a greater understanding of the mechanobiology of bone cells during the disease of osteoporosis.