Front-to-Rear Membrane Tension Gradient in Rapidly Moving Cells

Abstract

Membrane tension is becoming recognized as an important mechanical regulator of motile cell behavior. Although membrane-tension measurements have been performed in various cell types, the tension distribution along the plasma membrane of motile cells has been largely unexplored. Here, we present an experimental study of the distribution of tension in the plasma membrane of rapidly moving fish epithelial keratocytes. We find that during steady movement the apparent membrane tension is ∼30% higher at the leading edge than at the trailing edge. Similar tension differences between the front and the rear of the cell are found in keratocyte fragments that lack a cell body. This front-to-rear tension variation likely reflects a tension gradient developed in the plasma membrane along the direction of movement due to viscous friction between the membrane and the cytoskeleton-attached protein anchors embedded in the membrane matrix. Theoretical modeling allows us to estimate the area density of these membrane anchors. Overall, our results indicate that even though membrane tension equilibrates rapidly and mechanically couples local boundary dynamics over cellular scales, steady-state variations in tension can exist in the plasma membranes of moving cells.

Introduction

Membrane tension is an important mechanical regulator of cell motility, integrating mechanical cues across the cell and influencing protrusion and retraction dynamics along the cell boundary (1–5). Although membrane-tension measurements have been reported in various motile cell types, including fibroblasts (5), neutrophils (1), and fish keratocytes (3,6), the tension distribution in the plasma membrane of motile cells has remained largely unexplored. The plasma membrane exhibits properties of a two-dimensional fluid, so that in stationary cells, membrane tension has to be homogeneous and isotropic, whereas transient changes in tension should relax (7,8). The typical timescale for tension relaxation depends on the viscosity of the membrane and is relatively fast (on the order of milliseconds) compared to other cellular processes. During persistent cell movement, however, the plasma membrane undergoes a two-dimensional flow, and steady-state gradients in membrane tension could arise. Two recent studies (9,10) analyzed this situation theoretically and showed that the primary factor generating a steady-state gradient of membrane tension is an effective viscous friction associated with movement of the cell membrane relative to the actin cytoskeleton in motile cells. This friction is mainly due to transmembrane anchors and adhesion proteins that are bound to the actin network and treadmill rearward with it. The movement of these cytoskeleton-attached membrane proteins within the viscous lipid bilayer generates frictional drag. The cumulative drag force increases steeply with the area fraction of the transmembrane cytoskeleton-attached anchors (9,10).

Previous measurements of plasma membrane flow in motile cells indicated that the membrane passively translocates forward with respect to the extracellular substrate, staying essentially at rest in the cell frame of reference. This was shown for most motile cell types, including fibroblasts (11), keratocytes (12–14), leukocytes (15), and Dictyostelium amoebae (16). Membrane flows have been observed in neuronal growth cones (17), where continuous incorporation of membrane at the growth cone generates a steady flow of membrane from the growth cone toward the cell body. The lack of membrane flow in the cell frame of reference of motile cells implies that the tension gradient that develops in the membrane counterbalances the frictional drag on the membrane generated by the treadmilling cytoskeleton. The magnitude of the tension gradient is predicted to strongly depend on the density and distribution of the cytoskeleton-attached membrane anchors and adhesion complexes, and reasonable values of this density should lead to a considerable tension difference between the leading and trailing edges of motile cells (9,10). Here, we test these predictions experimentally by examining the membrane-tension distribution in fish epithelial keratocytes, which are notorious for their persistent and rapid movement (3,18,19).

Materials and Methods

Cell culture and pharmacological treatments

Primary keratocyte cultures are prepared from the Central American cichlid Hypsophrys nicaraguensis as described previously (3,20). One-day-old cultures are replated and cultured at room temperature in Leibovitz’s L-15 media (Gibco BRL, Grand Island, NY) and supplemented with 14.2 mM Hepes, pH 7.4, 10% fetal bovine serum (Invitrogen, Grand Island, NY), and 1% antibiotic-antimycotic (Gibco BRL). Keratocyte fragments are prepared as described previously (21). Cytochalasin treatment is done by adding 0.5 μM cytochalasin D (Sigma, St. Louis, MO) to the cell culture media. Tension measurements are done between 8 and 40 min after adding cytochalasin. Lamellipodial freezing is done by incubating cells in 75 μM blebbistatin for 3 min and subsequently adding 1.5 μM jasplakinolide (both from Sigma). Measurements are done 10–30 min after adding jasplakinolide.

Tether-pulling experiments and force measurements

Tether force measurements are carried out as in our previous work (3) with a laser tweezers system (PALM microtweezers, Carl Zeiss MicroImaging, Jena, Germany) using a 63× 1.2 NA water immersion objective and a motorized stage (Ludl Electronic Products, Hawthorne, NY) on an inverted microscope (Axiovert 200M, Carl Zeiss). Trapping is done with a 3 W, 1064 nm Nd:YAG laser focused to a diffraction-limited spot, and imaging by bright field is done simultaneously. Tether force measurements on cells are done by attaching concanavalin-A-coated beads to motile keratocytes and measuring the force after tether formation. At the front, a coated bead is brought into contact with the membrane on the dorsal surface of the lamellipodium. The bead is pulled toward the leading edge and beyond it to form a tether by moving the stage. At the back, a bead is brought into contact with the cell membrane at the rear part of the cell body and pulled away by moving the stage. We correct the measured tether force for the contribution of the dynamic friction due to stage movement, when relevant, as previously (3). The time intervals between sequential measurements within the same cell are between ∼20 s and a few minutes. The order of measurements (front before rear and vice versa) did not influence the results. Apparent membrane-tension values, T, are calculated from the tether force, F_T, using $T=\left(F_T^2/8{\pi }^{2}B\right)$, where $B=0.14\text{pN}\cdot \mu \text{m}$ is the measured bending modulus of the plasma membrane in keratocytes (3,22).

Results

Membrane tension is higher at the leading edge of motile keratocytes

To characterize the membrane-tension distribution in rapidly moving fish keratocytes, we measure tension, using a tether-pulling assay (3,22), at different positions along the cell boundary. Specifically, measurements are done (a) at the center of the leading edge and (b) behind the cell body at the rear (Fig. 1 and Movies S1 and S2, respectively, in the Supporting Material). Tethers are pulled from individual cells at both positions, often with more than one measurement performed at each location. The temporal order in which the front and rear measurements are performed does not matter. The population-averaged membrane tension at the cell front is 365 ± 26 pN/μm (mean ± SE), whereas the average tension at the rear is 280 ± 21 pN/μm (Fig. 1 C). Thus, the membrane tension is on average ∼30% higher at the leading edge compared to the trailing edge. The mean membrane-tension difference between the front and rear within individual cells is 85 ± 19 pN/μm (Fig. 1 D). Higher membrane-tension values at the leading edge compared to the trailing edge are also observed in cells treated with cytochalasin D (Fig. S1), which caps free barbed ends of actin filaments (23) and leads to a substantial reduction in membrane-tension values and speed (3). The average difference between sequential tension measurements in control experiments in which the membrane tension is repeatedly measured at the same location is not significantly different from zero (Fig. S2). Assuming that the membrane-tension gradient is distributed evenly from front to rear (9,10), we can estimate the magnitude of the gradient by dividing the measured front-to-rear tension difference by the front-to-rear length of cells (15.8 ± 0.5 μm; mean ± SE, N = 25), which gives an average membrane-tension gradient of ∼5 pN/μm².

Figure 1.

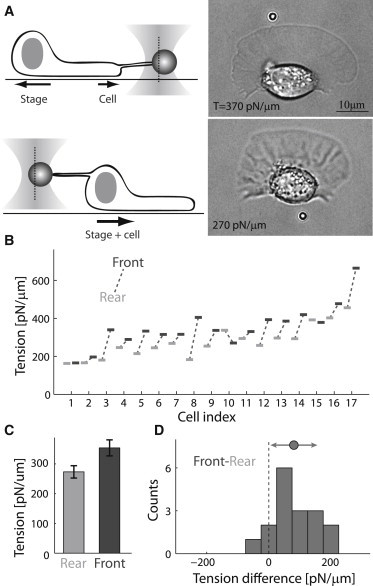
Membrane tension is higher at the leading edge of motile keratocytes. (A) Schematic illustrations (left) and bright-field images (right) of a motile keratocyte during membrane-tension measurements at the front (upper) and rear (lower). The time interval between the front and rear tension measurements was 22 s, and the tension value at each position is indicated in the images. The focal planes of the images are slightly shifted due to differences in bead height when pulling from the front as compared to pulling from the rear. (B) Front (dark) and rear (light) membrane-tension values are shown for 17 different cells. (C) Bar plot showing the population-averaged membrane-tension values at the front and rear of the cell (mean ± SE). The difference in the average tension between front and rear is statistically significant (p < 0.01). (D) Histogram of the front-to-rear membrane-tension difference distribution for the population of cells shown in (B). The mean and standard deviation are indicated above the histogram.

To examine the importance of cell movement in generating higher apparent tension at the leading edge, we examined keratocytes in which cell movement was abolished by treating the cells with blebbistatin followed by jasplakinolide (3,24). This combination treatment interferes with actin disassembly processes and leads to rapid cessation of movement, essentially freezing the lamellipodial actin network (24). In our previous work (3), we found that the apparent membrane tension was severely diminished by this treatment, and we attributed the residual tension in frozen cells to the contribution of membrane-cytoskeleton attachment energy. Interestingly, we find here that frozen cells have higher apparent tension at the cell rear than at the leading edge (Fig. 2), suggesting that membrane-cytoskeleton attachment energy is larger at the cortical region at the rear end of the cell body than at the leading edge. These results are in striking contrast to motile keratocytes, where the apparent tension is higher at the leading edge (Fig. 1), emphasizing the importance of cell movement for generating the observed front-to-rear tension difference.

Figure 2.

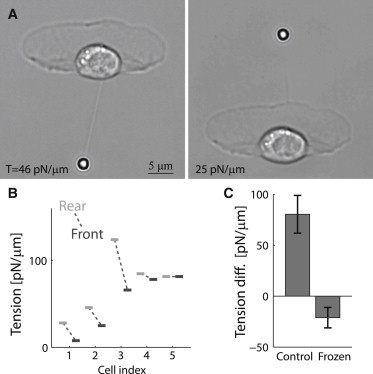
Membrane tension in frozen cells is higher at the rear. (A) Bright-field images of a cell that has stopped moving after treatment with blebbistatin followed by jasplakinolide, during membrane tension measurements at the front and rear. (B) Front (dark) and rear (light) membrane-tension values are shown for different frozen cells. (C) Bar plot showing the population-averaged membrane-tension difference between the front and rear of the cell (mean ± SE) in control cells and frozen cells. In contrast with control cells, the tension values in frozen cells are higher at the rear. The difference in the average tension difference between control cells and frozen cells is statistically significant (p < 0.01).

Membrane tension gradient in keratocyte fragments is similar to that in whole cells

Lamellipodial fragments of keratocytes, which lack nuclei, microtubules, and most organelles, move with speed and persistence similar to those of whole cells (21,25,26). These fragments are essentially stand-alone lamellipodia, containing little besides a treadmilling actin network enclosed by a membrane. As such, fragments present an ideal model system for studying the membrane-tension distribution during steady lamellipodial motility. The tension in motile fragments is measured using a tether-pulling assay as in whole cells, except that in fragments, tethers can be pulled directly from the lamellipodium at both ends, since the rear part of the lamellipodium is also accessible (Fig. 3). The values of membrane tension at the leading edge of fragments are similar to those in whole cells (Fig. 3 A), with a population average of 320 ± 19 pN/μm (mean ± SE, N = 22) in fragments, compared to 360 ± 26 pN/μm (N = 15) in whole cells. The front-to-rear membrane-tension difference in fragments is measured as in cells, by performing sequential measurements at the front and rear of the same fragment (Fig. 3, B and C; Movie S3). The resulting average front-to-rear membrane-tension difference in fragments is 50 pN/μm (N = 3), compared to 85 pN/μm (N = 25) in whole cells. However, since fragments are smaller in width, the estimated tension gradient in fragments is ∼5 pN/μm², as in whole cells.

Figure 3.

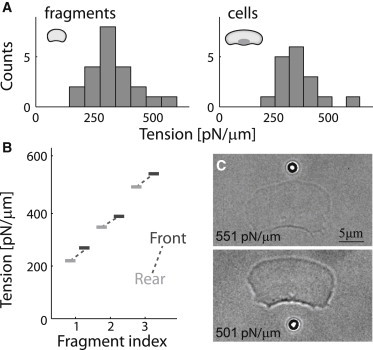
Membrane tension gradient in lamellipodial fragments. (A) Histograms of membrane tension values at the leading edge in a population of lamellipodial fragments (left) and whole cells (right). The membrane tension in fragments is comparable to that in cells (p > 0.1). (B) Front (dark) and rear (light) tension values are shown for three fragments. (C) Bright-field images of a fragment during membrane-tension measurements at the front and rear. The time interval between the front and rear tension measurements was 80 s.

Discussion

We measure the membrane-tension distribution in motile keratocytes and find a steady-state membrane-tension difference between the cell front and rear, with ∼30% higher apparent tension values at the leading edge (Fig. 1). Local variations in the apparent membrane tension have been reported previously in neurons (17) and epithelial cells (27). In epithelia, membrane-tension differences were measured between the apical and basal membranes and attributed to differences in membrane-cytoskeleton attachment energy (27). In growth cones, which are generally characterized by very low membrane-tension values, a small membrane-tension gradient appeared to drive a measurable membrane flow from the growth cone toward the cell body (17). How is the membrane tension distributed in motile cells like keratocytes, which move persistently yet exhibit no apparent membrane flow in the cell frame of reference? Previous studies generally have mostly assumed, based on the fluid nature of the membrane and the lack of bulk membrane flow, that the tension distribution is homogenous during steady movement (8,19,21). However, recent theoretical studies suggest that steady-state gradients in the lateral tension can develop in the membranes of moving cells (9,10). The measurements presented here indeed show that measurable tension gradients exist in steadily moving keratocytes.

The apparent membrane tension in keratocytes is dominated by the lateral tension in the membrane rather than the attachment energy between the cytoskeleton and the membrane (3). What is the origin of the observed front-to-rear membrane-tension gradient in these cells? Although we cannot completely rule out a contribution of local differences in the membrane-cytoskeletal attachment energy, our data strongly suggest that the observed front-to-rear membrane-tension difference arises primarily from variations in the lateral membrane tension associated with cell movement. First, our results with frozen cells show that in the absence of cell movement, the difference between the apparent tension at the front and rear becomes small and negative (Fig. 2). Second, keratocyte cells and fragments exhibit the same front-to-rear tension gradient, despite the rather different cytoskeletal organization near the location of the tether origin at the rear; in cells, the tether is pulled from a cortical region at the back of the cell body, whereas in fragments, the tether is pulled from the rear of the lamellipodium. Together, these results imply that differences in membrane-cytoskeleton attachment energy between the front and rear of the cell are minor, and that the main contribution to the front-to-rear membrane-tension gradient arises from differences in the in-plane (lateral) tension within the membrane of the moving cell.

Our measurements in keratocyte cells, and in particular in keratocyte fragments, can be interpreted based on a recent theoretical model for the distribution of lateral tension in the membranes of moving cells (9). This model assumes a simplified flat cell geometry, which lacks a cell body, and thus resembles the shape of a keratocyte fragment. According to the model, the membrane tension is generated by the protrusive force applied to the leading edge of the cell by the polymerizing actin filaments. The tension gradient is determined by the viscous friction forces between the plasma membrane and transmembrane protein anchors that are bound to the treadmilling actin network and hence move rearward relative to the bulk of the membrane. The model predicts that the tension gradient increases with the area density of cytoskeleton-bound membrane anchors but is only weakly dependent on the density of adhesion molecules, except at extremely low adhesion values (9). The density of cytoskeleton-bound protein anchors can be estimated based on the model: for a crawling speed of 0.2 μm/s, assuming an anchor cross section of 5 nm, the measured tension gradient of ∼5 pN/μm² corresponds to a membrane area fraction of ∼2% covered by the anchors. The distance between anchors in this case can be estimated as l ≈ 31 nm. The force exerted on one anchor by the membrane, originating from the membrane-anchor viscous friction, thus has an approximate value of $f\approx \left(dT/dr\right)l^2=5\text{pN}/\mu {\text{m}}^2\times {\left(0.031\mu \text{m}\right)}^2=0.005\text{pN}$. While this force leads to the observable tension gradient over cellular scales, it contributes only about 0.005 k_BT to the energy of anchor dissociation from the lamellipodial actin network, and therefore has a negligibly small influence on the dissociation kinetics of the anchors. An additional prediction of the model concerns a possible rolling of the membrane with respect to the cell’s leading edge, reminiscent of a tank-treading motion. For the estimated anchor area fraction, the membrane rolling speed is predicted to be ∼0.01 μm/s, which is an order of magnitude lower than cell speed and probably below the measurement detection limit (12–14).

Conclusions

Overall, our results show that persistent membrane tension gradients can occur in motile cells, despite the fluid nature of the membrane. Several recent studies have emphasized the important role of transient changes in membrane tension for coordinating and regulating cell boundary dynamics (1,5,28,29). Local variation in the apparent membrane tension can similarly be functionally relevant, imposing distinct constraints on cell boundary dynamics at different cellular locations. For example, differences in the apparent membrane tension between the apical and basal surfaces in epithelia (27) generate spatial variations in the energy requirements for clathrin-mediated endocytosis and thus differentially influence the actin dependence of clathrin-coat assembly at the apical and basal surface (30). The difference in the apparent membrane tension between the leading edge and the trailing edge could also have functional significance. For example, a front-to-rear gradient in membrane tension may assist directed membrane transport toward the leading edge by promoting exocytosis near the leading edge while favoring endocytosis at the trailing edge. Thus, a front-to-rear membrane tension could lead to net membrane transport to the leading edge which would accelerate cell movement. Further work is required to characterize the membrane-tension distribution in different motile cell types and to reveal its role under different conditions.

Supporting Material

Movie S1. Tether pulling at the leading edge of a cell

This movie shows bright-field images of a keratocyte during a tether-pulling experiment from the leading edge. An image of the whole cell (upper) is shown together with a zoomed view of the bead (inset). The location of the center of the laser trap is indicated (red cross). The presence of a tether, which is invisible by bright field, is evident from the displacement of the bead from the trap center. The field of view is 51 μm wide, and the movie is played at 4× real time.

Movie S2. Tether pulling from the cell body at the rear

This movie shows bright-field images of the same keratocyte shown in Movie S1 during a tether-pulling experiment from the rear of the cell body. An image of the whole cell (upper) is shown together with a zoomed view of the bead (inset). The location of the center of the laser trap is indicated (red cross). The tether force displaces the bead from the trap center. The field of view is 51 μm wide, and the movie is played at 4× real time.

Movie S3. Measurements of front-to-rear membrane-tension difference in fragments

This movie shows bright-field images of a keratocyte fragment during a tether-pulling experiment (upper) together with a zoomed view of the bead (inset). The location of the center of the laser trap is indicated (red cross). A membrane tether is first pulled from the leading edge of the fragment. The same bead is then brought into contact with the rear of the fragment by moving the stage. A tether is formed at the rear on the third attempt. The field of view is 45 μm wide, and the movie is played at 4× real time.