Abstract
As the major structural constituent of the cytoskeleton, microtubules (MTs) serve a variety of biological functions that range from facilitating organelle transport to maintaining the mechanical integrity of the cell. Neuronal MTs exhibit a distinct configuration, hexagonally packed bundles of MT filaments, interconnected by MT-associated protein (MAP) tau. Building on our previous work on mechanical response of axonal MT bundles under uniaxial tension, this study is focused on exploring the compression scenarios. Intracellular MTs carry a large fraction of the compressive loads sensed by the cell and therefore, like any other column-like structure, are prone to substantial bending and buckling. Various biological activities, e.g., actomyosin contractility and many pathological conditions are driven or followed by bending, looping, and buckling of MT filaments. The coarse-grained model previously developed in our lab has been used to study the mechanical behavior of individual and bundled in vivo MT filaments under uniaxial compression. Both configurations show tip-localized, decaying, and short-wavelength buckling. This behavior highlights the role of the surrounding cytoplasm and MAP tau on MT buckling behavior, which allows MT filaments to bear much larger compressive forces. It is observed that MAP tau interconnections improve this effect by a factor of two. The enhanced ability of MT bundles to damp buckling waves relative to individual MT filaments, may be interpreted as a self-defense mechanism because it helps axonal MTs to endure harsher environments while maintaining their function. The results indicate that MT filaments in a bundle do not buckle simultaneously implying that the applied stress is not equally shared among the MT filaments, that is a consequence of the nonuniform distribution of MAP tau proteins along the bundle length. Furthermore, from a pathological perspective, it is observed that axonal MT bundles are more vulnerable to failure in compression than tension.
Introduction
The cytoskeleton features a system of highly entangled protein filaments. Actin filaments, intermediate filaments, and microtubules (MTs) are the major structural components of the cytoskeleton filamentous network. Among these three principal constituents of the cytoskeleton, MTs are responsible for various essential biological functions that range from facilitating organelles transport to maintaining the mechanical integrity of the cells (1,2). MTs are hollow cylinders formed by, on average, 13 parallel longitudinally oriented protofilaments. These protofilaments are composed of α-β tubulin heterodimers (1,3–6). Their tubular structure bestows the MT filaments a high flexural rigidity (1,7,8). Although, MTs generally do not demonstrate any regular geometrical organization, neuronal axons present a well-organized morphology of MTs. Axonal MTs are bundled by interconnections mediated by MT-associated protein (MAP) tau and form polarized arrays located in the interior portion of the axon (9–12). It is known that MAP tau, an intrinsically unfolded protein, stabilizes MTs and promotes their assembly (11,13,14).
Cells are constantly involved in mechanotransduction events that help them carry out their functions (15). Cytoskeletal components work in concert to carry these mechanical forces and MTs play a substantial role in this process. Previously, we investigated the mechanical response of axonal MT bundles under uniaxial tension and demonstrated that the mechanical properties of the axonal MT bundle are influenced by tau protein interconnections (11). MTs are, however, primarily regarded as compression-bearing elements (11). A number of observations suggest that among all cytoskeletal components, MTs play a critical role in carrying compressive loads. Their curved conformation in cultured cells implies that they experience large compressive forces within the cytoplasm (2). In addition, as suggested by phenomenological models, MTs behave as compression-supporting elements that maintain cell shape by balancing the cytoskeletal prestress (1,16–18). In the chromosome segregation apparatus, MTs act as compression-supporting struts (19), and it is observed that MTs in PC12 neurites bear compression to partially support tension in actin networks (20,21). Buckling is the first expected consequence of compressive loads on column-like structures such as MTs. Many biological activities feature bending, looping, and buckling of MT filaments, e.g., MT assembly and growth against barriers, observed in in vitro and in vivo experiments (22–25), organelle movement along MTs (26), direct interactions with molecular motors such as dynein and kinesin (27,28), and actomyosin contractility (22,29) (also see (30) for a comprehensive review). Furthermore, it has been suggested that MT buckling and breaking is the major cause of MT reorganization in the central spindle (31). In addition to normal biological functions, MTs might also experience buckling and breaking in traumatic injuries. Axon compression is a common feature of traumatic injuries (32–35) and therefore axonal MT bundles may experience pathological compressive forces leading to their buckling and breaking.
Buckling of MTs has been studied through computational and experimental works in recent years. Some noticeable observations and outcomes are briefly tabulated in Table 1. Considering the large slenderness ratio, i.e., length to diameter ratio, of MTs (>100) (36), it is expected that MTs undergo classical Eulerian buckling, under the first mode, with a large wavelength under exceedingly small forces (∼1 pN) (36–38). However, it has been argued that in vivo MTs experience a short-wavelength buckling regime due to their mechanical coupling with the surrounding cytoskeleton, suggesting that this mechanism assists MTs in bearing large compressive force (2). Several computational approaches were subsequently exploited to determine the validity of this observation. Li (39) studied a single MT surrounded by a viscoelastic cytoplasm under compression and measured the buckling amplitude, wavelength, and growth rate based on the surrounding cytoplasm properties. The results agreed with those of Brangwynne et al. (2). Jiang and Zhang (40) modeled MTs as single elastic cylindrical tubes surrounded by the cytoplasm, and concluded that the cytoskeletal resistance to compressive forces depends on mechanical properties of the MTs as well as the cytoplasm where the stiff MTs embedded in the viscoelastic cytoplasm act as an effective composite material for bearing compressive forces. The data in Table 1 is reported in chronological order to indicate the rise in interest of the role of a supporting cytoplasm on the buckling behavior of in vivo MTs in recent years.
Table 1.
Studies conducted on buckling behavior of MT filaments, individually or in bundles (presented in chronological order of appearing in the literature)
| Critical load (Fcr) | Wavelength () | Methods and conditions | |
|---|---|---|---|
| Kurachi et al. (36) | ≈ 1 pN | – | In vitro experiment on an individual MT by optical trapping forces method |
| Elbaum et al. (37) | 10 pN (individual MT) | – | Micropipette aspiration of vesicles (Assumes Eulerian buckling to obtain flexural rigidity of MTs.) |
| 31 pN (MT Bundle) | |||
| Fygenson et al. (38) | ≥ 2 pN | – | Eulerian buckling due to growth of confined MTs |
| Gittes et al. (27) | 4–6 pN | – | Buckling of MTs due to the movement of kinesin motor molecule |
| Stamenović et al. (18) | ≈ 27 pN | 2.8 μm | MTs supported by continuous elastic intermediate filaments |
| Kerssemakers et al. (53) | 1.2 ± 0.2 pN | – | Eulerian long-wavelength buckling |
| Kikumoto et al. (6) | 0.11–1.35 pN | – | First mode Eulerian buckling |
| Howard (54) | 5–20 pN | 4–8 μm | Eulerian buckling with no supporting surrounding |
| Brangwynne et al. (2) | >100 pN | ≈ 2 μm (theoretical) | In vivo experiments. Theoretical method assumes an MT surrounded by elastic cytoskeletal network |
| ≈ 3 μm (experimental) | |||
| Li (39) | 232, 350, 500 pN | 2.6, 2.2, 1.8 μm | MTs embedded in a viscoelastic cytoplasm |
| Jiang and Zhang (40) | On the order of 100 pN (212 pN for MT surrounded by viscoelastic cytoplasm) | ≈ 3 μm (for viscoelastic surrounding) | MTs are assumed to be surrounded by whether elastic, viscous, or viscoelastic cytoplasm |
Computational modeling techniques are widely used for investigations of cytoskeletal filaments and networks (see (11) for a review). To the best of our knowledge, there is no specific computational study on compressive forces and buckling behavior of filamentous proteins. However, a recent study has exploited a similar computational approach to analyze buckling behavior of vertically aligned carbon nanotube arrays under compression (41). Here, we seek to characterize the mechanical behavior of individual as well as bundled MTs under compressive forces. The primary goal of this study is to characterize the role of viscous cytoplasm as well as bundled configuration on buckling behavior of MTs. The computational model we reported previously (11) has proved to be a powerful tool to accurately study such biological systems with moderate computational demands. The model is extended here to incorporate compressive loading scenarios. The proposed model allows for flexibility in determining various configurations of MTs, an ability to incorporate different mechanical properties for the cytoplasm, and accounts for all morphological features of MT bundles. Two different categories of intracellular MTs are studied here. First, intracellular MTs supported by viscous cytoplasm are subjected to axial compressive force to computationally investigate the influence of the environment on the critical load and buckling wavelength. Bundled MT models are then used to examine the buckling behavior of interconnected bundles in neuronal axons. The bundled configuration of axonal MTs and the MAP tau proteins are found to significantly influence the axonal response to compressive loads.
Materials and Methods
Discrete bead-spring model
Discrete bead-spring models are useful in simulating filamentous network configurations, enabling to accurately model intrinsically intricate geometries ubiquitous in cell biology studies (11,42–44). These models can handle sufficient complexity with modest computational demand. Previously, we presented a discrete bead-spring model that accounts for geometrical complexities of MTs and MT bundles (11). Here, we extend this model to enable compressive loading configurations and buckling modes of deformation.
Here, the MT filaments are represented by beads of mass m, interacting via potentials that represent elasticity and bending rigidity of MT filaments (see Fig. 1). Spring coefficients, denoted by ks and kb, stand for the axial and flexural rigidity of MTs, respectively. These spring constants are related to material properties of the filaments in the equations:
| (1) |
| (2) |
where E is the Young’s modulus of the filament, A is the cross-sectional area of the filament, l0 is the unstretched bead spacing, and EI is flexural rigidity of the filament. The flexural rigidity of a polymer can be calculated based on its persistence length:
| (3) |
where lp is the persistence length, kB is the Boltzmann constant, and T is the temperature.
Figure 1.
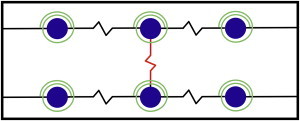
Schematics of the MT filaments and MAP tau proteins representation in the model. Black and red linear springs represent MT and MAP tau protein elasticity. Green torsion springs symbolize flexural rigidity of MTs. (Not drawn to scale.) To see this figure in color, go online.
Therefore, the axial and bending potential of the linear springs can be calculated by the following equations:
| (4) |
| (5) |
where r is the separation distance, θ is the angle between subsequent elements, and is the rest angle of the bend.
Given their tight packing configuration, MTs are likely to penetrate neighboring filaments in bundles. Therefore, it is essential to incorporate a repulsive force to prevent this unrealistic event. This was implemented in the model by introducing a regulatory steric repulsion potential between neighboring filaments shown in Eq. 1.
| (6) |
where is a scaling parameter, r is the distance between sterically interacting beads, and is the steric radius. Numerous trial and error attempts suggest values of 1 × 10−16 nm and 15 nm for the energy scaling parameter and steric radius, respectively. The cutoff radius for steric interaction was set to be 2.4 (11). In our model, the presence of the cytoplasm, which is assumed as a viscous environment, is represented by tangential and normal drag forces on the MT and MAP tau elements. The MT and tau protein resistance coefficients (Cn, Ct) describe the amount of drag force experienced by each of the elements, in this equation:
| (7) |
where Fdrag is the drag force, μ is fluid viscosity, and is instantaneous velocity of the element. Subscript i is either tangent or normal and superscript j is either MT or cross-link. A modified predictor-corrector velocity Verlet algorithm was employed to calculate the beads of MT filament trajectories. The compressive force was applied in a ramp and hold manner, i.e., reaching its maximum value in the first 10% of simulation. In addition, for the sake of stability and computational efficiency, a simulation time step of 0.1 ps was used. Considering that the forces used in this study are large enough, we can assume the system to be athermal and neglect the effect of thermal fluctuations in the system.
Individual MT compression
To investigate the in vivo buckling behavior of individual MTs, an individual MT filament embedded in the viscous cytoplasm is modeled (Fig. 2). Material properties of MTs, the surrounding cytoplasm, and their interactions are the same as those employed by Peter et al. (11), briefly tabulated in Table 2. A compressive force aligned with the MT main axis is applied to both ends of the MT to represent compressive stress exerted on it.
Figure 2.
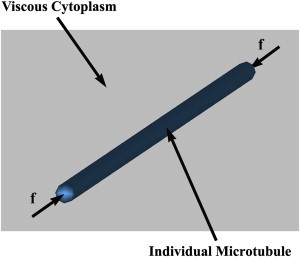
An individual MT surrounded by the viscous cytoplasm subjected to axial compressive force. To see this figure in color, go online.
Table 2.
Material parameters for MTs
| Parameter | Value |
|---|---|
| MT Young’s modulus, EMT | 1.5 GPa |
| MT persistence length, | 420 μm |
| MT flexural rigidity, (EI)MT | 2.0 × 10−23 Nm2 |
| MT element length, | 10 nm |
| MT axial spring constant, | 47.1 N/m |
| MT bending spring constant, | 1.8 × 10−16 Nm |
| MT bead mass, mMT | 1.48375 × 10−21 Kg |
| MT resistance coefficients, | 2.1191, 1.2700 |
In a fully viscous surrounding and with centrally aligned compressive forces, a pure compressive force would not lead to bending or buckling of the filament. Therefore, to define a more realistic environment, either an off-centered force or a slight additional transverse force should be applied to the filaments. The latter option is implemented to initiate lateral deformation and buckling.
MT bundle compression
The hexagonally packed bundle geometry presented by Peter et al. (11) (Fig. 3) is employed to investigate MT bundle behavior under compressive forces. MT filaments are interconnected by idealized linear elastic tau proteins (45). The mass of the tau cross-link is added to the bead where the cross-link is connected. The material and model properties of tau proteins are the same as those incorporated in (11) and are briefly tabulated in Table 3.
Figure 3.
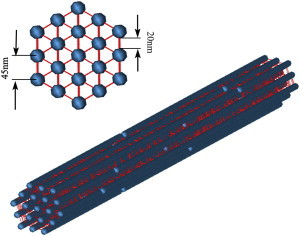
Bundle geometry, and its cross section, employed in this work. The picture depicts the hexagonal configuration and interconnections of the bundle mediated by MAP tau proteins (shown in red). A center-to-center distance of 45 nm between MT beads is enforced to correspond to 20 nm edge-to-edge spacing. The bundle consists of 19 rows of 8 μm MTs with one discontinuity in each filament. To see this figure in color, go online.
Table 3.
Material parameters of MAP tau cross-links
| Parameter | Value |
|---|---|
| Tau cross-link Young’s modulus, ECL | 5 MPa |
| Tau cross-link element length, | 45 nm |
| Tau cross-link axial spring constant, | 3.925 × 10−2 N/m |
| Tau cross-link bead mass, mCL | 2.0 × 10−22 Kg |
| MT resistance coefficients, | 5.9555, 4.9181 |
Tau proteins are known as intrinsically disordered proteins, characterized by a lack of stable secondary structure (46). Currently, there is not enough evidence that they can bear compressive forces. Therefore, although a significant number of MAP tau proteins experience compressive forces, in this study, they are modeled to only resist in tension.
An average spacing of 25 nm was applied to adjacent tau proteins, and a critical tensional strain of 1.0 was employed in accordance with the previous studies (11,47). It is worth mentioning that although average spacing between tau proteins is held constant, the MAP tau proteins are distributed unevenly along the length of MT filaments. As one of the most important features of the model, MTs are not continuous and each filament includes a discontinuity in the central 80% of its total length. As is the case for individual MTs, compressive forces are exerted at both ends of all of the filaments in the bundle. The desired stress is the total amount of forces applied to MT filaments divided by the cross-sectional area of the filaments. However, due to the presence of tau proteins and their asymmetric distribution along bundle length, no additional transverse force is required for buckling initiation.
Results and Discussion
Individual MT buckling
Simulations were first conducted using individual MTs wherein the effect of supporting cytoplasm was observed. Regardless of the magnitude of the applied force, MTs buckle in short wavelength rather than buckling in classical Eulerian long-wavelength modes (Fig. 4 a). This behavior was previously observed and reported in theoretical, computational, and experimental studies (2,18,30,40). However, to confirm that this behavior is a direct consequence of the support from the surrounding cytoplasm, an individual MT in a free environment, i.e., lacking the cytoplasm, was subjected to compression and was observed that the MT buckled in single wave classical Eulerian mode (data not shown).
Figure 4.

(a) Individual MT subjected to 1000 pN force resulting in wavelength of 1.3 μm. Decaying and localized buckling is observable. (b) The same MT subjected to the same force, whereas tangential support from the cytoplasm is ignored. Comparison between the two MTs indicates that decaying nature of MT buckling in the presence of the cytoplasm is primarily driven by tangential supportive force (2). To see this figure in color, go online.
The cytoplasm supports MTs in normal and tangential directions. As mentioned earlier, the supporting forces are simulated by normal and tangential components of the drag force derived from relative movement of MT filaments to the viscous cytoplasm. Our simulations demonstrate that the buckling wave does not progress beyond the tip of the filament and that the buckling amplitude decays along the MT length (Fig. 4 a) (2,48). This is a direct result of the drag force exerted on MTs by the viscous cytoplasm, previously referred to as the coupling of MT with the surroundings (2,48). To explore whether the two components of drag forces have distinct effects on MTs, a defective environment, lacking tangential resistance to relative displacement of MT filaments, was introduced into the model. Fig. 4 b shows that frequency of the waves are exactly the same along the MT, whereas no decaying of the waves is observed (2), demonstrating that the two components of the drag force have two distinguished responsibilities in support of the filament. Although normal supportive forces result in the short-wavelength buckling of MTs, tangential force accounts for the decayed response of MTs to compressive forces.
The tensile and bending energies of an individual MT filament subjected to a constant compressive force are presented in Fig. 5. The tensile energy increases gradually with time until the MT reaches the steady-state condition. At this stage, the MT filament is ready to buckle, but the initiation requires a trigger. An infinitesimal transverse force is applied to the MT to initiate bending and buckling of the MT. The buckling starts when the tensile energy dramatically decreases and bending energy increases markedly. In other words, the tensile energy is continually transformed to bending energy, denoting the progression of buckling. Buckling is a threshold phenomenon that progresses rapidly after its initiation (2). The aforementioned energy transformation was not observed in simulations that did not result in a buckled MT.
Figure 5.
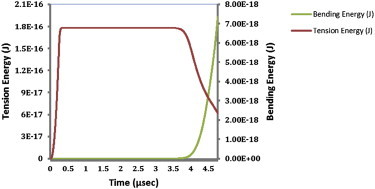
Individual MT tension and bending energies under compression. Buckling of MTs is characterized by a rapid decrease of tensional energy and corresponding dramatic increase in their bending energy. To see this figure in color, go online.
Fig. 6 shows buckling wavelengths (in μm) for different compressive loads (in pN) exceeding the critical force. The diagram indicates an expected decreasing trend for the wavelength with respect to the applied force (39). However, comparing the results for MTs supported by viscous cytoplasm (blue diamonds) to classical Eulerian buckling of an isolated MT in the absence of the supporting cytoplasm (red circles), it could be seen that the viscous cytoplasm can significantly strengthen the MT to bear much higher compressive forces (2).
Figure 6.
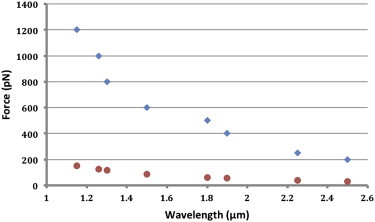
Applied compressive force as a function of MT buckling wavelength for individual MTs. Blue diamonds show results for MTs embedded inside the viscous cytoplasm, whereas red circles show data for classical Eulerian buckling of the same MT without presence of the cytoplasm. The significant difference between the forces in the two categories highlights the ability of MTs surrounded by the cytoplasm to carry much larger compressive forces. To see this figure in color, go online.
The critical buckling force of an individual MT surrounded by a viscous cytoplasm is reported frequently in literature through various techniques (see Table 1 for a brief review). In this study, the critical force was found through a trial and error procedure to be ∼200 pN with a corresponding wavelength of 2.5 μm (the largest corresponding wavelength in Fig. 6). These results agree with the reported experimental (2) and analytical (39,40) values. It should be noted that thermal fluctuations might affect how MTs mechanically behave, to the extent that they might influence active measurements of MT mechanical properties (49). However, experiments that involve force-induced deformations can likely dominate the role of thermal fluctuations in the overall behavior of the MT (49). Therefore, considering the large forces applied in these simulations, the effect of thermal fluctuations can be neglected.
Axonal MT bundle buckling
Short-wavelength, tip-localized buckling of the MT filament observed in the individual MTs is also discernible in MT bundles (Figs. 7 and 8). MT bundles resist higher compressive forces while experiencing the same buckling wavelength as individual MTs. This implies that short-wavelength buckling is primarily driven by supportive forces exerted by the cytoplasm, whereas critical buckling force is affected by any type of mechanical support, i.e., the cytoplasm and tau proteins. The critical buckling force of axonal MT filaments is found to be ∼400 pN for each filament, i.e., approximately twofold higher than that for the individual MT force. This demonstrates the reinforcing role played by the MAP tau proteins assisting bundled MTs to carry larger compressive forces without undergoing bending or buckling. It should be noted that the critical buckling force of MT bundles corresponds to a substantially lower stress relative to the critical tensional stress of MT bundles reported by Peter et al. (11). This suggests that, from a pathological viewpoint, MT bundles are more vulnerable to failure in compression than in tension. In traumatic and diffused axonal injuries, however, the axons are subject to a combination of various forces, i.e., tensional, compressive, and rotational.
Figure 7.
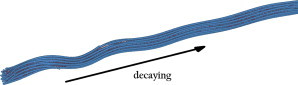
Buckled MT bundle. Buckling is localized at the tip of the bundle and its amplitude decays along MT length. Presence of MAP tau proteins assists bundled MTs to resist higher compressive forces, although their wavelengths are the same as those in individual MTs. To see this figure in color, go online.
Figure 8.
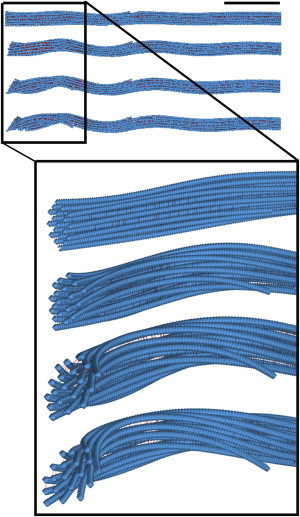
Buckling process in MT bundles. Half of the bundle is shown. It is clear that the buckling is localized at the tip of the bundle and waves decay as they get farther from the tip of the bundle. Scale bar represents 10% of bundle length. To see this figure in color, go online.
One other important characteristic of axonal bundles is related to the presence of MAP tau proteins that interconnect MT filaments in a hexagonally packed configuration. Tau binding helps decay the buckling along MT filaments, and, as a result, >60% of the bundle length remains intact (Fig. 8). This observation along with the aforementioned results on the ability of bundled MTs to resist higher compressive forces shall be treated as a potential explanation to the question of why axonal MTs bundle in such a specific geometrical configuration. The fact that the particular geometry featured by axonal MTs can prevent a large fraction of the bundle from being bent or buckled could be interpreted as a self-defense mechanism. In fact, individual MT filaments form bundles in axons to more efficiently withstand environmental changes and maintain their structure. In addition, axonal MTs play a key role in vital cell functions, serving as a track to transport organelles to major structural components of the axons. Axons are long projections of nerve cells and are prone to experience catastrophic stresses as a result of traumatic injuries. It can be hypothesized that axonal MTs in larger bundles may be able to handle stronger compressive forces despite their length.
Another expected yet interesting behavior of bundles is the nonsimultaneous buckling of comprising filaments (Fig. 9). The bending energy of all filaments of an axonal MT bundle is shown in Fig. 10. These results indicate different buckling starting points for different filaments in the bundle. However, Laan et al. (25) observed that MT filaments, growing together in parallel with no cross-links, equally share the compressive force. As the only difference between this study and Laan et al. (25) work is the presence of MAP tau proteins as tension-bearing elements, collectively, the two observations shed light on the influence of MAP tau on force-sharing of MT filaments in a bundle. In addition, several traces in Fig. 10 show a plateau-like behavior in their bending energy before failure. It could be speculated that this behavior of bending energy plots is showing a semi-equilibrium point for MT filaments. At the maximum bending energy point, where the filament has built up enough bending energy to resist the external force, the filament is in an unstable equilibrium. Therefore, a slight change in environmental conditions, e.g., a lateral force, leads to immediate buckling and failure of the filament. However, this hypothesis should be taken with a grain of salt. Further studies focused on the failure mechanism can reveal the exact behavior of filaments before failure.
Figure 9.

Different buckling behavior of different MT filaments in a bundle. Due to the unequal force-sharing configuration between MTs, due to the specific assembly of the filaments, i.e., the uneven distribution of MAP tau proteins along the filaments as well as presence of random discontinuities, MTs exhibit different behaviors under compressive forces, i.e., the buckling direction and amplitude vary among different filaments. Although the bending of MTs could potentially lead to penetration of filaments into each other, steric repulsion implementation in the model has efficiently inhibited the filaments to penetrate into others. To see this figure in color, go online.
Figure 10.
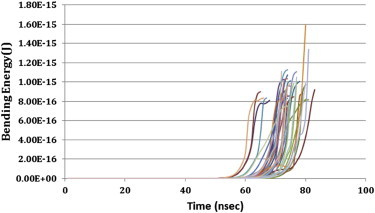
Bending energy of 38 filaments of MT bundle. Each line represents one of the filaments and different points of dramatic increase in bending energy show unequal fractions of compressive force carried by each filament in the bundle. To see this figure in color, go online.
Although bundles are under compression, a significant fraction of MAP tau cross-links experience tension. In contrast to failure of MT bundles under tension, which are primarily a result of the MAP tau protein letdowns (11), bundle failure is found to be primarily due to MT filament buckling. In fact, the mechanical support provided by cross-linking tau proteins enables MT bundles to bear significantly larger compressive forces before buckling.
To explore the role of bundle length (9,50) in buckling behavior, bundles of lengths 2 to 14 μm were studied under the same compressive force. Simulations show that bending energy increases with bundle length; however, this does not necessarily mean that longer bundles are more susceptible to buckling because this increase might be due to the larger number of elements undergoing bending in longer MT bundles. Therefore, bending energy per unit length is a more meaningful parameter for comparison purposes. Fig. 11 shows bending energy per unit length of the bundles of different lengths after a certain amount of simulation time. In general, as bundle length increases the bending energy per unit length is reduced. This counterintuitive observation is in direct agreement with the fact that a large fraction of the bundles remain intact and do not participate in bearing the compressive force, because bending and buckling are primarily localized at the tip of the bundle. Presumably, the fraction of bundle length involved in bending does not increase as much as the length of the bundle, resulting in reduction of the average bending energy of the bundle. Quantitatively, a sevenfold increase in length leads to only less than a threefold reduction in bending energy per unit length.
Figure 11.
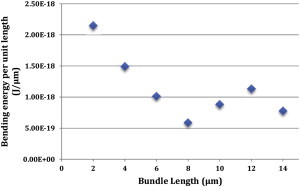
Bending energy per unit length versus bundle length. In general, as bundle length increases the bending energy per unit length is reduced. This observation confirms the fact that a large fraction of the bundle is not involved in bearing the external compressive force, highlighting the tip-localized buckling of MT bundles. To see this figure in color, go online.
Limitations
Although the model presented in this work accounts for several different aspects of individual and bundled MTs, like any other computational model it involves some limitations. It is conceivable that other factors such as the viscoelastic contribution of the cytoplasm, membrane elasticity, adhesion to the extracellular matrix, other MAP proteins present in the axon, could directly and indirectly influence mechanical response of MTs to external stresses. Although accounting for all these factors could result in a more comprehensive representation of MTs and their environment, it would make it challenging to explore the specific role of each element. In addition, lack of detailed information on how some of these elements are involved in MT response adds another layer of complexity to the model. Therefore, the aim of this study was to develop a minimalistic model that appropriately presents a fairly accurate picture of MT behavior under compressive forces. More specifically, one physical limitation of the model is the absence of other cytoskeletal filaments beside MTs. It has been widely reported that cytoskeletal elements are mechanically cross talking via several different proteins (22,51,52). This implies that other cytoskeletal elements, e.g., actin filaments, could have an important role in the mechanical behavior of MTs, e.g., buckling. Intuitively, other elements might act as further supporters of MTs to resist compressive forces. Therefore, one can speculate that the results obtained in this work are underestimating the critical compressive forces of in vivo MTs.
Conclusions
Bending and buckling of individual MT filaments have been previously studied in several experimental and computational investigations (Table 1). In this work, we sought to address some missing aspects of this phenomenon. Specifically, we explored the supportive role of viscous cytoplasm as well as the influence of bundled configuration of MTs within neural axons. Our discrete bead-spring model was further developed to account for compressive forces and buckling behavior of MT filaments. Both individual and bundled MTs displayed short-wavelength buckling, localized at the tip of the filament and decayed along its length. Such behavior is a direct consequence of coupling of MT filaments to their surrounding cytoplasm. The supportive influence of MAP tau protein cross-linkers on the ability of MTs to bear compressive forces is improved by a factor of two in MT bundles. The collective effect of cytoplasm, MAP tau interconnections, and specific hexagonal packing of axonal MT filaments results in extreme decay of buckling waves. The intact central core of the bundle could be interpreted as a self-defense mechanism for axonal MT bundles to stand higher stresses. The asymmetric distribution of tau proteins along bundle length results in nonsimultaneous buckling of filaments in a bundle. In fact, stress exerted on axonal bundles is not equally shared among MT filaments.
A previous study on uniaxial tension on MT bundles has shown the vital role of tau proteins in MT bundle response. Likewise, tau proteins are significant players in buckling of MT bundles under compression. For the bundle lengths we studied, MAP tau proteins collectively offer the same scale of support as the cytoplasm does on the MT filaments, because the critical buckling force of bundled MTs is observed to be twice that of individual MTs. Consequently, additive sources of support for individual and bundled MTs protect filaments against compressive applied forces and enable them to bear much larger stresses, which seems to be a vital property of long axons under various catastrophic external forces.
References
- 1.Mofrad M.R.K. Rheology of the cytoskeleton. Annu. Rev. Fluid Mech. 2009;41:433–453. [Google Scholar]
- 2.Brangwynne C.P., MacKintosh F.C., Weitz D.A. Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement. J. Cell Biol. 2006;173:733–741. doi: 10.1083/jcb.200601060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Desai A., Mitchison T.J. Microtubule polymerization dynamics. Annu. Rev. Cell Dev. Biol. 1997;13:83–117. doi: 10.1146/annurev.cellbio.13.1.83. [DOI] [PubMed] [Google Scholar]
- 4.Nogales E., Whittaker M., Downing K.H. High-resolution model of the microtubule. Cell. 1999;96:79–88. doi: 10.1016/s0092-8674(00)80961-7. [DOI] [PubMed] [Google Scholar]
- 5.Li C., Ru C.Q., Mioduchowski A. Length-dependence of flexural rigidity as a result of anisotropic elastic properties of microtubules. Biochem. Biophys. Res. Commun. 2006;349:1145–1150. doi: 10.1016/j.bbrc.2006.08.153. [DOI] [PubMed] [Google Scholar]
- 6.Kikumoto M., Kurachi M., Tashiro H. Flexural rigidity of individual microtubules measured by a buckling force with optical traps. Biophys. J. 2006;90:1687–1696. doi: 10.1529/biophysj.104.055483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mehrbod M., Mofrad M.R.K. On the significance of microtubule flexural behavior in cytoskeletal mechanics. PLoS ONE. 2011;6:e25627. doi: 10.1371/journal.pone.0025627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pampaloni F., Lattanzi G., Florin E.L. Thermal fluctuations of grafted microtubules provide evidence of a length-dependent persistence length. Proc. Natl. Acad. Sci. USA. 2006;103:10248–10253. doi: 10.1073/pnas.0603931103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yu W., Baas P.W. Changes in microtubule number and length during axon differentiation. J. Neurosci. 1994;14:2818–2829. doi: 10.1523/JNEUROSCI.14-05-02818.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Guzik B.W., Goldstein L.S. Microtubule-dependent transport in neurons: steps towards an understanding of regulation, function and dysfunction. Curr. Opin. Cell Biol. 2004;16:443–450. doi: 10.1016/j.ceb.2004.06.002. [DOI] [PubMed] [Google Scholar]
- 11.Peter S.J., Mofrad M.R.K. Computational modeling of axonal microtubule bundles under tension. Biophys. J. 2012;102:749–757. doi: 10.1016/j.bpj.2011.11.4024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Conde C., Cáceres A. Microtubule assembly, organization and dynamics in axons and dendrites. Nat. Rev. Neurosci. 2009;10:319–332. doi: 10.1038/nrn2631. [DOI] [PubMed] [Google Scholar]
- 13.Lee G., Rook S.L. Expression of tau protein in non-neuronal cells: microtubule binding and stabilization. J. Cell Sci. 1992;102:227–237. doi: 10.1242/jcs.102.2.227. [DOI] [PubMed] [Google Scholar]
- 14.Drubin D.G., Kirschner M.W. Tau protein function in living cells. J. Cell Biol. 1986;103:2739–2746. doi: 10.1083/jcb.103.6.2739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mofrad M.R.K., Kamm R.D., editors. Cellular Mechanotransduction: Diverse Perspectives from Molecules to Tissues. Cambridge University Press; New York: 2014. [Google Scholar]
- 16.Wang N., Butler J.P., Ingber D.E. Mechanotransduction across the cell surface and through the cytoskeleton. Science. 1993;260:1124–1127. doi: 10.1126/science.7684161. [DOI] [PubMed] [Google Scholar]
- 17.Wang N., Naruse K., Ingber D.E. Mechanical behavior in living cells consistent with the tensegrity model. Proc. Natl. Acad. Sci. USA. 2001;98:7765–7770. doi: 10.1073/pnas.141199598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Stamenović D., Mijailovich S.M., Wang N. Cell prestress. II. Contribution of microtubules. Am. J. Physiol. Cell Physiol. 2002;282:C617–C624. doi: 10.1152/ajpcell.00271.2001. [DOI] [PubMed] [Google Scholar]
- 19.Bouck D.C., Joglekar A.P., Bloom K.S. Design features of a mitotic spindle: balancing tension and compression at a single microtubule kinetochore interface in budding yeast. Annu. Rev. Genet. 2008;42:335–359. doi: 10.1146/annurev.genet.42.110807.091620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Joshi H.C., Chu D., Heidemann S.R. Tension and compression in the cytoskeleton of PC 12 neurites. J. Cell Biol. 1985;101:697–705. doi: 10.1083/jcb.101.3.697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dennerll T.J., Joshi H.C., Heidemann S.R. Tension and compression in the cytoskeleton of PC-12 neurites. II: Quantitative measurements. J. Cell Biol. 1988;107:665–674. doi: 10.1083/jcb.107.2.665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Waterman-Storer C.M., Salmon E.D. Actomyosin-based retrograde flow of microtubules in the lamella of migrating epithelial cells influences microtubule dynamic instability and turnover and is associated with microtubule breakage and treadmilling. J. Cell Biol. 1997;139:417–434. doi: 10.1083/jcb.139.2.417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Weisshaar B., Doll T., Matus A. Reorganization of the microtubular cytoskeleton by embryonic microtubule-associated protein 2 (MAP2c) Development. 1992;116:1151–1161. doi: 10.1242/dev.116.4.1151. [DOI] [PubMed] [Google Scholar]
- 24.Dogterom M., Yurke B. Measurement of the force-velocity relation for growing microtubules. Science. 1997;278:856–860. doi: 10.1126/science.278.5339.856. [DOI] [PubMed] [Google Scholar]
- 25.Laan L., Husson J., Dogterom M. Force-generation and dynamic instability of microtubule bundles. Proc. Natl. Acad. Sci. USA. 2008;105:8920–8925. doi: 10.1073/pnas.0710311105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jolly A.L., Kim H., Gelfand V.I. Kinesin-1 heavy chain mediates microtubule sliding to drive changes in cell shape. Proc. Natl. Acad. Sci. USA. 2010;107:12151–12156. doi: 10.1073/pnas.1004736107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gittes F., Meyhöfer E., Howard J. Directional loading of the kinesin motor molecule as it buckles a microtubule. Biophys. J. 1996;70:418–429. doi: 10.1016/S0006-3495(96)79585-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ferenz N.P., Wadsworth P. Prophase microtubule arrays undergo flux-like behavior in mammalian cells. Mol. Biol. Cell. 2007;18:3993–4002. doi: 10.1091/mbc.E07-05-0420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gupton S.L., Salmon W.C., Waterman-Storer C.M. Converging populations of f-actin promote breakage of associated microtubules to spatially regulate microtubule turnover in migrating cells. Curr. Biol. 2002;12:1891–1899. doi: 10.1016/s0960-9822(02)01276-9. [DOI] [PubMed] [Google Scholar]
- 30.Bicek A.D., Tüzel E., Odde D.J. Anterograde microtubule transport drives microtubule bending in LLC-PK1 epithelial cells. Mol. Biol. Cell. 2009;20:2943–2953. doi: 10.1091/mbc.E08-09-0909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Schiel J.A., Park K., Prekeris R. Endocytic membrane fusion and buckling-induced microtubule severing mediate cell abscission. J. Cell Sci. 2011;124:1411–1424. doi: 10.1242/jcs.081448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dyck P.J., Lais A.C., Engelstad J.K. Structural alterations of nerve during cuff compression. Proc. Natl. Acad. Sci. USA. 1990;87:9828–9832. doi: 10.1073/pnas.87.24.9828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Anthes D.L., Theriault E., Tator C.H. Characterization of axonal ultrastructural pathology following experimental spinal cord compression injury. Brain Res. 1995;702:1–16. doi: 10.1016/0006-8993(95)01028-6. [DOI] [PubMed] [Google Scholar]
- 34.Stichel C.C., Müller H.W. Experimental strategies to promote axonal regeneration after traumatic central nervous system injury. Prog. Neurobiol. 1998;56:119–148. doi: 10.1016/s0301-0082(98)00033-1. [DOI] [PubMed] [Google Scholar]
- 35.Hubbard R.D., Quinn K.P., Winkelstein B.A. The role of graded nerve root compression on axonal damage, neuropeptide changes, and pain-related behaviors. Stapp. Car Crash J. 2008;52:33–58. doi: 10.4271/2008-22-0002. [DOI] [PubMed] [Google Scholar]
- 36.Kurachi M., Hoshi M., Tashiro H. Buckling of a single microtubule by optical trapping forces: direct measurement of microtubule rigidity. Cell Motil. Cytoskeleton. 1995;30:221–228. doi: 10.1002/cm.970300306. [DOI] [PubMed] [Google Scholar]
- 37.Elbaum M., Kuchnir Fygenson D., Libchaber A. Buckling microtubules in vesicles. Phys. Rev. Lett. 1996;76:4078–4081. doi: 10.1103/PhysRevLett.76.4078. [DOI] [PubMed] [Google Scholar]
- 38.Fygenson D.K., Marko J.F., Libchaber A. Mechanics of microtubule-based membrane extension. Phys. Rev. Lett. 1996;79:4497–4500. [Google Scholar]
- 39.Li T. A mechanics model of microtubule buckling in living cells. J. Biomech. 2008;41:1722–1729. doi: 10.1016/j.jbiomech.2008.03.003. [DOI] [PubMed] [Google Scholar]
- 40.Jiang H., Zhang J. Mechanics of microtubule buckling supported by cytoplasm. J. Appl. Mech. 2008;75:061019. [Google Scholar]
- 41.Yang X., He P., Gao H. Competing elastic and adhesive interactions govern deformation behaviors of aligned carbon nanotube arrays. Appl. Phys. Lett. 2012;101:053105. [Google Scholar]
- 42.Kim T., Hwang W., Kamm R.D. Computational analysis of a cross-linked actin-like network. Exp. Mech. 2009;49:91–104. [Google Scholar]
- 43.Sandersius S.A., Newman T.J. Modeling cell rheology with the Subcellular Element Model. Phys. Biol. 2008;5:015002. doi: 10.1088/1478-3975/5/1/015002. [DOI] [PubMed] [Google Scholar]
- 44.Rodney D., Fivel M., Dendievel R. Discrete modeling of the mechanics of entangled materials. Phys. Rev. Lett. 2005;95:108004. doi: 10.1103/PhysRevLett.95.108004. [DOI] [PubMed] [Google Scholar]
- 45.Bathe M., Heussinger C., Frey E. Cytoskeletal bundle mechanics. Biophys. J. 2008;94:2955–2964. doi: 10.1529/biophysj.107.119743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wille H., Drewes G., Mandelkow E. Alzheimer-like paired helical filaments and antiparallel dimers formed from microtubule-associated protein tau in vitro. J. Cell Biol. 1992;118:573–584. doi: 10.1083/jcb.118.3.573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Rosenberg K.J., Ross J.L., Israelachvili J. Complementary dimerization of microtubule-associated tau protein: implications for microtubule bundling and tau-mediated pathogenesis. Proc. Natl. Acad. Sci. USA. 2008;105:7445–7450. doi: 10.1073/pnas.0802036105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Das M., Levine A.J., MacKintosh F.C. Buckling and force propagation along intracellular microtubules. Europhys. Lett. 2008;84:18003. [Google Scholar]
- 49.Taute K.M., Pampaloni F., Florin E.L. Extracting the mechanical properties of microtubules from thermal fluctuation measurements on an attached tracer particle. Methods Cell Biol. 2010;95:601–615. doi: 10.1016/S0091-679X(10)95030-9. [DOI] [PubMed] [Google Scholar]
- 50.Baas P.W., Vidya Nadar C., Myers K.A. Axonal transport of microtubules: the long and short of it. Traffic. 2006;7:490–498. doi: 10.1111/j.1600-0854.2006.00392.x. [DOI] [PubMed] [Google Scholar]
- 51.Applewhite D.A., Grode K.D., Rogers S.L. The spectraplakin short stop is an actin-microtubule cross-linker that contributes to organization of the microtubule network. Mol. Biol. Cell. 2010;21:1714–1724. doi: 10.1091/mbc.E10-01-0011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Salmon W.C., Adams M.C., Waterman-Storer C.M. Dual-wavelength fluorescent speckle microscopy reveals coupling of microtubule and actin movements in migrating cells. J. Cell Biol. 2002;158:31–37. doi: 10.1083/jcb.200203022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kerssemakers J.W.J., Janson M.E., Dogterom M. Optical trap setup for measuring microtubule pushing forces. Appl. Phys. Lett. 2003;83:4441–4443. [Google Scholar]
- 54.Howard J. Elastic and damping forces generated by confined arrays of dynamic microtubules. Phys. Biol. 2006;3:54–66. doi: 10.1088/1478-3975/3/1/006. [DOI] [PubMed] [Google Scholar]


