Abstract
Elastin, the principal component of the elastic fiber of the extracellular matrix, imparts to vertebrate tissues remarkable resilience and longevity. This work focuses on elucidating dynamical and structural modifications of porcine aortic elastin exposed to glucose by solid-state NMR spectroscopic and relaxation methodologies. Results from macroscopic stress-strain tests are also presented and indicate that glucose-treated elastin is mechanically stiffer than the same tissue without glucose treatment. These measurements show a large hysteresis in the stress-strain behavior of glucose-treated elastin—a well-known signature of viscoelasticity. Two-dimensional relaxation NMR methods were used to investigate the correlation time, distribution, and population of water in these samples. Differences are observed between the relative populations of water, whereas the measured correlation times of tumbling motion of water across the samples were similar. 13C magic-angle-spinning NMR methods were applied to investigate structural and dynamical modifications after glucose treatment. Although some overall structure is preserved, the process of glucose exposure results in more heterogeneous structures and slower mobility. The correlation times of tumbling motion of the 13C-1H internuclear vectors in the glucose-treated sample are larger than in untreated samples, pointing to their more rigid structure. The 13C cross-polarization spectra reveal a notably increased α-helical character in the alanine motifs after glucose exposure. Results from molecular dynamics simulations are provided that add further insight into dynamical and structural changes of a short repeat, [VPGVG]5, an alanine pentamer, desmosine, and isodesmosine sites with and without glucose. The simulations point to changes in the entropic and energetic contributions in the retractive forces of VPGVG and AAAAA motifs. The most notable change is the increase of the energetic contribution in the retractive force due to peptide-glucose interactions of the VPGVG motif, which may play an important role in the observed stiffening in glucose-treated elastin.
Introduction
Elastin is a long-lived extracellular protein found in various vertebrate tissues, such as the skin, that may suffer from cumulative biochemical degradation. For example, nonenzymatic glycation of elastin, where glucose directly condenses with free amino groups on lysine residues to form a Schiff base, has been shown to occur with aging (1). These glycated cross-links in elastin have been implicated in the stiffening of large vessels of diabetic patients (2). To understand the possible structural and functional alterations at the macroscopic level, we performed in vitro glycation of purified elastin. Glucose treatments were shown to stiffen arterial elastin (3,4), increase the storage and loss moduli (5), and modify the protein’s viscoelastic stress relaxation behavior (4). Glycation of elastin was shown to enhance its binding to metal ions such as calcium, which may be related to the observed accelerated calcification of tissues in diabetic patients (3).
Elastin is composed of tropoelastin, which is a large, 72 kDa protein rich in glycine, proline, valine, and alanine (see Rosenbloom et al. (6), Anwar (7), and Urry (8)) for reviews on elastin and the elastic fiber). Additional amino acids, such as phenylalanine, leucine, and isoleucine, are present at smaller concentrations ranging from 2–5%. Serine, threonine, and tyrosine are present at yet smaller quantities (9). Tropoelastin molecules may covalently bond with one another and form desmosine or isodesmosine cross-links which are unique to elastin. Desmosine and isodesmosine are assembled from four lysine/allysine residues that form pyridinium, which is polar and believed to make the cross-linking sites hydrophilic. In elastin, these cross-linking sites are often flanked by repeating alanine motifs such as the pentamer [AAAAA]. Elastin is not soluble and does not crystallize and therefore is not a good candidate for structural studies by liquid-state magnetic resonance or x-ray crystallography. Nevertheless, much structural and dynamical information has been gleaned from both short MD simulations and NMR experiments on mimetic sequences such as the hydrophobic-domain VPGVG (10–16) and LGGVG (17,18). One notable characteristic of the mimetic VPGVG is that the force-extension curve (measured with an atomic force microscope) exhibits no mechanical hysteresis; the process of stretching and releasing these short segments was found to be completely reversible, providing evidence that the source of elasticity for this one motif of elastin is largely entropic (19). In agreement with these experiments, previously reported short molecular dynamics simulations of the mimetic VPGVG demonstrated that the changes in energy of the peptide upon stretching were negligible in comparison to changes in entropy (20). Other simulation and experimental studies, by Floquet et al., focused on the motif VGVAPG, which was shown to exhibit a type VIII β-turn spanning the GVAP sequence (21). Notably, their work also demonstrated that this peptide adapted a more folded structure when the solvent was changed from water to a less polar solvent, such as dimethylsulfoxide or urea.
Elastin is a peculiar elastomer in that it requires water to maintain resilience; dehydrating elastin results in a brittle solid. Early work by Lillie and Gosline demonstrated the effects of changing the solvent polarity, sample temperature, and pulling rate on the stress-strain behavior of elastin (5,22). The dynamics of water in elastin and the impact of water hydration on protein dynamics have been measured by Samouillan et al. using dielectric spectroscopy (23,24). Those works offered further insight into the dynamics of water in elastin and provided a direct measurement of the glassy-point transition temperature as a function of hydration. The demonstration that the presence of crystallizable water prevents motions of some 10 nm along the polypeptidic chains is significant. In addition, NMR relaxation times measured in deuterium-hydrated elastin point to the presence of two associated reservoirs of water within the elastic fiber that are observable on a timescale of a few hundred microseconds to 1–2 s (25). More recently, the exchange times for the various reservoirs were measured and the dynamics of the waters of hydration in elastin were studied using magnetic resonance methodology (26). Similar two-dimensional NMR measurements showed that the correlation time of tumbling motion of water decreases as the polymer is strained (27). These measurements give evidence that the entropy of localized water increases as the protein elongates and that localized water does not bear the entropic elastomeric force when elastin is strained.
In this work, we report on the macroscopic changes to elastin after glucose exposure. Together, the changes in stiffness and size are correlated to microscopic dynamical and structural changes of the protein measured by 13C magic-angle-spinning (MAS) spectroscopic and relaxation NMR measurements. In addition, we measured the dynamics and populations of water in glucose-exposed elastin resolved by two-dimensional 2H NMR relaxometry. This experimental technique makes use of a two-dimensional radio-frequency pulse sequence that correlates the NMR T1 and T2 relaxation times of an ensemble of nuclear spins. A particularly useful feature of the experimental method is that it allows for the differentiation of reservoirs of water resolved on the timescale of the relaxation measurements, based on dynamical characteristics of the nuclear spins. This powerful method has been applied to probe the distribution of water in complex porous systems including potato tissue (28), cement pastes (29), bovine nuchal ligament and aortic elastins (26), spider dragline silks (30), and water-saturated sedimentary rock (31). Here, the technique is employed to probe the distribution and dynamical characteristics of water and to provide insight into morphological changes of elastin after glucose exposure. Results from short molecular dynamics simulations are provided to add insight into dynamical and structural changes of a small elastin repeat, [VPGVG]5, an alanine pentamer, and in a desmosine or isodesmosine cross-link bonded to alanine. The changes in the retractive entropy and energy forces for the short segments in water or in a glucose solution are studied by simulation.
Materials and Methods
Sample preparation
Elastin from porcine thoracic aortas was isolated using 50 mg/mL cyanogen bromide (CNBr) in 70% formic acid solution for 19 h at room temperature with gentle stirring. The samples were then gently stirred for 1 h at 60°C, followed by 5 min of boiling to inactivate the CNBr (32). For the glucose-treated sample, purified tissue was incubated in a 2 M glucose solution (Fisher Scientific, Waltham, MA) and allowed to equilibrate at 37°C for 28 days. Amino acid analysis was performed by New England Peptide (Gardner, MA) on a sample of untreated elastin to assess the degree of purification. Results from the amino acid analysis are provided in Table S1 in the Supporting Material. The amino acid concentration measured after purification is in good agreement with values reported in the literature for human and bovine nuchal ligament elastin and indicates the purity of the starting samples (33). The untreated (control) sample refers to the same starting material, after purification, without glucose exposure. For both glucose-exposed samples and untreated samples, the tissues were wet and held in a bath of water for all measurements.
Mechanical testing
The experimental settings for the biaxial tensile testing and elastin assays are provided in greater detail in a previous study (4,34). Sample sizes were ∼2 cm × 2 cm × 1.2 mm for the mechanical testing. Equibiaxial tension tests were performed using a biaxial tensile tester controlled by means of a custom LabVIEW program (National Instruments, Austin, TX). Load cells captured the applied load and the position of marker dots, which were tracked with a CCD camera to measure strain in the two directions. Sandpaper tabs were attached to the top and bottom faces along the edges of the tissue samples with cyanoacrylate glue (Elmer’s Products, Columbus, OH). Sutures were then looped through the sandpaper fold and connected to the linear positioners. After preconditioning, eight cycles of equibiaxial tension were applied to capture the mechanical behavior. Data used for the analysis came from the eighth cycle, when the stress-versus-strain curves had become stable. To compare the effects of glucose treatment on the mechanical properties of elastin samples, averaged Cauchy stress versus true strain was obtained for the samples between 0 and 80 kPa. Stresses and strains from both the loading and unloading curves were averaged among samples. Experimental data were summarized with the mean and standard deviations from our measurements. Comparisons of the strains in both the longitudinal and circumferential directions were made between untreated and treated elastin samples using generalized estimating equations that take into account repeated measures (35). A two-tailed two-sample t-test, p < 0.05, was considered statistically significant. Statistical analysis was performed using the JMP statistical package (version 11.1.1, SAS Institute, Cary, NC).
13C NMR relaxation and spectroscopy
13C cross-polarization (CP) and direct-polarization (DP) experiments were performed on a Bruker Avance 750 MHz system (Billerica, MA) at 37°C using a 3.5 mm rotor and 10 kHz MAS. The rotors were sealed using compression-style rotor caps in all the studies. Sample temperature was regulated to within 1°C and the rotor spinning speed was regulated to within 5 Hz. For the CP experiments, a 2.5 ms ramp on the 1H channel was used. All 13C experimental data were acquired with ∼8 × 104 Hz of 1H TPPM decoupling (36). The acquisition time in all studies was 15 ms and the spectral width was set to 299.5 ppm. All data were processed using 25 Hz of Gaussian broadening and the 13C chemical shifts were referenced to adamantane (tetramethylsilane scale). For the 13C T1ρ relaxation experiments, spin-locking fields of 30 kHz and 59 kHz were used for the DP experiments on the untreated and glucose-treated samples. Spin locking fields of 32 kHz and 62 kHz were used for the CP experiments for the glucose-treated sample. All 13C T1ρ experiments made use of pulse durations ranging from 50 μs to 8.5 ms. In these relaxation measurements, the 13C carrier during the locking pulse was offset to either 35 ppm or 173 ppm for measuring the aliphatic or carbonyl relaxation time, respectively. In hydrated elastin, 13C T1 relaxation times are on the order of 1 s (27,37). All measurements in this study were therefore performed with a recycle time of 5 s.
2H NMR relaxation
The 2H T1-T2 experiments were run on a 200 MHz Varian Unity system (Palo Alto, CA) at 37°C. The same samples used in the 13C NMR studies were soaked in 2H2O for a duration of ∼24 h before experiments were run. In these two-dimensional relaxation measurements, the interpulse spacing in the CPMG train was 700 μs and the 2H π/2 pulse was ∼28 μs. Stroboscopic detection of 6000 echo peaks was used to measure the T2 relaxation time, and 100 logarithmically spaced points ranging from 1 ms to 10 s were sampled in the T1 dimension. To analyze the 2H T1-T2 relaxation data, we applied a fast two-dimensional inverse Laplace transform (ILT) algorithm, as described elsewhere (38).
Simulations
Molecular dynamics simulations were performed with GROMACS (39) using the GROMOS 53a6 force field (40). The simulations were allowed to equilibrate for 20 ns and used the SPC-216 water model (41). The peptides [VPGVG]5 and [AAAAA] were separately simulated at a temperature of 310 K. Additional simulations of isodesmosine and desmosine cross-links with two or three alanine residues bonded to two neighboring lysine molecules were also performed. This structure was chosen because lysine and alanine occur in repeating motifs that include KAAK or KAAAK in tropoelastin (9). A schematic representation of the desmosine and isodesmosine molecules used in the simulations is shown in Fig. S1. These cross-link simulations included the additional step of topology generation using a stand-alone topology builder (42). Simulations were performed both in water and in a 2 M glucose solution to match the experimental conditions in this study, and stretched simulations were performed to determine retractive forces. The topology of the glucose molecule was built as with the cross-link simulations and used for mixed-solvent GROMACS simulations. The peptides were terminated as neutral molecules, and the velocity-rescaling thermostat (43) was used for the simulations. These simulations ran for 20 ns, and the final frame was used as a starting structure for the stretched and unstretched simulations presented here. For the stretched studies, the peptides were first stretched for 2 ns ([VPGVG]5) or 1 ns ([AAAAA]) using an umbrella potential and a rate constant of 5000 kJ/mol/nm2. After this, the peptides were held for 4 ns with a constant force potential and a rate constant of 1000 kJ/mol/nm2. The unstretched simulations were performed for an additional 4 ns for [AAAAA] and 60 ns for [VPGVG]5 and these additional times were used for all calculations. Desmosine and isodesmosine simulations involved no stretching and only a single 100 ns simulation for each case. The Ramachandran maps from the alanine pentamer and alanine trimer in desmosine and isodesmosine made use of the final 1 ns of data from the simulations.
Results and Discussion
Mechanical studies of glucose-treated elastin
Fig. 1 shows representative changes in the Cauchy stress-versus-true-strain behavior of glucose-treated elastin. For these data, the Cauchy stresses, σ, were calculated based on plane stress and incompressibility assumptions given by
| (1) |
In the above expression, F is the applied load, λ is the ratio of the deformed length to the initial length, L0 is the initial length, and t is the thickness of the sample. Subscripts 1 and 2 correspond to the longitudinal and circumferential directions, respectively, of the tissue sample. The true strain, , is defined as
| (2) |
The hysteresis of a material under mechanical deformation is a characteristic of viscoelasticity and is proportional to the energy dissipated within a loading cycle (44). In previous studies, glucose treatment has been shown to increase the mechanical relaxation time (5) and also to induce more relaxation (4). We observe an increase in the hysteresis of the stress-strain behavior (Fig. 1) from in untreated elastin () to after glucose treatment () (the percentage shown reflects the change in the slope of the stress-strain curves during the loading and unloading process). For untreated elastin samples, the loading and unloading stress-versus-strain curves almost overlap, i.e., the hysteresis is very small. Note that the stress-strain curves for the glucose-treated samples along the longitudinal and circumferential directions almost overlap. The untreated elastin shows an anisotropic stress-strain response, where the circumferential direction is stiffer than the longitudinal direction. However, this anisotropic behavior is lost upon exposure to glucose. Fig. 2 shows that glucose-treated elastin samples are significantly stiffer than untreated samples () in both the longitudinal and circumferential directions. The observed increase in stiffness correlates well with the work by Lillie and Gosline, who reported an increase in the tensile storage and loss modulus after exposure to glucose (5). Elastin is essential for the elasticity of the arterial wall, so the changes in its viscoelastic characteristics and loss of anisotropy in the stress-strain behavior may have important physiological and pathological implications.
Figure 1.
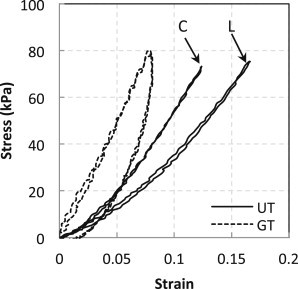
Representative plots of Cauchy stress versus true strain of untreated (UT) and glucose-treated (GT) elastin in the longitudinal (L) and circumferential (C) directions. Note that the Cauchy stress versus true strain curves for the glucose-treated sample overlap for both the longitudinal and circumferential directions and are therefore not labeled.
Figure 2.
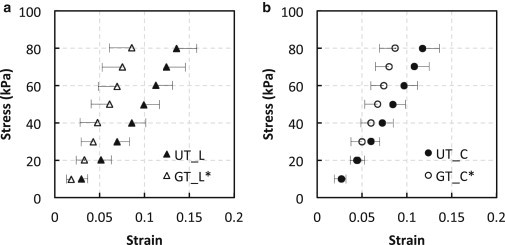
Averaged Cauchy stress versus true strain of untreated (UT) and glucose-treated (GT) elastin (n = 7) in the longitudinal (L) and circumferential (C) directions. One-sided error bars represent one standard deviation. ∗p < 0.05.
Exposing the elastin to glucose resulted in a decrease in the side lengths of the sample to of its original size along the longitudinal and along the circumferential direction. The thickness decreased to of its original dimensions (). The observed change in the macroscopic dimensions of the samples exposed to glucose is in good agreement with previously reported studies. Lillie and Gosline studied the swelling of pig thoracic aortas, purified by repeated autoclaving, in a 2 M glucose solution and reported a slight reduction in the mean swelling ratio (they defined the swelling ratio as the length of a piece of elastin in a given solution divided by the length of the same tissue in distilled water at 37°C). At higher glucose concentrations, Lillie and Gosline reported a further decrease in the swelling ratio (5). The macroscopic changes in tissue size presented here are also in good agreement with our previous work (4). Water is known to act as a plasticizer in the functionality of elastin, and the observed macroscopic reduction in tissue size suggests that the process of glucose exposure would be accompanied by water redistribution as well as structural and dynamical changes to the protein, as discussed below. The redistribution of water may be expected to modify somewhat the time-dependent mechanical characteristics of interstitial fluid flow in the elastin matrix or the dynamical and/or structural characteristics of the protein that provide its elastomeric attributes.
13C NMR chemical shifts and secondary structure of glucose-treated elastin
To probe microscopic dynamical and structural changes to elastin after glucose treatment, we studied 13C NMR chemical shifts using MAS methodology, as described in Materials and Methods. Two experiments were performed for each sample: a DP experiment, which allows observation of both mobile and rigid domains, and a CP experiment, wherein the polarization to 13C spins is transferred from all dipolar coupled 1H nuclei. The signal obtained in the CP experiments results solely from cross-polarized magnetization of dipolar coupled 1H nuclei.
Table 1 summarizes 13C chemical shifts and related secondary structures from values reported in the literature. The values presented include information from atomic coordinates in the Protein Data Bank and 13C NMR chemical-shift data reported for 40 proteins (45), as well as data from a protocol based on the joint probability of secondary structures tested on 36 proteins (46). The table also includes data collected for 13C-labeled Nephila clavipes dragline silk ((47) and data therein, including 13C chemical shifts from polypeptides with known secondary structures) and a secondary structure database of reference-corrected protein chemical shifts derived from the BioMagResBank (48). The 13C chemical shift data for the Cδ-isoleucine and Cγ-valine sites were obtained from an experimental study on a protected linear hexapeptide [Gly-Gly-X-Y-Gly-Gly] (49). Table 2 summarizes the results of the two samples studied in this work using values assigned in Table 1.
Table 1.
Ranges of the Cα, Cβ, and Cγ chemical shifts for the most abundant amino acids in elastin
| Assignment | α-helix (ppm) | β-sheet/turn (ppm) | Random coil (ppm) |
|---|---|---|---|
| Cβ-Ile | — | — | 11.2a |
| Cγ-Val | — | — | 18.4–19.2b |
| Cβ-Ala | 14.6–17.65 | 17.39–21.49 | 16.06–18.62 |
| Cβ-Ile | 34.75–37.05 | 36.18–40.24 | 34.50–38.64 |
| Cβ-Leu | 38.59–41.00 | 40.09–44.31 | 38.47–42.32 |
| Cβ-Phe | 35.72–38.70 | 38.10–41.59 | 35.77–39.73 |
| Cβ-Pro | 28.54–30.71 | 29.37–31.77 | 29.21–31.19 |
| Cβ-Thr | 65.96–68.35 | 67.01–71.23 | 66.76–69.75 |
| Cβ-Val | 28.97–30.51 | 30.32–33.90 | 29.22–32.74 |
| Cα-Ala | 49.00–54.18 | 47.90–51.31 | 49.21–52.78 |
| Cα-Gly | 42.50–46.31 | 41.50–44.69 | 42.20–44.86 |
| Cα-Leu | 54.59–57.05 | 51.05–53.69 | 51.36–54.94 |
| Cα-Phe | 57.21–61.01 | 53.32–56.54 | 53.26–58.30 |
| Cα-Pro | 62.71–64.87 | 59.87–62.31 | 60.51–63.09 |
| Cα-Val | 62.87–66.01 | 57.43–60.77 | 57.85–62.52 |
Shown are the maximum and minimum chemical shifts observed in previous studies (45–49,68). The maximum value was determined from the largest reported value plus its uncertainty and the minimum value from the smallest reported value minus its uncertainty. All values except those of Asakura et al. (45) were adjusted for the tetramethylsilane scale by subtracting 1.7 ppm (68), since the original references used 4,4-dimethyl-4-silapentane-1-sulfonic acid as the standard.
Values when the amino acid is followed by alanine.
Values when the amino acid is followed by proline.
Table 2.
Measured 13C chemical shifts and corresponding secondary structural assignments
| Assignment | Structure | ||
|---|---|---|---|
| Untreated sample | |||
| DP | CP | ||
| 11.9 ± 0.5 | 11.5 ± 0.5 | Cδ-Ile | RC |
| — | 17.9 | Cβ-Ala, Cγ-Val | β-sheet/turn or RC, RC |
| — | 17.2 | Cβ-Ala | α-helix or β-sheet/turn or RC |
| 18.3 ± 0.9 | 18.0 ± 0.5 | Cβ-Ala, Cγ-Val | β-sheet/turn or RC, RC |
| 19.0 ± 0.5 | 19.0 ± 0.5 | Cβ-Ala, Cγ-Val | β-sheet/turn, RC |
| 20.1 ± 0.5 | 20.1 ± 0.5 | Cβ-Ala, Cγ-Val | β-sheet/turn, RC |
| 22.5 ± 0.5 | 22.5 | — | — |
| 24.0 ± 0.5 | 23.7 | — | — |
| 25.7 ± 0.5 | 25.7 | — | — |
| 31.4 ± 0.9 | 31.4 ± 0.5 | Cβ-Val, Cβ-Pro | —, — |
| 37.8 ± 0.9 | 37.8 ± 0.5 | Cβ-Phe, Cβ-Ile | —, β-sheet/turn or RC |
| 41.0 ± 0.5 | — | Cβ-Phe, Cβ-Leu | β-sheet/turn, — |
| 44.2 ± 0.9 | 44.1 ± 0.5 | Cα-Gly, Cβ-Leu | —, β-sheet/turn |
| 49.2 ± 0.9 | — | Cα-Ala | β-sheet/turn or RC |
| 51.3 ± 0.7 | 51.6 ± 0.5 | Cα-Ala, Cα-Leu | β-sheet/turn or RC, β-sheet/turn |
| 53.8 ± 0.9 | — | Cα-Ala, Cα-Phe | α-helix or RC, RC or β-sheet/turn |
| 56.2 | — | Cα-Phe, Cα-Leu | β-sheet/turn or RC, α-helix |
| 58.0 ± 0.3 | — | Cα-Val, Cα-Phe | β-sheet/turn or RC, α-helix |
| 60.9 ± 0.5 | 60.8 ± 0.5 | Cα-Val, Cα-Pro | RC or β-sheet/turn, RC or β-sheet/turn |
| 61.9 ± 0.5 | 62.3 ± 0.5 | Cα-Val, Cα-Pro | RC or β-sheet/turn, — |
| 68.7 ± 0.5 | Cβ-Thr | β-sheet/turn or RC | |
| 71.2 ± 0.5 | Cβ-Thr | β-sheet/turn | |
| Glucose-treated sample | |||
| DP | CP | ||
| 11.9 ± 0.4 | 11.9 ± 0.5 | Cδ-Ile | RC |
| 16.9 ± 0.7 | 16.9 ± 0.7 | Cβ-Ala | RC or α-helix |
| 19.3 ± 0.4 | — | Cβ-Ala, Cγ-Val | β-sheet/turn, RC |
| 20.1 ± 0.4 | 20.1 ± 0.7 | Cβ-Ala, Cγ-Val | β-sheet/turn, RC |
| 22.5 ± 0.5 | 22.5 ± 0.4 | — | — |
| 24.0 ± 0.7 | 24.0 ± 0.7 | — | — |
| 25.7 ± 0.7 | 25.7 ± 0.9 | — | — |
| 31.1 ± 1.4 | 31.1 ± 1.4 | Cβ-Val, Cβ-Pro | —, — |
| 37.4 | 37.8 | Cβ-Phe, Cβ-Ile | —, β-sheet/turn or RC |
| 41.0 | 41.0 | Cβ-Phe, Cβ-Leu | β-sheet/turn, — |
| 42.4 | — | Cα-Gly, Cβ-Leu | —, β-sheet/turn or RC |
| 43.8 | 43.8 | Cα-Gly, Cβ-Leu | —, β-sheet/turn |
| 48.4 | 49.2 ± 0.7 | Cα-Ala | β-sheet/turn or RC |
| 50.9 | — | Cα-Ala | β-sheet/turn or RC |
| 53.8 ± 0.5 | Cα-Ala, Cα-Phe | RC or α-helix, β-sheet/turn or RC | |
| — | 58.0 | Cα-Val, Cα-Phe | β-sheet/turn or RC, α-helix |
Data are based on values in Table 1 for hydrated untreated and glucose-treated porcine aortic elastin under DP and CP conditions. RC, random coil; —, no signal was observed or no assignment could be made.
As shown in our amino acid analysis in Table S1, a well-known characteristic of elastin is the high abundance of alanine, glycine, proline, and valine residues that contribute to its assembly. Keeley and co-workers have analyzed the repeating motifs in elastin from genomic sequence data for 11 species of vertebrates (50). The pentameric unit VPGVG has been the focus of numerous experimental (10,13) and molecular dynamics studies (15,16,18,51) over the past 30 years. In human tropoelastin, this unit repeats nine times, whereas other glycine-rich pentamers, such as PGVGG or VGVAP, repeat six times. Alanine pentamers such as AAAAA repeat 14 times in human tropoelastin, whereas AAKAA and AAAKA repeat up to 11 times. The alanine-rich motifs of elastin frequently reside in close proximity to lysine in repeats such as KAAAK or KAAK (9). In elastin, oxidative deamination of three out of every four lysines yields desmosine or isodesmosine (52).
The spectra obtained under MAS conditions allowed for the assignment of Cα and Cβ aliphatic carbons from ∼16 ppm to ∼70 ppm (the tetramethylsilane scale). Methyl 13C NMR signals appear between 17 and 20 ppm, which previous studies of elastin and short elastin peptides have assigned to valine and alanine residues. Yao et al. assigned the peak at 19 ppm to the Cγ valine sites based on their results from a two-dimensional double quantum spectrum of Poly(Lys-25)[(VPGVG)4(VPGKG)]39 (14). Additional studies were carried out on the same peptide using 13C-13C and 15N-13C correlation experiments to resolve and assign isotropic chemical shifts of various sites. In that work, the Cβ-proline peak was observed at 30.5 ppm, and for the two valine residues, Val1 and Val4, chemical shifts of 31.3 and 30.1 ppm were reported. Shifts of 57.1 and 61.5 ppm were reported for the Cα-valine signals, and a shift of 60.8 ppm was reported for the Cα-proline (13). In a recent work, Pometum et al. reported that in bovine neck ligament elastin, the Cβ-proline and Cβ-valine chemical shifts were observed at 31.83 and 32.80 ppm, and the Cα chemical shifts for proline and valine occurred at 63.35 and 62.08 ppm, respectively (53). We measured a signal at ∼31 ppm in all samples studied, which we assigned to Cβ-valine or Cβ-proline. The Cα signals from valine and proline were also observable, except in the case of the glucose-treated sample, where they overlap with glucose signals (which appear in the range 70–80 ppm). In the untreated elastin sample, we observed signals at 60.9 and 61.9 ppm, which we assigned to either the Cβ-proline or Cβ-valine. In either case, based on the assignments in Table 1, these chemical shifts would point more to random coil or β-sheet/turn structures.
Fig. 3 shows the results from the 13C DP experiments from the two samples. In these spectra, no differences in the chemical shift of the Cα signal of glycine at ∼43 ppm were observed between the samples. This chemical shift does not point clearly to any well-defined structure, as the Cα-glycine chemical shifts for α-helical, β-spiral, and random coil structures overlap (see Table 1). The observed chemical shift agrees well with results of previous studies (14,53), discussed above, as well as a study of insoluble elastin synthesized in vitro with isotopically enriched glycine (37). However, the spectra show significant differences in resolution, with the untreated sample appearing narrower than the glucose-treated sample. Our interpretation of this finding is that there is a higher degree of structural heterogeneity revealed on the T2 timescale in the glucose-treated sample compared to the untreated sample. As discussed above, there does not appear to be a significant difference in Cβ-valine and Cβ-proline peaks at ∼30 ppm between the treated and untreated samples in terms of either the observed chemical shift values (Table 2) or the line widths (Fig. 3). However, the Cβ-alanine signals in the two samples appear markedly different. The Cβ-alanine signal in the glucose-treated sample (17 ppm) suggests a more α-helix-like structure, whereas that in the untreated sample (19 ppm) points to a random coil structure. The signals observed in Fig. 3 B2 at ∼62 ppm and between 70 and 80 ppm resulted from residual glucose present in the tissue. This was independently verified by measuring the 13C spectra from 2 M glucose (data not shown).
Figure 3.
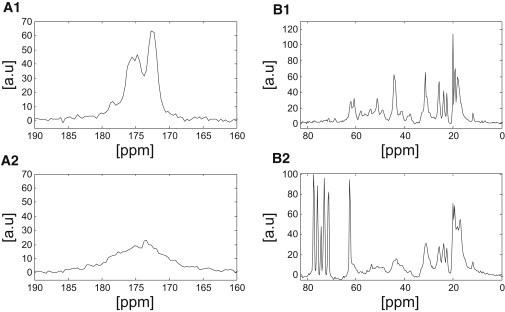
DP 13C NMR spectra of hydrated untreated (A1 and B1) and hydrated glucose-treated (A2 and B2) porcine aortic elastin samples. The peaks between 60 and 80 ppm in the glucose-treated samples arise from the glucose solution. Spectra correspond to the aliphatic region (B1 and B2) and the carbonyl region (A1 and A2). Differences are observed in the resolution of the various peaks between the samples, as discussed in the text. Note the different vertical scales.
Fig. 4 shows results from the 1H - 13C NMR CP experiments. These measurements indicate that the glucose-treated sample cross-polarizes significantly more than the untreated samples, pointing to more rigid structures and reduced dynamical characteristics. In addition, a chemical-shift difference is observed in the Cα- and Cβ-alanine signals between the glucose-treated and untreated samples, as was the case in the DP studies (Fig. 3). The Cβ-alanine signal at 17 ppm and the Cα-alanine signal at 54 ppm appear better resolved for the glucose-treated sample. As in the DP spectra of Fig. 3 discussed above, these observations again point to the presence of more α-helical characteristics in the alanine sites for this sample.
Figure 4.
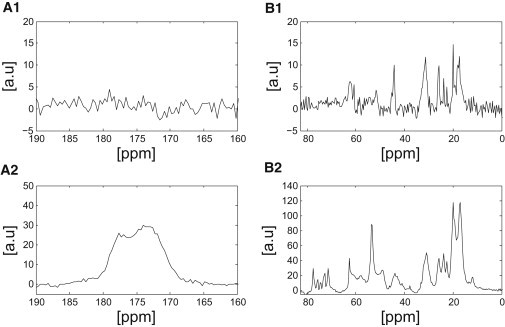
CP 13C NMR spectra of hydrated untreated (A1 and B1) and hydrated glucose-treated (A2 and B2) porcine aortic elastin samples. The peaks between 60 and 80 ppm in the glucose-treated samples arise from the glucose solution. Spectra correspond to the aliphatic region (B1 and B2) and the carbonyl region (A1 and A2). Differences are observed in the resolution of the various peaks between the samples as discussed in the text. Note the different vertical scales.
The CP data shown in Fig. 4 B2 indicate the presence of a glucose signal in the glucose-treated sample in the range 70–80 ppm and at 62 ppm. This may arise from a number of events that lead to anisotropic motion of the glucose molecules, which gives rise to inter- and/or intra-glucose 1H-13C dipolar couplings. The signature of a cross-polarized glucose signal may also indicate that elastin has been glycosylated via hydrogen bonds throughout the protein, at specific solvent-exposed sites, or covalently with the hydroxyl groups of tyrosine, threonine, or serine. As seen in Table S1, these amino acids comprise only ∼4.4% of the protein. Given our observations of the overall increased CP in the glucose-treated sample, it would appear more likely that the glucose has perturbed the water-protein interface throughout the protein. Cheng et al. performed MD simulations on RNase A linked to a single N-glycan and found that the presence of the glycan perturbs the local water hydrogen-bonding network, resulting in a burial of the hydrophobic surface and enhancement of protein folding (54). This effect would correlate with the observed reduction in the size of elastin treated with glucose, discussed earlier, and the increase in intensity of the CP signal, shown in Fig. 4. On the other hand, more recent simulations by Lu et al. show that glycan chains located at a specific site of hydrophilic amino acid residues of a β-barrel protein (which has 10 possible glycosylated variants) facilitate both collapse and rearrangement, whereas other glycan chains are observed to hinder the rearrangement of the protein (55). Below, we provide MD simulations on an elastin mimetic peptide, [VPGVG]5, and an alanine pentamer, AAAAA, as well as in desmosine and isodesmosine bonded to alanine. These simulations show how the presence of glucose modifies the water-peptide interface, as well as peptide dynamical and structural characteristics, thereby affecting both the entropy and energy contributions to retractive forces. Finally, we performed additional experiments of lyophilized glucose-treated and untreated elastin with CP (data not shown). Our data were similar to results published by Perry et al. in a study of the effects of hydration and temperature on elastin (56). These experiments did not allow for any useful chemical-shift assignment, because the backbone dynamics of elastin are quenched without the presence of a solvent, resulting in significant spectral overlap.
Protein dynamics and relaxation times of glucose-treated elastin
To further quantify protein dynamics, we measured 13C NMR relaxation times in the rotating frame. In these experiments, the 13C nuclear spin relaxation is dominated by the 1H-13C (I-S) dipolar interaction, and the 13C relaxation rate is given by (57,58)
| (3) |
where is the angle between and (here, ). The constant and are spin-lattice relaxation rates given by
| (4) |
and
| (5) |
In the above expressions, the spectral density is defined by , where x is a generalized order parameter that describes the amplitude of motion, denotes the angular rotational frequency of the rotor, and and are the proton and carbon Larmor frequencies. The constant quantifies the dipolar coupling between proton and carbon nuclear spins and is given by = . For our study, two different 13C locking fields, denoted , were applied to measure two different relaxation rates to determine the correlation time, , which quantifies the tumbling of 13C-1H internuclear vectors. For the glucose-treated sample, we conducted the same experiment with and without CP, whereas for the untreated sample, the measurements were only performed with DP, since the signal/noise ratio in CP was very weak.
Table 3 shows the results of the measured correlation times for each of the samples. The Cα-glycine, Cβ-valine, Cβ-proline, and Cα- and Cβ-alanine correlation times all appear larger for the glucose-treated sample than for the untreated sample. For the untreated sample, the average correlation time for the aliphatic carbons in aortic elastin was s, and that for the carbonyl was s. Both values are larger than those determined in a previous study in bovine nuchal ligament elastin that made use of a 13C spin-lattice relaxation time (T1) and a spin-lattice relaxation time in the rotating frame (T1ρ) in static samples. In unstrained nuchal ligament elastin, the average aliphatic correlation time measured was s (27) and that for the carbonyl was s (27) (the values in that article need to be divided by a factor of 2π, as they were given in units of s/cycle). Torchia and co-workers also have performed numerous NMR relaxation studies on elastin in various solvents, again in static conditions. In one study, they investigated the 13C NMR spin-lattice relaxation times of unstretched calf ligamentum nuchae in 0.15 M NaCl and found that ∼80% of the backbone carbonyl carbons exhibit a correlation time of ∼ s (estimated from a single relaxation time using Solomon’s equations) (59). This value is an order of magnitude smaller than that in the work presented here, but it appears to be in agreement with our previously reported value (27). In a later work, Lyerla and Torchia reported on the 13C correlation times of ligamentum nuchae elastin swollen by various solvents and found that the average backbone correlation time is reduced to s (60). They further suggested that glycine, proline, and valine residues are significantly more mobile than alanine residues, and that the water-swollen elastin is composed of a network of highly mobile chains, with the possible exception of the cross-linking sites. Fleming et al. also reported 13C-1H correlation times of purified labeled chick aorta in culture. Their correlation times ranged from 6 to s for all of the valine-labeled residues and from 5 × 10−8 to s for 75% of the alanine-labeled and 60% of the lysine-labeled resides; these values are somewhat closer to our measured values but still different by an order of magnitude (the values varied based on estimates that made use of the T1 relaxation time, the NMR line width, or the nuclear-Overhauser-effect signal intensity) (61). A likely cause for the differences in the correlation times measured in this work, as well as differences reported in previous studies, discussed above, may arise from the fact that we measured the relaxation times in the rotating frame. The relaxation time in the rotating frame has a different dependence on the spectral density than and is therefore sensitive to different timescales of motion.
Table 3.
Measured relaxation times for two different spin-locking fields for the samples
| Assignment | (ms) | (ms) | (s) |
|---|---|---|---|
| Untreated sample (DP) | = (Hz) | = (Hz) | |
| Cβ-Ala, Cγ-Val | |||
| 22.5 ppm | |||
| 25.7 ppm | |||
| Cβ-Val, Cβ-Pro | |||
| Cβ-Phe, Cβ-Ile | |||
| Cα-Gly, Cβ-Leu | |||
| Cα-Ala, Cα-Leu | |||
| C=O | |||
| Glucose-treated sample (DP) | = (Hz) | = (Hz) | |
| Cβ-Ala, Cγ-Val | |||
| Cβ-Ala, Cγ-Val | |||
| Cβ-Val, Cβ-Pro | |||
| Cα-Gly, Cβ-Leu | |||
| C=O | |||
| Glucose-treated sample (CP) | = (Hz) | = (Hz) | |
| Cβ-Ala, Cγ-Val | |||
| 22.5 ppm | |||
| 24.0 ppm | |||
| 25.7 ppm | |||
| Cβ-Val, Cβ-Pro | |||
| Cα-Ala, Cα-Phe | |||
| C=O |
Correlation times were determined from the ratio of the two times using Eq. 3. The applied locking field is determined by = .
Water dynamics and distribution in glucose-treated elastin
To probe the dynamics and distribution of water in each of the samples studied, we employed a T1-T2 two-dimensional relaxation method based on an ILT (38). Fig. 5 shows results from 2H T1-T2 relaxation experiments on deuterium-hydrated glucose-treated samples, as well as untreated porcine aortic elastin. Four reservoirs of water are resolved by the ILT algorithm for each sample. This experimental technique does not allow either association of the reservoir of water to a particular structural motif of elastin or association of reservoirs within the elastic fiber-water system; it only differentiates the relaxation characteristics of the 2H nucleus. The observation of four reservoirs of water in the elastin-water system agrees with previously reported measurements of water in bovine nuchal ligament and aortic elastin using the same experimental approach (27). Using the notation adopted in our earlier work, the four components in the 2H T1-T2 measurements were labeled , , β, and γ. The β and γ components are both characterized by relaxation times with T1 > T2 and T2 values shorter than those of and and therefore indicate comparatively more anisotropic motion. The peak denoted corresponds to bulk water (this was confirmed by simply running the same experiment on a sample of 2H2O). Blotting the hydrated elastin samples with a kimwipe (data not shown) suppresses both the and components in the 2H T1-T2 map. Thus, the peak denoted likely represents water between elastic fibers. In the remainder of this section, we therefore focus the discussion on the population and dynamics of the two components denoted β and γ as resolved by the two-dimensional relaxation method.
Figure 5.
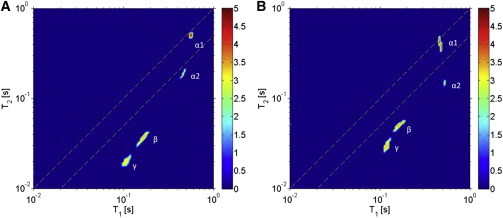
T1-T2 results from untreated (A) and glucose-treated (B) porcine aortic elastin at 37°C (intensity, indicated by the colorbar at right, is shown on a logarithmic scale). Four distinguishable peaks are observed in each sample, denoted by , , β, and γ. Differences in the relative populations of water in the assigned γ and β regions are observed between the samples, as discussed in the text. The numerical values of the T1 and T2 times and the relative intensities are provided in Table 4. To see this figure in color, go online.
Because the 2H-2H and 1H-2H nuclear dipolar couplings are negligible compared to the quadrupolar interaction, the dominant relaxation pathway for the 2H nucleus is quadrupolar to a good approximation. In this situation, the T1 and T2 relaxation times may be expressed as (62)
| (6) |
and
| (7) |
In the above equations, the constant is the effective quadrupolar coupling constant, given by
| (8) |
where is a motional averaging parameter. The spectral density is given by . The formulation of the above expressions assumes that the motion of the water molecule can be divided into fast oscillatory motions and slower diffusional processes. For short times, the orientational motion of the water molecule consists of fast librations about an equilibrium orientation in a random network of surrounding water (62). In our system, this network includes protein atoms. On a much longer timescale relative to the reorientation motion, the molecule will undergo diffusive motion, resulting in a rearrangement of the surrounding water and the protein atoms. The two motions are assumed to be separable, so that the cross correlation between the two relaxation pathways is negligible. The correlation time, , here quantifies the tumbling of the quadrupolar moment of the 2H nucleus with the electric field gradient and is intramolecular in origin. Using the measured T1 and T2 relaxation times, the correlation times for the tumbling motion of the water molecule in the two respective reservoirs β and γ were determined using Eqs. 6 and 7 and are tabulated in Table 4. The error bars shown in the table in each case were propagated from the distribution of the T1 and T2 values in the two-dimensional map. The correlation times indicate that the tumbling nature of water across the samples is similar, but that the γ component experiences less tumbling than the β component in both samples. Although changes in the protein dynamics were observed after glucose exposure, these changes did not alter the tumbling correlation time of 2H nuclei of 2H20.
Table 4.
Experimental 2H relative signal intensities, relaxation, and correlation times for the β and γ water components in purified porcine aortic elastin at 37°C
| Untreated sample | Glucose-treated sample | |
|---|---|---|
| γ component | ||
| (ms) | ||
| (ms) | ||
| (ns) | ||
| β component | ||
| (ms) | ||
| (ms) | ||
| (ns) | ||
| Signal intensity per unit dry sample mass (AU/g) | ||
| 1.18 | 2.32 | |
| γ | 0.43 | 1.15 |
| β | 0.75 | 1.17 |
Correlation times were determined using Eqs. 6 and 7. The uncertainties are determined from the distribution in the - map. The table also includes the signal intensity of each reservoir and the sum of the intensity in γ and β, determined from the integrated area in the two-dimensional ILT map per unit dry sample mass (AU/g). See Fig. 5 for denotation of β and γ water components.
We measured the concentration of water from the integrated intensity in the two-dimensional ILT map shown in Fig. 5 relative to the dry lyophilized sample weight (shown as arbitrary units per gram of sample (AU/g)). Note that the intensity in Fig. 5 is on a logarithmic scale (see color key). The glucose-treated sample has the highest concentration of the γ component (1.15 AU/g), which exhibits slower tumbling dynamics than the β component. The observed increase in water concentration in the γ reservoir for the glucose-treated sample appears to be correlated with the observed reduction in the size of this sample, discussed previously. The macroscopic reduction in size of the glucose sample may have resulted from a complex folding of the protein, which could lead to the presence of more structural features that give rise to water dynamics exhibiting characteristics of the γ reservoir (which has the larger correlation time). The structural changes, however, also result in an increase in the β water component for the glucose-treated sample relative to that for the untreated sample. Thus, the changes after exposure to glucose appear to alter the morphology of elastin, resulting in changes in the populations of both reservoirs of water revealed on the T1 and T2 timescale (milliseconds to seconds). Previous works have demonstrated the importance of hydration water to the resilience of elastin. For example, a 13C NMR work by Perry et al. demonstrated that lyophilized elastin exhibited reduced or quenched dynamics similar to those observed for frozen hydrated elastin (56). More recently, Samouillan et al. probed the dynamics of water and protein backbone motions in hydrated elastin by differential scanning calorimetry (24). The measurements from that study reflect the effect of water on the viscoelastic properties of elastin, through the analysis of the glass transition temperature, and demonstrate that noncrystallizable water linked to the polar atoms of the chain by hydrogen bonds plays a crucial role in increasing the mobility of elastin in the relaxed state. Although our measurements of water in glucose-treated elastin appear to indicate the presence of more water in both of the reservoirs, revealed by NMR relaxation, this does not result in an increase in mobility of the glucose-treated sample (measured per unit of dry sample mass, Table 4). Evidently, the presence of glucose alters the structural and dynamical characteristics of the protein, resulting in a change in its macroscopic mechanical characteristics.
Macroscopic and microscopic changes of elastin under glucose exposure
The total elastomeric restoring force (f) of a material is the result of an entropic () and an internal () energy change, (63). For an ideal elastomer driven solely by entropic changes, = 0 and . For natural rubber, the ratio is 0.18, and for elastin, it is ∼0.26 (64) (for a polypeptide consisting of [VPGVG]n segments, a value of ∼0.15 has been reported by Urry and co-workers (10)). One key finding in this work is the large mechanical hysteresis in the stress-strain curve of the glucose-treated sample, shown in Fig. 1. As discussed earlier, this is a characteristic of a solid that loses energy to its surroundings upon deformation. The data shown in this figure suggest either a change in interaction energy of elastin molecules at or near desmosine and isodesmosine sites or changes through intrachain and/or interchain interactions. An additional change in energy may have resulted from changes in the interactions with glucose and/or surrounding water. Although many of the well-resolved lines in our 13C NMR spectra were similar across the samples, differences were observed at the alanine sites, which are often in close proximity to desmosine and isodesmosine motifs. However, our 1H-13C NMR CP data (Fig. 4) and relaxation measurements showed that the dynamics of the protein appeared reduced in the glucose-treated sample, not only at a single site but throughout the aliphatic region. An additional mechanism for the observed increase in stiffness of the glucose-treated sample, then, is that dynamical changes throughout the protein change both the entropic and possibly the energetic contributions to the elastomeric force.
One model for elasticity proposed by Urry and co-workers, termed the librational entropic mechanism (65), involves the amplitude of librational motion being damped, resulting in a decrease in the overall entropy of the protein. In the librational entropy mechanism, atomic displacements are modeled by a harmonic oscillator of frequency , whose entropy is given by
| (9) |
In this treatment, the entropy of the system of atoms is determined by superposition over all atoms in the system. A well-known result from statistical mechanics of a harmonic oscillator is that a low-frequency mode has larger entropy than a higher-frequency mode. For a system that exhibits low-frequency vibrations, a change, , results in a larger fractional change in entropy, , in comparison to the same change in frequency of a system that exhibits high-frequency vibrations. If the only changes to the protein after glucose exposure are dynamical in nature, the larger correlation times observed in the glucose-treated sample would suggest comparatively smaller vibrational, librational, and rotational motion and higher entropy relative to the untreated samples. We note, however, that it is the change in entropy divided by the change in length that gives rise to an entropic force, . In addition, the changes in dynamics of the protein would also modify its internal energy and interaction with glucose and/or surrounding water. The changes in energy upon elongation add an additional contribution to the total force.
To give insight into the changes in the entropic and energetic forces after glucose exposure, we performed simulations of the motif [VPGVG]5 and an alanine pentamer. The quasiharmonic approach allows for an estimation of the peptide entropy based on atomic displacements. The entropy of the system may be determined from the equation (66)
| (10) |
where values come from the eigenvalues of the mass-weighted covariance matrix of the coordinate fluctuations σ, , and the sum is over all nonzero eigenvalues. Table 5 provides physical characteristics of the peptides in water and in glucose solution. The frequency of atomic displacements was determined using 4 ns of simulation (60 ns for unstrained [VPGVG]5). We observed that the entropy reached an asymptotic value as a function of sampling time, which is reported in Table 5. Fig. S2 shows the entropy versus simulation time under strained and unstrained conditions for both the glucose-treated and untreated peptides. A similar approach using the asymptotic value of the entropy determined in simulation was applied by Harris and Laughton to their study of the DNA sequences d(GC)30 and d(AT)30 (67) and recently by us in a simulation study of the elastin mimetic peptides VPGVG and LGGVG (18). Fig. S2 indicates that the entropy converges for either the [VPGVG]5 or the AAAAA motif; given that entropy is a measure of the number of configurations, these graphs indicate that the structural and dynamical information for either peptide from the simulations can be determined over the timescales shown (60 ns for [VPGVG]5 in the relaxed state, 4 ns for the stretched VPGVG5 peptide, and 4 ns for the stretched or relaxed AAAAA peptide.).
Table 5.
Simulated characteristics of [VPGVG]5 and AAAAA under strained and unstrained (relaxed) conditions in glucose or water
| Rg (nm) | Water-peptide energy (kJ/mol) | Peptide-peptide energy (kJ/mol) | Peptide-glucose energy (kJ/mol) | Entropy (J/(mol K)) | RMSF (nm) | Number of water molecules within 0.30 nm of peptide | Number of hydrogen bonds with water | Number of hydrogen bonds with glucose | |
|---|---|---|---|---|---|---|---|---|---|
| [VPGVG]5 | |||||||||
| 2 M glucose (strained) | −1126 | −314 | −938 | 1055 | |||||
| 2 M glucose (relaxed) | −847 | −740 | −1060 | 2534 | |||||
| Water (strained) | −1756 | −314 | — | 1152 | — | ||||
| Water (relaxed) | −1114 | −939 | — | 3500 | — | ||||
| AAAAA | |||||||||
| 2 M glucose (strained) | −230 | −86 | −224 | 161 | |||||
| 2 M glucose (relaxed) | −226 | −124 | −221 | 550 | |||||
| Water (strained) | −382 | −85 | — | 163 | — | ||||
| Water (relaxed) | −377 | −126 | — | 564 | — | ||||
Simulations were performed in water or 2 M glucose solution. The radius of gyration (Rg) is the RMS distance between the center of gravity of the peptides and their ends. Also shown are the accessible nonbonded energies between the peptides and water or glucose and the intrapeptide energy. The Coulomb potential includes a cutoff distance set to 0.9 nm and the long-range Coulomb energies are not accessible. RMSF is for fluctuations only in the Cα carbons of the peptides. Finally, we show the number of water molecules within 0.30 nm of the peptides and the number of hydrogen bonds for the peptide with water and with glucose. The radii of gyration, the RMSF values, and the numbers of water molecules are computed from data in the final 1 ns of the simulation. The determination of the entropy, using the quasiharmonic approach, made use of 4 ns (or 60 ns for relaxed [VPGVG]5 only) of simulation time with the entropy using the whole window reported. Details of the water model are provided in Materials and Methods.
As shown in Table 5, the root mean-square fluctuation (RMSF) of Cα for the [VPGVG]5 peptide in unstrained conditions in the glucose solution is smaller than that of the same peptide in water only. The changes in dynamics may be due to hydrogen bonding with the glucose molecule, which is also recorded in Table 5. This reduced RMSF after glucose exposure correlates well with the findings of our CP spectra and the measured correlation times. The strained peptides have more hydrogen bonds with water, since they are unfolded and are more accessible to the water molecules. The entropy is also larger for the unstretched peptides, as expected given their larger configurational entropy compared with the extended peptides. For [VPGVG]5, a significant energy contribution arises from interactions with glucose. The additional energy contribution, as discussed below, provides a partial explanation for the stiffening observed in glucose-exposed elastin.
Table 6 gives details of the entropic (fs = −TΔS/Δr), energy (fe = ΔU/Δr), and total forces () from accessible nonbonded interactions for the peptides. Note that the value of for the peptides in 2 M glucose is different from that in water, because the starting structures are different (for example, the VPGVG motif in glucose has a slightly larger radius of gyration). Both of the glucose-treated peptides exhibit a smaller entropic force, consistent with a smaller configurational space due to limited folding. Also shown are the accessible nonbonded energy contributions from Lennard-Jones and Coulomb interactions (the long-range Lennard-Jones potentials and short-range contributions for both, but without the inaccessible long-range Coulomb energy). The ratio for the [VPGVG]5 simulations with glucose as an added solvent is much larger than when the motif is only in water.
Table 6.
Simulation results for the retractive forces of a [VPGVG]5 and AAAAA peptide
| End-to-end displacement Δr (Å) | Entropic force (kJ/mol) | Energy force (kJ/mol) | Total force (kJ/(mol Ǻ)) | |
|---|---|---|---|---|
| [VPGVG]5 | ||||
| Water | 89.4 | 8.1 | −0.2 | 8.0 |
| 2 M glucose | 72.7 | 6.3 | 3.7 | 10.0 |
| AAAAA | ||||
| Water | 5.5 | 22.7 | 6.7 | 29.3 |
| 2 M glucose | 8.5 | 14.1 | 3.5 | 17.7 |
Entropic force and energy forces are computed from the values in Table 5. Entropic force is given by (T = 310 K) and energy force by .
Fig. 6 shows the Ramachandran maps for the alanine pentamer and for AAA alanine residues in desmosine and isodesmosine. In each image, the integrated intensity of the entire map is scaled to 1. In 2 M glucose, the MD simulations show that the isodesmosine and desmosine Ramachandran maps are unchanged in the presence of glucose, whereas a structural change is evident in the alanine pentamer. The structural changes in the alanine pentamer point to an α-helix in 2 M glucose, which appears to agree with what we observed in experiment. As a check of the convergence of the desmosine and isodesmosine simulations, we plotted the RMSD of the Cα in either 2 M glucose or water for either desmosine or isodemsosine (Fig. S3). The Ramachandran maps from the last 1 ns of a 100 ns or 20 ns simulation were very similar (data not shown).
Figure 6.
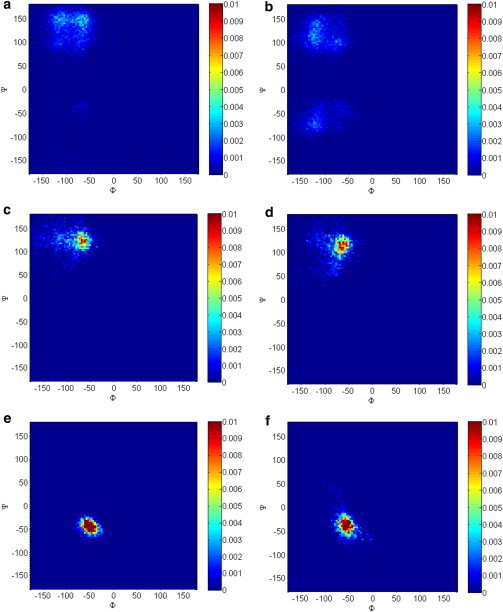
Ramachandran angles for the samples in water (a, c, and e) and 2 M glucose (b, d, and f). Samples included AAAAA (a and b), desmosine with alanine (c and d), and isodesmosine residues with alanine (e and f) (alanine Ramachandran angles are shown). The angles were calculated using the final 1 ns of the 20 ns simulations (images are shown in color). Note that for AAAAA in glucose, there is a change or increase from β-spiral to α-helical, consistent with the experimental NMR results. A schematic representation of the desmosine and isodesmosine molecules used in the simulations is shown in Fig. S1. To see this figure in color, go online.
The alanine pentamer behaves differently from a purely entropic elastomer, because its energy-force contribution to the total force is significant in either glucose or water. However, for the VPGVG motif, the energy contribution to the retractive force is close to zero in water (see Table 6). Most notably, after glucose exposure the total retractive force for AAAAA is reduced from 29.3 to 17.7 kJ/(mol Å), whereas for the [VPGVG]5 motif the retractive force increases from 8.0 to 10.0 kJ/(mol Å). These simulations therefore suggest that the observed stiffening in glucose-treated elastin arises at least partially from a solvent-peptide energetic contribution to the retractive forces of hydrophobic domains such as VPGVG, and not from the polyalanine domains.
One might speculate that the solvent-peptide energetic contribution to the retractive force in VPGVG may also be the cause of the observed viscoelasticity in glucose-exposed elastin (refer to Fig. 1). However, these energetic contributions are expected to be recoverable; any changes to the peptide-solvent energy (water or glucose) lost or gained upon deformation would be recovered upon release and would not give rise to viscoelastic behavior. A more likely cause for this behavior, as well as for the loss of anisotropy in the stress-strain behavior, is from interchain interactions occurring on a more macroscopic scale. Although our MD simulations do not offer insight into these effects, signatures of architectural changes were revealed in the redistribution of water in glucose-exposed elastin.
Conclusions
We report here on the macroscopic mechanical behavior and microscopic dynamical and structural modifications of porcine aortic elastin after glucose exposure. Mechanical stress-strain testing indicates that glucose-treated elastin is stiffer than control samples (with no exposure to glucose). In addition, glucose-treated samples exhibit a large hysteresis upon loading and unloading compared to the control. The observed hysteresis in the stress-strain behavior of glucose-treated elastin is a trademark signature of a loss of energy upon deformation. Our two-dimensional 2H T1-T2 measurements show the presence of four reservoirs of water in each of the samples studied and demonstrate that the glucose-treated sample has more overall water per unit of dry sample mass compared to the control. The two-dimensional 2H T1-T2 measurements also indicate a difference in the population of the different reservoirs of water in the samples studied, although the measured correlation times for tumbling motion were the same. The 13C MAS NMR spectra show that glucose-treated elastin cross-polarizes with higher efficiency compared to the untreated samples, indicating the presence of more rigid structural motifs in this sample. Our measurements also reveal a difference in the sites resolved by CP across the samples; for example, the peak at 53.4 ppm in the glucose-treated elastin assigned to the Cα-alanine peak cross-polarizes more efficiently than in the untreated samples. We observe a glucose signal in the CP spectra of the glucose-treated elastin, suggesting that the dynamics of the glucose molecule are restricted and/or anisotropic. 13C relaxation measurements allowed us to determine the correlation time of 13C-1H internuclear vectors; glucose-treated elastin has on average the largest correlation times of the two samples studied, pointing to slower dynamics and more rigid structural motifs. Molecular dynamics simulations reveal that the VPGVG repeat in water experiences an almost entirely entropic restoring force upon stretching, whereas in a 2 M glucose solution, the relative entropic contribution is smaller, indicating that the glucose degrades the ideal nature of this motif. This is consistent with the experimental stress-strain measurements reported, and in simulations, the folding of the VPGVG repeat is significantly affected by glucose. However, changes in the alanine pentamer in glucose are different; the sum of entropic and energetic contributions to the retractive force appears smaller than that observed in water. These simulations suggest that the observed stiffening arises from an energetic contribution to the retractive force in hydrophobic domains of the protein. Finally, in simulations of AAAAA there is an increase in the α-helical nature of the alanine peptides exposed to glucose, consistent with the NMR data.
Author Contributions
M.S. and K.B. performed NMR measurements and analysis and contributed to writing the manuscript. Y.W. and Y.Z. performed mechanical measurements and contributed to writing the manuscript. S.W.M. performed molecular dynamics simulations and analysis of these data and contributed to writing the manuscript. G.S.B. coordinated the study, performed NMR measurements and analysis, molecular dynamics simulations, and analysis, and contributed to writing the manuscript.
Acknowledgments
The authors thank Boris Itin, Antony Papaioannou, and Ivan Sergeyev for assistance in the NMR experiments and for useful discussions and Yi-Qiao Song of Schlumberger-Doll Research for allowing us to implement the ILT algorithm. G.S.B. is a member of the New York Structural Biology Center.
G.S.B. acknowledges support from the National Institutes of Health under award number 2SC1GM086268. Y.Z. acknowledges support from the National Science Foundation under award number CMMI 1100791 and the National Institutes of Health under award number R01HL098028. The content of this article is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Collection of data at the New York Structural Biology Center was made possible by a grant from NYSTAR. This research was supported, in part, by a grant of computer time from the City University of New York High Performance Computing Center under National Science Foundation grants CNS-0855217, CNS-0958379, and ACI-1126113.
Supporting Material
References
- 1.Konova E., Baydanoff S., Velkova A. Age-related changes in the glycation of human aortic elastin. Exp. Gerontol. 2004;39:249–254. doi: 10.1016/j.exger.2003.10.003. [DOI] [PubMed] [Google Scholar]
- 2.Sims T.J., Rasmussen L.M., Bailey A.J. The role of glycation cross-links in diabetic vascular stiffening. Diabetologia. 1996;39:946–951. doi: 10.1007/BF00403914. [DOI] [PubMed] [Google Scholar]
- 3.Winlove C.P., Parker K.H., Bailey A.J. Interactions of elastin and aorta with sugars in vitro and their effects on biochemical and physical properties. Diabetologia. 1996;39:1131–1139. doi: 10.1007/BF02658498. [DOI] [PubMed] [Google Scholar]
- 4.Zou Y., Zhang Y. The biomechanical function of arterial elastin in solutes. J. Biomech. Eng. 2012;134:071002. doi: 10.1115/1.4006593. [DOI] [PubMed] [Google Scholar]
- 5.Lillie M.A., Gosline J.M. Swelling and viscoelastic properties of osmotically stressed elastin. Biopolymers. 1996;39:641–652. doi: 10.1002/(sici)1097-0282(199611)39:5<641::aid-bip3>3.0.co;2-w. [DOI] [PubMed] [Google Scholar]
- 6.Rosenbloom J., Abrams W.R., Mecham R. Extracellular matrix 4: the elastic fiber. FASEB J. 1993;7:1208–1218. [PubMed] [Google Scholar]
- 7.Anwar R.A. Elastin: A brief review. Biochem. Educ. 1990;18:162–166. [Google Scholar]
- 8.Urry D.W. What is elastin; what is not. Ultrastruct. Pathol. 1983;4:227–251. doi: 10.3109/01913128309140793. [DOI] [PubMed] [Google Scholar]
- 9.Debelle L., Alix A.J. The structures of elastins and their function. Biochimie. 1999;81:981–994. doi: 10.1016/s0300-9084(99)00221-7. [DOI] [PubMed] [Google Scholar]
- 10.Urry D.W. Entropic elastic processes in protein mechanisms. I. Elastic structure due to an inverse temperature transition and elasticity due to internal chain dynamics. J. Protein Chem. 1988;7:1–34. doi: 10.1007/BF01025411. [DOI] [PubMed] [Google Scholar]
- 11.Urry D.W. Free energy transduction in polypeptides and proteins based on inverse temperature transitions. Prog. Biophys. Mol. Biol. 1992;57:23–57. doi: 10.1016/0079-6107(92)90003-o. [DOI] [PubMed] [Google Scholar]
- 12.Urry D., Parker T. Mechanics of elastin: molecular mechanism of biological elasticity and its relationship to contraction. In: Linke W.A., Granzier H.L., Kellermayer M., editors. Mechanics of Elastic Biomolecules. Springer; Dordrecht, The Netherlands: 2003. pp. 543–559. [PubMed] [Google Scholar]
- 13.Hong M., Isailovic D., Conticello V.P. Structure of an elastin-mimetic polypeptide by solid-state NMR chemical shift analysis. Biopolymers. 2003;70:158–168. doi: 10.1002/bip.10431. [DOI] [PubMed] [Google Scholar]
- 14.Yao X.L., Conticello V.P., Hong M. Investigation of the dynamics of an elastin-mimetic polypeptide using solid-state NMR. Magn. Reson. Chem. 2004;42:267–275. doi: 10.1002/mrc.1330. [DOI] [PubMed] [Google Scholar]
- 15.Li B., Alonso D.O., Daggett V. The molecular basis for the inverse temperature transition of elastin. J. Mol. Biol. 2001;305:581–592. doi: 10.1006/jmbi.2000.4306. [DOI] [PubMed] [Google Scholar]
- 16.Li B., Daggett V. Molecular basis for the extensibility of elastin. J. Muscle Res. Cell Motil. 2002;23:561–573. doi: 10.1023/a:1023474909980. [DOI] [PubMed] [Google Scholar]
- 17.Ohgo K., Niemczura W.P., Kumashiro K.K. Heterogeneity in the conformation of valine in the elastin mimetic (LGGVG)6 as shown by solid-state 13C NMR SPEctroscopy. Biomacromolecules. 2006;7:3306–3310. doi: 10.1021/bm0607168. [DOI] [PubMed] [Google Scholar]
- 18.Huang J., Sun C., Boutis G.S. On the inverse temperature transition and development of an entropic elastomeric force of the elastin mimetic peptide [LGGVG]3, 7. J. Chem. Phys. 2012;136:085101. doi: 10.1063/1.3685454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Urry D.W., Hugel T., Parker T. Elastin: a representative ideal protein elastomer. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2002;357:169–184. doi: 10.1098/rstb.2001.1023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chang D., Urry D. Polypentapeptide of elastin: damping of internal chain dynamics on extension. J. Comput. Chem. 1989;10:850–855. [Google Scholar]
- 21.Floquet N., Héry-Huynh S., Alix A.J. Structural characterization of VGVAPG, an elastin-derived peptide. Biopolymers. 2004;76:266–280. doi: 10.1002/bip.20029. [DOI] [PubMed] [Google Scholar]
- 22.Lillie M.A., Gosline J.M. The viscoelastic basis for the tensile strength of elastin. Int. J. Biol. Macromol. 2002;30:119–127. doi: 10.1016/s0141-8130(02)00008-9. [DOI] [PubMed] [Google Scholar]
- 23.Samouillan V., Tintar D., Lacabanne C. Hydrated elastin: dynamics of water and protein followed by dielectric spectroscopies. Chem. Phys. 2011;385:19–26. [Google Scholar]
- 24.Samouillan V., André C., Lacabanne C. Effect of water on the molecular mobility of elastin. Biomacromolecules. 2004;5:958–964. doi: 10.1021/bm034436t. [DOI] [PubMed] [Google Scholar]
- 25.Ellis G.E., Packer K.J. Nuclear spin-relaxation studies of hydrated elastin. Biopolymers. 1976;15:813–832. doi: 10.1002/bip.1976.360150502. [DOI] [PubMed] [Google Scholar]
- 26.Sun C., Boutis G.S. Measurement of the exchange rate of waters of hydration in elastin by 2D T2-T2 correlation nuclear magnetic resonance spectroscopy. New J. Phys. 2011;13:2–16. doi: 10.1088/1367-2630/13/2/025026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sun C., Mitchell O., Boutis G.S. NMR studies of localized water and protein backbone dynamics in mechanically strained elastin. J. Phys. Chem. B. 2011;115:13935–13942. doi: 10.1021/jp207607r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hills B., Costa A., Wright K. T1-T2 NMR correlation studies of high-pressure-processed starch and potato tissue. Appl. Magn. Reson. 2005;28:13–27. [Google Scholar]
- 29.McDonald P.J., Korb J.-P., Monteilhet L. Surface relaxation and chemical exchange in hydrating cement pastes: a two-dimensional NMR relaxation study. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;72:011409. doi: 10.1103/PhysRevE.72.011409. [DOI] [PubMed] [Google Scholar]
- 30.Ukpebor O.T., Shah A., Boutis G.S. Inverse temperature transition of elastin like motifs in major ampullate dragline silk: MD simulations of short peptides and NMR studies of water dynamics. Soft Matter. 2014;10:773–785. doi: 10.1039/C3SM52001C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kleinberg R., Farooqui S., Horsfield M. T1/T2 ratio and frequency dependence of NMR relaxation in porous sedimentary rocks. J. Colloid Interface Sci. 1993;158:195–198. [Google Scholar]
- 32.Lu Q., Ganesan K., Vyavahare N.R. Novel porous aortic elastin and collagen scaffolds for tissue engineering. Biomaterials. 2004;25:5227–5237. doi: 10.1016/j.biomaterials.2003.12.019. [DOI] [PubMed] [Google Scholar]
- 33.Mecham R.P. Methods in elastic tissue biology: elastin isolation and purification. Methods. 2008;45:32–41. doi: 10.1016/j.ymeth.2008.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zou Y., Zhang Y. An experimental and theoretical study on the anisotropy of elastin network. Ann. Biomed. Eng. 2009;37:1572–1583. doi: 10.1007/s10439-009-9724-z. [DOI] [PubMed] [Google Scholar]
- 35.Liang K.-Y., Zeger S. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73:13–22. [Google Scholar]
- 36.Bennett A.E., Rienstra C.M., Griffin R.G. Heteronuclear decoupling in rotating solids. J. Chem. Phys. 1995;103:6951–6958. [Google Scholar]
- 37.Perry A., Stypa M.P., Kumashiro K.K. Observation of the glycines in elastin using 13C and 15N solid-state NMR spectroscopy and isotopic labeling. J. Am. Chem. Soc. 2002;124:6832–6833. doi: 10.1021/ja017711x. [DOI] [PubMed] [Google Scholar]
- 38.Song Y.-Q., Venkataramanan L., Straley C. T1-T2 correlation spectra obtained using a fast two-dimensional Laplace inversion. J. Magn. Reson. 2002;154:261–268. doi: 10.1006/jmre.2001.2474. [DOI] [PubMed] [Google Scholar]
- 39.Pronk S., Páll S., Lindahl E. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics. 2013;29:845–854. doi: 10.1093/bioinformatics/btt055. http://bioinformatics.oxfordjournals.org/content/29/7/845 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Oostenbrink C., Villa A., van Gunsteren W.F. A biomolecular force field based on the free enthalpy of hydration and solvation: the GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 2004;25:1656–1676. doi: 10.1002/jcc.20090. [DOI] [PubMed] [Google Scholar]
- 41.Teleman O., Jönsson B., Engström S. A molecular dynamics simulation of a water model with intramolecular degrees of freedom. Mol. Phys. 1987;60:193–203. [Google Scholar]
- 42.Malde A.K., Zuo L., Mark A.E. An automated force field topology builder (ATB) and repository: version 1.0. J. Chem. Theory Comput. 2011;7:4026–4037. doi: 10.1021/ct200196m. [DOI] [PubMed] [Google Scholar]
- 43.Bussi G., Donadio D., Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007;126:014101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- 44.Humphrey J. Review Paper: Continuum biomechanics of soft biological tissues. Proc. R. Soc. Lond. A: Math. Phys. Eng. Sci. 2003;459:3–46. [Google Scholar]
- 45.Asakura T., Iwadate M., Williamson M.P. Structural analysis of silk with 13C NMR chemical shift contour plots. Int. J. Biol. Macromol. 1999;24:167–171. doi: 10.1016/s0141-8130(98)00082-8. [DOI] [PubMed] [Google Scholar]
- 46.Wang Y., Jardetzky O. Probability-based protein secondary structure identification using combined NMR chemical-shift data. Protein Sci. 2002;11:852–861. doi: 10.1110/ps.3180102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jenkins J.E., Creager M.S., Yarger J.L. Quantitative correlation between the protein primary sequences and secondary structures in spider dragline silks. Biomacromolecules. 2010;11:192–200. doi: 10.1021/bm9010672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Zhang H., Neal S., Wishart D.S. RefDB: a database of uniformly referenced protein chemical shifts. J. Biomol. NMR. 2003;25:173–195. doi: 10.1023/a:1022836027055. [DOI] [PubMed] [Google Scholar]
- 49.Wishart D.S., Bigam C.G., Sykes B.D. 1H, 13C and 15N random coil NMR chemical shifts of the common amino acids. I. Investigations of nearest-neighbor effects. J. Biomol. NMR. 1995;5:67–81. doi: 10.1007/BF00227471. [DOI] [PubMed] [Google Scholar]
- 50.He D., Chung M., Parkinson J. Comparative genomics of elastin: sequence analysis of a highly repetitive protein. Matrix Biol. 2007;26:524–540. doi: 10.1016/j.matbio.2007.05.005. [DOI] [PubMed] [Google Scholar]
- 51.Wasserman Z.R., Salemme F.R. A molecular dynamics investigation of the elastomeric restoring force in elastin. Biopolymers. 1990;29:1613–1631. doi: 10.1002/bip.360291211. [DOI] [PubMed] [Google Scholar]
- 52.Anwar R.A., Oda G. The biosynthesis of desmosine and isodesmosine. J. Biol. Chem. 1966;241:4638–4641. [PubMed] [Google Scholar]
- 53.Pometun M.S., Chekmenev E.Y., Wittebort R.J. Quantitative observation of backbone disorder in native elastin. J. Biol. Chem. 2004;279:7982–7987. doi: 10.1074/jbc.M310948200. [DOI] [PubMed] [Google Scholar]
- 54.Cheng S., Edwards S.A., Gräter F. Glycosylation enhances peptide hydrophobic collapse by impairing solvation. ChemPhysChem. 2010;11:2367–2374. doi: 10.1002/cphc.201000205. [DOI] [PubMed] [Google Scholar]
- 55.Lu D., Yang C., Liu Z. How hydrophobicity and the glycosylation site of glycans affect protein folding and stability: a molecular dynamics simulation. J. Phys. Chem. B. 2012;116:390–400. doi: 10.1021/jp203926r. [DOI] [PubMed] [Google Scholar]
- 56.Perry A., Stypa M.P., Kumashiro K.K. Solid-state 13C NMR reveals effects of temperature and hydration on elastin. Biophys. J. 2002;82:1086–1095. doi: 10.1016/S0006-3495(02)75468-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kurbanov R., Zinkevich T., Krushelnitsky A. The nuclear magnetic resonance relaxation data analysis in solids: general R1/R1(ρ) equations and the model-free approach. J. Chem. Phys. 2011;135:184104. doi: 10.1063/1.3658383. [DOI] [PubMed] [Google Scholar]
- 58.Farès C., Qian J., Davis J. Magic angle spinning and static oriented sample NMR studies of the relaxation in the rotating frame of membrane peptides. J. Chem. Phys. 2005;122:194908. [Google Scholar]
- 59.Torchia D.A., Piez K.A. Mobility of elastin chains as determined by 13C nuclear magnetic resonance. J. Mol. Biol. 1973;76:419–424. doi: 10.1016/0022-2836(73)90514-7. [DOI] [PubMed] [Google Scholar]
- 60.Lyerla J.R., Jr., Torchia D.A. Molecular mobility and structure of elastin deduced from the solvent and temperature dependence of 13C magnetic resonance relaxation data. Biochemistry. 1975;14:5175–5183. doi: 10.1021/bi00694a024. [DOI] [PubMed] [Google Scholar]
- 61.Fleming W.W., Sullivan C.E., Torchia D.A. Characterization of molecular motions in 13C-labeled aortic elastin by 13C-1H magnetic double resonance. Biopolymers. 1980;19:597–617. doi: 10.1002/bip.1980.360190311. [DOI] [PubMed] [Google Scholar]
- 62.Lang E., Lüdemann H.-D., Piculell L. Nuclear magnetic relaxation rate dispersion in supercooled heavy water under high pressure. J. Chem. Phys. 1984;81:3820–3827. [Google Scholar]
- 63.Flory P., Ciferri A., Hoeve C. The thermodynamic analysis of thermoelastic measurements on high elastic materials. J. Polym. Sci. Polym. Phys. 1960;45:235–236. [Google Scholar]
- 64.Tatham A.S., Shewry P.R. Elastomeric proteins: biological roles, structures and mechanisms. Trends Biochem. Sci. 2000;25:567–571. doi: 10.1016/s0968-0004(00)01670-4. [DOI] [PubMed] [Google Scholar]
- 65.Luan C.-H., Jaggard J., Urry D. On the source of entropic elastomeric force in polypeptides and proteins: backbone configurational vs. side-chain solvational entropy. Int. J. Quantum Chem. 1989;16:235–244. [Google Scholar]
- 66.Andricioaei I., Karplus M. On the calculation of entropy from covariance matrices of the atomic fluctuations. J. Chem. Phys. 2001;115:6289–6292. [Google Scholar]
- 67.Harris S.A., Laughton C.A. A simple physical description of DNA dynamics: quasi-harmonic analysis as a route to the configurational entropy. J. Phys. Condens. Matter. 2007;19:076103. doi: 10.1088/0953-8984/19/7/076103. [DOI] [PubMed] [Google Scholar]
- 68.Wishart D.S., Bigam C.G., Sykes B.D. 1H, 13C and 15N chemical shift referencing in biomolecular NMR. J. Biomol. NMR. 1995;6:135–140. doi: 10.1007/BF00211777. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


