Abstract
Förster resonance energy transfer (FRET) is a nonradiative process for the transfer of energy from an optically excited donor molecule (D) to an acceptor molecule (A) in the ground state. The underlying theory predicting the dependence of the FRET efficiency on the sixth power of the distance between D and A has stood the test of time. In contrast, a comprehensive kinetic-based theory developed recently for FRET efficiencies among multiple donors and acceptors in multimeric arrays has waited for further testing. That theory has been tested in the work described in this article using linked fluorescent proteins located in the cytoplasm and at the plasma membrane of living cells. The cytoplasmic constructs were fused combinations of Cerulean as donor (D), Venus as acceptor (A), and a photoinsensitive molecule (Amber) as a nonfluorescent (N) place holder: namely, NDAN, NDNA, and ADNN duplexes, and the fully fluorescent quadruplex ADAA. The membrane-bound constructs were fused combinations of GFP2 as donor (D) and eYFP as acceptor (A): namely, two fluorescent duplexes (i.e., DA and AD) and a fluorescent triplex (ADA). According to the theory, the FRET efficiency of a multiplex such as ADAA or ADA can be predicted from that of analogs containing a single acceptor (e.g., NDAN, NDNA, and ADNN, or DA and AD, respectively). Relatively small but statistically significant differences were observed between the measured and predicted FRET efficiencies of the two multiplexes. While elucidation of the cause of this mismatch could be a worthy endeavor, the discrepancy does not appear to question the theoretical underpinnings of a large family of FRET-based methods for determining the stoichiometry and quaternary structure of complexes of macromolecules in living cells.
Introduction
Förster resonance energy transfer (FRET) is a radiationless, extremely short-range (i.e., <10 nm) photophysical process of energy transfer from an excited donor (D) to a nearby acceptor (A) via dipole-dipole interaction (1–3). The theory that describes this process was introduced by Förster almost three quarters of a century ago (4–6) and has stood the test of time (2,3). Its broad application to biological systems has been greatly facilitated by the advent of fluorescent tags such as organic dyes (7–10) and variants of the green fluorescent protein (11–14). By acting as FRET donors and acceptors, the fluorescence tags allow the association of macromolecules to be investigated under a variety of conditions, including living cells (15–21).
An extension of FRET theory that accommodates multiple donors and acceptors within an oligomeric complex (22) has led to a method for determining the size and geometry of such structures. The apparent FRET efficiency (Eapp) is measured for each pixel within an image of a thin optical section of the sample (obtainable with the use of a multiphoton or confocal microscope), and the number of pixels falling within a certain interval of Eapp is plotted against the center of the interval to obtain a histogram, or distribution of FRET efficiencies, for the entire section of a cell or cellular region of interest (23). Such distributions are richer in information than the average efficiency over all pixels (24), because the peaks collectively constitute a unique fingerprint of a specific oligomeric arrangement (17). As demonstrated recently (25,26), the quaternary structure of a protein complex can be inferred from the number of peaks in the histogram and their mutual relationships. Because the approach delivers a characteristic FRET spectrum for a given complex, it is in effect a FRET-based spectrometric method, and has been referred to as “FRET spectrometry” (27).
To test the theory of FRET in complexes containing more than one acceptor, Koushik et al. (28) have developed a set of multiplexed fluorescent proteins comprising fused combinations of a donor (Cerulean, D) (13), an acceptor (Venus, A) (14) and a chromophore-deficient Venus-like molecule that cannot absorb or transfer energy (Amber, N). Four such units are contained in each of four cytoplasmic constructs: a fluorescent quadruplex in which all units are fluorescent (i.e., ADAA), and three fluorescent duplexes in which two units are fluorescent and two are dark (i.e., NDAN, ADNN, and NDNA) (28). Intriguingly, the measured transfer of energy within the quadruplex ADAA exceeded by a small but significant amount what was predicted from the transfer measured within the duplexes NDAN, ADNN, and NDNA.
Such discrepancies are not expected to arise when the multiplexed or multimeric nature of a protein is determined by FRET spectrometry (23,25,26,29), in which the extended theory of FRET that underlies the method accommodates structures containing several (i.e., >2) donors and acceptors (22). We therefore undertook an experimental study to put the theory further to the test. Our examination included the cytoplasmic constructs of Koushik et al. (28) as well as three novel membrane-bound fusion proteins in which multiplexed copies of GFP2 (D) (12) and eYFP (A) (11) were preceded by the acylated N-terminal segment of the α-subunit of Gi1 (MP) to form two duplexes (i.e., MP-DA and MP-AD) and a triplex (MP-ADA).
Each fusion protein was expressed in Chinese hamster ovary (CHO) cells, and the FRET efficiencies were measured at the level of single pixels using an imaging system designed for optical microspectroscopy (23,30). According to the theory (22), the apparent FRET efficiency of a fluorescent quadruplex containing multiple donors and acceptors (e.g., ADAA) can be predicted from measurements on analogs that contain a single donor and acceptor (e.g., NDAN, NDNA, and ADNN); similarly, the apparent FRET efficiency of a fluorescent triplex such as ADA can be predicted from the pairwise FRET efficiency measured for the duplexes DA and AD. By comparing the measured and predicted FRET efficiencies for ADAA and ADA, we were able to test the kinetic theory of FRET as commonly used in FRET imaging.
Theory of the method
FRET efficiency for multimeric complexes
The kinetic theory of FRET is based on the notion that the FRET efficiency in a multimeric complex of donors and acceptors may be generalized by taking the average of the individual FRET efficiency for each donor transferring energy to the acceptors within the complex, as we shall demonstrate next using the theory published previously in Raicu (22).
Consider an oligomer or multiplex containing n fluorophore-bearing protomers or subunits, of which k are identical donors and n–k are identical acceptors. We further assume that only one donor in a complex is in an excited state at a time. This may be easily achieved by keeping the intensity of excitation light low enough that the excitation rate of the donors is much lower than all the deexcitation rates of the donors. Each donor may transfer energy to the n–k acceptors, with a probability that depends on the acceptor distance and orientation relative to the donor. There accordingly is one pathway for each donor to lose excitation energy through radiative emission of a photon or nonradiative deexcitation via interactions with the environment, and there are n–k different ways to lose excitation energy via FRET with nearby acceptors. An example of all possible energy transfer pathways for a pentamer with two donors and three acceptors is shown in Fig. 1.
Figure 1.
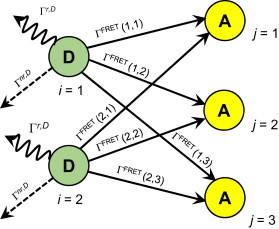
Schematic representation of a fluorescent oligomer, in this case a pentamer that comprises two donors (D, green) and three acceptors (A, yellow). The various arrows indicate possible pathways for energy loss or transfer from donors to acceptors. (Solid arrows) FRET (ΓFRET); (dashed arrows) nonradiative loss (Γnr,D); and (wavy arrows) radiative loss (Γr,D). To see this figure in color, go online.
In the absence of FRET, the quantum yields, QD, of all donors are equal to one another, as are the excitation rates of all acceptors, ΓA,ex. As it is well known, FRET does not modify either the excitation rate of the donors, Γex,D, or the quantum yield of the acceptors, QA. In the presence of FRET, the quantum yield of the ith donor is modified as expressed by the following equation (17,23):
| (1) |
The quantity
in Eq. 1 is the rate of transfer from the ith donor to the jth acceptor through FRET, ri,j is the distance between the fluorophores, R0i,j is the Förster radius (17,22), and
Note that, because the orientation factor can differ for different donor-acceptor pairs in an oligomer (2,3), the corresponding Förster radii also can differ. The FRET efficiency for the ith donor can be defined as
| (2) |
Equations 1 and 2 may be combined to obtain
| (3) |
which is in accord with the expectation that emission from the donor decreases upon the transfer of energy to the acceptor.
Similar arguments may be used to show that the excitation rate of the jth acceptor in the presence of donors is enhanced by FRET, as given by the expression
| (4) |
Using Eq. 3, the total number of photons emitted by all the k donors in an oligomer in the presence of acceptors (i.e., FRET) may be expressed as
while, using Eqs. 2 and 4, the total number of photons emitted by the n–k acceptors may be expressed as
Choosing appropriate notations, the last two equations may be written simply as
| (5) |
| (6) |
where FD(λex) = kΓex,DQD and FA(λex) = (n–k)Γex,AQA are the donor and acceptor emissions, respectively, in the absence of FRET
is the loss of emission from the donor due to FRET; and
is the corresponding gain in emission from the acceptor. In addition, by comparing the second terms on the right-hand sides of Eqs. 5 and 6, we obtain a third relationship,
| (7) |
By defining the FRET efficiency of the oligomer as the fraction of excitations of donors transferred to acceptors, that is,
| (8) |
we immediately obtain
which proves the statement made above that the FRET efficiency for an oligomer equals the average efficiency for all the donors in the oligomer.
Determination of the apparent FRET efficiency from spectrally resolved measurements of fluorescence intensity
The determination of apparent FRET efficiencies by spectrally resolved FRET imaging (23) relies on tagging the proteins of interest with fluorescent molecules that act as donors and acceptors of energy. Cells coexpressing donor- and acceptor-tagged proteins are irradiated at the wavelength corresponding to the excitation maximum of the donor, and an emission spectrum consisting of signals from donors and acceptors is acquired for every pixel in an image. Emission spectra also are acquired for cells expressing donors or acceptors alone, and the measured intensities are normalized to the maximum value to obtain elementary or standard spectra for the donor,
| (9) |
and the acceptor,
| (10) |
where il, …, il are the normalized intensities corresponding to each emission wavelength, λem,1, …, λem,1 (17). The presence of a third signal such as constant background noise, background autofluorescence (31), or the emission from a fluorescent sensor (e.g., for pH or voltage) can be accommodated by including an additional spectrum,
| (11) |
The emission spectrum of every pixel in the image of a sample containing all three signals is
which may be approximated by a linear combination of the three emission spectra as
| (12) |
This equation becomes an exact identity in the absence of experimental noise. The parameters kDA(λex), kAD(λex), and kF(λex) are proportional to the emission intensities of D in the presence of A, of A in the presence of D, and of the third fluorescent species unrelated to FRET, respectively. Their values are computed from the measured spectra using a least-squares minimization procedure (21,32) as described in Appendix SA in the Supporting Material. Those values can be used to determine the total number of photons emitted by the donor [i.e., FDA(λex)], the acceptor [FAD(λex)], and the third fluorophore if present [FF(λex)], as
| (13) |
| (14) |
| (15) |
where wD, wA, and wF are the integrals of the elementary emission spectra of the donor, the acceptor, and the third fluorophore.
Note that the first two of the above three quantities are the same as defined in the previous subsection and may be used to compute experimental values of the FRET efficiency of multimeric complexes containing donors and acceptors. Assuming that direct excitation of the acceptors is negligible at the wavelength of the incident light (i.e., FA(λex) ≈ 0), and using Eqs. 5–7, Eq. 8 becomes
| (16) |
Equation 16 has been used to determine the FRET efficiency at each pixel in a fluorescence image following a single scan of the sample at a single excitation wavelength. It circumvents difficulties associated with classical filter-based methods for the determination of FRET efficiency using two or more excitation scans (17).
Correction for direct excitation of the acceptor
To determine the apparent FRET efficiency at each image pixel according to Eq. 16, one aims to choose a laser operating at a wavelength that achieves maximal excitation of the donor with minimal excitation of the acceptor. That rarely is possible, however, and the acceptor typically is excited to some extent. Such an effect was expected to be small with the fluorescent proteins and excitation wavelengths used in this investigation, but it was taken into account nonetheless; the procedure is explained next.
In the presence of small but nonnegligible direct excitation of the acceptor (i.e., FA(λex) ≠ 0), Eq. 8 becomes
| (17) |
If the rate of direct excitation of the acceptor is assumed to be very low (Appendix SB in the Supporting Material), Eq. 17 may be reduced to the following simple form:
| (18) |
The correction factor αA in Eq. 18 is given by the expression
where Eapp is the FRET efficiency determined using Eq. 16; Γex,A and Γex,D are the excitation rates of the acceptor and donor, respectively; and n is the number of fluorophores (D and A) per oligomer or multiplex. Finally,
where [D]A and [A]D are the number of donors and acceptors, respectively, per oligomer. The rates Γex,A and Γex,D are proportional to the two-photon absorption cross sections of the fluorophores.
Prediction of the apparent FRET efficiency of fluorescent multiplexes
The apparent FRET efficiency of an oligomer or multiplex of one donor and n−1 acceptors is given by
| (19) |
with
| (20) |
These equations are in essence just a convenient restatement of Eq. 2, where we have also dropped the index i, for simplicity.
For the multiplexes containing more than one acceptor, such as ADAA (n−1 = 3) and ADA (n−1 = 2, see above), Eq. 19 may be expressed in terms of the measured efficiencies of cognate fluorescent duplexes containing one donor and one acceptor (i.e., NDNA, NDAN, ADNN, or AD and DA). Each duplex (i.e., n = 2), accounts for a single term in the sum in Eq. 19.
From Eq. 20, we obtain for each duplex
| (21) |
and, with this, Eq. 19 becomes
| (22) |
In the case of ADAA, for example, j in Eq. 19 denotes NDAN, ADNN, or NDNA; in the case of ADA, j denotes AD or DA. The error on Epredicted can be calculated according to the method of propagation of errors, which gives
| (23) |
Materials and Methods
FRET standards
The FRET theory outlined above was tested with fusion proteins that localized either in the cytoplasm or at the membrane of mammalian cells. Four constructs were expressed in the cytoplasm and have been described previously in Koushik et al. (28). Each is a linear array of four domains, the second of which is the donor (D, Cerulean) (13) as illustrated in Fig. 2. In one of the constructs, the other three positions are taken by the acceptor (A, Venus) (14) (i.e., ADAA). In the other constructs, one subunit is Venus and the remaining slots are filled by Amber (N) (33), a Venus-like mutant that does not form a fluorophore and therefore cannot participate in FRET. Amber serves as a place-holder as the single acceptor is moved from one position to another relative to the donor (i.e., NDAN, NDNA, and ADNN). This arrangement preserves the quadruplex configuration of ADAA in constructs that behave as fluorescent duplexes in the process of energy transfer. The emission spectrum of the donor alone was recorded from a fusion product of Amber and Cerulean (i.e., Amber-5-Cerulean, N5D).
Figure 2.
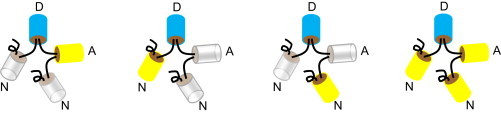
Schematic of the cytoplasmic FRET standards. A donor (D, Cerulean), an acceptor (A, Venus), and two nonfluorescent proteins (N, Amber) are joined by amino-acid linkers depicted (by curved lines connecting D, A, and N (28)). To see this figure in color, go online.
Three constructs were directed to the plasma membrane by the acylated amino-terminal segment of Gαi1, which was fused to the amino-termini of linked fluorophores as shown in Fig. 3. Complementary DNA (MP) coding for the first seven residues of αi1, the next 25 residues of αi1, and the six bases corresponding to the BamH1 restriction site was fused upstream of the cDNA coding for either GFP2 or eYFP to obtain MP-GFP2 and MP-eYFP, respectively. A second fluorescent domain was added to the 3′ end of the first via a linker of six bases corresponding to the BspE1 restriction site to create the duplexes MP-GFP2-eYFP (DA) and MP-eYFP-GFP2 (AD). A third fluorophore was added to the 3′ end of MP-eYFP-GFP2 via six bases corresponding to the AgeI restriction site to create the triplex MP-eYFP-GFP2-eYFP (ADA). The amino-terminal heptapeptide of αi1 (i.e., Met-Gly-Cys-Thr-Leu-Ser-Ala) contains the sites of attachment for myristoyl (M) and palmitoyl (P) groups, which are added at positions two and three, respectively, during biosynthesis.
Figure 3.
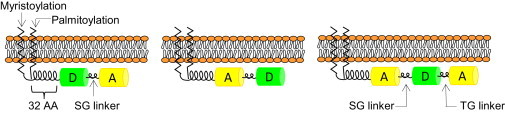
Schematic representation of membrane-bound duplex and triplex FRET constructs. Addition of a myristoylation and palmitoylation sequence derived from the αi1-subunit of Gi1 at the N-terminus of the first fluorophore anchors the fluorescent protein to the plasma membrane. The first two fluorophores are linked by the dipeptide Ser-Gly (SG), and eYFP (A) is linked to eYFP-GFP2 (AD) in the triplex configuration by Thr-Gly (TG). To see this figure in color, go online.
All fusions were ligated into the pcDNA3.1+ vector, and the sequences were confirmed by DNA sequencing.
Cell culture and transfection
CHO cells were grown in Dulbecco’s modified Eagle’s medium lacking sodium pyruvate, supplemented with fetal bovine serum (10%), L-glutamine (2 mM), penicillin/streptomycin (1%), and nonessential amino acids (1%). Cells for imaging on a two-photon microscope with spectral resolution built in-house as described previously in Raicu et al. (23) were cultured and seeded in six-well plates (3.5 cm diameter) at a density of 15,000–20,000 cells/cm2 and maintained at 37°C in a humidified environment with 5% CO2. After 24 h, when the cells were 40–45% confluent, each well was transfected with plasmid DNA (2 μg) and Lipofectamine 2000 (10 μL) (Invitrogen, Carlsbad, CA) diluted in OptiMEM medium (250 μL) (Invitrogen). The transfection procedure was similar to that described previously in Pisterzi et al. (29). Cells lacking plasmid but otherwise processed in the same manner were maintained as controls. Images generally were acquired ∼6, 10, 16, or 24 h after transfection, when the medium in each well was replaced with OptiMEM (250 μL; Invitrogen); the cells then were dislodged with a cell scraper and collected in 1 mL Eppendorf tubes. The different transfection times allowed us to investigate possible effects of concentrations and/or fluorophore maturity on the obtained FRET data. Approximately 10 μL of the suspension was placed on a microscope glass slide with a 0.3-mm coverslip and used for imaging. Cells to be imaged were cultured at a density of 8000–10,000 cells/cm2 in 35-mm Petri dishes with a 0.3-mm glass coverslip placed at the bottom (MatTek, Ashland, MA). Transfections were carried out with 2 μg of plasmid DNA per dish and other reagents in quantities proportional to those listed above. Other conditions were as described above, and the cells were imaged without being dislodged.
Image acquisition
Spectrally resolved fluorescence imaging was performed throughout at room temperature. Imaging experiments were performed using a replica of a commercial version of a two-photon microscope with spectral resolution described previously in Biener et al. (34), which is called an optical microspectroscope (Optimis TruLine, Aurora Spectral Technologies, Milwaukee, WI). The imaging system is equipped with a Ti-Sapphire laser (Tsunami, Spectra-Physics, Santa Clara, CA) with a tuning range of 690–1040 nm and delivering pulses with a width of <100 fs at a repetition rate of 80 MHz. For the membrane constructs, the system was upgraded to perform line scans rather than point scans by employing a curved mirror to shape the excitation beam into a line (34). This setup features a reduced acquisition time and increased overall sensitivity. The incident light was focused through an infinity-corrected oil-immersion objective (100× magnification, NA 1.45; Nikon Instruments, Melville, NY) to a line with diffraction-limited thickness on the sample. The emitted light was passed through a transmission grating and projected onto a cooled electron-multiplying charge-coupled device camera (iXon 897; Andor Technology, South Windsor, CT).
Determination of the emission spectra of donors and acceptors
To determine the emission spectrum of cytosolic Cerulean (i.e., the donor), CHO cells expressing N5D were imaged using Optimis TruLine (Aurora Spectral Technologies) at an excitation wavelength of 800 nm. The average excitation power was ∼67 mW per entire excitation line, as measured after the microscope objective. To determine the emission spectrum of cytosolic Venus (i.e., the acceptor), CHO cells expressing ADAA were irradiated at 1020 nm at average powers similar to those described above for N5D. Cerulean is not excited appreciably at that wavelength. The seven spectral images in Fig. 4 are selected from 200 images over the range from 400 to 600 nm and are representative of CHO cells expressing N5D or ADAA. The background-corrected intensity at each wavelength was averaged over pixels of nonzero intensity, selected as shown by the red circles, and the means were normalized to the maximum value to obtain the elementary emission spectra of Cerulean and Venus. Normalized spectra for the membrane-bound standards were obtained from CHO cells expressing MP-GFP2 or MP-YFP and irradiated at 800 nm and 970 nm, respectively, using an average laser power of ∼200 mW per line.
Figure 4.
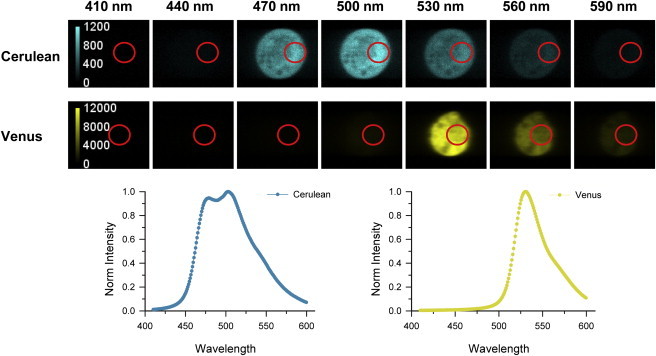
Spectral images of representative CHO cells expressing the cytoplasmic constructs N5D or ADAA. (Upper panels) The samples were irradiated by two-photon lasers at 800 and 1020 nm for Cerulean and Venus, respectively, to obtain the reconstructed images at the emission wavelengths shown. (Lower panel plots, cyan and yellow lines) Elementary emission spectra of Cerulean and Venus, respectively, averaged over nonzero pixels (region indicated by the red circle in each image).
Spectral unmixing and calculation of Eapp
Spectrally resolved images of CHO cells expressing the cytoplasmic and membrane-bound FRET standards were unmixed as described in the previous paragraph to obtain fitted estimates of kDA(λex) and kAD(λex) for the contribution of donor and acceptor at each pixel. Those values then were used together with the quantum yields of the fluorophores (QD, QA) and the integrals of the corresponding emission spectra (wD, wA) to calculate the apparent FRET efficiency (Eapp) at each pixel according to Eq. 16. To avoid instrumental and other noise in the image of Eapp, pixels with values of kDA(λex) or kAD(λex) below a certain threshold (corresponding to signal/noise = 0.5) of the donor signal corrected for FRET) were disregarded. Because excitation of the acceptor was disregarded in the calculation of kAD(λex) (Eqs. 9–15) and the apparent FRET efficiency (Eapp) (Eq. 16), estimates of pixel-level Eapp were corrected according to Eq. 18. The two-photon absorption cross sections of the fluorophores at 800 nm were as follows: Cerulean, 37.132 GM; Venus, 2.519 GM; GFP2, 6.43 GM; eYFP, 2.54 GM (Developmental Resource for Biophysical Imaging Opto-Electronics, Cornell University, Ithaca, NY; http://www.drbio.cornell.edu/). The number of fluorophores (n) and the probability of acceptors (PA) in each construct is as follows: n = 2 and PA = 1/2 for NDAN, ADNN, and NDNA; n = 4 and PA = 3/4 for ADAA; n = 2 and PA = 1/2 for DA and AD; and n = 3 and PA = ⅔ for ADA.
Results and Discussion
FRET efficiencies of the cytoplasmic constructs
Representative histograms of Eapp obtained for the cytosolic constructs NDAN, ADNN, NDNA, and ADAA in CHO cells are illustrated in Fig. 5, where the values are distributed using a bin size of 0.01 on a scale of 0:1. The pixel level Eapp values were corrected for direct excitation of acceptor according to Eq. 18, as described in Spectral Unmixing and Calculation of Eapp, above. The mean value of Eapp and its standard deviation were calculated for each cell from the Eapp histogram for that cell. From these values, we computed the weighted average and mean ± SE for each of the four constructs (see Appendix C in the Supporting Material). The resulting difference between the predicted Eapp for ADAA and the measured one (∼0.03 ± 0.05) was virtually nil. Note, however, that is not the result that should be retained from this study, because the distribution of primary values suffers from systematic effects as detailed in the analysis that follows.
Figure 5.
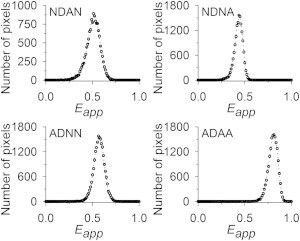
Distributions of Eapp for fluorescent duplexes and the quadruplex ADAA expressed in the cytoplasm of CHO cells. Values of Eapp were calculated for single pixels, as described in the text and plotted as histograms (bin size, 1%).
A relatively broad range of concentrations of these constructs was achieved by imaging the cells 6, 10, 16, or 24 h after transfection. Because each FRET construct contains only one donor, the concentration of the construct equals that of the donor, and it is proportional to the emission from the donor corrected for FRET. The latter was calculated according to the equation FD = kDAwD + kADwAQD/QA, which was derived by inserting Eqs. 6 and 7 into Eq. 5 and assuming as before that FA(λex) ≈ 0). The relationship between the average FRET efficiency and the level of expression [log (FD/a.u.)] is shown for NDAN, ADNN, NDNA, and ADAA in Fig. 6 a, where each data point represents one cell. Log (FD/a.u.) was divided into five intervals and the weighted mean Eapp and the standard error of the mean (mean ± SE) were determined for each construct. The predicted values were calculated for ADAA using Eq. 22 from the mean values of Eapp for NDAN, ADNN, and NDNA for each interval. The propagated errors for the predicted means for the five different intervals were computed using Eq. 23. The weighted average differences between the measured and predicted values of Eapp were then computed for ADAA (i.e., ΔEapp) for each interval (Fig. 6 b).
Figure 6.
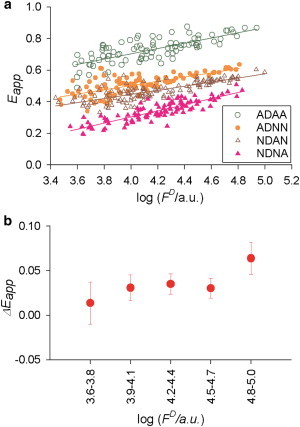
Dependence of the cellular average of the apparent FRET efficiency (Eapp) on the level of expression [log (FD/a.u.)]. The cytoplasmic constructs ADAA (open circles), ADNN (solid circles), NDAN (open triangles), and NDNA (solid triangles) were expressed in CHO cells for different periods of time after transfection, as described in the text. The level of expression was estimated from the spectral properties of the donor. (a) Each point represents the cellular average of Eapp corrected for acceptor direct excitation at image pixel level (before averaging) for a single cell transfected with one of the four constructs as shown. To avoid unnecessary clutter of the plots, the standard deviations were not plotted. (Lines) Obtained by linear regression, serving as a guide to the eyes. (b) Each point represents the difference between the measured and predicted values of Eapp for ADAA (i.e., , where and Epredicted are from Eqs. 18–22, respectively), plotted against the corresponding mean value of log (FD/a.u.) for the range shown on the abscissa. (Vertical bars) Propagated errors computed by adding the individual errors in quadrature. To see this figure in color, go online.
As seen in Fig. 6, the apparent FRET efficiency for each construct slightly increased with the level of expression (Fig. 6 a), as did a small but statistically significant difference between the measured and predicted values for ADAA (Fig. 6 b). The difference is between measured and predicted FRET, which ranges from 0.01 to 0.06 and is lower than that of 0.11, which was reported by Koushik et al. (28).
Regarding the causes for the dependence of average Eapp on the donor fluorescence corrected for FRET (i.e., FD), we may rule out contributions from stochastic or bystander FRET between neighboring fusion proteins (35), because such an effect becomes significant only for FRET constructs confined to two dimensions (i.e., at the plasma membrane) and comparatively large concentrations. Rough estimates based on a method described previously in Patowary et al. (25) and Singh et al. (26) place the concentrations of the cytoplasmic constructs in the range of 10−8 to 10−6 constructs/nm3. These would result in concentrations of <10−3 constructs/nm3 if the focal depth of the microscope (∼1000 nm) were to be sliced into layers of size equal to the size of the constructs (∼10 nm). Such concentrations would be too low to cause significant stochastic FRET even if all the constructs contained in such layers were forced to assume favorable orientations relative to one another (35). Because of this, the FRET efficiencies determined at higher concentrations are expected to remain unaffected by stochastic FRET.
A possible explanation for the dependence of average Eapp on log(FD/a.u.) is based on the observation that, because the average FRET efficiencies are computed over large regions of interest, over which the distribution of oligomers is not entirely homogeneous, these averages are reduced by contributions from regions with lower concentrations of complexes (24). Because the spatial distributions become more uniform at concentrations toward the higher end of the range investigated, and, aided by the image smearing effect caused by the point-spread function of the microscope, the reduction in the average FRET efficiency due to nonuniform distributions is gradually eliminated. A second possibility is that the apparent dependence on concentration is in effect caused by a difference in the maturation times of the two fluorophores, Cerulean and Venus. Populations of fusion proteins in which all fluorophores are mature cannot be distinguished from those in which only some are mature, and the relationship between the apparent FRET efficiency and the observed effect in fact may derive from a dependence on the time elapsed between transfection and acquisition of the image.
Both of those effects suggest an increased accuracy of the measurements performed after longer times from transfection, which happen to correlate with larger values of log(FD) in Fig. 6 b. This means that the larger difference between measured and predicted Eapp for ADAA (i.e., 0.064 ± 0.017, relative to the predicted value of 0.789) is the most reliable result of this set of measurements. This excess in the measured FRET efficiency corresponds to a total relative excess of 8% for the quadruplex or 2.7% per acceptor in a complex.
FRET efficiencies of the membrane-bound constructs
In principle, it is possible to avoid effects caused by differential fluorophore maturation times by performing measurements on constructs bound to the plasma membrane, because construct delivery to the membrane would presumably occur after it has folded properly. Our next step was therefore to perform measurements on a set of two membrane-bound duplexes (DA and AD) and a triplex (ADA), which were constructed in-house. Representative histograms of Eapp obtained for AD, DA, and ADA in CHO cells are illustrated in Fig. 7, and the mean values of Eapp for all cells are listed in Table 1 together with the predicted value for ADA. All values were calculated as described for the cytosolic constructs in the previous section.
Figure 7.
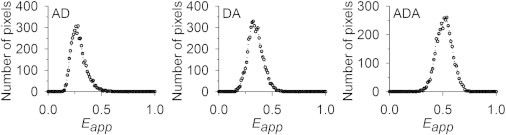
Distributions of Eapp for fluorescent duplexes AD and DA and the triplex ADA localized at the plasma membrane of CHO cells. Values of Eapp were calculated for single pixels as described in the text and plotted as histograms with a bin size of 1%.
Table 1.
Average mean ± SE of measured apparent FRET efficiencies of the cytoplasmic constructs
| Construct |
Eapp |
|
|---|---|---|
| Measured | Predicted | |
| DA | 0.368 ± 0.015 (54) | — |
| AD | 0.254 ± 0.012 (48) | — |
| ADA | 0.515 ± 0.009 (48) | 0.480 ± 0.033 |
The predicted mean ± SE value for the ADA construct is also listed. The number of cells is shown in parentheses.
Here again, a small (0.035 ± 0.034) but statistically significant difference was observed between the measured Eapp value for the ADA triplex and the value predicted by Eq. 22 using separate measurements for AD and DA. This excess in the measured FRET efficiency corresponds to a total relative excess of 7.2% for the triplex or 3.6% per acceptor. While identifying the main reason for these small discrepancies is outside of the scope of this work, we will next provide a quick assessment of the consequences of this result for FRET imaging, and in particular, FRET spectrometry.
Implications for FRET studies
As has been mentioned in the Introduction, in FRET spectrometry, the apparent FRET efficiency is measured for each pixel within a FRET-based image of a thin optical section of the sample, and the number of pixels falling within a certain interval of Eapp is plotted against the center of the interval to obtain a histogram of FRET efficiencies for the entire section of a cell or cellular region of interest (23). In its simplest form, this method relies on the assumption that only one complex (or, occasionally, very few complexes) resides at each pixel, and that a set of several pixels containing a single type of complex leads to formation of a peak in the Eapp histogram.
The observed relative Eapp excess was 2.7% per acceptor for the cytoplasmic quadruplex, and 3.6% per acceptor for the membrane-bound triplex. The results obtained for two different cytoplasmic constructs reported previously in Koushik et al. (28) appear to lie somewhere above these two values. We will take our lowest and highest surplus per acceptor as the best- and worst-case scenario, respectively.
It is instructive to estimate the effect of the observed surplus of energy transfer on the Eapp histogram of a rhombus tetramer, as described in, e.g., Raicu and Singh (27), with a pairwise FRET efficiency (Ep) of 0.200. For the complex containing a single acceptor and three donors, Eapp is roughly 2/3Ep = 0.133; the observed excess would shift that peak by 0.036 × 1 × 0.133 = 0.005 to 0.138. For the opposite case of three acceptors and one donor, the rhombus tetramer predicts an Eapp value of 3Ep/(1+2Ep) = 0.429, which would be shifted by 0.036 × 3 × 0.429 = 0.047 to become 0.476. The overall result of these two shifts is a corresponding shift between the lowest and highest peak value 0.047 – 0.005 = 0.042, the remaining three peaks being affected to different degrees in between the two extremes. This histogram shift is within the experimental errors of this method and should not affect the identification of the correct quaternary structure from Eapp histograms. In fact, the only undesired consequence of this peak shift is that Ep (which determines the position of all individual Eapp peaks simultaneously) would be inadvertently increased in order to fit the histogram to the theoretical model of a tetramer. This is rather inconsequential, because, due to the strongly nonlinear dependence of FRET efficiency on distance between fluorescent tags, such change in Ep results in only minute changes in distances.
For methods that rely on determination of average Eapp values over entire cells or regions of interest, assessing the effects of such a surplus as discussed above is more difficult. For such methods, FRET efficiencies from all possible combinations of donors and acceptors are averaged over with complexes containing only donors (i.e., Eapp = 0) to produce a single Eapp value for the regions of interest. However, at least for FRET spectrometry, the mismatch between the measured and predicted Eapp values for proteins with multiple acceptors does not appear to compromise the reliability of the results.
Conclusion
Using a technique based on spectrally resolved two-photon microscopy, we have tested the kinetic theory of FRET for multiplex complexes by means of fluorescent protein standards expressed in the cytoplasm and at the plasma membrane of CHO cells. The multiplexes comprised multiple fused fluorophores, thereby mimicking in a covalently determined manner the fluorescent complement of tagged protomers within an oligomer. The results show that the average FRET efficiency measured for the membrane-bound triplex ADA and the cytoplasmic quadruplex ADAA were slightly lower than could be predicted based on the measured FRET efficiencies for their corresponding duplexes.
We note in passing that multiplying the individual Eapp for all the FRET constructs considered in Koushik et al. (28) by the quantum yield of their respective donor not only results in significantly lower values of Eapp for each construct but also essentially eliminates the differences between measured and predicted values for the triplex and quadruplex oligomers (it actually inverts the surplus for the case of the quadruplex in this article). While this is not a mathematical proof that the kinetic FRET model is correct, it suggests that the greater effect observed by Koushik et al. may be related to how the FRET efficiency is defined and what approximations are made in its derivation. This is of significant concern, as one needs to be fully aware of such approximations if one is interested in quantitative analysis.
Detailed studies concerning the manner in which relevant quantities are defined and measured, and what approximations are made in FRET studies, will likely follow. For the time being, we only wish to reiterate that, because the observed effect was comparatively small under the conditions of the studies described here, which are typical of FRET investigations, it is highly unlikely to affect to any significant degree conclusions regarding the size and configuration of protein complexes as determined from FRET measurements (see, for example, Raicu and Singh (27) and Mishra et al. (36)). It nevertheless is a reminder of the need for continual efforts to improve existing FRET-based methods for investigating protein-protein interactions.
Acknowledgments
We are grateful to Dr. Stephen S. Vogel, National Institute on Alcohol Abuse and Alcoholism, for his generous gift of the cDNA constructs coding for the four cytoplasmic FRET standards (i.e., ADAA, NDAN, NDNA, and ADNN), and for useful discussions. We thank Dr. Julie Oliver for giving us access to mammalian cell culture facilities.
This work was supported by grants from the National Science Foundation (grant Nos. PHY-1058470, IIP-1114305, and PHY-1126386 to V.R.) and the Canadian Institutes of Health Research (grant No. MOP-97978 to J.W.W.).
Footnotes
Suparna Patowary’s present address is Division of Biology and Biological Engineering, California Institute of Technology, Pasadena, CA.
Supporting Material
References
- 1.Stryer L. Fluorescence energy transfer as a spectroscopic ruler. Annu. Rev. Biochem. 1978;47:819–846. doi: 10.1146/annurev.bi.47.070178.004131. [DOI] [PubMed] [Google Scholar]
- 2.Clegg R.M. Fluorescence resonance energy transfer. In: Wang X.F., Herman B., editors. Fluorescence Imaging Spectroscopy and Microscopy. Wiley-Interscience; New York: 1996. [Google Scholar]
- 3.Lakowicz J.R. Springer; New York: 2006. Principles of Fluorescence Spectroscopy. [Google Scholar]
- 4.Förster T. Energy migration and fluorescence [Energiewanderung und fluoreszenz] Naturwissenschaften. 1946;33:166–177. [Google Scholar]
- 5.Förster T. Fluorescence experiments with dye mixtures [Fluoreszenzversuche an farbstoffmischungen] Angew. Chem A. 1947;59:181–187. [Google Scholar]
- 6.Förster T. Intermolecular energy migration and fluorescence[Zwischenmolekulare energiewanderung und fluoreszenz] Ann. Phys. 1948;2:55–75. [Google Scholar]
- 7.Maurel D., Comps-Agrar L., Pin J.P. Cell-surface protein-protein interaction analysis with time-resolved FRET and snap-tag technologies: application to GPCR oligomerization. Nat. Methods. 2008;5:561–567. doi: 10.1038/nmeth.1213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Calebiro D., Rieken F., Lohse M.J. Single-molecule analysis of fluorescently labeled G-protein-coupled receptors reveals complexes with distinct dynamics and organization. Proc. Natl. Acad. Sci. USA. 2013;110:743–748. doi: 10.1073/pnas.1205798110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lowder M.A., Appelbaum J.S., Schepartz A. Visualizing protein partnerships in living cells and organisms. Curr. Opin. Chem. Biol. 2011;15:781–788. doi: 10.1016/j.cbpa.2011.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ward R.J., Pediani J.D., Milligan G. Ligand-induced internalization of the orexin OX1 and cannabinoid CB1 receptors assessed via N-terminal SNAP and CLIP-tagging. Br. J. Pharmacol. 2011;162:1439–1452. doi: 10.1111/j.1476-5381.2010.01156.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tsien R.Y. The green fluorescent protein. Annu. Rev. Biochem. 1998;67:509–544. doi: 10.1146/annurev.biochem.67.1.509. [DOI] [PubMed] [Google Scholar]
- 12.Zimmermann T., Rietdorf J., Pepperkok R. Spectral imaging and linear un-mixing enables improved FRET efficiency with a novel GFP2-YFP FRET pair. FEBS Lett. 2002;531:245–249. doi: 10.1016/s0014-5793(02)03508-1. [DOI] [PubMed] [Google Scholar]
- 13.Rizzo M.A., Springer G.H., Piston D.W. An improved cyan fluorescent protein variant useful for FRET. Nat. Biotechnol. 2004;22:445–449. doi: 10.1038/nbt945. [DOI] [PubMed] [Google Scholar]
- 14.Nagai T., Ibata K., Miyawaki A. A variant of yellow fluorescent protein with fast and efficient maturation for cell-biological applications. Nat. Biotechnol. 2002;20:87–90. doi: 10.1038/nbt0102-87. [DOI] [PubMed] [Google Scholar]
- 15.Vámosi G., Gohlke C., Clegg R.M. Fluorescence characteristics of 5-carboxytetramethylrhodamine linked covalently to the 5′ end of oligonucleotides: multiple conformers of single-stranded and double-stranded dye-DNA complexes. Biophys. J. 1996;71:972–994. doi: 10.1016/S0006-3495(96)79300-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lee N.K., Kapanidis A.N., Weiss S. Three-color alternating-laser excitation of single molecules: monitoring multiple interactions and distances. Biophys. J. 2007;92:303–312. doi: 10.1529/biophysj.106.093211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Raicu V. FRET-based determination of protein complex structure at nanometer length scale in living cells. In: Diaspro A., editor. Nanoscopy and Multidimensional Optical Fluorescence Microscopy. CRC Press; Boca Raton, FL: 2010. [Google Scholar]
- 18.Placone J., Hristova K. Direct assessment of the effect of the Gly380Arg achondroplasia mutation on FGFR3 dimerization using quantitative imaging FRET. PLoS ONE. 2012;7:e46678. doi: 10.1371/journal.pone.0046678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Miles T.F., Dougherty D.A., Lester H.A. The 5-HT3AB receptor shows an A3B2 stoichiometry at the plasma membrane. Biophys. J. 2013;105:887–898. doi: 10.1016/j.bpj.2013.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Alvarez-Curto E., Ward R.J., Milligan G. Ligand regulation of the quaternary organization of cell surface M3 muscarinic acetylcholine receptors analyzed by fluorescence resonance energy transfer (FRET) imaging and homogeneous time-resolved FRET. J. Biol. Chem. 2010;285:23318–23330. doi: 10.1074/jbc.M110.122184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Raicu V., Jansma D.B., Friesen J.D. Protein interaction quantified in vivo by spectrally resolved fluorescence resonance energy transfer. Biochem. J. 2005;385:265–277. doi: 10.1042/BJ20040226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Raicu V. Efficiency of resonance energy transfer in homo-oligomeric complexes of proteins. J. Biol. Phys. 2007;33:109–127. doi: 10.1007/s10867-007-9046-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Raicu V., Stoneman M.R., Saldin D.K. Determination of supramolecular structure and spatial distribution of protein complexes in living cells. Nat. Photonics. 2009;3:107–113. [Google Scholar]
- 24.Singh D.R., Raicu V. Comparison between whole distribution- and average-based approaches to the determination of fluorescence resonance energy transfer efficiency in ensembles of proteins in living cells. Biophys. J. 2010;98:2127–2135. doi: 10.1016/j.bpj.2010.01.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Patowary S., Alvarez-Curto E., Raicu V. The muscarinic M3 acetylcholine receptor exists as two differently sized complexes at the plasma membrane. Biochem. J. 2013;452:303–312. doi: 10.1042/BJ20121902. [DOI] [PubMed] [Google Scholar]
- 26.Singh D.R., Mohammad M.M., Raicu V. Determination of the quaternary structure of a bacterial ATP-binding cassette (ABC) transporter in living cells. Integr Biol (Camb) 2013;5:312–323. doi: 10.1039/c2ib20218b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Raicu V., Singh D.R. FRET spectrometry: a new tool for the determination of protein quaternary structure in living cells. Biophys. J. 2013;105:1937–1945. doi: 10.1016/j.bpj.2013.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Koushik S.V., Blank P.S., Vogel S.S. Anomalous surplus energy transfer observed with multiple FRET acceptors. PLoS ONE. 2009;4:e8031. doi: 10.1371/journal.pone.0008031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pisterzi L.F., Jansma D.B., Wells J.W. Oligomeric size of the M2 muscarinic receptor in live cells as determined by quantitative fluorescence resonance energy transfer. J. Biol. Chem. 2010;285:16723–16738. doi: 10.1074/jbc.M109.069443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Stoneman M.R., Patowary S., Raicu V. Quantifying the efficiency of various FRET constructs using OptiMiS (TM) Biotechniques. 2012;52:191–195. [Google Scholar]
- 31.Mannan M.A., Shadrick W.R., Dey M. An Ire1-Phk1 chimera reveals a dispensable role of autokinase activity in endoplasmic reticulum stress response. J. Mol. Biol. 2013;425:2083–2099. doi: 10.1016/j.jmb.2013.02.036. [DOI] [PubMed] [Google Scholar]
- 32.Epe B., Steinhäuser K.G., Woolley P. Theory of measurement of Förster-type energy transfer in macromolecules. Proc. Natl. Acad. Sci. USA. 1983;80:2579–2583. doi: 10.1073/pnas.80.9.2579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Koushik S.V., Chen H., Vogel S.S. Cerulean, Venus, and VenusY67C FRET reference standards. Biophys. J. 2006;91:L99–L101. doi: 10.1529/biophysj.106.096206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Biener G., Stoneman M.R., Raicu V. Development and experimental testing of an optical micro-spectroscopic technique incorporating true line-scan excitation. Int. J. Mol. Sci. 2014;15:261–276. doi: 10.3390/ijms15010261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.King C., Sarabipour S., Hristova K. The FRET signatures of noninteracting proteins in membranes: simulations and experiments. Biophys. J. 2014;106:1309–1317. doi: 10.1016/j.bpj.2014.01.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mishra A.K., Mavlyutov T., Raicu V. The σ-1 receptors are present in monomeric and oligomeric forms in living cells in the presence and absence of ligands. Biochem. J. 2015;466:263–271. doi: 10.1042/BJ20141321. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


