Estimating Drivers’ Stress from GPS Traces

Abstract

Driving is known to be a daily stressor. Measurement of driver’s stress in real-time can enable better stress management by increasing self-awareness. Recent advances in sensing technology has made it feasible to continuously assess driver’s stress in real-time, but it requires equipping the driver with these sensors and/or instrumenting the car. In this paper, we present “GStress”, a model to estimate driver’s stress using only smartphone GPS traces. The GStress model is developed and evaluated from data collected in a mobile health user study where 10 participants wore physiological sensors for 7 days ( for an average of 10.45 hours/day) in their natural environment. Each participant engaged in 10 or more driving episodes, resulting in a total of 37 hours of driving data. We find that major driving events such as stops, turns, and braking increase stress of the driver. We quantify their impact on stress and thus construct our GStress model by training a Generalized Linear Mixed Model (GLMM) on our data. We evaluate the applicability of GStress in predicting stress from GPS traces, and obtain a correlation of 0.72. By obviating any burden on the driver or the car, we believe, GStress can make driver’s stress assessment ubiquitous.

INTRODUCTION

Daily stress experienced during driving [17] may increase the likelihood of adverse events (e.g., accidents and traffic fatalities [12, 20]) and contribute to adverse health. Repeated occurrences of stress can cause or worsen cancer [37], heart diseases [7], hypertension [2], aging [29], shrinking of brain [16], fatigue, depression, and rage [24, 25]. Consequently, there has been tremendous interest in both the scientific community as well as the technology and automotive industry [5, 15, 43, 45] in developing systems to measure stress in real-time in order to enhance stress-awareness of drivers and to deliver just-in-time stress interventions [22, 27].

Driver stress had traditionally been measured post-hoc via self-reports [17] or biofluid assays [11]. Emergence of physiological sensors such as electrocardigram (ECG) and galvanic response (GSR) and their instrumentation on drivers [9] or in the car [5, 15, 43, 45] has made continuous stress measurement feasible. Research on developing accurate measure of stress during driving from physiological sensors has been an active area of research for more than a decade now [14, 41]. More recently, these physiological measures have been supplemented with data collected from the car about driving events such as steering wheel movements and braking episodes [36], and information about driving conditions from the environment [35]. In addition, video has been used to capture driver’s facial expressions to detect stress during driving [30]. Recent research is exploring the role of extraneous cognitive load on the driver (e.g., texting, navigation) [42] that may further escalate a driver’s stress.

Stress monitoring of drivers is yet to be ready for wider adoption, though. This is because monitoring of driver’s stress today requires either having the drivers wear physiological sensors or instrumenting the car with sensors and cameras. For stress monitoring to be widely available, a method is needed that can infer stress from data collected passively by commonly used existing technology, such as mobile phones.

In this paper, we propose a model named GStress to estimate the stress level of drivers from GPS traces. GPS sensors are readily available in current navigation systems and more and more smart phones are also equipped with GPS – making attainment of GPS traces in real-time increasingly feasible. Drivers can use the GStress model to become more aware of their stress during driving, overlay the stress data on a map to identify road segments frequently associated with elevated stress to plan their route accordingly, and adapt their driving behaviors if needed. GStress model can also help inform the design and use of in-vehicle technologies. For example, calls or texts can be blocked or postponed if the driver is stressed. Wide adoption of such models can be used to annotate traffic maps with current stress levels being experienced by drivers on various routes, similar to real-time traffic update displayed by the navigation systems. Such data can also be used by city planners to identify pain points in a city’s road network (e.g., difficult intersections that cause stress in many drivers).

To develop the GStress model, we used physiological data collected from 30 human volunteers who wore AutoSense [9] sensors for at least 10 hours/day for a week in their natural environment. However, 19 of these 30 volunteers were living on the university campus and rarely used a vehicle for commute. The remaining 11 participants had at least 10 driving episodes and in this paper we only report data collected from these participants.

We use GPS and self-report data to identify driving episodes from the entire day’s data. For model development, we first analyze driving episodes to identify events that have been shown to be stressful, which include stops, braking, and turns. Next, considering the wide variability across individuals in stress reactivity, we develop a Generalized Linear Mixed Model (GLMM) that separates the effects of between-person variability. The GLMM model also permits exploiting nonlinear relationships while retaining the simplicity of a linear regression. By using three factors (stops, turns, and braking) from the GPS traces, our model obtains an r value of 0.72 for predicting stress from GPS traces. We then obtain a population estimate of the person-specific biases and obtain a person-independent model. Using leave-one-subject-out evaluation, our model provides a median (across all participants) r value of 0.687 while a person-dependent model improves this median correlation to 0.762. We find that stops have the highest impact on stress, confirming the widespread belief that impedance is the genesis of stress during commute [17, 28], with quantitative data from real-life driving.

RELATED WORK

Assessment of driver’s stress is an active area of research. However, most of the existing research focus on measuring stress from physiological data [14, 41], video [30], and acoustic data [21]. More recently, these measurements have been supplemented with driving and traffic information [36, 42]. For example, [36] performed real-time stress detection using physiological signals and measurements obtained from the vehicle’s CAN-bus (e.g., speed, RPM, and throttle) and combined the physiological stress response with driving behaviors (e.g., overtake, hard brake, etc.) to improve accuracy. They trained a stress model from self-reported data. However, self-reports are episodic, prone to bias, noise, and misreport, and is less reliable for training stress models [32].

Measurement of driver’s stress has traditionally been confined to simulators due to the difficulty, effort, and risk involved in collecting data in the natural environment [22, 42]. The limited number of studies that are conducted in the natural environment followed scripted routes under supervision for a limited duration [14, 38, 41]. For example, in [14], four drivers wore physiological sensors during highway and urban driving episodes and self-report showed that urban driving was more stressful than highway, which, in turn, was more stressful than when parked in a garage. A continuous rating of stress was also obtained, however, this stress model was not validated against behaviorally accepted measures of stress.

To the best of our knowledge, this is the first study that collected continuous stress data from uncontrolled and unscripted driving episodes where participants drove their own vehicles. In addition, while most existing research utilize driving event measurements together with physiological measurements [14, 41] to improve stress measurement accuracy, we present a model for stress estimation using GPS traces obtained via smart phone alone.

DATA COLLECTION PROCEDURE

To obtain continuous stress measures experienced by drivers during (unscripted) driving, we conducted a week-long mobile health user study on stress, where participants wore a physiological sensor suite and carried a smart phone with GPS for at least 10 hours/day in their natural environment. The physiological data thus collected is processed (by applying a validated stress model [32]) to obtain a continuous measure of stress experienced by these participants and to identify association between stress and various driving events. In this section, we describe the devices and measures used in this study.

Participants

A total of 30 participants (15 females) completed the study. Our participants were university students with an average age of 24 years(SD = 4.5 years). The goal of the study was to assess stress in the natural environment where commute is a part of daily life. However, 19 of these 30 participants lived in or around campus and did not drive frequently, resulting is very few driving episodes. We excluded all data collected from participants with less than 10 driving episodes from our analysis and model development.

Sensor Suite

Our participants wore a wireless sensor suite called AutoSense [9] underneath their clothes. AutoSense consists of two unobtrusive, flexible bands worn about the chest and upper arm, respectively. The chest band provided respiration data by measuring the expansion and contraction of the chest via inductive plethysmography (RIP), two-lead electrocardiograph (ECG), and 3-axis accelerometer. Measurements collected by the sensors were transmitted wirelessly to a Sony Ericsson Xperia X8 smart phone. The sampling rates for the chest band were 21.33 HZ for RIP, 64 HZ for ECG, and 10.67 HZ for each of the three axes of accelerometers, and 1 HZ for battery level. These samples were sent 28 times/second with each packet containing 8 bytes of data and consisting of 5 samples.

Mobile Phone

Participants carried a smart phone customized to communicate with the sensor suite. The smart phone had three roles. First, it received and stored data transmitted by the sensor suite. Second, it stored data from the phone sensors, including GPS and accelerometers and these measurements were synchronized to the measurements transmitted from AutoSense. Finally, participants used the phone to complete system-initiated self-reports in the field.

Self-report Measures

In addition to the sensor measurements, data was collected from participants using self-reports, up to 20 times each day, which was administered on the study phone. The 42-item survey asked participants to rate their subjective stress level on a 6-point Likert scale [19] as well as provided additional contextual data such as whether the participant was riding or driving a vehicle. Participants were allowed to postpone or not answer a prompt. We note that data obtained using self-reports was only used for identifying drivers and not for modeling stress.

Continuous Stress Measure

The entire day (including the driving episodes) was divided into 30 second segments and the stress state for each segment was computed as a continuous measure in terms of posterior probability of being stressed using the model presented in [32]. Stress estimation from ECG has traditionally relied on a single feature (e.g., heart rate or heart rate variability) [24, 25]. Machine learning models that identify a more specific fingerprint of physiological activation began emerging in the past decade [14]. We utilized the model developed in [32] as it has been validated in the lab and the natural field environment. Although the initial model was developed to provide a binary stress output for each 1 minute of physiological data, we adapted the model to provide a stress state for each 30 second segment. We reduced the granularity from 1 minute to 30 seconds to capture stress levels associated with events such as braking, stops, and turns, events which may not last a minute. As the stress model uses statistics such as heart rate and heart rate variability, using a window smaller than 30 second will reduce the accuracy of the stress model to below 80%. This model provides a continuous stress measure that is normalized between 0 and 1, where stress values can be interpreted as No, Low, Moderate, High, and Extremely High stress for the ranges of 0–0.2, 0.2–0.4, 0.4–0.6, 0.6–0.8, and 0.8–1 respectively.

DETECTION OF TRAFFIC EVENTS

We now describe methods that we use to computationally detect potentially stressful driving events from GPS traces. We first define each event and then describe the computational method we use to detect them. In most cases, our goal is to compute the duration of these events.

Driving Episode

Definition

Vehicular movements are usually sandwiched between walking segments. Start time of a vehicular movement episode occurs when the speed (obtained from GPS samples) is over the maximum gait speed of 2.53 meter/sec [4]. A vehicular movement episode is considered a driving episode if the participant is the driver. A driving episode consists of various driving events such as stops, turns, congestions, etc.

Computation

In order to determine whether the participant was driving or riding in a commuting episode, we used participant’s response to the self-report question (completed upon conclusion of the driving episode): If you commuted since the last prompt, what type? with possible answers — Driving, Biking, Walking, Riding as a Passenger, Riding Public Transportation, and Did not commute.

Duration of Stop Segments

Definition

Stop segments refer to parts of the driving episode when the vehicular speed obtained from GPS reaches zero. Usually, stops occur when a vehicle encounters a road intersection and the traffic signal is red, there is a stop sign, or when the car is maneuvering (e.g., moving in or out of a drive-way). A stop segment can consist of multiple consecutive stops or a single stop. For our stress analysis, we separate stop events in parking lots and garages from stop events during driving by plotting the location of stops in Google Maps. We discard stop events in parking lots and garages from analysis. The total stop time is defined as the time taken between driver initiating a deceleration and the start of the following acceleration event.

Computation

To compute the duration of stop segments, we search backwards from the end time of a complete stop. We search for the moment when the driver starts decelerating. We consider prior 5 seconds from the final stop mark and compute the speed difference

$$dv=v_{t_{\text{start}}}-v_{t_{\text{end}}},$$ (1)

where t_end and t_start (= t_end – 5) are the end and start time of the 5 second window respectively, v_tend and v_tstart are the instantaneous speeds at time t_end and t_start respectively. We continue this process with 4 second overlaps (i.e. 1 second sliding) until the speed difference dv at t_end is less than 10% of the speed at t_start i.e., dv ≤ 0.1 × v_tstart and both of the two speeds (i.e., v_tstart and v_tend ) are above the maximum gait speed. We mark t_start as the start time of deceleration.

Merging of Closely Spaced Stops

We merge multiple stops that appear closely with slow moving driving segments among them. To merge these intermittent stops, we consider 5 seconds prior to the start (t_start) of each stop and compute the area under the speed curve as follows.

$${\mathit{Area}}_i=\underset{t_{\text{start}}-5}{\overset{t_{\text{start}}}{\int }}dv(t)dt,$$ (2)

where Area_i is the area associated with the i^th stop under the speed curve from time (t_start – 5) to t_start and dv is the change in speed during that time window. If Area_i < ε, then we consider this slow moving driving segment as part of the i^th stop and replace the speed values for this time period with zero. The backward propagation of the algorithm allows the detection and merging of a stop with the preceding slowly moving driving patterns until Area_i ≥ ε. The value of ε can be derived by taking the average of areas of all prior windows across all stops. For our dataset, ε = 10.87. Area under the speed curve represents distance travelled in 5 seconds.

Turn Detection

Definition

A turn is associated with a change in the driving direction (of more than 30° [33]) and a decrease in the speed of the vehicle. The geometric properties [13] of the curve determines the amount of change in driving direction and speed.

Computation

We detect turn from changes in driving direction obtained from GPS bearing using a modified approach proposed in [33, 46]. For speeds < 3m/s, when GPS bearing data is less accurate, we consider the heading at current sample and fifth previous sample from the current sample. For speeds ≥ 3m/s, we consider the heading at current sample and third previous sample from the current sample. A turn is detected when the absolute value of direction change (i.e. difference between heading at the two samples) is > 30° [33]. Sign of the direction change defines the turn type (right or left).

Duration of Braking and Acceleration After Braking & Stop

Definition

Braking is a driving event that results in an immediate deceleration and sometimes can result in a complete stop. In our analysis, we consider only those braking segments that are followed by an acceleration segment. Braking that leads to a stop are considered to be part of the corresponding stop event. As a result, some braking events within a driving episode are subsumed in stop segments. Intensity of deceleration defines the category of braking such as negligible, moderate, and severe [8, 18]. After braking, a driver usually starts to increase the speed up to an almost constant speed. For our analysis, we consider this segment of speed up after braking as an acceleration after braking segment. We also consider the speed up segment after a stop as an acceleration after stop segment in our analysis.

Computation

For braking, we first find the local minima in the speed curve of each driving segment and then identify the start time of deceleration. We use “Imregionalmin” [34] to find Regional minima and “PeakFinder” [31] to find local minima. To identify the start time of deceleration, we examine the speed difference between prior seconds following a similar approach that we used to identify deceleration start time for stops. The end time of a braking segment occurs when acceleration begins. We determine the end of an acceleration after braking segment by reversing the search process we use to find the start of a braking event. Similarly, we determine an acceleration after stop segment starting from the end of stop segment.

Duration of Congestion

Definition

When the demand of a road network exceeds its capacity, the network imposes additional travel cost to all users of the network, a situation known as vehicular congestion. It can happen on a regular, cyclic basis reflecting the social and economic activities of an area or happen irregularly in certain points in the network due to irregular occurrence of road work, breakdown, and/or accidents [44].

Computation

We use Density-Based Spatial Clustering of Applications with Noise (DBSCAN) [10] to detect traffic congestion. We did not have access to surrounding traffic and geographical information [3, 6] that could improve the detection accuracy. To apply DBSCAN, we define our core points as those points/sample that have ≥ 3 points/sample within the neighborhood of radius 15 meter since a driver moving as slowly as 5 m/s can pass 15 meters in 3 seconds and meanwhile the GPS receiver can gather 3 samples at a sampling rate of 1 Hz. After we find the core points, we consider them together to make congestion segments. We consider only ≥ 5 minutes long segments. We found only a few congestion segments in our dataset, due to unscripted natural driving.

Duration of Driving Segments

We consider those portions of a driving episode as driving segment that remains after extracting the stops, turns, braking, acceleration, and congestion segments.

G-STRESS MODEL

We first present a summary of our dataset, observed stress patterns from physiological data, and finally present the development and evaluation of the GStress model.

Data Summary

Of the 30 participants, 25 reported at least one instance of driving and we obtained a total of 372 driving episodes. For stress measurement and model development, we selected only those participants who reported at least 10 driving episodes, resulting in 11 participants who contributed 295 driving episodes. We further excluded data from one participant (ID# 31) as s/he reported having an unusually stressful week. Of these 295 episodes considered initially, we excluded episodes with low quality physiological data, resulting in 181 (37.05 hours) driving episodes. We identified 637 stops, 1120 turns, 840 braking, and 1477 acceleration segments within these 181 driving episodes. Figure 1 shows distribution of these driving segments. The average durations of stop, turn, braking, and acceleration after braking segments were 2.0389 minutes (SD = 1.72 minutes), 0.28 minutes (SD = 0.18 minutes), 0.20 minutes (SD = 0.32 minutes), and 0.44 minutes (SD = 0.51 minutes) respectively. We also observed five congestion segments with an average duration of 5.95 minutes (SD = 1.04 minutes).

Figure 1.

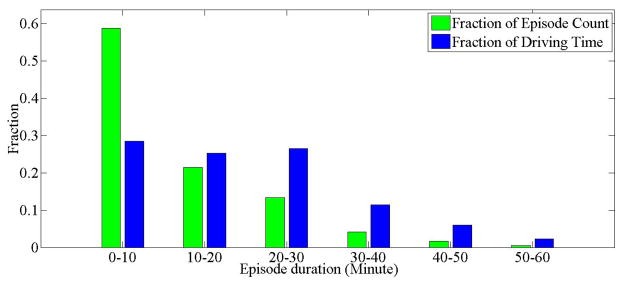
Distribution of driving episode counts and driving durations. We observe that a majority of driving episodes are ≤ 30 minutes.

Patterns of Stress from Physiological Data

The average stress levels (obtained by applying a stress model [32] on physiological data) during driving and rest of the day are 0.3992 and 0.2178 (with standard errors of 0.0041 and 0.0013) respectively. Thus, driving is 83% more stressful than rest of the day, which is consistent with existing literature [14, 36, 40, 41]. Figure 2 presents average stress level of 11 participants during driving and rest of the day.

Figure 2.

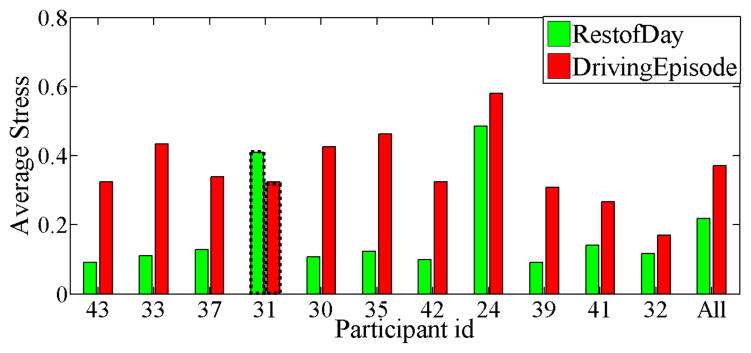
Average stress levels (obtained from physiological data) during driving and rest of the day for 11 selected participants.

To further examine the difference between stress during driving and rest of the day, we used a two sample t-Test with the null hypothesis, H₀ : μ_D = μ_RD, where μ_D and μ_RD are average stress during driving and rest of the day, respectively. We performed for individual participants and for the entire population, i.e. on all participants together. At α = 0.05 significance level, we reject the null hypothesis for both individual and population level with a p-value < 0.001. Therefore, participants’ average stress levels during driving and rest of the day are not equal. It is interesting to point out that, while calculating stress values, we observed an anomaly for Participant ID#31. This participant had three exams and a couple of deadlines during the study week, resulting in unusually high levels of stress for the rest of the day. During this study week, this participant used driving as a stress reduction technique as s/he mentioned enjoying driving a lot. Hence, P#31’s data was excluded from the analysis.

Development of the GStress Model

The goal of the GStress model is to estimate drivers’ stress level during a driving episode from GPS traces. For stress estimation, we used time duration of stops, turns, braking, and driving segments within a driving episode.

The simplest model is a linear regression model with the assumption that errors are normally distributed. This assumption does not hold when the response variable (Y ) refers to count, proportion, or positive continuous data. Our response variable (Y ) refers to average stress of a driving episode, a positive continuous data.

The next candidate is Generalized Linear Models (GLM) that does not assume normality. GLM assumes that a linear function (η = g(.)) of the mean (μ = E[Y ]) of the response variable is related to the predictors i.e. η = g(μ) = Xβ, where, X stands for predictor variables, and β are the fixed-effects regression coefficients. We use Gamma for the underlying distribution that is suitable for scenarios where the response variable are positive continuous data. We use identity as our transformation/link function (i.e. μ = (E[Y ]) = Xβ, where, Y = Xβ + ε). An advantage of using such a descriptive model is that, it enables us to determine the relative importance of each factor in measuring the response variable.

Driving in the natural environment, however, may involve unanticipated events such as phone calls/texts and adverse weather/road conditions in addition to the major events detected from GPS traces. These unaccounted factors and wide between-person variation in stress-reactivity limits the use of regression models such as GLM that rely on fixed effects only, i.e. effects that can be explained with known factors such as stops, turns, and braking.

To account for the random effects, we use Generalized Linear Mixed Model (GLMM), a widely used model in the health research domain. GLMM takes into account both the fixed effects and the random effects that cannot be estimated with fixed effects or errors. The general form of the model is Y = Xβ + Zγ + ε, where, Y, X, β, Z, γ, and ε stand for the response variable, predictor variables, fixed-effects regression coefficients, design matrix for random effects, random effects, and random errors or residuals, respectively.

Our predictor variables for the fixed effects are the amount of time (in terms of 30 second segments) affected by stop (x₃), braking (x₄), turn (x₅), acceleration after braking (x₆), acceleration after stop (x₇), and congestion (x₈). We consider these segments individually and independently. To determine which segment is affected by what type of driving event, we apply majority-voting on the duration of different driving events that occurs within or overlaps with an individual segment. We also include the stress level prior to driving (x₁) and the amount of driving time (x₂) not affected by these driving events. We scale all the predictor variables (except x₁) on a 0 to 1 scale by dividing the x_i’s with the duration of a driving episode. The output or response variable (y) is the average stress of a driving episode. We consider person-level variation as our random effect.

Our stress estimation model based on GPS traces, GStress is

$$y_{ij}=({\beta }_0+{\gamma }_j)+\sum _{k=1}^8{\beta }_k{x}_{\mathit{kij}}+\epsilon$$ (3)

where, y_ij is the average stress of i^th driving episode of person j; for k = 1, . . . , 8, β_k is the k^th fixed effect, x_kij is the k^th predictor variable for fixed effect in i^th episode of j^th person; β₀ is the fixed effect on intercept and γ_j is the random effect on intercept for the j^th person.

While building the GStress model, we did not find sufficient instances of congestion. We tested the significance of both “Congestion” and “Acceleration” (both after braking and stop) i.e. H₀ : β₆ = β₇ = β₈ = 0. We built two models — with and without the congestion and acceleration effects referred to as “gm44” and “gm33”, respectively. We could not reject the H₀ for χ² = 1.5678 and p-value = 0.2105 (see Table 1) at α = 0.05 significance level. Also, model “gm33” had lower Akaike Information Criterion (AIC) [1] and Bayesian Information Criterion (BIC) [39] (see Table 1), so the effect of “Congestion” and “Acceleration” was not significant in our dataset. However, in a dataset where instances of congestion is not minimal, congestion may have a significant impact.

Table 1.

χ² test to check the significance of “person random effect” and fixed effect “congestion” and “acceleration”.

Model	AIC	BIC	Deviance	χ2	p-value
gm11	−3367.1	−3341.4	−3383.1
gm22	−3447.3	−3418.4	−3465.3	82.245	< 0.001
gm33	−95.5	−69.9	−107.88
gm44	−95.074	−66.287	−109.35	1.5678	0.2105

We also examined whether the random effect of subject is significant i.e. H₀ : γ = 0. We built two models — with and without person random effect referred to as “gm22” and “gm11”, respectively. We rejected the null hypothesis for χ² = 3237.8 and p-value < 0.001 (see Table 1) at α = 0.001 significance level. Also, model “gm22” had lower AIC, and BIC (see Table 1). Hence, the person random effect is significant. Therefore, the final GStress model is $y_{ij}=({\beta }_0+{\gamma }_j)+{\sum }_{k=1}^5{\beta }_k{x}_{\mathit{kij}}+\epsilon$ Table 2 presents the proposed GStress model. Stress levels prior to driving (x₁), driving time without events (x₂), amount of driving time affected by stop (x₃) and affected by turn (x₅) were significant at α = 0.001, amount of time affected by braking(x₄) was significant at α = 0.01, and intercept was significant at α = 0.05. We observe that all significant fixed effect factors have positive coefficients, i.e. they increase stress while driving. Among all the driving events, stop has the highest weight (β₃ = 0.755).

Table 2.

G-Stress: Driving Stress Estimation Model. Here, SE stands for standard error.

Fixed effects	β	SE	t-value	p-value
Intercept	−0.445	0.181	−2.454	0.014147
x1	0.681	0.077	8.795	<0.001000
x2	0.682	0.188	3.632	0.000281
x3	0.755	0.207	3.655	0.000257
x4	0.668	0.210	3.178	0.001480
x5	0.703	0.200	3.523	0.000427

Evaluation of GStress

We obtained a Pearson Correlation, r = 0.722 for predicting stress from GPS traces via the GStress model (see Table 2). The variance for person variability, residual, and fixed effects were 0.002, 0.188, and 0.061, respectively. Therefore, $R_{\mathit{GLMM}}^2(c)=0.252$ [26], i.e. 25% variability of the data can be explained with both fixed effect and random effect.

To evaluate the applicability of the GStress model on participants on whom no training data has been collected, we trained the model on nine participants and applied it on the remaining one participant with a population estimate of the random effect and fixed effects. Figure 3 shows the correlation for each subject. For this leave-one-subject-out validation, we obtained a median correlation of 0.687.

Figure 3.

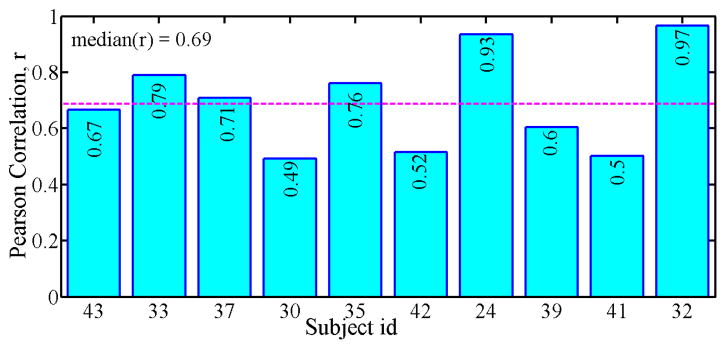
Pearson Correlation, r between actual and estimated average stress for “leave one subject out” validation. Horizontal magenta line corresponds to median correlation (0.687) from all 10 test subjects.

We also evaluated the GStress model using leave-one-episode-out validation, where we trained the model on n – 1 driving episodes out of n episodes from the same participant and applied it on the remaining one driving episode to estimate stress. We continued this process to get n estimated stress values for all n episodes and obtained correlation between the estimated and actual stress of all these n episodes. Similarly, we calculated correlation for all other subjects via the leave-one-episode-out approach. With this person-dependent model, we obtained a median correlation of 0.762 (Figure 4). We observed that the person-dependent model (Figure 4) has a better correlation than the person-independent model (Figure 3). The minimum correlation improves from 0.49 to 0.64. It suggests that the prediction accuracy is likely to improve over time for any user.

Figure 4.

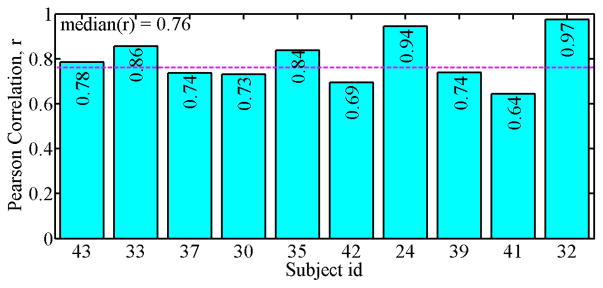
Pearson Correlation, r between actual and estimated average stress for “leave one driving episode out” validation. Horizontal magenta line corresponds to median correlation.

To further evaluate the performance of the GStress model, we analyzed the Bland-Altman plot [23](Figure 5). The plot shows moderate agreement between actual and predicted stress, however, lack of consistent agreement for values lower than 0.4 and variability above 0.4 were mainly observed within the 50% difference levels. From Figure 5, we cannot reject the null hypothesis, H₀, that “the actual and estimated stress values have same mean i.e. the mean of paired differences of actual average stress and predicted average stress is zero (0)” with a p-value = 0.8893 at α = 0.1 significance level (using paired t-test). Therefore, the two distributions, i.e. estimated average stress values obtained from the GStress model and the actual average stress values, were not significantly different.

Figure 5.

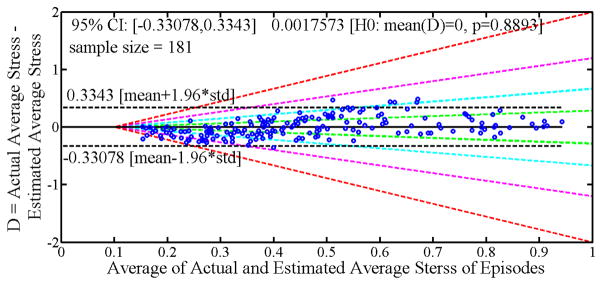
Bland-Altman plot for the actual and estimated average stress for all driving episodes obtained from GStress. Green, cyan, magenta and red dashed lines are for 25%, 50%, 75% and 100% difference respectively.

Contribution of Driving Events to Stress

We now quantify the contribution of each driving event to the total stress. The contribution of the events depend on two factors — how frequent they occur in a typical driving episode and their weight (β) in the driving stress model (Table 2). For the first, we compute the amount of time (in terms of number of 30 second segments) that are classified to be affected by a particular event. Figure 6(a) shows the fraction of time in a driving episode that corresponds to each of the driving events — stops, turns, brakings, and driving and Figure 6(b) shows the contribution of these events to the overall stress level. We observe that stops were more stressful than driving as stops contribute 27% to the stress even though they only occur 24% of the time. On the other hand, driving accounts for 32% of the time, but only contributes 28% to the total stress level. This may imply that reducing number of stops in a driving episode may be an effective approach to reducing stress during driving. We note that high occurrence of stops, turns, and braking in our dataset may be due to participants driving in university neighborhoods.

Figure 6.

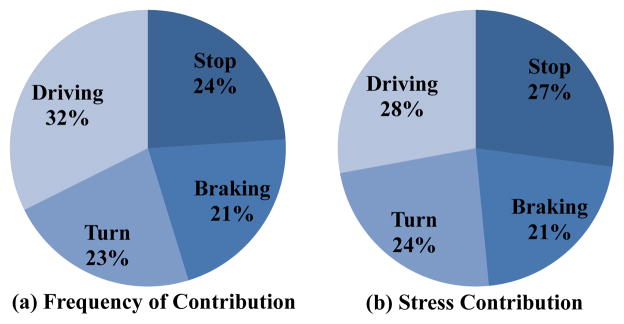
(a) shows the fraction of an average driving episode that is affected by various stressful factors i.e. frequency of events in an average driving episode. (b) shows the contribution of each factor to the total stress level.

CONCLUSIONS, LIMITATIONS, AND FUTURE WORK

Our work pointed out the feasibility of estimating drivers’ stress using only GPS traces collected from the driver’s smart phone. The proposed GStress model provides a correlation of over 0.7 by identifying major factors such as stops, turns, and braking associated with driving stress. This work has several limitations that may be addressed in future research. First, the accuracy of stress estimation can be improved by incorporating additional factors such as road information (e.g., complex intersections, number of lanes, type of road, speed limit, location of traffic light, curvature information, etc.) that can be obtained from a geographic database, real-time traffic conditions (e.g., level of congestion) and driving behaviors (e.g., patterns of acceleration and braking).

Second, dataset used in developing and evaluating GStress is limited to 10 drivers without any scripting of the roads on which they all drive. While it improves the ecological validity of the model, it prevents comparison with literature that mostly prescribed scripted routes to obtain uniformity of road conditions. A larger scale study that involves more participants for a much longer duration can generate data set that are large enough to compare the stress responses of several drivers when they happen to drive on the same road segments under similar conditions. That way comparison with existing works can be done while maintaining ecological validity. Third, even though GStress model is based on real-life dataset from 10 drivers, these are mostly college students. The stress response of young drivers may not accurately represent those experienced by other populations such as seniors, or those with a history with serious motor vehicle accidents. Fourth, stress experienced by drivers in a specific city (from where participants were selected for our study) may not accurately represent stress experienced during driving in other cities in the United States and more broadly in other parts of the world. Additional studies need to be conducted to evaluate the generalizability of GStress or to determine the adaptations necessary to improve its generalizability.

Finally, although GStress has a potential to improve stress awareness and reduce stress of drivers, this potential is yet to be demonstrated. Stress awareness applications or stress interventions that make use of the GStress model need to be developed and evaluated for its efficacy in diverse population in various driving environments to generate evidence of clinical utility of GStress in reducing drivers’ stress.