A Novel Approach for Identifying Causal Models of Complex Diseases from Family Data

Abstract

Causal models including genetic factors are important for understanding the presentation mechanisms of complex diseases. Familial aggregation and segregation analyses based on polygenic threshold models have been the primary approach to fitting genetic models to the family data of complex diseases. In the current study, an advanced approach to obtaining appropriate causal models for complex diseases based on the sufficient component cause (SCC) model involving combinations of traditional genetics principles was proposed. The probabilities for the entire population, i.e., normal–normal, normal–disease, and disease–disease, were considered for each model for the appropriate handling of common complex diseases. The causal model in the current study included the genetic effects from single genes involving epistasis, complementary gene interactions, gene–environment interactions, and environmental effects. Bayesian inference using a Markov chain Monte Carlo algorithm (MCMC) was used to assess of the proportions of each component for a given population lifetime incidence. This approach is flexible, allowing both common and rare variants within a gene and across multiple genes. An application to schizophrenia data confirmed the complexity of the causal factors. An analysis of diabetes data demonstrated that environmental factors and gene–environment interactions are the main causal factors for type II diabetes. The proposed method is effective and useful for identifying causal models, which can accelerate the development of efficient strategies for identifying causal factors of complex diseases.

MOST complex diseases involve a large number of genes and intricate patterns of inheritance. These heterogeneities result in difficulties in identifying genetic models using segregation analyses (Demenais and Elston 1981; Karunaratne and Elston 1998; SAGE 1994). The flexible framework based on variance components has enabled many extensions for fitting genetic models, with major causal factors of additive genetic effects, shared environment, and unique environment (Morton and MacLean 1974; Falconer and Mackay 1996; Rabe-Hesketh et al. 2008). Genetic models based on familial aggregation using relative risk and covariance could provide partial assessment of relevant parameters such as the number of loci and/or the disease allele frequencies (Elston and Campbell 1970; McGue et al. 1983; Risch 1990; Lange 2002; Slatkin 2008).

These genetic models are based on linear models that search the linear relationships between the trait and the causal components. The linear models in genetics were developed to be applicable to most kinds of genetics problems (Mackay 2014). While genetic epidemiologists have focused on the development of modern statistical technologies derived from Fisher’s variance components (Fisher 1918), the focus of epidemiologists has been the fundamental concept of causation. A cause is an event, condition, or characteristic that results in an effect (a disease), alone or in conjunction with other causes (Rothman 1976; Rothman et al. 2008). A sufficient cause is a minimal set of conditions and events that inevitably produces the disease (Rothman 1976; Rothman et al. 2008). Therefore, the sufficient component cause (SCC) model was designed to explain a complete causal mechanism (Rothman et al. 2008). Regarding causation in epidemiology, there are other types of concepts of causation such as probabilistic causation and counterfactuals (Parascandola and Weed 2001), which include elaborate efforts to apply genetic epidemiology to studying causation based on directed acyclic graphs (Pearl 2009a,b). Although there are debates about the best model (Parascandola and Weed 2001), the SCC model is useful for studying individual mechanisms of causation (Rothman et al. 2008).

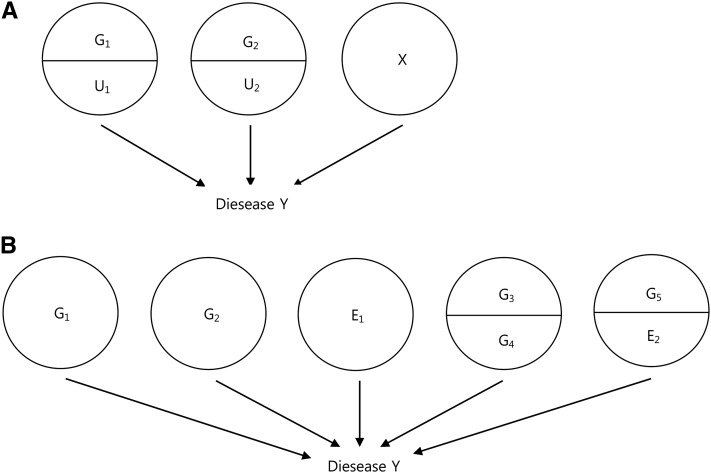
To identify causal components, the SCC model in epidemiology (Rothman 1976; Rothman et al. 2008) might be more straightforward than the conventional approaches in statistical genetics (Figure 1). Similar to the logic by Mackie (1980), the SCC model is composed of several sufficiently causal components, each of which is a set of minimal events that inevitably produce disease (Rothman 1976; Rothman et al. 2008; Madsen et al. 2011a). Therefore, each of the minimal events in a sufficient causal component is neither necessary nor sufficient. Several conventional genetic models, including the two-locus heterogeneity model could correspond to SCC models for certain circumstances (Madsen et al. 2011b). The two-locus heterogeneity model indicates that an individual is affected if one has a mutation in any two loci. Therefore, the two loci are parallel (or independent), as described previously (Darroch 1997). Through expansions of the conventional linear models in genetics (Yi et al. 2011), each sufficient cause could correspond to each component in genetic models, such as additive genetic components, shared environments, gene interactions, and others; however, the original framework of the SCC model, rather than the linear models, should be investigated in advance to minimize the parameter assumptions.

Figure 1.

Typical sufficient component cause (SCC) models for a causation of disease Y. (A) A typical model with more than two sufficient causes consisting of two genetic components (G₁ or G₂) with their causal partners (U₁ or U₂, respectively) and the rest of sufficient causes (X). (B) A model with five sufficient causes (two single genetic causes (G₁ and G₂), one environmental cause (E₁), one genetic interaction cause (causal partners: G₃ and G₄), and one gene–environment interaction cause (causal partners: G₅ and E₂).

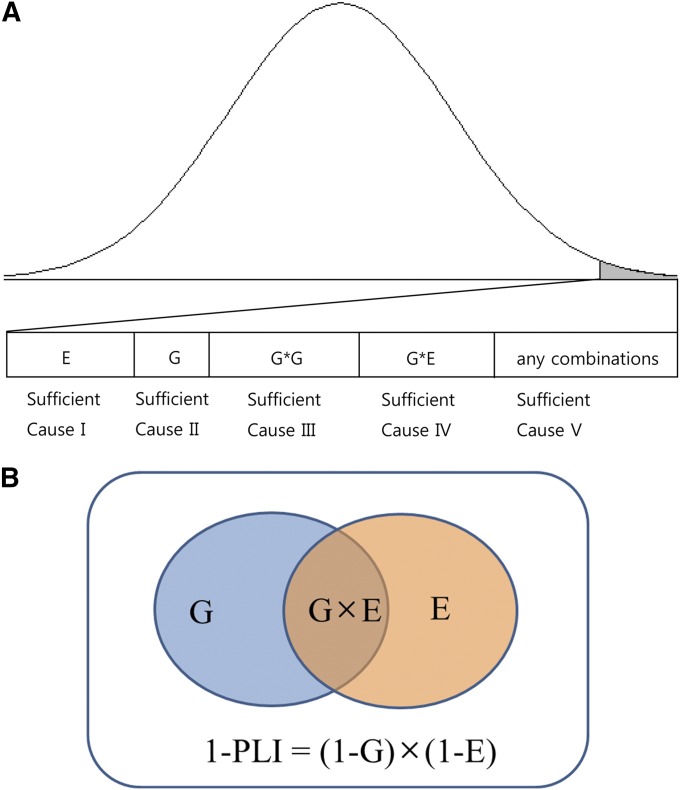
To identify causal models, an advanced framework based on the SCC model using the disease concordances of relative pairs with four causal components was proposed (Figure 2A), i.e., single genetic factors (G), complementary gene interactions (G × G), gene–environment interactions (G × E), and environmental factors (E). The four causal factors are parallel (Darroch 1997), as are the disease loci in the G component. The parallelism (independency) among the disease loci indicates that each disease genotype in the G component is epistatic, masking the effect of other genotypes based on the original Bateson definition (Phillips 2008). Therefore, the G component are composed of many parallel loci, each of which has rare or de novo mutations (Gratten et al. 2013) that are fully penetrant. Due to the existence of other sufficient components, each gene is sufficient, yet unnecessary, to the disease presentation.

Figure 2.

(A) Causal components and the population distribution of complex traits (the shaded region indicates the affected population). (B) A causal Venn diagram with two components of G and E.

Each G × G and G × E are composed of a set of minimal events, each of which is a disease gene or an causal environment. The events of G × G (or G × E) are synergistic, meaning that all of the events in G × G (or G × E) should occur for the disease presentation (Darroch 1997). Therefore, the partial concept of statistical gene interaction, defined as any statistical deviation from the additive combination of two loci in their effects on a phenotype (Phillips 2008), was applied to the G × G component, which is denoted by the term “complementary interaction” in this study (Strachan and Read 2004). Part of the genetics follows numerical expressions that were presented previously (Elston and Campbell 1970; Risch 1990). A standard Bayesian MCMC was implemented on the genetic model with four major causal factors to infer the proportion of these causal factors in disease presentation.

Materials and Methods

Reformulation of the concordance of relative pairs

In the SCC model, there are sufficient causal factors, each of which is independent. Figure 1A indicates one of the general SCC models (Rothman et al. 2008; Madsen et al. 2011a). If the disease Y is considered as a breast cancer as indicated in a previous example, G₁ could be causal mutations in BRCA1, with U₁ as the causal partner that causes a breast cancer in combination with G₁ (Madsen et al. 2011a). G₂ could be causal mutations in BRCA2, with U₂ as the causal partner of G₂, and X indicates all other sufficient causal factors of the breast cancer, as in the previous example (Madsen et al. 2011a). As indicated in the Introduction, the possible causal factors of complex diseases are G, E, G × G, and G × E. In Figure 1B, a complex disease (Y) having five sufficient causal factors is presented. G₁, G₂, and E₁ can solely cause the disease by itself, yet the G₃ and G₅ can cause the disease only when their causal partner exists. In Figure 1, each event happens separately; however, in reality, two or more sufficient causal factors happen coincidently as shown in Figure 2B. Assuming that causal factors are independent, the population with no disease during their lifetime is represented as 1–PLI (population lifetime incidence), which is the same value obtained when all fractions of the population without the risk factor are multiplied. If z_i indicates the proportion of a causal factor for k risk factors, the generalization of the population with no disease is expressed as follows for four causal factors:

$$1-\text{PLI}={\displaystyle \prod _{i=1}^k(1-z_i)}.$$ (1)

Considering the entire population, the normal–normal pairs were included in addition to the normal–disease and disease–disease pairs. For relative pairs, the probability of normal–normal (P_NN), normal–disease (P_ND), and disease–disease (P_DD) pairs for each relative pair can be expressed as

$$\begin{array}{l}{\displaystyle \prod _{i\in K}^{}{\displaystyle \sum _{}^{}{P}_i(X_1,X_2)}}=1,K=\left\{\text{1,2,3,4}\right\}\\ P_{\text{NN}}^i=P_i\left(X_1=0,X_2=0\right)\times P_{\text{NN}}^{i-1}\text{,}i=\text{2,3,4;}{P}^1=P_1\left(X_1,X_2\right)\\ P_{\text{ND}}^i=P_i\left(X_1=0,X_2=0\right)\times P_{\text{ND}}^{i-1}+\left\{P_i(X_1=0,X_2=1)+P_i(X_1=1,X_2=0)\right\}\times \left(P_{\text{NN}}^{i-1}+\frac{1}{2}{P}_{\text{ND}}^{i-1}\right).\\ P_{\text{DD}}^i=P_i\left(X_1=0,X_2=0\right)\times P_{\text{DD}}^{i-1}+\left\{P_i(X_1=0,X_2=1)+P_i(X_1=1,X_2=0)\right\}\times \left(P_{\text{DD}}^{i-1}+\frac{1}{2}{P}_{\text{ND}}^{i-1}\right)\\ +P_i\left(X_1=1,X_2=1\right).\end{array}$$ (2)

P_i indicates the probability of disease concordance for the ith causal factor, and Pⁱ indicates the probability of disease concordance at the ith iteration including up to ith causal factor. Because there are four causal factors, the number of iterations is three, starting from P¹_NN, P¹_ND, and P¹_DD for the first causal factor to yield the final probability of P_NN, P_ND, and P_DD. In P_i of each causal factor i, X_j indicates the causal status of individual j due to the corresponding causal factor i. For a G factor, X_j indicates the genotype of individual j, where 1 is the disease genotype and 0 is the normal genotype. Therefore, X_j = 0 means that the individual has normal genotypes for all of the disease loci of the G factor. For an E factor, X_j is 0 when the individual has a normal environment for one’s entire life, and 1 otherwise. For a causal factor of G × G, X_j is 1 when the individual has the disease genotypes in all of the corresponding pathway genes, and it is 0 otherwise. For a causal factor of G × E, X_j is 1 when the individual has a disease genotype (or disease genotypes) and experienced an interacting causal environment. Each gene is either dominant or recessive, and allelic heterogeneity in a gene is dealt with by considering a haplotype with any disease allele(s) as a disease allele.

The probabilities of P(X₁,X₂) must be derived, of which there are four, i.e., P(X₁ = 0,X₂ = 0), P(X₁ = 1,X₂ = 0), P(X₁ = 0,X₂ = 1), and P(X₁ = 1,X₂ = 1). The sum of all four probabilities is one. For the G factor, due to epistasis, when two or more disease genes are present, at least one disease genotype would result in the presentation of the disease. All possible combinations of genotypes were considered, and the probability, P(X₁,X₂) for n disease genes of the G factor, was obtained by

$$\begin{array}{l}P\left(X_1=0,X_2=0\right)={\displaystyle \prod _i^n\left\{{\displaystyle \sum _{j}P\left(G_j^N\right)\left({\displaystyle \sum _k{I}_{k}P\left(X_2=0|k,G_j^N\right)}\right)}\right\}}\\ P\left(X_1=0,X_2=1\right)+P\left(X_1=1,X_2=0\right)\\ ={\displaystyle \prod _i^n\left\{{\displaystyle \sum _{j}P\left(G_j\right)\left({\displaystyle \sum _k{I}_{k}P\left(X_2=0|k,G_j^{}\right)}\right)}\right\}}-{\displaystyle \prod _i^n\left\{{\displaystyle \sum _{j}P\left(G_j^N\right)\left({\displaystyle \sum _k{I}_{k}P\left(X_2=0|k,G_j^N\right)}\right)}\right\}}\\ +{\displaystyle \prod _i^n\left\{{\displaystyle \sum _{j}P\left(G_j^N\right)}\right\}}-P\left(X_1=0,X_2=0\right)\\ P\left(X_1=1,X_2=1\right)={\displaystyle \prod _i^n\left\{{\displaystyle \sum _{j}P\left(G_j\right)\left({\displaystyle \sum _k{I}_{k}P\left(X_2=1|k,G_j^{}\right)}\right)}\right\}}-{\displaystyle \prod _i^n\left\{{\displaystyle \sum _{j}P\left(G_j^N\right)\left({\displaystyle \sum _k{I}_{k}P\left(X_2=1|k,G_j^N\right)}\right)}\right\}},\end{array}$$ (3)

where G_j indicates the genotype j of the first individual, among which G^N indicates normal genotypes; I_k indicates the probability of the identical-by-descent (IBD) status, k (0, 1, or 2), between two individuals; and P(X₂|k,G_j) indicates the probability of the disease genotype status of the second individual for a given IBD and a given genotype of the first individual.

For P(X₁,X₂) for G × G with n disease genes, all of the genes should have their disease genotypes when an individual is affected. G_j indicates the genotype of gene, j. For each gene, there are two types of genotypes, normal and disease. G^D is the probability vector of disease genotypes, and G is the probability vector of all genotypes. For instance, if a gene is dominant with a disease allele (D) and a normal allele (d), G^D of gene, j, is a probability vector of DD and Dd genotypes and G is a probability vector of DD, Dd, and dd genotypes. If ID_j indicates the probability that the second individual has a disease genotype based on the IBD status of the first individual with the genotype, G_j, each probability can be expressed as

$$\begin{array}{c}{\text{ID}}_j={\displaystyle \sum _k{I}_{k}P\left(X_{2,j}=1|k,G_j\right)}\\ P\left(X_1=1,X_2=1\right)=\left({\otimes }^n{\mathbf{G}}^{\mathrm{D}}\right)•\left({\otimes }^n\mathbf{I}{\mathbf{D}}^{\mathrm{D}}\right)\\ P\left(X_1=1,X_2=0\right)=\left({\otimes }^n{\mathbf{G}}^{\mathrm{D}}\right)•\left[\mathbf{1}-\left({\otimes }^n\mathbf{I}{\mathbf{D}}^{\mathrm{D}}\right)\right]\\ P\left(X_1=0,X_2=0\right)=(\left({\otimes }^n\mathbf{G}\right))•\left[\mathbf{1}-\left({\otimes }^n\mathbf{ID}\right)\right]-\left({\otimes }^n{\mathbf{G}}^{\mathrm{D}}\right)•\left[\mathbf{1}-\left({\otimes }^n\mathbf{I}{\mathbf{D}}^{\mathrm{D}}\right)\right]\\ P\left(X_1=0,X_2=1\right)=1-\left({\otimes }^n{\mathbf{G}}^{\mathrm{D}}\right)•\mathbf{1}-P\left(X_1=0,X_2=0\right).\end{array}$$ (4)

Here, ID is the probability vectors corresponding to G, and ID^D is the probability vector corresponding to G^D. X_2,j indicates the disease genotype status of the second individual for gene, j. The Kronecker power (⊗ⁿ) indicates the n times of the Kronecker product of the following vector. For example, ⊗³G indicates G ⊗ G ⊗ G. Because equal frequencies were assumed in the current study, all Gs (or G^Ds) for dominant genes are identical, as are those for recessive genes. The vectors are indicated as boldface letters.

For a causal factor of gene–environment interactions (G × E), the calculation of the genetic component (G_E) interacting with the environment is identical to the calculation of the single genetic components (G) in Equation 3. In this case, however, an individual is affected only when the individual has the disease genotype (G_E) and is exposed to the environmental factor (E_G) that interacts with the disease genotype. The models can be extended to include the complementary gene interactions as the G_E component. In this case, the P(X₂,X₁) is based on Equation 4. Additional extensions for both single genetic components (G) and complementary gene interactions (G × G) interacting with environments are also possible.

Bayesian inference

For the Bayesian inference, the relative pairs with at least one affected individual are considered. The relative types include monozygotic twins (MZT), parent–offspring (P–O), dizygotic twins (DZT), siblings (sib), second-degree relative pairs (grandparent–grandchild and avuncular pairs), third-degree relative pairs (cousins), etc. The model contains four distinctive and independent causal factors to model disease presentations: E, G, G × G, and G × E. The Dirichlet distribution was used to model the proportions of four causal factors. Without any prior information, an uninformative prior is a common choice. By assuming α₁ = α₂ = α₃ = α₄ = 1, an uninformative prior on the causal factors was used, which was proper in the current situation,

$$Q=(pE,pG,p(G\times G),p(G\times E))\sim \text{Dir}({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4)$$

$$\text{Posterior}\propto \text{Likelihood}\times \text{Priors}\propto {\displaystyle \prod _i^{}P(Y_i|N_i,{\theta }_i)P(\alpha )P(K).}$$ (5)

Y_i is the number of pairs with disease concordance in the N_i pairs of the ith relative type, and θ_i is the concordance rate of the relative type i. In this equation, P(Y_i|N_i,θ_i) is the binomial density function. If a cohort family data set is available, the multinomial density function for NN, ND, and DD pairs can be used instead. Based on α, the rest of the latent parameters were determined to be the same as the MCMC update described below. K is a vector of gene numbers for each genetic component for which an uninformative prior (a uniform distribution from 0 to the maximum number of genes for each component) is also applied.

The MCMC simulations are performed based on the model (Figure 3). Because the differences in concordance rates between models with different numbers of genes approach a rapid convergence to 0 as the number of genes increases, a large number of genes is neither necessary nor efficient. Therefore, the number of genes in each causal factor is set to be uniformly distributed between 0 and 8, which, in Equations 2–4, is the maximum number of a matrix computation in regular 32-bit computing facilities. All other variables, except Q and K, are latent variables and are denoted as Z. Z includes each component of the dominant (G_D) and recessive (G_R) genes in the G × G term, each component of the genetic (G_E) and environment (E_G) fractions in the G × E term, and the frequencies of genes in each genetic component. For convenience, equal frequencies of variants in the same genetic component are assumed. The rest of unmentioned parameters were automatically determined on the basis of these parameters. If the model has distinctive concordance rates, the posterior means of latent variables also localize to the correct values.

Figure 3.

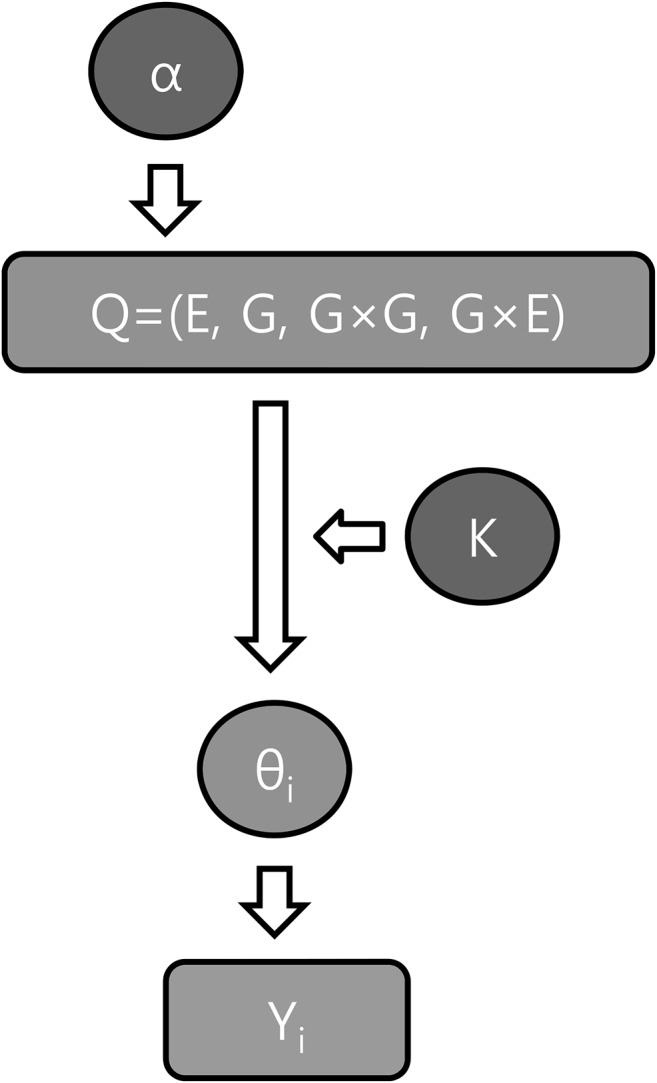
Graphical representation of the hierarchical mixture model (α, prior parameters; K, number of genes; Q, proportions of causal factors; θ_i, concordance rate of relative pair i; Y_i, concordance data of relative pair i).

A detailed MCMC update proceeds as follows. For the proper usage of Dirichlet distribution, log transformations are applied to Equation 1. Let c represent an arbitrary constant, and α is a vector of 1 with a length that corresponds to the matched parameters. For the genetic component (G) and the genetic component that interacts with the environment (G_E), there is at least more than one disease gene, either dominant or recessive. The terms f_D and f_{D|G × E} represent the frequency of dominant genes in the genetic (G) and gene–environment interaction (G × E) components, respectively. For the gene interaction component, pG_D and pG_R are the proportions of dominant genes and recessive genes, respectively.

K is a vector that lists the number of recessive genes for the G, G_R, and G_E terms and the number of dominant genes for the G_D term. In this model, because the concordance rates depending on the number of dominant genes are indistinguishable, except for the G × G component, it is assumed that there is one dominant gene for the G and G_E components. Because the model should contain the G × G term, the sum of the number of dominant genes and recessive genes should be more than zero in the G × G component. If one of the values is zero, then the responsible value is considered to be zero, and all of the G × G terms are considered to be the remainder. The detailed MCMC algorithm is described below:

• Step 1. Sample Q^t from Pr(Q|Q^t−1):

  $$Q|Q^{t-1}\sim \text{Dir}(\alpha +Q^{t-1}\times c)$$
• Step 2. Sample Z^t from Pr(Z|Q^t):

  $$p{G}_D,p{G}_R|Q^t\sim \text{Dir}\left({\alpha }_{G\times G}\right);$$

  $$p{G}_E,p{E}_G|Q^t\sim \text{Dir}\left({\alpha }_{G\times E}\right);$$

  $$f_D|pG\sim \text{uniform}\left(0,1-\sqrt{1-pG}\right);$$

  $$f_{D|G\times E}|p{G}_E\sim \text{uniform}\left(0,1-\sqrt{1-p{G}_E}\right);$$

  $$\mathit{K}\sim \mathrm{uniform}\left(0,8\right).$$

Derive Θ* from the sampled parameters based on Equation 2.

• Step 3. Accept and update all parameters with the probability

  $$\min \left(1,\frac{{\displaystyle {\prod }_{i}P\left(Y_i|{\theta }_i^{*}\right)/J_t\left({\theta }_i^{t-1}|{\theta }_i^{*}\right)}}{{\displaystyle {\prod }_{i}P\left(Y_i|{\theta }_i\right)/J_t\left({\theta }_i^{*}|{\theta }_i^{t-1}\right)}}\right).$$

From factorization, the sampling of Q^t is dependent only on Q^t−1, and the sampling of Z^t is dependent on Q^t. The conventional Gibbs sampling of each variable depends on all of the other variables and updates each variable separately. In the current study, updates that depend on all of the other variables result in restrictions to each update. These restrictions provide slightly skewed posterior distributions with inflated rejection rates. Therefore, to minimize the restrictions from the latent variables, the sampling procedure is performed as described above, and the acceptances of the sampled variables are decided after all of the samplings of each variable are conducted simultaneously. The sampling Q^t is based on the Dirichlet distribution dependent on the value at the previous time, Q^t−1, where the Dirichlet distribution is not symmetric. Therefore, the Metropolis–Hastings algorithm is used for the update.

The jumping rule at the current time, t, is indicated as J_t. Most parameters are canceled out, leaving the likelihood function and the jumping rule. The jumping rule follows the Dirichlet distribution, as indicated in step 1. MCMC was conducted in two stages: a mixing stage and a data collection stage. In the mixing stage, the sampling of Q^t was conducted using the Dirichlet distribution with 1500 iterations of the parameter, α = 1. The parameter was gradually increased with c in Dir(α + Q^t−1 × c) from 2 to 17 for 1500 iterations. After the mixing stage, 4000 iterations of the data were collected with a constant c. The convergence was diagnosed using the Gelman and Rubin diagnostics provided by the “coda” package for the R statistical package (http://cran.r-project.org/web/packages/coda/index.html). To reduce the estimating time, parallel computing was performed with ‘Rmpi’ by distributing each MCMC chain to each computing node (http://cran.r-project.org/web/packages/Rmpi/index.html).

Schizophrenia data

Data from the pooled results of relevant twin and family studies of schizophrenia in western Europe were used in the current study (Gottesman and Shields 1982; McGue et al. 1983). In the result table of the previous study (McGue et al. 1983; Risch 1990), the relative risks were presented for different types of relative pairs, i.e., MZT, P–O, DZT, sibs, grandparents and grandchildren pairs, uncle–niece pairs, and cousins. The relative risks were transformed into the concordance rates of each relative pair, with a population lifetime incidence of 0.0085 (Rao et al. 1981; McGue et al. 1983; Risch 1990). The concordance rates of available relative pairs were as follows: MZT, 0.44285 (106); P–O, 0.085 (1679); DZT, 0.1207 (149); sibs, 0.0731 (7523); grandparents and grandchildren pairs, 0.02805 (740); uncle–niece pairs, 0.02635 (3966); and cousins, 0.0153 (1601), where the numbers inside of the parentheses are the age-corrected sample sizes with a definite diagnosis (McGue et al. 1983; Risch 1990).

Diabetes data

Cohort–subject diabetes data were kindly provided by the Korean Healthy Twin Study team. The Korean Healthy Twin Study is a cohort of adult twin pairs (ages ≥20) and their family members who have been recruited since 2005 by advertisements at government health agencies and participating hospitals. The overall methodology and protocol of this multicenter survey were described previously (Sung et al. 2006). Of a total of 3800 participants, 3518 individuals who were 30 or older were included in the analysis. The type II diabetes subjects included 496 MZTs, 2026 P–O’s, 119 DZTs, 2237 sibs, and 159 avuncular pairs (Table 1). The other relative pair types with small numbers were excluded from the analysis. Individual twins and their families who were willing to participate in the Healthy Twin Study completed a questionnaire and visited one of the centers to undergo physical examinations, clinical tests, biochemical tests, and body measurements. Written, informed consent was obtained from all participants. The study protocol was approved by the ethics committees at the Samsung Medical Center and the Busan Paik Hospital.

Table 1. The probabilities of NN, ND, and DD pairs before and after age adjustment.

	After age adjustment				Before age adjustment
	NN	ND	DD	No. pairs	NN	ND	DD
MZT	0.6267	0.3110	0.0623	496	0.9395	0.0363	0.0242
P–O	0.6165	0.3301	0.0534	2026	0.7804	0.2058	0.0138
DZT	0.6367	0.3224	0.0408	119	0.9496	0.0504	0.0000
Sibs	0.6266	0.3262	0.0472	2237	0.9061	0.0881	0.0058
Avuncular	0.6916	0.2811	0.0273	159	0.9623	0.0377	0.0000

The diabetes data were obtained from the Korean Healthy Twin Study, and the adjustment was based on the Korean National Health and Nutrition Survey (NN, normal–normal pair; ND, normal–disease pair; DD, disease–disease pair).

The raw probabilities of NN, ND, and DD pairs were obtained and adjusted on the basis of the age-dependent population lifetime incidence, as indicated in a previous study (Robertson et al. 1996). The age-dependent population lifetime incidence was derived from the diabetes prevalence in the Korean National Health and Nutrition Survey for subjects who were 30 or older (Statistics Korea, 2011), assuming a lack of complete recovery. The population lifetime incidence was assumed to be 0.22 in this study, which was the peak prevalence that occurred among people in their sixties (Statistics Korea, 2011). The raw and adjusted probabilities for five relative pairs (MZTs, P–O’s, DZTs, siblings, and avuncular pairs) are shown in Table 1.

The original diabetes data showed larger ND and DD probabilities and a smaller NN probability of MZT than the probabilities derived by the genetic models with a PLI of 0.22. One possible reason for this difference is that individuals with the disease can be recruited more easily than normal twins. To avoid the discordance between data and PLI, the concordance rates were used in the Bayesian inference. The concordance rates of the diabetes data for MZT, P–O, sibling, and avuncular pairs were 0.167, 0.139, 0.126, and 0.0885, respectively. The rate of P–O pairs was slightly higher than the rate of sibling pairs, indicating the effect of parental care.

Results

Simulation results

The Bayesian MCMC method was applied to simulated data sets. For the data sets, the proportions of each causal factor were based on, but not limited to, the initial studies of simple causal models with G and E factors for schizophrenia and Type II diabetes (unpublished data). Simulated parameters of more complicated models with more causal factors have been based mostly on these initial values. Representative ones were summarized in Table 2. For most of the simulations, including those summarized in Table 2, PLI was set to 0.01, similar to schizophrenia. Numerous proportions were tested for the model containing E, E × G, G, and G × G, including those with one or more zero proportions. In addition, various numbers of genes were tested for each model. Disease concordances of nine relative pairs were derived from Equations 1–4 based on each model, and it was assumed that 1000 pairs were available for each relative pair.

Table 2. Posterior means of variable models with causal components: E, G, G × E, and G × G.

True ratio				Posterior means				Gelman & Rubin diagnostics				Rejection rate
E	G	G × E	G × G	E	G	G × E	G × G	E	G	G × E	G × G
1	1	1	7	0.079	0.297	0.115	0.509	1.021	1.023	1.019	1.021	0.593
1	4	2	3	0.106	0.385	0.162	0.347	1.006	1.070	1.117	1.034	0.612
2	2	3	3	0.191	0.272	0.212	0.325	1.004	1.008	1.007	1.015	0.459
3	2	3	2	0.227	0.246	0.294	0.233	1.014	1.076	1.072	1.022	0.462
5	2	2	1	0.303	0.210	0.330	0.156	1.033	1.015	1.016	1.003	0.447

The method worked well when the actual model contained E, G, and G × G components or simpler combinations of these three components regardless of the number of genes; the posterior distributions clearly were localized to the original model parameters with an excellent concordance to the parameters. In the models, the posterior means of most latent variables also were localized exactly to the original parameters. However, when both G × E and E terms were included in the model, the posterior distributions showed much more dispersed distributions. In comparing concordance rates between the three-component models of E, G, and G × E with the various ratios of causal components, models with different ratios of causal components showed almost identical concordance rates (supporting information, Table S1). These characteristics resulted in dispersed posterior distributions, as the updated parameters in the MCMC oscillated between these states. However, the posterior means of the four causal factors were represented of the original parameters with acceptable Gelman and Rubin diagnostics (Table 2).

The real model for a complex disease might not include one or more causal factors. In this case, serial deductions of causal factors could be used to infer the correct genetic model for a certain disease. For example, for a certain disease, there are only two causal factors, genetic and environmental factors. Because the causal factors affecting the disease presentation are unknown, the full model with all four causal factors should be examined first. If the model is overparameterized, the posterior distribution of the nonexisting causal factor will be localized close to zero. By eliminating the causal factors localized to zero, a better model that is closer to the real model can be derived. By repeating this elimination procedure until no causal factors are localized to zero, the actual model for a certain disease can be obtained. A relevant public program is available as an R package, IFP (identifying functional polymorphisms: http://cran.r-project.org/web/packages/IFP/index.html).

Bayesian inferences on schizophrenia and diabetes data

The proposed method was applied to the data of schizophrenia, which is one of the well-studied diseases that displays obvious heritability (McGue et al. 1983). The posterior means of causal factors were indicated in Table 3, which shows that the Gelman and Rubin diagnostics appeared to be accurate. In the results, all four causal factors had substantial proportions, supporting the strong heterogeneity in schizophrenia causation. For the genetic factors, the total dominant gene frequency converged to ∼0.0008. If there are numerous dominant genes, many of them could have de novo mutations. Based on the frequencies of the dominant genes, the frequencies of the recessive genes were between 0.01 and 0.003, depending on the number of genes. These results were in agreement with the previous studies that indicated that schizophrenia could be caused by rare variants (McClellan et al. 2007; Malhotra and Sebat 2012; Gratten et al. 2013).

Table 3. Posterior means of the model with the environmental and gene–environment components in the diabetes data.

	Schizophrenia			Diabetes
	Mean (± SD)	Conversion to true value	Diagnostics	Mean (± SD)	Conversion to true value	Diagnostics
E	0.230 (±0.136)	0.00196	1.007	0.568 (±0.263)	0.132	1.02
G × E	0.227 (±0.150)	0.00194	1.011	0.432 (±0.263)	0.102	1.02
G	0.198 (±0.097)	0.00169	1.023	∼0
G × G	0.345 (±0.143)	0.00294	1.007	∼0

Conversion to true value (z_i): the proportion of disease causation by the causal factor in the whole population; z_i = 1 − exp[y_i × log(1 − PLI)], in which y_i is the proportion of the causal factor i in PLI.

In addition to rare variants, the common variants are at least a contributing causal factor (Manolio et al. 2009; Ripke et al. 2011), possibly having multiple disease variants within a gene (Fellay et al. 2010; Thompson et al. 2010). In Table 3, the sum of G × G and G × E proportions is >50% of the total causal factors, indicating that there might be many common variants interacting with other genes or environments. A relatively large G × G proportion, including a large proportion of dominant genes compared to other factors, indicates that schizophrenia may be caused by several complementary genetic pathways that consist of mostly dominant genes. A study of a two-hit model in neuropsychiatric diseases supported this prediction (Girirajan et al. 2010). The sum of G and G × G was 0.543, which was smaller than the heritability estimate, 0.668 with a definite diagnosis (McGue et al. 1983); however, considering that G × E was 0.227 in Table 3, adding G_E would provide a similar number to the heritability estimate.

Bayesian inference of the diabetes data showed the importance of environmental factors in the presentation of type II diabetes. Using the full model with four causal factors, the posterior distribution converged poorly, and both the G × G and G terms were localized to zero. After eliminating the G and G × G components from the full model, the model with E and G × E showed a good convergence of posterior distributions, suggesting that the presentation of type II diabetes was influenced mostly by two causal factors: the environmental factor and gene–environment interactions.

The posterior means of the fractions of causal factors are indicated in Table 3. The fraction of the environmental causal component was 0.132, corresponding to Z_i in Equation 1, which indicated that the probability that a person could be exposed to the causal environmental factor during one’s lifetime was 0.132. The fraction of the causal factor due to gene–environment interactions was 0.102, which was a bit lower than the E component. In the fraction of gene–environment interactions, the fraction of the environmental factor interacting with the genetic factor was 0.28, and the fraction of the genetic factor interacting with the environmental factor was 0.461. The multiplication of these two factors does not yield the exact number of 0.102, probably because these are posterior means and there are slight inaccuracies. The substantial proportion of genetic factors that interact with the environment was not surprising considering that genome-wide association studies have found many loci associated with type II diabetes (Hanis et al. 1996; Zeggini et al. 2008).

Discussion

The current study provides an advanced framework for identifying major causal components and their fractions. This framework is flexible for handling both rare and common variants in a gene and across multiple genes. Based on this new formula, conventional Bayesian MCMC was used to obtain the fractions of each component in a model of a certain disease. Simulation studies showed that the method worked well but needed improvements for certain circumstances. Application to real data of schizophrenia and type II diabetes demonstrated excellent agreements with the molecular and clinical studies of these diseases.

Applying the models to schizophrenia data reinforced the complex causation of schizophrenia. All four causal factors showed substantial proportions in the population lifetime risk, suggesting the importance of all four causal factors in the presentation of schizophrenia. The G component in this study included many rare variants or de novo mutations in dominant and recessive genes. The substantial G component was in accordance with previous studies that indicated the genetic heterogeneity of schizophrenia and the contributions of many rare (possibly dominant) variants in schizophrenia (McClellan et al. 2007; Malhotra and Sebat 2012; Gratten et al. 2013). Consanguinity induces neuropsychological disorders due to homozygosity (Kurotaki et al. 2011), possibly suggesting many recessive genes for the causation of schizophrenia. From the posterior distributions of latent variables, the multiple-hit model with a majority of dominant genes, similar to the previous two-hit model (Girirajan et al. 2010), was the most likely explanation for the gene–gene interaction component of schizophrenia presentation.

In the type II diabetes data, the main causal factor was the environment, showing a proportion of 0.568. The remaining proportion of causation was due to gene–environment interactions, which had a proportion of 0.432, indicating that the causal factors of genetic or gene interactions could be minimal. This result was in agreement with previous findings indicating that the heritability estimate of type II diabetes mellitus is 0.26, and nongenetic factors are suspected to play a predominant role (Poulsen et al. 1999). The known causal environmental factors for diabetes include obesity, physical inactivity, and diet (Van Dam 2003). The genome-wide association studies (GWAS) successfully identified loci associated with type II diabetes; however, the effect sizes of these loci were very modest, ranging from 1.05 to 1.35, suggesting that common disease polymorphisms are weak risk predictors (Willems et al. 2011). In the current study, the gene interaction or gene–environment interactions increased the corresponding disease allele frequencies and decreased the effect sizes of the disease alleles. Therefore, the previous results from GWAS support the conclusion in this study that type II diabetes is primarily a result of environmental factors and gene–environment interactions. It should be noted that the current result does not completely exclude the existence of G and G × G components in the causations of type II diabetes, but the result emphasizes that the major players in type II diabetes are E and G × E components.

The current method requires several improvements, such as the incorporation of various environmental factors. The shared environmental factor and the childhood environmental factor could be applied, as indicated previously (Czene et al. 2002). Of the possible independent environmental components, the prenatal environment was separately examined in the current study. The common prenatal environment was numerically obtained when the NN, ND, and DD probabilities of MZTs were given. In the diabetes data, the assessment of the prenatal environmental component had a small and negative effect; therefore, it was excluded from this study. The exclusion of shared environmental components might result in inflated genetic factors. Further studies are required to conduct a comprehensive assessment of various environmental components. With the improvements described above, the framework also could be applicable to the extension of traditional linear models of genetics (Yi et al. 2011). Among causal inferences in epidemiology, the causal diagrams based on directed acyclic graphs were previously applied to the linear models in genetic epidemiology (Pearl 1995; Pearl 2009a). Currently, involving direct causal relationships in the current study provides too many complexities to identify actual models; however, in the future, the direct causal relationships could be studied with more information including environmental causation, as suggested previously (Pearl 1995; Pearl 2009a).

Based on the genetic models derived from the method described in this study, more suitable strategies for identifying genetic and environmental factors can be developed for each complex disease. For example, the genetic model of schizophrenia suggested that genetic studies on the rare single genetic factors and the complementary gene interaction factors should be conducted separately. In addition, the genetic factors that interact with the environment should be detected independently of the pure genetic factors. In the case of type II diabetes, efforts to find single or complementary gene interaction factors may fail. A better approach to understanding the presentation of type II diabetes might be to examine interactions between the environmental factors and the disease polymorphisms identified from GWAS.