Abstract
Objectives
Dynamic contrast enhanced (DCE) MRI exams of the kidneys provide quantitative information on renal perfusion and filtration. However, these exams are often difficult to implement because of respiratory motion and their need for a high spatiotemporal resolution and 3D coverage. Here, we present a free-breathing quantitative renal DCE MRI exam acquired with a highly accelerated stack-of-stars trajectory and reconstructed with 3D through-time radial GRAPPA, utilizing half and quarter doses of gadolinium contrast.
Materials and Methods
Data were acquired in ten asymptomatic volunteers using a stack-of-stars trajectory that was under sampled in-plane by a factor of 12.6 with respect to Nyquist sampling criterion and using partial Fourier of 6/8 in the partition direction. Data had a high temporal (2.1-2.9 s/frame) and spatial (approximately 2.2 mm3) resolution with full 3D coverage of both kidneys (350-370 mm2 × 79-92 mm). Images were successfully reconstructed with 3D through-time radial GRAPPA, and inter-frame respiratory motion was compensated by using an algorithm developed to automatically utilize images from multiple points of enhancement as references for registration. Quantitative pharmacokinetic analysis was performed using a separable dual compartment model.
Results
ROI pharmacokinetic analysis provided estimates (mean±std.dev.) of renal perfusion after half-dose: 218.1ml/min/100ml±57.1, plasma mean transit time: 4.8s±2.2, renal filtration: 28.7ml/min/100ml±10.0, and tubular mean transit time: 131.1s±60.2in 10 kidneys. ROI pharmacokinetic analysis provided estimates (mean±std.dev.) of renal perfusion after quarter-dose: 218.1ml/min/100ml±57.1, plasma mean transit time: 4.8s±2.2, renal filtration: 28.7ml/min/100ml±10.0, and tubular mean transit time: 131.1s±60.2 in 10 kidneys. 3D pixel wise parameter maps were also evaluated.
Conclusion
Highly under sampled data were successfully reconstructed with 3D through-time radial GRAPPA to achieve a high resolution 3D renal DCE MRI exam. The acquisition was completely free-breathing, and the images were registered to compensate for respiratory motion. This allowed for accurate high resolution 3D quantitative renal functional mapping of perfusion and filtration parameters.
Keywords: Renal Perfusion, DCE MRI, Through-time Radial GRAPPA
Introduction
Quantitative dynamic contrast enhanced (DCE) MRI exams of the kidneys can be used to provide valuable information on both renal perfusion and filtration by employing pharmacokinetic modeling of gadolinium-based contrast agents to obtain measurements of these physiologically relevant model parameters (1–7). This quantitative evaluation of the kidney has a broad potential for impact in clinical care, including evaluation of renal artery stenosis, renal transplants, and tumor characterization (8–12). Furthermore, it can be combined with other MR imaging methods, such as an MR angiography exam, for comprehensive assessment of the kidneys (10,13–17).
However, acquisition of DCE MRI data is not trivial, particularly if 3D and high resolution analysis is desired. These methods require high temporal resolution to appropriately sample the arterial input function and the enhancement of renal parenchyma tissue (18), and thus spatial resolution or volumetric coverage is typically sacrificed. View-sharing methods have been utilized to achieve 3D coverage (19–21), but a broad temporal footprint across the shared timeframes could affect the accuracy of the pharmacokinetic analysis (20). In addition to the resolution requirements, DCE-MRI scans also require sampling of the entire enhancement process, requiring scan times that exceed four minutes (18). This long enhancement time course means that respiratory motion is unavoidable and thus problematic. Repeated breath-holds can be employed but there is significant potential for motion due to incomplete breath-holds, especially as the patient tires. Moreover, the necessary rest phases between breath-holds result in data gaps that deleteriously affect the modeling.
In this study, we address all of these problems by performing a free-breathing, 3D high resolution renal perfusion exam. We utilize a highly-accelerated non-Cartesian stack-of-stars trajectory with a 3D through-time radial GRAPPA reconstruction (22,23) to achieve high spatiotemporal resolution acquisition with full volumetric coverage of the kidneys. The high temporal resolution free-breathing images are registered to correct for inter-frame motion, and then a separable two compartment renal pharmacokinetic model (7,24) is applied to estimate perfusion and filtration parameters.
Materials and Methods
Image Acquisition and Reconstruction
In this IRB-approved, HIPAA compliant study, ten asymptomatic volunteers (20 kidneys) were scanned after written informed consent. Volunteers were given no instructions regarding water, food, or caffeine intake prior to the study. Imaging was performed at 3.0T (Magnetom Skyra, Siemens Healthcare, Erlangen, Germany) with a 18 channel body matrix receive coil and spinal array coil (12-16 channels). The DCE-MRI exam was initiated immediately following injection of a half (in five volunteers) or quarter (in five volunteers) dose by weight, of Gadopentetate Dimeglumine (Magnevist, 0.05 and 0.025mmol/kg, Bayer, Berlin, Germany).
A spoiled gradient echo acquisition was performed with a stack-of-stars k-space trajectory. For this cylindrical-shaped trajectory, data were sampled in-plane with a radial trajectory that is replicated along the partition direction using Cartesian encoding. To accelerate the acquisition, only radial under sampling was used (as described in (25)). The in-plane radial trajectory was under sampled by a factor of eight such that 20 radial projections were acquired for each partition. This yields an acceleration factor of 12.6 with respect to the Nyquist sampling criterion. This highly accelerated acquisition yielded a temporal resolution of less than 3 seconds/frame. Scanning parameters were tailored to fit the anatomy of each volunteer while maintaining a scan time of less than 3 seconds per volume. Other scanning parameters include: oblique coronal slab orientation, repetition time: 3.02-3.78 ms, echo time: 1.3 ms, flip angle: 12°, field-of-view (FOV): 350-370mm2 × 79.2-92 mm, spatial resolution: 2.2-2.3 mm3, bandwidth: 710 Hz/pixel, partial Fourier in partition direction: 6/8, acquisition time: 2.1-2.9 s/frame, number of frames: 135, total DCE MRI acquisition time: 4.7-6.5 min.
As described above, the stack-of-stars data were under sampled in-plane in every partition to meet the stringent needs of the renal DCE MRI exam. This results in poor image quality with noise amplification and radial aliasing artifacts. To mitigate these artifacts, images were reconstructed with 3D through-time radial GRAPPA (22,23). In this reconstruction, GRAPPA weights are applied to the acquired radial projections to reconstruct the missing radial projections. These GRAPPA weights are calibrated for small segments of the radial trajectory using fully-sampled, 3D time-resolved calibration data (22,23). To perform the 3D through-time calibration, an additional fully-sampled dataset was acquired with the following parameters after the renal DCE-MRI exam: 160 projections/partition,8 low resolution partitions with the same field-of-view as the under sampled data, 16 temporal repetitions, segment size of 4 projections × 8 readout points, and a calibration acquisition time of approximately 1-1.3 minutes. Using this calibration data, GRAPPA weights were calculated and used to reconstruct the missing projections. The ‘through-time’ moniker in the name of this reconstruction method refers to the use of temporal repetitions for the GRAPPA weight calibration. No temporal filtering or view-sharing was utilized. Data were further accelerated with a partial Fourier acquisition along the partition encoding direction, and were reconstructed using projection onto convex sets (POCS) prior to performing a Fourier transform along the partition direction. Density compensation and the non-uniform fast Fourier transform (26) were then applied to the in-plane radial data to provide reconstructed images.
All reconstructions were performed offline using MATLAB (The Mathworks, Inc., Natick, MA). The 3D through-time radial GRAPPA reconstruction is entirely automated, and only requires the user to select calibration parameters (segment size, number of calibration repetitions and partitions) that have been previously optimized (22,23). Further reconstruction details can be found in (22,23) and open-source code for through-time radial GRAPPA can be found in (25).
Image Registration
All data were acquired without breath-holds, and volunteers were asked to breathe normally during data acquisition. Because of the free-breathing acquisition, respiratory motion between frames must be compensated prior to DCE-MRI analysis. Here, a registration technique was implemented based on work by Chen, et al. (27), which was previously applied to free-breathing, dynamic contrast-enhanced liver data.
Registration algorithms typically produce better results when applied to images with similar contrast or appearance. For example, registering images during the corticomedullary phase of enhancement to images during the nephrographic phase can be difficult due to the markedly different appearance of the kidneys at these times. To avoid this problem, this method utilizes several reference frames where the kidney is at the same spatial location but at different points in enhancement. The algorithm can then select the reference frame that is temporally nearest to each frame for registration.
This strategy requires that all reference frames have negligible motion between them. Thus, a canny edge filter was applied to a single coronal slice, and an automated algorithm detected the top edge of the liver throughout the acquisition to track motion. From these data, the most frequently occurring location was selected, and these frames were monitored to ensure that negligible motion occurred between the selected references. After the references were identified, the open-source FNIRT software (FMRIB's Non-linear Image Registration Tool) was utilized to register each frame to the temporally nearest reference frame (28,29).
DCE-MRI Analysis
A separable two-compartment pharmacokinetic model was used to quantitatively evaluate perfusion and filtration in the kidneys (7). This model describes the perfusion (FP, mL/100mL/min) of gadolinium from the arteries to the tissue, where it disperses over the tissue compartment volume (VP, mL/100mL). The model additionally considers the filtration rate (FT, mL/100mL/min) of gadolinium from the tissue into the renal tubules, where it disperses over tubular volume (VT, mL/100mL). The mean transit time (MTT) of the tracer in the tissue and renal tubular compartments are also denoted as TP and TT, respectively. As previously described by Sourbron, et al. (7), the concentration of contrast agent that is transferred to the tissue compartment can be described by the following equation:
where CA(t) is the arterial input function and CP(t) is the concentration of gadolinium in the tissue compartment. Note that the arterial input function is normalized to account for the hematocrit Hct(by a factor of (1-Hct), where Hct is assumed to be 0.45).
The contrast agent will be filtered from the renal tissue compartment to the tubular compartment as described in the following equation:
where CT is the concentration of gadolinium in the tubular compartment. This model also accounts for reabsorption of the contrast agent, which is denoted in the equation above as a fraction that is reabsorbed f. Note that the mean transit time of the tubular compartment will be normalized by the amount of concentration that is not reabsorbed (1-f), such that .
It is important to note that the tissue and tubular compartments cannot be separately measured, and thus a weighted sum of the two compartments reflects the concentration changes in acquired renal DCE MRI data:
where C(t) describes concentration of gadolinium for the whole kidney or the renal cortex. Because the arterial input function is used directly in this model, recirculation effects are accounted for. Using this model, four parameters can be independently estimated: FP (Perfusion rate), TP (MTT in the plasma compartment), FT (Filtration rate), and TT (MTT in the tubular compartment). Complete details of this model have been described previously (7,18).
In this study, an ROI in the aorta proximal to the renal arteries was used for the arterial input function. Based on the assumptions of the model (7), a ROI analysis was performed using a whole kidney ROI. Pixelwise parameter mapping was also performed on the renal cortex, which was segmented by thresholding signal intensity values in a frame during corticomedullary enhancement.
To convert signal intensity values to concentration of Gd-DTPA, the following equation was used (30):
Where T1, 0 is the baseline T1 of the tissue (used literature value (31)), T1 is its shortened value in the presence of Gd-DTPA, r is the relaxivity of the contrast agent (used literature value (32)), and C is the concentration of the contrast agent. T1 was computed using signal values and the FLASH signal intensity relationship (30). When converting signal to T1, it was assumed that there were no substantial changes in coil sensitivities (or other scaling factors) during the concentration time-courses. The resulting concentration time courses were used to estimate perfusion and filtration parameters (FP, TP, FT, and TT) with a non-linear least squares fit using MATLAB (‘fminsearch’ algorithm, The Mathworks, Inc., Natick, MA).
The accuracy of the perfusion and filtration parameter estimation is dependent on the SNR of the acquisition. To evaluate how acquisition noise may propagate to errors in parameter estimation, the noise level of the acquisition was measured using the bootstrapping method (33). In one volunteer, a noise scan was acquired in addition to the under sampled data (where the noise scan had the same acquisition parameters but no RF excitation). The contrast-enhanced scan was acquired after administration of a quarter dose of Gd-DTPA to evaluate noise propagation in the lower SNR case. The randomly reordered noise was added to the under sampled data, which were then reconstructed as described above. This process was repeated to generate 20 datasets. The ROI pharmacokinetic analysis described above was performed on each dataset, and FP, TP, FT, and TT were quantified.
Results
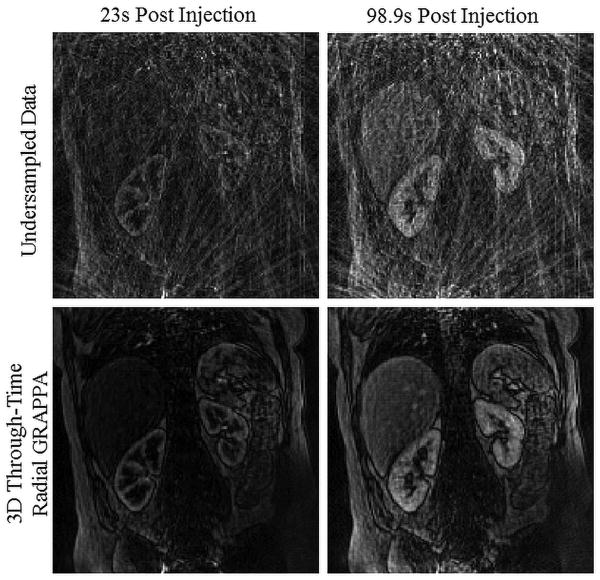
Using the 3D through-time radial GRAPPA reconstruction algorithm, highly under sampled data were acquired and successfully reconstructed to achieve a high spatiotemporal resolution. In Figure 1, a single partition from a 3D data set is shown at two time points during contrast enhancement. The top row in Figure 1 shows the reconstructed under sampled data to demonstrate the level of aliasing artifacts and noise amplification present in the underlying date. The second row shows these same images after reconstruction with 3D through-time radial GRAPPA, where the aliasing artifacts are successfully removed. The successful reconstruction of highly accelerated data with 3D through-time radial GRAPPA is also shown in Figure 2 for a second dataset. Here, three partitions of the 36 acquired partitions are shown at 3 different times during contrast enhancement. From these data, image details can be seen, such as corticomedullary differentiation during the arterial phase, despite using a highly under sampled and free-breathing exam. Furthermore, these data have a high spatiotemporal resolution without sacrificing 3D coverage.
Figure 1.
This figure demonstrates the successful reconstruction of highly accelerated stack-of-stars data with 3D through-time radial GRAPPA. These data were acquired at an acceleration of 12.6 with respect to Nyquist sampling criterion with a spatial resolution of 2.2mm3 and a temporal resolution of 2.3s/frame. The top row shows the original undersampled data with a gridding reconstruction to show the level aliasing artifacts and noise amplification present in the acquired data. The bottom row shows reconstructed images with the 3D through-time radial GRAPPA reconstruction. The undersampled and reconstructed images are shown for a single partition (from the 40 acquired partitions) at two different time points during contrast enhancement at the corticomedullary phase (23s post injection) and at the nephrographic phase (98.9s post injection).
Figure 2.
This figure shows reconstructed images for 3 partitions from the 36 acquired partitions and 3 time points during the corticomedullary, nephrographic, and excretory phases of enhancement. These data were acquired at an acceleration of 12.6 with respect to Nyquist sampling criterion with a spatial resolution of 2.2mm3 and a temporal resolution of 2.1s/frame. Despite the high level of acceleration and free-breathing nature of the acquisition, the images maintain excellent image quality.
After image reconstruction, the registration algorithm began by detecting motion that occurred at the top of the liver, which provides a pixel position over time as shown in Figure 3A. The most frequent position (marked by red ‘x’) are all used as reference images for image registration, and all other images are registered to the temporally nearest reference. Figure 3B shows images before and after registration is applied. Five adjacent time points during the excretory phase of enhancement were selected during a deep inhale by the volunteer (shown by red circles in Figure 3A). Source images are shown in the first five columns of Figure 3B before (top row) and after (bottom row) registration. The final column in Figure 3B shows a subtraction of the last time point from the first time point to demonstrate the change in signal. While respiratory motion of the kidney is relatively small, it can be seen in both the source and subtracted images in Figure 3B (top row). Figure 3B (bottom row) demonstrates the non-rigid 3D registration's ability to mitigate respiratory motion. Because the respiratory motion of the kidney is relatively small, an ROI analysis that evaluates the whole kidney is not substantially degraded by respiratory motion. However, this motion does degrade the quality of a pixelwise analysis as shown in Figure 3C. This figure shows the change in signal intensity in a single pixel at the edge of the renal cortex. The registration algorithm clearly reduces signal fluctuations due to respiratory motion in that pixel, which would affect the resulting pharmacokinetic analysis.
Figure 3.
Images are acquired with a free-breathing acquisition. Respiratory motion is observed by tracking motion at the top of the liver, which provides a pixel position over time as shown in Figure 3A. Images at the most frequently occurring position (marked by red ‘x’) are used as references for image registration. It is assumed that no motion occurs between these reference images. All other time frames are registered to their temporally adjacent neighbor. The motion observed during data acquisition and the successful registration of this data is shown in Figure 3b. The top row of images shows a single partition over fiver adjacent time points that were acquired during a deep inhale (time points noted by red circles in Figure 3A). The bottom row shows these images after registration. The last column shows a subtraction of the first and last source images. Figure 3B demonstrates that there can be problematic renal motion during the acquisition, and that this motion can be successfully compensated with the registration algorithm. Finally, Figure 3C shows a single pixel's signal intensity time course before and after image registration (pixel located at the top of the right renal cortex). By comparing these two plots, it is clear that oscillations due to respiratory motion are largely removed.
After reconstruction and registration, pharmacokinetic analysis was performed both with pixelwise mapping and using ROIs, to quantify perfusion, filtration rates and mean transit times. The measured arterial input and renal concentration time courses from ROIs in aorta and in a single slice of the renal parenchyma are shown in Figure 4A and 4B for data acquired after a half and quarter dose, respectively, and a representative model fit of the data is shown in Figures 4A-D. These data show typical concentration ranges that were seen across our population and also good model fit of the data. For each ROI analysis in 20 kidneys, an average root mean squared error of 1.7% was seen between the data and the model fit. The quantitative parameter estimation results from this analysis using an ROI on a single slice around the whole kidney can be seen in Table 1 where 10 kidneys were analyzed separately in five asymptomatic volunteers for each dose (total of 20 kidneys in ten volunteers). The bootstrap simulations resulted in a standard deviation of 7.6 ml/min/100ml for Fp, 0.09s for Tp, 0.7 ml/min/100ml for FT, 6.5s for TT.
Figure 4.
Figure 4A shows a representative arterial input function (AIF) and renal enhancement curves from ROIs placed in the aorta and around the whole kidney. Figures 4A and 4B also show the model fit of this data. This model fits the renal enhancement data well with very low residuals between the model and the data.
Table 1.
Summary of renal perfusion and filtration parameters using the separable compartment model for a whole kidney ROI analysis. Each column reports Mean ± Standard Deviation. A range of average values found in the literature for normal kidneys is also provided for reference.
| Half Dose (n=10 kidneys) | Quarter Dose (n=10 kidneys) | Pooled Data (n=20 kidneys) | Literature Values Refs. (7,10,12) | |
|---|---|---|---|---|
| Renal Perfusion (FP, ml/min/100ml) | 218.1 ± 57.1 | 212.5 ± 47.6 | 215.3 ± 51.3 | ∼ 171.5-229.0 |
| MTT in Plasma (TP, seconds) | 4.8 ± 2.2 | 3.3 ± 0.8 | 4.0 ± 1.8 | ∼6.5 |
| Renal Filtration (FT, ml/min/100ml) | 28.7 ± 10.0 | 25.8 ± 9.0 | 27.2 ± 9.4 | ∼21.3-31.0 |
| MTT in Tubules (TT, seconds) | 131.1 ± 60.2 | 124.2 ± 36.3 | 127.6 ± 48.5 | ∼125 |
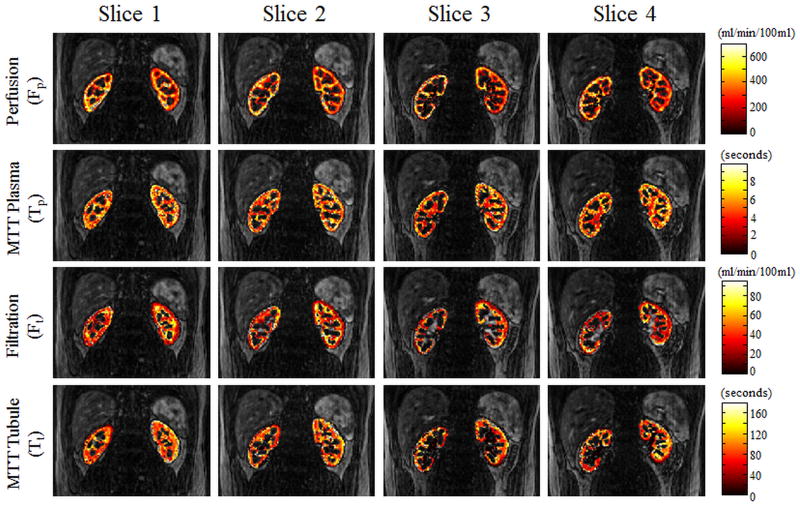
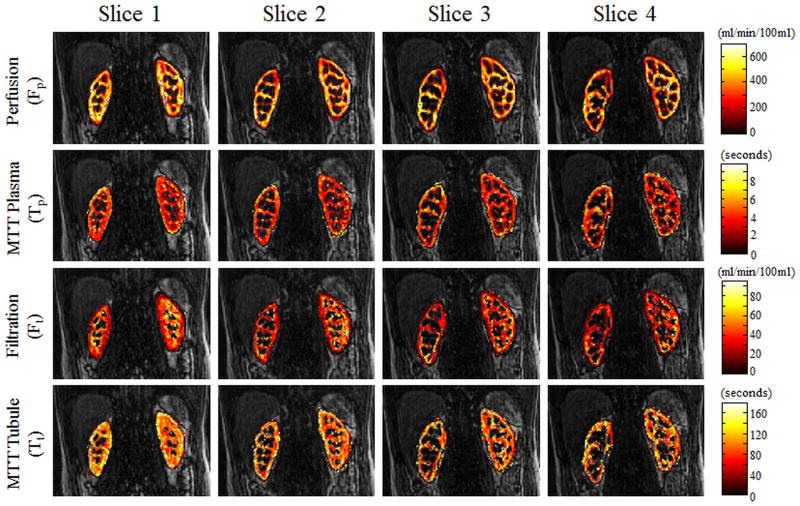
Figures 5 and 6 show perfusion rate, filtration rate, and mean transit time pixelwise parameter maps for several partitions from two different volunteers after administration of a half and quarter dose of Gd-DTPA. These parameters maps are overlaid on the anatomical images for reference. Although only 4partitions are shown here, more than 36 partitions were actually acquired for these high spatial resolution 3D acquisitions.
Figure 5.
Figure 5 shows pixelwise parameter maps of the four parameters (perfusion, filtration, and mean transit times of the plasma and tubule compartments) from the pharmacokinetic renal model in 4 of the 36 acquired slices. These data were acquired after administration of a half-dose (by weight) of Gd-DTPA.
Figure 6.
Figure 6 shows pixelwise parameter maps of the four parameters (perfusion, filtration, and mean transit times of the plasma and tubule compartments) from the pharmacokinetic renal model in 4 of the 40 acquired slices. These data were acquired after administration of a quarter-dose (by weight) of Gd-DTPA.
Discussion
While much of present clinical MRI focuses on anatomical imaging, techniques including DCE MRI are promising because they could add a quantitative underlay to renal imaging (8–12). The combination of perfusion quantification with anatomical imaging could provide complete renal assessment in a single comprehensive MRI exam (10,13–17). However, in order for perfusion measurements to find widespread utility in the clinical environment, the exams must be easy to implement, robust to patient compliance issues such as problems with breath-holding, and should be performed at clinically relevant resolutions with complete volumetric coverage. In this study, we aimed to provide a high spatiotemporal resolution exam with full coverage of the kidneys without breath-holding. To achieve the desired resolution and volumetric coverage, the data were acquired with a highly under sampled non-Cartesian trajectory and were reconstructed with 3D through-time radial GRAPPA (22,23). Furthermore, it can be easily implemented with real-time reconstructions (34). In addition, this entire technique is performed without breath-holds, which simplifies the exam for use in patients who have difficulty holding their breath, in and of itself a critical improvement in renal imaging.
3D through-time radial GRAPPA was used to successfully reconstruct data with a temporal resolution of better than 3s/frame using acceleration factor of 12.6 with respect to the Nyquist criterion and partial Fourier in the partition direction. Despite this high degree of under sampling, the images retain excellent quality, as can be seen in Figures 1 and 2. In contrast to other reconstruction techniques, an advantage of 3D through-time radial GRAPPA reconstruction is that the temporal footprint is the same as the temporal resolution, which for these exams ranged between 2.1 and 2.9s/frame. No view-sharing or temporal filtering was employed to reconstruct the data, thus guaranteeing a high fidelity reconstruction. This short, well-defined temporal footprint allowed for accurate pharmacokinetic analysis of renal enhancement, with obtained parameters in good agreement with the published literature.
For quantification of renal perfusion and filtration, images are acquired for several minutes after contrast administration. In order to avoid errors due to motion, image registration must be performed prior to pharmacokinetic analysis (35). While a lot of research has been explored for registration of dynamic data, the additional challenge of changing contrast throughout the acquisition must also be considered. Previous approaches have successfully utilized a wide range of registration techniques (7,36–43). Respiratory motion can be minimized by performing multiple breath-holds (2,21,37,44), but patient fatigue could affect compliance, and the exam is complex for both the patient and the clinical technologists. Moreover, motion between the multiple breath-holds is still problematic, and missing data between breath-holds could affect quantitative accuracy. In order to alleviate these problems, data acquisition in this study was completely free-breathing, and images were retrospectively registered using FNIRT. This approach has many advantages. First, because this is exam is completely free-breathing, patient comfort and compliance is greatly improved, and the scans are very easily performed. Second, the registration algorithm can be easily implemented offline using a canny edge detection algorithm (MATLAB) and open-source non-rigid registration methods. Because respiratory motion is relatively small for the kidneys, the effect of motion on signal intensity curves in the ROI analysis is minimal. However, motion is more problematic when generating a pixelwise parameter map as seen in Figure 3C. The registration results demonstrated in Figure 3 show that the algorithm works well despite large changes in contrast and non-rigid motion throughout the acquisition, which allowed for improved pixelwise quantitative analysis. Respiratory motion during the 2-3s acquisition of each individual frame was not corrected. However, as seen in the images in Figures 1-3, intra-frame respiratory motion was minimal and did not cause deleterious image artifacts.
Functional evaluation of both kidneys in ten volunteers was performed using a pharmacokinetic analysis that included renal perfusion and filtration parameters. Results shown in Figure 4 show a good model fit with low residual error with this ROI analysis. The bootstrap error analysis shows that measurement errors in FP, TP, FT, and TT are 6.5-20 times smaller than the physiological variations in these parameters (Table 1) seen across the study population. The resulting estimated perfusion parameters (as shown in Table 1) are in good agreement with those previously reported in the literature (7). The filtration rate parameter (FT) is directly proportional to GFR (referred to here as estimated GFR or GFRest) (7). In order to determine GFRest values, a typical single kidney weight of 200g and a tissue density of 1g/ml were assumed. For the half dose data, the mean (±standard deviation) single kidney GFRest was 57.4ml/min±20.0, and the mean (±standard deviation) GFRest per subject was 114.9ml/min±38.4. For the quarter dose data, the mean (±standard deviation) single kidney GFRest was 51.5ml/min±17.9, and the mean (±standard deviation) GFRest per subject was 103.0ml/min±36.5.
High resolution parameter mapping was also demonstrated in Figures 5-6. It should be noted that only a half-dose (by weight) of gadolinium contrast was utilized in Figure 5 and only a quarter-dose of gadolinium contrast was utilized in Figure 6. While previous studies have explored a low dose approach to renal DCE-MRI, these results demonstrate that a low dose exam can still be used for a pixelwise analysis with this highly accelerated 3D non-Cartesian parallel imaging acquisition and reconstruction. This opens the door for developing a low dose comprehensive renal exam, or alternatively, using a second half-dose of contrast for other purposes such as a high resolution breath-held angiography study.
A potential limitation for this methodology is that both the reconstruction and registration methods are computationally demanding and must be implemented properly to avoid clinically prohibitive durations. For this work, all image reconstructions and registrations were performed offline, and no parallelization or GPU processing was used. However, this implementation was too slow for clinical use, so a low-latency through-time radial GRAPPA reconstruction using GPU programming was also implemented. This method has previously been used to perform real-time reconstructions with 2D data (34), and was adapted to work with the 3D stack-of-stars data. With the GPU-based reconstruction, GRAPPA weight calculation took approximately 38.6 seconds, and reconstruction of each frame took approximately 15.6 seconds. Offline registration of the reconstructed data using FNIRT was approximately 9 min/frame using a single CPU core. The registration of each individual frame can be performed independent of all other frames, so registration could also benefit from parallelization.
In conclusion, 3D through-time radial GRAPPA was used to reconstruct data with a high temporal (2.1-2.9 s/frame) and spatial (approximately 2.2 mm3) resolutions with full 3D coverage of both kidneys and the aorta (350-370 mm2 × 79-92 mm). The acquisition was completely free-breathing, and the images were registered to compensate for respiratory motion. This allowed for accurate high resolution 3D quantitative renal functional mapping of perfusion and filtration parameters.
Acknowledgments
Funding Sources: NIH 1R01DK098503, and R00EB011527, 1R01EB017219. Siemens Healthcare.
References
- 1.Vallée JP, Lazeyras F, Khan H, Terrier F. Absolute renal blood flow quantification by dynamic MRI and Gd-DTPA. Eur Radiol. 2000;10(8):1245–1252. doi: 10.1007/s003300000434. [DOI] [PubMed] [Google Scholar]
- 2.Lee VS, Rusinek H, Johnson G, Rofsky NM, Krinsky GA, Weinreb JC. MR Renography with Low-Dose Gadopentetate Dimeglumine: Feasibility 1. Radiology. 2001;221(2):371. doi: 10.1148/radiol.2212010142. [DOI] [PubMed] [Google Scholar]
- 3.Hackstein N, Heckrodt J, Rau WS. Measurement of single-kidney glomerular filtration rate using a contrast-enhanced dynamic gradient-echo sequence and the Rutland-Patlak plot technique. J Magn Reson Imaging. 2003;18(6):714–25. doi: 10.1002/jmri.10410. [DOI] [PubMed] [Google Scholar]
- 4.Lee VS, Rusinek H, Noz ME, Lee P, Raghavan M, Kramer EL. Dynamic three-dimensional MR renography for the measurement of single kidney function: initial experience. Radiology. 2003;227(1):289–94. doi: 10.1148/radiol.2271020383. [DOI] [PubMed] [Google Scholar]
- 5.Hermoye L, Annet L, Lemmerling P, Peeters F, Jamar F, Gianello P, Van Huffel S, Van Beers BE. Calculation of the renal perfusion and glomerular filtration rate from the renal impulse response obtained with MRI. Magn Reson Med. 2004;51(5):1017–25. doi: 10.1002/mrm.20026. [DOI] [PubMed] [Google Scholar]
- 6.Dujardin M, Sourbron S, Luypaert R, Verbeelen D, Stadnik T. Quantification of renal perfusion and function on a voxel-by-voxel basis: A feasibility study. Magn Reson Med. 2005;54(4):841–849. doi: 10.1002/mrm.20608. [DOI] [PubMed] [Google Scholar]
- 7.Sourbron SP, Michaely HJ, Reiser MF, Schoenberg SO. MRI-measurement of perfusion and glomerular filtration in the human kidney with a separable compartment model. Invest Radiol. 2008;43(1):40–8. doi: 10.1097/RLI.0b013e31815597c5. [DOI] [PubMed] [Google Scholar]
- 8.Michaely HJ, Schoenberg SO, Oesingmann N, Ittrich C, Buhlig C, Friedrich D, Struwe A, Rieger J, Reininger C, Samtleben W, et al. Renal Artery Stenosis: Functional Assessment with Dynamic MR Perfusion Measurements—Feasibility Study. Radiology. 2006;238(2):586–596. doi: 10.1148/radiol.2382041553. [DOI] [PubMed] [Google Scholar]
- 9.Sun MRM, Ngo L, Genega EM, Atkins MB, Finn ME, Rofsky NM, Pedrosa I. Renal Cell Carcinoma: Dynamic Contrast-enhanced MR Imaging for Differentiation of Tumor Subtypes—Correlation with Pathologic Findings 1. Radiology. 2009;250(3):793. doi: 10.1148/radiol.2503080995. [DOI] [PubMed] [Google Scholar]
- 10.Attenberger UI, Sourbron SP, Schoenberg SO, Morelli J, Leiner T, Schoeppler GM, Samtleben W, Birkemeier KL, Glaser C, Reiser MF, et al. Comprehensive MR evaluation of renal disease: added clinical value of quantified renal perfusion values over single MR angiography. J Magn Reson Imaging. 2010;31(1):125–33. doi: 10.1002/jmri.21994. [DOI] [PubMed] [Google Scholar]
- 11.Wentland A, Sadowski E, Djamali A, Grist T. Quantitative MR Measures of Intrarenal Perfusion in the Assessment of Transplanted Kidneys: Initial Experience. Acad Radiol. 2009;16(9):1077–1085. doi: 10.1016/j.acra.2009.03.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Notohamiprodjo M, Sourbron S, Staehler M, Michaely HJ, Attenberger UI, Schmidt GP, Boehm H, Horng A, Glaser C, Stief C, et al. Measuring perfusion and permeability in renal cell carcinoma with dynamic contrast-enhanced MRI: a pilot study. J Magn Reson Imaging. 2010;31(2):490–501. doi: 10.1002/jmri.22028. [DOI] [PubMed] [Google Scholar]
- 13.Michaely HJ, Sourbron S, Dietrich O, Attenberger U, Reiser MF, Schoenberg SO. Functional renal MR imaging: an overview. Abdom Imaging. 2006;(December 2006):758–771. doi: 10.1007/s00261-006-9150-8. [DOI] [PubMed] [Google Scholar]
- 14.Prasad PV. Functional MRI of the kidney: tools for translational studies of pathophysiology of renal disease. Am J Physiol Renal Physiol. 2006;290(5):F958–74. doi: 10.1152/ajprenal.00114.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Notohamiprodjo M, Reiser MF, Sourbron SP. Diffusion and perfusion of the kidney. Eur J Radiol. 2010;76(3):337–347. doi: 10.1016/j.ejrad.2010.05.033. [DOI] [PubMed] [Google Scholar]
- 16.Attenberger UI, Morelli JN, Schoenberg SO, Michaely HJ. Assessment of the kidneys: magnetic resonance angiography, perfusion and diffusion. J Cardiovasc Magn Reson. 2011;13(1):70. doi: 10.1186/1532-429X-13-70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chandarana H, Lee VS. Renal functional MRI: Are we ready for clinical application? AJR Am J Roentgenol. 2009;192(6):1550–7. doi: 10.2214/AJR.09.2390. [DOI] [PubMed] [Google Scholar]
- 18.Michaely HJ, Sourbron SP, Buettner C, Lodemann KP, Reiser MF, Schoenberg SO. Temporal constraints in renal perfusion imaging with a 2-compartment model. Invest Radiol. 2008;43(2):120–8. doi: 10.1097/RLI.0b013e3181583b0c. [DOI] [PubMed] [Google Scholar]
- 19.Vakil P, Carr JC, Carroll TJ. Combined renal MRA and perfusion with a single dose of contrast. Magn Reson Imaging. 2012;30(6):878–85. doi: 10.1016/j.mri.2011.12.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Song T, Laine AF, Chen Q, Rusinek H, Bokacheva L, Lim RP, Laub G, Kroeker R, Lee VS. Optimal k-space sampling for dynamic contrast-enhanced MRI with an application to MR renography. Magn Reson Med. 2009;61(5):1242–1248. doi: 10.1002/mrm.21901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chandarana H, Amarosa A, Huang WC, Kang SK, Taneja S, Melamed J, Kim S. High temporal resolution 3D gadolinium-enhanced dynamic MR imaging of renal tumors with pharmacokinetic modeling: Preliminary observations. J Magn Reson Imaging. 2013 doi: 10.1002/jmri.24035. 000. [DOI] [PubMed] [Google Scholar]
- 22.Seiberlich N, Ehses P, Duerk J, Gilkeson R, Griswold M. Improved radial GRAPPA calibration for real-time free-breathing cardiac imaging. Magn Reson Med. 2011;65(2):492–505. doi: 10.1002/mrm.22618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wright KL, Lee GR, Ehses P, Griswold MA, Gulani V, Seiberlich N. Three-Dimensional Through-Time Radial GRAPPA for Renal MR Angiography. J Magn Reson Imaging. 2013 doi: 10.1002/jmri.24439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Annet L, Hermoye L, Peeters F, Jamar F, Dehoux JP, Van Beers BE. Glomerular filtration rate: assessment with dynamic contrast-enhanced MRI and a cortical-compartment model in the rabbit kidney. J Magn Reson Imaging. 2004;20(5):843–9. doi: 10.1002/jmri.20173. [DOI] [PubMed] [Google Scholar]
- 25.Wright KL, Hamilton JI, Griswold MA, Gulani V, Seiberlich N. Non-Cartesian parallel imaging reconstruction. J Magn Reson Imaging. 2014 doi: 10.1002/jmri.24521. 00. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fessler J, Sutton B. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans Signal Process. 2003;51(2):560–574. [Google Scholar]
- 27.Chen Y, Lee G, Wright K, Griswold M, Seiberlich N, Gulani V. Proc of the 21st Annual Meeting of the Int Soc Magn Reson Med. Vol. 21. Salt Lake City, USA: 2013. 3D high spatiotemporal resolution quantitative liver perfusion imaging using a stack-of-spirals acquisition and throughtime non-Cartesian GRAPPA acceleration; p. 0601. [Google Scholar]
- 28.Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM. Fsl. Neuroimage. 2012;62(2):782–90. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- 29.Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23(Suppl 1):S208–19. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- 30.Haacke M, Brown R, Thompson M, Venkatesan R. Magnetic resonance imaging: physical principles & sequence design. New York: John Wiley & Sons; 1999. [Google Scholar]
- 31.Stanisz GJ, Odrobina EE, Pun J, Escaravage M, Graham SJ, Bronskill MJ, Henkelman RM. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magn Reson Med. 2005;54(3):507–12. doi: 10.1002/mrm.20605. [DOI] [PubMed] [Google Scholar]
- 32.Pintaske J, Martirosian P, Graf H, Erb G, Lodemann KP, Claussen CD, Schick F. Relaxivity of gadopentetate dimeglumine (Magnevist), gadobutrol (Gadovist), and gadobenate dimeglumine (MultiHance) in human blood plasma at 0.2, 1.5, and 3 Tesla. Invest Radiol. 2006;41(3):213. doi: 10.1097/01.rli.0000197668.44926.f7. [DOI] [PubMed] [Google Scholar]
- 33.Riffe M, Blaimer M, Barkauskas K, Duerk J, Griswold M. SNR Estimation in Fast Dynamic Imaging Using Bootstrapped Statistics. Proc of the 15th Annual Meeting of the Int Soc Magn Reson Med. 2007;15:1879. [Google Scholar]
- 34.Saybasili H, Herzka D, Seiberlich N, Griswold M. Low-Latency Radial GRAPPA Reconstruction using Multi-Core CPUs and General Purpose GPU Programming. Proc of the 20th Annual Meeting of the Int Soc Magn Reson Med. 2012;20:2554. [Google Scholar]
- 35.Melbourne A, Hipwell J, Modat M, Mertzanidou T, Huisman H, Ourselin S, Hawkes DJ. The effect of motion correction on pharmacokinetic parameter estimation in dynamic-contrast-enhanced MRI. Phys Med Biol. 2011;56(24):7693–708. doi: 10.1088/0031-9155/56/24/001. [DOI] [PubMed] [Google Scholar]
- 36.Lietzmann F, Zöllner FG, Attenberger UI, Haneder S, Michaely HJ, Schad LR. DCE-MRI of the human kidney using BLADE: A feasibility study in healthy volunteers. J Magn Reson Imaging. 2011;874:868–874. doi: 10.1002/jmri.23509. [DOI] [PubMed] [Google Scholar]
- 37.Rusinek H, Boykov Y, Kaur M, Wong S, Bokacheva L, Sajous JB, Huang AJ, Heller S, Lee VS. Performance of an automated segmentation algorithm for 3D MR renography. Magn Reson Med. 2007;57(6):1159–67. doi: 10.1002/mrm.21240. [DOI] [PubMed] [Google Scholar]
- 38.Gupta SN, Solaiyappan M, Beache GM, Arai AE, Foo TKF. Fast method for correcting image misregistration due to organ motion in time-series MRI data. Magn Reson Med. 2003;49(3):506–14. doi: 10.1002/mrm.10394. [DOI] [PubMed] [Google Scholar]
- 39.Attenberger UI, Sourbron SP, Michaely HJ, Reiser MF, Schoenberg SO. Retrospective respiratory triggering renal perfusion MRI. Acta Radiol. 2010;51(10):1163–71. doi: 10.3109/02841851.2010.519717. [DOI] [PubMed] [Google Scholar]
- 40.Lin W, Guo J, Rosen Ma, Song HK. Respiratory motion-compensated radial dynamic contrast-enhanced (DCE)-MRI of chest and abdominal lesions. Magn Reson Med. 2008;60(5):1135–46. doi: 10.1002/mrm.21740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.De Senneville BD, Mendichovszky IA, Roujol S, Gordon I, Moonen C, Grenier N. Improvement of MRI-functional measurement with automatic movement correction in native and transplanted kidneys. J Magn Reson Imaging. 2008;28(4):970–8. doi: 10.1002/jmri.21515. [DOI] [PubMed] [Google Scholar]
- 42.Zöllner FG, Sance R, Rogelj P, Ledesma-Carbayo MJ, Rørvik J, Santos A, Lundervold A. Assessment of 3D DCE-MRI of the kidneys using non-rigid image registration and segmentation of voxel time courses. Comput Med Imaging Graph. 2009;33(3):171–81. doi: 10.1016/j.compmedimag.2008.11.004. [DOI] [PubMed] [Google Scholar]
- 43.Song T, Lee VS, Chen Q, Rusinek H, Laine AF. An automated three-dimensional plus time registration framework for dynamic MR renography. J Vis Commun Image Represent. 2010;21(1):1–8. [Google Scholar]
- 44.Bokacheva L, Rusinek H, Zhang JL, Chen Q, Lee VS. Estimates of glomerular filtration rate from MR renography and tracer kinetic models. J Magn Reson Imaging. 2009;29(2):371–82. doi: 10.1002/jmri.21642. [DOI] [PMC free article] [PubMed] [Google Scholar]