Children’s developing intuitions about the truth conditions and implications of novel generics vs. quantified statements

Abstract

Generic statements express generalizations about categories and present a unique semantic profile that is distinct from quantified statements. This paper reports two studies examining the development of children’s intuitions about the semantics of generics and how they differ from statements quantified by all, most, and some. Results reveal that, like adults, preschoolers (1) recognize that generics have flexible truth conditions and are capable of representing a wide range of prevalence levels; and (2) interpret novel generics as having near-universal prevalence implications. Results further show that by age 4, children are beginning to differentiate the meaning of generics and quantified statements; however, even 7- to 11-year-olds are not adult-like in their intuitions about the meaning of most-quantified statements. Overall, these studies suggest that by preschool, children interpret generics in much the same way that adults do; however, mastery of the semantics of quantified statements follows a more protracted course.

Statements such as ducks lay eggs, grass is green, and knives are dangerous, known as generics, express generalizations about the members of a kind (e.g., Carlson, 1977; Carlson & Pelletier, 1995; Leslie, 2008). These statements are commonplace in everyday conversation and convey much of what we know about categories in the world. Generics are intriguing to linguists (e.g., Carlson, 1977; Carlson & Pelletier, 1995), philosophers (e.g., Leslie, 2008), and psychologists (e.g., Gelman, 2004; Prasada, 2000) alike because they present a series of puzzles, including how to explain their semantics and the relation between their truth conditions and their implications. In this paper, we take a developmental approach to these puzzles. Specifically, we explore the development of children’s intuitions about the truth conditions and implications of generics, the relation between them, and how children’s intuitions about generics differ from their intuitions about statements using explicit quantifiers (e.g., all, most, some).

The Semantics of Generics

The question of how to characterize the semantics of generics presents a sizable challenge. Generics can express predicates that are believed to be true for the majority (e.g., birds fly), half (e.g., lions have manes) or even fewer than half (e.g., mosquitoes carry the West Nile Virus) of category members. Still other generics can be rejected even though they are true of many (e.g., lions are male) or even the majority of category instances (e.g., people are right-handed). This complex, often conflicting relation between the truth of a generic statement and the statistical prevalence of the property in question has received considerable attention in the linguistic and philosophical literatures and has led to many attempts to explain the semantics of generics (e.g., Carlson, 1977; Carlson & Pelletier, 1995; Cohen, 1996; Diesing, 1992; Greenberg, 2003; Heim, 1982; Leslie, 2007; Liebesman, 2011; Pelletier & Asher, 1997).

Recent work in psychology has offered a compelling theoretical framework to explain this puzzling set of truth conditions (Gelman, 2010; Leslie, 2008, 2012; Prasada, 2000). According to this view, generics articulate core conceptual beliefs about kinds. Debates exist over whether the kind-based generalizations that generics express are quantitative and statistical (e.g., Rosch, 1973) or more complex and theory-driven (e.g., Gelman, 2003; Prasada & Dillingham, 2006, 2009). Nevertheless, an explanation of how we represent kinds must consider more than just quantitative, statistical information about the features that co-occur with category membership; it must also consider the causal knowledge that people have about categories. Thus, the truth of a generic can be understood as a function of both quantitative information about the prevalence of the predicated property within the kind (see Prasada & Dillingham, 2006, 2009) and other causal and conceptual knowledge linking the property to the kind (e.g., whether the property is innate, acquired, or emerges over development; Cimpian, Gelman, & Brandone, 2010b; Gelman & Bloom, 2007; whether the property is particularly dangerous or distinctive; Cimpian, Brandone, & Gelman, 2010a; Leslie, 2007, 2008).

Another perplexing aspect of the semantics of generics is the relation between their truth conditions and their prevalence implications. Cimpian, Brandone, and Gelman (2010a) propose that there is an asymmetry at the core of generic meaning: Although the truth of a generic may be unrelated to the prevalence of the predicated property, this is not the case for the implications of generics. Generic statements have powerful prevalence implications. Imagine hearing the generic “parrots carry psittacosis.” Based on this statement, a reasonable assumption is that psittacosis is widespread among parrots and that all or at least a majority are carriers of this disease. Research confirms that adults indeed expect generics to apply to the vast majority of category members (Cimpian et al., 2010a; Gelman et al., 2002). Consistent with the proposal that generics have strong implications yet require little evidence to be judged true, Cimpian et al. found that adults interpreted novel generics (e.g., Lorches have purple feathers) as referring to nearly all members of a kind (roughly 95%), yet judged the same generics to be true at a wide range of prevalence levels (even as low as 10%).

This discrepancy between the truth conditions and implications of generics is not just an intriguing linguistic phenomenon. This asymmetry also shows up in and can shape real world thinking. Consider a stereotype such as “Boys are good at sports.” The flexible truth conditions of generics allow that a generalization such as this can be legitimized based on very little evidence. Once accepted, however, this generalization can imply a far more prevalent--even normative--fact with potential consequences for beliefs and behavior (e.g., Abelson & Kanouse, 1966; Cimpian, 2010; Rhodes, Leslie, & Tworek, 2012).

Importantly, the semantic idiosyncrasies described here are unique to generics. Quantified statements, in comparison, are relatively straightforward in their semantic interpretations¹. Quantifiers are used to express a more or less fixed prevalence (Carlson, 1977). For example, all statements refer to an entire category without exception; some statements are true as long as the property is present in at least a subset of category members; finally, most statements are true when greater than 50% of category members display the property. (Here we define the quantifiers some and most in terms of their lower bound—that is, the minimum prevalence required for them to be considered true. When used in conversation, these quantifiers are often assumed to have an upper bound, as well. For example, a most statement (e.g., Most people are right-handed) conveys that (to the speaker’s knowledge) the predicate applies to no more than most (i.e., not all) category members. In cases such as these, known as scalar implicatures, the semantic and pragmatic aspects of meaning differ (see Grice, 1989; Horn, 1992; Noveck, 2001). For the present purposes, however, we focus on the purely semantic interpretation of these quantifiers.)

Quantified statements are also relatively straightforward as compared to generics in that they do not show the asymmetry between prevalence implications and truth conditions observed for generics. Instead, they imply a prevalence that roughly matches that required to judge them true. For example, all statements imply that a property is shared by 100% of category members and require a prevalence of 100% to be deemed true. This claim has been validated for the quantifier most: Cimpian et al. (2010a) found that the prevalence that led adult participants to accept most-quantified statements (e.g., Most lorches have purple feathers) was statistically identical to the prevalence implied by them (roughly 80%).

Thus, overall, the literature suggests that generics present a complex and unique semantic profile that is distinct from that of quantified statements and has important implications for real world thinking. Of particular interest in the present paper is the question of how these semantic intuitions emerge during development.

The Semantics of Generics for Young Children

Existing research suggests that, despite the puzzles generics present to scholars, they are well within children’s grasp from early in development. Generics are frequent in the speech young children hear in natural conversation and they occur in children’s own spontaneous speech by 2½ years of age (e.g., Gelman, Coley, Rosengren, Hartman, & Pappas, 1998; Gelman, Goetz, Sarnecka, & Flukes, 2008; Pappas & Gelman, 1998; see Sneed, 2008 for a linguistic account of the acquisition of genericity). Preschoolers comprehend generics and are able to distinguish them from non-generics on the basis of lexical, morphosyntactic, and contextual cues (e.g., Cimpian & Markman, 2008; Gelman & Raman, 2003; Graham, Nayer, & Gelman, 2011). Moreover, preschoolers can use the distinction between generics and non-generics to guide the inferences they draw when acquiring new knowledge (e.g., Chambers, Graham, & Turner, 2008; Cimpian & Markman, 2009, 2011; Gelman & Bloom, 2007; Gelman, Ware, & Kleinberg, 2010; Graham et al., 2011; Hollander, Gelman, & Raman, 2009; Rhodes et al., 2012).

In contrast to the ease with which they acquire generics, quantified statements are relatively difficult for children to master. In recent years, children’s comprehension of sentences containing quantified expressions has received considerable attention (e.g., Brooks & Braine, 1996; Crain et al., 1996; Gualmini, 2004; Huang & Snedeker, 2009; Lidz & Musolino, 2002; Noveck, 2001; Papafragou & Musolino, 2003). Data suggest that, although even preschoolers appear to understand the semantic implications of some and all on simplified tasks (Barner, Chow, & Yang, 2009; Smith, 1979, 1980), children consistently make errors in interpreting the subtle aspects of the meaning of all (e.g., Brooks & Sekerina, 2006), some (e.g., Guasti, Chierchia, Crain, Foppolo, Gualmini, & Meroni, 2005; Hurewitz, Papafragou, Gleitman, & Gelman, 2006; Noveck, 2001), and most (Barner et al., 2009; Papafragou & Schwartz, 2006) until well into middle childhood. Controversy exists over the specific nature of children’s difficulty and the extent to which it is semantic or pragmatic (e.g., Crain et al., 1996; Musolino & Lidz, 2006; Papafragou & Musolino, 2003; Phillip, 1995; Pouscoulous et al., 2007; Sullivan & Barner, 2011). Nevertheless, children often differ from adults in the way they interpret sentences containing quantified expressions.

Intriguingly, when children’s understanding of generics and quantifiers has been examined in the same study, not only do quantified statements prove more challenging, they also appear to be misinterpreted at first as if they were generic. Hollander, Gelman, and Star (2002) found that when asked to evaluate the truth of generics and statements quantified by all or some (e.g., Are flowers/all flowers/some flowers yellow?), 4-year-olds and adults appropriately differentiated their responses to generics versus quantified statements. However, 3-year-olds gave the same pattern of responses regardless of whether they were given quantified statements or generics, and these responses were indistinguishable from the responses older children and adults gave in response to generics. To account for these findings, Leslie (2008, 2012) has proposed that generics express cognitively fundamental, default generalizations that are easier, more automatic, and appear developmentally earlier than other forms of generalization. In contrast, quantified statements express generalizations that are more cognitively complex and effortful, and thus appear later and prove more difficult for children to master (see Leslie & Gelman, 2012 for further evidence).

Although the existing literature and the generics-as-default proposal suggest that children master generics early in development, questions remain regarding the extent to which children share adults’ intuitions about the unique semantic profile of generics. In the current paper, we were interested in examining the development of children’s intuitions about the semantics of generics by systematically testing (1) how children evaluate the truth conditions and prevalence implications of generics, (2) the relation between them, and (3) how children’s intuitions about generics differ from their intuitions about statements quantified by all, most, and some.

Consider first the question of how children evaluate the truth conditions and prevalence implications of generics. Studies have shown that, like adults, preschoolers recognize that generics can be true despite salient exceptions (Gelman & Raman, 2003), understand that the truth of a generic depends on more than just the statistical prevalence of the predicated property (Brandone, Cimpian, Leslie, & Gelman, 2012), and interpret generics as broad in scope but tolerant of exceptions (Gelman et al., 2002). However, more research is needed to systematically test children’s intuitions about the precise truth conditions and implied prevalence of generics. In particular, we know that adults judge generics to be true at a wide range of prevalence levels (roughly 65% on average, but even as low as 10%; Cimpian et al., 2010a); however, it remains an open question whether young children also understand that generics can represent a broad range of prevalence levels. Moreover, we know that adults estimate the prevalence of a novel generic to apply to roughly 95% of category members (Cimpian et al., 2010a); yet, it remains an open question what prevalence level children assume given a novel generic.

Our second research question examines the relation between children’s intuitions about the truth conditions and implications of generics. Research with adults has shown that an important asymmetry exists such that adults interpret novel generics as referring to the vast majority of category members, but judge the same novel generics to be true given a wide range of prevalence levels—even 10 or 30% (Cimpian et al., 2010a). Here we provide the first test of whether this asymmetry also exists in children.

Note that these questions are not just interesting from a linguistic perspective; they also have important implications for understanding children’s conceptual development. Since generic concepts are central to human reasoning and provide insight into the nature of concepts (e.g., Prasada, 2000), determining how children interpret the truth conditions of generics can shed light on the nature of children’s early kind concepts. Moreover, because generic testimony from others serves as an important source of knowledge for young children (e.g., Gelman, 2009; Harris & Koenig, 2006; Rhodes et al., 2012), establishing what children see as the implications of generics can help us to understand the process by which children incorporate new information conveyed through generic language into their world knowledge.

Our final research question tests the uniqueness of the semantic profile of generics by asking whether children, like adults, differentiate the semantics of generics from those of statements quantified by all, most, and some. Studies have shown that children can distinguish the truth conditions of generics from all or some statements (Hollander et al., 2002) and that children show different patterns of inferences after hearing information about a familiar category presented in generic, all, and some form (Gelman et al., 2002). Yet data also suggest that children have difficulty mastering the semantics of quantified statements (e.g., Brooks & Sekerina, 2006; Hurewitz et al., 2006; Papafragou & Schwartz, 2006) and in some cases interpret some and all statements as though they were generic (Hollander et al., 2002). Finally, no studies have examined whether children differentiate the semantics of generics from statements quantified by most—the quantifier argued to come closest to capturing generic meaning (Carlson, 1977). Thus, further research is needed to systematically address the extent to which children differentiate the truth conditions and implications of generics and statements quantified by all, some, and most.

The Present Studies

Two experiments were conducted to systematically examine children’s intuitions about the semantics of generics and quantified statements referring to novel categories. Novel categories about which children had no prior knowledge were used to present a pure test of children’s semantic intuitions. To provide a thorough developmental account, each study included a sample of preschoolers (ages 4 and 5), older children (ages 7 to 11), and adults. In Study 1, we explored the truth conditions of generics and quantifiers. Specifically, we used a sentence verification task with novel animal categories to ask (a) whether children understand that generics are capable of representing a broad range of prevalence levels and (b) how children’s intuitions about the truth conditions of generics differ from their intuitions about statements quantified by all, most, and some. In Study 2, we explored the implied prevalence of generics and quantifiers. We asked (a) what prevalence level children assume upon hearing a generic about a novel category, and (b) whether children recognize the implications of generics as distinct from those of statements quantified by all, most, and some. Finally, to determine whether the asymmetry in generic meaning shown previously in adults (Cimpian et al., 2010a) extends to children, we compared responses across Study 1 and Study 2.

Consistent with evidence supporting young children’s skill in using and comprehending generics (e.g., Brandone et al., 2012; Cimpian & Markman, 2008; Gelman et al., 2008; Hollander et al., 2002) and theoretical claims that generics reflect default generalizations (Leslie, 2008, 2012), we predicted that both preschoolers and older children would demonstrate adult-like intuitions about the semantics of generic statements. Specifically, we predicted that preschoolers and older children would accept generics at a broad range of prevalence levels in Study 1 and assume widespread prevalence implications in Study 2. We also predicted that the asymmetry in generic meaning demonstrated in adults (Cimpian et al., 2010a) would be observed in children.

Regarding children’s comprehension of explicit quantifiers and their differentiation from generics, we made the following predictions. First, consistent with studies documenting children’s errors in interpreting quantified statements into middle childhood (e.g., Brooks & Sekerina, 2006; Hurewitz et al., 2006; Papafragou & Schwartz, 2006) and the theoretical claim that quantified statements communicate cognitively sophisticated generalizations (Leslie, 2008, 2012), we predicted that performance in response to quantified statements would be less adult-like than performance in response to generic statements and would become more adult-like with age. Second, in line with the generics-as-default hypothesis (Leslie, 2008, 2012) and Hollander et al.’s (2002) initial finding that 3-year-olds interpreted all and some statements about familiar categories as if they were generics, we predicted that preschoolers may treat quantified statements about novel categories in the current studies as though they were generic.

Study 1: Truth Conditions of Generics

In Study 1, we examined the truth conditions of generics and quantifiers using a sentence verification task with completely novel animal categories. We asked: (a) whether children understand that generics are capable of representing a broad range of prevalence levels and (b) how children’s intuitions about the truth conditions of generics differ from their intuitions about the truth conditions of quantified statements (e.g., some, most, all).

Method

Participants

Sixteen adults (3 males, 13 females), 16 older children (7.08 to 10.62 years; M = 8.56 years; 6 males, 10 females), and 24 preschoolers (4.11 to 5.73 years; M = 4.66 years; 12 males, 12 females) participated. Two additional preschoolers were tested and excluded from the final sample due to failure to comprehend the practice items. Preschoolers were recruited from in and around a Midwestern U.S. university town. Older children were recruited from a midsize city in the Northeastern U.S. Children were predominantly middle-class and white. Adults were undergraduate students in an Introduction to Psychology class at a large Midwestern university and participated for course credit.

Materials

Materials included 32 novel animal kinds each with a distinctive physical feature. There were four types of features: pattern (e.g., spots), color (e.g., red), part (e.g., wings), and part color (e.g., orange ears). Feature types were distributed over the 32 kinds such that 8 kinds displayed each of the 4 feature types. For each kind, images depicting a sample of 6 individuals were created. The number of individuals displaying the distinctive feature within each sample varied at the follow prevalence levels: 0 (0%), 2 (33%), 4 (67%), and 6 (100%) out of 6 (see Figure 1). These prevalence levels were selected to provide a range from 0 to 100% and to include both a minority and a majority sample. Which prevalence level was presented for each item was counterbalanced across participants. Each participant saw just one sample of each animal kind.

Figure 1.

Sample animal kind (“crullets”) showing target feature (“spots”) at each of 4 prevalence levels (0, 33, 67, and 100%).

Procedure

Children were tested individually with an experimenter in a quiet room. Adults were tested in groups in a written version of the task. For each item, participants saw one sample of an animal kind and were asked to indicate whether a corresponding statement (e.g., Crullets have spots) is right or wrong. Adults responded by circling their answer choice. Children responded by pointing to a picture of a happy (for right responses) or sad (for wrong responses) face. To motivate the task, children were introduced to a puppet named Droid, described as an alien from outer space who is trying to teach children about the animals on his planet. Children were told that Droid gets confused, so sometimes he says things that are wrong. Children were asked to help Droid by telling him whether each of his statements is right or wrong.

Practice trials

To convey that Droid’s statements could be either right or wrong, participants were first given a practice task consisting of four items—two designed to elicit right responses (e.g., a picture of bananas with the statement “This is a picture of bananas”) and two designed to elicit wrong responses (e.g., a picture of a white house with the statement “This house is blue”). Children were corrected in the practice task if they responded incorrectly. Two children who responded incorrectly on two or more trials were excluded from the final sample.

Primary task

Following the practice items, the primary task began. For each item, participants saw a single sample of an animal kind displaying a target feature at one of four prevalence levels (0, 33, 67, 100%). Participants were asked to indicate whether a corresponding statement was right or wrong. Statements were in one of the following wording conditions: generic (e.g., Ackles have spikes), some (e.g., Some taifels have pink feathers), most (e.g., Most ollers are green), or all (e.g., All noobs have hair). Animal names were always presented in the subject position. All generics used the bare plural form. Wording conditions (generic, some, most, all) were presented in blocks of 8 items. Each block included two items at each prevalence level and two items from each feature category (e.g., pattern, color, part, part color). Block order was counterbalanced using a Latin Square design.

Results and Discussion

Do children recognize that generics represent a broad range of prevalence levels?

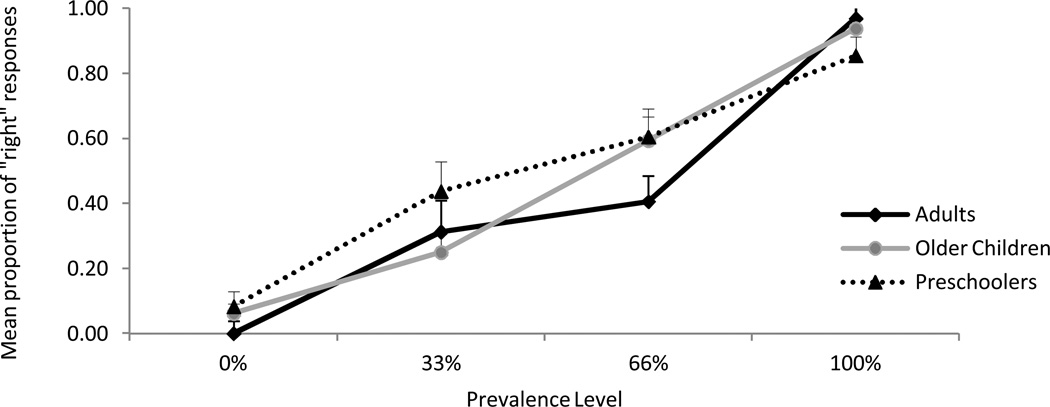
The first set of analyses examined the central question of whether children, like adults, understand that generics are capable of representing a broad range of prevalence levels. We performed a mixed 3 (age group: preschoolers, older children, adults; between) × 4 (wording order; between) × 4 (prevalence level: 0, 33, 67, 100%; within) ANOVA on the proportion of right selections in response to generic statements. Results revealed a significant main effect of prevalence level, F(3, 132) = 71.67, p < .001, η_p² = .62, and no significant effects or interactions with age. As shown in Figure 2, according to linear trend analyses, preschoolers, F(1, 20) = 146.18, p < .001, η_p² = .88, older children, F(1, 12) = 112.34, p < .001, η_p² = .90, and adults, F(1,12) = 1152.00, p < .001, η_p² = .99, all showed a linear effect of prevalence level such that the average proportion of right responses increased as the prevalence level increased.

Figure 2.

Mean proportion of “right” responses to generic statements on the truth condition task (Study 1) by age group

Notably, generics were periodically judged to be true even when the prevalence of the property was quite low: 12 out of 24 preschoolers, 5 out of 16 older children, and 5 out of 16 adults responded that a generic was true when the property in question was present in only 33% of category members. Participants offered right responses at this prevalence level an average of 34.8% of the time (43.8, 25.0, and 31.3% for preschoolers, older children, and adults, respectively. Analyses using the Generalized Estimating Equations (GEE) procedure (Liang & Zeger, 1986) revealed that, overall, the likelihood of judging a generic statement as right in response to the 33% prevalence level was significantly greater than the likelihood of doing so in response to the 0% prevalence level, χ²(1) = 26.86, p < .001. This comparison was significant for adults and preschoolers (ps < .05) and marginal for children in the older age group (p = .060). Together, these results confirm that both children and adults are sometimes willing to judge novel generic statements as true on the basis of little evidence.

Do children differentiate the truth conditions of generics and quantified statements?

Our next set of analyses asked whether children’s intuitions about the truth conditions of generics differ from those of statements quantified by some, most, or all. To address this question, we first examined the average prevalence level that led to right responses for each statement type². For example, if a subject selected right in response to generics whenever the prevalence was 67 or 100% and wrong for anything else, then that person’s average prevalence that led to right responses for generics would be 83.3%—the mean of 67 and 100%. These data were entered into a 3 (age group: preschoolers, older children, adults; between) × 4 (wording order; between) × 4 (wording: generic, all, most, some; within) ANOVA. Results revealed a main effect of wording, F(3, 132) = 65.55, p < .001, η_p² = .60, and an interaction of wording × age group, F(6, 132) = 2.78, p = .014, η_p² = .11. Bonferroni-adjusted pairwise comparisons revealed that the average prevalence level that led to right responses for all wording conditions differed significantly from each other (ps < .001; M_All = 94.95%, M_Most = 74.82%, M_Some = 62.28%, M_Generic = 81.85%). Separate ANOVAs analyzing the effect of wording within each age group revealed a similar pattern of results for children and adults. The average prevalence level that led to right responses for each wording condition at each age group is displayed in Table 1.

Table 1.

Mean prevalence level (SD) that led to “right” responses on the truth condition task (Study 1) and mean prevalence (SD) on the implied prevalence task (Study 2) by age group and wording

		Mean Prevalence Level (SD)
Age Group	Wording	Truth Condition (Study 1)	Implied Prevalence Task (Study 2)	Significant Task Effect
Adults	Generic	87.5 (15.5)	99.0 (4.2)	*
	All	99.3 (2.8)	100.0 (0.0)
	Most	74.0 (15.8)	67.2 (2.1)
	Some	58.2 (13.9)	42.7 (13.9)	*
Older Children	Generic	81.1 (15.0)	97.8 (8.6)	*
	All	95.0 (11.1)	100.0 (0.0)
	Most	73.0 (14.8)	91.1 (15.3)	*
	Some	62.0 (16.6)	53.9 (16.6)
Preschoolers	Generic	76.7 (15.7)	87.5 (16.5)	*
	All	90.1 (14.1)	95.5 (9.8)
	Most	77.1 (15.6)	84.0 (16.8)
	Some	66.3 (17.8)	66.3 (22.7)

^*Indicates p < .05 for task comparison within each wording condition and age group

To explore the perceived truth conditions of generics versus quantified statements in a more nuanced way, we next examined the proportion of right responses participants provided at each prevalence level. We performed a mixed 3 (age group: preschoolers, older children, adults; between) × 4 (wording order; between) × 4 (wording: generic, all, most, some; within) × 4 (prevalence level: 0, 33, 67, 100%; within) ANOVA. Results showed significant main effects of wording, F(3, 129) = 31.45, p < .001, η_p² = .42, and prevalence level, F(3, 129) = 146.39, p < .001, η_p² = .77, as well as significant interactions of wording × age group, F(6, 129) = 2.47, p = .027, η_p² = .10; wording × prevalence level, F(9, 387) = 30.82, p < .001, η_p² = .42; and wording × prevalence level × age group, F(18, 387) = 2.67, p < .001, η_p² = .11.

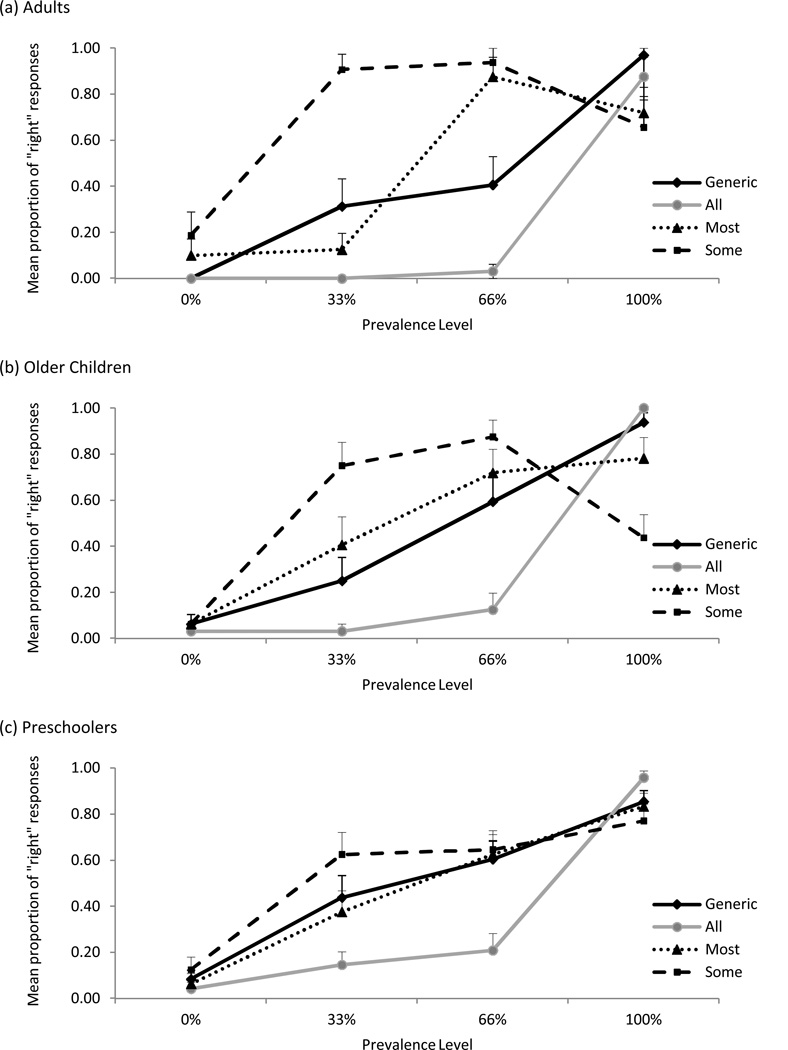
To disentangle the three-way interaction, we first examined the effects of prevalence level and age group within each wording condition (see Figure 3). Here we asked whether for each wording condition, preschoolers, older children, and adults responded differently to samples of varying prevalence levels. Results revealed a significant prevalence level × age group interaction in some wording conditions, but not others. In particular, the interaction was significant in both the most, F(6, 129) = 2.18, p = .049, η_p² = .092, and some conditions, F(6, 132) = 2.73, p = .016, η_p² = .11, suggesting that children and adults differ from one another in their intuitions about the prevalence required for most and some statements to be considered true. In contrast, in the generic and all conditions this interaction was nonsignificant (ps > .24), indicating that children and adults share the same intuitions about the prevalence required for generic and all statements to be considered true. These data suggest that children show adult-like reasoning about the truth conditions of generics and all statements; however, their reasoning about most and some statements is still maturing. In particular, for some statements, older children performed equivalently to adults whereas preschoolers did not, F(3,96) = 2.73, p =.048, η_p² = .079. In contrast, for most statements, children of both age groups performed differently from adults—significantly so for the younger age group, F(3, 93) = 3.91, p = .011, η_p² = .11, and marginally so for the older age group, F(3, 69) = 2.33, p = .082, η_p² = .092.

Figure 3.

Mean proportion of “right” responses on the truth condition task (Study 1) by age group: (a) adults, (b) older children, (c) preschoolers, wording, and prevalence level.

To further explore how participants in each age group differentiated the truth conditions of the generic and quantified statements, we next examined the effects of prevalence level and wording condition separately for each age group. Here we asked whether adults, older children, and preschoolers responded to the prevalence levels differently for each statement type.

As can be seen in Figure 3a, adults showed a different pattern of responses for each wording condition (ps < .01). Adults viewed all statements as correct only when 100% of category members displayed the key feature; they judged most statements as correct at prevalence levels of 67% or greater; and they judged some statements as correct at prevalence levels as low as 33%. Adults also showed evidence of scalar implicatures in the most and some conditions: That is, they showed an increased tendency to reject most and some statements when they were used to described the 100% samples. Finally, as mentioned previously, for generics adults showed a linear effect of prevalence level such that they were more likely to accept generics as right as the prevalence of the property increased (linear trend analysis). Adults did not show evidence of scalar implicature for generics. Overall, these data show that adults perceive generic, all, most, and some statements as each having their own unique set of truth-values³.

As can be seen in Figure 3b, the pattern of results for the older children was similar to that of adults with a few key exceptions. Like adults, older children viewed all statements as correct only when 100% of category members displayed the key feature. Also like adults, older children accepted some statements at prevalence levels as low as 33% and showed evidence of scalar implicature in their tendency to reject some-quantified statements at the 100% level. Unlike adults, however, for older children, the effect of prevalence level did not differ between most statements and generics, F(3, 36) = 1.51, p = .23, η_p² = .11. Linear trend analyses showed that a linear effect of prevalence level emerged in older children’s responses to both generics and most statements. Thus, older children differentiated each wording condition (all ps < .01) except most and generics.

Finally, the youngest age group showed a distinct pattern of results. As can be seen in Figure 3c, the effect of prevalence level in the all wording condition was different from that in the most, some, and generic wording conditions (all ps < .001). Like adults and older children, preschoolers viewed all-quantified statements as correct mainly at the 100% prevalence level. Preschoolers’ pattern of responses for the other wording conditions, however, was less differentiated: the effect of prevalence level was only marginally different in the comparison between most and some, F(3, 69) = 2.24, p = .092, η_p² = .089, with preschoolers accepting some statements marginally more often than most statements at the 33% level. This effect was also marginally different in the comparison between some statements and generics, F(3, 69) = 2.18, p = .098, η_p² = .087, with preschoolers accepting some statements marginally more often than generics at the 33% level. Finally, similarly to older children, but unlike adults, there was no difference in the effect of prevalence level on preschoolers’ reasoning about most statements and generics, F(3, 69) = .21, p = .89, η_p² = .009. A linear effect of prevalence level emerged in preschoolers’ responses to both generics and most statements (linear trend analysis). Note that preschoolers also did not show any sensitivity to scalar implicatures. Preschoolers were somewhat more (rather than less) likely to accept some- and most-quantified statements when they were used to describe 100% samples. These data suggest that by 4 to 5 years, children are beginning to differentiate the truth conditions of generics and quantifiers; however, their reasoning about most and some statements is still maturing and they do not appear to clearly distinguish the semantics of generics, most, and some statements.

Conclusions

Overall, the results of Study 1 support two main conclusions. First, by 4 to 5 years of age, children understand that generics are capable of representing a broad range of prevalence levels. Preschoolers and older children in the current study were willing to accept novel generics that were true of only a minority of category members (at the lowest non-zero prevalence level tested—33%). Crucially, because these studies used novel categories about which children had no prior knowledge, they provide a pure test of children’s understanding of the role that prevalence plays in generic meaning. Second, our data demonstrate that children are in the process of differentiating the truth conditions of generics and quantified statements throughout childhood. Children are sensitive to the difference between generics and all statements by preschool. By middle childhood (and to a much lesser extent during preschool), children are also sensitive to the difference between generics and some statements. However, preschoolers and older children do not appear to distinguish the truth conditions of generics and most statements. Although these conclusions are necessarily limited by the sensitivity of our methodology, they are consistent with the hypothesis that generics may be a kind of default (Hollander et al., 2002; Leslie, 2008, 2012). In support of this proposal, most-quantified statements were interpreted equivalently to generics by preschoolers and older children; some-quantified statements also showed a tendency to be interpreted as generic by preschoolers. Together these results suggest that children share adults’ intuitions about the flexible truth conditions of generics from an early age and continue to learn how the truth conditions of quantified statements are different from generics throughout childhood.

Study 2: Prevalence Implications of Generics

In Study 2, we further explored the development of intuitions about the meaning of generics by examining the implied prevalence of generics and quantified statements. We asked (a) what prevalence level children assume upon hearing a generic about a novel category, and (b) whether children recognize the implications of generics as distinct from those of statements quantified by all, most, and some. Crucially, to determine whether the asymmetry in generic meaning shown previously in adults (Cimpian et al., 2010a) extends to children, we also compared participants’ responses across Study 1 and Study 2.

Method

Participants

Sixteen adults (7 males, 9 females), 15 older children (7.04 to 11.25 years; M = 8.31 years; 7 males, 8 females), and 24 preschoolers (4.16 to 5.32 years; M = 4.64 years; 9 males, 15 females) participated. Participants were recruited as in Study 1. Five additional children were tested and excluded from the final sample for failing two or more practice items.

Materials

Materials were identical to those in Study 1.

Procedure

Children were tested individually with an experimenter. Adults were tested in groups with a written version of the task. For each item, participants were asked to indicate which of four samples best represents a corresponding statement (e.g., Which of these pictures best shows that crullets have spots?). Options included samples at each of the four prevalence levels (0, 33, 67, 100%). Materials were presented in pre-printed booklets with all four samples on a single page (see Figure 1). Adults responded by circling the sample they believed best represented each statement. Children responded by putting a sticker on the appropriate sample. To motivate the task, children were introduced to a puppet named Droid. Droid was described as an alien from outer space who is making a picture book to teach children about the different kinds of animals on his planet. Children were asked to help Droid decide which pictures to put in his book.

Practice trials

To convey that on a given item participants needed to select one of the four samples, participants completed two practice tasks. The first involved selecting the picture that matched the experimenter’s question from a set of four pictures. In this task, there were two items: one required finding the picture of bananas from a set of four foods; the other required finding the picture of a blue house from a set of four houses. The second task involved selecting a picture based on a precise quantification term. Participants were shown four samples of the same animal kind at varying prevalence levels and were asked to select the sample in which a specified number of animals displayed the target property (e.g., Which of these pictures best shows that two daxes have ears?) This task included four items—one targeting each prevalence level. Children were corrected if they responded incorrectly. Five participants who responded incorrectly on two or more practice items were excluded from the final sample.

Primary task

For a given item, participants saw four samples from the same animal kind. The prevalence of the distinctive feature within each sample varied with one sample at each of the four prevalence levels (0, 33, 67, 100%). The order in which the samples appeared on the page was systematically varied. Participants were asked to indicate which of the four samples best represents the given information. In the generic condition, participants were asked questions in generic form (e.g., What’s the best picture to show that ackles have spikes?). In the some, most, and all conditions, participants were asked questions quantified by some, most, and all, respectively (e.g., What’s the best picture to show that some/most/all ackles have spikes?). As in Study 1, animal names were always presented in the subject position and all generics used the bare plural form. Wording conditions (generic, some, most, all) were presented in blocks. Each block consisted of four items. Block order was counterbalanced using a Latin Square design. For a given participant, all four item sets within each block came from the same feature category (e.g., pattern, color, part, and part color). The order in which these feature categories were presented and the wording condition to which they were assigned were counterbalanced such that feature categories were presented in each of the four block positions and with each of the four wording conditions an equal number of times.

Results and Discussion

What is the implied prevalence of generics and quantifiers for children?

The goal of Study 2 was to determine what prevalence level children assume upon hearing a novel generic and whether children recognize the implied prevalence of generics as distinct from those of quantified statements. To address these questions, we performed a mixed 3 (age group: preschoolers, older children, adults; between) × 4 (wording order; between) × 4 (wording: generic, all, most, some; within) ANOVA on the average prevalence level participants selected. Results revealed main effects of wording, F(3, 129) = 116.27, p < .001, η_p² = .73, and age group, F(2,43) = 4.34, p = .019, η_p² = .17, that are best interpreted in light of a wording × age group interaction, F(2, 129) = 14.15, p < .001, η_p² = .40.

As can be seen in Table 1, the prevalence levels adults selected for the quantified statements differed significantly from each other (Bonferroni-adjusted pairwise comparisons; ps < .001). As expected, the implied prevalence of all was greater than most, which was greater than some. Adults tended to select the 100% sample for all, the 67% sample for most, and the 33% sample for some at levels significantly greater than chance (.25) (ps < .001; see Table 2 for the average proportion of selections at each prevalence level). Crucially, adults also differentiated the implied prevalence of generics and statements quantified by some and most (ps < .001): they assumed the prevalence of a novel generic to be greater than that of a some- or most- quantified statement. However, adults did not differentiate the implied prevalence of generics and all statements. When evaluating which picture best illustrates a generic property, adults selected the 100% prevalence level the vast majority of the time (see Table 2).

Table 2.

Mean proportion (SD) of times each prevalence level was selected in the implied prevalence task (Study 2) by age group and wording

		Prevalence Level
Age Group	Wording	0%	33%	67%	100%
Adults	Generic	0.00 (0.00)	0.02 (0.06)	0.00 (0.00)	0.98 (0.06)*
	All	0.00 (0.00)	0.00 (0.00)	0.00(0.00)	1.00 (0.00)*
	Most	0.00 (0.00)	0.00 (0.00)	0.95 (0.14)*	0.02 (0.06)
	Some	0.00 (0.00)	0.75 (0.39)*	0.22 (0.38)	0.03 (0.09)
Older Children	Generic	0.00 (0.00)	0.00 (0.00)	0.07 (0.26)	0.93 (0.26)*
	All	0.00 (0.00)	0.00 (0.00)	0.00(0.00)	1.00 (0.00)*
	Most	0.00 (0.00)	0.00 (0.00)	0.27 (0.46)	0.73 (0.46)*
	Some	0.00 (0.00)	0.42 (0.47)	0.55 (0.46)*	0.03 (0.09)
Preschoolers	Generic	0.00 (0.00)	0.08 (0.16)	0.21 (0.31)	0.71 (0.38)*
	All	0.01 (0.05)	0.01 (0.05)	0.08 (0.16)	0.90 (0.21)*
	Most	0.01 (0.05)	0.06 (0.13)	0.32 (0.34)	0.60 (0.40)*
	Some	0.00 (0.00)	0.33 (0.37)	0.38 (0.38)	0.29 (0.39)

^*Indicates greater than chance (.25) performance, p < .05

The pattern of responses for preschoolers was comparable, but different in several key ways. As can be seen in Table 1, the youngest children also differentiated the implied prevalence of the quantifiers (Bonferroni-adjusted pairwise comparisons; all ps < .003). Like adults, they judged the implied prevalence of all to be greater than most, which was greater than some. However, their responses differed significantly from those of adults in each wording condition except all (ps < .002), and preschoolers’ responses were more varied than those of adults. Preschoolers selected the 100% sample the vast majority of the time for all-quantified statements. But they selected both the 67 and 100% samples in response to most-quantified statements, and they selected the 33, 67, and 100% samples at chance levels in response to some-quantified statements (see Table 2)—suggesting a lack of sensitivity to the scalar implicature in statements quantified by most and some.

With respect to the key comparison between the implications of generics and quantified statements (see Table 1), preschoolers differentiated the implied prevalence of generics and some statements (p = .002). In addition, they showed a marginal tendency toward differentiating generics and statements quantified by all (p = .072). However, preschoolers did not differentiate the implications of generics and most-quantified statements (p = .73). These data suggest that preschool age children are beginning to distinguish the implications of generics and quantifiers; however, they appear not to discriminate the meaning of generics and most-quantified statements.

Finally, the pattern of responses for the older children fell in between that of preschoolers and adults. Older children responded statistically equivalently to adults in response to all, some, and generic statements (all ps > .39; Table 1). However, in response to most-quantified statements, older children provided unexpectedly high implied prevalence responses that were not significantly different from their responses to all-quantified statements. Older children selected the 100% sample at levels significantly greater than chance for both the all- and most- quantified statements—suggesting a lack of sensitivity to the scalar implicature in statements quantified by most⁴ (and, to some extent, in statements quantified by some; see Table 2).

With respect to the key comparison between the implications of generics and explicitly quantified statements (see Table 1), older children differentiated the implied prevalence of generics and statements quantified by some (p < .001). In addition, older children performed like adults in that they did not differentiate the implied prevalence of generics and statements quantified by all; however, older children also performed like preschoolers in that they did not differentiate the implied prevalence of generics and statements quantified by most (ps > .55)⁵. Altogether, these data suggest that children in middle childhood are adult-like in their reasoning about the semantic implications of generics; however, they appear to still be fine-tuning their intuitions about the implications of statements quantified by most.

Is there an asymmetry in generic meaning for young children?

The goal of the final set of analyses was to test for an asymmetry in generic meaning: namely, that generic statements have strong implications yet require little evidence to be judged true. As in Cimpian et al. (2010a), we compared the average prevalence level that led to right responses in the truth condition task (Study 1) with the average prevalence level selected for each type of statement in the implied prevalence task (Study 2). To do so, we performed a 2 (task: truth condition vs. implied prevalence; between) × 3 (age group: preschoolers, older children, adults; between) × 4 (wording: generic, all, most, some; within) ANOVA. Here we focus on effects and interactions involving the variable task (truth condition vs. implied prevalence). Results revealed a significant main effect of task, F(1, 105) = 4.50, p = .036, η_p² = .041, and a task × wording interaction, F(1, 192) = 6.76, p < .001, η_p² = .096 (see Table 1). The three-way interaction of age group × task × wording was only marginally significant, F(6, 315) = 2.04, p = .06, η_p² = .037. However, because our goal was to test whether an asymmetry is present in children’s judgments about generics, we evaluated the task × wording interaction separately for each age group.

We used tests of simple effects to check for an effect of task for adults and children within each wording condition. Of special interest was the generic condition. As can be seen in Table 1, results confirmed the predicted asymmetry for preschoolers, F(1, 43) = 5.15, p = .028, η_p² = .11, older children, F(1, 26) = 13.51, p = .001, η_p² = .34, and adults, F(1, 27) = 7.80, p = .009, η_p² = .22. The average prevalence that led participants to accept generics in the truth condition task (Study 1) was significantly lower than the average prevalence implied by them in Study 2. For the youngest children, this asymmetry was unique to reasoning about generics: the effect of task was non-significant for all, some, and most-quantified statements (all ps > .14). For older children, this asymmetry was also observed for most-quantified statements, F(1, 26) = 8.92, p = .001, η_p² = .33, confirming the older children’s lack of differentiation of generics and most statements. Finally, for adults, this comparison was non-significant for all and most quantified statements and the opposite effect was found for some-quantified statements: the prevalence that led adults to accept some statements was greater than the prevalence implied by them, F(1, 27) = 9.36, p = .005, η_p² = .26.

Conclusions

Overall, the results of Study 2 and the comparison between the truth condition task (Study 1) and the implied prevalence task (Study 2) support three main conclusions. First, for both children and adults, generics have powerful prevalence implications. Upon hearing a novel generic, adults and children as young as 4 years assume the property is true of the vast majority of category members. Second, between the ages of 4 and 11, children are beginning to differentiate the implications of generics and quantified statements; however, even 7- to 11-year-old children do not appear to be adult-like in their intuitions about the implications of some and most and how they differ from generics. Finally, our results confirm the presence of an asymmetry in reasoning about generics that is present as early as preschool. Both adults and young children assumed that generic statements about novel categories apply to nearly all members of the relevant categories; however, they often judged the same generic statements to be correct even when the prevalence of the property was much lower.

With respect to this asymmetry, it is important to note that the tasks assessing the truth conditions and implied prevalence of generics and quantified statements are not entirely symmetrical. The truth conditions task required participants to evaluate a range of prevalence levels as right or wrong, while the implied prevalence task asked participants to select just one (i.e., the best one). Because of this difference, the truth condition task may be measuring the average prevalence level whereas the implied prevalence task may be measuring the modal prevalence level. If this is the case, it still means that generics are distinctive in being used to refer to one set of prevalence levels (i.e., from 33 to 100%) but being interpreted according to a different set of prevalence levels (i.e., at or close to 100%). In a sense, this phenomenon can be considered parallel to what occurs in a scalar implicature. Although generics do not show scalar implicature like some and most statements, just as there is a distinction between what a some-quantified statement can mean (i.e., any non-null set) and what it implies (i.e., not more than some), in the case of generics there is a distinction between what the generic statement can mean (i.e., a wide range of prevalence levels) and what it implies (i.e., near-universal prevalence levels). Importantly, our data suggest that this asymmetry is present for generics as early as 4 years of age. We discuss the significance and implications of this phenomenon in the General Discussion.

General Discussion

The goal of this research was to explore the development of semantic intuitions about generics by investigating (1) how children evaluate the truth conditions and implications of generics, (2) whether the asymmetry observed in adults’ reasoning about the truth conditions and implications of generics is shared by children, and (3) whether children differentiate the unique semantics of generics from those of statements quantified by all, most, and some. Overall, our data reveal that young children share adults’ intuitions about the meaning of generics. Specifically, we found that, like adults, preschoolers and older children recognize that generics have flexible truth conditions and are capable of representing a wide range of prevalence levels (from 33 to 100%; Study 1). Additionally, we found that, like adults, preschoolers and older children interpret novel generics as having extremely high prevalence implications (Study 2). These studies thus provide the first evidence that for young children (like adults), generics embody a paradoxical combination of flexible truth conditions and near-universal prevalence implications. Finally, we found that between the ages of 4 and 11, children are working to master the semantics of statements quantified by all, some and, especially most, and to differentiate them from generics. We elaborate on each of these contributions in the sections below.

The Semantics of Generics

The current data extend and confirm previous research on the unique semantics of generics. In particular, research with adults has established that there is a loose, often negligible relation between the truth of a generic statement and the statistical prevalence of the property to which it refers. One explanation for this phenomenon is that generics reflect default ways of thinking about kinds (e.g., Leslie, 2008, 2012). On this view, the truth-values of generics are a function of not only the prevalence of the predicated property, but also other causal and conceptual knowledge that links that property to the kind (Cimpian et al., 2010a, 2010b; Gelman & Bloom, 2007; Leslie, 2008; Prasada & Dillingham, 2006, 2009). Previous research has provided some indication that children may appreciate this aspect of generic meaning—at least in the context of familiar categories. For example, when presented with questions expressing properties that were matched in prevalence but varied in whether or not adults accept them as generically true (e.g., “Do lions have manes? [True] vs. “Are lions boys?” [False]), children were more likely to affirm generics that express properties that are characteristic of familiar kinds than those that are statistically matched in prevalence yet not characteristic of the kinds (Brandone et al., 2012). Data from Study 1 extend these results in two key ways. First, our data establish that children can reason about the role of prevalence in generic meaning even in the context of completely novel categories about which they have no prior knowledge. Second, our findings provide the first systematic evidence that preschoolers are willing to endorse a generic that is true of only a minority of kind members (at the lowest non-zero prevalence level tested—33%). Together, these results demonstrate that by 4–5 years of age, children appreciate the nuanced relation between the statistical prevalence of a property and the truth of a generic.

The findings from Study 2 also add to the literature on the implications of generics. Although the question of what a novel generic implies to young children has been examined indirectly in previous research on the inductive inferences that generics license (e.g., Chambers et al., 2008; Gelman et al., 2002), the current research provides the first test of the prevalence level children assume upon hearing a novel generic. Our data indicate that novel generics imply near-universal scope to children—applying to roughly 87.5% and 97.8% of category members for preschoolers and older children, respectively.

It is interesting to note that this is an area in which the youngest children differed somewhat from adults and older children. Both children and adults assumed widespread prevalence upon hearing a novel generic; however, the responses of older children and adults were more extreme than those of preschoolers. Whereas preschoolers selected both the 100% sample and the 67% sample in response to generic statements (71 and 21% of the time, respectively), adults and older children selected the 100% sample almost exclusively (see Table 2). This finding is consistent with prior work by Gelman, Star, & Flukes (2002) examining the inductive inferences children and adults draw upon hearing novel generics about familiar categories (e.g., “Bears like to eat ants”). Gelman et al. found that 4-year-olds display a more conservative interpretation of generics than adults, showing less willingness to generalize from a generic statement to the category as a whole. Studies examining the role generics play in promoting essentialist reasoning regarding novel animal (Gelman et al., 2010) and social categories (Rhodes et al., 2012) have also shown somewhat weaker effects of generics for preschoolers than for adults. The explanation for this age difference remains unclear. One possibility is that this effect reflects performance factors or task demands. For example, in the current study, children may have had difficulty isolating the 100% sample from the other three samples, leading to noisier attempts to choose the 100% sample. Another possibility is that this effect reflects a legitimate age-related change in the semantics of generics. Perhaps preschoolers have a heightened awareness that generics admit exceptions and are thus more conservative in the inferences they draw on the basis of generics. Such an awareness could prevent children from making overly broad generalizations in the process of early conceptual development. If this is the case, our findings show that children shift from this more conservative reading of generics to the more generous reading favored by adults by 7–11 years of age; however, it remains an open question why or how this shift might occur. Exploring these possibilities is an important goal for future research.

Our data on the implied prevalence of generics also raise important broader questions about the role of generics in knowledge construction. Much of what children know about the world is learned through the testimony of others (e.g., Gelman, 2009; Harris & Koenig, 2006), and given the frequency with which generics occur in conversation with children (Gelman et al., 1998; Gelman et al., 2008), it important to consider what children learn through generic testimony (see also Cimpian & Markman, 2009, 2011; Gelman, 2003; Gelman et al., 2010; Hollander et al., 2009; Rhodes et al., 2012). Our data suggest that when children first hear a generic, they infer that the generic property applies to the vast majority of category members. This assumption is appropriate in many cases. For example, by means of generic statements, children could appropriately learn facts about the physical characteristics, eating habits, and behaviors of animals (e.g., lions have four legs, eat meat, roar, live in prides, etc.).

Note, however, that the observed asymmetry between the truth conditions and implications of generics complicates this matter. Some “true” generic statements express information that applies to only a minority of category members. For a child learning through generic testimony, however, these statements still imply widespread prevalence. For example, upon hearing “Lions have manes” or “Lions attack people” (both plausibly true generics that apply to fewer than half of lions), children may erroneously infer that these properties apply to the vast majority of category members. This issue is particularly problematic when considering how children interpret generics about social categories. Given that generics are a common vehicle for expressing stereotypes about groups of people (e.g., Girls are bad at math; Gelman, Taylor, & Nguyen, 2004), their near-universal prevalence implications could lead children to draw dangerous conclusions (see Rhodes et al., 2012 for a demonstration of how hearing generic language about novel social categories influences children’s category beliefs). Given the flexible truth-values of generics, these conclusions may be based on little evidence and may persist even when presented with extensive counterevidence. However, in these case children may also later revise downward their expectations about the prevalence of this property upon learning new information (e.g., about the infrequency of lion attacks or the frequency of girls who are good at math). Further exploring whether and how this revision process occurs and how generic testimony influences knowledge acquisition more broadly are important issues for future research.

Generics versus Quantified Statements

The current paper also contributes to the literature on children’s comprehension of the truth conditions and implications of quantified statements. The present studies reveal that by preschool age, children demonstrate some competence in understanding quantifiers. Specifically, by 4 to 5 years, children show a nascent understanding of the semantics of statements quantified by all and some and how they differ from generics even in the context of novel categories. In the truth condition task (Study 1), preschoolers appropriately viewed all-quantified statements as true at the 100% prevalence level and some-quantified statements as true at levels as low as 33%. Moreover, in the implied prevalence task (Study 2), preschoolers recognized the different prevalence implications of statements quantified by all and some. Thus, data suggest that preschoolers have mastered some key aspects of the semantics of quantifiers. However, consistent with previous research showing that explicitly quantified statements are relatively difficult for young children to master, our data also show that even 7–10-year-olds are not adult-like in their interpretations of quantifiers. In particular, children demonstrated a lack of sensitivity to scalar implicatures, experienced difficulty interpreting most-quantified statements, and showed a tendency to interpret quantified statements as generics.

First consider children’s sensitivity to scalar implicatures. Scalar implicatures appear in examples such as “Some politicians are corrupt”, where the speaker’s use of the quantifier some typically indicates that he or she had reasons not to use a stronger quantifier (e.g., all, most). Thus, in a conversational context, a statement such as “Some politicians are corrupt” yields the implicature that “Not all politicians are corrupt”. In the current studies, adults clearly showed evidence of computing scalar implicatures—rejecting some- and most-quantified statements when they were used to describe a sample where the target property was present in all category members (Study 1) and assuming “not more than some” and “not more than most” prevalence interpretations for some- and most-quantified statements, respectively (Study 2). However, consistent with prior research (e.g., Brooks & Sekerina, 2006; Crain et al., 1996; Gualmini, 2004; Guasti et al., 2005; Hurewitz et al., 2006; Lidz & Musolino, 2002; Noveck, 2001; Papafragou & Musolino, 2003; Papafragou & Schwartz, 2006), children were less sensitive to scalar implicatures in our tasks. Older children showed sensitivity to the implied upper bound of some-quantified statements, but failed to do so for statements quantified by most. Moreover, preschoolers showed no evidence of scalar implicatures on either task. These findings confirm that while even preschoolers recognize the basic semantics of the quantifiers some and all, they are not as sophisticated as adults in their ability to draw pragmatic inferences (see Crain et al., 1996; Musolino & Lidz, 2006; Papafragou & Musolino, 2003; Pouscoulous et al., 2007 for evidence showing that whether or not children compute scalar implicatures depends on a variety of factors ranging from children’s own information-processing abilities to details of the experimental context).

Findings from the current study also highlighted children’s difficulty interpreting most-quantified statements until well into middle childhood. Neither preschoolers nor older children showed clear understanding of the truth conditions of most-statements as demonstrated by their willingness to accept them at prevalence levels as low as 33%--the lowest non-zero prevalence tested. Children’s evaluation of the implications of most- statements were somewhat more appropriate; however, even 7- to 11-year-olds were not adult-like in their interpretations—selecting the 100% prevalence level the vast majority of the time in response to most statements. There are a number of possible explanations for why the semantics of most-quantified statements are particularly challenging for young children. First, most is used in a broad range of contexts and each context requires a subtly different interpretation. For instance, most can be used in a strictly comparative way in addition to indicating greater than 50%. For example, “I ate the most jellybeans” may indicate that the speaker took only a small fraction of the entire set, if others took even less. Thus, in learning the semantics of most, children must engage in the non-trivial task of sorting through its different uses and differentiating their meanings (Stickney, 2006). In addition, compared to quantifiers like some and all, most is unique in that it requires numerical knowledge: to make a judgment about a most-quantified statement, children must compare the cardinality of two sets (i.e., the number of crullets that have spots vs. the number that do not) (Barwise & Cooper, 1981; Halberda, Taing, & Lidz, 2008; Papafragou & Schwartz, 2006). Accordingly, there is some evidence to suggest that mature comprehension of most might await counting ability (Papafragou & Schwartz, 2006; but see Halberda et al., 2008).

An intriguing additional (not mutually exclusive) possibility is that when faced with this quantifier whose meaning they do not yet fully understand, children may default to a generic interpretation (see Leslie, 2008, 2012). In the current studies, children in fact responded to most-quantified statements as though they were generic. On both the truth condition and the implied prevalence tasks, preschoolers and older children (but not adults) failed to differentiate generics and most-quantified statements (see Hollander et al., 2002 for similar results with 3-year-olds and the quantifiers some and all). Moreover, children’s pattern of responses to both generic and most-quantified statements was comparable to adults’ pattern of responses to generics: they were accepted as true at a broad range of prevalence levels and implied near-universal prevalence. This finding is consistent with the recent theoretical framework proposing that generics express default generalizations about kinds, whereas quantified statements reflect generalizations that are cognitively more sophisticated (Leslie, 2008, 2012). Support for this proposal comes from recent studies documenting that generics are processed more rapidly (Meyer, Gelman, & Stilwell, 2011) and elicit fewer errors (Leslie & Gelman, 2012; Leslie, Khemlani, & Glucksberg, 2011) than quantified statements. On this view, when faced with taxing cognitive demands and a quantifier whose meaning they have not yet fully mastered, children default to a generic interpretation. It is important to note that conclusions regarding children’s lack of differentiation between generics and most statements are limited by the sensitivity of our methodology. It may be that the tasks used in the current studies were not sufficiently sensitive to detect differences in the semantics of generics and most quantified statements in children⁶. Thus, more work is needed to determine when children grasp the semantics of most and differentiate them from the semantics of generics. Nevertheless, the generics-as-default hypothesis is a promising avenue for future research.

Conclusion

Generic statements offer a commonplace way to express generalizations about categories and convey knowledge about the world. As a result, they have been argued to play a central role in human reasoning, to provide insight into the nature of concepts, and to be a significant contributor to children’s knowledge acquisition (e.g., Gelman, 2009; Prasada, 2000). For these reasons, it is important to understand both how children evaluate the truth and falsity of generics and what they see as the implications of novel generics. Results of the current studies confirm that by preschool age, children interpret generics in much the same way that adults do. Like adults, preschoolers recognize that generics embody flexible truth conditions as well as near-universal prevalence implications. Moreover, preschoolers share adults’ intuitions about the uniqueness of the semantics of generics as compared to quantifiers. These findings set the stage for further explorations into what generics reveal about children’s concepts and how generics influence conceptual development.