Abstract
Movement of ions (Ca2+, K+, Na+ and Cl-) and second messenger molecules like inositol 1, 4, 5-trisphosphate inside and in between different cells is the basis of many signaling mechanisms in the microcirculation. In spite of the vast experimental efforts directed towards evaluation of these fluxes, it has been a challenge to establish their roles in many essential microcirculatory phenomena. Recently, detailed theoretical models of calcium dynamics and plasma membrane electrophysiology have emerged to assist in the quantification of these intra and intercellular fluxes and enhance understanding of their physiological importance. This perspective reviews selected models relevant to estimation of such intra and intercellular ionic and second messenger fluxes and prediction of their relative significance to a variety of vascular phenomena such as myoendothelial feedback, conducted responses and vasomotion.
Keywords: Intercellular signaling, Ca2+ and IP3 fluxes, myoendothelial projections
Intercellular signaling allows for integration and coordination of responses in microcirculatory vessels, and is critical for local regulation of vascular tone and blood flow [1; 2; 3]. Cell - cell communication depends to a large extent on homocellular and heterocellular gap junction channels which form pathways for the diffusion of ionic species and second messengers. The exchange of current, calcium (Ca2+) and inositol 1,4,5-trisphosphate (IP3) through gap junctions, in particular, can readily initiate signaling events in neighboring cells and thus, these three fluxes can play a key role in vascular communication.
Ca2+ has been established as a key signaling molecule in the cardiovascular system that regulates a plethora of functions including tone development or the release of vasoactive mediators. It also modulates electrical properties and the membrane potential (Vm). Although Ca2+ homeostasis and intercellular fluxes have attracted most of the attention of investigators, other ionic species can influence Ca2+ dependent responses and participate in vascular signaling. K+, Cl-, and Na+ concentrations, for example, determine corresponding membrane currents and thus membrane potential and the activity of voltage-operated Ca2+ channels (VOCC) in smooth muscle cells (SMCs) [4]. Na+ balance has been suggested to affect intracellular Ca2+ via Na+-Ca2+ exchange in SMCs [5].
Direct Ca2+ diffusion through gap junction or indirect Ca2+ coupling through the diffusion of IP3 can provide a pathway for cell to cell communication. Intercellular Ca2+ fluxes have been suggested to synchronize SMCs in vasomotion [6] and IP3 and/or Ca2+ diffusion via heterocellular gap junctions may generate a myoendothelial feedback control loop that can modulate SM responses to vasoconstrictors [7; 8]. Current carried by the three major ionic species is also a key signal for coordinated vessel behavior. Current flow within the smooth muscle or endothelial layers, as well as between the two layers, play a central role in conducted responses [3] and Cl- currents have been suggested to coordinate SMCs during vasomotion [9]. Furthermore, experimental results indicate that intracellular ionic composition of endothelial cells (ECs) is altered after coupling to SMCs [10].
Despite several evidence that exchange of ions and second messenger occurs between vascular cells, it has been often difficult to assess their relative importance in different responses. A major limitation in investigations is the quantification of these intercellular fluxes experimentally. Thus, alternative hypotheses have often been proposed regarding the actual signaling mediator that contributes to a coordinated vessel behavior. Theoretical analyses and mathematical models can contribute in this discussion by providing estimates for the magnitude of these fluxes and their potential contribution in signaling. This perspective utilizes such approaches to examine the role of these mediators in myoendothelial communication, conducted responses and vasomotion.
Estimation of intercellular fluxes through gap junctions
Gap junctions allow for the transmission of electrical current between cells, as well as for the diffusion of second messengers such as Ca2+ and IP3. Current is carried mostly by the three major ionic species (i.e. K+, Cl-, Na+) and evokes changes in Vm. The fluxes of ions and second messengers depend on the electrochemical gradient as well as on the permeability and density of gap junctions between the two cells.
An unspecified electric current can be calculated from the membrane potential difference between two coupled cells n-th and m-th and the effective gap junction resistance (Rgj) [11]:
| (1) |
To estimate the intercellular exchange of a species, a flux proportional to concentration difference between two cells has often been assumed [12]:
| (2) |
where Pgj,S is the gap junction permeability to S (e.g., Ca2+, IP3, cyclic adenosine monophosphate (cAMP), cyclic guanosine monophosphate (cGMP)).
Current, however, is carried by ionic species and many second messengers are charged particles, and the simplified equations (1) and (2) do not account for exchange based on the combined electrochemical gradient. A linear model can be used to account for both chemical and electrical gradients acting on specified charged species S [9]:
| (3) |
where , and are the concentration difference and the average concentration across the gap junction (Fig. 1).
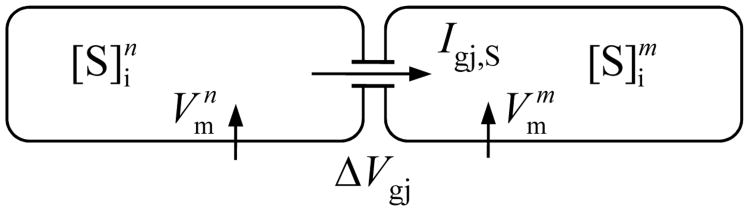
Fig. 1.
Schematic diagram of two cells, n and m, connected by nonselective gap junctions. The gap junctions are permeable to various ionic species and small molecules, S. The intercellular fluxes of individual species vary according to their corresponding concentration gradients and Vm difference between the two cells.
Current/flux of an ionic species via a gap junction can also be estimated from the nonlinear Goldman-Hodgkin-Katz (GHK) equation:
| (4) |
where zs, F, R and T are the valence of ion S, Faraday's constant, gas constant and temperature, respectively [13; 14]. It predicts a rectifying I-V relationship when ionic concentrations are unequal, with larger conductance when current flows from the side of higher concentration [15]. Under physiological range of concentration and potential differences, the GHK equation is similar to the Ohmic behavior from Eq. 3.
In most theoretical models, Rgj and Pgj are assumed constant in Eqs. 1 – 4. In general, gap junctions can be dynamically regulated by potential difference, phosphorylation and various second messengers, including Ca2+ [13; 16; 17; 18]. Theoretical models demonstrated that second messengers acting on gap junctions can produce 50-125 % changes in the number of recruited cells after local stimulation [12]. Modeling and patch-clamp studies also suggest that downregulation of intercellular communication is likely to be more physiologically important than upregulation due to relatively high open probabilities of gap junction channels [1]. The role of these changes in the regulation of vascular tone under control conditions remain unclear [19; 20], although some studies suggest that physiological concentrations of cytosolic Ca2+ can regulate the permeability of Cx43 in a calmodulin-dependent manner [21].
If the concentration of any charged particle is the same in the two cells, Eqs. 3 and 4 reduce to Eq. 1 and the flux depends only on Vm gradient. If there is no difference in Vm between the coupled cells then Eqs. 3 and 4 are reduced to Eq. 2 and intercellular flux is proportional to concentration difference between the two cells. In general, significant differences in both Vm and concentrations can appear between two cells particularly in heterocellular coupling or during asymmetric stimulations.
This approach allows us to partition the total gap junction current into the currents carried by individual ionic species:
| (5) |
The intracellular concentrations of K+, Cl- and Na+ are much larger than that of Ca2+ and other charged molecules permeable through gap junctions; thus, the total electric current is mediated mostly by these three ions. If there are small concentrations gradients across the gap junction for the three major ionic species, the total current is given by:
| (6) |
Vascular gap junctions are poorly selective for small ionic species M [1; 15], and thus, their ionic permeabilities Pgj,M should be similar and approximately equal to a common permeability Pgj. Pgj can then be estimated from Eq. 6 [14]:
| (7) |
Eq. 7 allows us to predict the ionic permeability from reported values of Rgj. Although the electrical resistance is easier to measure experimentally than the permeability, it is also associated with large uncertainty due to experimental limitations and tissue/preparation dependent variability. There are only few estimates of gap junction coupling between vascular cells, and thus the estimates for Pgj provide a first approximation. In general, endothelial gap junctions are more prevalent than smooth muscle and myoendothelial gap junctions.
Representative estimates for the Rgj often used in modeling studies are a low EC-EC resistance , an intermediate SMC-SMC resistance , and a high EC-SMC resistance per SMC [11]. Based on these values, gap junction permeabilities to K+, Cl-, Na+ and Ca2+ can be predicted assuming typical values of cytosolic concentrations for, K+, Na+ and Cl- ( , , and , where S = K+ Cl-, Na+ and Ca2+).
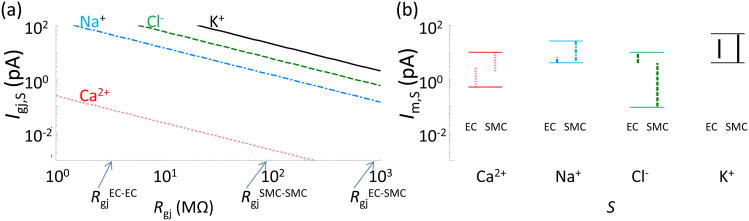
Similar values for the gap junction permeability for IP3 can be assumed as a first approximation, based on the similar diffusivities of IP3 and Ca2+ in un-buffered solution [22]. However, lower permeability for IP3 and other larger molecules is possible, since inside the pore, larger molecules may actually move slower than single atom ions. Fig. 2 shows ionic currents predicted by Eqs. 3 and 7 as a function of gap junctional resistance. Currents are based on an assumed electrical gradient (or equivalent concentration difference) between the two cells. An important prediction is that with similar permeabilities Pgj,S for the four ions, the predominant current carrier will be K+, due to its highest cytosolic concentration [13]. Contribution of Cl- and Na+ to electrical coupling will be approximately 3-and 12-fold smaller, respectively, based on their concentration ratio to K+. To assess the significance of these currents typical whole cell membrane currents under resting and stimulatory conditions are presented in Fig. 2b. Whole cell currents are predicted from our earlier theoretical models of isolated EC and SMC [23; 24]. The K+, Cl-, and Na+ gap junction currents induced by a small Vm gradient (i.e. ΔVgj = 3 mV) are comparable with the transmembrane currents, and therefore gap junctional currents for these three ions have the potential to induce significant Vm changes in neighboring cells.
Fig. 2.
a) Gap junction K+ (solid line), Cl- (dashed line), Na+ (dash-dot line), and Ca2+ (dotted line) currents as a function of Rgj predicted from Eq. 4 and 7; K+, Cl- and Na+ currents are estimated with ΔVgj = 3 mV (or equivalent Δ[K]gj = 17 mM, Δ[Cl]gj = 5 mM, Δ[Na]gj = 1.2 mM), and ΔVgj = 21 mV (or equivalent Δ[Ca]gj = 1 μM) for Ca2+ current. b) Range of total membrane currents in isolated EC and SMC at rest and during agonist stimulation predicted by theoretical models [23; 24].
Cytosolic Ca2+ concentration is about 105 times lower than that of K+, and thus gap junctional Ca2+ current has minimum effect on Vm. A significant Ca2+ concentration gradient across the gap junction (i.e. Δ[Ca]gj = 1 μM) results in a relative small Ca2+ flux (i.e. < 0.1pA) (Fig. 2a, red line) that is significantly lower than typical whole cell transmembrane Ca2+ currents in EC and SMC (Fig. 2b). Thus, the predicted magnitude of intercellular Ca2+ flux is rather small. In addition, the cells have the capacity to effectively absorb Ca2+ influx due to a significant buffering ability and the presence of effective Ca2+ extrusion pumps (i.e. PMCA and SERCA). Thus, these preliminary considerations question the ability of intercellular Ca2+ fluxes to affect global Ca2+ levels in neighboring cells.
The gap junction fluxes will affect membrane potential and cytosolic concentrations of ions according to the equations:
| (8) |
| (9) |
| (10) |
where Cm is the cell membrane capacitance, Im,k represents all membrane currents, vol is the cell volume, JSR - the Ca2+ exchange between the cytosol and sarco/endoplasmic reticulum, and Jbuffer accounts for Ca2+ buffering.
Fluxes in homocellular coupling
Gap junctions may allow the transient exchange of intercellular signals but also a sustained flux of various intracellular species. Homocellular gap junctions, i.e., SMC-to-SMC and EC-to-EC, are most likely to mediate transient signals with a zero net flux over time, assuming an absence of steady-state gradients between cells of the same type. Transient intercellular Ca2+ gradients may occur from spontaneous intracellular Ca2+ activity, (e.g., Ca2+ sparks and puffs). Whether such local heterogeneities may give rise to intercellular Ca2+ waves, manifested with a dramatic elevation of cytosolic Ca2+ relative to its resting value is under investigation.
Spread of a short term local Vm perturbation will be conducted mostly by K+. A Vm change can be accomplished without a significant modification of the cytosolic K+, Cl- or Na+. The amount of extra ions (ΔN) necessary to charge the membrane capacitance to a new Vm is very small compared to the total amount of ions (N) in the cytoplasm. For example, for a ΔVm of 5 mV only about 10-18 mol of K+ are required, compared to the N = 10-13 mol of the total cytosolic K+:
| (11) |
The Vm charging has a small time constant τ ≈ Rgj × Cm (e.g., 100 MΩ × 10 pF = 1 ms), thus the process is fast. If a Vm gradient persists beyond the time constant, an equilibrium point is reached where gap junction currents balance the total membrane current. However, at the new value of Vm the individual fluxes of ions will not be at equilibrium, and ionic concentrations will drift slowly with time to match the new Vm. For a sufficiently long perturbation (tens of minutes), a new true steady state will be reached, sustained by continuous gap junction fluxes. Vm gradients in homocellular coupling can appear during conducted responses and sustained gradients may also exist between SMCs in the vascular wall with multiple layers of smooth muscle. A radial asymmetry in the system may be created by ECs coupled to the innermost SM layer and/or by nonuniform innervations of the muscle cells.
Myoendothelial coupling
In heterocellular coupling, sustained gap junction fluxes are likely, although their presence, magnitude and significance remain controversial. Vascular ECs and SMCs express different set of membrane channels, and isolated, cultured or poorly coupled ECs have often resting Vm significantly different than SMCs [25; 26]. In guinea-pig mesenteric arterioles, the resting EC Vm is on average slightly less negative (few mV) than Vm in SMCs [10]. Furthermore, once the SM layer was removed, the resting Vm in EC layer depolarized significantly to the average of -4.2 mV. It was further suggested that ECs are dependent on SMCs not only for resting Vm but also their intracellular ionic concentration. Accordingly, the expression of Na+-K+ pump seems to be upregulated in isolated ECs as compared to ECs in arteries, which indicates persistent and physiologically important ionic exchange between ECs and SMCs [10]. A strong gap junction coupling in intact vessels may equilibrate EC and SMC Vm so that no significant differences can be recorded at rest [27; 28]. Different membrane composition can maintain continuous gap junction fluxes under such conditions, and a net myoendothelial current can be sometimes revealed by changes in Vm after application of gap junction uncouplers [29].
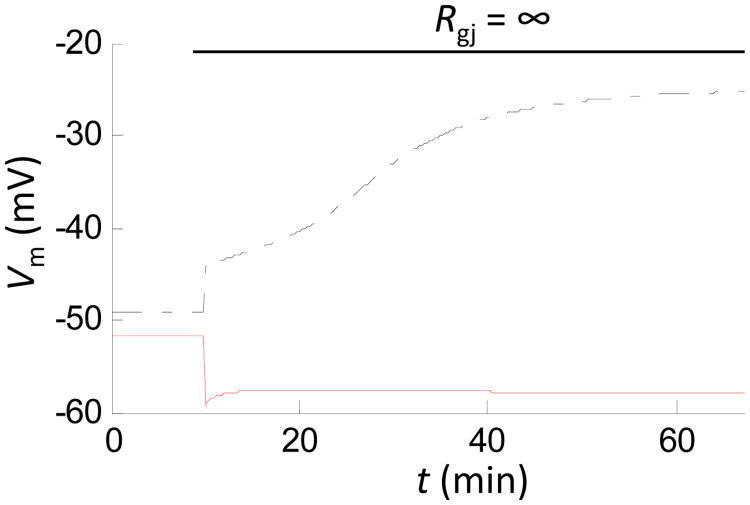
The equilibrium following acute uncoupling of EC and SMC will require balancing total membrane current as well as the balancing of transmembrane ionic fluxes for each cell. Thus, both Vm and ionic compositions in either cell are expected to change after uncoupling. Fig. 3 and Table 1 shows the predicted time course of EC and SMC Vm after gap junction uncoupling (t = 10 min) in an integrated EC-SMC model [14]. Table 1 presents predicted changes in ionic concentrations in the two cells from the same simulation. After gap junction uncoupling, myoendothelial current is blocked instantaneously (Igj, S=0). EC and SMC Vm change rapidly within ms (i.e. time constant, τ ≈ Rm × Cm) towards their Vm in the isolated state (i.e. Vm that gives a total transmembrane current (ΣIm, S) equal to zero (Eq. 8). This Vm change alters electrochemical gradients for the ions and thus, following this initial change in Vm, ionic concentrations will drift. Changes in ionic concentrations affect Nernst potentials and thus Vm will also drift until a steady-state is reached. The time course of the drift is relatively slow (Fig. 3) and depends on parameters such as cell volume, buffering, or membrane currents. Although the content of the individual ions changes significantly, their net electric charge remains constant (Table 1).
Fig. 3.
Changes in EC Vm (dashed-dotted line) and SMC Vm (solid line) after gap junction uncoupling (t = 10 min), predicted by theoretical model of EC-SMC communication utilizing Eqs. 8-10 [14]. EC and SMC Vm change rapidly after the uncoupling, indicating presence of steady myoendothelial ionic and current exchange under control conditions. Unbalanced ionic fluxes in the isolated cells cause slow drift of the cytosolic ion concentrations and Vm until a new steady state is reached.
Table 1.
Representative changes in Vm and ionic concentrations after gap junction uncoupling, predicted by theoretical model of EC-SMC communication [14].
| Rgj = 900 MΩ | Rgj = ∞ | |||
|---|---|---|---|---|
| SMC | EC | SMC | EC | |
| Vm (mV) | -52 | -49 | -59 | -25 |
| [Ca2+]i (nM) | 99 | 130 | 68.4 | 70 |
| [Na+]i (mM) | 9.4 | 18.7 | 8.3 | 9.4 |
| [K+]i (mM) | 121 | 116 | 126 | 152 |
| [Cl-]i (mM) | 42 | 46.3 | 46 | 73 |
| [Na+]i+[K+]i-[Cl-]i | 88.4 | 88.4 | 88.4 | 88.4 |
Similar fast and slow phases as well as concentration drifts may occur during cell stimulations. For example, activation of intermediate and small conductance Ca2+ activated K+ (IKCa/SKCa) channels by acetylcholine rapidly hyperpolarizes EC and SMC (through the gap junctions) towards the K+ Nernst potential until a new electric current balance is reached. If the agonist stimulation persists, the new electrochemical gradients will result in slow drifts in ionic concentrations and Vm towards a new steady state. In the simulations above we have assumed that cells do not regulate the presence or activity of the membrane components during uncoupling or stimulation. Regulatory mechanisms that will enable cells to control ionic concentrations and Vm in response to uncoupling or prolonged stimulations have not been identified at this point.
Can Ca2+ and IP3 fluxes engage in propagation of conducted responses?
The importance of gap junction communication in multicellular coordination has been established. Ionic (Ca2+, Na+, K+, and Cl-) and IP3 fluxes exist between cells and can communicate changes upon mechanical or agonist stimulation in neighboring cells. Rapid, long-range communication of local vasodilation or vasoconstriction (i.e. conducted responses) has been observed in many vascular beds and species [30; 31; 32; 33; 34; 35]. This phenomenon is critical for matching blood perfusion to local metabolic demand.
Electrical current passing through gap junctions is considered to be the major mechanism behind conducted responses. Experimental and theoretical attempts have investigated electrical spread through gap junctions and its potential for transmitting signals along the vessel [11; 36; 37; 38; 39]. The vessel segment can be viewed as a continuous wire with uniform axial and radial resistance along the vessel's length [37; 39]. The axial and radial resistivity will determine the attenuation of the spreading hyperpolarization/depolarization. Axial resistivity depends on gap junctional resistance (Rgj) and the number of open gap junctions along the current path. Radial resistivity determines current loss through the cell membrane and depends on whole-cell membrane conductance and the number of cells per vessel length. Attenuation of current spread with length constants in the order of millimeters have often been measured experimentally and predicted theoretically [36; 40]. Inhibition of BKCa and Kv channels enhanced conducted vasomotor responses in isolated segments of rat mesenteric terminal arterioles, and computer simulations identified these channels as the major pathways for current dissipation across the plasma membrane [41].
In some preparations, vasodilation spreads with minimal attenuation over significant distances [42]. Passive current diffusion cannot account for such experimental observations as dissipation of current by membrane ions channels should attenuate the transmitted hyperpolarization/depolarization along the vessel. Thus, investigators have looked for mechanisms that can regenerate/facilitate the transmitted signal. Inwardly rectifying potassium (Kir) channels can potentially facilitate transmission of hyperpolarization /depolarization provided that they are present in significant density and the characteristic negative conductance (i.e. negative slope of I-V curve) occurs over the Vm of interest [40]. Theoretical and experimental studies have demonstrated a positive effect of Kir current in the propagation of hyperpolarization [43; 44; 45]. However, the presence of Kir is tissue dependent [46; 47] and there is wide disparity in its expression among vessels [48; 49]. A non-linearity between the spread of hyperpolarization and vasodilation has been suggested by Wolfle et al. [50] to explain the inequality of their spread in arteries. Hyperpolarization may attenuate with distance from the site of stimulation; vasodilation however, remains maximal until a threshold potential is reached. The threshold potential was suggested to be the activation threshold for VOCC in SMC.
At this stage, most evidence suggests that conducted responses depend primarily on passive electrotonic spread. Theoretical [11] and experimental studies [51] have provided evidence for the importance of the endothelial layer in longitudinal signal transmission. This is attributed to the longitudinal orientation and the abundance of homocellular coupling that makes the EC layer a low resistance pathway for transmitting membrane potential changes [11]. Interestingly, mathematical models suggest ECs as the primary pathway for conduction of vasodilation as well as of vasoconstriction. SMC derived depolarization (and vasoconstriction) can be efficiently transmitted through the EC layer, provided that there is sufficient myoendothelial coupling and that enough SMCs have been stimulated to produce sufficient depolarizing current [11; 40].
A significant Ca2+ spread over long distances within the EC layer can provide an alternative mechanism for enhancing conduction of vasodilation/vasoconstriction along the vessel's length. Experiments have reported the activation of EC Ca2+ dependent pathways like NO and EDHF at distant sites following local EC stimulation[52; 53; 54]. Distant EC Ca2+ waves have been reported in different arteries [52; 53; 54] with speeds that cannot be accounted by IP3 and or Ca2+ diffusion and the involvement of a regenerative mechanism has been suspected. Endothelium independent fast and slow speed Ca2+ waves have also been observed in vessels and cultured SMCs. Fast Ca2+ waves may result from the spread of electrical depolarization and subsequent entry of Ca2+ by VOCC followed by Ca2+ induced Ca2+ release (CICR) and regeneration of depolarization by chloride channels [55]. Despite these observations a consistent mobilization of EC Ca2+ at distant sites has not been established nor a mechanism that will allow for a regenerative Ca2+ spread along the vessel axis.
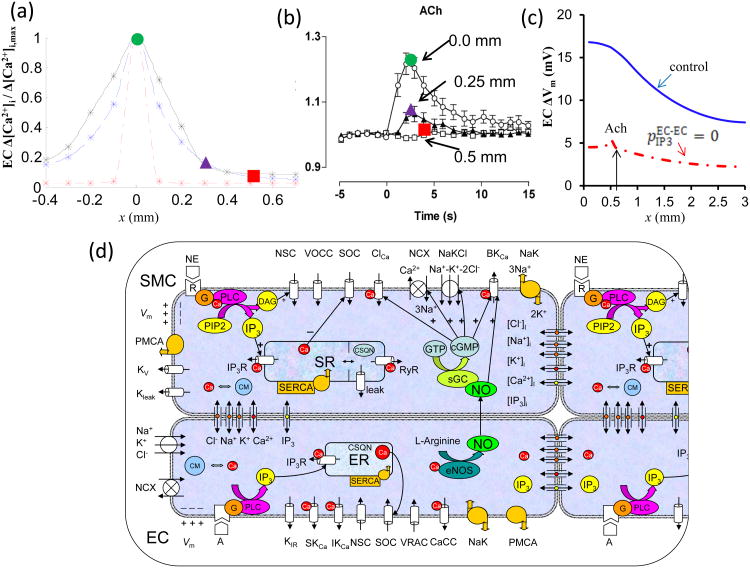
We have previously examined the potential of intercellular Ca2+ and IP3 diffusion in conducted responses utilizing a multicellular mathematical model (Fig. 4d) [40]. In the model, electrical coupling is the only signal strong enough to spread over long distances. Local Ca2+ transients do not propagate significantly along the vessel and they are restricted to only a couple of cells away from the stimulus site (Fig. 4a, dashed line). The limited Ca2+ spread was actually a result of IP3 rather than Ca2+ diffusion (Fig. 4a, dash-dot line). This limited IP3 mediated Ca2+ mobilization in neighboring cells could amplify the total current generated at the local site (Fig. 4c, dashed vs. solid line), thus contributing to the strength of the electrical signal spreading along the ECs. Thus, model simulations suggested a limited passive Ca2+ and IP3 spread which cannot facilitate signal transmission along the vessel but under some conditions can enhance distant responses by increasing local stimulus strength.
Fig. 4.
a) Normalized steady state endothelial Ca2+ profiles during local stimulation of 1 EC with Ach at x = 0 mm. Under control conditions (dashed line), the Ca2+ spread was limited to 300 μm (three ECs). Inhibition of axial IP3 diffusion (EC-EC pIP3 = 0) practically abolished the Ca2+ spread (dash-dot line). One hundred fold greater permeability of endothelial gap junctions to Ca2+ extended Ca2+ spread to 400 μm (black line). b) Ca2+ spread to Ach stimulation observed in an experimental study by Takano et al. [78] which is in agreement with predictions from the model. c) Predicted changes in EC Vm with respect to resting Vm during local Ach application to one EC with (solid line) and without (dashed line) endothelial IP3 diffusion (EC-EC pIP3 = 0) in a vessel prestimulated with NE. d) Schematic diagram of coupled ECs and SMCs used in the vessel model reproduced from [40]. Cells are coupled by nitric oxide (NO) and myoendothelial gap junctions permeable to Ca2+, Na+, K+, and Cl- ions, and IP3. Kir – inward rectifier K+ channel; VRAC – volume-regulated anion channel; SKCa, IKCa and BKCa – small-, intermediate-, and large-conductance Ca2+-activated K+ channels; SOC – store-operated channel; NSC – nonselective cation channel, CaCC and ClCa – Ca2+-activated chloride channel; NaK – Na+-K+-ATPase; PMCA – plasma membrane Ca2+-ATPase; NCX – Na+/Ca2+ exchanger; NaKCl – Na+-K+-Cl- cotransport; Kv – voltage-dependent K+ channel; Kleak – unspecified K+ leak current; VOCC – voltage-operated Ca2+ channels; SR/ER – sarco/endoplasmic reticulum; IP3R – IP3 receptor; RyR – ryanodine receptor; SERCA – SR/ER Ca2+-ATPase; CSQN – calsequestrin; CM – calmodulin; R – receptor; G – G protein; DAG – diacylglycerol; PLC – phospholipase C; sGC – soluble guanylate cyclase; cGMP – cyclic guanosine monophosphate.
Can the presence of local domains enhance the role of Ca2+ and IP3 fluxes?
Theoretical considerations suggest small gap junction fluxes for Ca2+ and IP3 and their limited role in spreading responses. The effect of these fluxes, however, may be amplified through a CICR mechanism. For example, weak Ca2+ and/or IP3 fluxes may be amplified and cause significant Ca2+ events near the gap junctions in the presence of localized ryanodine receptors (RyRs) and/or IP3Rs. Although such microdomains have not been reported around homocellular gap junctions, myoendothelial gap junctions (MEGJs) are usually colocalized with IP3Rs on cellular extensions known as myoendothelial projections (MPs). MPs have been identified in many tissues and species with numbers that increase with decreasing vessel size, an attribute shared by MEGJ expression and EDHF action [1; 56; 57; 58]. MPs consist of an extremely small fraction of total EC volume (<1%) and create restricted spaces within the EC where ions can potentially accumulate. Recent experimental evidence shows that key molecular elements like IP3Rs, IKCa and NaKATPases (NaK) [59; 60; 61] are localized close to MP. Localization of IP3R in such a restricted space can potentially allow IP3 and/Ca2+ diffusing from a stimulated SMC to accumulate in the MP and cause a rapid increase in local Ca2+ concentration. Localized Ca2+ events have been reported in and around these structures [61]. The proximity of such Ca2+ events to a localized density of IKCa channels or endothelial nitric oxide synthase (eNOS) can lead to EC hyperpolarizations that can feedback to the SMC or SMC relaxation via nitric oxide released in the EC. This myoendothelial feedback response can attenuate SMC response to vasoconstrictors.
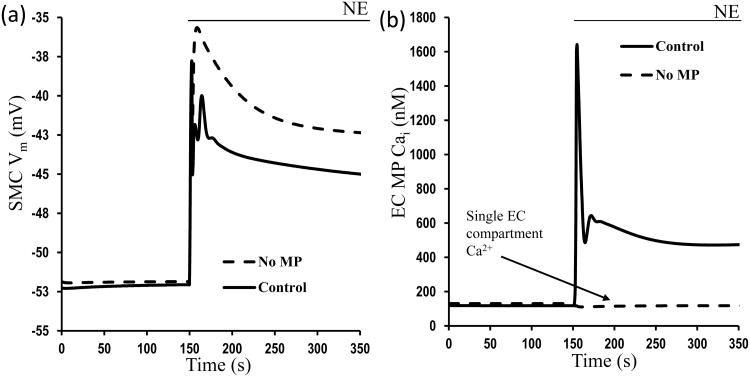
Despite the general agreement for the presence of myoendothelial feedback mechanism to SMC stimulation, several aspects of this response are still under investigation. An increasing amount of evidence supports a local rather than global myoendothelial feedback mechanism and a significant role of MPs in this response [62]. Theoretical simulations with finite element method models corroborate this opinion [63]. We also extended our integrated EC-SMC model [14] to incorporate an extra compartment in the EC representing a MP with localized IP3R and IKCa channels. Representative simulations in the presence and absence of the MP are shown in Fig. 5 following stimulation of the SMC with NE. A significant feedback response (i.e. few mV) is observed only when MP is present (Fig. 5a, solid line) and as a result SMC is less depolarized to NE in comparison with simulations without a MP (Fig. 5a, dashed line). This difference is attributed to a significant Ca2+ response in the confined space of the MP with high density of IP3Rs and IKCa channels (Fig. 5b, solid line). The amount of feedback depends on the assumed density of IKCa and IP3Rs in the MPs and on Rgj. Thus, quantification of IP3R and IKCa in the MPs will allow us to make better predictions for the myoendothelial feedback response. It also suggests that tissues and disease dependent differences in channel localization can affect the ability of the endothelium to modulate SMC constriction.
Fig. 5.
Changes in a) SMC Vm and b) EC projection Ca2+ after NE stimulation of SMC in the presence (solid line) and absence (dashed line) of MP in the EC.
Does Ca2+ or IP3 mediate the EC feedback response to SMC stimulation?
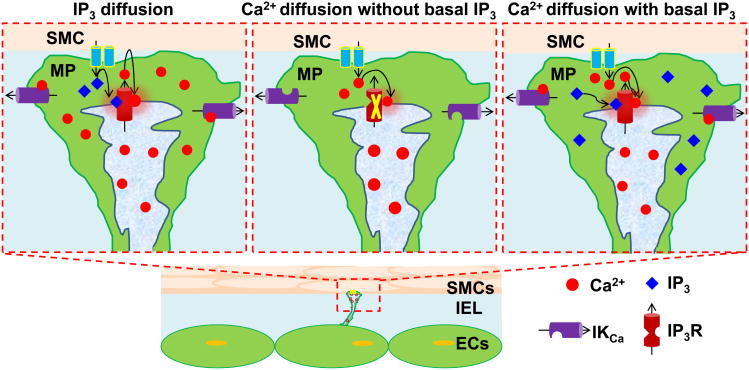
The SMC originating signal that initiates Ca2+ mobilization in the MP has not been determined. Ca2+ [7; 64] and IP3 [8; 65; 66] diffusion have been suggested to initiate this response (Fig. 6). Although Ca2+ ions and IP3 have similar MEGJ permeabilities, the intercellular Ca2+ flux is probably not sufficient to mediate the feedback response (Fig. 6b). Our model simulations (unpublished data) suggest that IP3 is more likely to be the mediator because of the localization of IP3Rs in the MP (Fig. 6a) (i.e. feedback is lost after blockade of intercellular IP3 diffusion but not of Ca2+).
Fig. 6.
Role of IP3 and Ca2+ diffusion from SMC to EC in myoendothelial feedback during a) IP3 diffusion b) Ca2+ diffusion without no basal IP3 in EC and c) Ca2+ diffusion with basal IP3 in EC. Ca2+ requires the presence of some basal IP3 to activate IP3R and both the diffusing Ca2+ as well as the Ca2+ released from store can potentially cause further release from localized IP3Rs.
No favorable RyR localization has been reported in MP (and limited presence of RyR overall is likely in ECs) to amplify the small Ca2+ influx by CICR. The diffusing Ca2+ could however induce CICR through IP3Rs which exhibit both Ca2+ dependent activation as well as inhibition [67]. However, for Ca2+ influx to induce a Ca2+ event in the MP, basal IP3 levels need to be present (Fig. 6c). The concentration of IP3 needs to be at a level adequate for significant opening of the receptor and to not induce significant CICR prior to stimulation. Resting MP Ca2+ levels should remain below the activation levels of the IP3R and at the same time the IP3Rs need to be sensitized so that a weak Ca2+ flux can cause significant CICR. It is not known if all of these conditions can exist at the same time. Most importantly, recent experimental data in hamster skeletal muscle arterioles provide evidence for IP3 mediated feedback and corroborate the theoretical predictions. When the smooth muscle was stimulated with an IP3 releasing vasoconstrictor (PE) a feedback response could be inhibited by blocking of EC IP3Rs (Xestospongin C). In contrast, depolarization and vasoconstriction with a voltage dependent potassium channels (Kv) blocker, 4-aminopyridine (4-AP) remain unchanged after similar blockade of IP3Rs in the endothelium [62].
Recent experimental data have shown local rather than global Ca2+ events in the endothelium upon SMC stimulation [62; 68; 69]. Mathematical models (unpublished data) corroborate these findings. The weak Ca2+ and IP3 fluxes described above can be amplified in the restricted volume of the MP (Fig. 5b, solid line); however, their concentrations quickly dissipate in the bulk cytosol. The rapid buffering of Ca2+ and the degradation of IP3 by cytosolic phosphatases [22; 66] are both unfavorable to their respective intracellular movement and weaken the possibility of a global EC response following SMC stimulation. Passive diffusion without a mechanism that will allow a regenerative Ca2+ wave seems to be insufficient for global Ca2+ mobilization.
Can intercellular IP3 and Ca2+ fluxes contribute to cell synchronization in vasomotion?
Although the physiological significance of the phenomenon of vasomotion is not completely understood, it is speculated that oscillation of arteriolar diameter might increase flow conductance and in some cases may improve oxygenation as compared to steady flow through the same average diameter [70]. Initiation of vasomotion requires the SMC's intrinsic ability for Ca2+ oscillations. In addition, a synchronizing mechanism needs to be in place that will enable a coordinate response in tone and diameter.
Electrical current through gap junctions can provide a signal that can spread rapidly across many cells, and thus represents the best candidate mechanism for synchronization in a vascular segment. Could Ca2+ or IP3 coupling also play a role in synchronization? Considerations presented above suggest that passive diffusion across gap junction yields weak Ca2+ and IP3 fluxes and their ability for global Ca2+ mobilization at distant sites is probably limited (at least in the absence of an amplification mechanism). However, the limited role that these fluxes may have in conduction does not necessarily mean a limited role in synchronization. A synchronizing signal has to affect only the phase of coupled self-sustained oscillators, and thus it can be relatively weak and is not required to produce forced Ca2+ oscillations or waves in neighboring cells. Local coordination of immediate neighbors can then synchronize larger population of SMCs. Furthermore, IP3 and/or Ca2+ fluxes may generate stronger effect in immediate neighbors than electrical coupling dissipated over multiple cells [71].
A number of experimental and theoretical studies have investigated potential mechanisms for synchronization. In a model for vasomotion in a population of SMCs by Jacobsen et al. [9], a cGMP sensitive chloride (Cl-) current was suggested to enhance the coupling between SMC Vm and Ca2+. SMC Vm depolarization can spread to adjacent cells and coordinate Ca2+ elevation in those cells by activation of VOCCs. The effect of Ca2+ diffusion was negligible in these models. Experimental evidence supports a role for cGMP (through ClCa channel activation) in promoting synchronization. In an experimental study by Peng et al. [72], a synchronization mechanism based on a Ca2+ and cGMP-activated inward current was shown for endothelium denuded vessels. In a more recent experimental study, transfecting rat mesenteric small arteries in vivo with siRNA specifically targeting bestrophin-3, inhibited cGMP dependent ClCa current and abolished vasomotion in isolated arteries [73]. However, in another study from the same group [74], 4,4′-Diisothiocyano-2,2′-stilbenedisulfonic acid (DIDS) and Zn2+, both blockers of ClCa,cGMP channels, did not inhibit vasomotion in intact small rat mesenteric arteries. The vasomotion was inhibited by Cl- substitution, suggesting that cGMP-independent Cl- channel may participate in synchronization. Cl- currents remain the only mechanism of synchronization tested through experimentation. Nevertheless, the role of Cl- in synchronization in intact vessels needs to be further elaborated upon, and possible contribution of other pathways should be also investigated.
The effect of Ca2+, IP3, and electrical coupling on synchronization in vasomotion was studied in multicellular mathematical models by Koenigsberger et al. [75; 76]. Intercellular Ca2+ fluxes have been suggested to be involved in synchronization of cells in close range. Homocellular and heterocellular gap junctions in a population of SMCs and ECs were simulated by combination of formulae (1, 2). In the models, Ca2+ flux between SMCs was necessary to override desynchronizing effect of large conductance calcium activated potassium channels (BKCa) channels. Although the model did not incorporate Ca2+ activated Cl- channels and did not identify any electrically mediated synchronizing pathway, it demonstrated that local Ca2+ coupling can synchronize a larger population of SMCs.
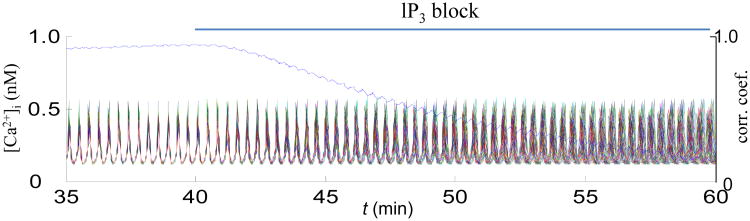
Both electrically and diffusion mediated synchronizing pathways were implemented in our multicellular ECs-SMCs model [77]. Previously recognized Cl- and Ca2+ synchronizing mechanisms were evaluated in a system of increased complexity and under different stimulatory scenarios. The study suggests two alternative pathways for synchronization in addition to Cl- current and direct Ca2+ diffusion. Intercellular diffusion of oscillatory IP3 (Fig. 7) and pulsatile current generated by nonselective cation channels has the potential to affect synchronization. Thus, coordination is achieved or lost as a result of the competition between synchronizing and desynchronizing factors, and there can be several mechanisms that work individually, in synergy or redundancy, depending on stimulatory conditions.
Fig. 7.
Simulations in a population of eighty SMCs and eighty ECs arranged into a cylinder. Each SMC within the cylinder is coupled to its four neighbors through Rgj = 87.4 MΩ, and to underlying ECs through the total myoendothelial Rgj = 900 MΩ per SMC. SMCs are stimulated by NE (0.8 μM), and ECs are stimulated by acetylcholine (1 a.u.). Shown are Ca2+ oscillations in the SMCs, and mean correlation coefficient indicating degree of synchronization. Under control conditions, SMCs are coordinated, but inhibition of intercellular IP3 diffusion desynchronizes Ca2+ oscillations.
Summary
Intercellular communication is essential for the coordination of microcirculatory reactivity. Continuous electrical and ionic movement occurs between coupled cells which affects resting cell states and enables transmission of signals. Based on available measurements for gap junction resistances and expected intercellular gradients of different ions and IP3, we can estimate the magnitudes of these fluxes in different scenarios. Electrical current through gap junctions (carried predominantly by K+ ions) is the primary signal that enables spreading responses. Ca2+ and IP3 fluxes are small and thus, their passive diffusion should have a limited effect on Ca2+ mobilization at distant sites. These weak fluxes may be adequate, however, to amplify local current in conducted responses and to promote synchronization of oscillations in neighboring SMCs and vasomotion. The effect of Ca2+ and IP3 diffusion can be amplified by the presence of molecular components like RyRs, IP3Rs and IKCa channels in microdomains close to the gap junctions. Such localized signaling machinery exists in myoendothelial projections and enables an endothelial feedback response that moderates SMC constriction. Myoendothelial IP3 diffusion is more likely than Ca2+ to mediate this response. Theoretical analyses can assist experimentation in elucidation of the complex mechanisms that regulate microcirculatory reactivity.
Acknowledgments
Sources of support: The corresponding author is supported by the NIH grant SC1HL95101
References
- 1.Christ GJ, Spray DC, el-Sabban M, Moore LK, Brink PR. Gap junctions in vascular tissues. Evaluating the role of intercellular communication in the modulation of vasomotor tone. Circ Res. 1996;79:631–646. doi: 10.1161/01.res.79.4.631. [DOI] [PubMed] [Google Scholar]
- 2.Segal SS. Regulation of blood flow in the microcirculation. Microcirculation. 2005;12:33–45. doi: 10.1080/10739680590895028. [DOI] [PubMed] [Google Scholar]
- 3.de Wit C, Griffith TM. Connexins and gap junctions in the EDHF phenomenon and conducted vasomotor responses. Pflugers Arch. 2010;459:897–914. doi: 10.1007/s00424-010-0830-4. [DOI] [PubMed] [Google Scholar]
- 4.Jackson WF. Ion channels and vascular tone. Hypertension. 2000;35:173–178. doi: 10.1161/01.hyp.35.1.173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Blaustein MP, Zhang J, Chen L, Song H, Raina H, Kinsey SP, Izuka M, Iwamoto T, Kotlikoff MI, Lingrel JB, Philipson KD, Wier WG, Hamlyn JM. The pump, the exchanger, and endogenous ouabain: signaling mechanisms that link salt retention to hypertension. Hypertension. 2009;53:291–298. doi: 10.1161/HYPERTENSIONAHA.108.119974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Koenigsberger M, Sauser R, Lamboley M, Beny JL, Meister JJ. Ca2+ dynamics in a population of smooth muscle cells: modeling the recruitment and synchronization. Biophys J. 2004;87:92–104. doi: 10.1529/biophysj.103.037853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dora KA, Doyle MP, Duling BR. Elevation of intracellular calcium in smooth muscle causes endothelial cell generation of NO in arterioles. Proc Natl Acad Sci U S A. 1997;94:6529–6534. doi: 10.1073/pnas.94.12.6529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lamboley M, Pittet P, Koenigsberger M, Sauser R, Beny JL, Meister JJ. Evidence for signaling via gap junctions from smooth muscle to endothelial cells in rat mesenteric arteries: possible implication of a second messenger. Cell Calcium. 2005;37:311–320. doi: 10.1016/j.ceca.2004.11.004. [DOI] [PubMed] [Google Scholar]
- 9.Jacobsen JC, Aalkjaer C, Nilsson H, Matchkov VV, Freiberg J, Holstein-Rathlou NH. A model of smooth muscle cell synchronization in the arterial wall. Am J Physiol Heart Circ Physiol. 2007;293:H229–237. doi: 10.1152/ajpheart.00727.2006. [DOI] [PubMed] [Google Scholar]
- 10.Yamamoto Y, Suzuki H. Dependency of endothelial cell function on vascular smooth muscle cells in guinea-pig mesenteric arteries and arterioles. J Smooth Muscle Res. 2005;41:77–85. doi: 10.1540/jsmr.41.77. [DOI] [PubMed] [Google Scholar]
- 11.Diep HK, Vigmond EJ, Segal SS, Welsh DG. Defining electrical communication in skeletal muscle resistance arteries: a computational approach. J Physiol. 2005;568:267–281. doi: 10.1113/jphysiol.2005.090233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Christ GJ, Brink PR, Ramanan SV. Dynamic gap junctional communication: a delimiting model for tissue responses. Biophys J. 1994;67:1335–1344. doi: 10.1016/S0006-3495(94)80605-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Verselis V, White RL, Spray DC, Bennett MV. Gap junctional conductance and permeability are linearly related. Science. 1986;234:461–464. doi: 10.1126/science.3489990. [DOI] [PubMed] [Google Scholar]
- 14.Kapela A, Bezerianos A, Tsoukias NM. A mathematical model of vasoreactivity in rat mesenteric arterioles: I. Myoendothelial communication. Microcirculation. 2009;16:694–713. doi: 10.3109/10739680903177539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hille B. Ionic channels of excitable membranes. 2nd. Sinauer Associates; Sunderland, Mass: 2001. [Google Scholar]
- 16.Moore LK, Beyer EC, Burt JM. Characterization of gap junction channels in A7r5 vascular smooth muscle cells. Am J Physiol. 1991;260:C975–981. doi: 10.1152/ajpcell.1991.260.5.C975. [DOI] [PubMed] [Google Scholar]
- 17.Moore LK, Burt JM. Gap junction function in vascular smooth muscle: influence of serotonin. Am J Physiol. 1995;269:H1481–1489. doi: 10.1152/ajpheart.1995.269.4.H1481. [DOI] [PubMed] [Google Scholar]
- 18.Straub AC, Johnstone SR, Heberlein KR, Rizzo MJ, Best AK, Boitano S, Isakson BE. Site-specific connexin phosphorylation is associated with reduced heterocellular communication between smooth muscle and endothelium. J Vasc Res. 2009;47:277–286. doi: 10.1159/000265562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Figueroa XF, Isakson BE, Duling BR. Connexins: gaps in our knowledge of vascular function. Physiology (Bethesda) 2004;19:277–284. doi: 10.1152/physiol.00008.2004. [DOI] [PubMed] [Google Scholar]
- 20.Brink PR, Ricotta J, Christ GJ. Biophysical characteristics of gap junctions in vascular wall cells: implications for vascular biology and disease. Brazilian Journal of Medical and Biological Research. 2000;33:415–422. doi: 10.1590/s0100-879x2000000400007. [DOI] [PubMed] [Google Scholar]
- 21.Lurtz MM, Louis CF. Intracellular calcium regulation of connexin43. Am J Physiol Cell Physiol. 2007;293:C1806–1813. doi: 10.1152/ajpcell.00630.2006. [DOI] [PubMed] [Google Scholar]
- 22.Allbritton NL, Meyer T, Stryer L. Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science. 1992;258:1812–1815. doi: 10.1126/science.1465619. [DOI] [PubMed] [Google Scholar]
- 23.Silva HS, Kapela A, Tsoukias NM. A mathematical model of plasma membrane electrophysiology and calcium dynamics in vascular endothelial cells. Am J Physiol Cell Physiol. 2007;293:C277–293. doi: 10.1152/ajpcell.00542.2006. [DOI] [PubMed] [Google Scholar]
- 24.Kapela A, Bezerianos A, Tsoukias NM. A mathematical model of Ca2+ dynamics in rat mesenteric smooth muscle cell: agonist and NO stimulation. J Theor Biol. 2008;253:238–260. doi: 10.1016/j.jtbi.2008.03.004. [DOI] [PubMed] [Google Scholar]
- 25.McSherry IN, Spitaler MM, Takano H, Dora KA. Endothelial cell Ca2+ increases are independent of membrane potential in pressurized rat mesenteric arteries. Cell Calcium. 2005;38:23–33. doi: 10.1016/j.ceca.2005.03.007. [DOI] [PubMed] [Google Scholar]
- 26.Siegl D, Koeppen M, Wolfle SE, Pohl U, de Wit C. Myoendothelial coupling is not prominent in arterioles within the mouse cremaster microcirculation in vivo. Circ Res. 2005;97:781–788. doi: 10.1161/01.RES.0000186193.22438.6c. [DOI] [PubMed] [Google Scholar]
- 27.Welsh DG, Segal SS. Endothelial and smooth muscle cell conduction in arterioles controlling blood flow. Am J Physiol. 1998;274:H178–186. doi: 10.1152/ajpheart.1998.274.1.H178. [DOI] [PubMed] [Google Scholar]
- 28.Yamamoto Y, Klemm MF, Edwards FR, Suzuki H. Intercellular electrical communication among smooth muscle and endothelial cells in guinea-pig mesenteric arterioles. J Physiol. 2001;535:181–195. doi: 10.1111/j.1469-7793.2001.00181.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Goto K, Fujii K, Kansui Y, Abe I, Iida M. Critical role of gap junctions in endothelium-dependent hyperpolarization in rat mesenteric arteries. Clin Exp Pharmacol Physiol. 2002;29:595–602. doi: 10.1046/j.1440-1681.2002.03689.x. [DOI] [PubMed] [Google Scholar]
- 30.Krogh A, Harrop GA, Rehberg PB. Studies on the physiology of capillaries: III. The innervation of the blood vessels in the hind legs of the frog. J Physiol. 1922;56:179–189. doi: 10.1113/jphysiol.1922.sp002000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Duling BR, Berne RM. Propagated vasodilation in the microcirculation of the hamster cheek pouch. Circ Res. 1970;26:163–170. doi: 10.1161/01.res.26.2.163. [DOI] [PubMed] [Google Scholar]
- 32.Segal SS. Microvascular recruitment in hamster striated muscle: role for conducted vasodilation. Am J Physiol. 1991;261:H181–189. doi: 10.1152/ajpheart.1991.261.1.H181. [DOI] [PubMed] [Google Scholar]
- 33.Gustafsson F, Holstein-Rathlou N. Conducted vasomotor responses in arterioles: characteristics, mechanisms and physiological significance. Acta Physiol Scand. 1999;167:11–21. doi: 10.1046/j.1365-201x.1999.00603.x. [DOI] [PubMed] [Google Scholar]
- 34.Dora KA, Xia J, Duling BR. Endothelial cell signaling during conducted vasomotor responses. Am J Physiol Heart Circ Physiol. 2003;285:H119–126. doi: 10.1152/ajpheart.00643.2002. [DOI] [PubMed] [Google Scholar]
- 35.Dora KA. Coordination of vasomotor responses by the endothelium. Circ J. 2010;74:226–232. doi: 10.1253/circj.cj-09-0879. [DOI] [PubMed] [Google Scholar]
- 36.Emerson GG, Neild TO, Segal SS. Conduction of hyperpolarization along hamster feed arteries: augmentation by acetylcholine. Am J Physiol Heart Circ Physiol. 2002;283:H102–109. doi: 10.1152/ajpheart.00038.2002. [DOI] [PubMed] [Google Scholar]
- 37.Hirst GD, Neild TO. An analysis of excitatory junctional potentials recorded from arterioles. J Physiol. 1978;280:87–104. doi: 10.1113/jphysiol.1978.sp012374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Haug SJ, Segal SS. Sympathetic neural inhibition of conducted vasodilatation along hamster feed arteries: complementary effects of alpha1- and alpha2-adrenoreceptor activation. J Physiol. 2005;563:541–555. doi: 10.1113/jphysiol.2004.072900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Crane GJ, Hines ML, Neild TO. Simulating the spread of membrane potential changes in arteriolar networks. Microcirculation. 2001;8:33–43. [PubMed] [Google Scholar]
- 40.Kapela A, Nagaraja S, Tsoukias NM. A mathematical model of vasoreactivity in rat mesenteric arterioles. II. Conducted vasoreactivity. Am J Physiol Heart Circ Physiol. 2010;298:H52–65. doi: 10.1152/ajpheart.00546.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hald BO, Jacobsen JC, Braunstein TH, Inoue R, Ito Y, Sorensen PG, Holstein-Rathlou NH, Jensen LJ. BK(Ca) and K(V) channels limit conducted vasomotor responses in rat mesenteric terminal arterioles. Pflugers Arch. 2012;463:279–295. doi: 10.1007/s00424-011-1049-8. [DOI] [PubMed] [Google Scholar]
- 42.Figueroa XF, Chen CC, Campbell KP, Damon DN, Day KH, Ramos S, Duling BR. Are voltage-dependent ion channels involved in the endothelial cell control of vasomotor tone? American journal of physiology. 2007;293:H1371–1383. doi: 10.1152/ajpheart.01368.2006. [DOI] [PubMed] [Google Scholar]
- 43.Jantzi MC, Brett SE, Jackson WF, Corteling R, Vigmond EJ, Welsh DG. Inward rectifying potassium channels facilitate cell-to-cell communication in hamster retractor muscle feed arteries. Am J Physiol Heart Circ Physiol. 2006;291:H1319–1328. doi: 10.1152/ajpheart.00217.2006. [DOI] [PubMed] [Google Scholar]
- 44.Smith PD, Brett SE, Luykenaar KD, Sandow SL, Marrelli SP, Vigmond EJ, Welsh DG. KIR channels function as electrical amplifiers in rat vascular smooth muscle. J Physiol. 2008;586:1147–1160. doi: 10.1113/jphysiol.2007.145474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rivers RJ, Hein TW, Zhang C, Kuo L. Activation of barium-sensitive inward rectifier potassium channels mediates remote dilation of coronary arterioles. Circulation. 2001;104:1749–1753. doi: 10.1161/hc4001.098053. [DOI] [PubMed] [Google Scholar]
- 46.de Wit C. Different pathways with distinct properties conduct dilations in the microcirculation in vivo. Cardiovasc Res. 2010;85:604–613. doi: 10.1093/cvr/cvp340. [DOI] [PubMed] [Google Scholar]
- 47.Goto K, Rummery NM, Grayson TH, Hill CE. Attenuation of conducted vasodilatation in rat mesenteric arteries during hypertension: role of inwardly rectifying potassium channels. J Physiol. 2004;561:215–231. doi: 10.1113/jphysiol.2004.070458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Crane GJ, Walker SD, Dora KA, Garland CJ. Evidence for a differential cellular distribution of inward rectifier K channels in the rat isolated mesenteric artery. J Vasc Res. 2003;40:159–168. doi: 10.1159/000070713. [DOI] [PubMed] [Google Scholar]
- 49.Quayle JM, Dart C, Standen NB. The properties and distribution of inward rectifier potassium currents in pig coronary arterial smooth muscle. The Journal of physiology. 1996;494(Pt 3):715–726. doi: 10.1113/jphysiol.1996.sp021527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wolfle SE, Chaston DJ, Goto K, Sandow SL, Edwards FR, Hill CE. Non-linear relationship between hyperpolarisation and relaxation enables long distance propagation of vasodilatation. The Journal of physiology. 2011;589:2607–2623. doi: 10.1113/jphysiol.2010.202580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Takano H, Dora KA, Spitaler MM, Garland CJ. Spreading dilatation in rat mesenteric arteries associated with calcium-independent endothelial cell hyperpolarization. J Physiol. 2004;556:887–903. doi: 10.1113/jphysiol.2003.060343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Uhrenholt TR, Domeier TL, Segal SS. Propagation of calcium waves along endothelium of hamster feed arteries. Am J Physiol Heart Circ Physiol. 2007;292:H1634–1640. doi: 10.1152/ajpheart.00605.2006. [DOI] [PubMed] [Google Scholar]
- 53.Domeier TL, Segal SS. Electromechanical and pharmacomechanical signalling pathways for conducted vasodilatation along endothelium of hamster feed arteries. J Physiol. 2007;579:175–186. doi: 10.1113/jphysiol.2006.124529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Tallini YN, Brekke JF, Shui B, Doran R, Hwang SM, Nakai J, Salama G, Segal SS, Kotlikoff MI. Propagated endothelial Ca2+ waves and arteriolar dilation in vivo: measurements in Cx40BAC GCaMP2 transgenic mice. Circ Res. 2007;101:1300–1309. doi: 10.1161/CIRCRESAHA.107.149484. [DOI] [PubMed] [Google Scholar]
- 55.Koenigsberger M, Seppey D, Beny JL, Meister JJ. Mechanisms of propagation of intercellular calcium waves in arterial smooth muscle cells. Biophys J. 2010;99:333–343. doi: 10.1016/j.bpj.2010.04.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Sandow SL, Gzik DJ, Lee RM. Arterial internal elastic lamina holes: relationship to function? J Anat. 2009;214:258–266. doi: 10.1111/j.1469-7580.2008.01020.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Heberlein KR, Straub AC, Isakson BE. The myoendothelial junction: breaking through the matrix? Microcirculation. 2009;16:307–322. doi: 10.1080/10739680902744404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Shimokawa H, Yasutake H, Fujii K, Owada MK, Nakaike R, Fukumoto Y, Takayanagi T, Nagao T, Egashira K, Fujishima M, Takeshita A. The importance of the hyperpolarizing mechanism increases as the vessel size decreases in endothelium-dependent relaxations in rat mesenteric circulation. J Cardiovasc Pharmacol. 1996;28:703–711. doi: 10.1097/00005344-199611000-00014. [DOI] [PubMed] [Google Scholar]
- 59.Crane GJ. Localized expression of an Ins(1,4,5)P3 receptor at the myoendothelial junction selectively regulates heterocellular Ca2+ communication. J Physiol. 2003;553:183–189. doi: 10.1242/jcs.037481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Sandow SL, Neylon CB, Shui B, Garland CJ. Functional architecture of inositol 1,4,5-trisphosphate signaling in restricted spaces of myoendothelial projections. J Anat. 2006;209:689–698. doi: 10.1073/pnas.0801963105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Dora KA, Gallagher NT, McNeish A, Garland CJ. Modulation of endothelial cell KCa3.1 channels during endothelium-derived hyperpolarizing factor signaling in mesenteric resistance arteries. Circ Res. 2008;102:1247–1255. doi: 10.1161/CIRCRESAHA.108.172379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Tran CH, Taylor MS, Plane F, Nagaraja S, Tsoukias NM, Solodushko V, Vigmond EJ, Furstenhaupt T, Brighan M, Welsh DG. Endothelial Ca2+ wavelets and the induction of myoendothelial feedback. Am J Physiol Cell Physiol. 2012 doi: 10.1152/ajpcell.00418.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Kapela A, Tsoukias NM. Multiscale FEM modeling of vascular tone: from membrane currents to vessel mechanics. IEEE Trans Biomed Eng. 2011;58:3456–3459. doi: 10.1109/TBME.2011.2162513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Schuster A, Oishi H, Beny JL, Stergiopulos N, Meister JJ. Simultaneous arterial calcium dynamics and diameter measurements: application to myoendothelial communication. Am J Physiol Heart Circ Physiol. 2001;280:H1088–1096. doi: 10.1152/ajpheart.2001.280.3.H1088. [DOI] [PubMed] [Google Scholar]
- 65.Isakson BE. Localized expression of an Ins(1,4,5)P3 receptor at the myoendothelial junction selectively regulates heterocellular Ca2+ communication. J Cell Sci. 2008;121:3664–3673. doi: 10.1242/jcs.037481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Isakson BE, Ramos SI, Duling BR. Ca2+ and inositol 1,4,5-trisphosphate-mediated signaling across the myoendothelial junction. Circ Res. 2007;100:246–254. doi: 10.1161/01.RES.0000257744.23795.93. [DOI] [PubMed] [Google Scholar]
- 67.Bezprozvanny I, Watras J, Ehrlich BE. Bell-shaped calcium-response curves of Ins(1,4,5)P3- and calcium-gated channels from endoplasmic reticulum of cerebellum. Nature. 1991;351:751–754. doi: 10.1038/351751a0. [DOI] [PubMed] [Google Scholar]
- 68.Ledoux J, Taylor MS, Bonev AD, Hannah RM, Solodushko V, Shui B, Tallini Y, Kotlikoff MI, Nelson MT. Functional architecture of inositol 1,4,5-trisphosphate signaling in restricted spaces of myoendothelial projections. Proc Natl Acad Sci U S A. 2008;105:9627–9632. doi: 10.1073/pnas.0801963105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kansui Y, Garland CJ, Dora KA. Enhanced spontaneous Ca2+ events in endothelial cells reflect signalling through myoendothelial gap junctions in pressurized mesenteric arteries. Cell Calcium. 2008;44:135–146. doi: 10.1016/j.ceca.2007.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Goldman D, Popel AS. A computational study of the effect of vasomotion on oxygen transport from capillary networks. J Theor Biol. 2001;209:189–199. doi: 10.1006/jtbi.2000.2254. [DOI] [PubMed] [Google Scholar]
- 71.Halidi N, Boittin FX, Beny JL, Meister JJ. Propagation of fast and slow intercellular Ca(2+) waves in primary cultured arterial smooth muscle cells. Cell Calcium. 2011;50:459–467. doi: 10.1016/j.ceca.2011.08.001. [DOI] [PubMed] [Google Scholar]
- 72.Peng H, Matchkov V, Ivarsen A, Aalkjaer C, Nilsson H. Hypothesis for the initiation of vasomotion. Circ Res. 2001;88:810–815. doi: 10.1161/hh0801.089603. [DOI] [PubMed] [Google Scholar]
- 73.Broegger T, Jacobsen JC, Secher Dam V, Boedtkjer DM, Kold-Petersen H, Pedersen FS, Aalkjaer C, Matchkov VV. Bestrophin is important for the rhythmic but not the tonic contraction in rat mesenteric small arteries. Cardiovasc Res. 2011;91:685–693. doi: 10.1093/cvr/cvr111. [DOI] [PubMed] [Google Scholar]
- 74.Boedtkjer DM, Matchkov VV, Boedtkjer E, Nilsson H, Aalkjaer C. Vasomotion has chloride-dependency in rat mesenteric small arteries. Pflugers Arch. 2008;457:389–404. doi: 10.1007/s00424-008-0532-3. [DOI] [PubMed] [Google Scholar]
- 75.Koenigsberger M, Sauser R, Meister JJ. Emergent properties of electrically coupled smooth muscle cells. Bull Math Biol. 2005;67:1253–1272. doi: 10.1016/j.bulm.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 76.Koenigsberger M, Sauser R, Beny JL, Meister JJ. Role of the endothelium on arterial vasomotion. Biophys J. 2005;88:3845–3854. doi: 10.1529/biophysj.104.054965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Kapela A, Parikh J, Tsoukias NM. Multiple factors influence calcium synchronization in arterial vasomotion. Biophys J. 2012;102:211–220. doi: 10.1016/j.bpj.2011.12.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Takano H, Dora KA, Garland CJ. Spreading vasodilatation in resistance arteries. J Smooth Muscle Res. 2005;41:303–311. doi: 10.1540/jsmr.41.303. [DOI] [PubMed] [Google Scholar]