Abstract
Although the coding transformation between visual thalamus and cortex has been known for over 50 years, whether a similar transformation occurs between auditory thalamus and cortex has remained elusive. Such a transformation may occur for time-varying sounds, such as music or speech. Most subcortical neurons explicitly encode the temporal structure of sounds with the temporal structure of their activity, but many auditory cortical neurons instead use a rate code. The mechanisms for this transformation from temporal code to rate code have remained unknown. Here we report that the membrane potential of rat auditory cortical neurons can show stimulus synchronization to rates up to 500 Hz, even when the spiking output does not. Synaptic inputs to rate-coding neurons arose in part from temporal-coding neurons but were transformed by voltage-dependent properties and push-pull excitatory-inhibitory interactions. This suggests that the transformation from temporal to rate code can be observed within individual cortical neurons.
Introduction
The temporal structure of the sounds of footsteps or a woodpecker are perceptually striking. In music and speech, temporal features over a wide range of time scales convey perceptually important information. The representation of such temporal structure appears to undergo a transformation between the auditory periphery and auditory cortex. In subcortical regions such as the cochlear nucleus (Langner, 1992), inferior colliculus (Batra et al., 1989), and auditory thalamus (Bartlett and Wang, 2007), most neurons explicitly encode the temporal structure of sounds with the temporal structure of their activity. In these cells, termed synchronized neurons (Lu et al., 2001), responses are phase-locked to temporal features of the stimulus. In auditory cortex, synchronized neurons can also be found — indeed, these are the only type of neuron observed under anesthesia (Wang, 2007). But in unanesthetized cats and primates, a separate population of neurons has been recently described that responds to time-varying sounds with an elevated firing rate but no phase-locking (Dong et al., 2011; Lu et al., 2001; Wang, 2007; Wang et al., 2008; Yin et al., 2011). These cells, termed non-synchronized neurons by Lu et al. (2001), appear to encode temporal structure using firing rate rather than using the explicit temporal structure of the response. This suggests that between thalamus and cortex, the coding strategy for time-varying sounds is at least in part transformed from a temporal code to a rate code. The mechanisms for this transformation have remained unknown.
Here we used whole-cell recordings to compare the coding strategy used by the inputs and the outputs of neurons in rat auditory cortex. We find that the membrane potential of nonsynchronized neurons shows phase-locking to the stimulus, up to rates as high as 500 Hz, even when the spiking output does not. This indicates that the synaptic inputs to non-synchronized neurons arise, at least in part, from synchronized neurons. These fast stimulus-locked membrane potential fluctuations were riding on a large sustained depolarization. To determine whether this sustained depolarization arises from non-synchronized input, or from temporal summation of synchronized input, we turned to a conductance-based neural model. By comparing the strength of membrane potential phase-locking in the model to that in real nonsynchronized neurons, we estimate that 38–82% of the presynaptic population must be synchronized. This suggests that a substantial amount of the transformation from a temporal code into a rate code can be observed within individual cortical neurons.
Results
We first verified that non-synchronized responses to time-varying stimuli can be observed in rat auditory cortex, since they have only previously been reported in auditory cortex in cats and primates. We used whole-cell methods to record membrane potential and spiking responses of 54 neurons in auditory cortex of unanesthetized rats to periodic click trains. We used two alternative methods to encourage animals to sit quietly during recording sessions: for 35 neurons in 20 animals, we acclimatized animals to handling and restraint over several days before and in between recording sessions; for 19 neurons in 23 animals we used a low dose of diazepam to reduce anxiety (See Methods). Figure 1a, b shows two examples of neurons that responded to click trains with sustained spiking responses that lasted as long as the click train. This elevated firing rate was produced by sustained depolarizations that also lasted as long as the click trains. Both firing rate and depolarization increased progressively for shorter and shorter inter-click intervals (ICIs, Fig. 2a, b). This preference for shorter ICIs was reflected in a significantly negative slope in the dependence of firing rate and depolarization on ICI (dashed lines in Fig. 2a, b). To assess whether these evoked spikes were phase-locked to the temporal structure of the stimulus, we used a common measure of phase-locking known as vector strength (see Methods). Evoked spiking responses in these neurons did not show significant vector strength, indicating that these are non-synchronized neurons similar to those described in primates (Lu et al., 2001). We defined neurons to be non-synchronized if they showed a preference for short ICIs but no phase-locking at these short ICIs, or in other words, neurons that showed a significantly negative dependence of either firing rate or depolarization on ICI (points in the lower left quadrant of Fig. 2c or d) and no significant phase-locking at ICI < 64 ms. By these criteria, 28% (15/54) of our neurons were non-synchronized, similar to the prevalence reported in primate auditory cortex (Lu et al., 2001).
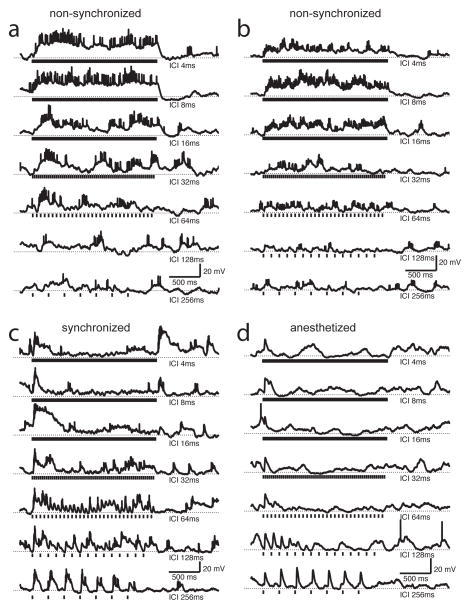
Figure 1.
Non-synchronized neurons in rat auditory cortex responded with sustained depolarizations and elevated firing rates to click trains with short inter-click intervals (ICIs). a, b) Two examples of non-synchronized neurons. The small action potential height is due to trial-averaging (5–6 trials in a and 8 trials in b). Vertical tick marks underneath each trace indicate each 1 ms click (for the shortest ICIs, these tick marks overlap but the actual stimuli did not). ICI is indicated at right. Dotted horizontal lines indicate resting membrane potential. c, d) Synchronized neurons showed phase-locked depolarizations and spiking at long ICIs, but for ICIs shorter than 64 ms only showed a transient response to the onset of the train. c) Neuron from unanesthetized animal. d) Neuron from ketamine-anesthetized animal. These are trial-averages (5 trials in c and 4 trials in d). The cell in c showed phase-locking of both spikes and membrane potential; the cell in d showed strong phase-locking of membrane potential but fired few spikes.
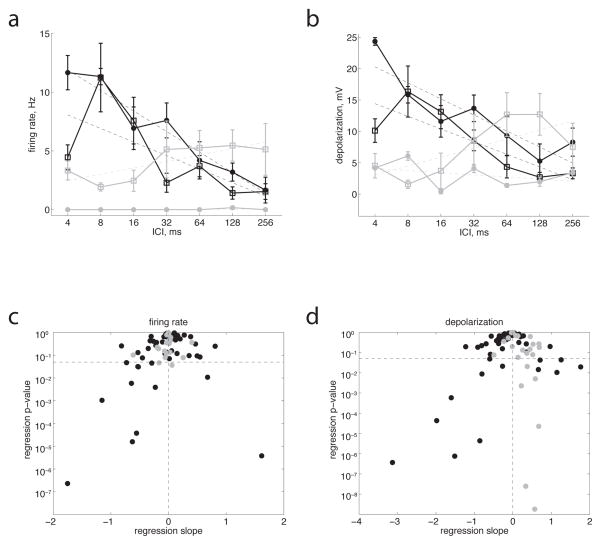
Figure 2.
Classification of synchronized and non-synchronized neuronal populations. a) Black lines show mean firing rate, averaged over the duration of the click train and across trials, for the two neurons in Fig. 1a, b. Error bars show s.e.m. Dashed lines show linear regression fits. Filled dots are from the neuron in Fig 1a (slope = −1.8 Hz/log2(ms), p < 10−6), open squares are from the neuron in Fig. 1b (slope = −1.2, p < 10−3). Gray lines show the same measure for the synchronized cells in Fig. 1c (open squares, slope = +0.6, n.s.) and Fig. 1d (filled dots, slope = 0.0, n.s.). b) Same neurons and format as a but for depolarization, averaged over the duration of the click train and across trials. Filled black dots, neuron in Fig. 1a, slope = −2.6, p < 10−4; open black squares, neuron in Fig. 1b, slope = −2.0, p < 10−4; Open gray squares, neuron in Fig. 1c, slope = +1.4, p < 0.05; filled gray dots, neuron in Fig. 1d, slope = −0.3, n.s. c, d) P-value vs. slope of linear regression fit of firing rate (c) or depolarization (d) to ICI, for all recorded neurons (black dots, 54 cells from unanesthetized animals; gray dots, 20 cells from anesthetized animals). The horizontal dashed line indicates p = 0.05. We defined non-synchronized cells as those in the lower left quadrant (i.e. with negative slope and p < 0.05) which did not show phase-locking at short ICIs.
We also observed synchronized neurons (Fig. 1c, d), which showed phase-locked spiking and/or membrane potential responses at the longest ICIs (256 ms), but progressively weaker responses at shorter ICIs, and only a transient response to the onset of the click train for ICIs shorter than 128 ms. The prevalence of these synchronized neurons in our sample (26%, or 13/54) was similar to that of non-synchronized neurons, and also to the prevalence of synchronized neurons reported in primate auditory cortex (Lu et al., 2001). These stimulus-synchronized responses closely resemble those seen under anesthesia (Fig. 1d shows an example from an anesthetized animal). Neurons recorded in ketamine-anesthetized rats invariably (100%, or 20/20) showed synchronized membrane potential responses to click trains. However, neurons in anesthetized rats responded with far fewer spikes (0.6 ± 0.8 Hz, compared to 2.4 ± 3.1 Hz in awake rats, p < 10−2), and only 20% (4/20) showed synchronized spiking responses. For example, the neuron in Fig. 1d fired only a few stray spikes, but showed prominent synchronized membrane potential responses to slow click trains. We never observed nonsynchronized neurons under anesthesia (Fig. 2, gray dots); responses sometimes depended significantly on ICI, but always with a positive slope, driven by the large stimulus-synchronized depolarizations at the longest ICIs (Fig. 2b, d, 1c, d). Four neurons recorded in unanesthetized rats were both synchronized (at long ICIs) and non-synchronized (at short ICIs) by our criteria, similar to the prevalence of such “mixed” responses reported previously in primates (Lu et al., 2001).
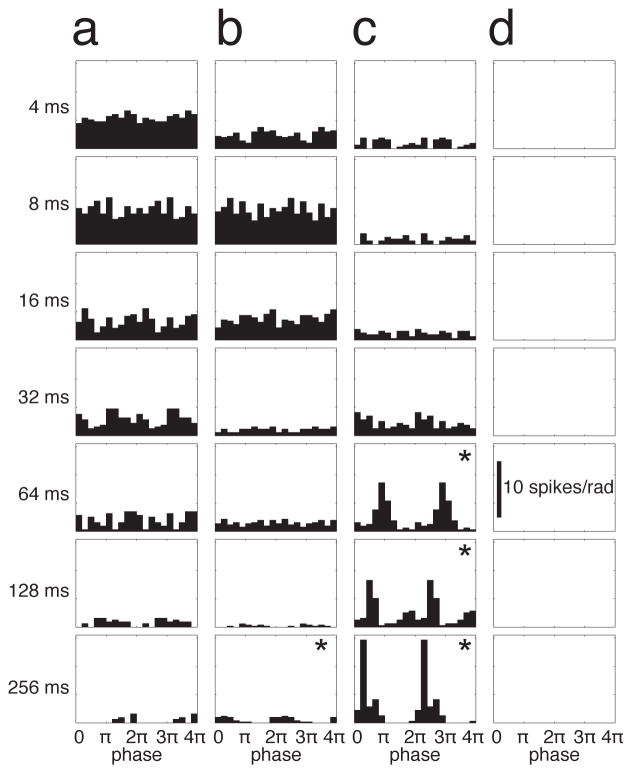
To more closely examine the phase-locking of spikes, we computed cycle histograms of spiking responses. Synchronized and non-synchronized neurons showed strikingly different patterns of phase-locking (Fig. 3, same example neurons as in Fig. 1). The non-synchronized neurons in Fig. 3a, b showed high spike rates, but little or no phase locking at the shortest ICIs. At the longest ICIs, these non-synchronized neurons were moderately phase-locked, but fired very few spikes. This was also true across the population of non-synchronized neurons (Fig. 5a), for which spiking vector strength was greatest for the longest ICI and progressively decreased for shorter ICIs. Synchronized neurons (Fig. 3c) showed the opposite: strong phase-locking at the longest ICIs, and little or no response at the shortest ICIs. Thus the strongest spiking responses of synchronized neurons were strongly stimulus-synchronized, whereas the strongest spiking responses of non-synchronized neurons were not stimulus-synchronized at all.
Figure 3.
Non-synchronized cells showed low spike rates and moderate phase-locking for long ICIs, and high spike rates but little or no phase locking at the shortest ICIs, whereas the opposite was true for synchronized cells. a–d) Cycle histograms of spiking responses for the example neurons shown in Fig. 1. Two complete cycles (0–4π) are shown. a, b) Non-synchronized neurons. c) Synchronized neuron. d) Neuron from an anesthetized animal, which showed stimulus-locked membrane potential responses (Fig. 4d) but no stimulus-locked spikes. * indicates significant phase-locking. Scale bar in d applies to all panels.
Figure 5.
Comparison of spiking and membrane potential phase-locking across the population. a) Vector strength (phase-locking index, varies from 0 to 1) of spiking output was greatest for the longest ICIs and weakest for shortest ICIs. Group data for all 15 non-synchronized neurons. Error bars are s.d. Dashed line is a linear regression fit (p < 10−9). b) Vector strength of membrane potential was greatest for shortest ICIs and weakest for longest ICIs. Dashed line is a linear regression fit (p < 10−2). c) Direct comparison of vector strength computed from spikes and from membrane potential. For the longest ICIs (open dots), spiking vector strength was significantly greater than membrane potential vector strength(p < 10−6). For the shortest ICIs (filled dots), membrane potential vector strength was significantly greater than spiking vector strength (p < 10−2). Dashed line indicates unity slope.
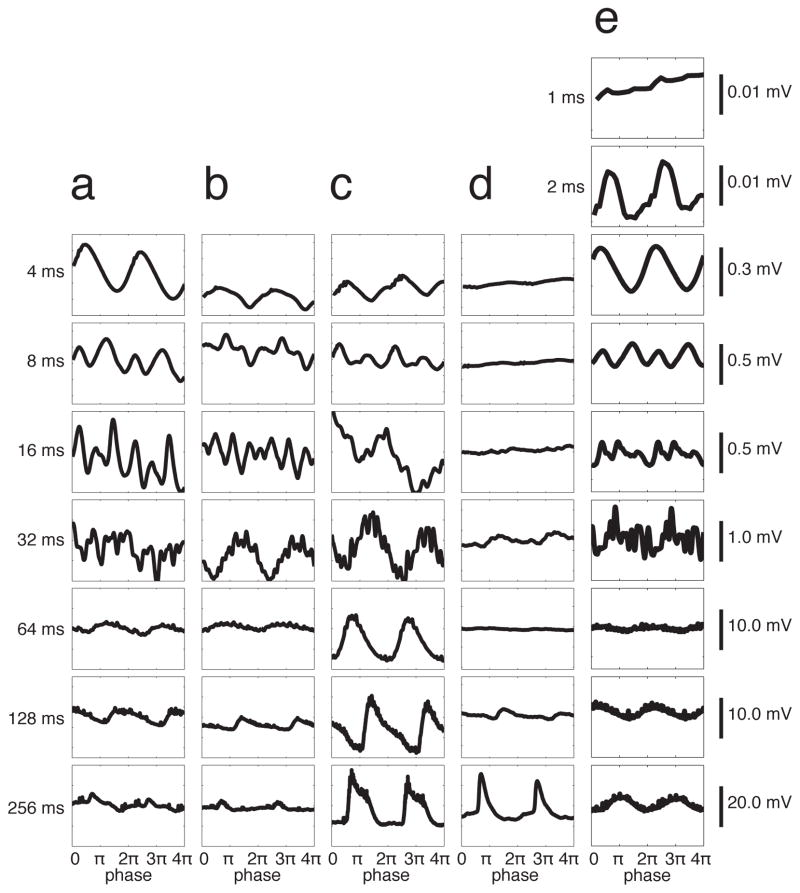
In contrast, the pattern of phase-locking of membrane potential responses was strikingly different. Cycle-averaged membrane potential responses revealed that non-synchronized neurons (Fig. 4a, b) showed strongly stimulus-synchronized membrane potential fluctuations, even at the shortest ICIs for which spikes were non-synchronized (compare Fig. 4a, b to 3a, b). These membrane potential fluctuations were small (< 1 mV), which could explain the absence of stimulus-synchronized spiking. Nevertheless, it is surprising that cortical neurons can exhibit stimulus-synchronized oscillations at 250 Hz (at the shortest ICI, 4 ms). In a subset of neurons, we then tested even shorter ICIs, and observed neurons (n=4) that showed small-amplitude but phase-locked membrane potential fluctuations at ICIs as short as 2 ms (500 Hz) (Fig. 4e), but not at an ICI of 1 ms. This pattern was similar across our population of non-synchronized neurons (Fig. 5b). The vector strength of membrane potential responses was greatest at the shortest ICIs, and progressively decreased with longer ICIs. This pattern is the opposite of that shown by the spiking responses in the same neurons (Fig. 5a). Across our sample of nonsynchronized neurons, the vector strength of the membrane potential was significantly higher than the vector strength of spiking responses at the shortest ICIs (p < 10−2, Fig. 5c, filled dots). This was not an artifact of comparing vector strengths of membrane potential and spiking responses, because the opposite was true for the longest ICIs (Fig. 5c, open dots). Because the membrane potential is a direct reflection of the synaptic input to a neuron, this indicates that these non-synchronized neurons (as defined by their spiking responses) receive inputs from synchronized neurons that phase-lock to stimuli up to 500 Hz. Because cortical neurons have not been reported to fire phase-locked spikes at these high rates (Langner, 1992; Liang et al., 2002; Lu et al., 2001), it is likely that these synaptic inputs are from subcortical neurons, and could be thalamocortical inputs from the medial geniculate nucleus of the thalamus. This suggests that at least some part of the transformation from a temporal code (in presynaptic synchronized neurons) into a rate code (in postsynaptic non-synchronized neurons) can be observed within individual cortical neurons at the level of the membrane potential.
Figure 4.
Non-synchronized cells showed synchronized membrane potential fluctuations at short ICIs. a–d) Cycle averages of membrane potential for the example neurons shown in Fig. 1. Scale bars at right apply to all panels in that row. Note that the non-synchronized cells in a–b showed stronger membrane potential phase-locking for short ICIs than for long ICIs. The opposite was true for synchronized cells in c–d. a, b) Non-synchronized neurons. c) Synchronized neuron. d) Neuron from an anesthetized animal, which showed stimulus-locked membrane potential responses. e) A non-synchronized neuron tested at shorter ICIs showed phase-locking at an ICI of 2 ms, but not at 1 ms. These are trial-averages of (in a–e) 5, 8, 4, 4, and 5 trials.
Interestingly, synchronized neurons in unanesthetized animals also showed small stimulus-synchronized membrane potential fluctuations at the shortest ICIs (Fig. 4c), but differed from non-synchronized neurons in the lack of sustained depolarization and spiking at these short ICIs, and in the prominent stimulus-synchronized responses at the longest ICIs (compare Fig. 1a, b to 1c, d). In anesthetized animals, synchronized neurons never showed stimulus-synchronized spiking responses or membrane potential fluctuations at short ICIs (Fig. 3d, 4d), ruling out the possibility of stimulus artifact.
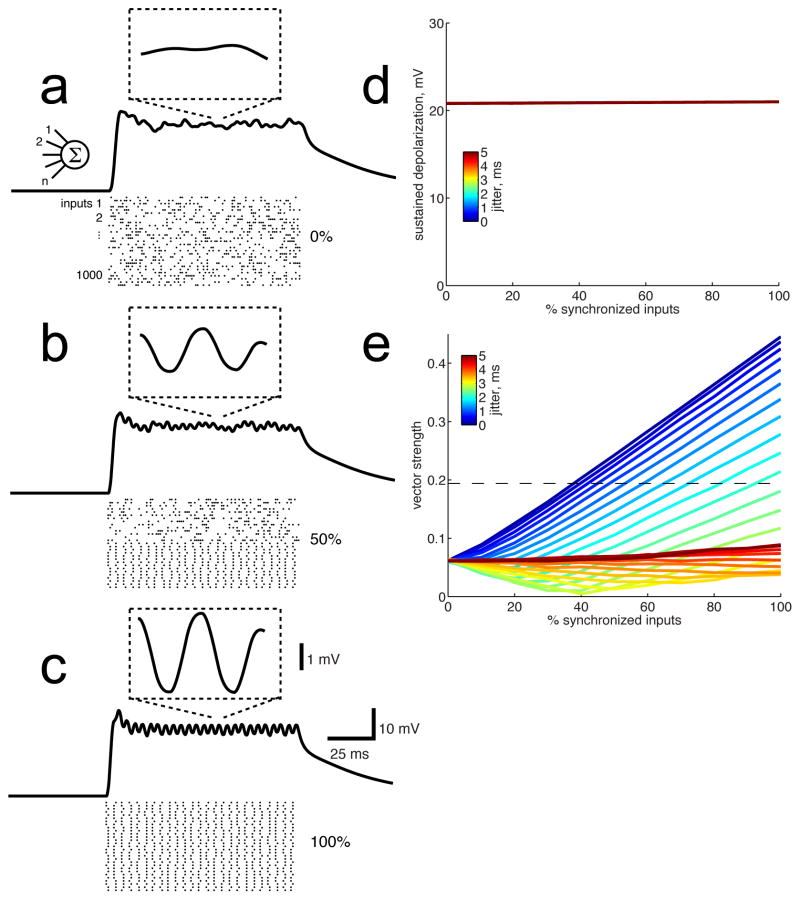
The synchronized membrane potential fluctuations we observed in non-synchronized cells were small (<1 mV) and were riding on large sustained depolarizations (10–20 mV). What are the sources of these two components? One possibility is that non-synchronized cortical neurons receive input from two distinct populations of presynaptic neurons: one that is synchronized (producing stimulus-locked fluctuations), and one that is non-synchronized (producing the sustained depolarization). Another possibility is that non-synchronized cortical neurons receive input from a single population of synchronized presynaptic neurons, but that temporal summation of those PSPs produces a sustained pedestal of depolarization along with stimulus-locked fluctuations. Between these two extremes lie a range of possible scenarios. To estimate the relative contribution of synchronized and non-synchronized input that would produce our observed results, we used a conductance-based neuronal model using biophysical parameters (input resistance, capacitance) measured from our whole-cell recordings, and which received 1000 synaptic inputs (Fig. 6, see Methods). When we varied the proportion of synchronized input, we found that the sustained depolarization was large (~20 mV), independent of the proportion of synchronized inputs, and independent of temporal jitter in the inputs (Fig. 6a–d). Thus temporal summation produces a large sustained pedestal of depolarization even when all presynaptic inputs are perfectly stimulus-locked. Small phase-locked membrane potential fluctuations, on the other hand, depended strongly on the proportion of synchronized inputs. Cycle-averaged membrane potential responses (Fig. 6a–c, insets) revealed that phase-locked fluctuations remained small (~1 mV) even when the presynaptic population was completely synchronized. Figure 6e shows how the vector strength of the membrane potential responses depended on the relative proportion of synchronized and non-synchronized inputs and the temporal jitter of synchronized spike trains. The mean vector strength of our sample of non-synchronized neurons (membrane potential) was 0.194 (at 4 ms ici, Fig. 5b), which is is indicated by the dashed horizontal line in Figure 6e. The minimum proportion of synchronized presynaptic neurons required to produce a vector strength of 0.194 was 38%, if those neurons were perfectly synchronized (i.e., no temporal jitter). The mean temporal jitter measured from recordings of synchronized neurons in the thalamus is 1.8 ms (Bartlett and Wang, 2007). With this degree of spike timing jitter, 82% of presynaptic neurons had to be synchronized to produce the degree of membrane potential phase-locking that we observed. While these simulations should not be considered definitive evidence for the true proportion of synchronized neurons that were pre-synaptic to our non-synchronized cortical neurons, they do illustrate that a sustained pedestal of depolarization is not necessarily produced by non-synchronized inputs. These results also provide an estimated lower bound of 38% for the proportion of synchronized input to our nonsynchronized cortical neurons.
Figure 6.
We used a conductance-based synaptic integration model to estimate the post-synaptic effect of varying proportions of synchronized and non-synchronized presynaptic neurons. a) Rasters show spike trains from presynaptic neurons, in this case all non-synchronized (i.e., 0% synchronized). The resulting membrane potential showed a sustained depolarization of ~20 mV, and the inset shows that the cycle-averaged membrane potential was flat. Only 30 of the 1000 excitatory and 1000 inhibitory input spike trains are shown; for clarity a 100 ms stimulus is illustrated, actual stimulus was 200 ms long. b) When half of the presynaptic population were synchronized (ICI 4 ms) and half were non-synchronized, the sustained depolarization remained ~20 mV but the phase-locked fluctuations (inset) are now ~1 mV in amplitude. c) With 100% of the input coming from synchronized neurons, the sustained depolarization remained ~20 mV and the phase-locked fluctuations were larger. In b–c, spikes from synchronized neurons were temporally jittered by 1.8 ms. d) The magnitude of the sustained depolarization was independent of the proportion of inputs that were synchronized. The magnitude was also independent of temporal jitter applied to individual spikes (0 to 5 ms, as indicated by color scale inset, note that all colored lines are superimposed). e) The degree of phase-locking of the membrane potential, as measured by vector strength, depended strongly on the proportion of inputs that were synchronized and on temporal jitter. The horizontal line indicates a vector strength of 0.194, which is the sample mean of our whole-cell recordings from non-synchronized neurons at an ICI of 4 ms. With no jitter (i.e. perfect phase-locking of input spike trains, blue line), 38% of presynaptic neurons had to be synchronized to produce this degree of phase-locking. With input jitter of 1.8 ms (as measured by Bartlett and Wang, 2007), an 82% synchronized input population was required.
What are the mechanisms underlying this coding transformation? One possibility is that precise temporal coding could be degraded by low-pass filtering of the membrane potential due to membrane capacitance. To investigate this possibility, we voltage-clamped neurons to to eliminate the effects of capacitance. If capacitive low-pass filtering reduces phase-locking, we should expect that the vector strength of the synaptic currents (measured in voltage clamp mode) should be greater than that of the membrane potential (measured in current-clamp mode). We found the opposite. Figure 7a shows that at the shortest ICIs (filled dots), the vector strength for membrane potentials was significantly greater than that for synaptic currents in the same neurons (p < 10−9). This difference was not an artifact of comparing vector strengths of synaptic current and membrane potential responses, because there was no difference in vector strength at the longest ICIs (Fig. 7a, open dots). This suggests that low-pass filtering by membrane capacitance does not account for the transformation from a temporal code to a rate code, at least not in auditory cortical neurons. Because we wished to observe coding by spikes, we did not include pharmacological blockers of voltage-dependent channels in our pipette internal solution. Since contributions from voltage-dependent channels are largely reduced or eliminated in our voltage-clamp conditions, but not in current-clamp conditions, such active currents could have amplified membrane potential fluctuations and thereby contributed to the stronger phase-locking of membrane potential compared to synaptic current seen in Fig. 7a.
Figure 7.
Non-synchronized cells showed synchronized push-pull synaptic excitation and inhibition. a) Vector strength for membrane potential was significantly greater than that for synaptic currents at 4 ms ICI (p < 10−9, filled dots), but not for 256 ms ICI (n. s., open dots). Group data for 12 non-synchronized neurons for which we were able to record both current-clamp (I=0) and voltage-clamp data. Synaptic currents were measured at hyperpolarized holding potentials (−83 ± 20 mV). Dashed line indicates unity slope. b) Cycle averages of excitatory (green) and inhibitory (red) synaptic conductances along with sinusoidal fits (same neuron as Fig 1a,4a,5a). Arrowheads indicate stimulus artifact. c) Phase difference between excitation and inhibition extracted from the sinusoidal fits in b. Dashed line is a linear regression fit (p < 10−2). Note that excitation and inhibition were in-phase at the longest ICI (256 ms) but nearly out of phase at the shortest ICIs (4–8 ms). d) Across all 11 non-synchronized neurons for which we were able to measure both excitation and inhibition, the phase difference between them depended significantly on ICI (p < 0.05). e) Across synchronized neurons (n=12), excitatory-inhibitory phase difference did not depend on ICI. Dashed lines in d–e are linear regression fits.
Cortical synaptic interactions are another possible mechanism underlying this coding transformation. For example, brief sounds evoke a stereotyped sequence of excitation and inhibition in auditory cortex, in which inhibition follows excitation after a brief delay of about 2 ms (Tan and Wehr, 2009; Wehr and Zador, 2003). For a long ICI such as 256 ms, this delay would produce a negligible phase difference (0.05 radians), such that excitation and inhibition are in-phase. However, this phase difference would progressively increase for shorter ICIs; at 4 ms, excitation and inhibition would be completely out of phase. This could produce a push-pull effect, amplifying the membrane potential response. To further investigate this possibility, we voltage-clamped neurons to multiple holding potentials in order to estimate excitatory and inhibitory synaptic conductances. Figure 7b shows the cycle-averaged excitatory and inhibitory conductances for the neuron shown in Figs. 1a,4a,5a. The phase difference between excitation and inhibition progressively increased from in-phase at long ICIs to nearly anti-phase at shorter ICIs (Fig. 7c). Across our sample of non-synchronized neurons, the phase difference between excitation and inhibition progressively increased with shorter ICIs (Fig. 7d, p < 0.05), but this was not true for our sample of synchronized neurons (Fig. 7e, n. s.). Excitatory-inhibitory phase differences for non-synchronized cells were significantly different compared to synchronized cells at the shortest ICIs (8 ms: p<0.01, 4 ms: p<0.05) but not at the longest ICI (256 ms, N.S.). Similarly, the regression slopes for non-synchronized neurons (computed individually) were significantly more negative than those from synchronized neurons (p<0.05). While small in magnitude, these anti-phase synaptic interactions in non-synchronized neurons could help explain why phase-locking of the membrane potential was greater than that of synaptic current.
Because inhibition received by cortical neurons is generated by local inhibitory interneurons (Markram et al., 2004; Thomson and Lamy, 2007), the existence of these phase-locked inhibitory synaptic conductances (Fig. 7b) indicates that at least a subset of cortical inhibitory interneurons must exhibit synchronized spiking responses to click trains up to at least 125 Hz (i.e. ICI 8 ms). This is faster than nearly all reports of synchronized spiking boundaries in auditory cortex (Langner, 1992; Liang et al., 2002; Lu et al., 2001). Fast-spiking interneurons such as parvalbumin-expressing basket cells would be well-suited to provide this inhibition.
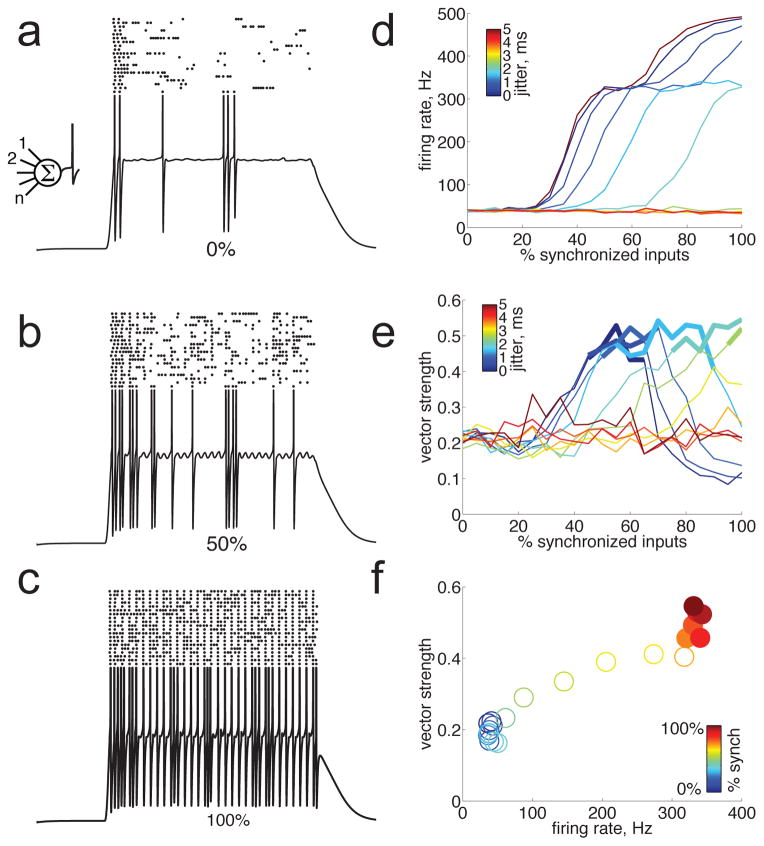
How might this push-pull synaptic amplification contribute to spiking output? Because rapid membrane potential fluctuations are particularly effective in triggering action potentials (Azouz and Gray, 1999; Mainen and Sejnowski, 1995), we wondered whether push-pull amplification of these fluctuations could partially contribute to increased firing at short ICIs in these neurons. To test this idea, we added a Hodgkin-Huxley spiking mechanism — which is one of the simplest spiking models for which spike probability is sensitive to dV/dt — to our conductance-based model (Fig. 8). Increasing the proportion of synchronized pre-synaptic inputs produced stronger stimulus-locked membrane potential fluctuations, which were more effective at driving spikes (Fig. 8a–c). As the presynaptic population became more synchronized and drove stronger membrane potential fluctuations, the evoked spike count increased several-fold (Fig. 8d). Not surprisingly, these added spikes had a tendency to be stimulus-locked, such that the vector strength of the spiking output also increased as the presynaptic population became more synchronized (Fig. 8e). Yet, importantly, firing rate increased between 7- and 9-fold before the vector strength reached significance, depending on the temporal jitter of presynaptic spike trains (Fig. 8d–e). For example, using the experimentally measured value of 1.8 ms for temporal jitter (Fig. 8f; Bartlett and Wang, 2007), the evoked spike count increased over 8-fold before those evoked spikes became significantly synchronized. This indicates that stimulus-locked membrane potential fluctuations can have a substantial impact on firing rate without producing significantly synchronized spike trains. This effect was not seen with an integrate-and-fire model that used a fixed spiking threshold and was therefore insensitive to dV/dt (not shown). These simulations suggest that the dependence of spike initiation on dV/dt is an important mechanism contributing to the transformation from temporal to rate coding. We found that stimulus-locked membrane potential fluctuations were maximal when excitation and inhibition were completely out of phase (as in Fig. 8), but were reduced by 89% when excitation and inhibition were completely in-phase and therefore canceled each other out, reducing spiking responses by 88–100%. This suggests that push-pull synaptic amplification of membrane potential fluctuations substantially enhances spiking responses for short ICIs, and likely contributes to the transformation from synchronized input to non-synchronized spiking output.
Figure 8.
Push-pull amplification of membrane potential fluctuations enhanced firing rate well before producing significantly synchronized spiking output. We added a Hodgkin-Huxley spiking mechanism to the conductance-based integrate and fire model shown in Fig. 6. a) When none of the 1000 presynaptic neurons were synchronized (0%), the membrane potential responded to a click train (4 ms ICI) with a sustained depolarization and a weak spiking response. The trace shows a single representative trial (spikes are clipped), rasters show spiking output responses on 20 trials. b–c) Increasing the proportion of synchronized pre-synaptic inputs to 50% (b) or 100% (c) produced progressively stronger stimulus-locked membrane potential fluctuations, which were more effective at driving spikes. (d) Spike count increased sharply with the proportion of synchronized presynaptic inputs. This effect was reduced by temporal jitter in the pre-synaptic spiketrains (and eliminated as jitter approached the ICI of 4 ms); the experimentally measured jitter value of 1.8 ms is shown in blue. (e) Vector strength of the spiking output increased with the proportion of synchronized presynaptic inputs. Again, this effect was reduced by temporal jitter (as in d). Significant vector strength is indicated by bold lines. (f) Direct comparison of evoked firing rate and vector strength as a function of the proportion of synchronized presynaptic inputs (indicated by color). Temporal jitter was 1.8 ms. Significant vector strength is indicated by filled circles. Note that firing rate increased 8-fold before the vector strength reached significance.
Discussion
In the auditory cortex of awake animals, time-varying signals are represented differently by two distinct classes of neurons: synchronized neurons that faithfully encode the temporal structure of the stimulus, and non-synchronized neurons that instead represent temporal structure with a rate code. These populations appear to constitute steps along a transformation in the representation of time-varying stimuli from a temporal code to a rate code (Langner, 1992; Wang, 2007). Here we have demonstrated that non-synchronized neurons exist in awake rats, with properties similar to those seen in primates, suggesting that they may be a general feature of mammalian auditory systems. We found that non-synchronized spiking responses are produced by sustained depolarizations, which are rare in auditory cortex even in awake animals (DeWeese and Zador, 2006; Hromadka and Zador, 2009). Furthermore, we found that the membrane potential of non-synchronized cortical neurons can be phase-locked to the stimulus up to rates as high as 500 Hz, even when the spiking output is not. This indicates that the synaptic inputs to nonsynchronized neurons arise, at least in part, from synchronized neurons. Simulations of synaptic integration indicate that the amount of synaptic input arising from synchronized neurons was likely substantial (38–82%). In other words, for a considerable fraction of the synapses onto these neurons, upstream of the synapse is a synchronized neuron, and downstream of the synapse is a non-synchronized neuron. This suggests that at least part of the transformation from a temporal code into a rate code can be observed within individual cortical neurons at the level of the membrane potential.
What are the mechanisms underlying this coding transformation? Low-pass filtering by biophysical properties such as capacitance has been proposed to explain the progressive slow-down of synchronization limits from the periphery to auditory cortex (Langner, 1992; Wang, 2007). However, we found that phase-locking of membrane potential responses was greater than that of synaptic currents recorded in voltage-clamp mode. This suggests that low-pass filtering does not contribute to the transformation of synchronized to non-synchronized responses, at least not in auditory cortical neurons. However, we did observe push-pull excitatory-inhibitory interactions that likely amplified the membrane potential responses to fast click trains. The brief (~2 ms) delay between excitation and inhibition (Wehr and Zador, 2003) produced a shift from in-phase to out-of-phase inhibition as the inter-click interval decreased from long (256 ms) to very short (4 ms) intervals. Although these excitatory-inhibitory interactions were small in magnitude, it is becoming increasingly clear that relatively subtle shifts in the balance of excitation and inhibition can often have a substantial impact on the spiking output of cortical neurons (Isaacson and Scanziani, 2011; Wu et al., 2008). Intrinsic properties also likely contributed to the fast membrane potential fluctuations we observed at short ICIs. Because we did not include any channel blockers in our whole-cell pipettes, the membrane potential in current-clamp mode was driven by a combination of both synaptic and voltage-dependent currents. The double- and triple-cycle membrane potential fluctuations we observed at 8 and 16 ms ICI (Fig. 4a, b) likely reflect a contribution from intrinsic properties, because they were absent in voltage-clamp conditions (Fig. 7b). Nevertheless, the fact that synaptic current and membrane potential fluctuations were synchronized to the stimuli indicates that they are driven mainly by synaptic input.
Many questions remain about the mechanisms underlying the transformation from synchronized to non-synchronized coding. Why do synchronized membrane potential fluctuations not produce more synchronized spiking output? One possibility is that these membrane potential fluctuations are riding on large sustained depolarizations, which likely dominate spike production. The source of these sustained depolarizations is still not clear, but our modeling results suggest that they can be produced by either synchronized and non-synchronized synaptic input. Even perfectly synchronized presynaptic neurons produced a large pedestal of sustained depolarization, due to post-synaptic temporal integration. Based on our model and the observed size of phase-locked membrane potential fluctuations, it seems likely that a substantial fraction of input is from synchronized neurons (38–82%). This suggests that non-synchronized spiking output is partially computed within auditory cortical neurons, but also partially inherited. This leaves open the question of where and how this encoding scheme is originally computed, although it seems likely that the mechanisms described above progressively enhance the degree of nonsynchronization. However, these mechanisms are unlikely to explain why non-synchronized neurons show little or no response to click trains with long ICIs, or why synchronized neurons show only a transient onset response to click trains with very short ICIs. Instead it seems likely that these response properties must be due to different patterns of input. Synchronized neurons likely get only transient input for click trains with very short ICIs, whereas non-synchronized neurons likely get no input for long ICIs. An important future goal will be to characterize the specific population(s) of neurons presynaptic to both synchronized and non-synchronized neurons, in order to identify the circuit mechanisms involved in these coding transformations.
The representation of time-varying stimuli appears to shift from exclusively synchronized responses in the cochlear nucleus (Frisina et al., 1990), to progressively greater proportions of non-synchronized neurons in the inferior colliculus (Batra et al., 1989; Langner and Schreiner, 1988), medial geniculate (Bartlett and Wang, 2007), primary auditory cortex (Bendor and Wang, 2007; Liang et al., 2002; Lu et al., 2001; Yin et al., 2011), and rostral auditory cortical fields (Bendor and Wang, 2007, 2008; Brugge et al., 2009). This suggests that early in the auditory hierarchy, temporal structure in the stimulus is represented directly by temporal structure in the response. At subsequent stages, the representation no longer faithfully replicates the temporal structure in the stimulus, shifting instead to a rate code (Wang, 2007). Why should the auditory system switch to a less faithful representation? One explanation is that rate codes could support multi-sensory integration in higher cortical areas. Information from sensory areas with different peripheral receptor dynamics may need to be converted into a common rate code to be meaningfully combined (Wang, 2007). In the somatosensory cortex, an analogous coding transformation occurs between S1 and S2 (Salinas et al., 2000). There, the representation of vibrations of the skin is transformed from a largely temporal code in S1 to a rate code in S2. This suggests that the transformation from temporal encoding of temporal structure into a common firing rate code could be a general principle of cortical operation. Whether similar cellular and circuit mechanisms perform this transformation in each of these cortical areas remains an open question.
The perception of periodic stimuli such as the click trains we used undergoes a categorical transition as the ICI decreases. At long ICIs, click trains produce a rhythmic percept in which each click is distinct. As ICI is decreased beyond a perceptual boundary at ~25–50 ms, click trains instead produce a buzzy pitch percept (periodicity pitch), in which individual clicks are no longer distinct. Interestingly, this perceptual boundary roughly corresponds to the limit beyond which synchronized neurons can no longer phase-lock, and at which non-synchronized neurons begin to fire in a non-stimulus-synchronized fashion. It is tempting to speculate that this perceptual transition could arise from a changeover in the representation of periodic stimuli from synchronized to non-synchronized populations of neurons (Langner, 1992). Lesion studies have shown that the auditory cortex is required for periodicity pitch perception (Whitfield, 1980), and imaging studies suggest that that periodicity pitch may be represented orthogonally to the topographic frequency axis in primary auditory cortex (Langner et al., 2009; Langner et al., 1997). The mechanisms by which periodicity selectivity is computed are still unclear (Langner, 1992).
Because we used clicks with a fixed amplitude, the average sound level of the entire click train depended on ICI (i.e., short-ICI click trains had higher average sound level than long-ICI click trains). However, several lines of evidence suggest that the greater response of nonsynchronized neurons to short ICIs was not driven simply by sound level. First, we never observed non-synchronized neurons in anesthetized animals, whereas a trivial effect of sound level would not be expected to depend on anesthesia. Second, not all neurons in unanesthetized animals were non-synchronized, also arguing against a trivial effect of sound level. Third, for the key comparison between the phase-locking of membrane potential and spiking responses for a given ICI (Fig. 5c), the sound level is identical. Finally, previous studies have shown that nonsynchronized neurons have similar response properties across a variety of level-normalized, energy-normalized, or non-normalized periodic stimuli (Lu et al., 2001), and that most auditory cortical neurons in awake animals show level-invariant coding (Sadagopan and Wang, 2008).
Is there an equivalent in A1 of orientation selectivity in V1? Despite extensive study, this question remains controversial (King and Nelken, 2009; Wang, 2007; Winer et al., 2005). Vision is inherently spatial, and accordingly the formation of orientation selectivity between LGN and V1 is a spatial transformation. Sounds such as music and speech inherently unfold over time, and given the exquisite sensitivity of the auditory system to temporal structure, it seems fitting that between MGB and A1 there appears to be a coding transformation for temporal structure. Moreover, we find that push-pull synaptic interactions, which contribute to the spatial coding transformation in simple cells in V1 (Hirsch et al., 1998), also contribute to the temporal coding transformation in A1. It is very intriguing that similar underlying thalamocortical circuitry could compute a spatial transformation in one modality, and a temporal transformation in another. Moreover, the responses of synchronized cells resemble the temporally modulated responses of simple cells to drifting gratings, whereas the responses of non-synchronized cells resemble the phase-insensitive responses of complex cells. The circuit mechanisms responsible for the formation of orientation selectivity between LGN and V1 remain controversial (Fig. 9f; Alitto and Dan, 2010; Ferster and Miller, 2000; Hirsch and Martinez, 2006; Monier et al., 2003; Sompolinsky and Shapley, 1997). Likewise, the circuitry involved in the transformation from a synchronized to a non-synchronized representation in auditory cortex is still unclear. The lack of nonsynchronized firing rate responses and fast (>250 Hz) phase-locked membrane potential fluctuations under anesthesia suggests that the neurons producing these two response properties are silenced by anesthesia, but it is not clear whether both properties arise from a single class of neurons, or from distinct classes of neurons (Langner, 1992). It will be interesting to more completely elucidate the circuit mechanisms that perform this coding transformation.
Methods
All procedures were in strict accordance with the National Institutes of Health guidelines as approved by the University of Oregon Animal Care and Use Committee.
Surgery
We anesthetized 25–29 day old rats with 2% isoflurane, implanted a headpost, and performed a craniotomy over left auditory cortex, which we then covered with a polyethylene chamber and a protective silicone elastomer cap. Animals were given 8 mg/kg dexamethasone and 5 mg/kg ketoprofen after surgery.
Physiology
After at least 18 hours of recovery, we restrained animals by mounting the headpost in a clamp, and obtained whole-cell recordings using standard blind patch clamp methods (Scholl et al., 2010). Animals had 1–3 recording sessions/day (<2 hours each) for 1–3 days. We used two alternative methods to encourage animals to sit quietly during recording sessions. For 35 neurons in 20 animals, we acclimatized animals to handling and restraint over several days before and in between recording sessions; for 19 neurons in 23 animals we used a low anxiolytic dose (5 mg/kg) of diazepam prior to recording sessions to reduce anxiety. The incidence of nonsynchronized neurons in animals that had received diazepam (42%, or 8/19) was not significantly different from the incidence of non-synchronized neurons in animals that had not received diazepam (17%, or 6/35; χ2=1.55, ν=1, n.s.). Neurons were located in layer 2/3 (depths were <325 um, as determined from micromanipulator travel). Neurons were most likely in primary auditory cortex or the ventral auditory field, although it is possible that some neurons were in neighboring auditory cortical fields. Internal solution contained, in mM, K-gluconate 140, HEPES 10, MgCl2 2, CaCl2 0.05, MgATP 4, NaGTP 0.4, Na2Phosphocreatine 10, BAPTA 10, pH 7.25, diluted to 290 mOsm. Because the internal solution contained no channel blockers, cells were free to spike in current clamp mode. Current-clamp recordings were made in I=0 mode, except for 2 cells in which we injected less than 200 pA of hyperpolarizing current to improve recording stability. Our methods for extracting excitatory and inhibitory conductances from synaptic currents recorded in voltage clamp are similar to those described previously (Wehr and Zador, 2003) except that we used only two holding potentials (mean ± s.d.: −83 ± 20 mV, and −19 ± 13 mV), and when stepping to depolarized holding potentials we waited until depolarization block occurred in order to minimize active conductances and thereby isolate synaptic conductances. Series resistance was 47 ± 24 MΩ, input resistance was 34 ± 22 MΩ, and whole-cell capacitance was 1.5 ± 0.9 nF (mean ± s.d.). We also recorded from 20 neurons in 8 rats anesthetized with ketamine (30 mg/kg) and medetomidine (0.24 mg/kg), using standard whole-cell methods as described previously (Wehr and Zador, 2003).
Acoustic stimuli
We presented pseudorandomly interleaved click trains that were 2 s long, with ICIs of 4, 8, 16, 32, 64, 128, and 256 ms. The interval between click trains was 1 s. Clicks were 1 ms, 80 dB SPL white noise bursts. For 4 cells, we added ICIs of 0.25, 0.5, 1, and 2 ms; for these stimuli all clicks were 0.1 ms 70 db SPL square pulses. Stimuli were delivered using a free-field calibrated sound delivery system in an acoustic isolation chamber as previously described (Scholl et al., 2010).
Analysis
We measured evoked responses (depolarization, firing rate, or phase-locking) during the entire duration of the 2s click trains, excluding the first 100 ms. We measured the degree of phase-locking using vector strength, which varies from 0 to 1 (where 0 indicates no phase-locking, and 1 indicates perfect phase-locking). For spikes, we used the conventional discrete definition of vector strength:
where θ is the phase of each spike in radians, and n is the number of spikes. For membrane potential, we used an extension of vector strength to sampled continuous signals:
where θ is the phase of each sample, Vθ is the membrane potential at that sample (normalized to lie between 0 and 1), and n is the number of samples. Vector strength of the synaptic current was computed similarly. Sampling rate was 10 kHz. Note that this measure is independent of sampling rate. We assessed the significance of phase-locking using Rayleigh’s statistic, p = e−nr2, where r is the vector strength (Zar, 1999), and used p < 0.001 as the criterion for significant phase-locking consistent with previous work (Liang et al., 2002; Lu et al., 2001; Yin et al., 2011). We compared the vector strength of spiking and membrane potential responses (Fig. 5c) using a paired one-tailed t-test; the use of a t-test to compare vector strengths is valid for these data because they were normally distributed (Lilliefors test, n.s.). We compared excitatory-inhibitory phase differences using the one-tailed Wilcoxon ranksum test. We compared regression slopes of excitatory-inhibitory phase differences vs. ICI, computed individually, using the Wilcoxon ranksum test.
We assessed the dependence of firing rate and depolarization on ICI using linear regression. We defined neurons to be non-synchronized if they showed a significantly (p < 0.05) negative dependence of either firing rate or depolarization on ICI (points in the lower left quadrant of Fig. 2c or d) and no significant phase-locking at ICIs < 64 ms. This definition is similar to those used in previous studies (Bendor and Wang, 2007; Lu et al., 2001) but extended to include depolarization. Cycle histograms used π/5 radian bins. We defined neurons to be synchronized if they showed significant phase-locking of spiking responses at the longest ICI (256 ms).
We used a conductance-based synaptic integration model to estimate the post-synaptic effect of varying proportions of synchronized and non-synchronized presynaptic neurons. Model parameters were either measured from our data or taken from published measurements or estimates (Bartlett and Wang, 2007; DeWeese and Zador, 2006; Gil et al., 1999; Stevens and Zador, 1998). The input consisted of 1000 excitatory and 1000 inhibitory neurons, which has been reported as an estimate for the size of the presynaptic population giving rise to typical stimulus-evoked membrane potential responses in auditory cortical neurons (DeWeese and Zador, 2006). We varied the proportion of non-synchronized and synchronized presynaptic neurons from 0 to 100%. For excitatory neurons, synchronized spike trains included a spike for every click in a 200 ms click train with 4 ms ici. We applied varying amounts of temporal jitter to each spike (0 to 5 ms, in 0.2 ms increments). The actual jitter applied to each spike was random within the bound set by the jitter value; for example, for a jitter value of 2 ms, each spike was shifted by a random value between 0 and 2 ms. Note that the mean temporal jitter measured from recordings of synchronized neurons in the thalamus is 1.8 ms (Bartlett and Wang, 2007). Nonsynchronized input spike trains were generated by a poisson process with the equivalent firing rate. For both synchronized and non-synchronized spike trains, each excitatory spike was followed by an inhibitory spike 2 ms later (Wehr and Zador, 2003). Post-synaptically, each input spike produced a 0.1 nS conductance change with a time course given by an α-function with a time constant of 3 ms (DeWeese and Zador, 2006). Input resistance was 34 MΩ and total cell capacitance was 1.5 nF (given by the sample means of our whole-cell recordings). Excitatory reversal potential was 0 mV, and inhibitory reversal potential was −85 mV (determined by our internal solution). We measured the vector strength of the resulting membrane potential the same way as for our whole-cell recordings. We measured the sustained depolarization as the mean membrane potential during the stimulus period, excluding the initial 20 ms. We also extended the model to include a Hodgkin-Huxley spiking mechanism (with voltage dependent Na+ and K+ conductances), using published cortical neuron parameters (Pospischil et al., 2008). We also verified that results were similar across a range of Hodgkin-Huxley parameter values.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Bibliography
- Alitto HJ, Dan Y. Function of inhibition in visual cortical processing. Curr Opin Neurobiol. 2010;20:340–346. doi: 10.1016/j.conb.2010.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azouz R, Gray CM. Cellular mechanisms contributing to response variability of cortical neurons in vivo. J Neurosci. 1999;19:2209–2223. doi: 10.1523/JNEUROSCI.19-06-02209.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartlett EL, Wang X. Neural representations of temporally modulated signals in the auditory thalamus of awake primates. J Neurophysiol. 2007;97:1005–1017. doi: 10.1152/jn.00593.2006. [DOI] [PubMed] [Google Scholar]
- Batra R, Kuwada S, Stanford TR. Temporal coding of envelopes and their interaural delays in the inferior colliculus of the unanesthetized rabbit. J Neurophysiol. 1989;61:257–268. doi: 10.1152/jn.1989.61.2.257. [DOI] [PubMed] [Google Scholar]
- Bendor D, Wang X. Differential neural coding of acoustic flutter within primate auditory cortex. Nat Neurosci. 2007;10:763–771. doi: 10.1038/nn1888. [DOI] [PubMed] [Google Scholar]
- Bendor D, Wang X. Neural response properties of primary, rostral, and rostrotemporal core fields in the auditory cortex of marmoset monkeys. J Neurophysiol. 2008;100:888–906. doi: 10.1152/jn.00884.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brugge JF, Nourski KV, Oya H, Reale RA, Kawasaki H, Steinschneider M, Howard MA., 3rd Coding of repetitive transients by auditory cortex on Heschl’s gyrus. J Neurophysiol. 2009;102:2358–2374. doi: 10.1152/jn.91346.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeWeese MR, Zador AM. Non-Gaussian membrane potential dynamics imply sparse, synchronous activity in auditory cortex. J Neurosci. 2006;26:12206–12218. doi: 10.1523/JNEUROSCI.2813-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong C, Qin L, Liu Y, Zhang X, Sato Y. Neural responses in the primary auditory cortex of freely behaving cats while discriminating fast and slow click-trains. PLoS One. 2011;6:e25895. doi: 10.1371/journal.pone.0025895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferster D, Miller KD. Neural mechanisms of orientation selectivity in the visual cortex. Annu Rev Neurosci. 2000;23:441–471. doi: 10.1146/annurev.neuro.23.1.441. [DOI] [PubMed] [Google Scholar]
- Frisina RD, Smith RL, Chamberlain SC. Encoding of amplitude modulation in the gerbil cochlear nucleus: I. A hierarchy of enhancement. Hear Res. 1990;44:99–122. doi: 10.1016/0378-5955(90)90074-y. [DOI] [PubMed] [Google Scholar]
- Gil Z, Connors BW, Amitai Y. Efficacy of thalamocortical and intracortical synaptic connections: quanta, innervation, and reliability. Neuron. 1999;23:385–397. doi: 10.1016/s0896-6273(00)80788-6. [DOI] [PubMed] [Google Scholar]
- Hirsch JA, Alonso JM, Reid RC, Martinez LM. Synaptic integration in striate cortical simple cells. J Neurosci. 1998;18:9517–9528. doi: 10.1523/JNEUROSCI.18-22-09517.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirsch JA, Martinez LM. Circuits that build visual cortical receptive fields. Trends Neurosci. 2006;29:30–39. doi: 10.1016/j.tins.2005.11.001. [DOI] [PubMed] [Google Scholar]
- Hromadka T, Zador AM. Representations in auditory cortex. Curr Opin Neurobiol. 2009;19:430–433. doi: 10.1016/j.conb.2009.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isaacson JS, Scanziani M. How inhibition shapes cortical activity. Neuron. 2011;72:231–243. doi: 10.1016/j.neuron.2011.09.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King AJ, Nelken I. Unraveling the principles of auditory cortical processing: can we learn from the visual system? Nat Neurosci. 2009;12:698–701. doi: 10.1038/nn.2308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langner G. Periodicity coding in the auditory system. Hear Res. 1992;60:115–142. doi: 10.1016/0378-5955(92)90015-f. [DOI] [PubMed] [Google Scholar]
- Langner G, Dinse HR, Godde B. A map of periodicity orthogonal to frequency representation in the cat auditory cortex. Front Integr Neurosci. 2009;3:27. doi: 10.3389/neuro.07.027.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langner G, Sams M, Heil P, Schulze H. Frequency and periodicity are represented in orthogonal maps in the human auditory cortex: evidence from magnetoencephalography. J Comp Physiol A. 1997;181:665–676. doi: 10.1007/s003590050148. [DOI] [PubMed] [Google Scholar]
- Langner G, Schreiner CE. Periodicity coding in the inferior colliculus of the cat. I. Neuronal mechanisms. J Neurophysiol. 1988;60:1799–1822. doi: 10.1152/jn.1988.60.6.1799. [DOI] [PubMed] [Google Scholar]
- Liang L, Lu T, Wang X. Neural representations of sinusoidal amplitude and frequency modulations in the primary auditory cortex of awake primates. J Neurophysiol. 2002;87:2237–2261. doi: 10.1152/jn.2002.87.5.2237. [DOI] [PubMed] [Google Scholar]
- Lu T, Liang L, Wang X. Temporal and rate representations of time-varying signals in the auditory cortex of awake primates. Nat Neurosci. 2001;4:1131–1138. doi: 10.1038/nn737. [DOI] [PubMed] [Google Scholar]
- Mainen ZF, Sejnowski TJ. Reliability of spike timing in neocortical neurons. Science. 1995;268:1503–1506. doi: 10.1126/science.7770778. [DOI] [PubMed] [Google Scholar]
- Markram H, Toledo-Rodriguez M, Wang Y, Gupta A, Silberberg G, Wu C. Interneurons of the neocortical inhibitory system. Nat Rev Neurosci. 2004;5:793–807. doi: 10.1038/nrn1519. [DOI] [PubMed] [Google Scholar]
- Monier C, Chavane F, Baudot P, Graham LJ, Fregnac Y. Orientation and direction selectivity of synaptic inputs in visual cortical neurons: a diversity of combinations produces spike tuning. Neuron. 2003;37:663–680. doi: 10.1016/s0896-6273(03)00064-3. [DOI] [PubMed] [Google Scholar]
- Pospischil M, Toledo-Rodriguez M, Monier C, Piwkowska Z, Bal T, Fregnac Y, Markram H, Destexhe A. Minimal Hodgkin-Huxley type models for different classes of cortical and thalamic neurons. Biol Cybern. 2008;99:427–441. doi: 10.1007/s00422-008-0263-8. [DOI] [PubMed] [Google Scholar]
- Sadagopan S, Wang X. Level invariant representation of sounds by populations of neurons in primary auditory cortex. J Neurosci. 2008;28:3415–3426. doi: 10.1523/JNEUROSCI.2743-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salinas E, Hernandez A, Zainos A, Romo R. Periodicity and firing rate as candidate neural codes for the frequency of vibrotactile stimuli. J Neurosci. 2000;20:5503–5515. doi: 10.1523/JNEUROSCI.20-14-05503.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholl B, Gao X, Wehr M. Nonoverlapping sets of synapses drive on responses and off responses in auditory cortex. Neuron. 2010;65:1–10. doi: 10.1016/j.neuron.2010.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sompolinsky H, Shapley R. New perspectives on the mechanisms for orientation selectivity. Curr Opin Neurobiol. 1997;7:514–522. doi: 10.1016/s0959-4388(97)80031-1. [DOI] [PubMed] [Google Scholar]
- Stevens CF, Zador AM. Input synchrony and the irregular firing of cortical neurons. Nat Neurosci. 1998;1:210–217. doi: 10.1038/659. [DOI] [PubMed] [Google Scholar]
- Tan A, Wehr M. Balanced tone-evoked synaptic excitation and inhibition in mouse auditory cortex. Neuroscience. 2009 doi: 10.1016/j.neuroscience.2009.07.032. [DOI] [PubMed] [Google Scholar]
- Thomson AM, Lamy C. Functional maps of neocortical local circuitry. Front Neurosci. 2007;1:19–42. doi: 10.3389/neuro.01.1.1.002.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X. Neural coding strategies in auditory cortex. Hear Res. 2007;229:81–93. doi: 10.1016/j.heares.2007.01.019. [DOI] [PubMed] [Google Scholar]
- Wang X, Lu T, Bendor D, Bartlett E. Neural coding of temporal information in auditory thalamus and cortex. Neuroscience. 2008;154:294–303. doi: 10.1016/j.neuroscience.2008.03.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wehr M, Zador AM. Balanced inhibition underlies tuning and sharpens spike timing in auditory cortex. Nature. 2003;426:442–446. doi: 10.1038/nature02116. [DOI] [PubMed] [Google Scholar]
- Whitfield IC. Auditory cortex and the pitch of complex tones. J Acoust Soc Am. 1980;67:644–647. doi: 10.1121/1.383889. [DOI] [PubMed] [Google Scholar]
- Winer JA, Miller LM, Lee CC, Schreiner CE. Auditory thalamocortical transformation: structure and function. Trends Neurosci. 2005;28:255–263. doi: 10.1016/j.tins.2005.03.009. [DOI] [PubMed] [Google Scholar]
- Wu GK, Arbuckle R, Liu BH, Tao HW, Zhang LI. Lateral sharpening of cortical frequency tuning by approximately balanced inhibition. Neuron. 2008;58:132–143. doi: 10.1016/j.neuron.2008.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin P, Johnson JS, O’Connor KN, Sutter ML. Coding of amplitude modulation in primary auditory cortex. J Neurophysiol. 2011;105:582–600. doi: 10.1152/jn.00621.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zar JH. Biostatistical analysis. 4. Upper Saddle River, N.J: Prentice Hall; 1999. [Google Scholar]