Detection of circular permutations within protein structures using CE-CP

Abstract

Motivation: Circular permutation is an important type of protein rearrangement. Natural circular permutations have implications for protein function, stability and evolution. Artificial circular permutations have also been used for protein studies. However, such relationships are difficult to detect for many sequence and structure comparison algorithms and require special consideration.

Results: We developed a new algorithm, called Combinatorial Extension for Circular Permutations (CE-CP), which allows the structural comparison of circularly permuted proteins. CE-CP was designed to be user friendly and is integrated into the RCSB Protein Data Bank. It was tested on two collections of circularly permuted proteins. Pairwise alignments can be visualized both in a desktop application or on the web using Jmol and exported to other programs in a variety of formats.

Availability and implementation: The CE-CP algorithm can be accessed through the RCSB website at http://www.rcsb.org/pdb/workbench/workbench.do. Source code is available under the LGPL 2.1 as part of BioJava 3 (http://biojava.org; http://github.com/biojava/biojava).

Contact: sbliven@ucsd.edu or info@rcsb.org.

1 Introduction

Circular permutation describes a relationship between two proteins where the N-terminal portion of one protein is related to the C-terminal portion of the other. While the order of amino acids changes, circularly permuted proteins are generally found to assume the same structure. Circular permutation has been documented to naturally occur in a number of protein families, such as lectins (Cunningham et al., 1979) and DNA methyltransferases (Jeltsch, 1999). Two general mechanisms for the evolution of circularly permuted proteins are known, so detecting such events can shed light on the evolutionary history of protein families (Weiner and Bornberg-Bauer, 2006). Circular permutation can influence protein folding, dynamics and function (Bliven and Prlić, 2012). Synthetic circular permutants have been engineered to alter activity, control regulation and improve stability (Ostermeier, 2005; Whitehead et al., 2009; Yu and Lutz, 2011).

Natural circular permutants generally have quite low sequence similarity, with previous studies finding <0.3–2.6% of proteins share >30% identity (Jung and Lee, 2001; Lo and Lyu, 2008). Thus, including structural information is essential for detecting circular permutations. Many structural alignment algorithms are unable to detect rearrangements in sequence, while general sequence-order independent methods lack a clear evolutionary mechanism by which complex rearrangements could occur. Therefore, algorithms that specifically search for circular permutations are needed. Several existing algorithms have been reported, including SHEBA (Jung and Lee, 2001) and CPSARST (Lo and Lyu, 2008).

Here we describe a method, Combinatorial Extension with Circular Permutations (CE-CP), for the identification of circular permutations based on protein structure.

2 Methods

CE is a rigid-body structural comparison algorithm (Shindyalov and Bourne, 1998). It uses dynamic programming to identify regions of local similarity between the alpha carbons of two protein structures, followed by iterative refinement to find a global superposition with low RMSD and high number of aligned residues.

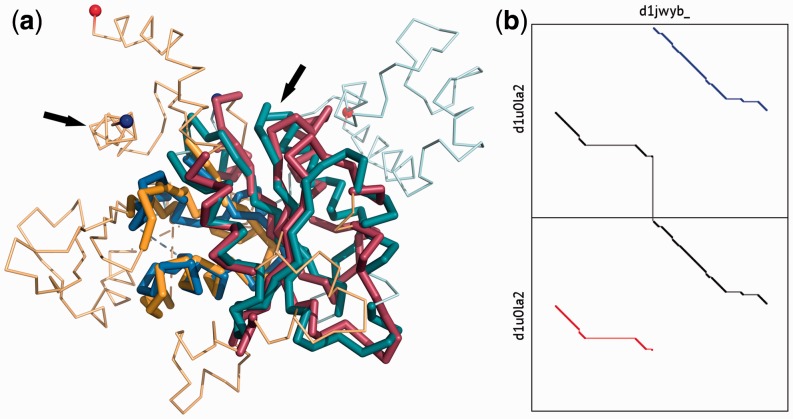
To adapt CE to quickly find circular permutations, we use an algorithm analogous to that proposed by Uliel et al. (1999) for detecting circular permutations by sequence similarity. The atoms of the shorter structure are virtually duplicated. This allows the alignment of the first protein to wrap around from the carboxyl terminus to the amino terminus of the second protein (see Fig. 1b). Thus, the path with optimal structural similarity will contain some residues from each copy of the duplicated protein, allowing the permutation site to be identified. In the case of structures that are not circular permuted, two equivalent paths are possible.

Fig. 1.

(a) CE-CP alignment of the dynamin A GTPase domain (yellow and red, SCOP:d1jwyb_) and the YjeQ protein (blue and green, SCOP:d1u0la2). N- and C-termini are shown with blue and red spheres. Arrows indicate the positions of the circular permutation. (b) Dotplot of the alignment with YjeQ duplicated. The optimal alignment is shown in black, with the inferred equivalent positions in blue and red

After identifying the highest scoring alignment to the duplicated protein, the result is processed to map the alignment onto the original query. While this is generally unambiguous for high-scoring alignments, it is possible that a single residue in the duplicated protein will align to multiple residues. In this case, a single aligned residue is chosen such that the total alignment length is maximized.

This technique is agnostic to the details of the actual alignment algorithm. Thus, it could be easily adapted to allow other sequence-order dependent alignment algorithms to detect circular permutations. For instance, CE-CP was used in our recent tool CE-Symm for identifying internally symmetric structures (Myers-Turnbull et al., 2014).

To reduce computational time, CE by default limits gap sizes to 30 residues. As terminal insertions are common in protein structures, due to both biological variability in tail regions and experimental tags and artifacts, this limit is often restrictive for circularly permuted proteins, and all gaps are considered used in CE-CP by default. This ensures that the optimal path can be found regardless of insertions and deletions.

3 Results and discussion

CE-CP is integrated into the RCSB PDB Comparison Tool, along with several other algorithms for structural alignment (Prlić et al., 2010). Two user interfaces are available: a web version, and a standalone Java application that can be downloaded or run via Java Web Start.

CE-CP results are presented to the user graphically, using the Jmol visualization program, and as a pairwise alignment. The portions before and after the permutation site are displayed in different colors if a permutation is found. The alignment is also available for export in a variety of formats, including a parsable text format or a two-model PDB file containing the two superimposed structures. The standalone application provides additional features, such as the ability to compare custom PDB files and perform full database searches.

As shown in Figure 1, CE-CP is able to identify the conserved structural core between highly divergent structures. It is robust to insertions and deletions, making it suitable for the detection of circular permutations in multi-domain structures.

No large, balanced benchmarks of circularly permuted structures are available. However, CE-CP performance was evaluated on the small but accurate RIPC benchmark (Mayr et al., 2007), as well as compared to results from the semi-automated circular permutation database (CPDB) (Lo et al., 2009).

The RIPC dataset is a small benchmark of ‘challenging’ manual alignments, due to the presence of insertions, conformational variability and permutations. All 11 pairs of circularly permuted proteins from the dataset were correctly identified by CE-CP, with most residues matching the reference alignment within 0–4 residues.

The CPDB contains 4169 pairs of circularly permuted proteins, as identified by the CPSARST algorithm, followed by manual screening for false positives. Thus, entries contain a plausible circular permutation but are not verified as evolutionarily related. CE-CP identified a circular permutation in 3666 (88%) of CPDB pairs. Of the cases where a permutation was not detected, many are internally pseudosymmetric structures that have reasonable sequential alignments. As both circularly permuted proteins and internally symmetric proteins can evolve through duplication and fusion mechanisms, the high correlation between the two phenomena should be unsurprising. A portion of these symmetric cases may prove to be false positives from CPSARST given additional evolutionary or functional data.

CE-CP is a readily available and easy to use tool for detecting circular permutations from protein structures. It is incorporated into the RCSB PDB Comparison Tool, which allows the comparison of structures through a variety of methods both on the RCSB PDB website and via a Java Webstart executable. CE-CP is available as part of the BioJava open source project (Prlić et al., 2012).

Funding

This work was supported by the National Science Foundation [grant number DBI-1338415]; the Intramural Research Program of the National Center for Biotechnology Information, National Library of Medicine; National Institutes of Health [grant number T32GM8806]; and the Department of Energy.

Conflict of Interest: none declared.