Abstract
Motor, sensory, and cognitive learning require networks of neurons to generate new activity patterns. Because some behaviors are easier to learn than others1,2, we wondered if some neural activity patterns are easier to generate than others. We asked whether the existing network constrains the patterns that a subset of its neurons is capable of exhibiting, and if so, what principles define the constraint. We employed a closed-loop intracortical brain-computer interface (BCI) learning paradigm in which Rhesus monkeys controlled a computer cursor by modulating neural activity patterns in primary motor cortex. Using the BCI paradigm, we could specify and alter how neural activity mapped to cursor velocity. At the start of each session, we observed the characteristic activity patterns of the recorded neural population. These patterns comprise a low-dimensional space (termed the intrinsic manifold, or IM) within the high-dimensional neural firing rate space. They presumably reflect constraints imposed by the underlying neural circuitry. We found that the animals could readily learn to proficiently control the cursor using neural activity patterns that were within the IM. However, animals were less able to learn to proficiently control the cursor using activity patterns that were outside of the IM. This result suggests that the existing structure of a network can shape learning. On the timescale of hours, it appears to be difficult to learn to generate neural activity patterns that are not consistent with the existing network structure. These findings offer a network-level explanation for the observation that we are more readily able to learn new skills when they are related to the skills that we already possess3,4.
Some behaviors are easier to learn than others1–4. We hypothesized that the ease or difficulty with which an animal can learn a new behavior is determined by the current properties of the networks of neurons governing the behavior. We tested this hypothesis in the context of brain-computer interface (BCI) learning. In a BCI paradigm, the user controls a cursor on a computer screen by generating activity patterns across a population of neurons. A BCI offers advantages for studying learning because we can observe all of the neurons that directly control an action, and we can fully specify the mapping from neural activity to action. This allows us to define which activity patterns will lead to task success and to test whether subjects are capable of generating them. Previous studies have shown that BCI learning can be remarkably extensive5–10, raising the intriguing possibility that most or all novel BCI mappings are learnable.
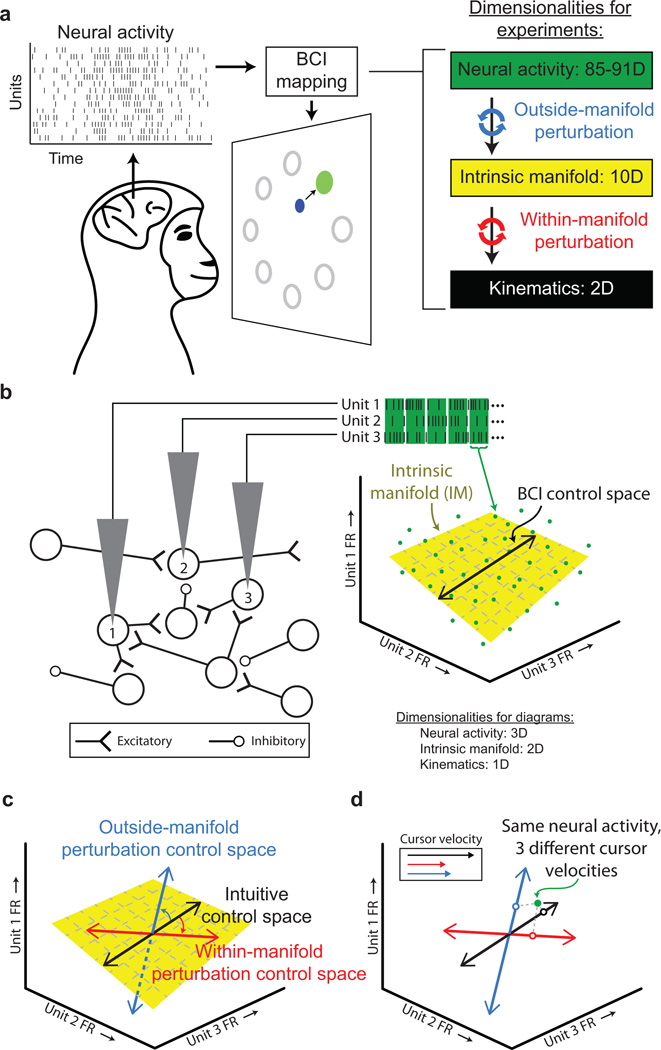
Two Rhesus monkeys were trained to move a cursor from the center of the screen to one of eight radially arranged targets by modulating the activity of 85 – 91 neural units (i.e., threshold crossings on each electrode) recorded in the primary motor cortex (M1) (Fig. 1a). To represent the activity of the neural population, we defined a high-dimensional space (called the neural space) where each axis corresponds to the firing rate of one neural unit. The activity of all neural units during a short time period is represented as a point in this space (Fig. 1b). At each timestep, the neural activity (i.e., a green point in Fig. 1b) is mapped onto a control space (e.g., black line in Fig. 1b; two-dimensional plane in the actual experiments, corresponding to horizontal and vertical cursor velocity) to specify cursor velocity. This is the geometrical representation of a BCI mapping. At the start of each day, we calibrated an intuitive mapping by specifying a control space that the monkey used to move the cursor proficiently (Extended Data Fig. 1).
Figure 1. Using a brain-computer interface to study learning.
a, Monkeys moved the BCI cursor (blue circle) to acquire targets (green circle) by modulating their neural activity. The BCI mapping consisted of first mapping the population neural activity to the IM using factor analysis, then from the IM to cursor kinematics using a Kalman filter. This two-step procedure allowed us to perform outside-manifold perturbations (blue arrows) and within-manifold perturbations (red arrows). b, A simplified, conceptual illustration using three electrodes. The spike counts observed on each electrode in a brief epoch define a point (green ●) in the neural space. The IM (yellow plane) characterizes the prominent patterns of co-modulation. Neural activity maps onto the control space (black line) to specify cursor velocity. c, Control spaces for an intuitive mapping (black), within-manifold perturbation (red), and outside-manifold perturbation (blue). d, Neural activity (green ●) elicits different cursor velocities (○ and inset) under different mappings.
At the beginning of each day, we also characterized how the activity of the recorded neurons covaried. In the simplified network in Fig. 1b, neurons 1 and 3 positively covary due to common input, whereas neurons 1 and 2 negatively covary due to an indirect inhibitory connection. Such co-modulations among neurons mean that neural activity does not uniformly populate the neural space11–16. We identified the low-dimensional space that captured the natural patterns of co-modulation among the recorded neurons. We refer to this space as the intrinsic manifold (IM, yellow plane in Figs. 1b and c). By construction, the intuitive mapping lies within the IM. Our key experimental manipulation was to change the BCI mapping so that the control space was either within or outside of the IM. A within-manifold perturbation was created by re-orienting the control space but keeping it within the IM (depicted as the red line in Fig. 1c). This preserved the relationship between neural units and co-modulation patterns, but it altered the way in which co-modulation patterns affected cursor kinematics (red arrows, Fig. 1a). An outside-manifold perturbation was created by re-orienting the control space but allowing it to depart from the IM (depicted as the blue line in Fig. 1c). This altered the way in which neural units contributed to co-modulation patterns, but it preserved the way in which co-modulation patterns affected cursor kinematics (blue arrows, Fig. 1a). In both cases, performance was impaired once the new mapping was introduced, and we observed whether the monkeys could learn to regain proficient control of the cursor.
To restore proficient control of the cursor under a within-manifold perturbation, the animals had to learn new associations between the natural co-modulation patterns and the cursor kinematics (Fig. 1d). To restore proficient control of the cursor under an outside-manifold perturbation, the animals had to learn to generate new co-modulation patterns among the recorded neurons. Our hypothesis predicted that within-manifold perturbations would be more readily learnable than outside-manifold perturbations.
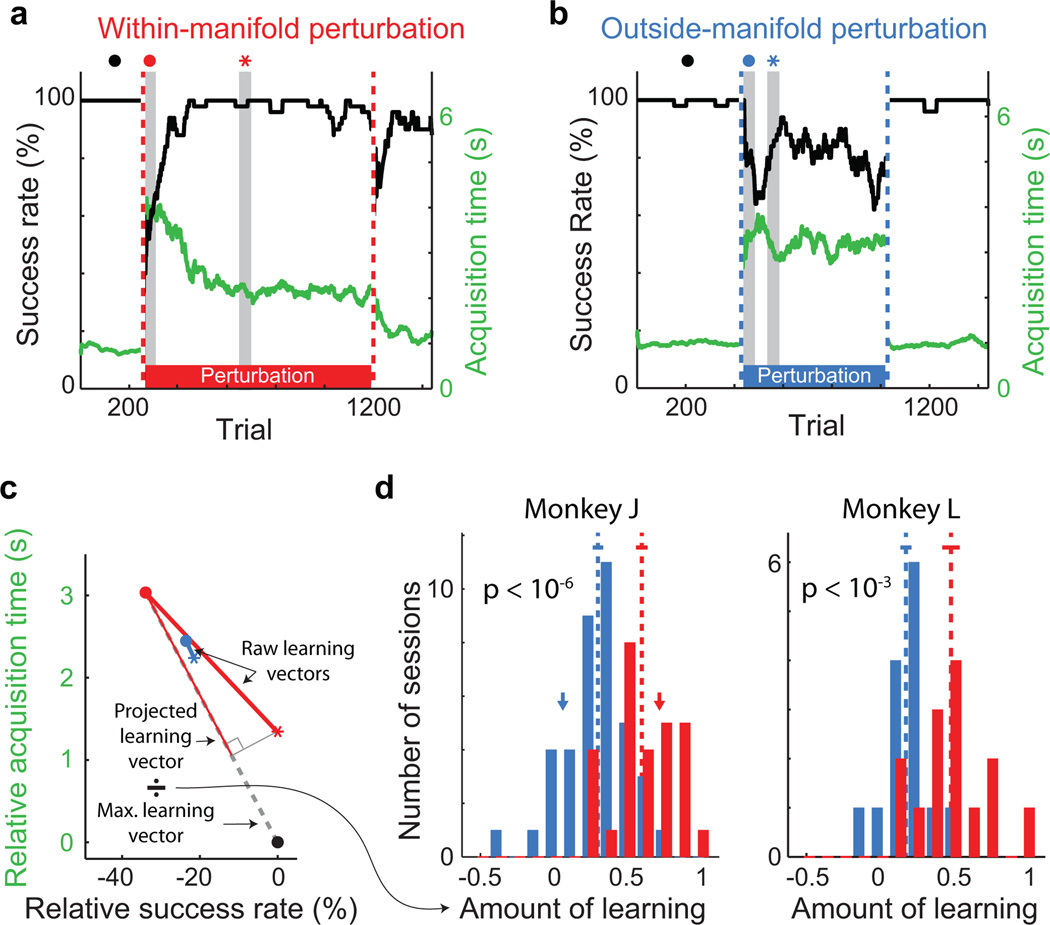
Just after the perturbed mappings were introduced, BCI performance was impaired (representative sessions: Figs. 2a and 2b, first gray vertical band). Performance improved for the within-manifold perturbation (Fig. 2a), showing that the animal learned to control the cursor under that mapping. In contrast, performance remained impaired for the outside-manifold perturbation (Fig. 2b), showing that learning did not occur. To compare learning across sessions, we quantified the extent to which BCI performance recovered to the level attained while using the intuitive mapping (Fig. 2c). For within-manifold perturbations, the animals regained proficient control of the cursor (red histograms in Fig. 2d and Extended Data Fig. 2), indicating that they could learn new associations between natural co-modulation patterns and cursor kinematics. For outside-manifold perturbations, BCI performance remained impaired (blue histograms in Fig. 2d and Extended Data Fig. 2), indicating that it was difficult to learn to generate new co-modulation patterns, even when those patterns would have led to improved performance in the task. These results support our hypothesis that the structure of a network determines which patterns of neural activity (and corresponding behaviors) a subject can readily learn to generate.
Figure 2. Greater learning for within-manifold perturbations than outside-manifold perturbations.
a,b Task performance during one representative within-manifold perturbation session (a) and one representative outside-manifold perturbation session (b). Black trace: success rate. Green trace: target acquisition time. Dashed vertical lines indicate when the BCI mapping changed. Gray vertical bands: 50-trial bins used to determine initial (red and blue ●) and best (red and blue ∗) performance with the perturbed mapping. c, Quantifying the amount of learning. Black ●: performance with the intuitive mapping. Red and blue ●: performance (success rate and acquisition time relative to performance with intuitive mapping) just after the perturbation was introduced for sessions in Fig. 2a and Fig. 2b. Red and blue ∗: best performance during those perturbation sessions. Dashed line: max. learning vector for the session in Fig. 2a. The amount of learning for each session is the length of the raw learning vector projected onto the max. learning vector, normalized by the length of the max. learning vector. A value of 1 indicates complete learning of the relationship between neural activity and kinematics, and 0 indicates no learning. d, Amount of learning for all sessions. Learning is significantly greater for within-manifold perturbations (red, n = 28 (monkey J), 14 (monkey L)) than for outside-manifold perturbations (blue, n = 39 (monkey J), 15 (monkey L)). Arrows indicate the sessions shown in Fig. 2a (red) and Fig. 2b (blue). Dashed lines: means of distributions. Solid lines: mean +/− SEM. p-values: two-sided t-tests.
Two additional lines of evidence show that within-manifold perturbations were more learnable than outside-manifold perturbations. First, perturbation types differed in their aftereffects (Extended Data Fig. 3). After a lengthy exposure to the perturbed mapping, we again presented the intuitive mapping (following the second dashed vertical line in Figs. 2a and 2b). Following within-manifold perturbations, performance was impaired briefly, indicating that learning had occurred17. Following outside-manifold perturbations, performance was not impaired, which is consistent with little, if any, learning. Second, the difference in learnability between the two types of perturbation was present from the earliest sessions, and over the course of the study the monkeys did not improve at learning (Extended Data Fig. 4).
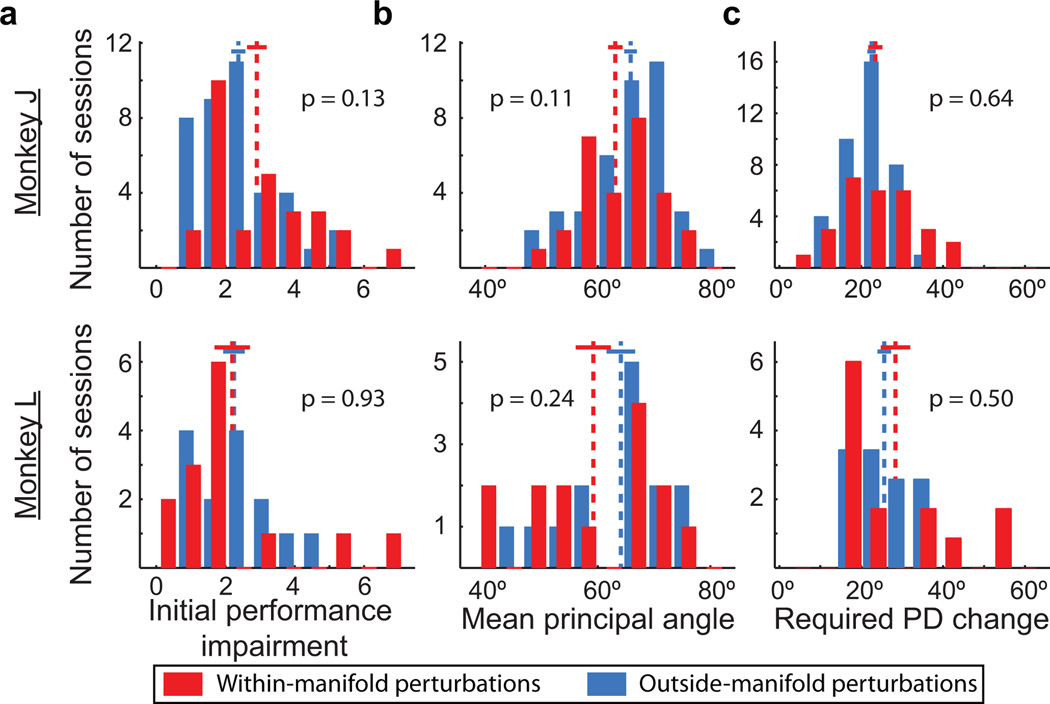
These results show that the IM was a reliable predictor of the learnability of a BCI mapping: new BCI mappings that were within the IM were more learnable than those outside of it. We considered five alternative explanations for the difference in learnability. First, we considered whether mappings that were more difficult to use at first might be more difficult to learn. We ensured that the initial performance impairments were equivalent for the two perturbation types (Fig. 3a).
Figure 3. Alternative explanations do not explain the difference in learnability between the two types of perturbation.
a, Performance impairment immediately following within-manifold perturbations (red) and outside-manifold perturbations (blue). Dashed lines: means of distributions. Solid lines: mean +/− SEM. b, Mean principal angles between intuitive and perturbed mappings. c, Mean required change in preferred direction (PD) for individual neural units. All panels: p-values are for two-sided t-tests; same number of sessions as in Fig. 2d.
Second, we posited that the animals must search through neural space for the new control space following the perturbation. If the control spaces for one type of perturbation tended to be farther from the intuitive control space, then they might be harder to find, and thus, learning would be reduced. We ensured that the angles between the intuitive and perturbed control spaces did not differ between the two perturbation types (Fig. 3b). Incidentally, Fig. 3b also shows that the perturbations were not pure workspace rotations because in that case, the angles between control spaces would have been zero.
Third, we considered how much of an impact the perturbations exerted on the tuning of neural units. Learning is manifested (at least in part) as changes in the preferred direction (PD) of individual neurons7,18. If learning one type of perturbation required larger changes in PDs, then those perturbations might be harder to learn. We predicted the changes in PDs that would be required to learn each perturbation while minimizing changes in firing rates. We ensured that learning the two perturbation types required comparable PD changes (Fig. 3c). Fourth, for one monkey (L), we ensured that the sizes of the search spaces for finding a strategy to proficiently control the cursor were the same for both perturbation types (see Methods: Choosing a perturbed mapping). Fifth, hand movements were comparable and nearly non-existent for both perturbation types (Extended Data Fig. 5).
We conclude from these analyses that the parsimonious explanation for BCI learning is whether or not the new control space is within the IM. These alternative explanations did reveal interesting secondary aspects of the data: the explanations partially explained within-category differences in learnability, albeit in an idiosyncratic manner between the two monkeys (Extended Data Fig. 6).
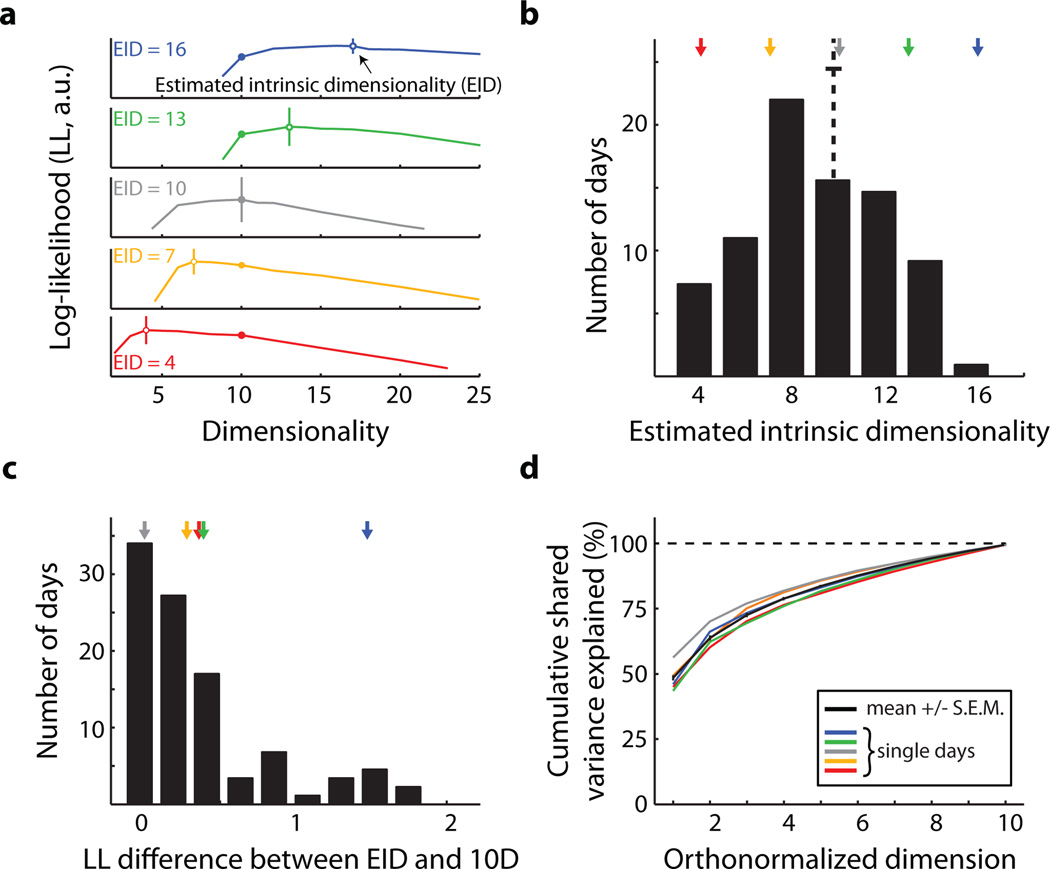
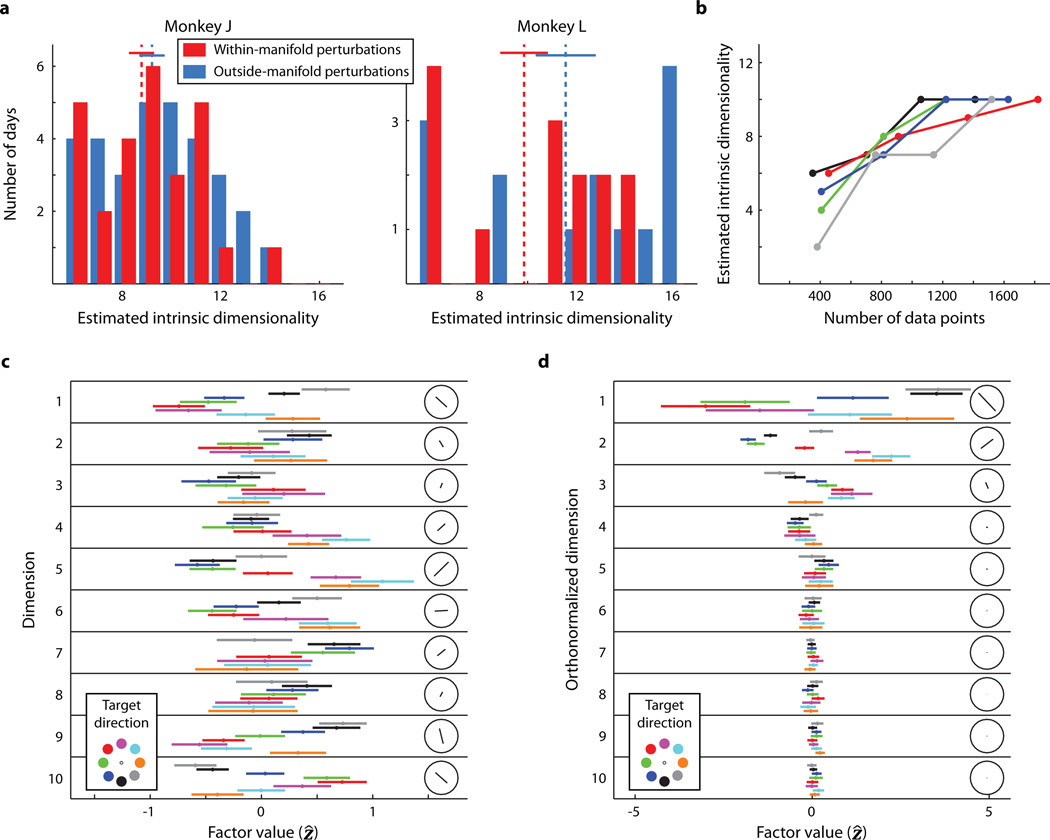
A key step in these experiments is the identification of an IM using dimensionality reduction11. Although our estimate of the IM can depend on several methodological factors (see Extended Data Fig. 7 caption), the critical property of an IM is that it captures the prominent patterns of co-modulation among the recorded neurons, which presumably reflect underlying network constraints. For consistency, we estimated a linear, 10-dimensional IM each day. Post hoc, we considered whether our choice of 10 dimensions had been appropriate (Fig. 4). We estimated the intrinsic dimensionality of the neural activity for each day (Fig. 4a). The average dimensionality was about 10 (Fig. 4b). Even though the estimated dimensionalities ranged from 4 to 16, the selection of 10 dimensions still provided a model that was nearly as good as the best model (Fig. 4c). Because the top few dimensions captured the majority of the co-modulation among the neural units (Fig. 4d), we likely could have selected a different dimensionality within the range of near-optimal dimensionalities and still attained similar results (see Extended Data Fig. 7 caption). We note that we cannot make claims about the 'true' dimensionality of M1 in part because it likely depends on considerations such as the behaviors the animal is performing and perhaps its level of skill.
Figure 4. Properties of the intrinsic manifold.
a, Cross-validated log-likelihoods (LL) of the population activity for different days. The peaks (○) indicate the estimated intrinsic dimensionality (EID). Vertical bars indicate the standard error of LL, computed across 4 cross-validation folds. We always used a 10-dimensional IM for the experiments (●). b, EID across all days and both monkeys (mean +/− SEM: 9.81 +/− 0.31). c, Difference between the LL for the 10-dimensional model and the EID model. Units are the number of standard errors of LL for the EID model. For 89% (78/88) of the days, the LL for the 10-dimensional model was within 1 standard error of the EID model. All sessions were less than 2 standard errors away. d, Cumulative shared variance explained by the 10-dimensional IM used during the experiment. Colored curves correspond to the experimental days shown in Fig. 4a. The black curve shows the mean +/− SEM across all days (n = 88; monkey J: 58, monkey L: 30).
Sensory-motor learning likely encompasses a variety of neural mechanisms, operating at diverse timescales and levels of organization. We posit that learning a within-manifold perturbation harnesses the fast-timescale learning mechanisms that underlie adaptation19, whereas learning an outside-manifold perturbation engages the neural mechanisms required for skill learning20,21. This suggests that learning outside-manifold perturbations could benefit from multi-day exposure5,22. Such learning might require the IM to expand or change orientation.
Other studies have employed dimensionality-reduction techniques to interpret how networks of neurons encode information11–16 and change their activity during learning23,24. Our findings strengthen those discoveries by showing that low-dimensional projections of neural data are not only visualization tools – they can reveal causal constraints on the activity expressed by networks of neurons. Our study also indicates that the low-dimensional patterns present among a population of neurons may better reflect the elemental units of volitional control than do individual neurons.
In summary, a BCI paradigm enabled us to reveal neural constraints on learning. The principles we observed may govern other forms of learning4,25–28 and perhaps even cognitive processes. For example, combinatorial creativity29, which involves re-combining cognitive elements in new ways, might involve the generation of new neural activity patterns that are within the IM of relevant brain areas. Transformational creativity, which creates new cognitive elements, may result from generating neural activity patterns outside of the relevant IM. More broadly, our results help to provide a neural explanation for the balance we possess between adaptability and persistence in our actions and thoughts30.
Methods
Electrophysiology and behavioral monitoring
We recorded from the proximal arm region of the primary motor cortex (M1) in two male Rhesus monkeys (Macaca mulatta, aged 7 and 8 years) using 96-channel microelectrode arrays (Blackrock Microsystems, Salt Lake City, UT, USA) as the monkeys sat head-fixed in a primate chair. All animal handling procedures were approved by the University of Pittsburgh Institutional Animal Care and Use Committee. At the beginning of each session, we estimated the RMS voltage of the signal on each electrode while the monkeys sat calmly in a darkened room. We then set the spike threshold at 3.0 times the RMS value for each channel. Spike counts used for BCI control were determined from the times at which the voltage crossed this threshold. Hereafter, one neural unit corresponds to the threshold crossings recorded on one electrode. We used 85 – 91 neural units each day. We did not use an electrode if the threshold crossing waveforms did not resemble action potentials or if the electrode was electrically shorted to another electrode. The data were recorded approximately 19 – 24 months after array implantation from Monkey J and approximately 8 – 9 months after array implantation for Monkey L.
We monitored hand movements using an LED marker (PhaseSpace, Inc., San Leadro, CA, USA) on the hand contralateral to the recording array. The monkeys' arms were loosely restrained. The monkeys could have moved their forearms by approximately 5 cm off of their arm rests, and there were no restrictions on wrist movement. The hand movements during the BCI trials were minimal, and we observed that the monkeys' movements did not approach the limits of the restraints. Extended Data Fig. 5a shows the average hand speed during the BCI trials. For comparison, Extended Data Fig. 15b shows the average hand speed during a standard point-to-point reaching task. We also recorded the monkeys' eye gaze direction (SR Research Ltd, Ottawa, ON, Canada). Those data are not analyzed here.
Task flow
Each day began with a calibration block during which we determined the parameters of the intuitive mapping. The monkeys then used the intuitive mapping for 400 trials (monkey J) or 250 trials (monkey L) during the baseline block. We then switched to the perturbed mapping for 600 trials (monkey J) or 400 trials (monkey L) for the perturbation block. This was followed by 200-trial washout block with the intuitive mapping. Together, the perturbation and washout blocks comprised a perturbation session. The transitions between blocks were made seamlessly, without an additional delay between trials. We gave the monkey no indication which type of perturbation would be presented. On most days, we completed one perturbation session (monkey J: 50/58 days, monkey L: 29/30 days). On nine days, we completed multiple perturbation sessions.
Experimental sessions
We conducted 78 (30 within-manifold perturbations; 48 outside-manifold perturbations) sessions with monkey J. We conducted 31 sessions (16 within-manifold perturbations; 15 outside-manifold perturbations) with monkey L. For both monkeys, we did not analyze a session if the monkey attempted fewer than 100 trials with the perturbed mapping. For monkey J, we did not analyze 11 sessions (2 within-manifold perturbations; 9 outside-manifold perturbations). For monkey L, we did not analyze 3 sessions (2 within-manifold perturbation; 1 outside-manifold perturbation).
BCI calibration procedures
Each day began with a calibration block of trials. The data that we recorded during these blocks were used to estimate the intrinsic manifold and to calibrate the parameters of the intuitive mappings. For Monkey J, we used two calibration methods (only one on a given day), and for Monkey L, we used one method for all days.
The following describes the BCI calibration procedures for monkey J. The first method for this monkey relied on the neural signals being fairly stable across days. At the beginning of each day, the monkey was typically able to control the cursor proficiently using the previous day's intuitive mapping. We collected data for calibration by having the monkey use the previous day's intuitive mapping for 80 trials (10 per target).
We designed the second method because we were concerned about the potential for carry-over effects across days. This method relied on passive observation of cursor movement31. The monkey observed the cursor automatically complete the center-out task for 80 trials (10 per target). At the beginning of each trial, the cursor appeared in the center of the monkey's workspace for 300 ms. Then, the cursor moved at a constant velocity (0.15 m/s) to the pseudo-randomly chosen target for each trial. When the cursor reached the target, the monkey received a juice reward. After each trial, there was a blank screen for 200 ms before the next trial.
For both methods for monkey J, we used the neural activity recorded 300 ms after the start of each trial until the cursor reached the peripheral target for BCI calibration.
The following describes the BCI calibration procedure for monkey L. We observed that neural activity for this monkey was not as stable from day to day as it was for monkey J. As a result, we could not use the calibration procedure relying on the previous day's intuitive mapping. Additionally, the observation-based calibration procedure was not as effective at generating an intuitive decoder for monkey L as it had been for monkey J. Therefore, we utilized a closed-loop calibration procedure of the type utilized by Velliste and colleagues32 to generate the intuitive decoder. The procedure began with 16 trials (2 to each target) of the observation task. We calibrated a decoder from these 16 trials in the same manner as the first method for monkey J. We then switched to the BCI center-out task, and the monkey controlled the velocity of the cursor using the decoder calibrated on the 16 observation trials. We restricted movement of the cursor so that it moved in a straight line towards the target (i.e., any cursor movement perpendicular to the straight path to the target was scaled by a factor of 0). After 8 trials (1 to each target), we calibrated another decoder from those 8 trials. The monkey then controlled the cursor for 8 more trials with this newly calibrated decoder with perpendicular movements scaled by a factor of 0.125. We then calibrated a new decoder using all 16 closed-loop trials. We repeated this procedure over a total of 80 trials until the monkey was in full control of the cursor (perpendicular velocity scale factor = 1). We calibrated the intuitive mapping using the 80 trials during which the monkey had full or partial control of the cursor. For each of those trials, we used the neural activity recorded 300 ms after the start of the trial until the cursor reached the peripheral target.
BCI center-out task
The same closed-loop BCI control task was used during the baseline, perturbation, and washout blocks. At the beginning of each trial, the cursor (circle, radius = 18 mm) appeared in the center of the workspace. One of eight possible peripheral targets (chosen pseudorandomly) was presented (circle; radius = 20mm, 150 mm (monkey J) or 125 mm (monkey L) from center of workspace, separated by 45°). A 300 ms freeze period ensued, during which the cursor did not move. After the freeze period, the velocity of the cursor was controlled by the monkey through the BCI mapping. The monkey had 7500 ms to move the cursor into the peripheral target. If the cursor acquired the peripheral target within the time limit, the monkey received a juice reward. After 200 ms, the next trial began. With the intuitive mappings, the monkeys' movement times were near 1000 ms (Extended Data Fig. 1), but the monkeys sometimes exceeded the 7500 ms acquisition time limit with the perturbed mappings. If the cursor did not acquire the target within the time limit, there was a 1500 ms timeout before the start of the next trial.
Estimation of intrinsic manifold
We identified the intrinsic manifold (IM) from the population activity recorded during the calibration session using the dimensionality reduction technique factor analysis (FA)33,34. The central idea is to describe the high-dimensional population activity (u) in terms of a low-dimensional set of factors (Z). Formally, this can be written as:
| (1) |
| (2) |
where u ∈ ℝq×1 is a vector of z-scored spike counts taken in non-overlapping 45 ms bins across the q neural units, and Z ∈ ℝ10×1 contains the 10 factors. The z-scoring was performed separately for each neural unit. The IM is defined as the column space of Λ. Each factor, or latent dimension, is represented by a column of Λ. We estimated Λ, μ, and ψ using the EM algorithm. The data collected during the calibration sessions had 1470 +/− 325 (monkey J, mean +/− standard deviation) and 1379 +/− 157 (monkey L) samples.
Intuitive Mappings
The intuitive mapping was a modified version of the standard Kalman filter35. A key component of the experimental design was to use the Kalman filter to relate factors (Z) to cursor kinematics rather than to relate neural activity directly to the cursor kinematics. This modification allowed us to perform the two different types of perturbation. We observed that performance with our modified Kalman filter is qualitatively similar to performance with a standard Kalman filter (data not shown).
The first step in the construction of the intuitive mapping was to estimate the factors using FA (equations 1 and 2). For each z-scored spike count vector ut, we computed the posterior mean of the factors Ẑt = E[Zt|ut]. We then z-scored each factor (i.e., each element of Ẑt) separately.
The second step was to estimate the horizontal and vertical velocity of the cursor from the z-scored factors using a Kalman filter:
| (3) |
| (4) |
where xt ∈ ℝ2×1 is a vector of horizontal and vertical cursor velocity at timestep t. We fit the parameters A, b, Q, C, d, and R using maximum likelihood by relating the factors to an estimate of the monkeys' intended velocity during the calibration sessions. At each timepoint, this intended velocity vector either pointed straight from the current cursor position to the target with a speed equal to the current cursor speed36 (monkey J, first calibration task) or pointed straight from the center of the workspace to the target with a constant speed (0.15 m/s, monkey L and monkey J, second calibration task).
Because spike counts were z-scored prior to FA, μ = 0. Because factors were z-scored prior to decoding into cursor velocity, d = 0. Because calibration kinematics are centered about the center of the workspace, b = 0.
The decoded velocity that was used to move the cursor at timestep t was . We can express x̂t in terms of the decoded velocity at the previous timestep x̂t−1 and the current z-scored spike count vector ut:
| (5) |
| (6) |
| (7) |
| (8) |
As part of the procedure for z-scoring factors, ΣZ is a diagonal matrix where the (p, p) element is the inverse of the standard deviation of the pth factor. K is the steady-state Kalman gain matrix. We z-scored the spike counts and the factors in the intuitive mappings so that the perturbed mappings (which were based on the intuitive mappings) would not require a neural unit to fire outside of its observed spike count range.
Perturbed mappings
The perturbed mappings were modified versions of the intuitive mapping. Within-manifold perturbations altered the relationship between factors and cursor kinematics. The elements of the vector Ẑt were permuted before being passed into the Kalman filter (red arrows, Fig. 1b). This preserves the relationship between neural units and the IM, but changes the relationship between dimensions of the IM and cursor velocity. Geometrically, this corresponds to re-orienting the control space within the intrinsic manifold.
The following equations describe within-manifold perturbations:
| (9) |
| (10) |
where ηWM is a 10 × 10 permutation matrix defining the within-manifold perturbation (i.e., the within-manifold perturbation matrix). Each element of a permutation matrix is either 0 or 1. In each column and in each row of a permutation matrix, one element is 1, and the other elements are 0. In other words, ηWMΣZβut is a permuted version of ΣZβut.
Outside-manifold perturbations altered the relationship between neural units and factors. The elements of ut were permuted before being passed into the FA model (blue arrows, Fig. 1b). This preserves the relationship between factors and cursor velocity, but changes the relationship between neurons and factors. Geometrically, this corresponds to re-orienting the control space within the neural space and outside of the IM.
The following equations describe outside-manifold perturbations:
| (11) |
| (12) |
where ηOM is a q × q permutation matrix defining the outside-manifold perturbation (i.e., the outside-manifold perturbation matrix). In other words, ηOMut is a permuted version of ut.
Choosing a perturbed mapping
We used data from the first 200 trials (monkey J) or 150 trials (monkey L) of closed-loop control during the baseline blocks to determine the perturbation matrix that we would use for the session. The procedure we used had three steps (detailed below). First, we defined a set of candidate perturbations. Second, we predicted the open-loop cursor velocities for each candidate perturbation. Third, we selected one candidate perturbation. We aimed to choose a perturbation such that the perturbed mapping would not be too difficult for the monkeys to use nor so easy that no learning was needed to achieve proficient performance.
For monkey J, we often alternated perturbation types across consecutive days. For monkey L, we determined which type of perturbation we would use each day prior to the first experiment. That order was set randomly by a computer. We did this in order to avoid a detectable pattern of perturbation types.
The following describes the first step in choosing a perturbed mapping: defining the candidate perturbations. For within-manifold perturbations, ηWM is a 10 × 10 permutation matrix. The total number possible ηWM is 10 factorial (3,628,800). We considered all of these candidate within-manifold perturbations.
For outside-manifold perturbations, ηOM is a q × q permutation matrix, where q is the number of neural units. For a population of 90 neural units, there are 90 factorial (> 10100) possible values of ηOM. Due to computational constraints, we were unable to consider every possible ηOM as a candidate perturbation. We used slightly different procedures to determine the candidate outside-manifold perturbations for the two monkeys.
The procedure we used for monkey J is as follows. We permuted the neural units independently. We chose to permute only the neural units with the largest modulation depths (mean number of units permuted: 39 +/− 18). Permuting the units with larger modulation depths impacted the monkey's ability to proficiently control the cursor more than would permuting units with smaller modulation depths. For each session, we randomly chose 6 million ηOM that permuted only the specified units. This formed the set of candidate outside-manifold perturbations.
The procedure we used for monkey L is as follows. To motivate it, note that for monkey J, the two perturbation types altered the intuitive mapping control space within a different number of dimensions of the neural space. Within-manifold perturbations were confined to 10 dimensions of the neural space, but outside-manifold perturbations were confined to N dimensions of the neural space (where N is the number of permuted units; 39 on average). Thus, the dimensionality of the search space for the perturbed mappings was larger for the outside-manifold perturbations than for the within-manifold perturbations. We recognized that this difference may have affected the monkey's ability to learn outside-manifold perturbations. For monkey L, we equalized the size of the search space for the two perturbation types. We did this by constraining ηOM so that the number of possible ηOM was equal to the number of candidate within-manifold perturbations. We then considered all ηOM to be candidate outside-manifold perturbations. To construct outside-manifold perturbations, we assigned each neural unit to one of eleven groups. The first 10 groups had an equal number of neural units. The eleventh group had the remaining neural units. We specifically put the neural units with the lowest modulation depths in the eleventh group. The 10m (where m is the number of neural units per group) neural units with the highest modulation depths were randomly assigned to the first 10 groups. We created outside-manifold perturbations by permuting the first 10 groups, keeping all the neural units within a group together. Thus, the number of possible ηOM is 10 factorial, all of which were considered as candidate outside-manifold perturbations. We did not alter the procedure for defining candidate within-manifold perturbations.
We attempted to keep these groupings as constant as possible across days. On some days, one electrode would become unusable (relative to the previous day) as evident from the threshold crossing waveforms. When this occurred, we kept all of groupings fixed that did not involve that electrode. If an electrode in one of the first ten groups became unusable, we would substitute it with a neural unit from the eleventh group.
The following describes the second step in choosing a perturbed mapping: estimating the open-loop velocities of each candidate perturbation. The open-loop velocity measurement captures how the neural activity updates the velocity of the cursor from the previous time step, whereas the closed-loop decoder (equation 5) includes contributions from the decoded velocity at the previous time step (M1x̂t−1) and from the neural activity at the current time step (M2ut). To compute the open-loop velocity, we first computed the average z-scored spike counts of every neural unit in the first 200 (monkey J) or 150 (monkey L) trials of the baseline block. We binned the spike counts from 300 ms to 1300 ms (monkey J) or 1100 ms (monkey L) after the beginning of each trial, and then averaged the spike counts for all trials to the same target. Together, these comprised 8 spike count vectors (one per target). For each of the spike count vectors, we computed the open-loop velocity for the candidate perturbations:
| (13) |
where is the mean z-scored spike count vector for the ith target. M2,P is M2,WM for within-manifold perturbations and M2,OM for outside-manifold perturbations.
The following describes the third step in choosing a perturbation: selecting a candidate perturbation. For each candidate perturbation, we compared the open-loop velocities under the perturbed mapping to the open-loop velocities under the intuitive mapping on a per target basis. We needed the velocities to be dissimilar (to induce learning) but not so different that the animal could not control the cursor. We measured the angles between the 2D open-loop velocity vectors. We also measured the magnitude of the open-loop velocity for the perturbed mapping. For each session, we defined a range of angles (average minimum of range across sessions: 19.7° +/− 7.0°; average maximum of range across sessions: 44.4° +/− 8.9°) and a range of velocity magnitudes (average minimum of range across sessions: 0.7 mm/s +/− 0.4 mm/s; average maximum of range across sessions: 5.5 mm/s +/− 4.0 mm/s). Note that when the monkey controlled the cursor in closed-loop (equation 5), the cursor speeds were much greater than these ranges of open-loop velocities. This is because M1 was nearly an identity matrix for our experiments. Thus, the term M1x̂t−1 is expected to be larger than the term M2ut. We found all candidate perturbations for which the angles and magnitudes for all targets were within the designated ranges. From the candidate perturbations that remained after applying these criteria, we arbitrarily chose one to use as the perturbation for that session.
Amount of learning
This section corresponds to Fig. 2c. For each session, we computed the amount of learning during perturbation blocks as a single, scalar value that incorporated both changes in success rate (percent of trials on which the peripheral target was acquired successfully) and target acquisition time. We sought to use a metric that captured how much the monkeys' performance improved throughout the perturbation block relative to how much it was impaired at the beginning of the perturbation block. Having a single value for each session allowed us to more easily compare learning across sessions and to relate the amount of learning to a variety of properties of each perturbation (Extended Data Fig. 6). We also analyzed each performance criterion individually for each monkey without any normalization (Extended Data Fig. 2). We saw consistent differences in learnability. Thus, our results do not rely on the precise form of our learning metric, but the form provides a convenient summary metric.
Because success rate and target acquisition time are expressed in different units, we first normalized each metric. We found the mean and standard deviation of the success rates and target acquisition times across all non-overlapping 50-trial bins in the baseline, perturbation, and washout blocks for each monkey. We then z-scored the success rates and target acquisition times separately for each monkey. Fig. 2c shows normalized performance projected onto veridical units.
For each session, we computed the average z-scored success rate and the average z-scored target acquisition time across all bins in the baseline block.
| (14) |
where PB is the performance, SB is the average normalized success rate, and aB is the average normalized acquisition time during the baseline block (monkey J: 386.9 +/− 82.5 trials; monkey L: 292.1 +/− 43.5 trials).
We also computed the normalized success rates and acquisition times for all bins in the perturbation blocks.
| (15) |
where PP(j) is the performance, SP(j) is the normalized success rate, and aP(j) is the average normalized acquisition time during the jth 50-trial bin of the perturbation block.
Empirically, we observed that the monkeys' performance during the perturbation blocks did not exceed the performance during the baseline blocks. Therefore, we define a maximum learning vector (L⃗max) as a vector that extends from the performance in the first bin with the perturbed mapping to the point corresponding to baseline performance (Fig. 2c).
| (16) |
The length of this vector is the initial performance impairment because it describes the drop in performance that resulted when we switched from the baseline block to the perturbation block (shown in Fig. 3a and Extended Data Fig. 6a). For each bin (j) within the perturbation blocks, we defined a raw learning vector (L⃗raw(j)). This vector extended from the point corresponding to initial performance during the perturbation block to the point corresponding to performance during each bin.
| (17) |
We projected the raw learning vectors onto the maximum learning vector. These were termed the projected learning vectors (L⃗proj(j)).
| (18) |
The lengths of the projected learning vectors relative to the lengths of the maximum learning vectors define the amount of learning in each 50-trial bin (Lbin(j)).
| (19) |
An amount of learning of 0 indicates that the monkey did not improve performance, and a value of 1 indicates that the monkey fully improved (up to the level during the baseline block). For each session, we computed the amount of learning for all bins, and we selected the largest one as the amount of learning for that session.
| (20) |
Fig. 2c shows the raw learning vectors for one bin in each of two sessions (thick blue and red lines), along with the projected learning vector (thin red line) and the maximum learning vector (dashed gray line) for one of those sessions.
Principal angles between intuitive and perturbed control spaces
This section corresponds to Fig. 3b and Extended Data Fig. 6b. The control spaces for the intuitive and perturbed BCI mappings in our experiments were spanned by the rows of M2 for the intuitive mapping, M2,WM for within-manifold perturbations, and M2,OM for outside-manifold perturbations. Because we z-scored spike counts in advance, the control spaces for each day intersected at the origin of the neural space. The two principal angles37 between the intuitive and perturbed control spaces defined the maximum and minimum angles of separation between the control spaces (Fig. 3b).
Required preferred direction changes
This section corresponds to Fig. 3c and Extended Data Fig. 6c. One way in which learning is manifested is by changes in preferred directions of individual neurons7,18. For each session, we sought to compute the required changes in preferred direction for each neural unit that would lead to proficient control of the cursor under the perturbed mapping. One possibility would be to examine the columns of M2 and M2,P. Each column can be thought of as representing the pushing direction and pushing magnitude of one unit (i.e., the contribution of each neural unit to the velocity of the cursor). We could simply estimate the required change in preferred direction by measuring the change in pushing directions for each unit between the intuitive and perturbed mappings. However, this method is not suitable for the following reason. For outside-manifold perturbations for monkey J, we permuted only a subset of the neural units. As a result, the columns of M2,OM corresponding to the non-permuted units were the same as in M2. By estimating the required changed in preferred direction as the difference in directional components of M2 and M2,OM, we would be implicitly assuming that the monkey is capable of identifying which units we perturbed and changing only their preferred directions, which appears to be difficult to achieve in the timeframe of a few hours7. Therefore, we sought a more biologically-plausible method of computing the required preferred direction changes.
Using a minimal set of assumptions, we computed the firing rates that each unit should show under one particular learning strategy. Then, we computed the preferred direction of each unit using those firing rates and compared them to the preferred directions during the baseline block. The following were the assumptions used to compute the firing rates:
We assumed the monkeys would intend to move the cursor to each target at the same velocity it exhibited under the intuitive mapping. Fitts' Law predicts that movement speed depends on movement amplitude and target size38.
The firing rates for the perturbed mapping should be as close as possible to the firing rates we recorded when the monkeys used the intuitive mapping. This keeps the predicted firing rates within a physiological range and implies a plausible exploration strategy in neural space.
We used the following procedure to compute the required preferred direction changes. First, we found the average normalized spike count vector across timepoints (300 ms – 1000 ms after the start of the trial) and all trials to each target (i) during the baseline blocks. We minimized the Euclidian distance between and , the normalized spike count vector for the perturbed mapping (assumption 2), subject to (assumption 1). (the open-loop velocity for the intuitive mapping) is known from the baseline block. For a given perturbed mapping (with M2,P), we sought to find that would lead to the same open-loop velocity, which has a closed-form solution:
| (21) |
For each neural unit (k), we computed its preferred direction θB(k) with the intuitive mapping by fitting a standard cosine tuning model.
| (22) |
where is the kth element of , mk is the depth of modulation, bk is the model offset of unit k, and θi is the direction of the ith target. We also computed the preferred direction of each unit for the perturbed mapping (θP(k)) in the same way. Fig. 3c shows histograms of
| (23) |
averaged across all units for each session.
Estimation of intrinsic dimensionality
This section accompanies Fig. 4a–c. During all experiments, we identified a 10-dimensional IM (i.e., 10 factors). Offline, we confirmed this was a reasonable choice by estimating the intrinsic dimensionality of the data recorded in each calibration block. For each day, we performed a standard model selection procedure to compare FA models with dimensionalities ranging from 2 to 30. For each candidate dimensionality, we used 4-fold cross-validation. For each fold, we estimated the FA model parameters using 75% of the calibration data. We then computed the likelihood of the remaining 25% of the calibration data with the FA model. For each dimensionality, we averaged the likelihoods across all folds. Each day's intrinsic dimensionality was defined as the dimensionality corresponding to the largest cross-validated data likelihood of the calibration data for that day.
Measuring the cumulative shared variance explained
This section corresponds to Fig. 4d. Factor analysis partitions the sample covariance of the population activity (cov(u)) into a shared component (ΛΛT) and an independent component (ψ). In offline analyses, we sought to characterize the amount of shared variance along orthogonal directions within the intrinsic manifold (akin to measuring the lengths of the major and minor axes of an ellipse). These shared variance values are given by the eigenvalues of ΛΛT, which can be ordered from largest to smallest. Each eigenvalue corresponds to an 'orthonormalized latent dimension', which refers to identifying orthonormal axes that span the intrinsic manifold. Each orthonormalized dimension is a linear combination of the original 10 dimensions. The cumulative shared variance curve is thus informative of how 'oblong' the shared variance is within the manifold, and it can be compared across days. By definition, the cumulative shared variance explained reaches 100% using all 10 dimensions, and none of the independent variance (ψ) is explained by those latent dimensions.
Blinding
Investigator blinding was ensured because all sessions were analyzed in the same way, by the same computer program. This parallel and automatic treatment of the two perturbation types eliminated investigator biases. The animals were blinded to the test condition delivered each day. If the animals knew which of the two conditions they were presented with, that might have biased our findings. Blinding was achieved before-the-fact with a random and/or unpredictable ordering of experiments, and after-the-fact with control analyses to ensure that conditions were matched as closely as we could detect.
Statistics
For the histograms in Figs. 2d and 3, Extended Data Figs. 1b, 2, and 7a, the significances of the differences in distributions between within-manifold perturbation samples and outside-manifold perturbation samples were determined with two-tailed Student's t-tests assuming unequal variance between the samples. We ensured that each histogram followed a normal distribution (KS test). In Extended Data Figs. 1a and 3, the histograms did not follow a normal distribution (KS test). For those figures, we used the Wilcoxon rank-sum test to determine the significance of the difference in the distributions. For the linear regressions in Fig. 4 and Extended Data Figs. 4 and 6, we determined the significance level of the slopes being different from 0 using F-tests. We determined whether the difference between two slopes was significant using two-tailed Student's t-tests. For all tests, we used p = 0.05 as the significance threshold.
Extended Data
Extended Data Figure 1. Performance during baseline blocks.
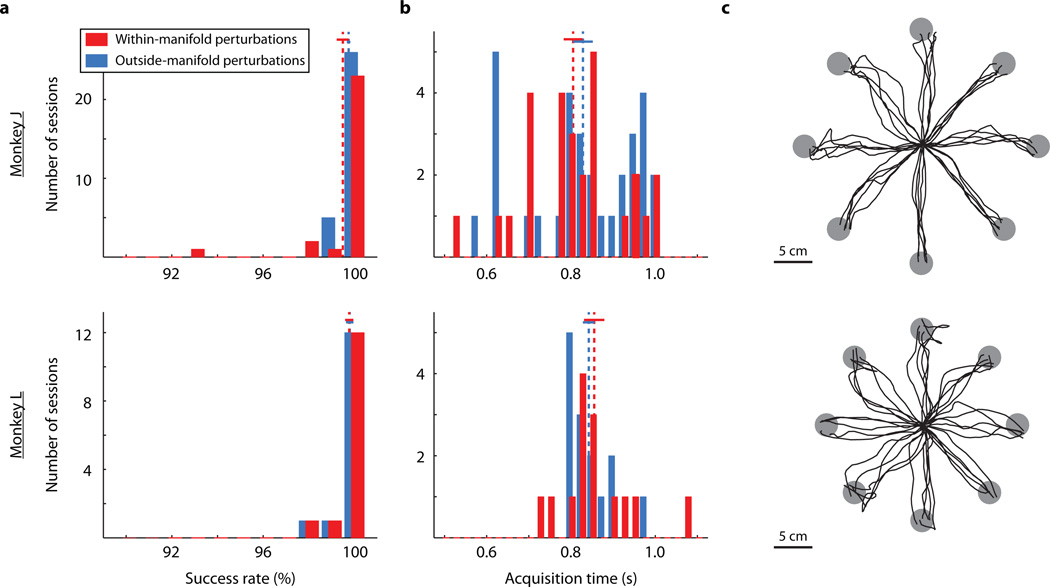
a, Histograms of success rate during the baseline blocks on days when the perturbation would later be within-manifold (red) and outside-manifold (blue) for monkey J (top) and monkey L (bottom). For days with multiple perturbation sessions, the data are colored according to the first perturbation type. Dashed lines: means of distributions. Solid lines: mean +/− SEM. b, Histograms of target acquisition time during baseline blocks. Number of days for panels a and b: within-manifold perturbations: n = 27 (monkey J), 14 (monkey L); outside-manifold perturbations: n = 31 (monkey J), 14 (monkey L) c, Sample cursor trajectories to all eight targets.
At the beginning of each day, the monkeys used the intuitive mapping for 250 – 400 trials. The monkeys were able to use these mappings to control the cursor proficiently from the outset (as measured by success rate and acquisition time). On all sessions, the success rates were near 100%, and the acquisition times were between 800 and 1000 ms. No performance metrics during the baseline blocks were significantly different between within-manifold perturbation sessions and outside-manifold perturbation sessions (p > 0.05; success rate: Wilcoxon rank-sum test, acquisition time: t-test).
Extended Data Figure 2. Changes in success rate and acquisition time during perturbation blocks.
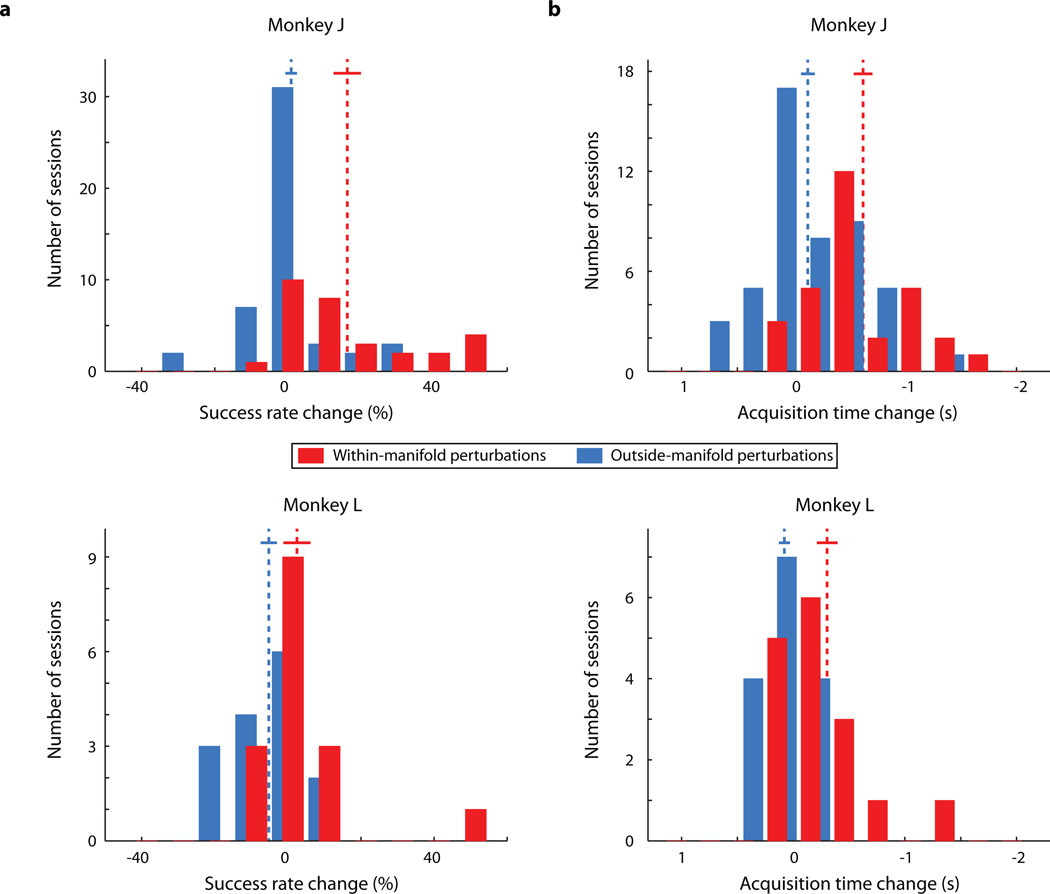
In Fig. 2d, we quantified the amount of learning in each session using a single metric that combined improvements in success rate and acquisition time. Here, we consider each metric separately. In each comparison, better performance is to the right. a, Change in success rate from the first 50-trial bin in the perturbation block to the bin with the best performance. The change in success rate was significantly greater for within-manifold perturbations than outside-manifold perturbations for monkey J (top, p < 10−3, t-test). For monkey L (bottom), the change in success rate was greater for within-manifold perturbations than for outside-manifold perturbations, and the difference approached significance (p = 0.088, t-test). b, Change in acquisition time from the first 50-trial bin in the perturbation block to the bin with the best performance. For both monkeys, the change in acquisition time for within-manifold perturbations was significantly greater than for outside-manifold perturbations (monkey J (top): p < 10−4, t-test; monkey L (bottom): p = 0.0014, t-test). Note that an acquisition time change less than 0 indicates performance improvement (i.e., targets were acquired faster). Number of within-manifold perturbations: n = 28 (monkey J), 14 (monkey L); outside-manifold perturbations: n = 39 (monkey J), 15 (monkey L)
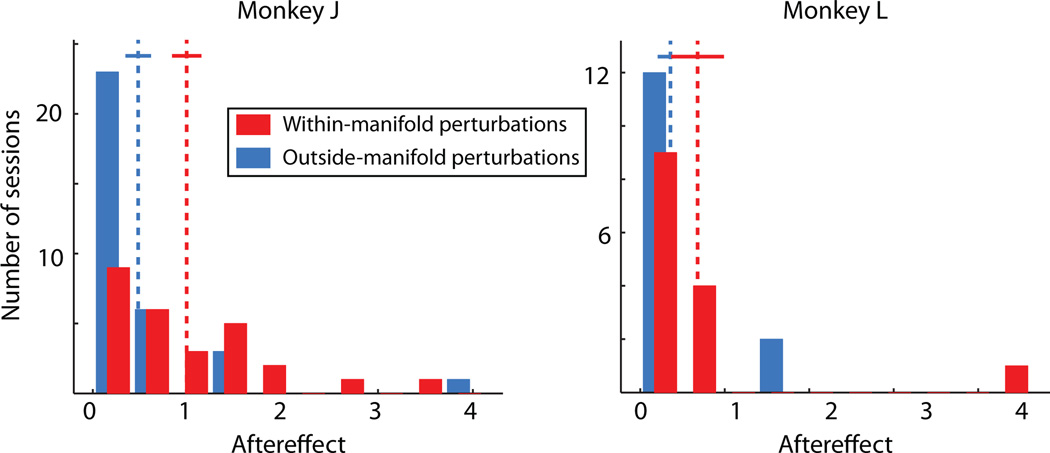
Extended Data Figure 3. Aftereffects during washout blocks.
After 600 (monkey J) or 400 (monkey L) trials using the perturbed mapping, we re-introduced the intuitive mapping to observe any aftereffects of learning. We measured the aftereffect as the size of the performance impairment at the beginning of the washout block in the same way that we measured the performance impairment at the beginning of the perturbation block. A larger aftereffect indicates more learning had occurred in response to the perturbation. For monkey J (left), the aftereffect was significantly larger for within-manifold perturbations (red) than for outside-manifold perturbations (blue) (Wilcoxon rank-sum test, p < 10−3). For monkey L (right), the trend is in the same direction as monkey J, but the effect did not achieve significance (Wilcoxon rank-sum test, p > 0.05). These data are consistent with the hypothesis that relatively little learning occurred during the outside-manifold perturbations in comparison to the within-manifold perturbations. Number of within-manifold perturbations: n = 27 (monkey J), 14 (monkey L); outside-manifold perturbations: n = 33 (monkey J), 15 (monkey L)
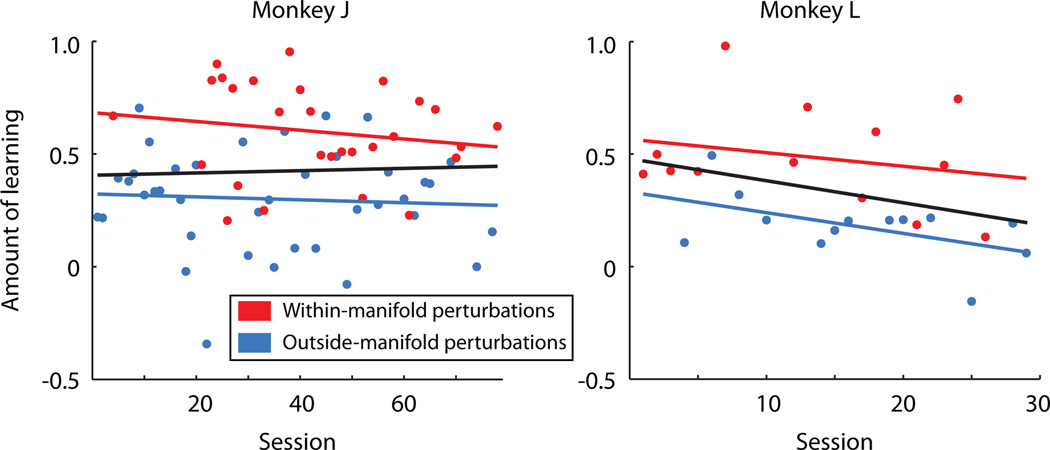
Extended Data Figure 4. Learning did not improve over sessions.
It might have been that, over the course of weeks and months, the animals improved at learning to use perturbed mappings, either one type or both types together. This did not occur. Within-manifold perturbations showed more learning than outside-manifold perturbations across the duration of experiments. Animals did not get better at learning to use either type of perturbation separately (red and blue regression lines, F-test, p > 0.05 for all relationships) nor when considering all sessions together (black regression line, F-test, p > 0.05). Same number of sessions as in Extended Data Fig. 2. Each point corresponds to one session.
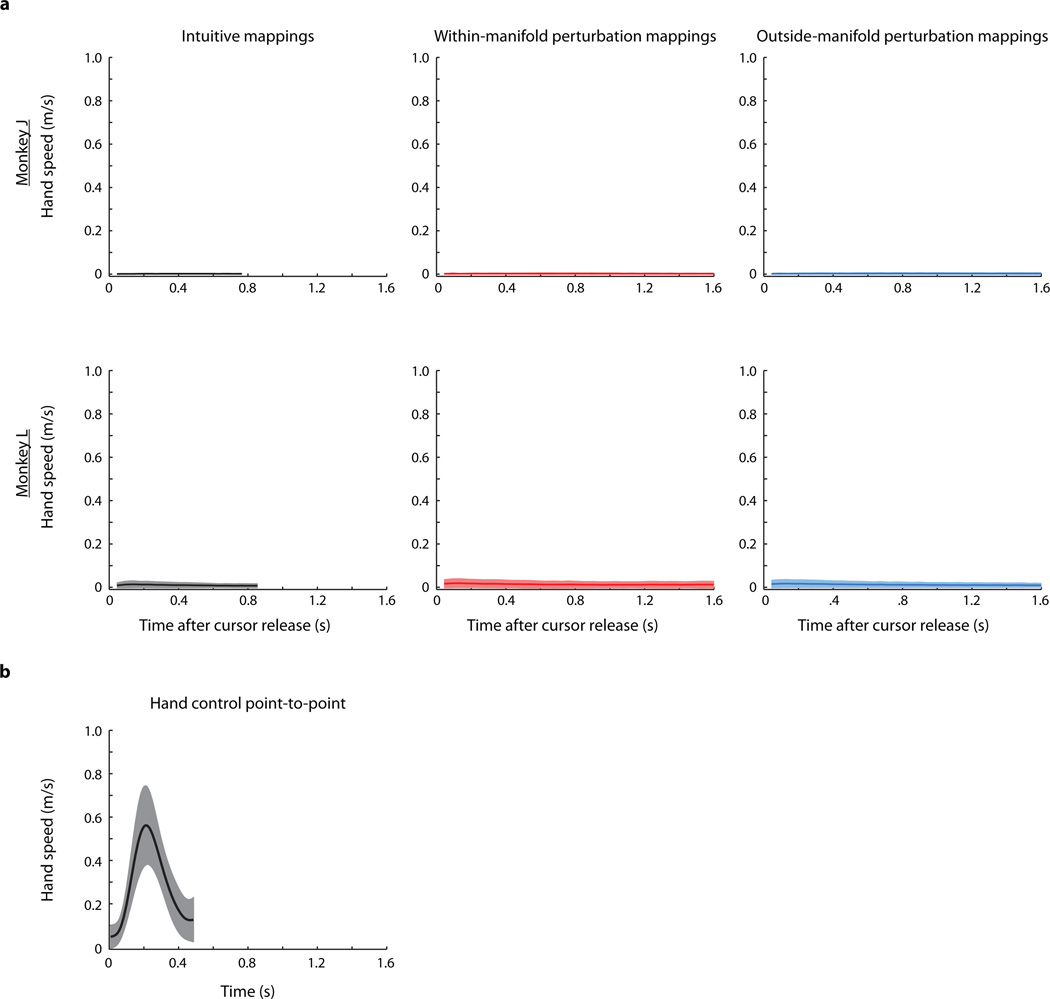
Extended Data Figure 5. Hand speeds during BCI control and hand control.
We loosely restrained the monkeys' arms to the chair's armrest during experiments. The monkeys minimally moved their hands, but the movements did not approach the limits of the restraints. a, Average hand speeds across all trials in all sessions for the baseline blocks (left column), within-manifold perturbation blocks (middle column), and outside-manifold perturbation blocks (right column) for monkey J (top row) and monkey L (bottom row). b, Average hand speed during a typical point-to-point reaching task (monkey L). Thus, the hand movements for the BCI tasks are substantially smaller than for the reaching task.
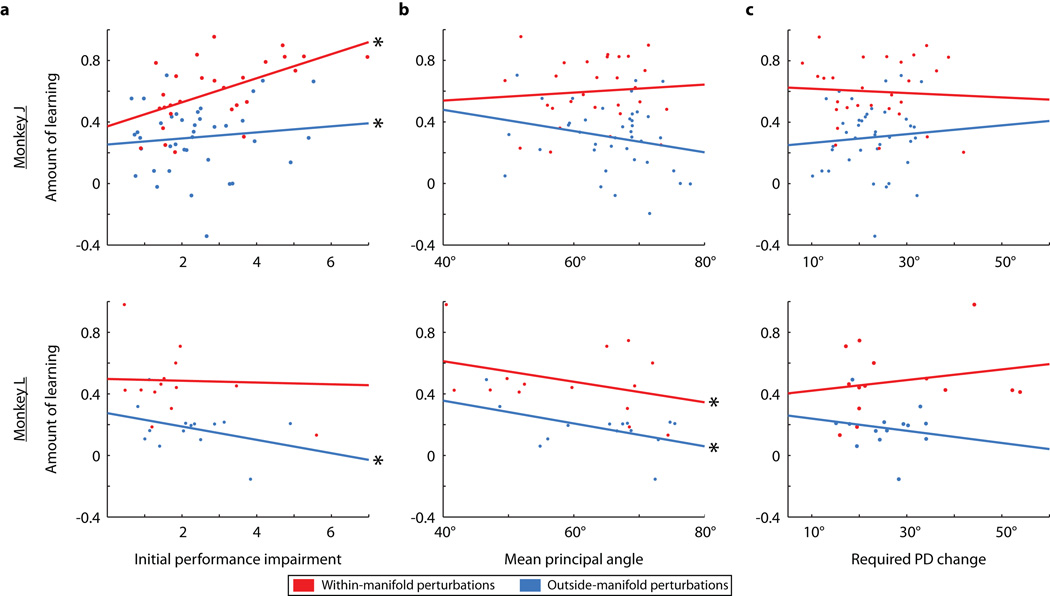
Extended Data Figure 6. Accounting for within-class differences in learning.
a, Relation between amount of learning and initial impairment in performance for monkey J (top) and monkey L (bottom). Each point corresponds to one session. Lines are linear regressions for the within-manifold perturbations and outside-manifold perturbations. ∗: slope significantly different than 0 (F-test, p < 0.05). b, Relation between amount of learning and mean principal angles between control spaces for perturbed and intuitive mappings. c, Relation between amount of learning and mean required PD change. Same number of sessions as in Extended Data Fig. 2.
Fig. 3 showed that the properties of the perturbed mappings (other than whether their control spaces were within or outside the IM) could not account for differences in learning between the two types of perturbation. However, as is evident in Fig. 2d, within each type of perturbation, there was a range in the amount of learning, including some outside-manifold perturbations that were learnable5,7. In this figure, we examined whether learning within each perturbation type could be accounted for by considering other properties of the perturbed mapping. We regressed the amount of learning within each perturbation type against the various properties we considered in Fig. 3. Panel a shows the initial performance impairment could explain a portion of the variability of learning within both classes of perturbation for monkey J. That monkey showed more learning on sessions when the initial performance impairment was larger. For monkey L, the initial performance impairment could account for a portion of the within-class variation in learning only for outside-manifold perturbations; this monkey showed less learning when the initial performance impairment was larger. We speculate that monkey J was motivated by more difficult perturbations while monkey L could be frustrated by more difficult perturbations. Panel b shows that the mean principal angles between control planes were related to learning within each class of perturbation for monkey L only. Larger mean principal angles between the control planes led to less learning. Panel c shows that the required PD changes were not related to learning for either type of perturbation for both monkeys. This makes the important point that we were unable to account for the amount of learning by studying each neural unit individually.
Extended Data Figure 7. Offline analyses of intrinsic manifold properties.
a, The intrinsic dimensionalities for all sessions for monkey J (left) and monkey L (right). For both monkeys, the intrinsic dimensionalities were not significantly different between days when we performed within-manifold perturbations and days when we performed outside-manifold perturbations (t-test, p > 0.05). Dashed lines: means of distributions. Solid lines: mean +/− SEM. Same number of days as in Extended Data Fig. 1. b, Relation between intrinsic dimensionality and the number of data points used to compute intrinsic dimensionality. For each of 5 days (one curve per day), we computed the intrinsic dimensionality using 25%, 50%, 75%, and 100% of the total number of data points recorded during the calibration block. As the number of data points increased, our estimate of the intrinsic dimensionality increased in a saturating manner. c, Tuning of the raw factors. These plots exhibit the factors that were shuffled during within-manifold perturbations. We show for one typical day the average factors (Ẑ) corresponding to the 10 dimensions of the IM over a time interval of 700 ms beginning 300 ms after the start of every trial. Within each row, the colored bars indicate the mean +/− standard deviation of the factors for each target. The line in each circular inset indicates the axis of 'preferred' and 'null' directions of the factor. The length of the axis indicates the relative depth of modulation. The tuning is along an axis (rather than in a single direction) because the sign of a given factor is arbitrary. d, Tuning of the orthonormalized factors. Same session and plotting format as c. The orthonormalized dimensions are ordered by the amount of shared variance explained, which can be seen by the variance of the factors across all targets. Note that the axes of greatest variation are separated by approximately 90° for orthonormalized dimensions 1 and 2. This property was typical across days.
The post hoc estimate of intrinsic dimensionality (Fig. 4 and Extended Data Fig. 6a) may depend on the richness of the behavioral task, the size of the training set (Extended Data Fig. 6b), the number of neurons, the dimensionality reduction method, and the criterion for assessing dimensionality. Thus, the estimated intrinsic dimensionality should only be interpreted in the context of these choices, rather than in absolute terms.
The key to the success of this experiment was capturing the prominent patterns by which the neural units covary. As shown in Fig. 4d, the top several dimensions capture the majority of the shared variance. Thus, we believe that our main results are robust to the precise number of dimensions used during the experiment. Namely, the effects would have been similar as long as we had identified at least a small handful of dimensions. Given the relative simplicity of the BCI and observation tasks, our estimated intrinsic dimensionality is likely an underestimate (i.e., a richer task may have revealed a larger set of co-modulation patterns that the circuit is capable of expressing). Even so, our results suggest that the IM estimated in the present study already captures some of the key constraints imposed by the underlying neural circuitry. The likely underestimate of intrinsic dimensionality may explain why a few ostensible outside-manifold perturbations were readily learnable (cf. Fig 2d).
It is worth noting that improperly estimating the intrinsic dimensionality would only have weakened the main result. If we had overestimated the dimensionality, then some of the ostensible within-manifold perturbations would actually have been outside-manifold perturbations. In this case, the amount of learning would tend to be erroneously low for nominal within-manifold perturbations. If we had underestimated the dimensionality, then some of the ostensible outside-manifold perturbations would actually have been within-manifold perturbations. In this case, the amount of learning would tend to be erroneously high for outside-manifold perturbations. Both types of estimation error would have decreased the measured difference in the amount of learning between within-manifold perturbation and outside-manifold perturbations.
Acknowledgements
We thank A. Barth, C. Olson, D. Sussillo, R. J. Tibshirani, and N. Urban for helpful discussions; S. Flesher for help with data collection; R. Dum for advice on array placement. This work was funded by NIH NICHD CRCNS R01-HD071686 (A.P.B. and B.M.Y.), NIH NINDS R01-NS065065 (A.P.B.), Burroughs Wellcome Fund (A.P.B.), NSF DGE-0549352 (P.T.S.), and NIH P30-NS076405 (Systems Neuroscience Institute at the University of Pittsburgh).
Footnotes
Author Contributions P.T.S., K.M.Q., M.D.G., S.M.C., B.M.Y., and A.P.B. designed the experiments. S.I.R. and E.C.T-K implanted the arrays. P.T.S. collected and analyzed the data. P.T.S., B.M.Y., and A.P.B. wrote the paper. B.M.Y. and A.P.B. contributed equally.
The authors declare no competing financial interests.
References
- 1.Krakauer JW, Mazzoni P. Human sensorimotor learning: adaptation, skill, and beyond. Curr. Opin. Neurobiol. 2011;21:636–644. doi: 10.1016/j.conb.2011.06.012. [DOI] [PubMed] [Google Scholar]
- 2.Ranganathan R, Wieser J, Mosier KM, Mussa-Ivaldi Fa, Scheidt Ra. Learning Redundant Motor Tasks with and without Overlapping Dimensions: Facilitation and Interference Effects. J. Neurosci. 2014;34:8289–8299. doi: 10.1523/JNEUROSCI.4455-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Thoroughman K, Taylor J. Rapid reshaping of human motor generalization. J. Neurosci. 2005;25:8948–8953. doi: 10.1523/JNEUROSCI.1771-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Braun D, Mehring C, Wolpert D. Structure learning in action. Behav. Brain Res. 2010;206:157–165. doi: 10.1016/j.bbr.2009.08.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ganguly K, Carmena JM. Emergence of a stable cortical map for neuroprosthetic control. PLoS Biol. 2009;7:e1000153. doi: 10.1371/journal.pbio.1000153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fetz EE. Operant Conditioning of Cortical Unit Activity. Science. 1969;163:955–958. doi: 10.1126/science.163.3870.955. [DOI] [PubMed] [Google Scholar]
- 7.Jarosiewicz B, et al. Functional network reorganization during learning in a brain-computer interface paradigm. Proc Natl Acad Sci USA. 2008;105:19486–19491. doi: 10.1073/pnas.0808113105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hwang EJ, Bailey PM, Andersen RA. Volitional Control of Neural Activity Relies on the Natural Motor Repertoire. Curr. Biol. 2013;23:1–9. doi: 10.1016/j.cub.2013.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rouse AG, Williams JJ, Wheeler JJ, Moran DW. Cortical adaptation to a chronic micro-electrocorticographic brain computer interface. J. Neurosci. 2013;33:1326–1330. doi: 10.1523/JNEUROSCI.0271-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Engelhard B, Ozeri N, Israel Z, Bergman H, Vaadia E. Inducing γ oscillations and precise spike synchrony by operant conditioning via brain-machine interface. Neuron. 2013;77:361–375. doi: 10.1016/j.neuron.2012.11.015. [DOI] [PubMed] [Google Scholar]
- 11.Cunningham JP, Yu BM. Dimensionality reduction for large-scale neural recordings. Nat. Neurosci. doi: 10.1038/nn.3776. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mazor O, Laurent G. Transient dynamics versus fixed points in odor representations by locust antennal lobe projection neurons. Neuron. 2005;48:661–673. doi: 10.1016/j.neuron.2005.09.032. [DOI] [PubMed] [Google Scholar]
- 13.Mante V, Sussillo D, Shenoy KV, Newsome WT. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature. 2013;503:78–84. doi: 10.1038/nature12742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rigotti M, et al. The importance of mixed selectivity in complex cognitive tasks. Nature. 2013;497:585–590. doi: 10.1038/nature12160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Churchland MM, et al. Neural population dynamics during reaching. Nature. 2012;487:51–56. doi: 10.1038/nature11129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Luczak A, Barthó P, Harris KD. Spontaneous events outline the realm of possible sensory responses in neocortical populations. Neuron. 2009;62:413–425. doi: 10.1016/j.neuron.2009.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Shadmehr R, Smith M, Krakauer J. Error correction, sensory prediction, and adaptation in motor control. Annu. Rev. Neurosci. 2010;33:89–108. doi: 10.1146/annurev-neuro-060909-153135. [DOI] [PubMed] [Google Scholar]
- 18.Li CS, Padoa-Schioppa C, Bizzi E. Neuronal correlates of motor performance and motor learning in the primary motor cortex of monkeys adapting to an external force field. Neuron. 2001;30:593–607. doi: 10.1016/s0896-6273(01)00301-4. [DOI] [PubMed] [Google Scholar]
- 19.Salinas E. Fast remapping of sensory stimuli onto motor actions on the basis of contextual modulation. J. Neurosci. 2004;24:1113–1118. doi: 10.1523/JNEUROSCI.4569-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Picard N, Matsuzaka Y, Strick PL. Extended practice of a motor skill is associated with reduced metabolic activity in M1. Nat. Neurosci. 2013;16 doi: 10.1038/nn.3477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rioult-Pedotti M-S, Friedman D, Donoghue JP. Learning-Induced LTP in Neocortex. Science (80-.) 2000;290:533. doi: 10.1126/science.290.5491.533. [DOI] [PubMed] [Google Scholar]
- 22.Peters AJ, Chen SX, Komiyama T. Emergence of reproducible spatiotemporal activity during motor learning. Nature. 2014;510:263–267. doi: 10.1038/nature13235. [DOI] [PubMed] [Google Scholar]
- 23.Paz R, Natan C, Boraud T, Bergman H, Vaadia E. Emerging patterns of neuronal responses in supplementary and primary motor areas during sensorimotor adaptation. J. Neurosci. 2005;25:10941–10951. doi: 10.1523/JNEUROSCI.0164-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Durstewitz D, Vittoz NM, Floresco SB, Seamans JK. Abrupt transitions between prefrontal neural ensemble states accompany behavioral transitions during rule learning. Neuron. 2010;66:438–448. doi: 10.1016/j.neuron.2010.03.029. [DOI] [PubMed] [Google Scholar]
- 25.Jeanne JM, Sharpee TO, Gentner TQ. Associative learning enhances population coding by inverting interneuronal correlation patterns. Neuron. 2013;78:352–363. doi: 10.1016/j.neuron.2013.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gu Y, et al. Perceptual learning reduces interneuronal correlations in macaque visual cortex. Neuron. 2011;71:750–761. doi: 10.1016/j.neuron.2011.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ingvalson EM, Holt LL, McClelland JL. Can native Japanese listeners learn to differentiate /r–l/ on the basis of F3 onset frequency? Biling. Lang. Cogn. 2011;15:255–274. doi: 10.1017/S1366728912000041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Park DC, et al. The impact of sustained engagement on cognitive function in older adults: the Synapse Project. Psychol. Sci. 2014;25:103–112. doi: 10.1177/0956797613499592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Boden MA. Creativity and artificial intelligence. Artif. Intell. 1998;103:347–356. [Google Scholar]
- 30.Ajemian R, D’Ausilio A, Moorman H, Bizzi E. A theory for how sensorimotor skills are learned and retained in noisy and nonstationary neural circuits. Proc. Natl. Acad. Sci. U. S. A. 2013;110:E5078–E5087. doi: 10.1073/pnas.1320116110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tkach DC, Reimer J, Hatsopoulos NG. Observation-based learning for brain-machine Interfaces. Curr. Opin. Neurobiol. 2008;18:589–594. doi: 10.1016/j.conb.2008.09.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Velliste M, Perel S, Spalding MC, Whitford AS, Schwartz AB. Cortical control of a prosthetic arm for self-feeding. Nature. 2008;453:1098–1101. doi: 10.1038/nature06996. [DOI] [PubMed] [Google Scholar]
- 33.Santhanam G, et al. Factor-Analysis Methods for Higher-Performance Neural Prostheses. J. Neurophysiol. 2009;102:1315–1330. doi: 10.1152/jn.00097.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Yu BM, et al. Gaussian-Process Factor Analysis for Low-Dimensional Single-Trial Analysis of Neural Population Activity. J. Neurophysiol. 2009;102:614–635. doi: 10.1152/jn.90941.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wu W, Gao Y, Bienenstock E, Donoghue JP, Black MJ. Bayesian population decoding of motor cortical activity using a Kalman filter. Neural Comput. 2006;18:80–118. doi: 10.1162/089976606774841585. [DOI] [PubMed] [Google Scholar]
- 36.Gilja V, et al. A high-performance neural prosthesis enabled by control algorithm design. Nat. Neurosci. 2012;15:1–49. doi: 10.1038/nn.3265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Björck Å, Golub GH. Numerical Methods for Computing Angles Between Linear Subspaces. Math. Comput. 1973;27:579–594. [Google Scholar]
- 38.Fitts PM. The information capacity of the human motor system in controlling the amplitude of movement. J. Exp. Psychol. Gen. 1954;121:262–269. doi: 10.1037//0096-3445.121.3.262. [DOI] [PubMed] [Google Scholar]