Pyramidal Cell-Interneuron Interactions Underlie Hippocampal Ripple Oscillations

SUMMARY

High-frequency ripple oscillations, observed most prominently in the hippocampal CA1 pyramidal layer, are associated with memory consolidation. The cellular and network mechanisms underlying the generation, frequency control, and spatial coherence of the rhythm are poorly understood. Using multisite optogenetic manipulations in freely behaving rodents, we found that depolarization of a small group of nearby pyramidal cells was sufficient to induce high-frequency oscillations, whereas closed-loop silencing of pyramidal cells or activation of parvalbumin-(PV) or somatostatin-immunoreactive interneurons aborted spontaneously occurring ripples. Focal pharmacological blockade of GABA_A receptors abolished ripples. Localized PV inter-neuron activation paced ensemble spiking, and simultaneous induction of high-frequency oscillations at multiple locations resulted in a temporally coherent pattern mediated by phase-locked inter-neuron spiking. These results constrain competing models of ripple generation and indicate that temporally precise local interactions between excitatory and inhibitory neurons support ripple generation in the intact hippocampus.

INTRODUCTION

A key physiological pattern in hippocampus-dependent memory consolidation is the sharp wave-ripple complex, occurring mainly during slow wave sleep (SWS), immobility, and consummatory behaviors (Buzsáki et al., 1983; Wilson and McNaughton, 1994). Sharp waves (SPW) reflect convergent depolarization of CA1 neurons as a consequence of coincident activity at multiple locations in the recurrent excitatory networks of the hippocampal CA3 region (Buzsáki et al., 1983). This excitatory drive can induce a local, fast oscillatory event in the CA1 region, known as “fast gamma” (90–140 Hz; Sullivan et al., 2011) or “ripple” (140–180 Hz; O’Keefe and Nadel, 1978; Buzsáki et al., 1992), with frequency depending on the magnitude of the excitatory SPW and decelerating during the course of the event (Sullivan et al., 2011). The cycles of the local field potential (LFP) ripple coincide with the sequential activity of neurons, the identity of which is influenced by previous experience (Buzsáki, 1989; Wilson and McNaughton, 1994). The neuronal sequence is often similar to place cell sequences observed during exploration (Foster and Wilson, 2006; Diba and Buzsáki, 2007; Karlsson and Frank, 2009). Selective elimination of ripples during post-learning results in impairment of memory performance (Girardeau et al., 2009; Jadhav et al., 2012). Despite the critical role of ripples for information transfer from the hippocampus to the neocortex and for memory consolidation, and their postulated role in epilepsy (“fast ripples”; Bragin et al., 1999; Le Van Quyen et al., 2008), the local network mechanisms underlying the generation of ripples are not well understood (Buzsáki and Silva, 2012).

Three classes of models for ripple generation have been proposed. The first postulates that spikes of CA1 pyramidal cells propagate at the rhythm of the ripple both orthodromically and antidromically in an electrically coupled axonal plexus (Figure 1A) (Draguhn et al., 1998; Traub and Bibbig, 2000; Schmitz et al., 2001; Maier et al., 2003, 2011; Bähner et al., 2011; Traub et al., 2012). According to the second class of models, SPW-associated depolarization excites perisomatic-targeting interneurons that, due to the synaptic time constants of reciprocal inhibition, co-oscillate at ripple frequency and generate periodic inhibition that entrains the population of pyramidal cells (Figure 1B) (Buzsáki et al., 1992; Ylinen et al., 1995; Whittington et al., 1995; Traub et al., 1996; Brunel and Hakim, 1999; Geisler et al., 2005; Rácz et al., 2009; Taxidis et al., 2012). In the third class of models, the fast rhythm is generated by short-lived interactions between interneurons and pyramidal cells rather than by the interactions among interneurons (Figure 1C) (Buzsáki et al., 1992; Ylinen et al., 1995; Brunel and Wang, 2003; Klausberger et al., 2003; Memmesheimer 2010). Testing of these models has been hampered by the correlative nature of most in vivo studies. On the other hand, interpretation of in vitro studies is constrained because many applied drugs are not selective for specific neuron types and can affect both SPW and ripple generation mechanisms, thus limiting separation into specific effects. Furthermore, many in vitro studies investigated CA3 ripples, which are neither prominent in vivo nor coherent with CA1 ripples (Buzsáki 1986; Sullivan et al., 2011). To examine the mechanisms of ripple generation and propagation in the intact brain, and to reconcile the merits and drawbacks of the existing models, we used optogenetic, pharmacological, and closed-loop feedback tools in behaving and anesthetized mice and rats. We demonstrate that pyramidal neuron activity is a necessary requirement for ripple generation and that inhibitory interactions play a critical role in rhythm generation and synchronizing independent ripple oscillators (Figure 1D).

Figure 1. Network Models of Ripple Oscillations.

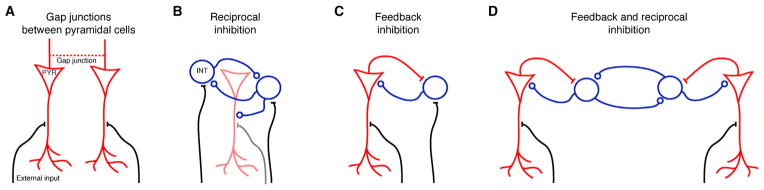
(A) Axonal net. The axons of pyramidal neurons (PYRs) are assumed to be connected via electrical synapses (gap junctions). Upon external input during a CA3-generated SPW (black), orthodromic spikes generated by one PYR also propagate antidromically to synchronize with other PYR; the rhythm frequency may be determined by the sparseness of the connectivity graph.

(B) Pacing by reciprocal inhibition. CA1 interneurons (INT) are assumed to be reciprocally connected via chemical synapses and, at the population level, can spike at ripple frequency due to the GABA_A synaptic time constants. Spikes of PYR (possibly receiving external input; gray) are paced by the inhibitory network.

(C) Pacing by feedback inhibition. Both pyramidal cells and interneurons receive external input, and the rhythm is dictated by the time constants of synaptic interaction between the two populations.

(D) PYR-INT-INT model suggested by the current study. Pyramidal cells receive tonic external input that activates both pyramidal cells and the reciprocally connected inhibitory network. Reciprocal inhibition paces the excited pyramidal cells, which in turn generate an LFP ripple. A SPW sweeping through the CA1 network can induce disparate oscillators, which are temporally coordinated by reciprocal inhibition.

RESULTS

We used high-density extracellular recordings coupled with multisite optogenetic manipulations in awake behaving rodents (n = 26 mice; n = 5 rats) and urethane-anesthetized mice (n = 16; Table S1 available online). Fast-gamma and ripple events (Figure 2A) appeared spontaneously and with similar properties in all animals, regardless of species and genotype (median frequency, 148 Hz; power, 9.1 SD; duration, 43 ms; 115,204 ripples) (Figure S1A). Because SPW-associated fast-gamma and ripple events differ only in frequency and amplitude distributions (Sullivan et al., 2011), for simplicity, we will refer to them as ripples.

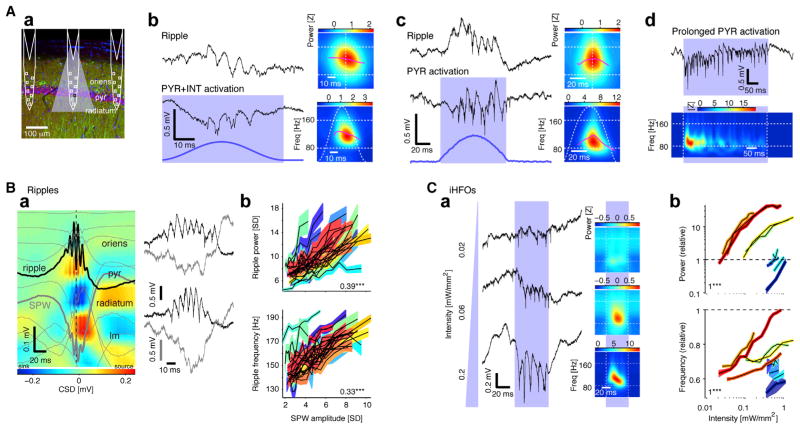
Figure 2. Local Activation of Pyramidal Cells Induces High-Frequency Oscillations.

(Aa) Schematic of three diode-probe shanks overlaid on a confocal image of ChR2 expression in CA1 pyramidal cells (CaMKII, red; EYFP, green; DAPI, blue; pyr, CA1 pyramidal layer).

(Ab) Spontaneous ripple and iHFOs recorded by the same electrode (freely moving CAG::ChR2 rat; single-shank illumination; peak light intensity at the middle of the CA1 pyramidal layer: 0.11 mW/mm²). Right: time-frequency decomposition (average of n = 458 spontaneous or n = 10 induced events).

(Ac) HFOs induced in a freely moving CaMKII::ChR2 mouse (0.14 mW/mm²). Right: time-frequency decomposition (n = 367 spontaneous or n = 20 induced events).

(Ad) Prolonged illumination (400 ms light pulses; n = 20) induces oscillations that decrease in frequency and amplitude (same recording site as in [Ac]).

(B) Ripple power and frequency increase with SPW amplitude.

(Ba) Left: depth profile of averaged sharp-wave ripples in a freely moving mouse (n = 961 events; vertical site separation: 100 μm). Voltage traces (light gray) are superimposed on current-source density (CSD) map. Black trace: site of maximum amplitude ripple; heavy gray trace: site of maximum amplitude SPW. pyr, pyramidal layer; lm, str. lacunosum-moleculare. Right: examples of lower (top) and higher (bottom) amplitude SPWs recorded from the same mouse.

(Bb) Ripple power and frequency increase with SPW amplitude (colored bands correspond to n = 26 experiments in four freely moving mice equipped with 32-site linear probes; bands: mean ± SEM over ripple events). Numbers indicate median rank correlation; ***p < 0.005, Wilcoxon’s signed-rank test.

(C) iHFO power and frequency increase with light intensity.

(Ca) Left: traces during individual pulses (50 ms), plotted versus light intensity at the middle of the CA1 pyramidal layer. Right: time-frequency decomposition (n = 20 induced events). Weaker light only induces spiking, whereas oscillations of increasing amplitude and frequency are induced with stronger light.

(Cb) Power and frequency (scaled by the properties of the same-site spontaneous ripples; bands: mean ± SEM, n = 10 experiments in four freely moving CaMKII::ChR2 mice) increase with light intensity.

Optogenetically Induced High-Frequency Oscillations Provide a Model for Spontaneous Ripples

Previous research has suggested that the excitatory CA3 input in the form of a SPW is a necessary but insufficient condition for ripple occurrence (Buzsáki et al., 1992; Chrobak and Buzsáki, 1996; Csicsvari et al., 2000) and that ripples are not transferred from upstream regions but rather emerge from local mechanisms in CA1 (Buzsáki, 1986; Csicsvari et al., 2000; Sullivan et al., 2011) (Figure 1). To directly test this hypothesis, we focally perturbed the spiking activity of distinct cell types in CA1 (Figure S2). In CAG::ChR2 animals, brief localized optogenetic depolarization of pyramidal cells (PYRs) and interneurons (INTs) with a half-sine waveform, designed to mimic the SPW envelope (Figure 2Ab, bottom; estimated light intensity: 0.11 mW/mm² at the center of the CA1 pyramidal layer; Stark et al., 2012), induced spiking that organized into high-frequency oscillations resembling spontaneous ripples recorded at the same site (Figure 2Ab, top). We will refer to these artificially generated patterns as induced high-frequency oscillations (iHFOs). Simultaneous direct optogenetic INT activation was not necessary, since iHFOs resembling the spontaneous ripples were readily induced in CaMKII::ChR2 animals by depolarization of PYRs) (Figure 2Ac). Rectangular waveforms were equally effective in inducing local iHFOs, and therefore, for simplicity, we used square pulses in CaMKII::ChR2 animals in all subsequent experiments. Individual brief pulses (≤10 ms) occasionally induced an LFP wave or two associated with spiking, reminiscent of ripple cycles, but regular HFOs were not induced.

As reported previously in rats (Ponomarenko et al., 2004; Nguyen et al., 2009; Sullivan et al., 2011), the frequency of ripples decelerated from the mean peak of ~150 Hz to ~120 Hz (Figures 2Ab and 2Ac, top, purple lines). Similar to spontaneous ripples, the induced oscillation frequency decelerated during the iHFO events (Figures 2Ab and 2Ac, bottom). Upon prolonged illumination (e.g., 400 ms square pulse), the amplitude of the oscillatory waves waxed and waned, and the frequency decreased (Figure 2Ad), although this change can also reflect opsin desensitization (Lin et al., 2009). SPW amplitude was positively correlated with spontaneous ripple power (median rank correlation, 0.39; p < 0.001; 26 sessions in four freely moving mice equipped with 32-site linear probes) and frequency (0.33; p < 0.001; Figure 2B). At low light intensities, the mean frequency of the iHFO was typically lower than the frequency of same-site ripples, but increasing light intensity (for example, 50 ms square pulses, 0.01–1 mW/mm² at the center of the CA1 pyramidal cell layer) (Figure 2Ca) enhanced iHFO power (median rank correlation, 1; p = 0.002, Wilcoxon’s paired signed-rank test; n = 10 experiments in four freely moving CaMKII::ChR2 mice) and frequency (median rank correlation, 1; p = 0.002) (Figure 2Cb). Thus, the excitatory drive, provided either by the SPW or optogenetic PYR activation, is positively correlated with oscillation power and frequency in the CA1 pyramidal layer. At maximum light intensity, as many as 80–100 CA1 PYR were directly illuminated (Experimental Procedures), suggesting that the minimal network that can support ripple generation is small.

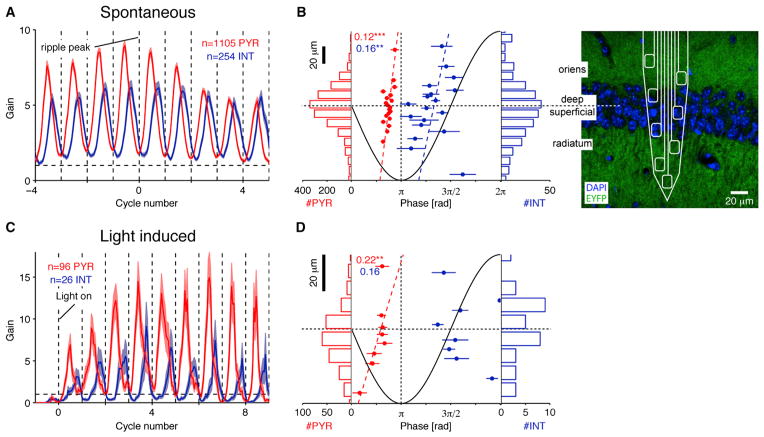
Next, we compared the temporal relationship between unit firing during ripples and iHFOs. Units were classified as putative PYR or INT on the basis of optogenetic responses and physiological criteria (Stark et al., 2013). During spontaneous ripple events, CA1 neurons increased their firing rate approximately 6-fold (relative to no-ripple epochs, “gain”; Figures S1B and S1C). Although the overall probability of spiking during an individual ripple event was higher for INT than for PYR (50% versus 9% of the ripple events, p < 0.001, Mann-Whitney U test, 369 INT and 1,864 PYR; 4.8% versus 0.8% of the ripple cycles, p < 0.001) (Figure S1D), PYR spiking gain was consistently higher than INT gain during the first half of the ripple (p = 0.003, Bonferroni corrected U test) (Figure S1B, bottom, red bar). Spikes of CA1 units were phase-locked to the ripple cycles (PYR: 1105/1864, 59%; INT: 254/369, 69%), and PYR spiked about 90° earlier than INT (mean ± SEM phases: PYR, 157° ± 1°; INT, 242° ± 4°; 0° corresponds to an LFP peak) (Figure S3Aa) on every ripple cycle (Figure 3A). For quantification of iHFOs, we defined a “threshold” light intensity in each experiment as the lowest intensity that generated iHFOs with comparable (equal to or higher) power to spontaneous ripples. Similarly to spontaneous ripples, CA1 spiking was phase-locked to LFP iHFO waves induced at the threshold light intensity (PYR: 96/254, 38%; INT: 26/37, 70%), and PYR spiked earlier than INT (mean ± SEM phases: PYR, 137° ± 4°; INT, 288° ± 10°) (Figure S3Ba) on every iHFO cycle (Figure 3C). When compared to spontaneous ripples, PYR spiked relatively earlier, and INT spiked later during iHFOs (PYR mean ± SEM phase difference: 20° ± 3°, p < 0.001, Wilcoxon’s paired signed-rank test; INT, 35° ± 7°; p < 0.001). However, on a unit-by-unit basis, spike phases during iHFOs and spontaneous ripples were correlated (circular-circular correlation: PYR, 0.7, p < 0.001; INT: 0.42, p = 0.009, χ² test).

Figure 3. Spatiotemporal Spiking Dynamics during Spontaneous Ripples and iHFOs.

(A) PYR spike earlier than INT on every ripple cycle. Cycle-resolved spiking during spontaneous ripples (data from 19 awake behaving mice and three rats). Bands: mean ± SEM; only phase modulated units (p < 0.05, Rayleigh test) are included.

(B) Superficial neurons spike earlier than deep neurons during the ripple cycle. Data are the same as in (A). Center: ripple phase of spiking (population mean ± SEM) versus depth in layer (see confocal image at far right), binned for presentation purposes only. Dashed lines show circular-linear model fit, and numbers indicate circular-linear correlation coefficients between phase and depth; **/***p < 0.01/0.005, χ² test. Histograms show the number of units recorded at each depth. Although the distribution of recorded units is approximately symmetric, superficial PYR and INT spike earlier than their deeper peers.

(C and D) These properties are also apparent during iHFOs. Data are from four freely moving CaMKII::ChR2 mice, and phase-resolved spiking is aligned to light onset (threshold intensity). As during spontaneous ripples, PYR spiking precedes INT spiking (C) and superficial PYR spike earlier than their deeper peers (D). See also Figure S3.

Because the deep and superficial substrata of the CA1 pyramidal layer have different physiological features (Mizuseki et al., 2011), we investigated the spatial distribution of unit spiking during spontaneous ripples and iHFOs. While roughly equivalent numbers of neurons were sampled in deep (toward str. oriens; 994 units) and superficial (toward str. radiatum; 1,131 units) sublayers (Figure 3B), we found that entrainment to spontaneous ripples was more ubiquitous in superficial PYR than deep PYR (609/954, 64%, versus 478/842, 57%; p < 0.001, Fisher’s exact test) and that superficial PYR had higher peak gain (mean ± SEM. PYR gain, 12.4 ± 0.5 versus 9.2 ± 0.5; p < 0.001, U test) (Figure S3Ab). Conversely, a larger fraction of deep INT than superficial INT was entrained (116/152, 76% versus 114/177, 64%; p = 0.006). Superficial PYR and INT spiked earlier than deep cells during the ripple cycle (circular-linear correlation, 254 INT: 0.16, p = 0.01, χ² test; 1105 PYR, 0.12, p < 0.001; circular-linear model: Φ(PYR) = 2π(0.44+0.55•d)) (Figure 3B). These sublayer differences were retained during iHFOs: superficial pyramidal cells spiked earlier on the iHFO cycle than their deeper peers (circular-linear correlation: 0.22, p = 0.006; circular-linear model: Φ(PYR) = 2π(0.4+2.85•d)) (Figures 3D and S3Bb).

Selective optogenetic activation of excitatory cells could also induce HFOs in dentate regions and in layer 5 of the somatosensory cortex (n = 2 rats and n = 4 CaMKII::ChR2 mice) (Figure S3Ca), and concurrent activation of excitatory cells and inter-neurons generated iHFOs in both CA1 and dentate regions (n = 3 CAG::ChR2 rats) (Figure S3Cb). These findings indicate that iHFOs can be evoked in various cortical networks as long as local excitatory cells are sufficiently activated (Kandel and Buzsáki, 1997; Grenier et al., 2001). In sum, although some differences were observed between spontaneous CA1 ripples and the artificially induced HFOs, these results suggest that within a local network, similar cellular-network mechanisms are involved in the generation of both phenomena.

Fast Inhibition Is Necessary for iHFO Generation

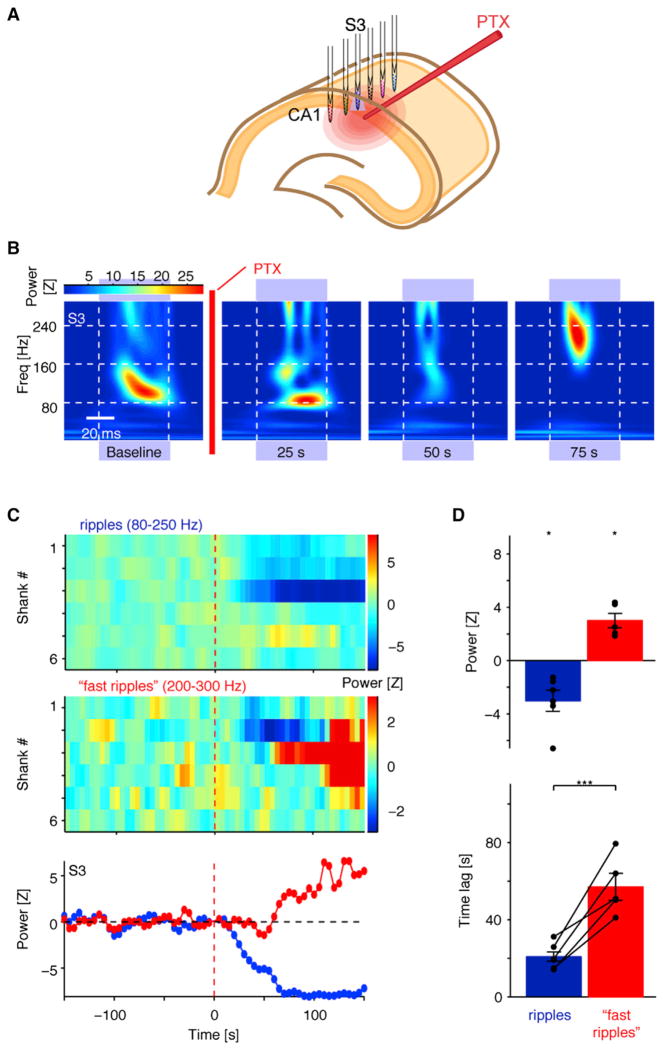
The experiments reported above demonstrated that direct PYR activation is a precondition for iHFO generation and possibly for spontaneous ripples. With this model in hand, we asked whether—in addition to PYR activation—synaptic inhibition is critical for the generation of LFP ripple oscillations. Because drugs applied in vivo may exhibit transient effects (see below) and spontaneous ripples occur sparsely, we examined the outcome of local GABA_A receptor blockade using sequentially triggered (single shank at a time) iHFOs in CaMKII::ChR2 urethane-anesthetized mice (Figure 4A). As in the freely moving animals, single-shank illumination (50 ms pulses; 470 nm, ~0.05 mW/mm²) generated localized LFP iHFOs (Figure 4B, left). Following focal infusion of the GABA_A receptor blocker picrotoxin (PTX) (1 mM in PBS; 13–52 nl, 26 nl/s), iHFOs were abolished on the shank closest to the pipette (p = 0.033, Wilcoxon’s signed-rank test with zero null, six experiments in four mice) (Figure 4D, top). This effect was specific in time and space, because iHFOs on adjacent shanks were either unperturbed or affected after a delay, presumably corresponding to limited diffusion of the drug to more distal sites (Figure 4C, top). The full suppression of local iHFOs following GABA_A receptor blockade indicates that PYR-PYR interactions alone (Figure 1A) are not sufficient for ripple generation and highlights the critical contribution of fast inhibition.

Figure 4. Local GABA_A-Receptor-Mediated Inhibition Is Necessary for Ripple Generation.

(A) During optical-pharmacological experiments, a six-shank/six-LED diode probe was positioned in CA1 pyramidal layer (urethane-anesthetized CaMKII::ChR2 mouse), and a glass pipette with PTX was positioned next to one of the shanks. Light pulses were applied sequentially to all shanks to obtain a baseline, after which PTX was infused while photostimulation was continued.

(B) Light-induced ripples are disrupted following local PTX infusion. Panels show the time-frequency decomposition of the pyramidal layer CSD trace during illumination (~0.05 mW/mm²). Baseline: average of 30 sequential pulses; other panels are for single light pulses. Note disruption of iHFOs following GABA_A receptor blockade.

(C) GABA_A receptor blockade disrupts induced ripples locally. Full spatiotemporal profile of induced events, summarized separately for ripple (top) and “fast ripple” (center) frequency bands. Each color-coded rectangle shows the power of the locally induced oscillations during a single light pulse. Ripple disruption is early and localized to shank 3 (S3), while “fast ripple” appearance is delayed and more distributed, consistent with drug diffusion. Bottom: time plot of ripple (blue) and “fast ripple” (red) power on S3.

(D) Local GABA_A receptor blockade consistently disrupts iHFOs (blue) before amplifying “fast ripples” (red). Mean ± SEM of six experiments in four animals; dots indicate individual experiments. *p < 0.05, Wilcoxon’s signed-rank test (zero null); ***p < 0.005, U test. See also Figure S4.

The selective suppression of iHFOs by PTX was transient (~1 min; Figure 4C) and was followed by the emergence of higher-frequency, nonphysiological epileptic oscillations (200–300 Hz “fast ripples”) (Bragin et al., 1999) (Figure 2B, far right). Induced “fast ripples” initially appeared on the same shank as the disrupted iHFOs and subsequently spread to neighboring recording sites (Figure 4C, middle). The emergence of the induced “fast ripples” always lagged behind the disruption of the iHFOs (Figure 4C, bottom; p = 0.004, U test, six experiments; Figure 4D, bottom), likely following the course of drug diffusion. In a third phase, large amplitude “fast ripples” appeared spontaneously between light stimuli (Figure S4). During the supersynchronous “fast ripples,” action potentials of individual neurons could not be discriminated due to the temporally superimposed spikes of many neurons. Activity returned to physiological baseline after approximately 60 min.

Pyramidal Cell Activity Is Critical for the Maintenance of Spontaneous Ripples

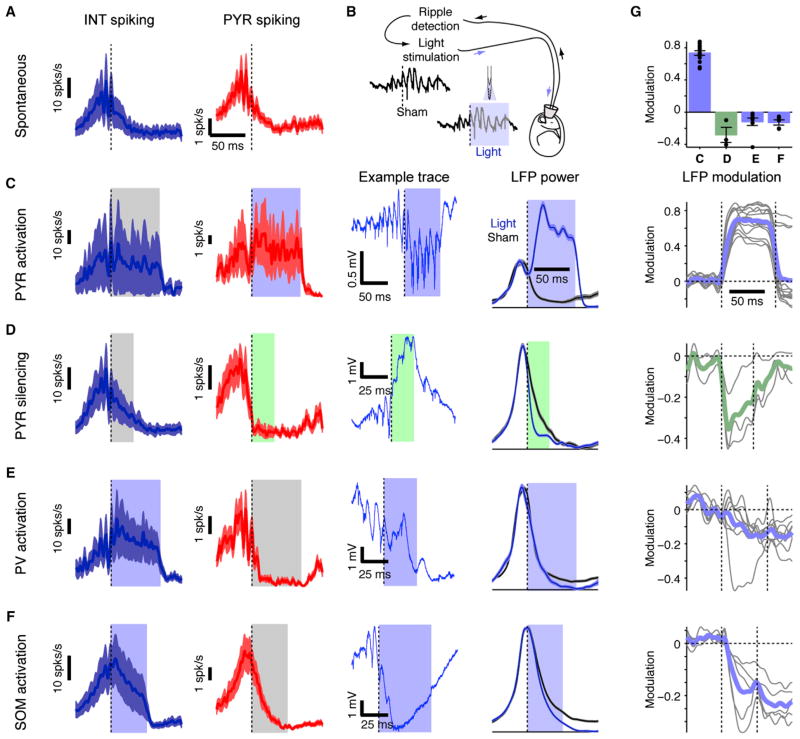
After establishing that activation of pyramidal cells and fast inhibition are, respectively, a precondition and a necessary condition for iHFO generation, we examined how excitation and inhibition contribute to spontaneous ripples. We used closed-loop optogenetic perturbations, contingent on real-time detection of spontaneous ripples (Figures 5A and 5B). In CaMKII::ChR2 animals, feedback illumination increased local spiking rate and prolonged high-frequency oscillations (p < 0.001, U test, for each of n = 14 experiments in one rat and three mice) (Figures 5C and 5G), while leaving firing rate and ripple power unaffected at nonilluminated shanks (Figure S5A). Thus, even during the postripple window of decreased pyramidal cell spiking (Figure S1B), PYR activation can induce HFOs.

Figure 5. Pyramidal Cell Activity Is Necessary for Ripple Maintenance.

(A) Ensemble spiking activity is oscillatory during ripples. Example shows ripple-triggered peri-event time-histogram during spontaneous ripples (mean ±SEM of ten simultaneously recorded INT, left; and 54 PYR, right).

(B) During closed-loop experiments, ripples are detected in real-time about three cycles after onset, and the detection triggers illumination on one or more shanks. Control (sham) and light trials are interleaved.

(C) Ripple-contingent activation of PYR (single-shank illumination; freely moving CaMKII::ChR2 mouse) drives PYR and increases duration of spontaneously occurring ripples (205 light and 301 sham events; p < 0.001, U test). Example wide-band (1–5,000 Hz) trace shows a single closed-loop event. LFP power: integrated power (80–250 Hz) of the CSD trace in the middle of the CA1 pyramidal cell layer (mean ±SEM) with and without illumination.

(D) Direct silencing of PYR (single-shank illumination; urethane-anesthetized CaMKII::Arch mouse) shortens spontaneously occurring ripples (815 light and 375 sham events; p < 0.001, U test).

(E) Indirect PYR silencing via PV activation (four-shank illumination; freely moving PV::ChR2 mouse) shortens ripples (109 light and 496 sham events; p < 0.001, U test).

(F) Indirect PYR silencing via SOM activation (freely moving SOM::ChR2 mouse) shortens ripples recorded on the illuminated shanks (1,325 light and 1,335 sham events; p < 0.001, U test).

(G) Closed-loop interference with PYR activity disrupts ripples. Modulation: the difference between ripple-power during light and sham trials, divided by the sum. Top: average modulation (mean ±SEM 30 ms postdetection; dots represent individual experiments, repeated 14, 3, 8, and 5 times for [C] through [F], respectively). Panels below show the full time course (colored lines, group averages; gray lines, individual experiments). See also Figure S5.

In support of a critical role of pyramidal neurons, local PYR silencing terminated the ripple events. Ripple-contingent illumination in CaMKII::Arch mice for 20–50 ms resulted in localized suppression of PYR spiking and ripple power (p < 0.001, U test, each of three experiments in two mice) (Figures 5D and 5G). At adjacent shanks, PYR spiking was not affected, and ripples were not disrupted (Figure S5B). These findings further demonstrate that the minimal network underlying the generation of ripples is small (see also Figure 7, below). Indirect, closed-loop silencing of PYR via activation of parvalbumin (PV)- or somatostatin (SOM)-immunoreactive interneurons also interrupted ongoing ripples. Ripple-contingent illumination in PV::ChR2 mice resulted in increased PV spiking and decreased PYR spiking (Figures 5E and S5C), as well as in aborting ongoing ripples on the illuminated shanks (p < 0.001, U test; p < 0.05 in 6/8 experiments in three mice) (Figures 5E and 5G). Likewise, feedback illumination in SOM::ChR2 mice resulted in SOM cell activation (Figure S5D), silencing of PYR and other interneurons (Figure 5F), and disruption of ripple power on the illuminated shanks (p < 0.001, U test, each of five experiments in three mice) (Figures 5F and 5G). Thus, intact activity of a small network of pyramidal cells is necessary for the generation and maintenance of spontaneous local ripples, and silencing pyramidal cells either directly or indirectly via interneuron-mediated inhibition aborts spontaneous ripples. Moreover, these results indicate that LFP ripples are not maintained during inter-neuron activation in the absence of increased pyramidal cell activity, at odds with the simple version of the IN-INT model (Figure 1B).

Figure 7. Interneuron Spiking Mediates the Coordination of Local Oscillators.

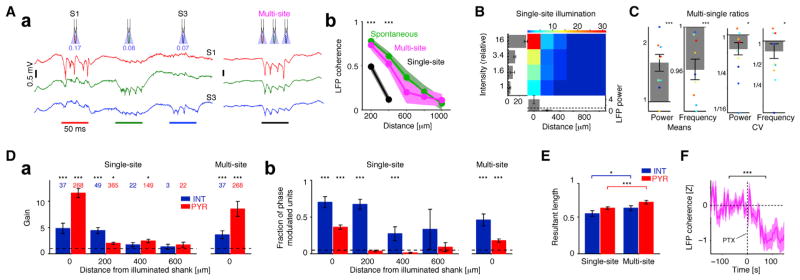
(Aa) Wide-band traces from the center of the CA1 pyramidal layer (freely moving mouse; CaMKII::ChR2) during sequential (single-site at a time, left) and same-intensity simultaneous, multisite (right) illumination. Illumination time is indicated by colored bars at bottom, and 470 nm light intensity (mW/mm²) is indicated below the schematic of each shank.

(Ab) Ripple-band coherence is similar (p > 0.05, all pairs) during spontaneous ripples and multisite illumination but lower during single-site illumination. During single-site illumination, ripple coherence for shanks >400 μm apart is at chance level. Data are from nine experiments in four freely moving CaMKII::ChR2 mice and five experiments in five urethane-anesthetized mice; bands: mean ±SEM; */*** here and in (C) and (E): p < 0.05/p < 0.005, Wilcoxon’s paired signed-rank test.

(B) iHFOs generated by single-site illumination are localized events. LFP power is scaled by spontaneous ripple power (dashed lines), and light intensity is scaled by threshold intensity. Bars below are group means ±SEM for the threshold intensity, and bars at the left refer to the local shank.

(C) During multisite illumination, ripple-band power is higher and frequency is lower, compared to same-intensity single-site illumination (left two panels). Intersite variability (coefficient of variation [CV]) is lower for both power and frequency. Bars here and in (D), (E), and (F) are mean ±SEM; colored dots, individual experiments (four freely moving mice).

(D) During single-site illumination, firing rate of distant INT is not altered, but their spikes are phase-locked to the induced ripples.

(Da) Spiking rate gain of PYR and INT at various distances from a single illuminated shank (left) or during multisite illumination (right). Number of cells per group are shown (11 experiments in four freely moving mice); *p < 0.05; ***p < 0.005, Wilcoxon’s signed-rank test (unity gain null; dashed line).

(Db) Fraction of phase-modulated (Rayleigh test, p < 0.05; dashed line) cells in each group. ***p < 0.005, exact binomial test.

(E) Phase-locking is stronger during multisite than single-site illumination.

(F) During multisite illumination, ripple-band coherence is reduced following local GABA_A receptor blockade (PTX; see Figure 4). For each pair of nearby sites (<400 μm; n = 36 pairs from three urethane-anesthetized CaMKII::ChR2 mice), ripple-band coherence was normalized by the preinjection baseline. ***p < 0.005, Wilcoxon’s paired signed-rank test. See also Figure S7.

PV Interneurons Can Pace Ensemble Activity at the Ripple Frequency

To test the prediction of the INT-INT model (Figure 1B) and its potential contribution to LFP ripple oscillations, we directly activated PV cells in freely moving PV::ChR2 mice (n = 7). During single-shank illumination, PV cells increased their firing rate, while PYR recorded on the same shank were suppressed (Figure 5A). However, LFP iHFOs were not observed, either during sequential (single-shank at a time; Figure 6A) or during simultaneous multisite diode-probe stimulation (four 470 nm LEDs, 1–1.5 mW/mm² per site; Figure S6A). Moreover, LFP iHFOs were not observed even during PV activation with strong light intensities (up to 100 mW/mm²; Figure S6A). Thus, in contrast to PYR activation, which readily generates iHFOs (Figure 2), non-rhythmic activation of PV interneurons cannot induce LFP oscillations, indicating that a simple version of the INT-INT model (Figure 1B) cannot account for the generation of LFP ripples.

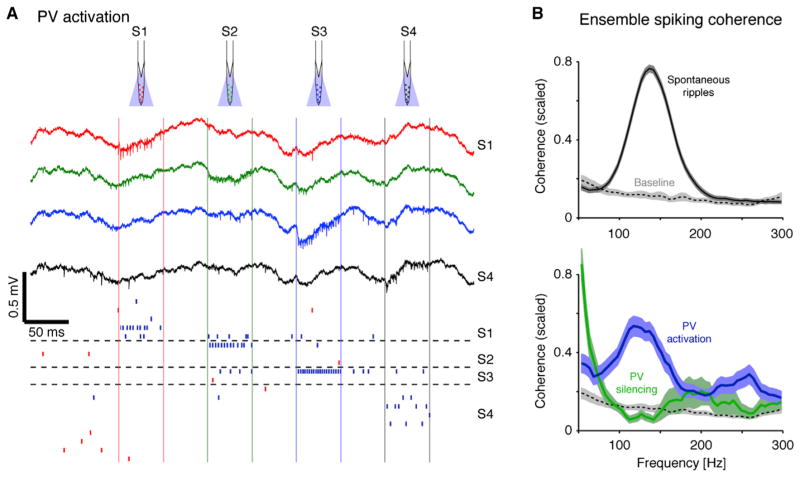
Figure 6. PV Interneuron Activity Does Not Induce LFP Ripples but Can Pace Ensemble Spiking.

(A) PV activation does not induce LFP ripples. Wide-band traces recorded at 200 μm intervals during sequential illumination (square pulses, light intensity: 1–1.5 mW/mm²; PV::ChR2 mouse) of the CA1 pyramidal layer. Vertical colored lines delimit illumination on each shank, and horizontal dashed lines separate units recorded on distinct shanks. Red/blue ticks indicate PYR/INT spike times, each row corresponding to a single unit. Note locally induced INT spiking but no LFP oscillations.

(B) Ensemble spiking coherence. Cross-shank spiking coherence was computed between agglomerated spike trains (summed PYR spikes, spikes of all PYR recorded on the same shank; summed INT spikes: same, for INT). Bands show mean ±SEM scaled (0–1) values of coherent spike train pairs (p < 0.05, Bonferroni-corrected F test); dashed lines show baseline coherence (in the lack of ripples or light) for the same pairs. Note coherent summed PYR and summed INT spike trains at ripple frequency during spontaneous ripples (258/737 pairs from 21 awake behaving mice and four rats) and single-shank PV activation (41/212 pairs; five freely moving PV::ChR2 mice) but not during PV silencing (14/32 pairs; four awake behaving mice). See also Figure S6.

However, the lack of induced LFP oscillations does not rule out a potential role of INT-INT interactions in pacing intraripple frequency of neuronal firing. To increase the power of detecting second order relations between spike trains, we agglomerated the spikes of all PYR recorded on the same shank (median, 6 PYR; range, 1–33) into “summed PYR” activity and all INT spikes into “summed INT” (median, 2 INT; range, 1–9) and quantified the coherence between the resulting spike trains recorded on different shanks. During spontaneous ripples, 258/737 (35%) of the summed PYR-summed INT pairs exhibited significant coherence (p < 0.05, Bonferroni-corrected F test; mean ± SEM frequency, 140 ± 2 Hz; data from 21 awake behaving mice and four rats) (Figure 6B, top). For comparison, when the same analysis was applied to exactly the same spikes yet with the original tagging of single neurons, only 790/6369 (12.4%) of the PYR-INT pairs were coherent (148 ± 1.5 Hz; Figure S6Ba). Consistent with the ripple-related spiking coherence, ensemble spiking was also coherent during iHFOs induced by single-shank PYR activation (e.g., 18/136 [13%] summed PYR-summed INT pairs were coherent; five freely moving CaMKII::ChR2 animals) (Figure S6Bb).

PV activation, while suppressing PYR and other INT, may still exert a coherent inhibitory timing effect on the remaining spikes of the target population. Whereas during PV activation LFP iHFOs could not be detected, presumably due to the lack of PYR spiking (Figures 6A and S6A), coherent ensemble spiking was consistently induced. During single-shank PV activation, 41/212 (19.3%) of the summed INT-summed PYR pairs and 43/137 (31%) of the summed PYR-summed PYR pairs were coherent at the ripple frequency (summed INT-summed PYR: 150 ± 10 Hz; summed PYR-summed PYR: 149 ± 11 Hz; five freely moving PV::ChR2 mice) (Figure 6B, bottom; similar results were obtained for single-unit coherence, Figure S6Bc). In contrast, simultaneous multisite PV silencing (in four awake behaving PV::Halo mice) mainly resulted in increased coherence at the low (<60 Hz) and supra-ripple frequency ranges (Figures 6B, bottom, and S6), consistent with disinhibited PYR spiking and increased supraripple LFP power (similar to the second phase of the focal PTX effect) (Figure 4). Thus, although tonic light activation of PV interneurons cannot induce LFP ripples, it can organize neuronal ensemble spiking into coherent ripple-frequency oscillations, consistent with a modified version of an INT-INT-based timing mechanism (Figure 1D).

Interneurons Mediate Phase Coupling of Spatially Distributed iHFO Events

Spontaneous ripples can be coherent over distances of several mm (Buzsáki et al., 1992; Ylinen et al., 1995) (Figure 7Ab, green) and thus differ from the optogenetically induced local iHFOs (Figure 7Ab, black). To examine the mechanisms that support such coherence, we generated iHFOs sequentially (single site at a time) or simultaneously at multiple sites (CaMKII::ChR2 animals: n = 2 rats, n = 4 freely moving mice, and n = 5 urethane-anesthetized mice). During single-site illumination, iHFO power declined progressively on other shanks with increased distance (Figures 7Aa and 7B). Two shanks away (400 μm), oscillation power was 2% ± 0.3% of the local power (mean ±SEM; 14 experiments in nine mice; p < 0.001, Wilcoxon’s signed-rank test with a zero-power null) (Figure 7B), while >400 μm away, induced power was indistinguishable from baseline (0.3% ± 0.1%; p > 0.05). For comparison, the power of spontaneous ripples recorded in the same animals was 89% ± 11% at 400 μm and above 40% at all distances up to 1 mm. Thus, iHFOs generated by threshold single-shank illumination involve a smaller network than typical spontaneous ripples, indicating that the coherence of ripples across multiple sites observed during spontaneous ripples is not a volume-conducted effect but rather an outcome of temporally correlated SPW input to multiple oscillators.

To examine whether multiple iHFOs are coupled, we illuminated all shanks simultaneously, keeping all other parameters identical to the sequential (single-site) stimulation (Figure 7Aa). Simultaneous multisite illumination resulted in phase-coherent oscillations on all shanks (Figures 7A and S7). Coherence between nearby sites (≤400 μm separation) was always higher during multi-site than single-site illumination (200 μm: p = 0.003, Wilcoxon’s paired signed-rank test; 400 μm: p < 0.001; 14 experiments in nine mice; Figure 7A). Coherence between distant sites (>400 μm separation) during single-shank illumination was at chance level, whereas simultaneous stimulation generated intersite coherence similar to that observed during spontaneous ripples (p > 0.05; Figure 7A). Compared to single-site illumination, multi-site illumination triggered iHFOs with higher power (p = 0.0015, Wilcoxon’s paired signed-rank test; nine experiments in four freely moving mice) and lower global frequency (p = 0.001) and reduced intersite variability (power: p = 0.03; frequency: p = 0.04; Figure 7C). Thus, during coincident input, multiple oscillators phase-lock and form a single global oscillator.

To understand how oscillators can phase-lock, we examined the concurrent spiking activity. Units recorded on the illuminated shank increased their firing rate (37 INT and 268 PYR from four freely moving mice; p < 0.001, Wilcoxon’s signed-rank test, unity gain null) (Figure 7Da) and were phase-locked (p < 0.05, Rayleigh test) to the iHFOs (p < 0.001, exact Binomial post hoc test; Figure 7Db), whereas PYR recorded on nonilluminated shanks were rarely phase-locked (p > 0.05; Figure 7Db). In contrast, INT recorded on nonilluminated shanks (“non-local” INT) were phase-locked to iHFOs (p < 0.001, exact Binomial test) without a mean change in firing rates (p > 0.05; Figure 7D) (e.g., 400 μm from the illuminated shank, 6/22 or 27% of the INT but only 2/149 PYR were significantly phase-locked) (Figure S7C). Phase-locking magnitude (quantified by the circular resultant length) of nonlocal INT was similar to that which was observed for the same units during spontaneous ripples (e.g., 0.50 ± 0.03 [single-site] versus 0.41 ± 02 [spontaneous] at 200 μm; p > 0.05 at all distances, Wilcoxon’s paired signed-rank test) and higher than during single-shank illumination (p = 0.017, Wilcoxon’s paired signed-rank test, 26 phase-modulated INT) (Figure 7E). We examined the causal role of inhibition in phase-locking by simultaneous illumination of multiple shanks before and after focal application of PTX (three urethane-anesthetized CaMKII::ChR2 mice). Following GABA_A receptor blockade, the ripple-band coherence between iHFOs recorded on nearby recording sites (≤400 μm separation) decreased progressively over time (p < 0.001, Wilcoxon’s paired signed-rank test, 36 site pairs) (Figure 7F). In most cases (22/36 site pairs; 61%) the decrease in coherence was significant (p < 0.05, U test), resulting in a median reduction of the coherence by 23%. Thus, interneuron spiking facilitates the phase-locking of locally emerging iHFOs (Figure 1D).

DISCUSSION

Using a combination of high-density extracellular recordings, multisite/multicolor closed-loop optical stimulation, and pharmacological intervention in freely behaving and urethane-anesthetized mice and rats, we examined the mechanisms of SPW-induced fast gamma/ripple generation. Our principal findings are as follows: (1) activation of a small group of pyramidal cells is sufficient to generate iHFOs. (2) Fast GABA_A-mediated inhibition is critical for the generation of iHFOs. (3) Pyramidal cell activity is critical for the maintenance of ripples. (4) PV interneurons can pace spiking in local populations. (5) Multisite activation induces temporally coherent ripples mediated by phase-locked interneuron spiking. These findings are consistent with a model of ripple generation based on PYR-INT-INT interactions (Figure 1D).

Mechanisms of Ripple Generation In Vivo

Emergent population bursts in the hippocampal CA3 region generate a sweep of excitation in the CA1 str. radiatum, as reflected by the SPW (Buzsáki et al., 1983; Patel et al., 2013). This excitatory drive, in turn, can induce fast oscillatory events in the CA1 region, known as fast-gamma (90–140 Hz; Sullivan et al., 2011) or “ripple” (140–180 Hz; O’Keefe and Nadel, 1978; Buzsáki et al., 1992), with frequency depending on the magnitude of the excitatory SPW, as shown also in our work. The frequency of ripples decelerates from the mean peak of ~150 Hz to ~120 Hz (Ponomarenko et al., 2004; Nguyen et al., 2009; Sullivan et al., 2011; present findings). By substituting the CA3-induced depolarization with optogenetic stimulation, we were able to induce oscillations that shared the above features of ripples. Further similarities between spontaneous ripples and iHFOs include the sublayer-specific recruitment of CA1 pyramidal cells and the phase/time shifted firing of pyramidal cells and interneurons in the sublayers. CA1 superficial neurons were recruited earlier and at a higher probability compared to deep layer cells, in line with a recent report showing stronger excitation of basket cells by superficial pyramidal cells and stronger basket-cell-mediated inhibition of deep layer pyramidal cells (Lee et al., 2014).

However, differences were also noted, such as a relatively lower mean frequency of iHFOs associated with a relatively larger phase separation between pyramidal cells and interneurons during iHFOs. Such differences might be explained by the activating mechanisms: during spontaneous ripples, INT receive excitatory input from diverse CA3 loci and CA1 pyramidal cells, whereas during iHFOs they are driven only by the local CA1 PYR. In transgenic mice we cannot exclude the possibility that terminals of the CA2/CA3 inputs were also activated by light, but the consistent observations in virus-injected wild-type animals indicate that direct activation of CA1 pyramidal cells is the main cause of iHFOs. Our experiments identified two cardinal components for ripple generation. First, activity of a few dozen pyramidal neurons is necessary for ripple generation. Second, fast GABA_A-receptor-mediated inhibition is an additional requisite for the generation of high-frequency oscillations. The necessary and sufficient requirements are further illustrated by the induction of iHFOs in deep neocortical layers and in the dentate gyrus. The neocortical iHFOs may be related to LFP ripples reported in deep neocortical layers upon strongly synchronized population bursts of activity (Kandel and Buzsáki, 1997; Grenier et al., 2001). How the optogenetically induced HFOs affect the spike content, incidence, and sequential neuronal activity during native ripples remains to be addressed.

The involvement of pyramidal neurons in ripple generation has been portrayed differently in the various models. A prominent computational model assumes that axo-axonal gap junctions connect the CA1 pyramidal neurons into a sparse electrically coupled network (Figure 1A). Critical assumptions of this model are that spikes in the axonal plexus excite pyramidal cells in both antidromic and orthodromic directions and that the connectivity graph and speed of propagation in the axonal network set the ripple frequency (Draguhn et al., 1998; Traub and Bibbig 2000; Traub et al., 2003). The strongest support for the axon-net model is that gap junction blockers abolish ripples both in vivo (Ylinen et al., 1995) and in vitro (Draguhn et al., 1998; Schmitz et al., 2001; Maier et al., 2003). However, connexin coupling between CA1 pyramidal cells have not been demonstrated, and gap junction blockers often interfere with receptor-mediated inhibition (Schmitz et al., 2001). Electrical coupling between interneurons, mediated by connexin 36 gap junction protein, is well demonstrated (Gibson et al., 1999), yet genetic ablation of connexin 36 does not alter in vivo ripples (Buhl et al., 2003; Pais et al., 2003). Furthermore, it is unclear how SPW-related excitation of the dendrites of CA1 pyramidal cells and interneurons would lead to the activation of the axonal plexus. One hypothesis is that tonic release of GABA can facilitate axonally generated spikes (Traub et al., 2003; Bähner et al., 2011). Our findings question this mechanism, because activation of PV and SOM interneurons, accompanied by presumed increase of released GABA, aborted rather than facilitated spontaneous ripples. Recurrent excitation by the sparse collaterals of CA1 pyramidal neurons has also been hypothesized as a mechanism for ripple timing (Memmesheimer 2010; Maier et al., 2011). Yet, this hypothesis does not explain why ripples in the CA3 region with its rich recurrent network are less expressed and more variable (Sullivan et al., 2011). Our observation that optogenetic activation and suppression of pyramidal neurons can induce and abolish ripples, respectively, clearly shows that pyramidal cell activation is a necessary (albeit not sufficient; see below) condition for ripple generation.

Despite the repeated observation that PV basket neurons fire phase-locked to ripple cycles and often at ripple frequency both in vivo (Buzsáki et al., 1992; Ylinen et al., 1995; Csicsvari et al., 1999; Klausberger et al., 2003; Klausberger and Somogyi, 2008; Rácz et al., 2009; Varga et al., 2012) and in vitro (Maier et al., 2003, 2011; Bähner et al., 2011; Hájos et al., 2013; Karlócai et al., 2014), the role of inhibition in ripple pacing has been debated. An early model assumed that SPW-related excitation of CA1 interneurons is sufficient to periodically inhibit CA1 pyramidal cells at ripple frequency (Figure 1B) (Ylinen et al., 1995; Whittington et al., 1995; Traub et al., 1996; Brunel and Hakim, 1999; Geisler et al., 2005; Taxidis et al., 2012). Yet, several studies dismissed the importance of inhibition altogether (Draguhn et al., 1998; Maier et al., 2011), despite the fact that ripples in vitro were abolished by blockade of GABA_A receptors (Maier et al., 2003), because fast oscillations could be reinstated by local puff of KCl (Nimmrich et al., 2005). Furthermore, perfusion of hippocampal slices with the GABA_A-receptor-positive allosteric modulator diazepam or a GABA reuptake inhibitor did not affect ripple frequency (Viereckel et al., 2013). These studies promoted the view that phasic inhibition is not responsible for setting the frequency of ripples. However, the KCl-induced oscillations were very fast (>200 Hz) and were coupled with long spike bursts of pyramidal cells, unlike naturally occurring ripples. On the other hand, systemic injection of diazepam and zolpidem in sleeping rats reduced the oscillation frequency (Ponomarenko et al., 2004), suggesting that inhibition may play a role in pacing ripple frequency. However, interpretation of this latter in vivo observation is also problematic, because the drugs also reduced the occurrence, amplitude, and duration of ripples.

Our findings demonstrate that fast GABA_A-receptor-mediated inhibition is critical for ripple generation. Focal application of the GABA_A receptor-antagonist PTX fully abolished iHFOs in a small drug-perfused volume. This finding demonstrates that even if axo-axonal interactions contributes to ripples (Figure 1A), fast inhibition is an obligatory condition. Inhibition can pace ripple frequency in two different ways. First, timing can be determined by the PYR-INT loop (Figure 1C). However, when the excitatory connections between pyramidal cells and interneurons were genetically compromised, ripples were not abolished, and instead, ripple power somewhat increased (Rácz et al., 2009). Second, ripple timing can be set by the interactions among interneurons. While interneuron activation alone (without pyramidal cell activation) could not generate LFP ripples (consistent with modeling studies; Schomburg et al., 2012), optogenetic activation of PV interneurons brought about ripple-frequency patterning of interneuron and pyramidal cell spikes, implying that ripple timing can be set by interactions among PV interneurons (Figure 1B), possibly enhanced by fast dendritic Ca²⁺ events in their dendrites (Chiovini et al., 2014). The correlation between SPW amplitude and ripple amplitude and frequency on the one hand and the correlation between light intensity and iHFO amplitude and frequency on the other hand can also be explained by excitation-mediated activation of the frequency-determining PV population. We therefore suggest that a hybrid model that includes SPW-induced transient excitation of pyramidal cells, combined with the pacing ability of interneuron interactions (Figure 1D; PYR-INT-INT model), can account for all known features of SPW-ripples in vivo and with most in vitro observations. It is important to emphasize that for ripple-related synchronization of pyramidal cells, it is sufficient that the rising phase of GABA_A-receptor-mediated inhibition is fast, because pyramidal neurons typically spike only once per ripple (Figure S1D), and different sets of pyramidal cells fire on subsequent ripple cycles.

“Fast Ripples” in the Absence of Inhibition

The SPW-ripple complex represents the most synchronous population pattern in brain networks (Buzsáki et al., 1992) and is controlled by a delicate spatiotemporal balance between excitation and inhibition (Figure 3). Such a high-risk balance is perhaps what makes the hippocampus the most epileptogenic zone of the brain. Focal application of PTX completely abolished optically induced ripples, followed by large-amplitude, fast LFP oscillations (>200 Hz) at variable delays, presumably when GABA_A receptor blockade affected larger numbers of pyramidal cells. These events resemble the “fast ripples” observed in the epileptic human hippocampus (Bragin et al., 1999) and occasionally in ripple models in vitro (Draguhn et al., 1998; Nimmrich et al., 2005). Although the receptor blockade and some optogenetic manipulations were carried out in anesthetized animals, several control experiments suggested that the results apply to the drug-free brain.

Our experiments demonstrate that physiological ripples and “fast ripples” arise from different mechanisms, since loss of fast inhibition disrupts the first and induces the latter. Similarly to our observations, perfusion of hippocampal slices with PTX generates “interictal spikes” (Wong and Traub, 1983) reminiscent of the “fast ripples” that we observed with PTX injection (Figure S4), in which nearly all pyramidal neurons participate in every event, typically firing a spike burst. Our findings illustrate that a shift in the excitatory-inhibitory balance may rapidly induce a qualitative change in the mechanisms underlying the generation of high-frequency oscillations, converting physiological ripples (generated by PYR-INT-INT interactions; Figure 1D) into larger amplitude, shorter, and faster pathological events (generated by inhibition-independent mechanisms).

Spatial Coherence of Locally Generated Ripples

When a CA3-generated SPW sweeps through the septo-temporal axis of the CA1 region, multiple foci of local ripples are generated (Patel et al., 2013). Consistent with this natural variability, the focally induced iHFOs can differ in power, frequency, and phase. On the other hand, when multiple CA1 locations are activated simultaneously, the local events become coherent and the frequency and phase differences between different sites are reduced (Figure 7). Our results show that interneurons are phase-locked to the light-induced oscillations even on those shanks where pyramidal cells are not directly activated by light and no LFP oscillations are detected. Furthermore, the high iHFO coherence between simultaneously activated loci is reduced by blocking fast inhibition, indicating that interneurons are critical for maintaining spatial coherence of ripples (Traub et al., 1996). Thus, in addition to the CA3-generated sweep that induces local oscillations, CA1 interneuron-interneuron interactions are likely responsible for coordinating multiple local ripple events at the temporal resolution of a single cycle and combining them into a spatially coherent event.

CA1 pyramidal cells represent the sole corticopetal output from the hippocampus. During SPW-ripples, they undergo spatiotemporally organized spiking reflected by population bursts (Foster and Wilson, 2006; Diba and Buzsáki, 2007; Karlsson and Frank, 2009). A potential goal of the synchronized CA1 ripples is to amplify the output messages of the hippocampus both by synchronizing the selected local pyramidal cells and by coordinating their activity patterns within the hippocampus. From this perspective, the physiological role of the interactions between the excitatory and inhibitory processes during ripples may be to rapidly select the dominant and suppress the competing assemblies and thereby propel forward temporally organized and strongly synchronous messages to downstream cortical and subcortical structures (Logothetis et al., 2012).

EXPERIMENTAL PROCEDURES

A total of 3,885 putative single cells (pyramidal cells and interneurons) were recorded extracellularly from the hippocampal CA1 region of 47 animals (five rats, 26 awake behaving mice, and 16 urethane-anesthetized mice); all animals expressed light-sensitive opsins in pyramidal cells, PV, and/or SOM interneurons and were implanted with single- or multi-shank silicon probes equipped with one or more optical fibers (Table S1). All animal handling procedures were approved by the Rutgers University and New York University Animal Care and Facilities committees. Optical stimuli (60–120 half-sine waves or 20–400 ms square pulses) were applied either to a single shank at a time or to multiple shanks simultaneously to induce or block high-frequency oscillations. For pharmacological experiments with CaMKII::ChR2 mice, animals were anesthetized with urethane (1.5 g/kg) and the GABA_A receptor blocker PTX was injected stereotactically into CA1 about 50–100 μm from the silicon probe.

Number of Illuminated Cells

The precise number of illuminated PYR may vary with light intensity, but an upper bound for somatic illumination in CA1 pyramidal layer may be obtained as follows. The optical fibers used (core radius, r₀ = 25 μm; etched to a cone, NA_eff = 0.37; Stark et al., 2012) were oriented perpendicularly to and ended at a distance of h ≤ 190 μm above the CA1 pyramidal layer (50 μm above the top recording site of a silicon probe shank spanning 140 μm). Thus, a disk of approximately V = Hπr² was illuminated, where H is the thickness of the CA1 pyramidal cell layer (~50 μm) and r = r₀+h•tan[sin⁻¹(NA_eff/n_out)]. Assuming a brain refractive index n_out = 1.36 (Binding et al., 2011) and CA1 neuronal density of 10⁵ mm⁻³ (West et al., 1991), the disk spans up to V = 10⁻³ mm³ and contains 1–100 somata (depending on h), which may consist of about 80 PYR and 20 INT. This upper bound ignores dendritic illumination, and thus the actual number of depolarized cells may be higher. Conversely, the estimate ignores optical shadowing by the probe shank (affecting about half of the disk volume), assumes that all cell bodies are light sensitive (incorrect even for pan-neuronal expression due to incomplete penetration), and assumes that the spiking threshold is infinitesimal (which is certainly incorrect); thus, the actual number of cells induced to spike is likely to be lower.

Closed-Loop Experiments

A single channel from the middle of the CA1 pyramidal cell layer was selected for real-time processing by a programmable DSP running at 25 kHz (RX6, Tucker-Davis Technologies). The root-mean-square (RMS) of the band-pass filtered (80–250 Hz) signal was computed in two running windows: long (2 s; RMS1) and short (8 ms; RMS2). Ripples were defined as events with RMS2 exceeding three times RMS1 (range, 3–3.5) for at least 8 ms. This resulted in online detection of the majority of the ripples two or three cycles after they were detected offline (median detection lag: 15 ms; range 12–24 ms; median false negative rate, 27%; range: 7%–45%, ground truth being the offline-detected ripples in the absence of light). Light stimulation was applied in alternation, yielding sham (detection/without stimulation) and light (detection and stimulation) conditions.

Offline Detection of Ripples

Ripples were detected independently at each recording site. The wide-band signal was band-pass filtered (80–250 Hz; difference-of-Gaussians, DOG; zero-lag, linear phase FIR), and instantaneous power was computed by clipping extreme values to 5 SD (to minimize ripple-rate induced biasing), rectifying, and low-pass filtering. The band-pass filtering specifics were chosen to minimize ringing and phase distortions that often occur upon using other parameters (for instance, a 100–300 Hz bandpass is inadequate for spontaneous ripples that typically peak at 110–180 Hz during waking and may be as low as 90 Hz during anesthesia) (Figure S1). The low-pass filter cutoff was at a frequency corresponding to π cycles of the mean band-pass (52.5 Hz). The mean and SD were computed from the power of the clipped signal during SWS (defined as non-theta, non-movement periods) in the absence of light stimulation. Subsequently, the power of the original trace was computed, and all events exceeding 5 SD from the mean were selected. Short events (duration <15 ms) were discarded, and adjacent events (gap <15 ms) were merged. Events were then expanded until the power fell below 2 SD and aligned by the trough (of the nonrectified signal) closest to the peak power. This procedure was carried out independently on every recording site of each shank. The site with the maximal ripple amplitude was determined for each shank separately; this was defined as the center of the CA1 pyramidal cell layer (Mizuseki et al., 2011), and subsequent analyses were based on ripples detected or iHFOs generated at that recording site.

Offline Analysis of Closed-Loop Experiments

For the purpose of determining the contribution of specific neuronal types to spontaneous ripples, detection misses are of little importance, whereas false detections are critical, as they may erroneously suggest a ripple interruption effect. Thus, for each experiment separately, online-detected events were classified as true-positive (TP) or false-positive (FP), as follows. First, sham events were tagged as TP or FP based on their temporal overlap with offline-detected ripples. Second, the median detection lag for the TP sham events was determined relative to the onset of offline-detected ripples, and the predetection power during this time was computed for all events. Third, a Mahalanobis-based classifier was built based on the distributions of the predetection power of the tagged sham events, each (sham and light) online-detected event was classified as TP or FP, and all FP events were excluded. The Bayes error of this classifier (determined by the classified versus tagged sham events) was 16% (median; range: 9%–28%), which is the asymptotic fraction of nonripple events that were detected as ripples online—in both sham and light conditions. We verified that any observed effects are not due to classification errors by assuming a worst case scenario, thereby excluding the corresponding fraction of events (lowest predetection power) only from the light-condition. All results were maintained regardless of this manipulation, and therefore, the unmodified results are reported in the main text.