Two-Part Test of Vaccine Effect

SUMMARY

Vaccine benefit is usually two-folded: (1) prevent a disease, or, failing that, (2) diminish the severity of a disease. To assess vaccine effect, we propose two adaptive tests. The weighted two-part test is a combination of two statistics, one on disease incidence and one on disease severity. More weight is given to the statistic with the larger a priori effect size, and the weights are determined to maximize testing power. The randomized test applies to the scenario where the total number of infections is relatively small. It uses information on disease severity to bolster power while preserving disease incidence as the primary interest. Properties of the proposed tests are explored asymptotically and by numerical studies. Though motivated by vaccine studies, the proposed tests apply to any trials that involve both a binary and a continuous outcome for evaluating treatment effect.

1 Introduction

Some vaccines may have two benefits: (1) prevent a disease or, failing that, (2) diminish the severity of a disease. For example, an HIV vaccine should first and foremost prevent HIV, but failing that, it might lower the viral loads of people who get HIV. Thus, data consist of pairs (X_i, Y_i), where X_i is the indicator that the person gets the disease and Y_i is the viral load if the person gets the disease. If the person is disease-free, Y_i = 0.

One approach would consider the outcome to be Y, and then test whether Y values in the vaccine group tend to be lower than Y values in the placebo group. This is a test of the total “burden of illness.” This approach creates “lumpy” data because the nonzero Y values may be quite far from 0. Having a bolus of zeroes could seriously inflate the variance if a t-test is used, leading to poor power [1]. Avoiding this problem by using a rank test creates another problem: tied ranks from the zeroes. This is not problematic if the number of zeroes is small, but naturally we hope that the vaccine will create many zeroes. A further criticism of trying to summarize the entire effect with the single variable Y is that it may obscure what is usually considered the most important part of a vaccine, namely preventing disease.

Another approach is to test separately the two components, disease incidence and viral load of those who get disease. Let Z_X be the z-statistic comparing the proportions infected in the vaccine and placebo arms, and Z_Y be the t-statistic comparing log viral loads of those infected. Under the null hypothesis that viral loads of those infected are not altered by the vaccine, Z_Y has mean 0. Lachenbruch’s test refers $Z_X^2+Z_Y^2$ to a chi-square distribution with 2 degrees of freedom [2]. The justification is that under the null hypothesis of no effect of vaccine on viral load, Z_X and Z_Y are approximately independent (see Section 2).

One criticism of Lachenbruch’s test is that Z_Y is defined for people who get the disease. If the vaccine has some effect on disease prevention, the people in the placebo group getting the disease may be different from the people in the vaccine group getting the disease. For example, suppose that only people with weak immune systems get the disease, and that the vaccine prevents some of them from getting it by boosting their immune systems; the vaccinees who do get it must have had very weak immune systems such that even the vaccine’s boost could not prevent disease. Therefore, people in the vaccine group with disease tend to have weaker immune systems at baseline than people in the placebo group with disease. If infected vaccinees are inherently different from infected placebo participants, it may be difficult to interpret the results of Z_Y [3] [4].

A second criticism of Lachenbruch’s test is that Z_X may be negative (indicating harm on disease incidence), whereas Z_Y may be positive (indicating benefit on viral load), or vice-versa. Such conflicting results should decrease, not increase, our confidence in the vaccine. It would seem preferable to use (Z_X + Z_Y)/2^1/2 as the test statistic so that conflicting directions of effect make statistical significance more difficult to achieve.

A third criticism of Lachenbruch’s test is that $Z_X^2+Z_Y^2$ gives equal weight to the statistics testing disease incidence and viral load. It seems preferable to give more weight to the more important outcome of disease prevention.

Our goal is to develop an adaptive combination test of Z_X and Z_Y. We first consider a weighted two-part test, which is a weighted linear combination of Z_X and Z_Y. It gives more weight to the statistic with the larger a priori effect size, and the weights are determined to maximize power of the test. We next investigate the scenario in which the total number of infections is relatively small, either by design or because of a lower than expected event rate. This leads us to propose a randomized test, which preserves the preeminence of Z_X but still uses Z_Y to bolster power. It is a compromise between the test of the most clinically relevant outcome (disease incidence) and the most powerful linear combination test. The proposed adaptive tests circumvent the last two criticisms for Lachenbruch’s test, where the randomized test additionally alleviates the first criticism.

2 Test Statistics and Their Approximate Joint Distribution

2.1 Test Statistics

The data for the n_C control and n_V vaccine participants consist of a 2 × 2 table summarizing the random numbers M_C and M_V of infections in each arm (Table 1), and the viral loads of those infected in each arm. The total numbers of participants and infected participants are n and M, respectively.

Table 1.

Infection results.

	Infected
Control	MC		nC
Vaccine	MV		nV
	M		n

To test the incidence null hypothesis ${\mathrm{H}}_0^X:p_C=p_V$ where p_C and p_V are the probabilities of infection in the two arms, form the usual z-score comparing proportions:

$$Z_X=\frac{{\widehat{p}}_C-{\widehat{p}}_V}{\sqrt{\widehat{p}(1-\widehat{p})(1/n_C+1/n_V)}},$$ (1)

where ${\widehat{p}}_C=M_C/n_C$, ${\widehat{p}}_V=M_V/n_V$ and $\widehat{p}=M/n=(n_C{\widehat{p}}_C+n_V{\widehat{p}}_V)/n$. A closely related z-statistic compares the observed number of people in the upper left cell of Table 1 to the number expected from its central hypergeometric null distribution:

$${Z\prime }_X=\frac{\text{Observed}-\text{Expected}}{\sqrt{\text{var}(\text{Observed})}}=\frac{M_C-{\mathit{Mn}}_C/n}{\sqrt{\frac{n_C{n}_{V}M(n-M)}{n^2(n-1)}}}.$$

It is easy to show that ${Z\prime }_X=\sqrt{(n-1)/n}{Z}_X$. If we remove the square root sign in the denominator, we get an estimator of the log odds ratio:

$$\ln (\mathrm{OR})\approx \frac{\text{Observed}-\text{Expected}}{\text{var}(\text{Observed})}=\frac{M_C-{\mathit{Mn}}_C/n}{\frac{n_C{n}_{V}M(n-M)}{n^2(n-1)}}.$$

Let Z_Y be the t-statistic testing the viral load (VL) null hypothesis ${\mathrm{H}}_0^Y:{\mu }_C={\mu }_V$ that appropriately transformed (e.g., log-transformed) viral loads have the same means in the two arms:

$$Z_Y=\frac{{\overline{Y}}_C-{\overline{Y}}_V}{\sqrt{{\widehat{\sigma }}^2(1/M_C+1/M_V)}},$$ (2)

where ${\widehat{\sigma }}^2$ is the usual pooled variance estimate, $\{(M_V-1)s_V^2+(M_C-1)s_C^2\}/(M-2)$.

We determine next the approximate joint distribution of (Z_X, Z_Y), showing that Z_X and Z_Y are approximately independent under typical assumptions.

2.2 Approximate Independence of Z_X and Z_Y

In this section we show that Z_X and Z_Y are asymptotically independent under the assumptions we commonly make in clinical trials. Assume first the null hypothesis $H_0^Y$ of no effect of vaccine on viral load of people who get the disease (we make no assumption about whether the vaccine affects disease incidence). Condition on (M_C, M_V), and suppose that M_C and M_V are large. The test statistic Z_Y comparing viral loads might depend on (M_C, M_V); for instance, under normality, the t-statistic (2) has degrees of freedom (d.f.) M_C + M_V − 2. Nonetheless, the t-distribution is virtually indistinguishable from the standard normal if the d.f. is large. Therefore, the conditional distribution of Z_Y given (M_C, M_V) is virtually the same—approximately standard normal—for any (M_C, M_V). Because the conditional distribution of Z_Y given (M_C, M_V) essentially does not depend on (M_C, M_V) for large M_C and M_Y, Z_Y is approximately independent of (M_C, M_V) when n is large. Also, Z_X is a function of (M_C, M_V), so Z_X is approximately independent of Z_Y as well. We implicitly assumed normality of log viral loads, but the t-distribution holds asymptotically even without this assumption. Therefore, we have argued that under the viral load null hypothesis $H_0^Y$ Z_X and Z_Y are approximately independent for large sample sizes irrespective of whether log viral loads are normally distributed and irrespective of whether the incidence null hypothesis holds.

The two statistics Z_X and Z_Y are approximately independent even under local alternative hypotheses (see appendix). Simulation results support this conclusion. Figure 1 shows the correlation between Z_X and Z_Y for alternatives close to the null for incidence (left panel) and for log viral load (right panel) where the sample size is 1000 per arm. The left panel shows that when the odds ratio for incidence is 1.2, the correlation between Z_X and Z_Y is close to 0 even if the effect on log viral load is fairly large; e.g., the mean difference in log viral load is ±2 standard deviations. Likewise, the right panel shows that when the mean difference in log viral load is 0.20 standard deviations, the correlation between Z_X and Z_Y is mostly between −0.05 and 0.05 even if the odds ratio for incidence is 0.5 or 2.0.

Figure 1.

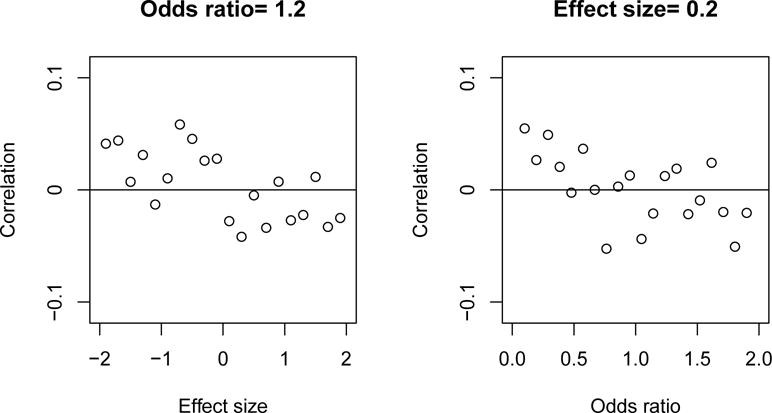
Correlation between Z_X and Z_Y under a local alternative for vaccine effect on incidence (left panel) and a local alternative for vaccine effect on viral load (right panel).

When large sample sizes are affordable, clinical trials usually target local alternatives. Therefore, Z_X and Z_Y are approximately independent. When sample sizes are not very big, the asymptotic independence may not hold. In the next section, two versions of the two-part test are developed, the asymptotically weighted test and the conditional test. The former applies to large sample size trials and the latter does not require a large sample size.

3 Weighted Two-Part Test

3.1 Asymptotic Weighted Two-Part Test

For w ∈ [0, 1], consider weighted combinations

$$Z_w=\sqrt{w}{Z}_X+\sqrt{1-w}{Z}_Y$$ (3)

of the disease incidence and viral load test statistics. Under local alternatives for disease incidence and viral load, Z_X and Z_Y are approximately independent, both asymptotically normally distributed with unit variance. Therefore, Z_w is approximately normally distributed with unit variance and mean

$$E_w=\sqrt{w}{E}_X+\sqrt{1-w}{E}_Y,$$ (4)

where E_X = E(Z_X) and E_Y = E(Z_Y | M_C, M_V).

Since most vaccine trials are powered for the disease endpoint, we usually have a projected value for E_X. It may be more difficult to specify E_Y, see section 5 for an example. The optimal weight w_opt should maximize (4) over w ∈ [0, 1]. We can find w_opt by solving dE_w/dw = 0 or using the geometrical argument that the vector $(w_{\mathrm{opt}}^{1/2},{(1-w_{\mathrm{opt}})}^{1/2})$ should have the same direction as (E_X, E_Y). Either way, we obtain

$$w_{\mathrm{opt}}=\frac{E_X^2}{E_X^2+E_Y^2};Z_{w_{\mathrm{opt}}}=\frac{E_X{Z}_X+E_Y{Z}_Y}{\sqrt{E_X^2+E_Y^2}}.$$ (5)

The mean of $Z_{w_{\mathrm{opt}}}$ is ${(E_X^2+E_Y^2)}^{1/2}$, so the power at treatment effect E_X and E_Y is approximately

$$\text{Power}(Z_{\mathrm{wopt}})=1-\mathrm{\Phi }(z_{\alpha }-\sqrt{E_X^2+E_Y^2}).$$

When E_X = E_Y = E, the optimal weighted combination, (Z_X + Z_Y)/2^1/2, weights the two z-statistics equally, and power is approximately 1 − Φ(Z_α − 2^1/2E). Thus, if each z-statistic has one-tailed α = 0.025 and 85% power, then E ≈ 1.96 + 1.04 = 3, and power for the weighted test is approximately 1 − Φ(−2.28) = 0.99. Therefore, there is a substantial power advantage of the weighted statistic over the disease incidence statistic. This is borne out in Figure 2, which shows that the weighted combination is more powerful than both Fisher’s exact test and Lachenbruch’s test.

Figure 2.

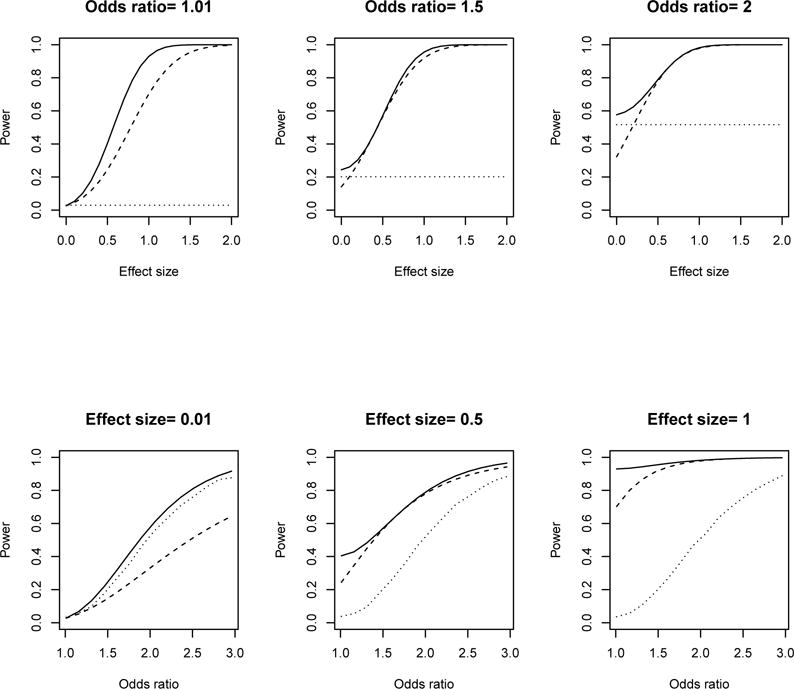
Power for the weighted two-part test (solid line), Fisher’s exact test (dotted line), and Lachenbruch’s test (dashed line) over prospective vaccine effect on incidence and effect size of viral load at n_C = n_V = 250.

The above development is based upon the asymptotic properties of Z_X and Z_Y. When the sample size is not large, Z_w may not be close to normally distributed with unit variance. Consequently, the optimal weights in (5) may be not correct. The following section introduces the conditional two-part test where a large sample size is not required.

3.2 Conditional Two-Part Test

Sometimes the number of disease events is not large enough to rely on asymptotics. In this case one can construct an exact test using the weighted combination (3) that maximizes power conditional on the lumped data from the two arms. Remaining blinded, we observe M = m and the lumped variance ${\widehat{\sigma }}_L^2$ of the log viral loads of all participants in the two arms. Let $\theta =\{p_C/(1-p_C)\}/\{p_V/(1-p_V)\}$ be the control to vaccine odds ratio. Given M = m, M_C follows a noncentral hypergeometric distribution:

$$P_{\theta }(M_C=m_C|M=m)=\frac{\left(\begin{array}{c}{n}_C\\ m_C\end{array}\right)\left(\begin{array}{c}{n}_V\\ m-m_C\end{array}\right){\theta }^{m_C}}{{{\displaystyle \sum }}_{k=0}^m\left(\begin{array}{c}{n}_C\\ k\end{array}\right)\left(\begin{array}{c}{n}_V\\ m-k\end{array}\right){\theta }^k}.$$ (6)

Under the null hypothesis, θ = 1 and (6) simplifies to

$$P_1(M_C=m_C|M=m)=\frac{\left(\begin{array}{c}{n}_C\\ m_C\end{array}\right)\left(\begin{array}{c}{n}_V\\ m-m_C\end{array}\right)}{\left(\begin{array}{c}n\\ m\end{array}\right)}.$$ (7)

Consider the weighted combination (3) at a given w, where Z_X = Z_X(M_C) depends on M_C. Determine the critical value c solving:

$$\begin{array}{l}\alpha =P(\sqrt{w}{Z}_X(M_C)+\sqrt{1-w}{Z}_Y\ge c|M=m)\\ ={\displaystyle \sum }_{m_C=0}^m\{1-G_{m-2}(\frac{c-\sqrt{w}{Z}_X(m_C)}{\sqrt{1-w}}\left)\right\}{P}_1(M_C=m_C|M=m),\end{array}$$

where G_m−2 is the cumulative distribution function of the central t-distribution with m − 2 degrees of freedom, α is the nominal type-I error rate and P₁(M_C = m_C | M = m) is from Equation (7).

Once c has been determined, compute power as follows. Let ${\widehat{E}}_Y$ be the estimated expected value of Z_Y at the hypothesized effect size of vaccine effect on viral loads. Let $G_{m-2,{\widehat{E}}_Y}$ be the cumulative distribution function of the noncentral t-distribution with m − 2 degrees of freedom and noncentrality parameter ${\widehat{E}}_Y$. Power is estimated by

$${\displaystyle \sum }_{m_C=0}^m\{1-G_{{\widehat{E}}_Y}(\frac{c-\sqrt{w}{Z}_X(m_C)}{\sqrt{1-w}}\left)\right\}{P}_{\theta }(M_C=m_C|M=m),$$

where P_θ(M_C = m_C | M = m) is given by (6). The optimal weight w_opt is picked over w ∈ [0, 1] to maximize the power.

4 Randomized Test

Even though (5) is optimal in terms of power, it is not necessarily optimal in terms of clinical importance. The primary endpoint in vaccine trials is usually disease incidence, which corresponds to w = 1. Therefore, we seek ways to improve power while still maintaining the preeminence of the disease incidence endpoint. One way is to use disease incidence as the primary endpoint, and Z_wopt as a secondary endpoint. An alternative to ensure that the test on incidence is primary, while still incorporating information from the test on viral load, is to use a randomized test of incidence. With a nonrandomized test and a discrete test statistic, the type I error rate can fall short of the desired level. For example, when rejecting the null hypothesis for large values of a discrete statistic T_d, we may find that P(T_d ≥ 10) = 0.01, whereas P(T_d ≥ 9) = 0.028. If we are using a nonrandomized, one-sided test at level 0.025, the rejection region is T_d ≥ 10, and its actual type I error rate is 0.01 instead of 0.025. We would not be able to reject the null hypothesis if T_d = 9. If we use a randomized test, then we would reject with probability p if T_d = 9, where p is such that P₀(T_d ≥ 10) + pP₀(T_d = 9) = 0.025, and P₀ denotes probability computed under the null hypothesis $H_0^X$.

Randomized tests are uncommon and have been ridiculed. In the following is an example that the authors learned from Dr. Debabrata Basu through personal communication. Let X₁, …, X₁₀ be outcomes of 10 coin flips with probability π of heads, and test H₀ : π = 1/2 versus H₁ : π > 1/2 at α = 1/2⁹. The most powerful test rejects if all 10 flips are heads, and P(10 heads) = 1/2¹⁰. If we also reject for 9 heads, then the type I error rate is too large: 1/2¹⁰ + 10/2¹⁰ > 1/2⁹. To achieve α = 1/2⁹, reject with probability 1/10 if 9 heads occur. If 9 heads, reject ⇔ the lone tail is the 10th flip. The rejection region is then: HH … HH or HH … HT; i.e., we reject ⇔ the first 9 flips are heads. How, critics argue, could the most powerful test actually throw out the 10th observation?

Notwithstanding the strange example in the preceding paragraph, the main arguments against a randomized test are 1) it seems wrong to increase the probability of rejection based solely on a random event, and 2) repeating the test with the same data might give a different answer. The randomized test we propose suffers neither of these shortcomings.

Here is how we propose to use a randomized test with vaccine data. With Fisher’s exact test on incidence, the actual type I error rate for a nonrandomized test can be substantially less than α if the total number of infections is not very large. For example, Table 2 shows hypothetical results for a trial randomizing 60 participants in a 2:1 fashion to vaccine or placebo. With 20 total infections, the one-tailed p-values for M_C = 10 and M_C = 11 are 0.05101 and 0.01365, respectively. To ensure a one-tailed error rate of 0.025, we reject the null hypothesis for a nonrandomized test if M_C is 11 or more. The actual type I error rate is about half of the intended level.

Table 2.

Infection results.

	Infected
Control	MC		20
Vaccine	MV		40
	20		n

A randomized test rejects the null hypothesis with probability 1 if M_C ≥ 11, and with probability p if M_C = 10, where P(M_C ≥ 11 | M = 20) + pP(M_C = 10 | M = 20) = 0.025. That is, the test rejects the null hypothesis with probability p = (0.025 − 0.01365)/P(M_C = 10 | M = 20) = 0.304 if M_C = 10. The type 1 error rate for this randomized test is 0.025. Instead of introducing auxiliary randomization independent of the data from the trial, we exploit the fact that under the null hypothesis, the viral load test statistic is independent of the incidence test statistic. Conditioned on M_C and M_V, the p-value p_Y for the t-test on log viral loads has a uniform [0, 1] distribution under the null hypothesis. Therefore, we can perform a randomized test by rejecting the null hypothesis if p_Y ≤ 0.304. This randomized test keeps the best of both worlds: it retains the incidence test statistic as the primary outcome, but in borderline settings, it incorporates corroborative information from the vaccine’s effect on log viral load to justify a declaration of statistical significance.

Figure 3 shows power of the randomized test (dotted-dashed line) and Fisher’s exact test (dotted line) for the example in Table 2, where the odds ratio is 3 and the effect size of the vaccine effect on viral loads ranges from 0 to 2. In such a setting of smaller than expected number of disease endpoints, the randomized test increases power over Fisher’s test while still maintaining incidence as primary outcome. Also shown are the weighted two-part test (solid line) and Lachenbruch’s test (dashed line). These have substantially greater power than Fisher’s test and the randomized test in this example, but they may fail the goal of preserving disease incidence as the primary interest.

Figure 3.

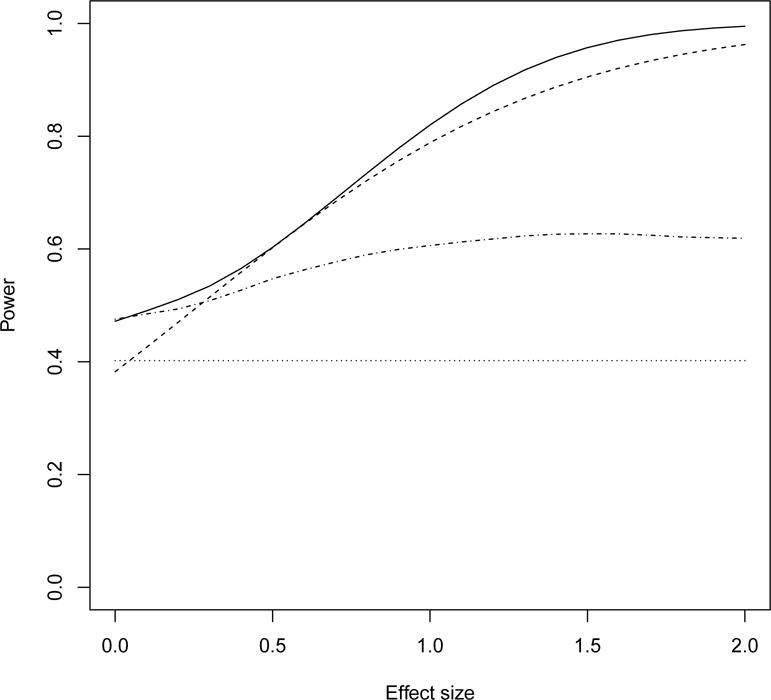
Power of the randomized test (doted-dashed line), Fisher’s exact test (dotted line), the weighted two-part test (solid) and Lachenbruch’s test (dashed line) for the example in Table 2.

5 Example

We illustrate the proposed two-part test with a Phase 3 HIV-1 preventive vaccine trial VAX004. This trial, evaluating a recombinant glycoprotein 120 vaccine for prevention of HIV, randomized 3598 participants to vaccine and 1805 to placebo [5]. The primary endpoint was HIV infection. Imagine, hypotheti-cally, that in the planning phase, the designers of VAX004 were considering the use of a two-part test. Given the very large size of the trial, the randomized test in Section 4 would be nearly identical to Fisher’s exact test on incidence, so we do not consider that test further. Instead, consider the approximately optimal weighted test. Trial planners would probably argue that the weighted two-part test should be a secondary analysis because, after all, HIV infection should be the most important outcome. The next thing they would have to specify in advance for this secondary analysis is the relative effect of the vaccine on infection versus log viral load. Suppose they believed that the relative effect (in terms of expected z-score) on incidence should be twice as great as the relative effect on log viral load; E_X = 2E_Y Then the optimal weight is $w_{\mathrm{opt}}=E_X^2/(E_X^2+E_Y^2)=4E_Y^2/(4E_Y^2+E_Y^2)=0.80$. That is, the weighted test statistic is $\sqrt{0.80}{Z}_X+\sqrt{1-.080}{Z}_Y=0.894Z_X+0.447Z_Y$. If the type I error rate is 0.025 and the power for the incidence endpoint is 0.90, then E_X = 1.96 + 1.28 = 3.24, and E(Z_wopt) = 0.894(3.24) + 0.447{(1/2)3.24} = 3.62. Power for the weighted combination test is approximately Φ(3.62 − 1.96) = 0.95.

Unfortunately, the data for VAX004 shown in Table 3 reveal that neither the infection nor log viral load results were close to being statistically significant; the control to treatment odds ratio was 1.09, Z_X = 0.71, while the control to treatment difference in mean log viral loads was −0.035, Z_Y = −0.37. The two-tailed p-values for Fisher’s exact test, Lachenbruch’s test, and the optimal weighted combination test are 0.48, 0.72, and 0.87, respectively. Note that results for viral load were slightly in the adverse direction, which properly increased the p-value of Z_opt because results for incidence and log viral load conflicted (although both were consistent with chance).

Table 3.

Results of VAX004 HIV vaccine trial.

	Control	Vaccine	Z-Score
Sample Sizes (nC, nV)	1805	3598
HIV Infections (mC, mV)	123	227	ZX = +0.71
Log VL ( $\overline{Y}\pm s$)	4.152 ± 0.84	4.187 ± 0.86	ZY = −0.37

6 Discussion

This paper on two-part tests in a vaccine setting shows that a weighted combination of z-statistics on incidence and log viral load can be substantially more powerful than alternatives such as Fisher’s exact test on incidence and Lachenbruch’s sum of squares test statistic. We derive the optimal weighting based on the pre-specified expected effects on the two endpoints, and show how to compute its approximate power. But because incidence is usually considered the most important outcome, this optimal weighted combination is probably best suited as a secondary analysis.

In some cases the total number of infections may not be large. One could then modify the procedure by using the conditional exact procedure described in Section 3.2. We also present a method that attempts to balance the countervailing properties of increasing power and maintaining incidence as the most important outcome in the setting of a relatively small number of infections. This randomized test incorporates information from the log viral load outcome to “break the tie” when the infection test statistic is borderline. We believe that both the weighted test and randomized test have distinct advantages over currently used procedures, and should be used in vaccine trials.

This work considers the vaccinated subjects falling into two categories: not infected or infected with detectable viral loads. When viral load readings are subject to censoring, for example, due to detection limits, methods in [6] may be considered.

Appendix: Approximate Independence of (Z_x, Z_y) under a Local Alternative for Viral Load

Now consider an alternative hypothesis under which the vaccine has an effect on viral load. If we fix the vaccine’s effect on viral load, then power approaches 1 as the sample size tends to infinity. But a typical clinical trial has, say, 80% or 90% power. Therefore, to do asymptotics in a way that represents what might actually happen in a clinical trial, we let the size of the effect tend to 0 as the sample size tends to infinity in such a way that the power of Z_Y approaches a limit other than 1. This is very analogous to approximating a binomial (n, p_n) probability with a Poisson (λ) probability when n → ∞ and p_n → 0 such that np_n → λ. The viral load ‘local’ alternative hypothesis we consider is

$$\frac{{\mu }_C-{\mu }_V}{\sigma }={\delta }_n,\text{where}\sqrt{n}{\delta }_n\to A\text{as}n\to \infty$$ (8)

for some constant A. Suppose that n_C/n → λ as n → ∞. The conditional distribution of Z_Y given M_C and M_V is approximately normal with unit variance and mean

$$\begin{array}{l}{E}_Y=\mathrm{E}(Z_Y|M_C,M_V)\\ =\frac{\sqrt{n}{\delta }_n}{\sqrt{n(1/M_C+1/M_V)}}\\ =\sqrt{n}{\delta }_n\sqrt{\frac{M_C}{n_C}\frac{M_V}{n_V}\frac{n_C}{n}\frac{n_V}{n}\frac{1}{(\frac{M_C}{n_C}\frac{n_C}{n}+\frac{M_V}{n_V}\frac{n_V}{n})}}\\ \to A\sqrt{\frac{p_C{p}_V\lambda (1-\lambda )}{\lambda p_C+(1-\lambda )p_V}}.\end{array}$$ (9)

The specific mean (9) is not important; what matters is that it does not depend on M_C and M_V. Therefore, the conditional distribution of Z_Y given (M_C, M_V) is approximately the same—normal with unit variance and mean given by (9)— regardless of (M_C, M_V). This means that Z_Y is approximately independent of (M_C, M_V), and therefore of any function of (M_C, M_V), including Z_X. We conclude that Z_X and Z_Y are approximately independent under a local alternative hypothesis for viral load, irrespective of whether the incidence null hypothesis holds.