Mechanism of substrate translocation by a ring-shaped ATPase motor at millisecond resolution

Abstract

Ring-shaped, hexameric ATPase motors fulfill key functions in cellular processes, such as genome replication, transcription or protein degradation, by translocating a long substrate through their central pore powered by ATP hydrolysis. Despite intense research efforts, the atomic-level mechanism transmitting chemical energy from hydrolysis into mechanical force that translocates the substrate is still unclear. Here we employ all-atom molecular dynamics simulations combined with advanced path sampling techniques and milestoning analysis to characterize how mRNA substrate is translocated by an exemplary homo-hexameric motor, the transcription termination factor Rho. We find that the release of hydrolysis product (ADP+Pi) triggers the force-generating process of Rho through a 0.1 millisecond-long conformational transition, the time scale seen also in experiment. The calculated free energy profiles and kinetics show that Rho unidirectionally translocates the single-stranded RNA substrate via a population shift of the conformational states of Rho; upon hydrolysis product release, the most favorable conformation shifts from the pre-translocation state to the post-translocation state. Via two previously unidentified intermediate states, the RNA chain is seen to be pulled by six K326 side chains, whose motions are induced by highly coordinated relative translation and rotation of Rho’s six subunits. The present study not only reveals in new detail the mechanism employed by ring-shaped ATPase motors, for example the use of loosely bound and tightly bound hydrolysis reactant and product states to coordinate motor action, but also provides an effective approach to identify allosteric sites of multimeric enzymes in general.

Introduction

One of the most remarkable inventions of biological evolution are molecular motors driven by energy released from ATP hydrolysis. Among such motors, ring-shaped, hexameric motors participate in many vital processes, such as DNA replication, transcription, chromosome segregation, protein degradation and maintenance of pH homeostasis;^1,2 most of these hexameric motors belong to the so-called Additional Strand Catalytic glutamatE (ASCE) superfamily of proteins.¹ Emerging evidence shows that a number of these hexameric motors can be targets for cancer therapy.^3–6 Characterizing the atomic level mechanism of their function on a biologically relevant time scale (millisecond or longer) could aid the development of anticancer drug design.⁷

The function of the ring-shaped motors is carried out in a series of repeated steps, by generating linear force or torque on the substrate (nucleic acid strand, polypeptide or central stalk) inside the central pore of the ring. Each step of the motors contains, according to single-molecule observation, a dwell phase of relative long duration and a motor-action phase.² During the dwell phase, the motor is energetically charged through the occurrence of three chemical processes, namely (1) ATP binding, (2) release of existing (i.e. “old”) ATP hydrolysis product, and (3) hydrolysis of ATP into “new” product, before the next motor-action phase takes place. This scenario is illustrated schematically in Figure S1 in Supporting Information. Interestingly, none of the three chemical processes during the dwell phase are directly involved in mechanical force generation since these processes happen at subunit-subunit interfaces along the ring, distant from the substrate binding site inside the central pore where mechanical force is actually being applied. The question addressed in the present study is how the free energy stored in the motor during the dwell phase is transferred to power substrate motion in the motor-action phase.

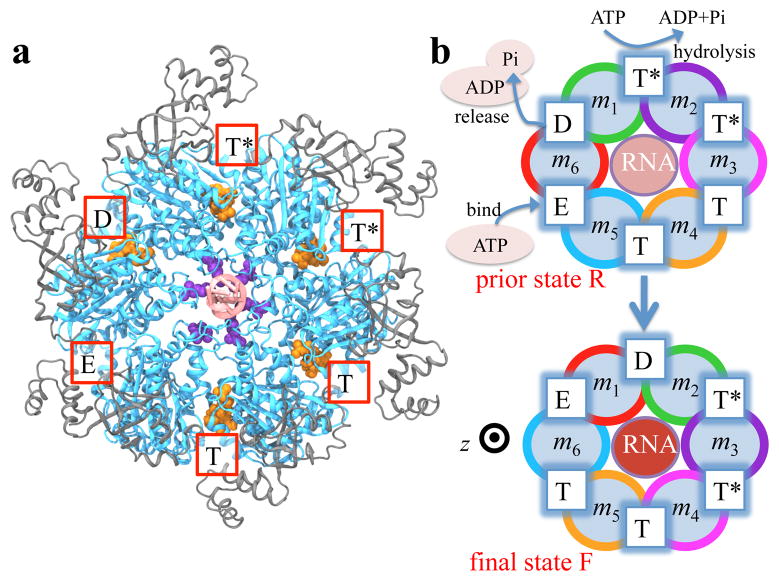
Crystal structures of hexameric helicases^8–10 and F₁-/V₁-ATPase ^11,12 with substrates and ligands (ATP-mimic molecules) bound provide evidence that large-scale conformational transitions are responsible for the substrate movement. In the present study we focus on an exemplary homohexameric helicase, Rho, whose equilibrium structure in complex with its RNA substrate and ligands (ATP analogue ADP · BeF₃) has been solved. 9 Rho is a key factor in bacterial gene expression and regulation,¹³ with a primary role in transcription termination through translocating the nascent mRNA in the 5′ → 3′ direction and terminating transcription upon reaching the RNA polymerase.^14–16 The asymmetric structure of Rho⁹ reveals that the six interfaces between Rho’s six subunits exhibit a specific circular pattern of different conformational states in the ATP hydrolysis cycle, the states being related to six sequential ligand binding states T*, T*, T, T, E, D shown and defined in Figure 1a. According to the crystal structure, Rho translocation, driven by ATP binding, hydrolysis and product release processes, should involve rotary reaction steps (Figure 1b). In each step the mentioned circular conformational pattern is shifted by one subunit or, rather, by 60° around the Rho ring. Such a rotary reaction mechanism, postulated originally by Boyer for F₁-ATPase, ¹⁷ has also been suggested, based on crystal structures, for other hexameric helicases^8,10 and F₁-/V₁-ATPase, ^11,12 the latter of which share considerable sequence and structural similarities with Rho.¹⁸

Figure 1.

Structure and proposed rotary reaction mechanism of Rho hexameric helicase. (a) Structure modeled based on the reported Rho crystal structure (pdb code: 3ICE⁹). Rho subunits consist of a C-terminal domain (blue) and an N-terminal domain (grey). Active sites of the ATPase cycle are located at the subunit-subunit interfaces and are labeled according to the state of ATP at the respective sites, namely, hydrolysis-competent (T*), ATP-bound (T), “old” product (D) and empty (E) state, respectively. ATP, ADP and Pi are shown in orange. K326 residues (purple), contributed by each subunit and altogether arranged in a roughly helical stair case fashion, are located in the central channel of the Rho hexamer where RNA (pale red) is bound, likewise in a roughly helical conformation. (b) Proposed rotary reaction mechanism.⁹ Rho’s six identical subunits are labeled m₁, m₂, …, m₆; the different colors of the six subunits’ circular peripheries indicate schematically that the subunits assume different interface conformations in prior state R. In binding ATP, releasing ADP+Pi and hydrolyzing ATP to ADP, the pattern of ligand binding states corresponding to the surface conformations in the prior state R, T*T*TTED, shifts to DT*T*TTE in the final state F. As one can easily recognize, the ligand binding states of R, after a 60° clockwise rotation around the z-axis, are the same as those of F. In going from R to F, RNA is propelled as indicated by pale (RNA further away from viewer) and intense red (RNA closer to viewer) coloration.

Despite the valuable information provided by the crystal structure,⁹ various biochemistry experiments^19–21 and a single-molecule study²² on Rho, the following three questions remain unanswered: (i) The rate limiting step in the Rho hydrolysis cycle, the latter combining dwell phase and motor-action phase, seems to be release of “old” hydrolysis product as suggested by experiments,^19,20 but whether and how this product release triggers the ring to exert force on the RNA substrate is unknown. (ii) A specific direction (clockwise in the case of Rho) of the rotary reaction steps, along with an asymmetry pattern of the ring subunits interacting with the substrate,²³ is required for the substrate’s unidirectional translocation.¹ How is the direction of the rotary reaction step selected and maintained, or in how far is the transition involved in Rho’s motor-action phase (Figure 1b) energetically favorable? (iii) What conformational transition arises at the “new” product binding site such that “new” product turns into “old” product, and can be released.

Previous computational studies on ring-shaped motors have shed light on the coupling between substrate dynamics and coordinated subunit conformational transition during the ATP hydrolysis cycle; however the studies included only coarse-grained simulations^24–27 or enforced-rotation simulations of the central stalk in the all-atomic F₁-ATPase system;^28–30 furthermore, the studies could not answer the above questions due to model resolution or time scale limitations. Today all-atom molecular dynamics (MD) simulations can achieve very large and very long simulations of protein dynamics, as reported recently in the cases of HIV capsid assembly³¹ and protein folding.³² However due to the millisecond scale of the Rho conformational transition along with Rho’s large size, straightforward MD simulations cannot reach the time scale of the transitions. Fortunately, transition pathway techniques for sampling rare transition events in protein conformational dynamics^33,34 can be utilized to overcome the timescale challenge; here we carry out MD simulations employing the string method^7,35 and the milestoning technique^36–39 to characterize the conformational transition pathway of Rho’s action phase along with associated free energy profile and kinetic rates in the Rho-RNA complex.

The transition pathway determined at atomic resolution reveals the relative translation and rotation of the six subunits that unidirectionally translocate RNA. The six-subunit-motion induces RNA translocation mainly through six lysine residues arranged in the pore along a spiral staircase, one (K326) contributed by each subunit. We find that, during one rotary reaction step, the force generation process is induced by release of “old”, actually loosely bound, product and eventually leads to one K326 residue (belonging to subunit m₁ in Figure 1b), namely the one at the top of the staircase, being pulled away from the RNA substrate, while the interactions between the second- and third-to-top K326 residues with RNA are firmly held. The disengagement between the top K326 and RNA exhibits the slowest ~0.1 ms transition between two key intermediate states. The directionality of the rotary reaction in Rho’s action phase, which starts upon completion of the three ligand state changes during the dwell phase, is induced by a 1.5 kcal/mol drop in free energy between pre-translocation and post-translocation states, suggesting a population shift mechanism for the force generation. Furthermore, among functionally important residues identified, a small subset of residues is found to form an allosteric pathway that couples unbinding of K326 from RNA with product release; this allosteric regulation changes a tight binding of the “new” hydrolysis product into a loose binding, so that the product changes its characteristic to that of “old” product that can be released in the subsequent dwell phase initiating the next motor-action phase.

Results

In the following the basic rotary reaction step from prior state R to final state F, as defined in Figure 1b, is described in detail. We first characterize the millisecond-scale conformational transition of the Rho-RNA complex along with the associated free energy profiles and kinetics. We then show in atomic level detail the relative motion of the six subunits, in particular the motion of the six lysines K326, and demonstrate how these motions unidirectionally translocate RNA. Finally, based on the transition pathway, we identify residues involved in an essential allosteric control pathway that synchronizes RNA translocation and the ATP hydrolysis cycle.

Thermodynamics and kinetics of a basic rotary reaction step

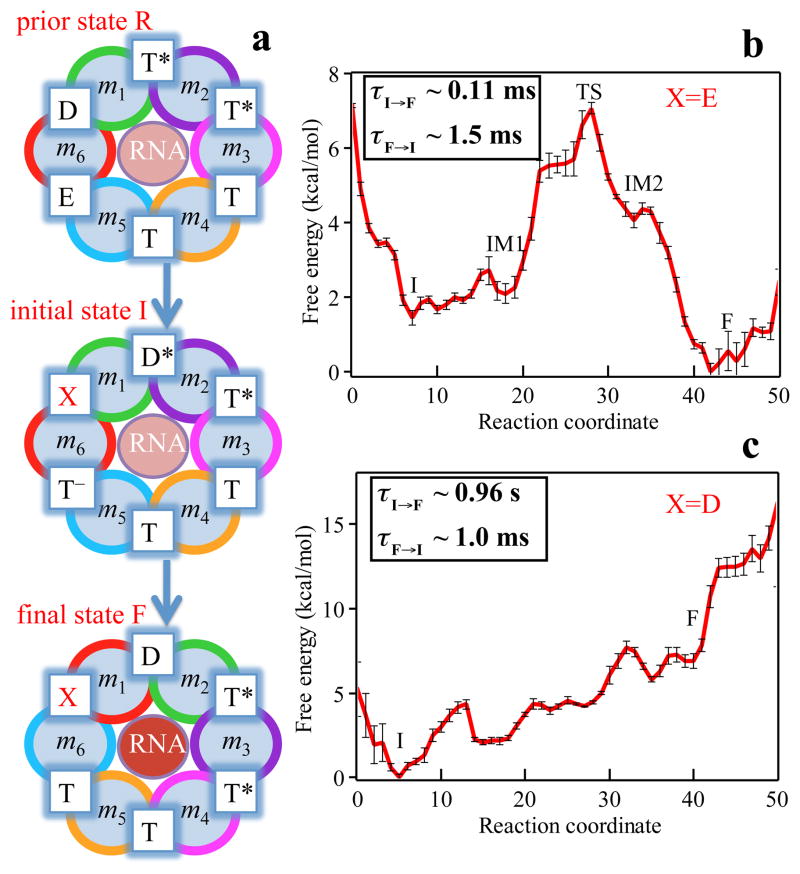
The rotary reaction R → F (Figures 1b and 2a) is driven by ligand state changes of the ATP hydrolysis cycle. The state R represents a stable state corresponding to the crystal structure; in this state Rho does not transition spontaneously to F. Three subprocesses occurring during Rho’s dwell phase (see Figure S1) are required to bring about a motor-action phase transition towards F: (1) binding of ATP to the empty site, namely E → T; (2) release of “old” hydrolysis product (ADP+Pi), namely D → E; (3) formation of “new” hydrolysis product through the reaction ATP → ADP + Pi, namely T* → D*. D represents here a state of loosely bound (“old”) product and D* a state of tightly bound (“new”) product.

Figure 2.

Free energy profiles and mean first passage times characterizing the rotatory reaction step of Rho. (a) Rotary reaction scheme. Details of how states R, I and F have been constructed are described in Methods. The ligand state X at the interface between subunits m₆ and m₁ is assumed to be in one case the empty state E and in another case the (“old”) product bound state D. The free energy profiles during the transition I → F for cases X = E and X = D are shown in (b) and (c), respectively. The standard error shown is estimated by repeating the free energy calculations with half of the trajectories. Insets in (b) and (c) show both the forward and backward mean first passage times. In case X = E the rotary reaction is exergonic whereas in case X = D the rotary reaction is strongly endergonic.

The subprocesses (1, 2, 3) take place somewhere along the transition R → F. Based on experimental studies,^19,20 subprocess (2) is considered rate limiting. Accordingly, we assume in our study that subprocesses (1, 3) take place at the very beginning of the R → F transition; to elucidate the rate limiting nature of subprocess (2) we introduce at the m₆/m₁ interface a ligand state X = E or D that we choose to have, respectively, product released right away or not released at all. The transition modeled by us is then actually R → I → F, where I is introduced and shown in Figure 2a; I differs from R by the change in ligand configuration T*, T*, T, T, E, D (state R) → D*, T*, T, T, T⁻, X (state I) (see Methods for details of R, I and F modeling based on the crystal structure and biochemical measurements).

We first describe the optimal I → F pathway for the choice of X = E. As shown in Figure 2b the reaction starts in the first local minimum at state I and, eventually, the system reaches the final state F, which is seen to lie energetically below I, namely by ΔG_I,F = − 1.5 kcal/mol; this energy drives the rotary reaction forward. The I → F transition happens in three steps, namely by overcoming a barrier of height ε₁ = 1.3 kcal/mol and reaching a first intermediate IM1, by overcoming a second barrier of height ε₂ = 5.0 kcal/mol at the main transition state (TS) and reaching a second intermediate IM2, and finally by overcoming a third, small energy barrier of height ε₃ = 0.3 kcal/mol and reaching the final state F. The conformations of the intermediates IM1 and IM2 arising in case of X = E will be discussed further below. The calculated mean first passage time (MFPT) from I to F is evaluated to be about 0.11 ms, consistent with the experimentally estimated value shown in Table 1. The forward rate constant for the I → F transition is about 15 times larger than the reverse rate constant. As listed in Table 1, the rate limiting step for the I → F transition, namely the step with the highest free energy barrier, is actually the IM1 → IM2 step.

Table 1.

Comparison between calculated and experimental mean first passage times ( MFPTs ).

	tI→IM1	tIM1→IM2	tIM2→F	tI→F
calculateda	183 ns	107 μs	2.75 μs	0.11 ms
experimentalb	-	-	-	10−1 ms to 1 ms (Ref. 19)

^aResults from the simulation for X = E;

^bExperimental MFPTs for the protein conformational transitions are order of magnitude estimates as reported in the references.

We also find the I→F transition pathway for the case X = D (hydrolysis product is not released from the m₆/m₁ interface binding pocket). The free energy and mean first passage times are presented in Figure 2c. A comparison of Figure 2c and Figure 2b shows clearly that the rotary reaction proceeds much better when the product release happens early on in state I. In fact, without product release the overall reaction is strongly endergonic (ΔG_I,F = +7 kcal/mol) and the forward rate constant is 1000 times smaller than the reverse rate constant. The results suggest that the conformations of states I and F exist in both X = E and X = D situations; hydrolysis product release shifts the relative population of these conformations and makes the state F more favorable.

Relative translation and rotation of six Rho subunits accompanied by the opening of the empty interface

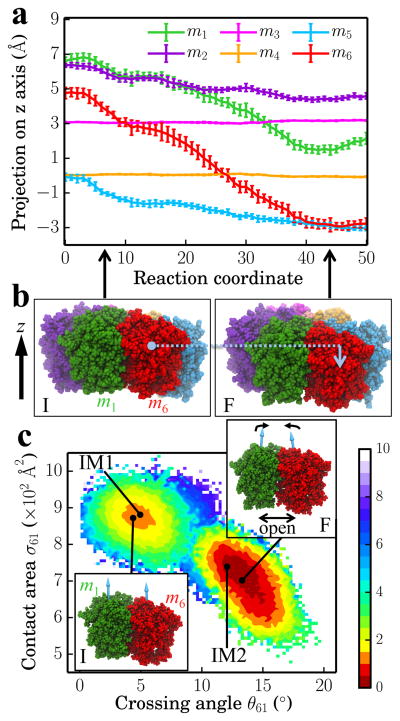
In the following we analyze the characteristics essential for Rho’s overall motion along the transition pathway after product release. Figure 3a shows the overall translational motion of the six Rho subunits along the z-axis. To simplify the description we introduced a moving coordinate system in which the z-coordinates of subunits m₃ and m₄ remain constant. The remaining subunits engage all into downward movement, subunits m₁ and m₆ exhibiting the most significant movement. In state I, five of the subunits (m₁, m₂, …, m₅) are arranged roughly like a downward staircase (Z(m₁) > Z(m₂) > Z(m₃) > Z(m₄) ~ Z(m₅)) where Z(m_i) is the position of subunit m_i on the z-axis. m₆ is the out-of-order subunit with Z(m₂) > Z(m₆) > Z(m₃). In state F, the five subunits (m₂, m₃ …, m₆) form a downward staircase (Z(m₂) > Z(m₃) > Z(m₄) > Z(m₅) ~ Z(m₆)) with m₁ being now the out-of-order subunit with Z(m₃) > Z(m₁) > Z(m₄). The vertical positions of the Rho subunits in states I and F are roughly shifted counterclockwise by one subunit. Figure 3b shows the front view of six subunits in states I and F, with m₆ moving down by 7 Å and m₁ by 5 Å.

Figure 3.

Relative translational and rotational motion of subunits during the I → F transition. (a) Projection of subunit positions (center of mass of each subunit’s atoms in the collective variable set) on the z-axis as a function of the progress along the discrete reaction coordinate (0, 1, …, 50), namely the image numbering representing the progress of the transition pathway. (b) Front view of the six subunits in the initial state I (left) and in the final state F (right). The motion of m₆ along the z-axis is indicated by a blue arrow. The subunit colors are consistent with (a). (c) Two-dimensional free energy landscape generated using the contact area between m₁ and m₆ (σ₆₁) and the crossing angle between the principal axes of m₁ and m₆ (θ₆₁) as coordinates. The unit for the free energy is kcal/mol. States I, IM1, IM2 and F (as labeled in Figure 2b) are shown as black dots. Insets demonstrate the relative orientations between m₁ and m₆ in state I (bottom left inset) and in state F (top right inset).

The release of “old” hydrolysis product (the D → E subprocess) happens at the interface between m₆ and m₁ and exerts a big influence on the conformational dynamics of that interface. We monitored the two-dimensional free energy map for the contact area between m₆ and m₁ and the crossing angle between principal axes of m₆ and m₁ (Figure 3c). During the I → F transition, the m₆/m₁ interface (the empty interface) turns into an open binding site via the four states I, IM1, IM2 and F as described previously in Figure 2b. Interestingly, a main free energy barrier of height 4 kcal/mol is found between states IM1 and IM2 in the 2-D map, indicating the opening of the m₆/m₁ interface is a key transition event during the I → F transition. Two insets in Figure 3c show that the crossing angle becomes larger as the two subunits rotate relative to each other. After product release, the empty interface can adopt either a more stable “open” conformation or a less stable “closed” conformation; ATP binding in the next rotary reaction step would shift the population towards the closed conformation. Clearly, an empty interface is essential for hexameric motor function as proposed for several systems.^8,9,40

How unidirectional RNA translocation is coupled to Rho conformational transitions

The coordinated motion of Rho’s subunits as seen in the simulations serves the purpose of translocating the bound RNA along Rho’s central pore. The translocation results from a coupling between Rho subunits and RNA, actually involving mainly interactions between six lysines K326 of subunits m₁, m₂, …m₆ and the RNA backbone. The Q loops of the subunits directed towards the central pore also contributes to RNA translocation, however, the contribution of the K326 side chains in translocating RNA is larger (see Figure S6a in Supporting Information).

In the I → F transition, the individual subunits m₁, m₂, …m₆ play different roles. In regard to the interaction between Rho and RNA, K326 of m₁ disengages from an interaction with phosphate group P₃ of the RNA backbone; K326 of m₄ engages into a new interaction with P₆; K326 of m₂ and m₃ continue their strong interaction with P₄ and P₅, respectively; K326 of m₅ and m₆ do not engage in significant interactions with RNA. The placement of RNA in the Rho channel and the translocation step is illustrated in movie S1 in Supporting Information.

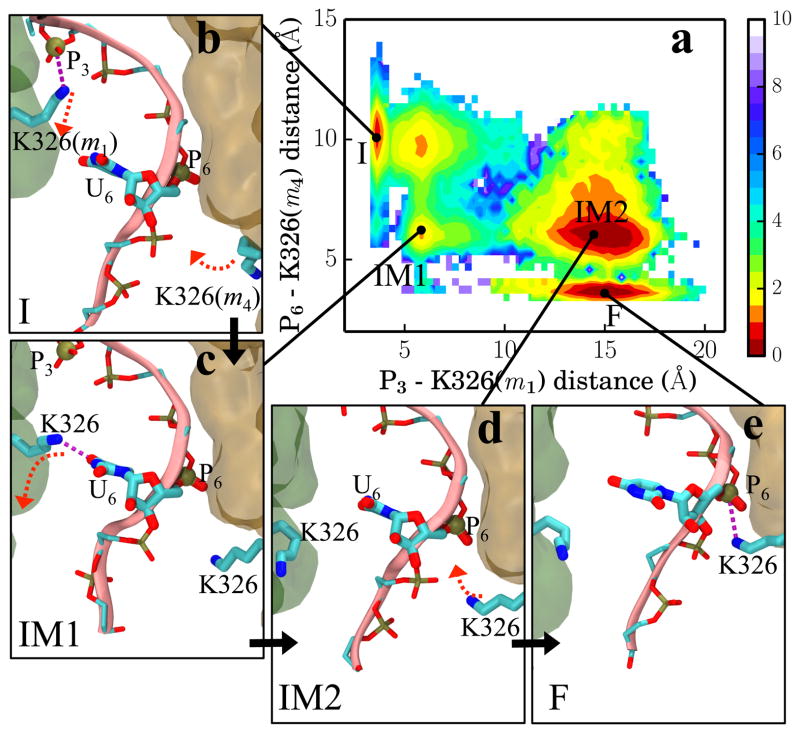
The above important switching of interactions between K326 and RNA backbones can be illustrated by measuring the distances between P₃ - K326(m₁) and P₆ - K326(m₄) along the transition pathway. Figure 4a shows the two-dimensional free energy landscape generated using the distances P₃ - K326(m₁) and P₆ - K326(m₄). The configurations of four local minima corresponding to states I, IM1, IM2 and F are shown in Figure 4b – 4e. During the I → IM1 stage, K326(m₁) first breaks its contact with P₃, after which K326(m₄) reduces its distance to P₆ by 4 Å but not engage yet with P₆. In the state IM1, K326(m₁) forms contact with RNA base U₆ (Figure 4c), indicating a different RNA sequence could give a different free energy profile. During the IM1 → IM2 transition, the distance between P₃ - K326(m₁) gradually increases at which point K326(m₁) loses all contact with RNA. During the last, IM2 → F, transition, K326(m₄) eventually coordinates with RNA phosphate P₆. Since crossing of the transition state (TS) happens during the IM1 → IM2 transition, the disassociation of RNA from K326(m₁) rather than the association of RNA with K326(m₄) is the rate limiting processes for the overall rotary step characterized by the I → F transition. The interaction strengths between the six Rho subunits and RNA residues in states I, IM1, IM2 and F are shown in Figure S4. Interestingly, discrete transitions of side chain conformations are also seen in the case of myosin whose recovery stroke involves side chain motions activated between a few discrete states as reported by Elber et al.⁴¹

Figure 4.

Key interactions between RNA and Rho during the I → F transition. (a) Free energy landscape along distances P₃-K326(m₁) and P₆-K326(m₄). The position of the phosphorus atoms of the phosphate group and NZ atoms of K326 define the corresponding distances. (b–e) Configurations in states I, IM1, IM2 and F, accounting for the key steps of RNA binding and release that induce RNA translocation. Red dashed arrows indicate large side chain movements before the next state is reached. m₁ (green) and m₄ (orange) are shown in transparent surfaces.

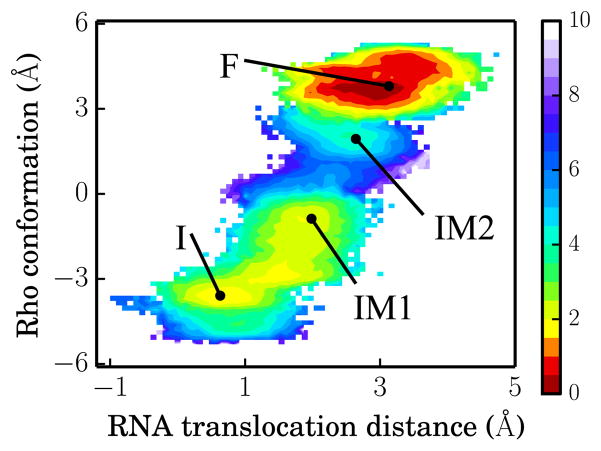
To inspect along the I → F transition overall RNA translocation and Rho conformational change, the latter property was characterized for this purpose through ΔRMSD = RMSD(Y, I) – RMSD(Y, F);⁴² here RMSD(Y, Z) is the conformational RMSD difference between two conformations Y and Z (Z in state I or F). The free energy landscape presented in Figure 5 reveals an RNA translocation distance of about 2.4 Å in going from state I to state F, which is commensurate with the helical rise per base pair seen in the Rho-RNA complex; ΔRMSD varies from −4 Å to 4 Å in going from state I to state F, implying that the full conformational change is necessary in realizing the RNA translocation. For comparison, we present in Figure S5 the free energy map for the unreleased product case X = D (see Figure 2c), which shows transition from a stable state I to a very unstable state F, clearly an unfavorable process.

Figure 5.

Free energy landscape for RNA translocation distance and Rho conformation for X = E. The energy values are defined by the color bar in units of kcal/mol. States I, IM1, IM2 and F are labeled with black dots. The RNA translocation distance is defined as the center of mass distance between RNA backbone (residues 3 – 8) and Rho backbone (C-terminal domain). The Rho conformational coordinate is defined in the text.

Extension from a single rotary reaction step to multiple steps

The scenario described above for one rotary reaction step can be readily extended to an arbitrary number of such steps.⁹ As shown in Table S4 the step 1 hexatuples of ligand states (T^*T^*TTED → DT^*T^*TTE) corresponding to the transition R → F can be continued by shifting the step 1 ligand states by one Rho subunit. Table S4 provides the detailed ligand states for step 2, 3, … 7, where step 7 exhibits again the same ligand states as step 1; the shifts complete in step 6 a full cycle (360°) through all six Rho subunits. For example, step 2 involves then ligand state changes DT^*T^*TTE → EDT^*T^*TT; step 7 involves ligand state changes T^*T^*TTED → DT^*T^*TTE. The RNA translocation in a full cycle (six steps) is illustrated in Movie S1. Movie S2 shows the relative motion of six Rho subunits in a full cycle. The reader is urged to view both videos for better comprehension of the simulation results.

Allosteric pathway that couples RNA translocation to hydrolysis product release

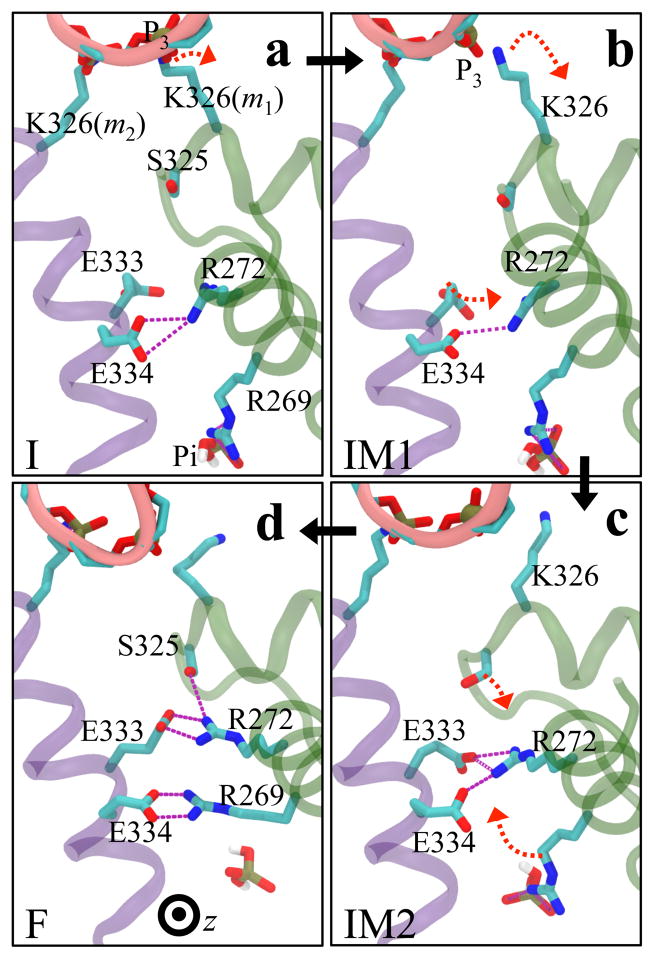
RNA translocation after step 1 requires at the beginning of step 2 the release of hydrolysis product ADP + Pi at the m₁/m₂ interface. In fact, when we assumed for step 1 that the respective release of “old” product at the m₆/m₁ interface does not take place, the rotatory reaction step is endergonic and cannot proceed (see case X = D in Figure 2c). Likewise, for step 2, the hydrolysis product at the m₁/m₂ interface must be released before the next step of RNA translocation can proceed. For this purpose the hydrolysis product at the m₁/m₂ interface, which we termed “new” product, must experience a change from being tightly bound (D^* state, see Figure 2a) to being loosely bound (D state) and, therefore, ready for subsequent release. One may hypothesize then that the initiation of step 2 in the form of a D → E transition at the m₁/m₂ interface during the next dwell phase should actually be prepared when state F is reached in step 1. It appears that such lockstep synchronization is indeed achieved by Rho through an allosteric pathway that links disengagement of K326(m₁) from RNA backbone phosphate P₃ (see Figure 4) to a liberation of inorganic phosphate Pi from a salt bridge with R269(m₁). This liberation looses the binding of Pi; we show below that the nearby ADP moiety becomes also more flexible.

We discovered the allosteric pathway by monitoring the interaction energy deviation along the simulated pathway between residue s of Rho and all residues of neighboring subunits, ΔE_s^{subunit-subunit} (see SI Text and Figure S6b). The larger ΔE_s^{subunit-subunit} is, the more important contribution residue s will make to the relative stability of different states along the pathway. Such residues s, namely those with ΔE_s^{subunit-subunit} > 5 kcal/mol, are listed in Table S3. Among the residues listed R272(m₁), E333(m₂), E334(m₂), and R269(m₁) participate in the stated allosteric coupling between RNA and Pi. The corresponding pathway is illustrated in Figure 6.

Figure 6.

Allosteric coupling between RNA translocation and Pi of the hydrolysis product. The coupling is established through a link between the disengagement of K326(m₁) from RNA phosphate P₃ and release of Pi from a salt bridge with R269(m₁). The figure shows in (a, b, c, d corresponding to states I, IM1, IM2, F, respectively) top-down views (same view of Rho as in Figure 1a) the conformational changes of residues R272(m₁), E333(m₂), E334(m₂), and R269(m₁) at the m₁/m₂ interface during transitions I → IM1 → IM2 → F. The three transitions are shown as black arrows; red arrows indicate large side chain movements occurring before the next transition takes place. RNA is shown as a pink ribbon with phosphate P₃ highlighted as a tan sphere.

The suggested allosteric mechanism at the m₁/m₂ interface (i.e., the interface involved in the T^* → D^* → D transition) is seen clearly when one follows the conformations of residues R272(m₁), E333(m₂), E334(m₂), and R269(m₁) during the I → IM1 → IM2 → F transitions in Figure 6a–d. One can recognize that K326(m₁) disengages from P₃ of RNA during the initial I → IM1 transition (Figures 6a,b and Figure 4b); the disengagement triggers a downward motion of m₁ (Figure 3a). During the IM1 → IM2 transition, E333(m₂) forms a contact with R272(m₁) during the sliding motion between subunits m₁ and m₂ (Figure 3a). In the final transition IM2 → F, S325(m₁), on the same R loop as K326(m₁), engages R272(m₁). Meanwhile the salt bridge network at the m₁/m₂ interface further adjusts its configuration: R272(m₁), which is coordinated with E334(m₂) in state IM2, establishes a firm contact with E333(m₂) in state F; R269(m₁) disengages from Pi and forms a salt bridge with E334(m₂), weakening its interactions with Pi considerably. As a result, Pi becomes weakly bound at the very end of step 1.

Comparing trajectories (carried out in Voronoi cells as described in Methods) at the beginning (state I) and the end (state F) of the motor-action phase shows that along with the loosening of Pi binding also the ADP moiety bound at the m₁/m₂ interface becomes more loosely bound as reflected in its position deviation shown in Figure S10. The average deviation changes from 0.6 Å to 1.4 Å, illustrating that the ADP molecule upon the I → F transition along with Pi becomes loosely bound and ready for release.

Discussion and Conclusion

The present study investigated through molecular dynamics simulations how the homohexamer Rho translocates RNA during the ATP hydrolysis cycle. The modeling is based on the important crystallographic structure⁹ that showed the identical and circularly arranged Rho subunits m₁, m₂, … m₆ with the hexameric symmetry broken through adoption of anasymmetric pattern of six ligand states. The result of the molecular dynamics simulations going beyond the stated structure is the actual detailed conformational transition pathway of the Rho-RNA complex via four key states (I, IM1, IM2, F), along with the associated free energy, kinetic information and, in particular, the coupling and synchronization between Rho’s ligand state changes and RNA translocation.

The all-atom millisecond dynamics of the Rho-RNA complex describes the force-generation mechanism for Rho in unprecedented detail and applies likely to other hexameric ring-type ATPase motors. As shown in Figure S1, Rho dynamics involves a dwell phase in which ATP binding, release of “old” product and ATP hydrolysis into “new” product take place and a motor action phase (I → F). The rate-limiting release of “old” product ends the dwell phase and triggers the motor-action phase, as demonstrated in Figure 2. The dynamics underlying RNA translocation during the motor-action phase involves highly coordinated translational and rotational movements of the six subunits in the Rho ring, but not internal motion of the individual subunits. The force-generation process, linked to the crossing of the major free energy barrier along the I → F transition, is actually associated with the disengagement of K326 of the leading subunit (the top position of the six K326 residues arranged in a spiral staircase) from an RNA phosphate; the barrier crossing corresponds to the 107 μs slow IM1 → IM2 transition. A non-native interaction between the side chain of K326 and an RNA base appears at the state IM1, suggesting sequence dependent activity of Rho.⁴³

The directionality of RNA translocation is determined by the interaction pattern between RNA backbone and the ring-shaped motor, as well as the direction of the rotary ATP hydrolysis cycle along the ring.¹ We found that the forward R → F reaction is triggered by release of “old” hydrolysis product; the reverse rotary reactions F → I and I → R are highly unfavorable, since the former step is endergonic (Figure 2b) and the later step is extremely hard to happen due to irreversibility of ADP/Pi release and ATP hydrolysis.^19,20 Upon completion of ligand state changes in a rotary reaction step, both conformational states (I and F) exist; however only state F is ready for ligand state changes in the next step. For example, as the simulations revealed, RNA translocation is allosterically coupled to loosening the binding of the “new” hydrolysis product, initially in state D^* and transitioning to state D, such that product is ready to be released in the subsequent dwell phase.

Due to the large number of residues involved in the transition pathway, we had to apply in the present study a statistical analysis to capture the residues that make significant contributions to the changes in the subunit-subunit interaction energy along the transition pathway. These residues exert their influence on the relative stability of different conformational states, as well as on the friction⁴⁴ at interfaces between subunits. For example, a salt bridge, R272-E333, stabilizes the state IM2; another salt bridge, R269-E334, stabilizes the state F. Among the list of identified residues (listed in Tables S2 and S3) about half of the residues are connected with mutations that have been demonstrated already in respective experiments to lead to functional deficiencies, including residues K326, R272, E333, E334, R269 and other allosteric residues as reported in Refs. 43,45–48; the remaining listed residues, not tested yet in mutagenesis studies, are good candidates for future experiments that further explore the structure-function relationship of Rho. The electrostatic nature of the allosteric pathway increases the friction at interfaces⁴⁴ and slows down the motor dynamics to a millisecond time scale.

The rotary reaction step investigated here is also found in other hexameric motors. Crystal structures of bovine papillomavirus E1 and Bacillus stearothermophilus DnaB hexameric helicase reveal asymmetric functional states in the ATPase cycle (like the prior R state in Figure 1). E1 is proposed to translocate one nucleotide of ssDNA every rotary reaction step;⁸ the non-planar DnaB structure indicates that DnaB can translocate two nucleotides of ssDNA per rotary reaction step, given that each subunit of DnaB accommodates two nucleotides.¹⁰

F₁-/V₁ -ATPases share an evolutionary link with, and are homologous to, Rho.^18,49,50 We note that the sequences of the ATPase domain of F₁-/V₁ -ATPases are about 50–100 aa longer than the ATPase domain of Rho; the additional 50–100 aa residues form a C-terminal domain that can swing relative to a central domain of F1-/V1 -ATPases. Such a feature is important for rotating their central stalks instead of moving substrate linearly. Though carrying out a very different function, F₁-/V₁ -ATPase and Rho share similarities in their ATPase cycle. Single-molecule and biochemical studies^51,52 show that V₁-ATPase pauses its central stalk every 120° without any submillisecond substeps, similar to the rotary step of 60° in the case of Rho. Recently, a series of intermediate structures of E. hirae V₁-ATPase were reported,^12,53 suggesting a pathway of a rotary reaction step: after ATP hydrolysis, ADP/Pi release is the rate-limiting process that would induce the 120° central stalk rotation (ATP binding is relatively fast); as a result of the stalk rotation, the prior ATP bound interface will change from state T to state T^*. The Rho transition pathway shows similarities with the rotary reaction step in V₁-ATPase: ATP hydrolysis, ATP binding and ADP/Pi release take place during Rho’s dwell phase before they trigger RNA translocation. As the main barrier crossing event for RNA translocation happens at the IM1 → IM2 stage (as demonstrated in Figures 4a and 5), the T → T^* transition (documented in Figures S8–S9), which occurs during the IM2 → F stage, is preceded by RNA translocation.

The coordination of catalytic processes at the subunit interfaces is important for hexameric motors’ function.² The central stalk rotation of E. coli F₁-ATPase, repeated in 120° steps, involves two sub-steps.^54,55 In each of the 120° steps, ATP binding, ATP hydrolysis and product release processes are separated into two dwell phases, namely a first binding dwell before a 80° sub-rotation and a second catalytic dwell before a 40° sub-rotation. However for V₁-ATPase and Rho, there are no sub-steps, and thus the three catalytic processes all happen before the hexameric motors carry out work (see Figure S1). The timing of when catalytic processes are ready to take place is controlled by the conformational transitions of the motors. Once the corresponding interfaces are competent to carry out the respective reactions, the reactions occur stochastically with first-order kinetics whose rates are determined by the local binding sites.^29,56 Four key transitions were observed in our simulations: (1) the allosteric regulation at the m₁/m₂ interface (D^* → D) renders ADP+Pi competent to be released; (2) the m₆/m₁ interface opening renders the interface capable of binding a new ATP molecule; (3) the ATP binding transition at the m₅/m₆ interface (Figure S7) moves the ATP into the binding pocket; (4) the transition T→T^* at the m₃/m₄ interface (Figures S8, S9) renders ATP competent to be hydrolyzed. In our simulations, we observed the ordering of transitions, namely (3) → (2) → (1), (4).

Recent single-molecule fluorescence studies have provided unprecedented insight into the dynamic unwinding processes of hexameric helicases. A recent single-molecule fluorescence study of T7 gp4 hexameric helicase,⁵⁷ together with a high resolution measurement on the chemical step size of T7,⁵⁸ suggests that the ratio between number of nucleotides hydrolyzed and number of bp unwound is 1 : 1. However, for G-C base-pairs, the unwinding signal shows stochastic pauses every 2–3 bp, implying 2–3 bp are unwound after enough elastic energy is stored when 2–3 ATP got hydrolyzed. For A-T base-pairs, a sequential reaction mechanism with 1 bp step size is proposed, similar to the case of the present study. Thus, the free energy landscape of conformational transitions during rotary steps needs to be adapted to accommodate different types of nucleotide substrates. Nevertheless, the free energy release of Rho during its I → F transition, G_I – G_F, is 1.5 kcal/mol, comparable to the ~1 kcal/mol (A-T) or ~2 kcal/mol (C-G) base-paring free energy.⁵⁹ The molecular basis for unwinding by hexameric helicase, unfolding by proteasome and stalk rotation by F₁-/V₁ -ATPases can be explored in future studies following the computational approach employed in the present study.

Methods

Here we describe first the molecular modeling of the hexameric helicase Rho and the procedures used for the MD simulations. Then, we introduce the string method³⁵ that we apply to calculate the most probable transition path (MPTP).^35,60 Finally, we outline how the milestoning method^37,39,61 allowed us to calculate free energy and kinetics along the Rho-RNA transition pathway. We note that the total simulation time, including string method calculation and enhanced sampling for free energy and kinetics, adds up to ~10 μs and involves ~0.4 million atoms.

Molecular modeling and simulation setup

Our molecular dynamics study is based on a crystal structure of Rho loaded with RNA (six uracil nucleobases) from Escherichia coli (pdb code: 3ICE; see Figure 1). In our simulations we replaced the ATP-mimics (ADP·BeF₃) in the crystal structure by the equivalent ATP molecules in the T^* and T states, introduced an ADP and an inorganic phosphate (modeled as

${\mathrm{H}}_2{\text{PO}}_4^{-}$)⁶² in case of the D state, and removed the loosely bound ATP-mimic in the E state. Structural analyses^63,64 have demonstrated that non-hydrolyzable ADP · BeF₃ can successfully mimic the ATP and ADP · Pi binding states in F₁-ATPase; different ATP analogues produce actually similar binding conformations. We also added to the six uracil nucleobases of the RNA in the structure three uracil nucleobases to the 3′ end, such that the simulated system contained RNA with nine uracil nucleobases. We denote by P_j the RNA backbone phosphate groups and by U_j the nucleobase of the RNA residue for j = 1, …, 9.

The protein-ligand-RNA system was solvated in a 120 Å×170 Å×170 Å water box with 150 mM NaCl; the simulated system involved altogether ~0.36 million atoms. After a 4000-step energy minimization, the system was heated in the NPT ensemble (1 atm) to 300 K in 50 ps, employing harmonic constraints with 1 kcal/(mol Ų) spring constant to the heavy atoms. Keeping the spring constant, a 1 ns equilibration in the NPT ensemble (1 atm at 300 K) was carried out, followed by a 4 ns NVT-ensemble simulation, gradually decreasing the spring constant to zero during the latter stage. In the following, we refer to the state of the resulting protein-RNA system as the prior state R (see Figure 1b). All MD simulations in our study were performed using NAMD 2.9⁶⁵ with the CHARMM27 force field and CMAP corrections.

The aim of our study is to identify the mechanism of an elementary propagation step of Rho. The step involves a prior state R and a final state F that are to be linked through a conformational transition. As the actual propagation (R → F) occurs typically on a millisecond time scale, straightforward MD simulation cannot simulate this transition and enhanced conformational sampling based on a so-called string method is employed instead. In the present case the hexameric symmetry of Rho dictates that F, in principle, is identical to R with all subunits shifted by one. To construct F one needs to permute the geometries of S₁(R), S₂(R), . . . S₆(R), where S_j(R) [S_j(F)] denotes the geometry of subunit j in Rho state R [state F] as follows: S₁(F) = S₆(R), S₂(F) = S₁(R), . . . S₆(F) = S₅(R).

We introduce an initial state I (see Figure 2a) between R and F. State I represents a state of Rho, in which ATP hydrolysis and new ATP binding in the prior state R have just taken place such that Rho is driven to a new geometry of its subunits, namely the one corresponding to state F. In other words, I represents a state energized through changes in ligand binding states. I is constructed from the prior state R as follows: at the m₁/m₂ interface one hydrolyzes one ATP molecule by superimposing an ADP and Pi onto the ATP position (T^* → D^*; D^* denotes the state of “new” product that presumably is more tightly bound than “old” product in state D); at the m₅/m₆ interface one docks one incoming ATP molecule into the loosely bound ATP-mimic position (E → T⁻; T⁻ represents a state with a loosely bound ATP); at the m₁/m₆ interface, we actually adopt two alternatives for the ligand state, referring to either state as X: in the first case, referred to as X = E, we removed ADP/Pi (D → E) and in the second case, referred to as X = D, we left ADP/Pi unchanged in the pocket; the other three ligand states remain unchanged at the m₂/m₃ interface (T^*), m₃/m₄ interface (T), and m₄/m₅ interface (T).

The resulting state I system was then equilibrated for 30 ns and the final snapshot was taken as the initial state I. To compare the conformational changes between state I and the crystal structure, binding pocket C_α RMSDs of subunits are listed in Table S5; the RMSD values listed are small, indicating that the non-hydrolyzable ADP · BeF₃ employed in the crystal structure has binding conformations that are very similar to those of ATP/ADP · Pi molecules employed in our simulations and in functional Rho.

The modeling of I adopted in the present study is justified for the following reasons. First, the time scale for ATP hydrolysis estimated from experiments to be 1 ms (Ref. 20) or 6.7 ms (Ref. 19) is shorter than the rate-limiting time for ADP release (10 ms, Ref. 20) or Pi release (20 ms, Ref. 19). As R resembles the catalytic dwell structure (the crystal structure⁹ was obtained while binding to Rho a non-hydrolyzable ATP analogue), ATP hydrolysis in R will necessarily precede the conformational transition towards F. Second, for the metabolite concentration of ATP in E. coli (~10 mM)⁶⁶ the time scale for ATP binding is less than 0.5 ms (Ref. 19,20), which is much shorter than the time scales of the other two processes (ATP hydrolysis and product release). Thus one ATP molecule will very likely diffuse to the E (empty) site of R and become weakly bound in I (E → T⁻ at the m₅/m₆ interface) before the other two ligand processes take place. In the simulation, we have four ATP bound in R. Since each Rho hexamer accommodates around 3.5 ATP on average under saturating conditions,¹⁹ one ATP hydrolysis reaction (T^* → D^*), namely the one at the m₁/m₂ interface in state I, will keep a suitable number of ATP molecules bound in Rho. Whether product release process is important to trigger the conformational transition is explored by simulations assigning for state X either state E or state D.

String method protocol

In the present study we opted for the so-called “string method with swarms-of-trajectories” ³⁵ to describe the roughly millisecond-scale I → F transition pathway which is represented by a “string” in a space of “collective variables” z(x), z being n-dimensional functions of Cartesian coordinates x of the system (x ∈ ℝ^3N). The string is discretized into M +1 equally spaced images, which are conformational states of Rho along the I → F transition and are characterized by the set of collective variables z⁽⁰⁾, z⁽¹⁾, ..., z^(M) (here M = 50). A swarm of short trajectories (4 ps) is launched for each image and the image evolves according to the average drift of its trajectory swarm during one iteration. The pathway is then optimized iteratively until it converges to the the most probable transition path.

Due to the high dimensionality of the movement in the I → F transition we needed to modify the string method protocol introduced in Refs. 35. On the one hand, we had to select z through a systematic computational procedure as the large number of collective variables needed could not be hand-picked (Rho has altogether ~ 40,000 atoms); on the other hand we had to employ multidimensional curve fitting, as used previously in simulation studies,^67,68 in order to reduce the noise arising from a thermal multidimensional system, appearing here in the form of noisy kinks in the transition pathway (string). The collective variables suitable for the present case should describe the dominant changes that arise during the I → F transition. These collective variables were identified to be the positions of key residues at the six subunit-subunit interfaces of the hexamer. We determined the residue-based interaction energy contribution of Rho subunits as shown in Figure S2b, the energy serving as a collective variable selection criterion as explained in Supporting Information. From this procedure resulted eventually 660 × 3 = 1980 coordinate positions.

Our implementation of the string method benefitted from a scalable multiple copy algorithm⁶⁹ which enables launching thousands of trajectories simultaneously on a petascale supercomputer. The total simulation time needed for the sum of all string method trajectories amounted to 8 μs for the two pathways depicted in Figure 2. More details of our protocol, including choice of collective variables, generation of initial configurations, evolution of the string, and convergence of the final pathway are provided in Supporting Information.

Free energy and kinetics calculations

In order to compute the free energy profile along the two I → F transition pathways for X = E and X = D we employed the enhanced sampling method described in Refs. 39,61. For this purpose we applied a Voronoi tessellation³⁹ in the collective variable space with M = 51 cells, whose centroids are the images z^{α} of the converged transition path. The points z(x) assigned to a Voronoi cell B_i are characterized through the Voronoi tessellation rule (Eq. S8, Supporting Information). In order to enhance the sampling, twenty conventional 0.8 ns-long MD simulations were carried out in each Voronoi cell with random seed employing reflective boundaries at the cell interfaces. The implementation details of the sampling along with the calculation of the equilibrium probability π_i and free energy G_i for the system in cell B_i can be found in Supporting Information (Eq. S9–S11).

Through the milestoning method developed in Refs. 37,39,61, the mean first passage times (MFPTs) for traversing from state I to state F can be computed. The kinetic rates predicted by milestoning have been shown to be comparable to experimental values.^41,70 In milestoning,^36,37 instead of performing a long-time MD trajectory, the transition event is split into short trajectories crossing a set of “milestones” (hypersurfaces) along the pathway between the initial and final states. Here the interfaces of Voronoi cells B_i and B_j are chosen as milestones, labeled by indices 0, 1, . . . , N_T (N_T ≠ M). Statistical properties of crossing the set of milestones are utilized to reconstruct the information of the transition rates; the rate matrix q_ij of instantaneous transition from milestone i to milestone j is obtained by Eq. S13^39,61 in Supporting Information and is based on the confined simulations within the Voronoi cells introduced above. The MFPTs from milestone m to milestone n, τ_m,n, can be then obtained by solving the system of N_T linear equations,^37,39,61,71

$$\sum _{\begin{array}{l}m=0\\ m\ne n\end{array}}^{N_T}{q}_{km}{\tau }_{m,n}=-1,k\ne n.$$ (1)

The sampling inside all Voronoi cells required a total simulation time of 1.6 μs for two free energy profiles and associated MFPTs between states I and F along the reaction coordinate in Figures 2b, c (0.8 μs each).