Abstract
This study employed functional magnetic resonance imaging (fMRI)-based dynamic causal modeling (DCM) to study the effective (directional) neuronal connectivity underlying inhibitory behavioral control. fMRI data were acquired from 15 healthy subjects while they performed a Go/NoGo task with two levels of NoGo difficulty (Easy and Hard NoGo conditions) in distinguishing spatial patterns of lines. Based on the previous inhibitory control literature and the present fMRI activation results, 10 brain regions were postulated as nodes in the effective connectivity model. Due to the large number of potential interconnections among these nodes, the number of models for final analysis was reduced to a manageable level for the whole group by conducting DCM Network Discovery, which is a recently developed option within the Statistical Parametric Mapping software package. Given the optimum network model, the DCM Network Discovery analysis found that the locations of the driving input into the model from all the experimental stimuli in the Go/NoGo task were the amygdala and the hippocampus. The strengths of several cortico-subcortical connections were modulated (influenced) by the two NoGo conditions. Specifically, connectivity from the middle frontal gyrus (MFG) to hippocampus was enhanced by the Easy condition and further enhanced by the Hard NoGo condition, possibly suggesting that compared with the Easy NoGo condition, stronger control from MFG was needed for the hippocampus to discriminate/learn the spatial pattern in order to respond correctly (inhibit), during the Hard NoGo condition.
Key words: : dynamic causal modeling, Go/NoGo, impulsivity, inhibitory control, top-down
Introduction
One of the main behavioral deficits associated with the clinical construct of impulsivity (Moeller et al., 2001) is impaired inhibitory behavioral control (Enticott et al., 2006; Logan et al., 1997). Meta-analyses (e.g., Buchsbaum et al., 2005; Simmonds et al., 2008; Swick et al., 2011) of neuroimaging studies to investigate inhibitory control revealed that frontal, subcortical, insula (INS), and parietal regions are active during Go/NoGo tasks. Within the prefrontal cortex, it has been hypothesized that the dorsolateral prefrontal cortex, pre-supplementary motor area, and ventrolateral prefrontal cortex are key structures subserving NoGo or the inhibitory control component during Go/NoGo tasks (Chikazoe, 2010).
One theory of inhibitory behavioral control hypothesizes that successful inhibition is dependent on top-down control by a prefrontal, reflective system over a subcortical, impulsive system (a largely amygdala [AMG]-striatum dependent system) (Bechara, 2005; Heatherton and Wagner, 2011; Noël et al., 2013). In humans, traditional regional activation studies have been unable to answer questions about whether a particular neuronal region (“R1”) directionally influences another region (“R2”). Although a correlation between activity in R1 and R2 could be demonstrated, until recently it has been difficult to clarify the direction of the association: whether R1 influences R2, or R2 influences R1, or both. In this study, we addressed this limitation by employing dynamic causal modeling (DCM) (Friston et al., 2003; Li et al., 2011) to study the effective (directional) neuronal connectivity underlying inhibitory behavioral control. DCM is particularly appropriate for analyzing whether the connectivity between regions is modulated (i.e., enhanced or reduced transmission between nodes) by experimental conditions (Friston, 2011). The DCM analysis in this study was conducted based on functional magnetic resonance imaging (fMRI) data acquired from 15 normal healthy subjects while they performed a Go/NoGo task with two levels of difficulty (Easy NoGo and Hard NoGo respectively) in the NoGo conditions (Lane et al., 2007). We hypothesized that the NoGo conditions modulate the effective connectivity from prefrontal regions to sub-cortical regions, consistent with the hypothesis of top-down inhibitory control. We used cortical and sub-cortical regions co-activated by the Go/NoGo task as the nodes of DCM. Specifically, we hypothesized that the prefrontal-subcortical effective connectivity was gradually enhanced from Go trials, to Easy NoGo, and Hard NoGo trials. To test this, we inverted a model with full parameters and pruned any surplus parameters using post-hoc optimization (Friston and Penny, 2011). We then performed post-hoc statistical tests on the parameters of the reduced model to confirm or reject the hypothesis that it was the top-down rather than the bottom-up connections which were more fundamentally modulated by NoGo conditions during the Go/NoGo task.
Methods
Subjects
The study was approved by the local Committee for the Protection of Human Subjects and was performed in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki). Normal healthy subjects were recruited through advertisements. Informed consent was obtained from all subjects. As a part of another study to investigate pharmacological influences of medication versus placebo on brain connectivity to be published at a later date, all fMRI scans in this study were acquired at 90 min after each subject was orally administered a placebo capsule containing cornstarch.
Subject inclusion criteria were as follows: (1) between 18 and 55 years old; (2) right handed; (3) no history of any Diagnostic and Statistical Manual-IV (American Psychiatric Association, 2000) substance use or psychiatric disorder; and (4) no metal fragments or other bodily metal or significant claustrophobia. Exclusion criteria were (1) any neurological, psychiatric, or medical disorders or medication therapy that may affect the brain; (2) claustrophobia during MRI simulator sessions; (3) positive urine drug screen or positive breath alcohol screen; (4) positive pregnancy test; and (5) any definite or suspected clinically significant abnormalities of the brain on MRI scans as read by a board-certified radiologist (Co-Investigator L.A.K.).
Among the 17 subjects who complete the experiment, 15 satisfied the inclusion criteria and were included for final analysis. Among them (all right handed), there were eight women and seven men. The ages were 31.8±8.6 years (mean±standard deviation), ranging from 19.8 to 43.6 years, and the education durations were 13.9±2.2 years, ranging from 11.0 to 17.0 years.
Go/NoGo response inhibition task
A rapid-presentation event-related Go/NoGo task (Lane et al., 2007) was used for fMRI of response inhibition. For each subject, there were two Go/NoGo fMRI runs. During each fMRI run, 208 visual stimuli (consisting of Go, Easy NoGo, or Hard NoGo, please see below for details) were sequentially presented in random order. Each stimulus was displayed for 500 msec, and neighboring stimuli in time were separated by a blank screen lasting 1900, 2100, or 2300 msec (jittered randomly). Each stimulus consisted of line segments enclosed within two boxes that were presented simultaneously side by side on the same screen (Fig. 1). The subjects were instructed to discriminate the direction of the lines by pressing a button using their right index finger when both boxes showed parallel diagonal lines in the same direction in both boxes (Go trial). The subjects were instructed not to press the button when both boxes showed horizontal lines (“Easy” NoGo trial), or when one box contained diagonal lines that were in the opposite direction of the diagonal lines in the other box (“Hard” NoGo trial). The “Easy” and “Hard” NoGo conditions were defined based on a previous behavioral laboratory study with a different group of subjects, in which behavioral performance was found to be significantly poorer during Hard NoGo trials than during Easy NoGo trials (Lane et al., 2007). For Go trials, a correct response was defined as a key-press completed greater than 100 msec and less than 600 msec after the stimulus. For NoGo trials, an incorrect response was defined as a key-press completed within 600 msec after the stimulus. Each fMRI run duration was 10 min 40 sec, and included 156 Go trials (75%), 26 Easy NoGo trials (12.5%), and 26 Hard NoGo trials (12.5%). There were no “null” (i.e., resting) trials in this event-related paradigm. Each subject earned $0.04 for a correct Go response or $0.12 for a correct NoGo response, lost $0.02 for an incorrect Go response or $0.06 for an incorrect NoGo response. These monetary performance contingencies were balanced using the β opt criterion (Gescheider, 1985), which maximizes earnings for overall performance (high discriminability and low response bias), while discouraging highly variable performance resulting from unequal attention toward a single trial type or response strategy. While the fMRI protocol precluded presentation of trial-by-trial feedback about performance, subjects were instructed in simple terms about the contingencies for performance and were informed of their earnings after each test session. In addition, all subjects completed a practice Go/NoGo test during a mock fMRI session in order to stabilize performance and provide familiarity with the task before actual MRI scanning.
FIG. 1.

Examples of the stimuli used in the Go/NoGo response inhibition task. (A) Go stimulus; (B) Easy NoGo stimulus; and (C) Hard NoGo stimulus.
fMRI data acquisition
MRI data were acquired on a Philips 3.0 T Intera system with an eight-channel receive head coil (Philips Medical Systems, Best, Netherlands). Single-shot spin-echo echoplanar imaging (EPI) was used for acquiring fMRI data. The spin-echo EPI sequence eliminates signal losses caused by through-slice dephasing in medial orbitofrontal cortex (Kruger et al., 2001) and is sensitive (Moeller et al., 2010; Norris et al., 2002) to blood oxygen level-dependent (BOLD) signal in fMRI. The fMRI acquisition parameters were SENSE acceleration factor 2.0, repetition time 2500 msec, echo time 75 msec, flip angle 90°, field of view 240×240 mm, in-plane resolution 3.75×3.75 mm, 25 axial slices, slice thickness 3.75 mm, interslice gap 1.25 mm, 256 repetitions per run after 10 dummy acquisitions, and total duration per run 10 min 40 sec. Each subject had two fMRI runs. A T1-weighted three-dimensional Spoiled Gradient Recalled anatomical scan (in-plane resolution 0.94×0.94 mm, slice thickness 1 mm) was acquired for co-registration with the fMRI images. A Fluid Attenuated Inversion Recoveryscan and T2-weighted spin-echo scan were acquired that were read by a board-certified radiologist (co-investigator L.A.K.) to rule out incidental brain abnormalities. Although we acquired two fMRI runs for each subject, some subjects only had one usable fMRI run. Thus, we decided to use only one fMRI run for all the subjects in order to avoid potential bias effects.
fMRI preprocessing
During an fMRI run, individual scans in which the MRI signal exceeded plus or minus four standard deviations from the mean for the run were considered outliers and were replaced by the mean of the two nearest neighbors using the Analysis of Functional NeuroImages (AFNI) (Cox, 1996) software command “3dDespike” (http://afni.nimh.nih.gov/afni/). All subsequent preprocessing used Statistical Parametric Mapping 8 (SPM8) software (http://fil.ion.ucl.ac.uk/spm/) implemented in Matlab R2007b (Mathworks, Inc., Sherborn MA). After slice-timing correction, the fMRI series was realigned to the first image to correct for head motion. Runs with head motion >1 voxel (3.75 mm translation on any axis) or rotation >3.75° were removed from the analysis. For each subject, the first run without artifacts and without excessive motion was included in the analysis. The anatomical image was coregistered to the fMRI images and spatially transformed to Montreal Neurological Institute (MNI) standard atlas coordinates using the SPM8 Normalize module with the SPM8 T1 MNI template image. The transformation parameters were applied to the fMRI images, which were resliced to 2 mm isotropic resolution and spatially smoothed with a Gaussian filter of 8 mm isotropic full width at half maximum.
SPM univariate analysis
The univariate statistical analyses of the fMRI data was conducted using SPM8. After specifying the design matrix, the parameters for the effects of different conditions were estimated at the first level for each subject as an event related design according to the general linear model at each voxel, using stick functions modeling the onsets of correct NoGo trials convolved with the SPM8 canonical hemodynamic response function as a basis function. Standard SPM8 basis functions for temporal and dispersion derivatives were also included in the model. Incorrect trials were entered as a separate covariate of no interest so that the remaining implicit baseline consisted only of the correct Go trials. A 128 sec high-pass temporal filter was applied. One contrast image was constructed for each subject for each of the following contrasts of parameter estimates: (1) correct Easy NoGo relative to correct Go (“E” activation); (2) correct Hard NoGo relative to correct Go (“H” activation); and (3) correct Hard NoGo relative to correct Easy NoGo (“H–E” activation). In the remaining part of this article, for brevity the word “correct” will be omitted, but the NoGo and Go conditions will be understood to consist only of correct responses.
A separate SPM8 second-level (Random Effects) statistical analysis was conducted voxel-wise throughout the whole brain for each of the contrast images listed in the earlier paragraph. For each contrast, the SPM8 second-level one-sample t-test with the default settings was used to determine BOLD activations significantly different from zero. For all SPM second-level analyses, statistical significance was defined as false discovery rate (FDR)-corrected cluster probability (p)<0.05, after being further corrected to account for two tails; and trend toward significance was defined as FDR-corrected cluster p less than 0.1 but greater or equal to 0.05, after being further corrected to account for two tails. We corrected the SPM t-test results from one tail FDR to two-tails FDR (used a corrected FDR criterion p value of 0.025 instead of 0.050), because SPM only provides one-tail FDR corrected results, but we examined contrasts in both directions, and, thus, we individually examined both of these one-tail FDR-corrected contrasts. The cluster-defining threshold was t=2.4. Approximate anatomical labels for regions of activation were determined using the Anatomical Automatic Labeling toolbox (Tzourio-Mazoyer et al., 2002).
In addition to the main SPM univariate analysis, we conducted an alternate SPM first-level general linear model (GLM) analysis (see Supplementary Materials; Supplementary Data are available online at www.liebertpub.com/brain) for each subject in which one regressor in the GLM was the combined Easy NoGo and Hard NoGo conditions (“NoGo” condition), and the other regressor in the GLM was NoGo task difficulty (“Difficulty”). For each subject, a contrast image of the parameter estimate resulting from this analysis for combined Easy and Hard NoGo relative to Go was constructed, which was then entered into a second-level SPM one-sample t-test for group analysis. Similarly, a contrast image was constructed consisting of the parameter estimate for Difficulty, which was also then entered into a second-level SPM8 one-sample t-test for group analysis.
Stochastic DCM
DCM (Friston et al., 2003), as implemented in DCM12 (SPM12b revision 5763), was used for effective connectivity analysis. DCM has been described elsewhere (Friston et al., 2003; Ma et al., 2012, 2014). DCM is a biophysical model of the underlying neuronal connectivity and of how the neuronal connectivity generates the observed BOLD signal (Friston et al., 2003). In brief, the mathematical model of the underlying neuronal connectivity among an a priori selected set of brain regions (nodes) is a system of bilinear differential state equations with coefficients specified by three matrices (A matrix, B matrix, and C matrix) (Friston et al., 2003). In this model, experimental conditions (e.g., Go, Easy NoGo, or Hard NoGo) can serve as inputs to the model as either driving inputs or modulatory inputs. The DCM analysis determines which particular nodes in the model exhibit directional (“effective”) connectivity with other specific nodes in the model, which nodes receive driving inputs from experimental conditions in the model, and which specific connections between nodes in the model are modulated by experimental conditions. A node in the model that receives driving inputs, as quantified by the C matrix parameters, is the brain region among the nodes in the model which first experiences a change in neuronal activity from experimental conditions. The node that receives the driving input then influences (“drives”) the connectivity to other nodes in the model. The endogenous (or fixed) connectivity in DCM is quantified by the A matrix parameters, which measure the effective connectivity strengths (in units of Hz) between nodes, regardless of the moment-to-moment switching on and off of inputs. Experimental conditions can modulate the endogenous connectivity between nodes, and these modulation effects are quantified by the B matrix parameters as increased or decreased connectivity strength relative to the endogenous connectivity at different times in the experiment that are related to the timing of changes in the particular experimental conditions. Nonlinear connectivity effects that are gated by other regions in the system can be modeled by an optional additional matrix (D matrix) (Stephan et al., 2008). In this study, the nonlinear option was not applied, and, thus, the term “modulation effects” in this article denotes bilinear modulation effects, where “bilinear” refers to the mathematical form of the equations determining the B matrix parameters. In addition, “center input” (mean center of the inputs) option was not chosen. Furthermore, the stochastic option for DCM was used, in which random fluctuations were modeled as inputs to the system in addition to the driving inputs due to experimental conditions (Daunizeau et al., 2009, 2012, 2013; Li et al., 2011). The stochastic fluctuations in physiological noise may contribute to the system connectivity input (Li et al., 2011) due to stochastic fluctuations in neuronal and vascular responses (Kruger et al., 2001; Li et al., 2011). Li and colleagues (2011) have demonstrated that stochastic DCM can improve parameter estimation over deterministic DCM. In addition, Daunizeau and colleagues (2012) have validated stochastic DCM and shown that stochastic DCM is superior to deterministic DCM in both model structure inference and model parameter inference.
Regions of interest
Following the procedures in Ma and associates (2012, 2014), the anatomical regions (nodes) for the DCM analysis in this study were chosen based on meeting all three of the following criteria: (1) the region should show significant (or trend significant, i.e., FDR-corrected cluster p less than 0.1 but greater or equal to 0.05) activation in the present univariate SPM second-level analysis (see Supplementary Materials); (2) the region should also show activation in previous fMRI studies using Go/NoGo tasks (e.g., Buchsbaum et al., 2005; Simmonds et al., 2008; Swick et al., 2011); and (3) the region should also be regarded in the previous literature to be involved in inhibitory control (e.g., Bechara, 2005; Chikazoe, 2010; Heatherton and Wagner, 2011; Volkow et al., 2011). Based on simultaneously meeting all three of the earlier criteria, the following 10 nodes were used for the DCM analyses in this study: (1) left (L) middle frontal gyrus (MFG); (2) right (R) MFG; (3) L pre-supplemental motor area (pre-SMA); (4) R pre-SMA; (5) L posterior parietal cortex (PPC); (6) R PPC; (7) R putamen (PUT); (8) R AMG; (9) L hippocampus (HIP); and (10) R INS. In addition, following Aron and colleagues (2007), pre-SMA was segmented from SMA using y>0 mm (MNI space) as the threshold, and the plane at x=0 mm (MNI space) was used as the border between L SMA and R SMA.
Volumes of interest and time series extraction
We followed the method that was described in Ma and associates (2012, 2014) of constructing the volumes of interest (VOIs). The atlas-derived binary masks corresponding to the 10 nodes mentioned earlier were obtained from the AAL atlas (Tzourio-Mazoyer et al., 2002) as implemented in the Wake Forest University PickAtlas SPM toolbox (Maldjian et al., 2003, 2004). Each VOI was obtained by the set-theoretic intersection of the atlas-based binary masks and the significant (or trend significant) activation clusters that were determined by the second-level random effects of univariate SPM analysis. The standard SPM procedure in which NoGo and Go conditions were explicitly modeled was conducted by using the principal eigenvariate of each VOI as a summary of the functional activity time series in that VOI (Ma et al. 2014) and each principal eigenvariate time series was adjusted for the F-contrast of effects of interest (Stephan et al., 2010). The same VOIs were used for all subjects. The number of voxels, volume, and center of mass of the 10 VOIs used as nodes for the DCM analysis are listed in Table 1. Due to the intersection of the atlas region with the activation cluster from the SPM analysis, the MFG VOI was not the whole gyrus, but a part of it. Approximately 40% of the volume of the MFG VOI in this study was within the broad range of dorsolateral prefrontal cortex, as defined in the human postmortem histological study by Rajkowska and Goldman-Rakic (1995). The Neurosynth automated meta-analysis at http://neurosynth.org/features/dlpfc/ (Yarkoni et al., 2011) showed that the posterior part of the MFG VOI in this study extended to the pre-motor cortex (Brodmann Area 6), but that most of the VOI was located in the dorsolateral prefrontal cortex as defined by the forward inference map, corresponding to the regions most consistently activated in studies that use the term “dorsolateral prefrontal cortex” (Yarkoni et al., 2011). The online Brodmann areas (Lacadie et al., 2008) in the MNI to Talairach atlas (http://noodle.med.yale.edu/∼papad/mni2tal/) of the Yale BioImage Suite (Papademetris et al.) showed that the MFG VOI in this study was located mostly in Brodmann Area 8 and a small part in rostral Brodmann Area 6. According to Petrides and Pandya (1999), Brodmann Area 8 and rostral Brodmann Area 6 are dorsolateral frontal areas underlying the maintenance of specifically spatial information.
Table 1.
Number of Voxels, Volume, and Center of Mass of Each of the 10 Volumes of Interest Used as Nodes in the Dynamic Causal Modeling Analysis
| VOI | Number of voxels | Volume (mL) | Center of mass MNI coordinates [x y z] (mm) |
|---|---|---|---|
| L MFG | 48 | 0.384 | −35, 8, 53 |
| R MFG | 190 | 1.520 | 38, 2, 58 |
| L pre-SMA | 59 | 0.472 | −12, 10, 64 |
| R pre-SMA | 176 | 1.408 | 4, 7, 64 |
| L PPC | 74 | 0.592 | −42, −34, 48 |
| R PPC | 242 | 1.936 | 37, −56, 52 |
| R putamen | 29 | 0.232 | 30, −1, −9 |
| R amygdala | 52 | 0.416 | 29, −2, −15 |
| L hippocampus | 31 | 0.248 | −15, −7, −20 |
| R insula | 31 | 0.248 | 34, 16, −13 |
VOI, volumes of interest; MNI, Montreal Neurological Institute; MFG, middle frontal gyrus; SMA, supplemental motor area; PPC, posterior parietal cortex.
DCM network discovery
DCM structure inference, as applied to fMRI activation experiments such as this study, searches for a model of the underlying neuronal connectivity among an a priori selected set of brain regions, in which the combined presence of some effective-connectivity interconnections (and/or modulation/driving input effects) and the absence of some other interconnections (and/or modulation/driving input effects) best explain the observed fMRI data. In this study, DCM structure inference was conducted using DCM Network Discovery (DND) (Friston et al., 2011). DND works in a data-driven fashion by identifying the sparse structure (i.e., absence of endogenous interconnections, driving input, or modulation effects) that best explains the observed fMRI data (Friston et al., 2011). The DND technique is useful for DCM studies with large numbers of nodes, such as this study, because with the increase in the number of nodes, the total number of free parameters and the number of models in the model space to be estimated for each subject increases quadratically (Seghier and Friston, 2013). When the number of models in the model space increases, it becomes increasingly impractical to conduct Bayesian model selection analysis, which selects the best model among a group of inverted (estimated) models (model space), because inverting all the models in the model space becomes an unsustainable computational load and storage load. DND overcomes this limitation (Friston et al., 2011), and in this study, DND efficiently selected for the whole group the model with optimal structure.
Two key routines are available in DCM12b for DND analysis: spm_dcm_post_hoc and spm_dcm_search (Friston and Penny, 2011). The former routine searches over all possible reduced models of a full model (in the sense of having the maximum number of free parameters) and uses post hoc model selection to select the optimal one (Friston and Penny, 2011). When a group of models are optimized together (e.g., group studies), these models are checked to ensure the same free parameters have been specified and the log evidences are pooled in a fixed-effects fashion (Friston and Penny, 2011). The latter routine operates on different a priori specified models to identify the best model (Friston and Penny, 2011). It estimates the “union” model (in the sense of having free parameters that are the union of all free parameters in each model specified) (Friston and Penny, 2011). The routine then uses post hoc selection to evaluate the model evidence of each model specified (Friston and Penny, 2011).
In this study, DND was conducted using the spm_dcm_post_hoc routine in the SPM12b software. Before the DND analysis was conducted, an initial single “full” model (Friston et al., 2011) was specified for each subject. The term “full” is used here in the sense that (1) each of the three experimental conditions (Go, Easy NoGo, and Hard NoGo) can be a driving input and a modulatory input; (2) each of the putative driving inputs entered all of the 10 nodes; (3) each node was putatively interconnected to all other nodes, and (4) each of the modulatory inputs putatively modulated all of the 90 interconnections between nodes. Since the incorrect responses were very few and sporadic, only stimuli corresponding to correct responses were included in the DCM analysis. The full models were inverted for all subjects. Group level post-hoc optimization was conducted by selecting all inverted “full” models (one per subject). The optimal sparse model was found at the group level, using Bayesian parameter averaging, which is integrated in the spm_dcm_post_hoc routine.
Results
Statistics on behavoral measures
The discrimination accuracy measure d′ (Forman et al., 2004; Gescheider, 1985; Lane et al., 2007) was used to measure behavioral performance on the Go/NoGo task in the scanner. For the 15 included subjects, the mean discrimination accuracy d′ during the Easy NoGo condition was 3.5999±0.4990 (corresponding to 98.72%±2.37% correct response), and the mean d′ during the Hard NoGo condition was 2.4647±0.5940 (corresponding to 81.54%±14.98% correct response). A two-sample Student's t-test analysis revealed that the d′ during the Easy NoGo condition was significantly greater than the d′ during the Hard NoGo condition (t=5.4751; df=28; p=0.00005). The means of the number of correct/incorrect responses are: 141.2±11.7 (correct Go), 14.8±11.7 (incorrect Go), 25.7±0.6 (correct Easy NoGo), 0.3±0.6 (incorrect Easy NoGo), 21.2±3.9 (correct Hard NoGo), and 4.8±3.9 (incorrect Hard NoGo).
SPM univariate analysis
SPM8 second-level random-effects one-sample t-test analysis revealed several statistically significant clusters for Easy, Hard, and Hard-Easy activations, which spanned to frontal, subcortical, and other brain regions. These regions included L MFG, R MFG, L pre-SMA, R pre-SMA, L PPC, R PPC, R PUT, R AMG, L HIP, and R INS, which were used as the regions of interest or nodes of the DCM. Please see the Supplementary Materials for the details of the SPM univariate analysis results.
DCM network discovery analysis
Starting from an initial full model, post-hoc optimization revealed an optimum sparse model structure at the group level. The DCM parameters of this optimum sparse model can be divided into two categories: parameter value=0 (corresponding to posterior probability=0) and parameter value=nonzero (corresponding to posterior probability >0.999). In this study, posterior probability >0.999 was used as the threshold to determine whether a DCM parameter is significantly different from zero.
The optimum sparse structure regarding driving inputs into the model is demonstrated in Supplementary Table S6, which shows the posterior mean strength for each driving input and each location. As evidenced by Supplementary Table S6, R AMG and L HIP were the driving input locations for all the three driving inputs into the model (Go, Easy NoGo, and Hard NoGo). In addition, R pre-SMA was the driving input location for Easy NoGo and Hard NoGo. Furthermore, L pre-SMA was the driving input location for Easy NoGo.
The group-level sparse structure regarding the endogenous connections is demonstrated in Supplementary Table S7. As shown in Supplementary Table S7, 12 connections (L MFG to R PUT, R MFG to L PPC, R MFG to R PUT, L pre-SMA to R AMG, R pre-SMA to R PUT, R pre-SMA to R INS, R PPC to R INS, R PUT to R MFG, R AMG to L pre-SMA, R AMG to R PPC, L HIP to L PPC, and R INS to L MFG) were switched off (connection strength=0, and posterior probability=0) by the post-hoc optimization among the 90 connections.
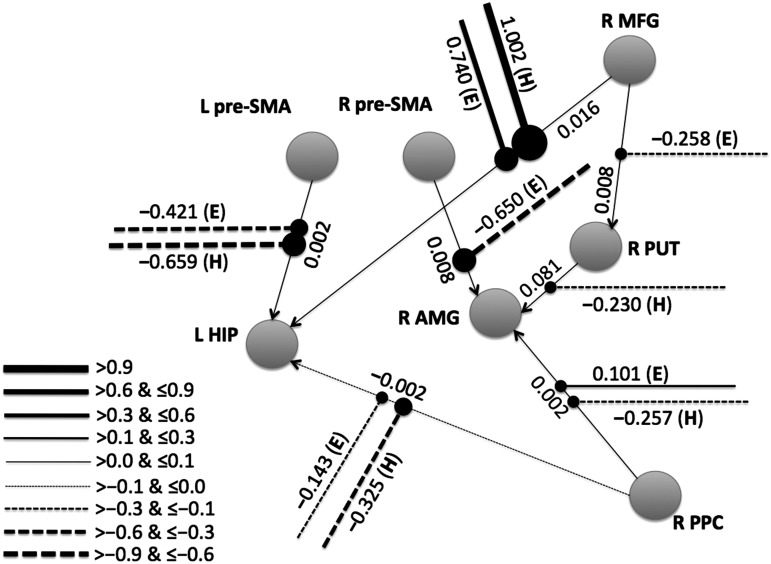
The group-level optimum sparse structure regarding modulation effects is shown in Supplementary Table S8. Due to the large number of connections, only those that had a posterior probability of modulation effect >0 are shown in Supplementary Table S8. As shown in Supplementary Table S8, seven connections were modulated by the NoGo conditions but not by the Go condition. Connections that were modulated by NoGo conditions (but not Go conditions) are shown in Figure 2. Note that Figure 2 only includes brain regions related to these connections. The strengths of the endogenous connections and modulation effects are also shown in Figure 2. It should be noted that connectivity from the R MFG to L HIP was relatively strongly positively modulated during both Easy and Hard NoGo conditions, and connectivity from L pre-SMA to L HIP was relatively strongly negatively modulated during both Easy and Hard NoGo conditions. Two connections (R MFG to R PUT, and R pre-SMA to R AMG) were only modulated by the Easy NoGo condition, and one connection (R PUT to R AMG) was only modulated by the Hard NoGo condition. Connectivity from the R MFG to R PUT was negatively modulated during the Easy NoGo condition, and connectivity from R PUT to R AMG was negatively modulated during the Hard NoGo condition (and not modulated by the other experimental conditions). Connectivity from R pre-SMA to R AMG was negatively modulated during Easy NoGo (and not modulated by the other experimental conditions). On the other hand, connectivity from L pre-SMA to R AMG was positively modulated during Easy NoGo (but negatively modulated during Hard Nogo and Go conditions).
FIG. 2.
Schematic diagram representing effective connectivity only modulated by the NoGo conditions. The endogenous connections are denoted by lines with arrows. The modulation effects are depicted by lines ending with a black dot. The legend in the bottom-left corner provides rough information about the relationship between line thickness (or line type) and effective connectivity strength. The mean strengths (in units of Hz) of the modulation effects exerted by the Easy (E) or Hard (H) NoGo condition are shown separately. For clarity, not all nodes and endogenous connections are shown in this figure. Only the connections that were modulated by NoGo conditions (but not Go conditions) and only the brain regions related to these connections are included. L, left. R, right.
Four connections (L pre-SMA to R AMG, L PPC to L HIP, R PPC to L pre-SMA, and L pre-SMA to R PUT) were modulated by Go and at least one of the NoGo conditions. Fourteen connections (L MFG to R AMG, R MFG to R PPC, L pre-SMA to R pre-SMA, L pre-SMA to L PPC, L pre-SMA to R INS, R pre-SMA to L PPC, R pre-SMA to R PUT, R pre-SMA to L HIP, R pre-SMA to R INS, R PPC to R pre-SMA, R PPC to R PUT, R PPC to R INS, R PUT to L hippocamups, and R INS to R AMG) were only modulated by the Go condition.
We conducted a post-hoc analysis using Bayesian contrasts of connections to test whether one condition had a significantly greater modulation effect than the other. The results of this post-hoc analysis are shown in Table 2. Only the modulation effects on the connection from R MFG to L HIP demonstrated the pattern of Hard NoGo>Easy NoGo>Go.
Table 2.
The Results of Bayesian Contrasts of Connections on the Modulation Effects Exerted by Hard NoGo (H), Easy NoGo (E), and Go Condition
| Connection | H>E | E>GO | H<E | E<GO | H>GO | H<GO |
|---|---|---|---|---|---|---|
| R MFG→L HIP | 0.999 | 0.999 | 0 | 0 | 0.999 | 0 |
| L pre-SMA→L HIP | 0 | 0 | 0.999 | 0.999 | 0 | 0.999 |
| R PPC→L HIP | 0.007 | 0 | 0.993 | 0.999 | 0 | 0.999 |
| R pre-SMA→R AMG | 0.999 | 0 | 0 | 0.999 | 0 | 0 |
| R MFG→R PUT | 0.999 | 0 | 0 | 0.999 | 0 | 0 |
| R PUT→R AMG | 0 | 0 | 0.999 | 0 | 0 | 0.999 |
| R PPC→R AMG | 0 | 0.999 | 0.999 | 0 | 0 | 0.999 |
Only the connections shown in Figure 2 were considered (i.e., connections that were modulated only by the NoGo conditions). All the numbers are probabilities.
HIP, hippocampus; PUT, putamen; AMG, amygdala.
Since the connection from R MFG to L HIP is the only connection that showed a pattern of modulation effects of Hard NoGo>Easy NoGo>Go, we conducted a post-hoc exploratory correlation analysis to test whether this MFG-HIP effective connectivity was associated with behavioral performance. Spearman nonparametric correlation analysis showed that the modulation effect on this connection was not significantly correlated with the d′ performance measure for the Hard NoGo condition (Rho=− 0.3821, uncorrected p=0.1607). Another correlation analysis showed that the correlation between the MFG-HIP effective connectivity (endogenous connectivity+modulation effect) and d′ was a trend toward significance for the Hard NoGo condition (Rho=−0.5393, corrected p=0.0814). Correlation analysis was not conducted for the Easy NoGo condition because of the lack of individual differences in behavioral performance during Easy NoGo condition (d′=3.5999±0.4990, corresponding to 98.72%±2.37% correct responses).
We also conducted several alternative DCM analyses using different procedures; the results of these alternative analyses are reported in the Supplementary Materials.
Discussion
In order to investigate the neural network underpinning inhibitory control, we examined the effective connectivity in 15 normal healthy subjects during performance in a Go/NoGo task with two levels of difficulty. Stochastic DCM was used to investigate which of the neural interconnections underlying inhibitory control were modulated by the NoGo conditions. We conducted network discovery analysis based on reducing an initial full model in which each of the three contextual conditions (Easy NoGo, Hard NoGo, and Go) separately served as driving inputs to all nodes, and also modulated all the connections. To the best of our knowledge, this is the first study that used the DCM Network Discovery technique to mechanistically depict the inhibitory control system.
The DCM Network Discovery analysis revealed that at the group level, both Go and NoGo conditions were driving inputs into the model at the R AMG and L HIP, consistent with a previous DCM study showing that different driving inputs can enter DCM network model through multiple nodes (Stephan et al., 2007). The network discovery analysis revealed that the Easy NoGo condition also was a driving input to the model at LR pre-SMA, and that the Hard NoGo condition also was a driving input to the model at R pre-SMA. These results reflect dynamic changes of the information propagation within the underlying neuronal network during the Go/NoGo task.
Consistent with our hypothesis, the DCM analysis found a cortical-subcortical connection (from right MFG to left HIP) in which both Easy and Hard NoGo conditions showed significantly greater modulation compared with Go, and in which the modulation effect for Hard (1.002 Hz) was significantly greater than the modulation effect for Easy (0.740 Hz). In addition, the main DCM analysis showed that both Easy and Hard NoGo conditions showed significantly stronger negative modulation compared with Go in the cortical-subcortical connection from left pre-SMA to left HIP, and that there was significantly greater negative modulation for Hard (−0.659 Hz) compared with Easy (−0.421 Hz) for this connection. The DCM analysis showed a similar finding (i.e., greater negative modulation effect for Hard vs. Easy) for the cortical-subcortical connection from right posterior parietal cortex to left HIP. Focusing on the connection on which the modulation effects showed the pattern of Hard NoGo>Easy NoGo>Go, we found that the correlation between the strength of the MFG-HIP effective connectivity and the behavioral performance d′ was a trend toward significance during the Hard NoGo condition in this small sample size. Future studies with larger sample size would be needed to clarify whether the MFG-HIP effective connectivity is significantly correlated with the behavioral performance.
An important component of inhibitory control is discrimination of signal, for example, initial signal processing or encoding (Forman et al., 2004; Green and Swets, 1966). In this study, since the Go trials are prepotent and the response should be made rapidly, difficulty in discriminating the signal increases the difficulty in inhibiting the (prepotent) response. In other words, greater signal processing demands produce more inhibitory errors when there is time pressure on the response (Forman et al., 2004; Green and Swets, 1966). Consistently, the behavioral performance was significantly worse during the Hard NoGo condition compared with Easy NoGo condition; and the modulation effect on the connection from R MFG to L HIP exerted by the Hard NoGo condition was significantly higher than that exerted by the Easy NoGo condition. Previous studies have shown that the HIP is critical for visual discrimination performance, especially when spatial processing is needed (Graham et al., 2006; Lee et al., 2005a, b). A recent study has shown that the HIP supports visual discrimination through learning spatial pattern (Kim et al., 2011). In addition, it has been theorized that one of the functions of MFG is stimulus-response associative learning (Goldstein and Volkow, 2011). Taken together, our results may reflect that compared with the Easy NoGo condition, stronger control from MFG was needed for the HIP to discriminate/learn the spatial pattern in order to respond correctly (inhibit), during the Hard NoGo condition. We can speculate that the difficulty of the Hard NoGo trials may have been frustrating and may have activated emotional circuits related to anxiety. Previous studies have shown that greater HIP volume was associated with high scores on the sensitivity to punishment scale (Levita et al., 2014) and that hippocampal activation was related to monitoring of threat level during a human approach-avoidance task that emulated rodent anxiety paradigms (Bach et al., 2014). Thus, an alternative interpretation of our results would be that stronger control from MFG to HIP may have been related to anxiety during Hard NoGo than during Easy NoGo.
The main DCM post-hoc statistical tests on the DCM parameters (see “Results” section in the main text) revealed that for each connection in the model, the modulation effects for the Hard NoGo condition were significantly different than the modulation effects for the Easy NoGo condition. In addition, the pattern of the modulation effects exerted by the Easy or Hard NoGo conditions was complicated, and showed different effects for different neural connections, and most of these modulation effects were not generally monotonically associated with NoGo task difficulty. In other words, in some connections, Hard NoGo showed greater modulation effect compared with Easy NoGo, but vice versa in other connections. Thus, these findings may explain why the alternate DCM analysis (see Supplementary Materials) that used the combined NoGo condition and/or the interaction of NoGo×Difficulty as modulatory inputs did not find reliable group-level modulation effects. Another potential reason may be that the regions of interest (ROIs) for DCM analysis did not include the significantly active brain regions for the combined NoGo condition (See the Supplementary Materials). These brain regions did not satisfy the following ROI selection criteria in the “Methods” section: (1) that the region should also show activation in previous fMRI studies using Go/NoGo tasks, and (2) that the region should also be regarded in the previous literature to be involved in inhibitory control.
Consistent with the opinion that stochastic DCM is appropriate for assessing the relative contributions of experimental stimulations (modulation effects) (Kahan and Foltynie, 2013), we have used stochastic DCM in this study. Unlike deterministic DCM in which random fluctuations were not modeled, stochastic DCM takes into account stochastic (random) fluctuations in the evolution of regional activity (Li et al., 2011). The stochastic fluctuations in physiological noise may contribute to the system connectivity input (Li et al., 2011) due to stochastic fluctuations in neuronal and vascular responses (Kruger et al., 2001; Li et al., 2011). Li and colleagues (2011) have demonstrated that stochastic DCM can improve parameter estimation over deterministic DCM. In addition, Daunizeau and colleagues (2012) have validated stochastic DCM and shown that stochastic DCM is superior to deterministic DCM in both model structure inference and model parameter inference. Furthermore, Daunizeau and colleagues (2013) studied conjoint empirical electroencephalography (EEG) and fMRI data and found that neural fluctuations which were inferred using stochastic DCM from fMRI data have an electrophysiological underpinning, providing empirical evidence supporting the predictive validity of stochastic DCM for fMRI data. For comparison with stochastic DCM, we used an alternate deterministic DCM analysis to conduct network discovery on the same data set (see the Supplementary Materials). Stochastic DCM analysis found significant results on driving inputs, whereas the alternate deterministic DCM analysis did not find any significant results on driving inputs, consistent with previous studies showing that stochastic DCM is superior over deterministic DCM in both model structure inference and model parameter inference (Duanizeau et al., 2012; Li et al., 2011).
How to optimize DCM experimental design is still an open question. In order to avoid susceptibility artifacts in the medial orbitofrontal area, we used spin-echo EPI in this study. Spin-echo EPI has better signal homogeneity; on the other hand, it has relatively lower signal amplitude compared with gradient echo EPI for the BOLD response. Only a few studies have investigated how to optimize a DCM experimental design (e.g., Daunizeau et al., 2011a, b; Goulden et al., 2012), and they have not ruled out spin-echo EPI as an approach for DCM analysis. We also used a rapid event-related design. Although it has been shown that compared with block design, event-related design is suboptimal for DCM analysis (Daunizeau et al., 2011b), event-related design is more appropriate for Go/NoGo studies (Simmonds et al., 2008). Our own data in this study showed that an fMRI experimental design combining spin-echo EPI and rapid event-related design can result in reliable DCM parameters, including modulation effects.
This study has several limitations. (1) It is possible that other neural interconnections may exist which are important for inhibitory control but not included in this study, because the regions to which they connect were not included as nodes for the present DCM analysis. One reason for the exclusion of potential nodes for this study was the lack of sufficient activation on fMRI, possibly related to the relatively small sample size (n=15). Future studies with more subjects will be helpful in providing greater insights into the neuronal effective connectivity underlying inhibitory control. (2) In addition, due to small sample size, it is difficult to evaluate the sex effect (eight women and nine men) in this study. (3) This study only included carefully screened healthy subjects, and it is quite possible that subjects with neurological, psychiatric, or substance use disorders may have different effective connectivity during response inhibition. (4) As a part of a larger study, all the subjects in this study received a placebo capsule, which may have contributed to unknown sources of variability in both the behavioral and brain activation data. (5) We have shown that effective connectivity was modulated by the NoGo conditions; however, it is unknown which brain regions mechanistically caused these modulation effects. This question could be addressed in future studies using non-linear DCM (Stephan et al., 2008). (6) The Go/NoGo paradigm has been used as a popular tool for investigating response inhibition mechanisms. However, fMRI activations elicited by Go/NoGo tasks are not necessarily directly related to response inhibition (Criaud and Boulinguez, 2013). In order to avoid the emergence of trivial strategies (e.g., always responding to all stimuli would automatically lead to 75% correct performance), we motivated subjects by setting higher reward values for NoGo trials than for Go trials (thrice, either in terms of gain or loss). Thus, the activations found in this study probably reflect the engagement of different cognitive processes, for example, attention, reward, and/or motivation, in addition to response inhibition. Thus, our results are difficult to disentangle from simple response inhibition. In this study, subjects had no explicit knowledge about the reward contingencies on the task, nor were they provided feedback about individual-trial earnings, block-level earnings, or performance accuracy. They were only told that the contingencies are such that maximal earnings will be obtained by responding on all Go trials and not responding on NoGo trials. The lack of detail in the instructions and absence of real-time feedback negate the possibility that subjects could discriminate reward density (i.e., which was “more reinforced”) during the rapid stream of stimuli and responses during the fMRI run. (7) The HIP has been used as a VOI based on group-level activation. The anterior HIP is vulnerable to inter-subject variation and is near the AMG. In order to clarify whether the group-derived HIP VOI in MNI space extended into each individual subject's AMG in the subject's native space, we reverse transformed the group-level hippocampal mask, which was in standard MNI space, back to each subject's native space. The hippocampal mask in native space was then overlaid on the subject's structural image in his/her native space. Among the 15 subjects, 12 of them showed no overlap between the hippocampal mask and the subject's AMG in native space. There was slight overlap between the hippocampal mask and the subject's AMG for the remaining three subjects.
In conclusion, the DCM Network Discovery analysis revealed that given the nodes in our network model, the locations of the driving input into the model by all the experimental stimuli were the AMG and the HIP, which then influenced other nodes in the model. The strengths of several cortico-subcortical connections were modulated by the two NoGo conditions. Specifically, connectivity from the MFG to HIP was enhanced by the Easy condition and further enhanced by the Hard NoGo condition, possibly suggesting that compared with the Easy NoGo condition, stronger control from MFG is needed for HIP to discriminate/learn the spatial pattern in order to respond correctly (inhibit), during the Hard NoGo condition.
Supplementary Material
Acknowledgments
This work is financially supported by the National Institute on Drug Abuse (NIDA) Grants # R01 DA034131 (L.M.), P50 DA009262 (F.G.M./J.L.S.), P50 DA018197 (T.R.K.), K05 DA020087 (K.A.C.), P50 DA033935 (K.A.C.), P20 DA024157 (K.A.C.), and MCRR Shared Instrumentation Grant # 1 S10 RR019186-01 (P.A.N.). The authors thank Zahra N. Kamdar, Vipulkumar S. (Vips) Patel, and Edward A. Zuniga for their excellent technical support. They also thank the anonymous reviewers for their constructive comments, which have resulted in significant improvement of this article.
Author Disclosure Statement
No competing financial interests exist.
References
- American Psychiatric Association. 2000. Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition, Text Revision. Washington, DC: American Psychiatric Association [Google Scholar]
- Aron AR, Behrens TE, Smith S, Frank MJ, Poldrack RA. 2007. Triangulating a cognitive control network using diffusion-weighted magnetic resonance imaging (MRI) and functional MRI. J Neurosci 27:3743–3752 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bach DR, Guitart-Masip M, Packard PA, Miro J, Falip M, Fuentemilla L, Dolan RJ. 2014. Human hippocampus arbitrates approach-avoidance conflict. Curr Biol 24:541–547 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bechara A. 2005. Decision making, impulse control and loss of willpower to resist drugs: a neurocognitive perspective. Nat Neurosci 8:1458–1463 [DOI] [PubMed] [Google Scholar]
- Buchsbaum BR, Greer S, Chang WL, Berman KF. 2005. Meta-analysis of neuroimaging studies of the Wisconsin card-sorting task and component processes. Hum Brain Mapp 25:35–45 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chikazoe J. 2010. Localizing performance of go/no-go tasks to prefrontal cortical subregions. Curr Opin Psychiatry 23:267–272 [DOI] [PubMed] [Google Scholar]
- Cox RW. 1996. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res 29:162–173 [DOI] [PubMed] [Google Scholar]
- Criaud M, Boulinguez P. 2013. Have we been asking the right questions when assessing response inhibition in go/no-go tasks with fMRI? A meta-analysis and critical review. Neurosci Biobehav Rev 37:11–23 [DOI] [PubMed] [Google Scholar]
- Daunizeau J, David O, Stephan KE. 2011a. Dynamic causal modelling: a critical review of the biophysical and statistical foundations. NeuroImage 58:312–322 [DOI] [PubMed] [Google Scholar]
- Daunizeau J, Friston KJ, Kiebel SJ. 2009. Variational Bayesian identification and prediction of stochastic nonlinear dynamic causal models. Phys D 238:2089–2118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daunizeau J, Lemieux L, Vaudano AE, Friston KJ, Stephan KE. 2013. An electrophysiological validation of stochastic DCM for fMRI. Front Comput Neurosci 6:(Article 103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daunizeau J, Preuschoff K, Friston K, Stephan KE. 2011b. Optimizing experimental design for comparing models of brain function. PLoS Comput Biol 7:e1002280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daunizeau J, Stephan KE, Friston KJ. 2012. Stochastic dynamic causal modeling of fMRI data: should we care about neural noise? Neuroimage 62:464–481 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enticott PG, Ogloff JRP, Bradshaw JL. 2006. Associations between laboratory measures of executive inhibitory control and self-reported impulsivity. Pers Individ Dif 41:285–294 [Google Scholar]
- Friston KJ. 2011. Functional and effective connectivity: a review. Brain Connect 1:13–36 [DOI] [PubMed] [Google Scholar]
- Friston KJ, Harrison L, Penny W. 2003. Dynamic causal modelling. Neuroimage 19:1273–1302 [DOI] [PubMed] [Google Scholar]
- Friston KJ, Li B, Daunizeau J, Stephan KE. 2011. Network discovery with DCM. Neuroimage 56:1202–1221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Penny W. 2011. Post hoc Bayesian model selection. Neuroimage 56:2089–2099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forman SD, Dougherty GG, Casey BJ, Siegle GJ, Braver TS, Barch DM, Stenger VA, Wick-Hull C, Pisarov LA, Lorensen E. 2004. Opiate addicts lack error-dependent activation of rostral anterior cingulate. Biol Psychiatry 55:531–537 [DOI] [PubMed] [Google Scholar]
- Gescheider GA. 1985. Psychophysics: Method, Theory, and Application. Hillsdale, NJ: Erlbaum [Google Scholar]
- Goldstein RZ, Volkow ND. 2011. Dysfunction of the prefrontal cortex in addiction: neuroimaging findings and clinical implications. Nat Rev Neurosci 12:652–669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goulden N, Elliott R, Suckling J, Williams SR, Deakin JF, McKie S. 2012. Sample size estimation for comparing parameters using dynamic causal modeling. Brain Connect. 2:80–90 [DOI] [PubMed] [Google Scholar]
- Graham KS, Scahill VL, Hornberger M, Barense MD, Lee AC, Bussey TJ, Saksida LM. 2006. Abnormal categorization and perceptual learning in patients with hippocampal damage. J Neurosci 26:7547–7554 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green DM, Swets JA. 1966. Signal Detection Theory and Phychophysics. New York: Wiley [Google Scholar]
- Heatherton TF, Wagner DD. 2011. Cognitive neuroscience of self-regulation failure. Trends Cogn Sci 15:132–139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahan J, Foltynie T. 2013. Understanding DCM: ten simple rules for the clinician. NeuroImage 83:542–549 [DOI] [PubMed] [Google Scholar]
- Kim S, Jeneson A, van der Horst AS, Frascino JC, Hopkins RO, Squire LR. 2011. Memory, visual discrimination performance, and the human hippocampus. J Neurosci 31:2624–2629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruger G, Kastrup A, Glover GH. 2001. Neuroimaging at 1.5 T and 3.0 T: comparison of oxygenation-sensitive magnetic resonance imaging. Magn Reson Med 45:595–604 [DOI] [PubMed] [Google Scholar]
- Lacadie CM, Fulbright RK, Rajeevan N, Constable RT, Papademetris X. 2008. More accurate Talairach coordinates for neuroimaging using non-linear registration. Neuroimage 42:717–725 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lane SD, Moeller FG, Steinberg JL, Buzby M, Kosten TR. 2007. Performance of cocaine dependent individuals and controls on a response inhibition task with varying levels of difficulty. Am J Drug Alcohol Abuse 33:717–726 [DOI] [PubMed] [Google Scholar]
- Lee AC, Buckley MJ, Pegman SJ, Spiers H, Scahill VL, Gaffan D, Bussey TJ, Davies RR, Kapur N, Hodges JR, Graham KS. 2005a. Specialization in the medial temporal lobe for processing of objects and scenes. Hippocampus 15:782–797 [DOI] [PubMed] [Google Scholar]
- Lee AC, Bussey TJ, Murray EA, Saksida LM, Epstein RA, Kapur N, Hodges JR, Graham KS. 2005b. Perceptual deficits in amnesia: challenging the medial temporal lobe ‘mnemonic’ view. Neuropsychologia 43:1–11 [DOI] [PubMed] [Google Scholar]
- Levita L, Bois C, Healey A, Smyllie E, Papakonstantinou E, Hartley T, Lever C. 2014. The behavioural inhibition system, anxiety and hippocampal volume in a non-clinical population. Biol Mood Anxiety Disord 4:4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li B, Daunizeau J, Stephan KE, Penny W, Hu D, Friston K. 2011. Generalised filtering and stochastic DCM for fMRI. Neuroimage 58:442–457 [DOI] [PubMed] [Google Scholar]
- Logan GD, Schachar RJ, Tannock R. 1997. Impulsivity and inhibitory control. Psychol Sci 8:60–64 [Google Scholar]
- Ma L, Steinberg JL, Hasan KM, Narayana PA, Kramer LA, Moeller FG. 2012. Working memory load modulation of parieto-frontal connections: evidence from dynamic causal modeling. Hum Brain Mapp 33:1850–1867 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma L, Steinberg JL, Hasan KM, Narayana PA, Kramer LA, Moeller FG. 2014. Stochastic dynamic causal modeling of working memory connections in cocaine dependence. Hum Brain Mapp 35:760–778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maldjian JA, Laurienti PJ, Burdette JH. 2004. Precentral gyrus discrepancy in electronic versions of the Talairach atlas. Neuroimage 21:450–455 [DOI] [PubMed] [Google Scholar]
- Maldjian JA, Laurienti PJ, Kraft RA, Burdette JH. 2003. An automated method for neuroanatomic and cytoarchitectonic atlas-based interrogation of fMRI data sets. Neuroimage 19:1233–1239 [DOI] [PubMed] [Google Scholar]
- Moeller FG, Barratt ES, Dougherty DM, Schmitz JM, Swann AC. 2001. Psychiatric aspects of impulsivity. Am J Psychiatry 158:1783–1793 [DOI] [PubMed] [Google Scholar]
- Moeller FG, Steinberg JL, Schmitz JL, Ma L, Liu S, Kjome KL, Rathnayaka N, Kramer LA, Narayana PA. 2010. Working memory fMRI activation in cocaine dependent subjects: association with treatment response. Psychiatry Research Neuroimaging 181:174–182 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noël X, Brevers D, Bechara A. 2013. A neurocognitive approach to understanding the neurobiology of addiction. Curr Opin Neurobiol 23:632–638 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norris DG, Zysset S, Mildner T, Wiggins CJ. 2002. An investigation of the value of spin-echo-based fMRI using a Stroop color-word matching task and EPI at 3 T. Neuroimage 15:719–726 [DOI] [PubMed] [Google Scholar]
- Papademetris X, Jackowski M, Rajeevan N, Okuda H, Constable RT, Staib LH. BioImage suite: an integrated medical image analysis suite. Section of Bioimaging Sciences, Dept. of Diagnostic Radiology, Yale School of Medicine; http://bioimagesuite.org [Google Scholar]
- Petrides M, Pandya DN. 1999. Dorsolateral prefrontal cortex: comparative cytoarchitectonic analysis in the human and the macaque brain and corticocortical connection patterns. Eur J Neurosci 11:1011–1036 [DOI] [PubMed] [Google Scholar]
- Rajkowska G, Goldman-Rakic PS. 1995. Cytoarchitectonic definition of prefrontal areas in the normal human cortex: II. Variability in locations of areas 9 and 46 and relationship to the Talairach coordinate system. Cereb Cortex 5:323–337 [DOI] [PubMed] [Google Scholar]
- Seghier ML, Friston KJ. 2013. Network discovery with large DCMs. Neuroimage 68:181–191 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmonds DJ, Pekar JJ, Mostofsky SH. 2008. Meta-analysis of Go/No-go tasks demonstrating that fMRI activation associated with response inhibition is task-dependent. Neuropsychologia 46:224–232 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephan KE, Kasper L, Harrison LM, Daunizeau J, den Ouden HE, Breakspear M, Friston KJ. 2008. Nonlinear dynamic causal models for fMRI. Neuroimage 42:649–662 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephan KE, Marshall JC, Penny WD, Friston KJ, Fink GR. 2007. Interhemispheric integration of visual processing during task-driven lateralization. J Neuroscience 27:3512–3522 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephan KE, Penny WD, Moran RJ, den Ouden HE, Daunizeau J, Friston KJ. 2010. Ten simple rules for dynamic causal modeling. Neuroimage 49:3099–3109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swick D, Ashley V, Turken U. 2011. Are the neural correlates of stopping and not going identical? Quantitative meta-analysis of two response inhibition tasks. Neuroimage 56:1655–1665 [DOI] [PubMed] [Google Scholar]
- Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M. 2002. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 15:273–289 [DOI] [PubMed] [Google Scholar]
- Volkow ND, Wang GJ, Fowler JS, Tomasi D, Telang F. 2011. Quantification of Behavior Sackler Colloquium: Addiction: Beyond dopamine reward circuitry. Proc Natl Acad Sci U S A 108:15037–15042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarkoni T, Poldrack RA, Nichols TE, Van Essen DC, Wager TD. 2011. Large-scale automated synthesis of human functional neuroimaging data. Nat Methods 8:665–670 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.