Comparative Study of Outcome Measures and Analysis Methods for Traumatic Brain Injury Trials

Abstract

Batteries of functional and cognitive measures have been proposed as alternatives to the Extended Glasgow Outcome Scale (GOSE) as the primary outcome for traumatic brain injury (TBI) trials. We evaluated several approaches to analyzing GOSE and a battery of four functional and cognitive measures. Using data from a randomized trial, we created a “super” dataset of 16,550 subjects from patients with complete data (n=331) and then simulated multiple treatment effects across multiple outcome measures. Patients were sampled with replacement (bootstrapping) to generate 10,000 samples for each treatment effect (n=400 patients/group). The percentage of samples where the null hypothesis was rejected estimates the power. All analytic techniques had appropriate rates of type I error (≤5%). Accounting for baseline prognosis either by using sliding dichotomy for GOSE or using regression-based methods substantially increased the power over the corresponding analysis without accounting for prognosis. Analyzing GOSE using multivariate proportional odds regression or analyzing the four-outcome battery with regression-based adjustments had the highest power, assuming equal treatment effect across all components. Analyzing GOSE using a fixed dichotomy provided the lowest power for both unadjusted and regression-adjusted analyses. We assumed an equal treatment effect for all measures. This may not be true in an actual clinical trial. Accounting for baseline prognosis is critical to attaining high power in Phase III TBI trials. The choice of primary outcome for future trials should be guided by power, the domain of brain function that an intervention is likely to impact, and the feasibility of collecting outcome data.

Introduction

Traumatic brain injury (TBI) is an important public health problem worldwide.¹ Every year, more than 53,000 people die in the United States alone due to TBI.² Moreover, it is estimated that 2% of the U.S. population currently suffers from long-term TBI-related cognitive, functional, and behavioral disabilities.³ The annual burden of TBI on the U.S. economy is estimated to be more than $75 billion.⁴

Despite the dire consequences of TBI, no acute treatment has proven beneficial in clinical trials.^5,6 Hence, there have been calls for more well-designed randomized controlled trials (RCTs) to test new interventions that may mitigate the substantial effects of TBI.⁷ Rigorously conducted RCTs are considered the definitive tool to test the efficacy of new interventions.⁸ Choosing the primary outcome for an RCT is a critical step that requires a careful balance among multiple factors, including minimization of type I and II error rates, comprehensive representation of the full spectrum of clinically important effects that an intervention may have, significance to stakeholders, and feasibility.^9,10 The diverse and multidimensional nature of TBI impact on an individual patient poses a unique challenge in selecting the primary outcome for RCTs of TBI.

The Extended Glasgow Outcome Scale (GOSE) is a global measure of long-term functional outcome for TBI victims with excellent reliability and validity.^11–14 Traditionally, GOSE and its predecessor, the Glasgow Outcome Scale, have been used as the single primary outcome in RCTs of new interventions for patients with moderate to severe TBI, and it is often dichotomized into favorable and unfavorable outcomes for analysis.^13,15 However, GOSE has been criticized for its failure to capture the multifaceted effects of TBI and its insensitivity to subtle changes, especially in the cognitive dimension; hence, some have questioned its suitability as the sole primary outcome for TBI treatment trials.^15,16 Composite outcomes, including batteries of both functional and cognitive measures, have been proposed as preferable alternatives, because of their better representation of the spectrum of long-term TBI outcomes and their theoretically superior statistical properties.^15,17–20 However, these composite measures have not been empirically shown to be superior to GOSE in minimizing type I and II error rates using clinical data with complex distributional challenges.

To address this evidence gap, we conducted a study using data from a recent RCT to compare the statistical properties of two types of primary outcome measures for Phase III TBI trials—GOSE and a battery of functional and cognitive performance measures, using several analytic strategies for each.

Methods

Study design

The source of patient-level data was a recent Phase III clinical trial, Magnesium Sulfate for Neuroprotection after TBI.¹⁹ After simulating multiple treatment effects across multiple outcome measures, we generated a large number of samples via bootstrapping from the available clinical trial data. Bootstrapping simply draws a random sample from the clinical trial data, with replacement.²¹ We made no assumptions about the sampled population other than the trial used being representative of patient outcomes following moderate to severe TBI. For each sample, we used a suite of statistical techniques to test the null hypothesis that the simulated treatment had no effect on the outcome measures. The primary objective of this study was to determine the power and corresponding type I error rate associated with each primary outcome measure and statistical technique. The study was approved by the Research Ethics Board of Sunnybrook Health Sciences Center, Toronto, Ontario, and the Institutional Review Board at the University of Washington, Seattle, Washington.

Data source

This simulation study used clinical data derived from a randomized controlled trial on TBI patients.¹⁹ The trial enrolled 499 patients aged 14 years or older (mean age - 34 years) with moderate or severe TBI who were admitted to a Level I regional trauma center in the United States between August 1998 and October 2004. The trial patients were randomly assigned one of two doses of magnesium or a placebo within 8 h of injury and continued the treatment for 5 d. The primary outcome was a composite of mortality, seizures, functional measures, and neuropsychological tests assessed six months after the injury. Although we had at least some outcome data available on 461 of the subjects (92%), we utilized only the data for the 331 subjects (66%) for whom data were known for all four outcome measures used in our study, which included those who had died or who were unable to take some of the tests due to neurological impairment. There were no significant differences in the primary or secondary outcomes between the treatment and control groups; therefore, data from both groups were included in the population used to draw the bootstrapped samples.

The reference values corresponding to normal levels of cognitive and functional performance were derived from patients who experienced trauma to parts of the body other than the head in the Patient Characteristics Study.²² These 132 participants were seen in the emergency department following trauma not involving the brain, with 71% having severe enough injuries to be admitted to the hospital. Ninety-two percent of subjects (n=121) returned at one year post-injury for neuropsychological assessment. Data from this study was used to establish normal levels of cognitive and functional performance for the purpose of defining the reduction in deficit and therefore simulating the desired treatment effects in the mock clinical trials.

Outcome measures

The two outcomes used for comparison were GOSE and a battery of four functional and cognitive measures. GOSE scores range from 1 to 8, with lower scores indicating a poorer functional outcome. The eight categories are: Dead, Vegetative State, Lower Severe Disability, Upper Severe Disability, Lower Moderate Disability, Upper Moderate Disability, Lower Good Recovery, and Upper Good Recovery.¹¹ The components of the four-measure battery are: GOSE,¹¹ Digit Symbol,^23,24 Selective Reminding Test Sum of Recall,²⁵ and Trail Making Test B (time to complete).²⁶ The three neuropsychological tests examine episodic memory, information processing speed, and executive functions.^23–27 For neuropsychological test scores, deaths were not considered to be missing data but rather were assigned a pseudoscore worse than the worst observed score. Those who were too neurologically impaired to take the test were assigned a pseudoscore better than those who died but worse than the worst score in the dataset. These neuropsychological tests were chosen, because they represent cognitive domains likely to be affected by TBI, they were among the outcome measures used in the Magnesium trial,¹⁹ and we had data on performance of control subjects who had other injuries but not ones involving the brain.²²

Statistical analysis

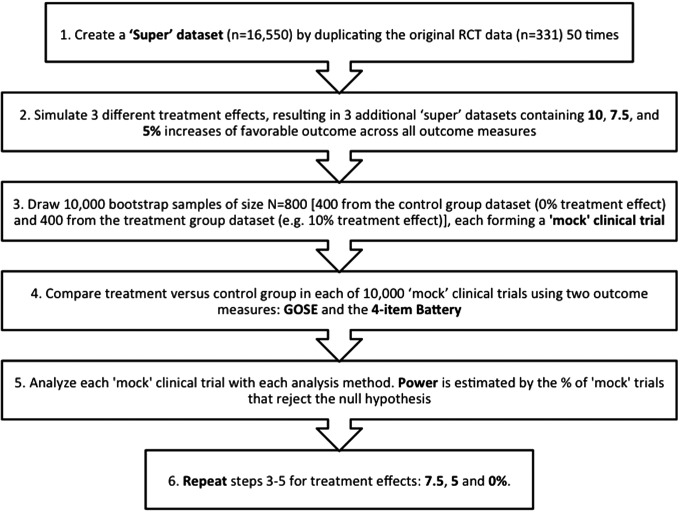
An overview of our statistical analysis is shown as a flowchart in Figure 1.

FIG. 1.

Flow diagram of the simulation design.

Generating the data with the desired treatment effect

To ensure that we could achieve the target outcome distribution equivalent to the desired treatment effect with a high precision, we first generated a “super” dataset of 16,550 subjects by replicating the original dataset (n=331) 50 times. Then, we simulated the desired treatment effect (i.e., shifted the outcome distribution to achieve the target treatment effects) in each version of the super datasets. We simulated three different treatment effect magnitudes, resulting in datasets containing 10.0, 7.5, and 5.0 percentage point increases of favorable outcome based on the dichotomized GOSE (i.e., GOSE 5–8). Simulated treatment effects were applied to the data by systematically improving the observed scores until the overall means and frequencies reached specific target values. Both the calculation of the target values and the assignment of the new scores are described below.

First, we calculated the target percentage in the favorable category for the GOSE (i.e., GOSE 5–8) by adding the posited treatment effect to the observed percentage in the favorable category and calculated the resulting odds ratio. We then constructed target frequencies for each individual GOSE category such that every possible dichotomization of the GOSE scale would yield an odds ratio equivalent to this value. Target values for the other outcome measures were achieved by re-expressing the treatment effect as a “reduction of deficit” as measured against published reference data on patients without TBI.²² For example, if 45% of the original RCT dataset and 95% of trauma controls had a favorable outcome, then the deficit would be seen to be 50 percentage points. Consequently, if the treatment effect was defined as a 10 percentage point increase on favorable outcome, this would correspond to a 20% reduction of this deficit (i.e., 10/50). This scalar could then be projected onto the other measures in a similar fashion. Thus, if the Selective Reminding Sum of Recall mean for the original RCT dataset was 30 words, and the trauma-control mean was 50 words, then the deficit would be 20 words, and the corresponding improvement due to the treatment effect would be 20% of this deficit (i.e., four words).

Once the target values were established, the posited treatment effect was infused into the original RCT dataset by improving the individual scores in a systematic and uniform manner until those values were realized. For the GOSE, this was achieved by randomly selecting subjects to improve by one category (or two categories if necessary). When such promotions on the GOSE involved subjects who were dead or too neurologically impaired to be tested on some or all of the other measures and thus required a battery that was more appropriate to their new GOSE level, they were assigned one from a randomly-chosen subject in that same level. For all of the other outcome measures, scores were improved using the same “reduction of deficit” methodology described above, except using ceiling values defined by observed maximums in the dataset rather than trauma control means (to ensure that no scores would actually worsen due to the treatment effect). Finally, all adjusted scores were rounded to emulate actual observed scores. This procedure resulted in three simulated datasets, each with a different treatment effect (10.0, 7.5, and 5.0 percentage points) in addition to the original data (which corresponded to a 0% treatment effect).

Forming the “mock clinical trials.”

The above simulations formed four sets of treatment data with 0, 5.0, 7.5, and 10.0 percentage points treatment effect, each drawn from a super dataset. We drew samples of n=400 from each of these datasets with replacement (i.e., bootstrapping) to create mock clinical trials with the desired treatment effect. For example, for a 10% treatment effect mock clinical trial, a sample of 400 subjects was drawn from the 10% treatment effect dataset and a sample of 400 subjects was drawn from the 0% treatment effect (control) dataset. This was done 10,000 times (each N=800), and then the process was repeated for the 7.5, 5.0, and 0% treatment effect simulations.

Determining power

We tested the null hypothesis of no treatment effect on both types of outcome measures, using multiple statistical techniques on each of the 10,000 simulated mock clinical trials, and for each of the desired treatment effects (5.0, 7.5, and 10.0 percentage points). Then, we computed the percentage of mock trials where the null hypothesis was rejected (i.e., how many were statistically significant defined as the two-sided p value<0.05). In this way, the estimated power for each outcome and analytical technique was calculated. By applying the same analytic approach to the dataset with the 0% treatment effect, we estimated the type I error rate.

Analysis of GOSE

First, GOSE was dichotomized into favorable (a score of 5 to 8 on the GOSE) and unfavorable (a score of 1 to 4 on the GOSE) outcomes, and a chi-square test (without continuity correction) was used to compare proportions. This is labeled “Fixed dichotomy of GOSE” in the tables and figures. This analytic technique, based on a dichotomization that is the same for all study participants, is commonly used to analyze GOSE.

Second, proportional odds regression²⁸ was used as an additional technique to analyze GOSE data under the assumption that the odds ratio for the treatment variable is the same for all possible ways of collapsing the ordinal outcome scale (i.e., GOSE) into a better and a worse category. The likelihood ratio test evaluates whether this odds ratio differs from 1. This is labeled “Proportional odds regression (GOSE).” The assumption of a consistent odds ratio for all dichotomization points was satisfied in the simulated data, because of the way we generated each treatment effect.

Third, we analyzed the GOSE data using a sliding dichotomy technique as described previously.^29,30 This method aims to improve sensitivity by stratifying according to baseline prognosis, with each stratum having a GOSE cutpoint that yields a more even split of favorable and unfavorable outcomes. For example, for patients with a poor prognosis, non-vegetative survival (i.e. GOSE scores of 3–8) would be considered favorable, whereas for patients with a good prognosis, only GOSE scores of 7 or 8 might be considered favorable.

In this procedure, dichotomization of GOSE was based on baseline prognostic risk. For each patient, the baseline prognostic risk score (BPRS) for the usually defined unfavorable outcome at six months (GOSE ≤4) was calculated based on three factors: age, Glasgow Coma Scale (GCS) motor score, and pupillary reactivity, using the International Mission for Prognosis and Analysis of Clinical Trials (IMPACT) core prognostic model.³¹ The original sample was ordered into tertiles based on the BPRS: best prognosis, intermediate prognosis, and worst prognosis. Within each tertile, the point of dichotomization for GOSE was chosen as the value closest to a 40:60 split between better and worse outcomes in the original dataset (Table 1). This split was chosen so that there would be nearly the optimal 50:50 split when the treatment effect was added. Thus, each patient's outcome was dichotomous (favorable or unfavorable) but the GOSE category they needed to obtain to be considered to have favorable outcome depended on their prognostic group. The treatment groups were compared using a chi-square test (without continuity correction). This is labeled “Sliding dichotomy of GOSE (3 prognostic groups).”

Table 1.

Illustration of Sliding Dichotomy Method (3 Prognostic Groups)

	Strata of probabilities of unfavorable outcome*
GOSE	Best prognosis	Intermediate prognosis	Worst prognosis
Death	Unfavorable	Unfavorable	Unfavorable
Vegetative
Lower severe disability			Favorable
Upper severe disability
Lower moderate disability
Upper moderate disability		Favorable
Lower good recovery	Favorable
Upper good recovery

^*Probabilities of unfavorable outcome (a score of 1 to 4 on the GOSE) were calculated using the International Mission for Prognosis and Analysis of Clinical Trials (IMPACT) core prognostic model.

GOSE, Extended Glasgow Outcome Scale.

Fourth, we used the same sliding dichotomy technique except with 10 prognostic groups instead of three, allowing finer distinctions between what would be considered favorable for an individual (Table 2). This is labeled “Sliding dichotomy of GOSE (10 prognostic groups).”

Table 2.

Illustration of Sliding Dichotomy Method (10 Prognostic Groups)

	Strata of probabilities of unfavorable outcome*
GOSE	1 (Lowest)	2	3	4	5	6	7	8	9	10 (Highest)
Death	Unfavorable				Unfavorable		Unfavorable			Unfavorable
Vegetative										Favorable
Lower severe disability							Favorable
Upper severe disability
Lower moderate disability
Upper moderate disability					Favorable
Lower good recovery	Favorable
Upper good recovery

^*Probabilities of unfavorable outcome (a score of 1 to 4 on the GOSE) were calculated using the International Mission for Prognosis and Analysis of Clinical Trials (IMPACT) core prognostic model. Stratum 1 is the decile of patients with the lowest probability of unfavorable outcome and stratum 10 is the decile with the highest probability of unfavorable outcome.

GOSE, Extended Glasgow Outcome Scale.

Fifth, the previous four analyses were repeated after adjusting each one for the baseline probability of unfavorable outcome (GOSE 1–4), as calculated using the IMPACT core prognostic model, using regression-based methods (noted on Table 2 as “Regression-Adjusted”). This provided us with adjusted fixed dichotomy using logistic regression, adjusted proportional odds regression, and adjusted sliding dichotomy using logistic regression (for three and 10 prognostic groups).

Analysis of four-measure battery

First, we dichotomized each of the component measures into favorable or unfavorable responses (based on the closest round number below the median score for subjects in the original dataset). Then, the null hypothesis was tested with logistic regression computed with the use of generalized estimating equations (GEE) to analyze all measures in the composite outcome simultaneously.²⁰ This technique assumes that the odds ratio is the same for each outcome and tests for whether that average odds ratio differs from 1. When analyzing the data using GEE, we tested two correlation structures: exchangeable (assumes equal correlation for all pairs of measures) and unstructured correlation (no assumption about correlation). These are labeled “Logistic regression with GEE (Exchangeable correlation)” and “(Unstructured correlation).” Similar analytic methods were used in the tissue plasminogen activator (t-PA) for acute ischemic stroke trial^8,32 and the Citicoline Brain Injury Treatment trial.¹⁸

Second, for the average percentile method, each subject's percentile in the full study sample was determined separately for each of the four measures in the battery, and the overall outcome for each subject was the average of the four percentiles. The range was 0 to 100, with a higher percentile indicating a better outcome. The t-test and Wilcoxon rank-sum tests were used to compare average percentile distributions between treatment and control groups. This method was used in the Magnesium trial¹⁹ and the recent BEST-TRIP intracranial pressure monitoring trial in TBI.¹⁷

Finally, with regard to GOSE, we looked to see whether analyzing the data with adjustment for baseline prognostic risk using regression methods increased power. This was done by including the baseline prognostic risk (i.e., the probability of unfavorable outcome on GOSE as calculated using the IMPACT model) in the logistic regression with GEE for the four-measure battery, and in the linear regression for the average percentile method. Note that here, as well, the word “Adjusted” is added to the beginning of the title of the relevant technique.

All of the statistical analyses were performed using SAS software (version 9.3, SAS Institute, Cary, NC), and statistical significance was defined by a two-tailed significance level of 0.05.

Results

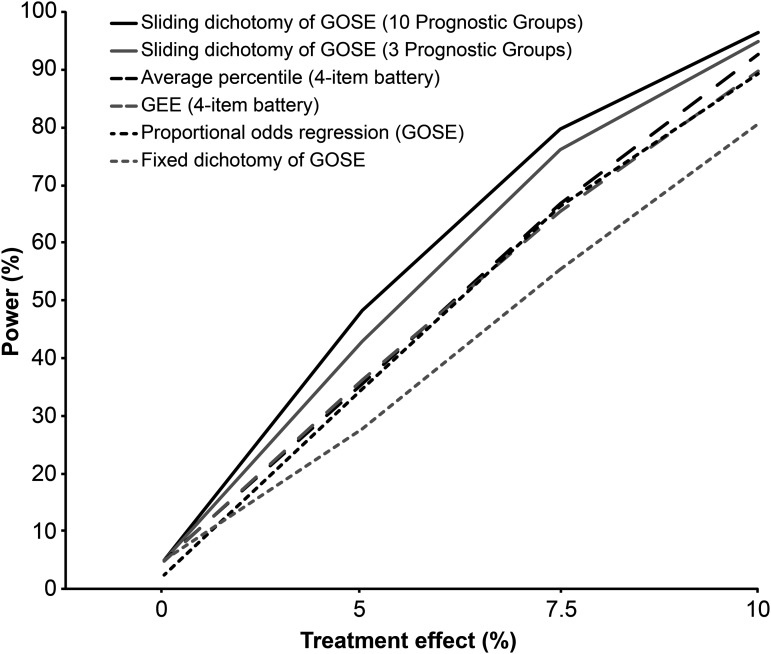
Table 3 summarizes the results of power calculations for both outcome measures across multiple analytic strategies. Analysis of the GOSE using the sliding dichotomy method (three or 10 prognostic groups) offered higher power across all treatment effects as compared to the methods for analyzing the GOSE or the four-measure battery that did not explicitly adjust for baseline prognosis (Fig. 2). Increasing the baseline prognostic groups from three to 10 in the sliding dichotomy method further increased the power to detect a treatment effect. Analyzing GOSE using the conventional fixed dichotomy method provided the lowest overall power. In other words, use of the sliding dichotomy would allow about a 30% to 40% decrease in sample size, compared with the fixed dichotomy without adjustment for baseline risk.

Table 3.

Summary of Power Calculations by Treatment Effect, and Type I Error Rate, over 10,000 Bootstrap Samples^a

	Treatment effecta
Outcome measure and analysis method	0%	5%	7.5%	10%
GOSE
Fixed dichotomy (chi-square)	5.0%	27.7%	55.4%	80.6%
Proportional odds regression	2.4%	34.6%	66.4%	89.4%
Sliding dichotomy method (3 prognostic groups)b	4.9%	42.9%	76.1%	95.0%
Sliding dichotomy method (10 prognostic groups)b	4.9%	48.2%	79.8%	96.4%
Regression-adjusted analysis of GOSEc
Adjusted fixed dichotomy d	2.4%	38.5%	70.8%	91.6%
Adjusted proportional odds regression	2.4%	52.4%	85.6%	98.4%
Adjusted sliding dichotomy method (3 prognostic groups)d	2.5%	42.9%	76.1%	94.9%
Adjusted sliding dichotomy method (10 prognostic groups)d	2.5%	48.2%	79.8%	96.3%
Four-Item batterye
Logistic regression with GEE (exchangeable correlation)	4.8%	36.3%	65.5%	89.7%
Logistic regression with GEE (unstructured correlation)	4.9%	35.7%	65.3%	89.8%
Average percentile method (t-test)	4.7%	35.4%	66.6%	92.3%
Average percentile method (Wilcoxon rank sum test)	4.9%	35.5%	66.7%	92.8%
Regression-adjusted analysis of four-item batteryc
Adjusted logistic regression with GEEf	4.8%	52.9%	83.8%	98.0%
Adjusted linear regression of average percentileg	4.9%	51.4%	84.8%	98.7%

^aCells report the proportion of 10,000 bootstrap samples where the null hypothesis was rejected (i.e., power when null hypothesis is false (5.0, 7.5 or 10.0% treatment effect), and type I error rate when null hypothesis is true (0% treatment effect)).

^bTreatment groups were compared using a chi-square test in the sliding dichotomy method calculated using the International Mission for Prognosis and Analysis of Clinical Trials (IMPACT) core prognostic model.

^cAdjusted for the baseline probability of unfavorable outcome (i.e., GOSE categories: 1–4), as calculated using the International Mission for Prognosis and Analysis of Clinical Trials (IMPACT) core prognostic model.

^dAnalysis was adjusted using a logistic regression model that includes the dichotomized GOSE as the dependent variable.

^eThe components of the four-item battery are: GOSE, Digit Symbol, Selective Reminding Sum of Recall and Trail Making Test B.

^fExchangeable correlation structure was assumed.

^gAnalysis was adjusted using a linear regression model that includes the average percentile as the dependent variable.

GOSE: Extended Glasgow Outcome Scale; GEE: generalized estimating equations.

FIG. 2.

Power curves for different outcome measures and analysis methods (sample n=400 per treatment group). For average percentile method, only results from Wilcoxon rank sum test are displayed in the figure (similar results were noted with t-test). For GEE, we only show the results under the assumption of exchangeable correlation structure (similar results were noted under the assumption of unstructured correlation). GOSE, Extended Glasgow Outcome Scale; GEE, generalized estimating equations.

When analyzing the four-measure battery without adjustment for baseline prognosis, the average percentile method provided higher power than a global test statistic computed using GEE but not as high as the power offered by an analysis of the GOSE using the sliding dichotomy method (Table 3; Fig. 2). Using a Wilcoxon rank-sum test instead of a t-test to compare the distribution of the average percentiles between the treatment groups did not change the results. In calculating a global test statistic using GEE, changing the assumption of exchangeable correlation structure to unstructured correlation also did not affect the power.

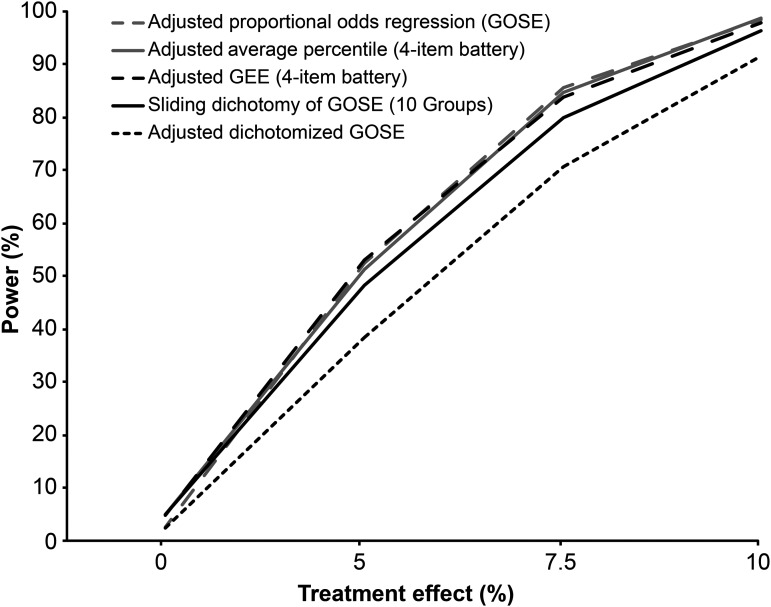
Adjustment for baseline characteristics using regression-based methods increased the power as measured by either GOSE or the outcome battery but notably not for the sliding dichotomy method with either three or 10 prognostic groups (Table 3; Fig. 3). The highest power across all outcome measures and analytic techniques was obtained using proportional odds regression including baseline risk to analyze GOSE, or using regression-based adjusted analysis of the four-measure battery (Table 3; Fig. 3). In terms of sample size, accounting for baseline prognosis using multivariate proportional odds regression or either adjusted analysis of the four-item battery would allow a 45% to 50% decrease in sample size—relative to fixed dichotomy method to analyze GOSE without adjustment for baseline prognosis—to yield comparable power.

FIG. 3.

Power curves for adjusted analyses using regression-based methods (sample n=400 per treatment group). Analyses were adjusted for the baseline probability of unfavorable outcome (i.e., GOSE categories: 1–4), as calculated using the International Mission for Prognosis and Analysis of Clinical Trials (IMPACT) core prognostic model. Power curve for sliding dichotomy method (10 prognostic groups) is shown for comparison (red curve). For average percentile method, only results from Wilcoxon rank sum test are displayed in the figure (similar results were noted with t-test). For GEE, we only show the results under the assumption of exchangeable correlation structure (similar results were noted under the assumption of unstructured correlation). GOSE, Extended Glasgow Outcome Scale; GEE, generalized estimating equations.

When analyzing the mock clinical trials with 0% treatment effect, proportional odds regression to analyze GOSE provided the lowest type I error rate (2.4%). Indeed, all of the statistical techniques used to analyze either outcome measure had acceptable rates of type I error (≤5%; Table 3).

Discussion

Choosing the primary outcome measure represents a critical step in designing Phase III clinical trials. Minimization of type II errors (i.e. maximizing the power) while keeping type I errors at or below the nominal figure is an important goal when deciding on the primary outcome measure.^9,10 Such errors can have a profound impact on the interpretation of study results and on planning future trials to address the same research question.

Historically, the U.S. Food and Drug Administration has accepted GOSE as the single primary outcome measure for TBI treatment trials.^{15,30,33–35} However, many have recently criticized GOSE as an insensitive measure of the multifaceted effects of TBI, especially when cognitive functioning is thought to be a major target of the treatment under investigation.^15,36 As an alternative to GOSE, batteries of functional (measured by GOSE) and cognitive (measured by neuropsychological tests) performance have recently been proposed by investigators—including those of the TBI Clinical Trials Network Outcome Measures subcommittee¹⁵—and have been used in a number of RCTs based on theoretical and practical considerations.^17–19 Among the main theoretical advantages of using a composite measure as the primary outcome instead of GOSE alone are the greater statistical power to detect a treatment effect than any single measure (provided the treatment effect is constant across all component measures), and the expectation that cognitive measures might be more sensitive.¹⁵ However, this has not been empirically shown using actual clinical data. Our study's findings challenge this notion.

In using multiple approaches to analyze actual clinical data, we found that several analytic methods can improve power over more commonly used techniques for analyzing primary outcome measures in TBI trials. Accounting for baseline prognosis, either by using sliding dichotomy for GOSE or using regression-based methods, substantially increased the power over corresponding analyses that did not account for prognosis. The highest overall power was obtained by using proportional odds regression that adjusted for baseline risk to analyze GOSE, or by using either of the regression-based adjusted analyses of the four-measure battery of functional and cognitive performance. Analyzing GOSE using the fixed dichotomy method, even with accounting for prognosis using logistic regression, provided substantially lower power.

This is the first study to compare GOSE with a battery of functional and cognitive measures from a TBI trial using actual clinical data. The distribution of outcome data for patients with moderate to severe TBI can be highly skewed, and a considerable proportion of patients might be too neurologically impaired to undergo neuropsychological testing. By using a bootstrapping technique to redraw a large number of samples from a super dataset, we ensured stability of the results across potentially complex distributional challenges commonly encountered in clinical data on TBI patients.²¹ Therefore, this technique helped to minimize the effect of random sampling errors on power calculations, without having to make assumptions of normality.²¹

Previous studies have compared multiple statistical techniques to analyze the 5-point GOS and 8-point GOSE.^29,37,38 The sliding dichotomy and proportional odds regression method were found to be more sensitive for detecting a treatment effect than the conventional fixed dichotomy in analyzing the GOS and GOSE.^29,39,40 Our results agree with these findings. In addition, we found that increasing the baseline prognostic groups from three to 10 as described in the original sliding dichotomy technique significantly increased statistical power. More importantly, if all measures have an equal decrease in deficit, our findings suggest that GOSE, if analyzed using the multivariate proportional odds regression or sliding dichotomy method, is as sensitive or only slightly less sensitive than a battery of functional and cognitive measures analyzed using regression-based adjustment for baseline prognosis.

The assumption of equal reduction in deficit is strong. Many might expect neuroprotective agents to have a larger effect on cognitive measures, which would lead to higher power for a battery that includes or is restricted to cognitive measures relative to GOSE alone. Similarly, a behavioral intervention might be hypothesized to have substantial effects on functional outcome, quality of life, or emotional wellbeing but little effect on cognition.⁴¹ However, cognitive and functional measures relate to severity of TBI, while emotional and quality of life measures have little or no relationship to severity.⁴² Since there have been no neuroprotection studies that have shown a positive effect of treatment, we could not determine which measures were most successful in picking up an actual neuroprotective effect. Instead, we simulated treatment effects.

In simulating the different treatment effects, we assumed similar percent reduction in deficit across all component measures for each treatment scenario. Therefore, our findings are limited to situations where the assumption of similar improvement using this metric across all component measures is satisfied. This may not be true in an actual clinical trial. Nevertheless, the validity of an outcome battery (i.e., a composite outcome measure) depends on the similarity in treatment effect across all of its component measures.⁴³ In other words, investigators are expected to construct batteries in which biology should lead to expect similar improvement across all components.⁴³ In cases where this assumption is not expected to hold, the use of composite measures is not recommended. In addition to the interpretational difficulty of an outcome battery when its constituents do not move in line with each other, less rather than more statistical power to detect effects on the primary end point would be expected.^20,44

Alternative approaches to simulate the treatment effect might yield different results. The treatment effect postulated for the dichotomized GOSE was propagated to the other possible GOSE cutpoints exactly as assumed for the proportional odds regression. Additionally, the adjusted proportional odds regression model assumes that the odds ratio for each covariate, including but not limited to the assigned treatment, is the same for all possible ways of collapsing the GOSE into a better and a worse category.⁴⁵ This assumption might be hard to verify a priori when designing a clinical trial.⁴⁵ If the treatment had a larger effect on some GOSE categories than on others, the power for the proportional odds regression might decrease. However, this needs to be confirmed by future studies. Further, as part of the analysis plan, one should test if the proportionality assumption holds prior to analyzing the data using the proportional odds regression method.²⁹ If not satisfied, one should consider using another analysis method that does not require the proportionality assumption, such as the sliding dichotomy technique, to provide a robust estimate of treatment effect.²⁹

Limited by the available dataset, we compared GOSE to only one potential outcome battery for TBI trials. Therefore, our findings may not be applicable to other outcome batteries of different component measures. However, these neuropsychological tests were chosen because they represent cognitive domains most likely to be affected by TBI. In addition, we speculate that similar results may be found if different neuropsychological tests were used to construct the composite outcome, because of the likely distributional similarity of cognitive outcome measures in patients with moderate to severe TBI. Nevertheless, only further studies using clinical data can confirm the generalizability of our study findings to other TBI outcome batteries.

In choosing a primary outcome for a TBI trial, there are other considerations, in addition to power. GOSE has some advantages over a battery of functional and cognitive measures. The GOSE can be administered over the telephone and can even be done with someone in close contact with the participant if need be. Cognitive tests must be done face-to-face with the participant. It takes less time and training to administer the GOSE than cognitive measures. Therefore, one is likely to have higher follow-up rates and less cost per person if the primary outcome is the GOSE. Further, clinicians may find measuring a treatment effect using a favorable-versus-unfavorable outcome dichotomy, as provided by the sliding dichotomy method, is more familiar and easier to understand than either an overall test based on multiple measures in a battery or odds ratios derived from multivariate regression analysis.⁴⁶

GOSE is an estimate of the overall functional outcome of TBI patients but it may not be an adequate measure of other dimensions of TBI effect, especially in the cognitive domain.^15,36 Future Phase III TBI trials testing treatments expected to mainly impact the functional domain may consider including neuropsychological tests as secondary outcomes to overcome this limitation without compromising the statistical power offered by GOSE as the sole primary outcome measure. Conversely, treatments that are most likely to affect cognition might be best examined in trials with neuropsychological measures as the primary outcome and GOSE as a secondary endpoint. Input from preclinical data and Phase I-II trials may help identify which outcome domain an intervention is most likely to impact, and thereby guide the choice of the primary outcome for a planned Phase III TBI treatment trial.

Conclusion

Accounting for baseline prognosis is critical to attaining high power in Phase III TBI trials. GOSE, if analyzed using the multivariate proportional odds regression or sliding dichotomy method, is as sensitive or only slightly less sensitive than a battery of functional and cognitive measures analyzed using regression-based adjustment for baseline prognosis, assuming equal treatment effect across all components. Analyzing GOSE using a fixed dichotomy provided the lowest power for both unadjusted and regression-adjusted analyses. The choice of primary outcome for future trials should be guided by power, the domain of brain function that an intervention is likely to impact, and the feasibility of collecting outcome data.

Acknowledgments

This work was supported in part by a Canada Research Chair Program in Systems of Trauma Care (to A.B.N.) and by DoD grant W81XWH-08-2-0159 (to N.T). Clinical trial data were collected under NIH grant R01 NS19643.

Author Disclosure Statement

No competing financial interests exist.