Skip to main content
PMC home page
Journal of Computational Biology logoLink to Journal of Computational Biology
. 2015 Apr 1;22(4):324–333. doi: 10.1089/cmb.2015.0010

cDREM: Inferring Dynamic Combinatorial Gene Regulation

Aaron Wise 1, Ziv Bar-Joseph 1,✉
PMCID: PMC4394168  PMID: 25844671

Abstract

Genes are often combinatorially regulated by multiple transcription factors (TFs). Such combinatorial regulation plays an important role in development and facilitates the ability of cells to respond to different stresses. While a number of approaches have utilized sequence and ChIP-based datasets to study combinational regulation, these have often ignored the combinational logic and the dynamics associated with such regulation. Here we present cDREM, a new method for reconstructing dynamic models of combinatorial regulation. cDREM integrates time series gene expression data with (static) protein interaction data. The method is based on a hidden Markov model and utilizes the sparse group Lasso to identify small subsets of combinatorially active TFs, their time of activation, and the logical function they implement. We tested cDREM on yeast and human data sets. Using yeast we show that the predicted combinatorial sets agree with other high throughput genomic datasets and improve upon prior methods developed to infer combinatorial regulation. Applying cDREM to study human response to flu, we were able to identify several combinatorial TF sets, some of which were known to regulate immune response while others represent novel combinations of important TFs.

Key words: : computational molecular biology, gene chips, gene expression, gene networks, HMM, machine learning, regulatory networks

1. Introduction

Gene expression is controlled, in part, by transcription factors (TFs), proteins which bind DNA and activate or repress their targets. Though genome-wide experimental techniques (including ChIP-chip and ChIP-seq) have been developed to establish the set of genes that each TF can regulate (Ren et al., 2000; ENCODE Project Consortium, 2012), such (often static) datasets only provide a partial picture of gene regulatory networks. First, regulation is a dynamic process that changes over time and in different conditions. In addition, genes are often combinatorially regulated by multiple transcription factors (TFs) (Brent and Ptashne, 1985). These factors either coactivate or corepress a gene or utilize a more complicated logic function (Yuh et al., 1998).

Modeling dynamic combinatorial networks is challenging. First, very little experimental data is available for directly studying such combinatorial regulation in vivo. Simple organisms such as yeast have more than 200 TFs, while the number is estimated to be more than 2000 for humans (Babu et al., 2004). Even looking at the most simple combinatorial subset, pairs of TFs, leads to an increase of two to three orders of magnitude in the number of regulators to be considered—around 20,000 for yeast and 2,000,000 for human cells. Combinatorial modules with more than 2 TFs are also possible, expanding the search space exponentially further. Additionally, given that combinatorial TF activity may be condition and time specific, experimentally interrogating the set of all possible modules is clearly impossible. Thus, tools that predict combinatorial binding are required to narrow the range of experiments that must be performed to identify combinatorial modules.

Given the importance of combinatorial binding, the question has been studied for over a decade. Pilpel et al. (2001) were one of the first to combine expression and sequence information for the analysis of co-occurring motifs in yeast. Their method searches for pairs of TFs whose target gene sets are more correlated in expression than either of the target sets of each TF alone. Other methods have primarily focused on using TF-gene-binding information to predict combinatorial TF binding in a more global context. For example, Yu et al. (2006a) used sequence and motif information in order to find pairs of S. cerevisiae transcription factors with statistically significant motif co-occurrence. A similar analysis for human data was also performed (Yu et al., 2006b). Another approach (Beyer et al., 2006) used a variety of data sources (including ChIP-chip data and sequence information) to predict TF-gene-binding in yeast. They then predicted combinatorial binding by identifying “modules” of at least two genes that had statistically enriched binding co-occurrence. Zinzen et al. (2009) combined ChIP-chip data with known enhancer binding patterns to predict cis-regulatory modules in Drosophila. A method by Gertz et al. (2008) used a synthetic library of promoter regions to develop a thermodynamic model of binding cooperativity between transcription factors.

While the above methods have provided valuable insights regarding combinatorial regulation, they often did not address two important issues. First, the exact logic used by the TFs (for example, AND or OR regulation) was usually not studied. Instead, the focus has primarily been on identifying the group of TFs rather than their influence. Second, even those methods that considered combinatorial logic did not model the dynamics of combinatorial regulation. So far, these methods were mostly focused on static/steady state analysis. Such analysis can miss cases where combinatorial binding is restricted to specific time points as we show in the Results Section.

To overcome these issues we developed a new method, cDREM, to model combinatorial dynamic regulation. Our method uses a probabilistic HMM-based model to integrate time series gene expression data with mostly static protein–DNA interaction data. To model combinatorial regulation we utilize a sparse group Lasso logistic regression method that attempts to explain dynamic changes in expression pattern using a (small) subset of combinatorially active TFs. The sets we consider include both logical AND and OR relationships, and these are assigned by the model to regulate genes at specific time points. We applied cDREM to time series data from yeast and human. In both cases, it was able to identify several combinatorial relationships, including logical AND relationships. Many of these were validated using additional high throughput datasets while others are novel, pointing to potential combinatorial interactions between key TFs.

2. Methods

2.1. Dynamic regulatory events miner (DREM)

cDREM extends the dynamic regulatory events miner (DREM) (Ernst et al., 2007) to infer and use combinatorial regulation. DREM uses an input–output hidden Markov model (IOHMM) to reconstruct dynamic regulatory networks. DREM integrates time series gene expression data with static protein–DNA interaction data (from DNA binding motifs, ChIP-chip or ChIP-seq data). The IOHMM is used to identify and learn parameters for regulatory events: points in the time series where a set of genes that were previously coexpressed diverge. These splits, which correspond to states in the HMM, are annotated by DREM with the TFs that are predicted to regulate genes in the outgoing upward and/or downward paths allowing us to associate temporal information (the timing of the splits, see Fig. 1) with the static protein–DNA interaction data.

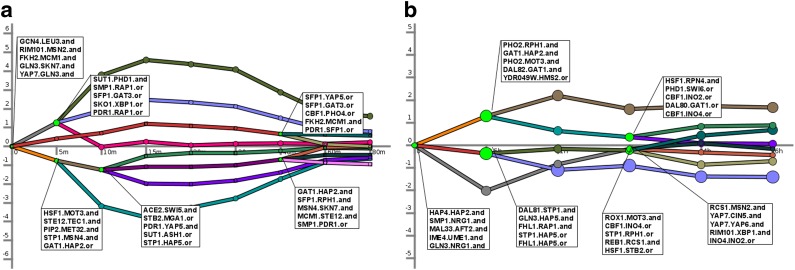
FIG. 1.

FIG. 1.

Open in a new tab

Reconstructed networks for yeast response to stress. We used cDREM to reconstruct combinatorial networks for yeast heat shock response and yeast response to amino acid starvation. Each path represents a set of genes that are found to be expressed and regulated in a similar manner. Bright green nodes represent splits where a regulatory event is predicted to occur. The splits are associated with a predicted set of transcription factors (TFs) indicating that these TFs are responsible for the changes in gene expression at that time point. For each split we display the top five significant combinatorial relationships identified. Note that, because the focus here is on combinatorial analysis, we omit the single activators identified (e.g., HSF1 is found on the first upregulated path in heat shock). See Supplementary Data for a list of all predictions.

To determine the set of TFs associated with each split, DREM learns an L1-regularized logistic regression classifier. The classifier uses the binding profile of a gene (the set of TFs that regulate it) to predict its next state going out of the split (up or down, see Fig. 1).

DREM has proven to be successful at modeling several biological processes and systems in multiple organisms, including stress response in yeast and E. coli (Ernst et al., 2007, 2008; Gitter et al., 2013), human and mouse development (Schulz et al., 2013; Roy et al., 2010; Mendoza-Parra et al., 2011), and immune and disease progression (Gitter and Bar-Joseph, 2013; Zinman et al., 2011; Laurenti et al., 2013).

2.2. From additive to combinatorial regulatory models

While DREM is useful for modeling dynamics, the logistic regression model that it relies on assumes independence between regulating TFs. Thus, the effect of multiple TFs is assumed to be additive in the DREM model, which ignores the combinatorial effects observed for sets of TFs.

To address this issue we developed cDREM. cDREM is designed to identify sets of combinatorially active TFs that dynamically regulate gene expression. It does this through a three-step process: (1) we identify a large set of TFs that are likely to work together (in a condition/time independent manner). Since the number of sets of size k is O(nk) where n is the number of TFs, prescreening is required to reduce the run time of the IOHMM and logistic regression algorithms. (2) We develop a new regression model based on the sparse group Lasso (Friedman et al., 2010), which can account for the relationships between sets of TFs identifying both AND and OR relationships within such sets (both for activators and repressors). AND relationships within a set indicate that all TFs are required to activate the gene, whereas OR relationships indicate that even one of the TFs in this set is enough. Both cases have been well documented in biological systems (Yuh et al., 1998). While more complex models can be generated from these two logic gates (for example, a combination of ANDs and ORs), there are very few documented examples of such relationships in regulatory networks, and due to their combinatorial complexity, we do not consider them in this work. (3) In a post-processing step, we analyze the putative TF subsets that are significantly associated with the learned splits to determine their interactions and impact on transcriptional regulation.

2.3. Identifying candidate transcription factor pairs

The first step is to prescreen the set of all possible TFs for subsets that are likely to interact. This is necessary since, as mentioned above, the number of such sets is exponential in k.

We use a greedy approach akin to Sinha et al. (2008) to screen for such an initial subset. We start by computing the significance of the overlap between the targets of all pairs of TFs using the hypergeometric test. We retain all pairs (a, b) below a certain p-value. Next, for each pair we retain we compute the significance of the overlap between targets of both TFs and targets of all other TFs c (one at a time) and again, retain all significant triplets. For this computation we use the intersection of a and b thereby defining a “new” TF construct ab that has as targets all genes that are bound by both TFs. This process is continued until we reach subsets of size k. The total run time of this algorithm is O(nk), which for small values of k is reasonable (we do not expect genes to be combinatorially controlled by tens of factors). When limiting our sets to pairs (k = 2), we perform Bonferroni correction to find all pairs of a certain significance. For higher values of k, we use a cutoff that is informed by the practical consideration of identifying a manageable number of TF combinations. The Lasso algorithm will then be used to further refine this set.

Once we have identified candidate subsets, we determine the targets of their OR and AND combination and add both types of logic sets as potential regulators in cDREM. These AND and OR combinations are explicitly modeled as regulators in cDREM. To do this, we must identify their targets. We define the targets of OR and AND sets in the following way. Let S be one of the subsets of TFs that was identified in the screening step. Let SI be the intersection of all targets of TFs in S (i.e., genes that are bound by all TFs in S), and let SU be the union of that set. We use SI as the potential targets of the AND logic gate for TFs in S and SU as potential targets for the OR function of the TFs in S.

2.4. Training using the sparse group Lasso

After identifying our potential subsets, we learn an IOHMM that models the dependency of gene expression on these logical TF subsets. To do this, we extend DREM using the sparse group Lasso. The sparse group Lasso extends the standard Lasso by taking into account relationships among the variables. The standard Lasso objective function is of the form:

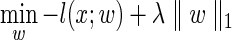graphic file with name eq1.gif

Here, l(x; w) is the log likelihood of our model and λ∥w∥1 is an L1 penalty term. In our case, we are using a logistic regression function to learn transition probabilities and so the penalized likelihood function is:

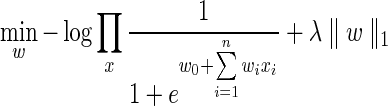graphic file with name eq2.gif

where wi is the weight learned by cDREM for the ith regulator, and xi is our confidence in the interaction between TF i and a target gene x, which is provided as input [this could either be a binary indicator or a continuous value between 0 and 1, see Schulz et al. (2012) for details].

The effect of the L1 term is to promote the sparsity of our weights wi, corresponding to regulators we expect to be involved in binding events. This is desirable in several optimizations and is also a reasonable assumption in biology since most regulatory events are caused by the specific effect of a small number of regulators (compared to the total number of TFs expressed).

The sparse group Lasso adds an additional penalty term to the Lasso, resulting in a new objective function:

graphic file with name eq3.gif

where γ is a group penalty term, G is the set of groups in the model, and ||w(g)||2 is the L2 norm of the weights of all members of the gth group. In our case, each group corresponds to a transcription factor and all of the subsets added to DREM that include that factor. (Thus, a TF can belong to multiple groups when it is in more than one logical set.) The group penalty term allows us to control the selection of different subsets associated with the same TF and to reduce the overall number of different TF combinations associated with a split. For more details on training the group lasso, see the Supplementary Material (available online at www.liebertpub.com/cmb).

2.5. Post-processing to identify the set of active TF sets for each split

To select the subset of combinatorial sets for further analysis, we combine the hypergeometric p-value (which is calculated based on the target genes associated with a split) with the logistic regression model coefficient for this set. Since the model employs a sparsity constraint, such combination allows us to prioritize sets identified by the Lasso as important for the split. Thus, we use a hypergeometric threshold of p < 0.1, and then take the regulators with the highest model score.

3. Results

We first tested cDREM using four different stress response time series datasets from S. cerevisiae: amino acid starvation response (Gasch et al., 2000), heat shock (Gasch et al., 2000), and osmotic stress (Gasch et al., 2000; Romero-Santacreu et al., 2009). The main reason we started with yeast is because a lot is known about regulation in this species, and several complementary high throughput datasets exist. This allowed us to rigorously test and compare cDREM with other methods. We next applied cDREM to study combinatorial regulation in human immune response. While cDREM identified both logical AND and OR relationships as can be seen in Figure 1, we have focused here on AND relationships. First, standard logistic regression can capture at least some OR relationships (or other additive function), while AND cannot be captured by most current regression algorithms. In addition, it is harder to validate OR relationships. Though we expect many AND pairs to physically interact, for OR pairs that is much less likely. Finally, most prior work focused on AND relationships (Pilpel et al., 2001; Yu et al., 2006a), making comparison harder for ORs.

While we tested cDREM with sets up to size three (and discuss some of the triplets we found below), we focus our analysis on cDREM models using only TF pairs, as they are easier to evaluate using available complementary data. See the Supplementary Material for results with k = 3.

3.1. Combinatorial binding in S. cerevisiae

3.1.1. Analysis of yeast stress response

Figure 1 displays two of the models learned by cDREM for yeast stress response (heat shock and amino acid starvation), highlighting some of the pairs identified. Several of the TF pairs displayed are known to interact to regulate expression in yeast. For example, the STE12-TEC1 and STE12-DIG1 pairs are known to physically interact to regulate filamentation (Chou et al., 2006). In our triplet model of heat shock, we find the AND triplet STE12-TEC1-DIG1. This triplet is a known complex (Chou et al., 2006). (See the Supplementary Material for the triplet model.)

Another example is the MBP1-SKN7 pair, which are known to be in the same complex (Bouquin et al., 1999), and have cell cycle and heat shock–related functions (Raitt et al., 2000). Similarly, FHL1-RAP1 are known to combinatorially regulate ribosomal protein production (Rudra et al., 2007). We also find the FHL1-YAP5 pair. The triplet FHL1-YAP5-RAP1 is a module that has been implicated in several studies as regulating ribosomal genes (Nagamine et al., 2005; Manke et al., 2003). The full set of predicted TF pairs (both AND and OR) can be found in the Supplementary Material.

To analyze the TF sets identified by cDREM in a more systematic way, we first looked at which of the predicted pairs were known to interact. For this, we used the BioGRID interaction database (Stark et al., 2006). We compared the enrichment of BioGRID annotated TF pairs in three sets: (1) The set of all TF pairs; (2) the 636 TF pairs used as input to cDREM, identified by using only the protein–DNA interaction data (overlap of at least 10 genes with corrected p < 10−5); and (3) the 93 putative combinatorial AND pairs identified in one of the four cDREM models. Only 4.9% of all TF pairs were interacting according to BioGRID. In the subset of pairs with significant overlap in targets, 113 pairs (17.8%) were interacting. However, for the cDREM selected set the percentage was much higher; 28 of the 93 pairs (30.1%) interact according to BioGRID (Table 1). Thus, by integrating the time series expression of TF targets, cDREM was able to improve upon only using the ChIP-chip data alone.

Table 1.

BioGRID Enrichment by Data Set

Data set No. of putative pairs Of which in BioGRID Percentage in BioGRID
Heat shock 36 10 27.8
Osmotic stress (Gasch) 23 8 34.8
Osmotic stress (Romero) 21 8 38.1
Amino acid starvation 26 7 26.9
Open in a new tab

For each of the four yeast data sets, we report the number of combinatorial AND predictions our method discovers, as well as the number and proportion of these pairs that are annotated in BioGRID.

3.1.2. Knockout expression correlation

We further investigated TFs identified by cDREM to control splits using an AND relationship. If both are required to combinatorially regulate a set of genes, we would expect that knocking out either one would lead to repression of these targets (or activation if they are repressors). We tested this by determining whether our putative combinatorial regulators had statistically significantly similar expression profiles under knockout. We compiled data from Reimand et al. (2010), which provided the set of differentially expressed genes from 269 TF knockout mutants. For each knocked out TF t, we have a vector kt containing its knockout effect on each of the genes (up, down, or no effect). We define the similarity score of two TFs A and B as:

graphic file with name eq4.gif

Note that with this score, if one TF's expression profile is a perfect subset of another, they will have the maximal score (1).

To determine the significance of our results we first computed the distribution of our score for all TF pairs. We then tested the hypothesis that the cDREM pairs have higher correlation scores than the overall set of pairs using the Mann–Whitney U test. We found that indeed, the cDREM sets were significantly more correlated (p = 1.3 * 10−5). We also compared the cDREM selected AND pairs to all 636 pairs that were input to cDREM (based on ChIP-chip data). As expected, the average correlation of the cDREM selected pairs was higher (p = 2.4 * 10−3) (see Fig. 2a).

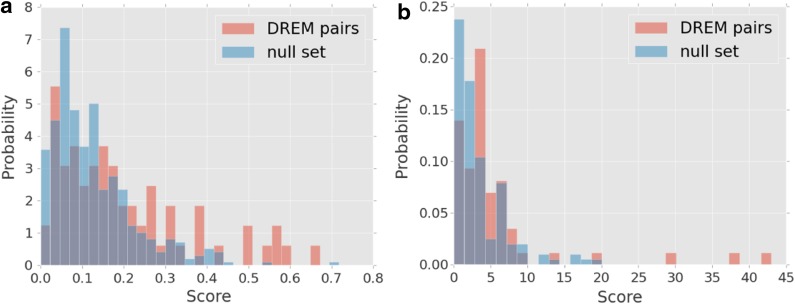
FIG. 2.

FIG. 2.

Open in a new tab

Histograms of two scoring metrics. Comparison of the distribution of the cDREM-predicted pairs and the set of pairs used as input to the algorithm on two metrics: pair knockout expression correlation and pair ChIP-chip colocalization. Note that the “null” set is our set of 636 input pairs to DREM, excluding all pairs selected by DREM (and thus it is already filtered for high overlap between known targets).

3.1.3. Knockout phenotype correlation

We also tested the hypothesis that pairs we identified from cDREM would have more correlated knockout phenotypes than our input pairs. That is, pairs of TFs that work together should cause similar phenotypic perturbations when knocked out. We tested this using the knockout phenotypic profiles from the Saccharomyces Genome Database. This data contains observations for various knockouts, including changes to oxidative stress resistance, chemical response, or growth rate. Thus, for each TF t, we have a list of annotations at, and the similarity of two TFs A and B is defined as the ratio of the intersection of the two lists divided by their union.

We first compared our putative combinatorial binders to random TF pairs creating a distribution of phenotypic pair correlations for random TFs. We then used the Mann–Whitney U test to test the hypothesis that the cDREM pairs have more correlated phenotype than the random pairs (p = 6.2 * 10−34). We performed the same test to compare the cDREM selected pairs to the input set and again found a higher average similarity score for the cDREM pairs (p = 0.07).

3.1.4. Correlation with ChIP-chip data

We further analyzed the locations of the experimentally derived binding sites for our putative TF pairs. Short distances between these sites increase our belief in their combinatorial regulatory interactions, since TFs often form complexes in order to recruit the transcriptional machinery (Brent and Ptashne, 1985). For this analysis we used data from Harbison et al. (2004), which contained short (<10 bp) windows that they defined as binding sites for 203 TF.

We developed a score that measures how frequently pairs of TFs colocate. To do this, we identified for each TF pair the number of instances where the two TFs had nonoverlapping binding sites within 20 bp of each other. We specifically exclude overlapping binding sites, as that would preclude complementary binding activity. We then compared the distribution of these scores among the cDREM pairs with randomly selected TF pairs. Compared to random TF pairs, the cDREM set was highly significant (p = 4.5 * 10−9, again using the Mann–Whitney U test). We also compared the scores of the cDREM pairs to the scores for the TF pairs in cDREM's input that were not selected by cDREM. Again, the cDREM pairs had significantly higher scores than non-selected-pairs (p = 0.003) (see Fig. 2b).

We further compared the properties of our cDREM AND and OR pairs on these three metrics. As expected, AND TF pairs were much more likely to be statistically related through knockout expression, phenotype, and ChIP-chip colocalization (see the Supplementary Material for details).

3.1.5. Comparison of cDREM combinatorial pairs to combinatorial pairs from other methods

To compare the results of cDREM with previous methods we first attempted to use the method from Pilpel et al. (2001), but were unable to obtain their code, and given the time that has passed since the publication of their article, it was difficult to map their yeast motif predictions to TFs. Instead, we compared our results to two other articles that provided a predicted list of combinatorial interactions.

The first is from Yu et al. (2006a) and involved the identification of 294 TFs with statistically enriched motif co-occurrences. We also compared cDREM to the method of Beyer et al. (2006), which used a naive Bayes model to combine ChIP-chip binding, expression, and interaction data to identify TF modules. We used their list of TF modules (their Table S2) to develop a list of predicted combinatorial binding pairs that we can compare to our method. We focus exclusively on their set of modules of size 2 (combinatorial pairs) and select the 176 pairs with reported p-value of less than 0.01.

Looking at knockout expression correlations we found that cDREM pairs were significantly more correlated than pairs from the other two methods (compared to Yu: p = 3.8 * 10−5; compared to Beyer: p = 0.01, U test). We also looked at agreement with BioGRID and found that 16% of the Yu et al. pairs and 29.7% of the Beyer set were annotated as interacting (the corresponding result for cDREM is 30.1%). We did not see a statistically significant difference in the ChIP-chip peak colocalization results (p = 0.068 compared to Yu, 0.349 compared to Beyer). Overall, these results indicate that cDREM is able to find a more relevant set of combinatorially acting TFs compared to other methods. While all methods identify TFs that occur proximal to each other, cDREM's pairs have higher knockout effect similarity, which is an expected quality of AND modules. We also compared cDREM to the original version of DREM and concluded that cDREM is able to identify a better set of combinatorial TFs (Supplementary Material).

3.2. Predicting human TFs combinatorial binding

To test cDREM on human data we used a time-series expression from Huang et al. (2011), which studied a patient undergoing a symptomatic flu infection. Due to the many more possible TF sets in humans, we used a two-step process to select our input set. As in yeast, we chose sets that had statistically significant overlap in the genes they regulated. However, unlike yeast, where we used a Bonferroni corrected p-value of 10−5, in human sets we simply chose the top 500 pairs based on the overlap p-value.

To guarantee that we had good coverage of TF pairs that were relevant to our experimental condition, we added a second set of condition-targeted pairs to our set of 500 pairs. For this, we ran cDREM with only single TFs as potential regulators. We next selected the top TFs at each split and included all pairs of such TFs that had a target overlap with corrected p < 0.001 in the new input set.

The reconstructed network can be seen in Figure 3. cDREM identified 14 AND relationships, several of which were among well-known immune regulators. Many of our predictions involve IRF (interferon regulatory factor) proteins, which are known to regulate immune response. For example, cDREM predicts the relationship between STAT1 and IRF1, which has been previously documented (Chatterjee-Kishore et al., 2000). Overall, 3 of the 14 (21.4%) pairs identified by cDREM were found in BioGRID. Other predicted pairs are not in BioGRID, but are supported in the literature. For example, IRF1 and IRF7 were found to colocalize on the GBP gene to control expression (Farlik et al., 2012). Another interesting pair is IRF1 and IRF2, which are known to participate in competitive binding (Harada et al., 1989). Thus, it is likely that we have captured a different kind of AND relationship here, where genes that can be bound by both TFs are downregulated compared to genes that are only bound by IRF1.

FIG. 3.

FIG. 3.

Open in a new tab

Reconstructed network for human response to flu. Several of the pairs identified by cDREM contain TFs that are known to combinatorially regulate immune response. Though our model incorporates both AND and OR pairs, here we only show AND pairs.

We additionally determined GO enrichment for paths in our model with and without the use of combinatorial binding and determined that explicitly modeling combinatorial binding leads to better enrichment for relevant categories (Supplementary Material).

4. Discussion

We have presented cDREM, a new method for reconstructing models of combinatorial gene regulation. Extending a previous method for HMM modeling of dynamic regulatory networks, cDREM utilizes a sparse group Lasso function to select a subset of potential TF sets and associate them with the genes they regulate and their time of activation. In contrast to previous methods, cDREM is able to take advantage of time series expression data when selecting the combinatorial sets and can also determine for some of the sets their combinatorial logic (AND or OR activation).

Simulation analysis is extremely problematic for methods that integrate a large number of diverse datasets (time series expression, binding data, sequence motifs). For example, simulating dynamic continuous expression values and their relationships to combinatorial binding requires making several arbitrary decisions, which are not well supported by current biological knowledge. Instead, we have tested our method using data from a well studied model organism, yeast, for which several complementary datasets exist. Applying cDREM to yeast, we showed that the set of pairs it identifies agrees well with such high throughput complementary data. Moreover, cDREM was able to correctly distinguish between AND and OR activation for several of the identified pairs. Comparison to prior methods indicates that cDREM improves upon the sets detected by these methods, in some cases significantly so. Application of cDREM to study immune response in humans led to the identification of a number of novel combinatorial pairs and has also improved the assignment of genes to paths (representing clusters of coexpressed and coregulated genes).

While cDREM was able to correctly identify several combinatorial regulatory events, there are several places where it can be extended and improved. First, it would be useful to improve the filtering used to select an input subset. One way is to incorporate additional types of data to the filtering step (for example PPI). Another important extension is to expand the set of combinatorial logic that cDREM supports. While such a step leads to many more potential candidate sets (for example combination of AND and ORs) with interesting logic function, a key challenge is that unlike classic AND and OR functions, it is hard to validate that these more complicated logic predictions are correct.

Supplementary Material

Supplemental data
Supp_Cdrem.zip (42.2MB, zip)

Acknowledgments

Work supported in part by National Institute of Health (grant 1 U54 HL127624-01 to Z.B.J.), by the National Science Foundation DBI-1356505 to Z.B.J.), and by the James S. McDonnell Foundation Scholars Award in Studying Complex Systems.

Author Disclosure Statement

No competing financial interests exist.

References

  1. Babu M.M., Luscombe N.M., Aravind L., et al. . 2004. Structure and evolution of transcriptional regulatory networks. Curr. Opin. Struct. Biol. 14, 283–291 [DOI] [PubMed] [Google Scholar]
  2. Beyer A., Workman C., Hollunder J., et al. . 2006. Integrated assessment and prediction of transcription factor binding. PLoS Comput. Biol. 2, e70. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bouquin N., Johnson A.L., Morgan B.A., and Johnston L.H.1999. Association of the cell cycle transcription factor mbp1 with the skn7 response regulator in budding yeast. Mol. Biol. Cell 10, 3389–3400 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Brent R., and Ptashne M.1985. A eukaryotic transcriptional activator bearing the dna specificity of a prokaryotic repressor. Cell 43, 729–736 [DOI] [PubMed] [Google Scholar]
  5. Chatterjee-Kishore M., van den Akker F., and Stark G.R.2000. Adenovirus e1a down-regulates lmp2 transcription by interfering with the binding of stat1 to irf1. J. Biol. Chem. 275, 20406–20411 [DOI] [PubMed] [Google Scholar]
  6. Chou S., Lane S., and Liu H.2006. Regulation of mating and filamentation genes by two distinct ste12 complexes in saccharomyces cerevisiae. Mol. Cell. Biol. 26, 4794–4805 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. ENCODE Project Consortium. 2012. An integrated encyclopedia of dna elements in the human genome. Nature 489, 57–74 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Ernst J., Beg Q.K., Kay K.A., et al. . 2008. A semi-supervised method for predicting transcription factor–gene interactions in escherichia coli. PLoS Comput. Biol. 4, e1000044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Ernst J., Vainas O., Harbison C., et al. . 2007. Reconstructing dynamic regulatory maps. Mol. Syst. Biol., 3, 74. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Farlik M., Rapp B., Marie I., et al. . 2012. Contribution of a tank-binding kinase 1–interferon (ifn) regulatory factor 7 pathway to ifn-γ-induced gene expression. Mol. Cell. Biol. 32, 1032–1043 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Friedman J., Hastie T., and Tibshirani R.2010. A note on the group lasso and a sparse group lasso. arXiv:1001.0736 [Google Scholar]
  12. Gasch A., Spellman P., Kao C., et al. . 2000. Genomic expression programs in the response of yeast cells to environmental changes. Sci. Signal. 11, 4241. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gertz J., Siggia E.D., and Cohen B.A.2008. Analysis of combinatorial cis-regulation in synthetic and genomic promoters. Nature 457, 215–218 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gitter A., and Bar-Joseph Z.2013. Identifying proteins controlling key disease signaling pathways. Bioinformatics 29, i227–i236 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Gitter A., Carmi M., Barkai N., and Bar-Joseph Z.2013. Linking the signaling cascades and dynamic regulatory networks controlling stress responses. Genome Res., 23, 365–376 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Harada H., Fujita T., Miyamoto M., et al. . 1989. Structurally similar but functionally distinct factors, irf-1 and irf-2, bind to the same regulatory elements of ifn and ifn-inducible genes. Cell 58, 729–739 [DOI] [PubMed] [Google Scholar]
  17. Harbison C.T., Gordon D.B., Lee T.I., et al. . 2004. Transcriptional regulatory code of a eukaryotic genome. Nature 431, 99–104 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Huang Y., Zaas A.K., Rao A., et al. . 2011. Temporal dynamics of host molecular responses differentiate symptomatic and asymptomatic influenza a infection. PLoS Genet. 7, e1002234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Laurenti E., Doulatov S., Zandi S., et al. . 2013. The transcriptional architecture of early human hematopoiesis identifies multilevel control of lymphoid commitment. Nat. Immunol. 14, 756–763 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Manke T., Bringas R., and Vingron M.2003. Correlating protein–dna and protein–protein interaction networks. J. Mol. Biol., 333, 75–85 [DOI] [PubMed] [Google Scholar]
  21. Mendoza-Parra M.A., Walia M., Sankar M., and Gronemeyer H.2011. Dissecting the retinoid-induced differentiation of f9 embryonal stem cells by integrative genomics. Mol. Syst. Biol. 7, 538. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Nagamine N., Kawada Y., and Sakakibara Y.2005. Identifying cooperative transcriptional regulations using protein–protein interactions. Nucleic Acids Res. 33, 4828–4837 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Pilpel Y., Sudarsanam P., and Church G.M.2001. Identifying regulatory networks by combinatorial analysis of promoter elements. Nat. Genet. 29, 153–159 [DOI] [PubMed] [Google Scholar]
  24. Raitt D.C., Johnson A.L., Erkine A.M., et al. . 2000. The skn7 response regulator of saccharomyces cerevisiae interacts with hsf1 in vivo and is required for the induction of heat shock genes by oxidative stress. Mol. Biol. Cell 11, 2335–2347 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Reimand J., Vaquerizas J.M., Todd A.E., et al. . 2010. Comprehensive reanalysis of transcription factor knockout expression data in saccharomyces cerevisiae reveals many new targets. Nucleic Acids Res. 38, 4768–4777 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Ren B., Robert F., Wyrick J.J., et al. . 2000. Genome-wide location and function of dna binding proteins. Science 290, 2306–2309 [DOI] [PubMed] [Google Scholar]
  27. Romero-Santacreu L., Moreno J., Pérez-Ortín J., and Alepuz P.2009. Specific and global regulation of mrna stability during osmotic stress in saccharomyces cerevisiae. RNA 15, 1110–1120 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Roy S., Ernst J., Kharchenko P.V., et al. . 2010. Identification of functional elements and regulatory circuits by drosophila modencode. Science 330, 1787–1797 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Rudra D., Mallick J., Zhao Y., and Warner J.R.2007. Potential interface between ribosomal protein production and pre-rrna processing. Mol. Cell. Biol. 27, 4815–4824 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Schulz M., Devanny W., Gitter A., et al. . 2012. Drem 2.0: Improved reconstruction of dynamic regulatory networks from time-series expression data. BMC Syst. Biol. 6, 104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Schulz M.H., Pandit K.V., Cardenas C.L.L., et al. . 2013. Reconstructing dynamic microrna-regulated interaction networks. Proc. Natl. Acad. Sci. USA 110, 15686–15691 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Sinha S., Adler A.S., Field Y., et al. . 2008. Systematic functional characterization of cis-regulatory motifs in human core promoters. Genome Res. 18, 477–488 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Stark C., Breitkreutz B.-J., Reguly T., et al. . 2006. Biogrid: a general repository for interaction datasets. Nucleic Acids Res. 34, D535–D539 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Yu X., Lin J., Masuda T., et al. (2006b). Genome-wide prediction and characterization of interactions between transcription factors in saccharomyces cerevisiae. Nucleic Acids Res. 34, 917–927 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Yu X., Lin J., Zack D.J., and Qian J. (2006a). Computational analysis of tissue-specific combinatorial gene regulation: predicting interaction between transcription factors in human tissues. Nucleic Acids Res. 34, 4925–4936 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Yuh C.-H., Bolouri H., and Davidson E.H.1998. Genomic cis-regulatory logic: experimental and computational analysis of a sea urchin gene. Science 279, 1896–1902 [DOI] [PubMed] [Google Scholar]
  37. Zinman G., Brower-Sinning R., Emeche C.H., et al. . 2011. Large scale comparison of innate responses to viral and bacterial pathogens in mouse and macaque. PloS One 6, e22401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Zinzen R.P., Girardot C., Gagneur J., et al. . 2009. Combinatorial binding predicts spatio-temporal cis-regulatory activity. Nature 462, 65–70 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental data
Supp_Cdrem.zip (42.2MB, zip)

Articles from Journal of Computational Biology are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES