Skip to main content
PMC home page
Brain Connectivity logoLink to Brain Connectivity
. 2015 Apr 1;5(3):137–146. doi: 10.1089/brain.2014.0299

Associations of Resting-State fMRI Functional Connectivity with Flow-BOLD Coupling and Regional Vasculature

Sungho Tak 1,✉, Jonathan R Polimeni 2, Danny JJ Wang 3, Lirong Yan 3, J Jean Chen 1
PMCID: PMC4394176  PMID: 25384681

Abstract

There has been tremendous interest in applying functional magnetic resonance imaging-based resting-state functional connectivity (rs-fcMRI) measurements to the study of brain function. However, a lack of understanding of the physiological mechanisms of rs-fcMRI limits their ability to interpret rs-fcMRI findings. In this work, the authors examine the regional associations between rs-fcMRI estimates and dynamic coupling between the blood oxygenation level-dependent (BOLD) and cerebral blood flow (CBF), as well as resting macrovascular volume. Resting-state BOLD and CBF data were simultaneously acquired using a dual-echo pseudocontinuous arterial spin labeling (pCASL) technique, whereas macrovascular volume fraction was estimated using time-of-flight MR angiography. Functional connectivity within well-known functional networks—including the default mode, frontoparietal, and primary sensory-motor networks—was calculated using a conventional seed-based correlation approach. They found the functional connectivity strength to be significantly correlated with the regional increase in CBF-BOLD coupling strength and inversely proportional to macrovascular volume fraction. These relationships were consistently observed within all functional networks considered. Their findings suggest that highly connected networks observed using rs-fcMRI are not likely to be mediated by common vascular drainage linking distal cortical areas. Instead, high BOLD functional connectivity is more likely to reflect tighter neurovascular connections, attributable to neuronal pathways.

Key words: : blood volume fraction, CBF-BOLD coupling, cerebral blood flow, MR angiography, resting-state BOLD, resting-state functional connectivity

Introduction

Functional magnetic resonance imaging (fMRI) has consistently revealed resting-state functional connectivity (rs-fcMRI) in the brain, predominantly through correlated spontaneous fluctuations in the blood oxygenation level-dependent (BOLD) signal across brain regions (Biswal et al., 1995; Fox et al., 2005; Greicius et al., 2003). Resting-state fcMRI has enabled the mapping of major functional networks of the brain, starting with the motor network (Biswal et al., 1995) and expanding to include other highly reproducible networks such as the default mode network (Greicius et al., 2003) and the frontoparietal network (Fox et al., 2005; Markett et al., 2014; Toro et al., 2008). Today, the impact of rs-fcMRI in basic neuroscience and clinical research is immense (Buckner et al., 2013; Fox and Greicius, 2010).

Importantly, the rapid growth of rs-fcMRI has highlighted the general lack of understanding of the physiological mechanisms behind rs-fcMRI measurements. Specifically, as rs-fcMRI is estimated using the BOLD signal, which is an indirect measure of neuronal activity, functional connectivity is unfortunately sensitive to non-neural confounds. These include, among others, head motion (Van Dijk et al., 2012) and physiological noise arising from respiration and cardiac activity (Birn et al., 2006; Chang and Glover, 2009). This is particularly detrimental to the usefulness of rs-fcMRI, as physiological noise, such as respiration and cardiac pulsation, has been shown to be more dominant near large vessels, where neuronal specificity is minimal (Tong et al., 2011). Thus, it has been suggested that spurious correlations in rs-fcMRI can originate from macrovascular draining routes across distal brain regions rather than from neuronal activity itself (Jo et al., 2010). This possibility severely limits their ability to interpret the rs-fcMRI findings and reinforces the importance of understanding the link between functional connectivity and neurovascular factors (Buckner et al., 2013).

The manner in which resting-state neuronal activity manifests as the BOLD fluctuations depends on the contribution of neurovascular factors (Liu, 2013). In support of this, several studies have addressed the influence of static content of neurovascular factors, including cerebral blood flow (CBF) and cerebral metabolic rate of oxygen (CMRO2) on the rs-fcMRI (Chuang et al., 2008; Fukunaga et al., 2008; Viviani et al., 2011; Wu et al., 2009). Specifically, Wu and colleagues (2009) observed a spatial correspondence between resting-state BOLD- and CMRO2-based functional connectivity maps, and Fukunaga and colleagues (2008) found similar metabolic involvement during resting-state and visual tasks using the ratio of BOLD and CBF fluctuations as an indicator of metabolic demand.

In their previous work, using simultaneous BOLD-CBF measurements as well as MR angiography (MRA), they probed the contribution of various neurovascular components to the resting-state BOLD signal (Tak et al., 2014). They observed significant coupling between resting-state BOLD and CBF signal in the regions of major resting-state networks, and found that the degree of this coupling diminishes as macrovascular fraction increases. However, there has been limited work quantitatively assessing regional effects of these neurovascular factors on rs-fcMRI measurements per se. Understanding such effects is critical for expanding the application of rs-fcMRI, particularly neurovascular abnormalities are often implicated in normal aging (Gauthier et al., 2012) as well as numerous brain diseases (Girouard and Iadecola, 2006). In this study, the authors explore the associations of rs-fcMRI strength with CBF-BOLD coupling and macrovascular volume fraction, and determine whether these relationships apply in a specific functional network or are generalizable.

Materials and Methods

Participants

The authors studied nine healthy participants (three men), aged from 18 to 32 years (mean=26.7 years, SD=4.3 years). Participants were recruited through the Baycrest Participants Database. The study was approved by the Baycrest Research Ethics Board (REB), and the experiments were performed with the written consent of each participant according to REB guidelines.

MRI acquisition

All images were acquired using a Siemens TIM Trio 3 Tesla System (Siemens, Erlangen, Germany). The scans employed 32-channel phased-array head coil reception and body-coil transmission.

To concurrently acquire resting-state CBF and BOLD data, they used dual-echo pseudocontinuous arterial spin labeling (pCASL) (Dai et al., 2008): repetition time (TR)=3500 msec, echo times (TE)1/TE2=10/25 msec, field of view=220×220 mm, 18 slices (ascending interleaved order), voxel size=3.4×3.4×5.0 mm3, 100 frames, bandwidth=2520 Hz/pixel and GRAPPA=2. The labeling duration was 1500 msec, and the postlabeling delay was 1000 msec with a mean Gz of 0.6 mT/m was selected to achieve transit time insensitivity. During the resting-state scan, all participants were instructed to keep their eyes closed and remain awake.

A 3D T1-weighted anatomical scan was acquired using MPRAGE, with detailed scanning protocol parameter values as follows: voxel resolution=1 mm3 isotropic, TR=2400 msec, inversion time (TI)=1000 msec, TE=2.43 msec, flip angle=8°, field of view=256×256 mm2 (sagittal), 192 partitions, bandwidth=180 Hz/pixel, and GRAPPA factor=2.

To measure the resting macrovascular volume fraction, a 3D multi-slab whole brain time-of-flight (TOF) MRA was used with TR=20 msec, TE=3.59 msec, field of view=200×181 mm, matrix size=768×696×200, number of averages=1, spanning six slabs with a distance factor of 20%, TONE ramp=70%, voxel size=0.26×0.26×0.5 mm3, bandwidth=165 Hz/pixel, and GRAPPA acceleration factor=2. To image venous as well as arterial contributions, no superior saturation band was used.

Data analysis

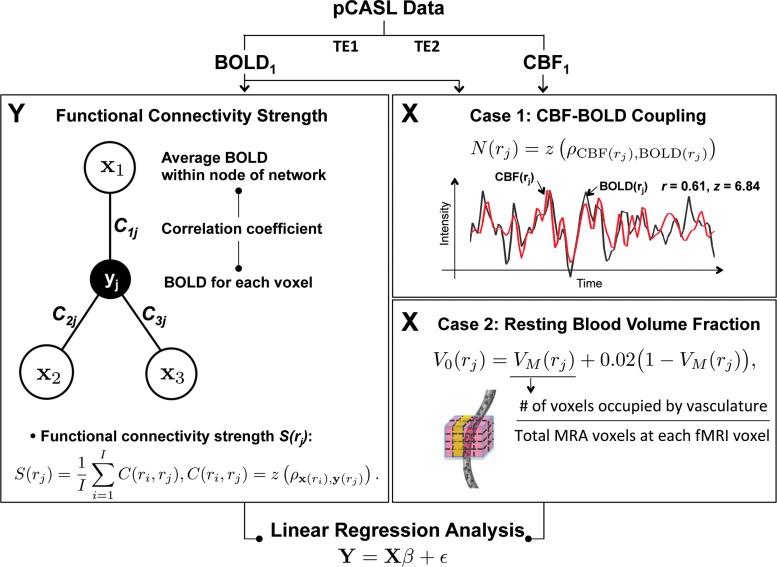
To investigate the regional association between rs-fcMRI, dynamic CBF-BOLD coupling and macrovascular volume fraction, they performed two sets of linear regression analyses, each addressing one of these associations (Fig. 1).

FIG. 1.

FIG. 1.

Open in a new tab

Schematic of proposed methods. The main modules are linear regression analyses of rs-fcMRI estimate strengths within specific functional networks against the CBF-BOLD coupling (case I) and macrovascular volume fraction (case II). Regionally specific functional connectivity strengths are assessed by calculating the sum of connectivity strengths in major nodes of predefined resting-state networks. For this purpose, they selected the default mode network, frontoparietal network, and primary sensory-motor network. BOLD, blood oxygenation level-dependent; CBF, cerebral blood flow.

Image preprocessing

The tag and control images in the pCASL data were separately preprocessed using the SPM8 (www.fil.ion.ucl.ac.uk/spm/software/spm8/) (Friston et al., 2011). The first four time frames were discarded to ensure MR steady state. Preprocessing of functional data included retrospective motion correction, slice-timing correction, spatial transformation into the Montreal Neurological Institute (MNI) space, and spatial smoothing with a 6-mm full-width at half-maximum Gaussian kernel. Anatomical images were coregistered with the realigned functional data and then segmented into gray matter, white matter, and cerebrospinal fluid (CSF) probability maps. Physiological noise removal within the tag and control images was performed separately by regressing out four significant principal components derived from the white matter and CSF signals (Behzadi et al., 2007).

TOF MRA data were coregistered with the functional data, following which the vessel structures were isolated using histogram thresholding (Otsu, 1975), given that signal intensities of blood vessels are higher than those of the surrounding tissues. Before thresholding, they removed nonbrain tissue using the brain-extraction tool (BET2) of FSL software (fsl.fmrib.ox.ac.uk/fsl/fslwiki/BET) (Jenkinson and Pechaud, 2005), and corrected intensity nonuniformity in MRA using the nonparametric nonuniform intensity normalization (Sled et al., 1998).

Estimation of dynamic CBF-BOLD coupling

To estimate the CBF signal minimizing BOLD contamination, the ASL time course, taken as a series of tag and control signals acquired at the first echo of the dual-echo acquisition, was high-pass filtered then demodulated (Chuang et al., 2008). This method is a generalized version of direct subtraction of time-matched upsampled followed by sinc interpolation of tag and control frames—sinc subtraction is equivalent to filtering the demodulated ASL data with an ideal low-pass filter (Liu and Wong, 2005). To estimate the BOLD signal while minimizing perfusion weighting, they applied a low-pass filter with a cutoff frequency of half of the Nyquist frequency (i.e., 1/4TR) to the tag and control time series acquired at the second echo (Liu and Wong, 2005). For details please refer to their earlier work (Tak et al., 2014).

Potential time shifts between BOLD and CBF signals were determined by maximizing their cross correlation within the physiological range of −3.5 to +3.5 sec (Fukunaga et al., 2008). The CBF signal for each voxel was then shifted in time to better match the BOLD signal, allowing dynamic CBF-BOLD coupling to be assessed, in this case by Pearson correlation between time series of CBF and BOLD signal (Tak et al., 2014). The correlation estimates were converted to z-scores using the Fisher transformation (Fisher, 1915).

Estimation of macrovascular volume fraction

The BOLD signal (in this case gradient-echo) results from an intravascular and an extravascular contribution, both of which can arise from either the microvasculature or macrovasculature. The macrovasculature, particularly the pial vessels that drain blood from large cortical domains, substantially bias the BOLD signal toward lower neuronal specificity (Boxerman et al., 1995). This bias has important implications for rs-fcMRI. In this work, they measured the resting macrovascular fraction, V0, as the ratio of blood vessels to tissue volume in the fMRI measurements (Buxton et al., 1998), and V0 can be calculated as a combination of small-vessel fraction VS and MRA-derived macrovascular fractions VM (Hu et al., 2012):

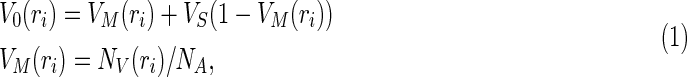graphic file with name eq1.gif

where ri is the ith voxel position in the fMRI image volume, i=1,…, N, VS is assumed as 0.02 (Hu et al., 2012), NV(ri) is the number of voxels occupied by the segmented vasculature at the ith fMRI voxel, and NA is the number of MRA voxels at each voxel of fMRI volume. Note that as the MRA images were transformed into MNI space and resampled to a 0.5-mm isotropic grid, the resulting voxel size of the MRA data (0.5×0.5×0.5 mm3) is much smaller than the voxel size of their fMRI dataset (2×2×2 mm3 after resampling). Therefore, in their dataset, NA was 64 for all voxels, and NV(ri) was between 0 and 64.

Estimation of functional connectivity strength

The authors estimated rs-fcMRI strength based on Pearson's correlation. Regionally the specific functional connectivity strength S(ri) was assessed by averaging correlation coefficients between each voxel and major nodes of established resting-state networks (Rubinov and Sporns, 2010; Van Dijk et al., 2012):

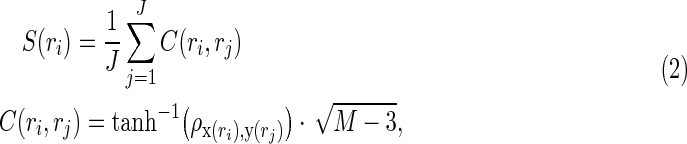graphic file with name eq2.gif

where x(ri) is the resting-state BOLD time series at the ith voxel, y(rj) is the average BOLD time series within the jth network node, 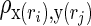Inline graphic is the Pearson correlation coefficient between x(ri) and y(rj), C(ri, rj) is the connectivity between the ith voxel and the jth major node; J is the total number of nodes (ROIs) within a predefined network, and M is the total number of time points. Note that the rs-fcMRI-strength map is simply an average of functional connectivity maps generated using all seeds of the selected resting-state network (Biswal et al., 1995; Fox et al., 2005; Liu et al., 2010), and this measure has been used in numerous studies that investigate the nature of resting-state functional connectivity (Liang et al., 2013; Liu et al., 2010; Markett et al., 2014; Van Dijk et al., 2012). Thus, correlations-based rs-fcMRI estimation is also their metric of choice, as they would like to maximize the applicability of their findings to the field.

Functional networks and seed locations

The resting-state networks considered in their analysis include (a) the default mode network (Greicius et al., 2003), (b) the frontoparietal network (Fox et al., 2005; Markett et al., 2014; Toro et al., 2008; Vincent et al., 2008), and (c) the primary sensory-motor (including motor, auditory, and visual) network (Biswal et al., 1995). These are among the most consistent and extensively studied in the literature. Their definitions of the networks are: (a) default mode network: posterior cingulate cortex, medial prefrontal cortex, lateral parietal cortex, and the parahippocampal region; (b) frontoparietal network: dorsolateral/anterior prefrontal cortex, inferior/superior parietal lobule, and anterior insula; (c) the primary sensory-motor network: bilateral regions similar in function, such as the motor, visual, and auditory cortices. The primary sensor and motor regions exhibit high levels of local connectivity consistent with a modular organization that is likely to reflect interactions between nearby areas (see Fig. 3 in Sepulcre et al., 2010).

FIG. 3.

FIG. 3.

Open in a new tab

Sample individual maps of the functional connectivity strength of the default mode network, dynamic CBF-BOLD coupling, and macrovascular volume fraction. Maps of (a) functional connectivity strength (in terms of z-statistics) and (b) CBF-BOLD coupling are both overlaid on a cortical surface model. (a) Connectivity is shown at this point for the default mode network. (b) Significantly positive CBF-BOLD coupling is detected in the main regions of networks such as default mode and frontoparietal networks. (c) Macrovascular volume fraction includes the resting blood volume fractions of both pial vessels and intracranial vessels. The regional association between the dynamic CBF-BOLD coupling and macrovascular volume fraction with functional connectivity strength was quantitatively explored using an ROI analysis.

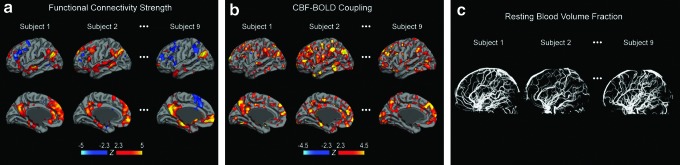
The authors used the anatomical locations of seed voxels reported by Toro and colleagues (2008), Fox and colleagues (2005), Vincent and colleagues (2008), Van Dijk and colleagues (2010), and Biswal and colleagues (1995) to generate the rs-fcMRI maps of the above networks, and calculate the corresponding rs-fcMRI strength maps. The MNI coordinates of the seeds for each network are summarized in Table 1, and are shown overlaid on the anatomical brain template and seed-based rs-fcMRI maps in Figure 2. A sphere with a radius of 8 mm centered at each of the seed voxels was used to construct each network node ROI.

Table 1.

Montreal Neurological Institute Coordinates of Regions of Interest Within the Three Predefined Networks

Region x y z
Default mode network
 PCC −6 −58 28
  6 −46 8
 MPFC −2 46 −4
  6 50 28
 lLPC −46 −66 24
 rLPC 53 −67 36
 lparaHipp −22 −22 −20
 rparaHipp 18 −22 −20
Frontoparietal network
 lMT+ −45 −69 −2
 rMT+ 50 −69 −3
 laPFC −36 57 9
 raPFC 34 52 10
 lFEF −25 −8 50
 rFEF 27 −8 50
 lSPL −27 −52 57
 rSPL 24 −56 55
 ldlPFC −50 20 34
 rdlPFC 46 14 43
 laINS −31 21 −1
 raINS 31 22 −2
 laIPL −52 −49 47
 raIPL 52 −46 46
Motor network
 lMot −42 −25 63
 rMot 42 −25 63
Auditory network
 lVis −43 −26 12
 rVis 43 −26 12
Visual network
 lAud −30 −88 0
 rAud 30 −88 0
Open in a new tab

aIPL, anterior inferior parietal lobule; aINS, anterior insula; aPFC, anterior prefrontal cortex; Aud, auditory cortex; dlPFC, dorsolateral prefrontal cortex; FEF, frontal eye fields; LPC, lateral parietal cortex; Mot, motor cortex; MPFC, medial prefrontal cortex; MT+, middle-temporal area; paraHipp, parahippocampal region; PCC, posterior cingulate cortex; SPL, superior parietal lobule; Vis, visual cortex.

FIG. 2.

FIG. 2.

Open in a new tab

Anatomical locations of seed regions within the predefined networks. The predefined functional network regions, shown in blue, include the (a) default mode network, (b) frontoparietal network, and (c) primary sensory-motor (visual, auditory, and motor) network. Seed positions for each network are overlaid on the anatomical brain template and the corresponding fcMRI maps. The anatomical template is taken from the MRIcro software (publicly available at: www.mccauslandcenter.sc.edu/mricro/mricron/). aINS, anterior insula; aIPL, anterior inferior parietal lobule; aPFC, anterior prefrontal cortex; FEF, frontal eye fields; dlPFC, dorsolateral prefrontal cortex; LPC, lateral parietal cortex; MPFC, medial prefrontal cortex; MT+, middle temporal area; paraHipp, parahippocampal region; PCC, posterior cingulate cortex; SPL, superior parietal lobule.

Associating rs-fcMRI strength with CBF-BOLD coupling and macrovascular content

A linear regression analysis was performed to identify the relationship between neurovascular factors and rs-fcMRI strength. Specifically, they modeled the dependent variable, namely the estimated rs-fcMRI strength, with an explanatory variable, namely either the dynamic CBF-BOLD coupling or the MRA-derived resting macrovascular fraction. All parameters were calculated for each voxel within the predefined ROIs of each network (Table 1), and then averaged across each network node, for the left and right hemispheres separately. In the regression analysis, they only considered regions associated with significant CBF-BOLD coupling (p<0.01, uncorrected). For the regression between rs-fcMRI strength and CBF-BOLD coupling, the number of data points (n) was 36, 62, and 27 for the default mode network, the frontoparietal network, and the primary sensory-motor network, respectively. For the regression between rs-fcMRI strength and macrovascular volume fraction, n=36, 39, and 18 for the default mode network, the frontoparietal network, and the primary sensory-motor network, respectively. Note that since not every ROI contains a large vessel, the number of samples used in the regression analysis between connectivity strength and macrovascular volume fraction was slightly decreased from these numbers. They performed the same linear regression analyses on regions of noninterest to verify that the relationship between neurovascular factors and rs-fcMRI strength is indeed specific to regions covered by the resting-state networks. Again, all parameters were calculated for each voxel and then averaged across the left and right hemispheres of each subject, separately. Again, the authors limited the analysis to regions of significant CBF-BOLD coupling for a fair comparison, whereas CBF and BOLD fluctuations were much less coupled outside the main regions of resting-state networks (Tak et al., 2014). Linear regression was then performed by minimizing the sum of squared residuals.

Results

Sample maps of rs-fcMRI strength in the default mode network as well as whole-brain CBF-BOLD coupling maps and macrovascular volume fractions are shown in Figure 3 for three representative participants. Their rs-fcMRI maps (z-scores) are similar to those reported previously (Biswal et al., 1995; Fox et al., 2005; Greicius et al., 2003; Van Dijk et al., 2010; Vincent et al., 2008). Volumetric z-maps for rs-fcMRI strength and CBF-BOLD coupling are overlaid on a cortical surface atlas constructed using the Freesurfer (surfer.nmr.mgh.harvard.edu) (Dale et al., 1999), thresholded at a significance level of uncorrected p<0.01. While the CBF-BOLD coupling (Fig. 3b) is highly variable across the brain, the most significant coupling is found in the major nodes of the default mode network and frontoparietal network. More details on this spatial distribution can be found in their previous work (Tak et al., 2014). In addition, the macrovasculature map (Fig. 3c) demonstrates that the MRA data was able to capture both pial vessels and intracranial vessels.

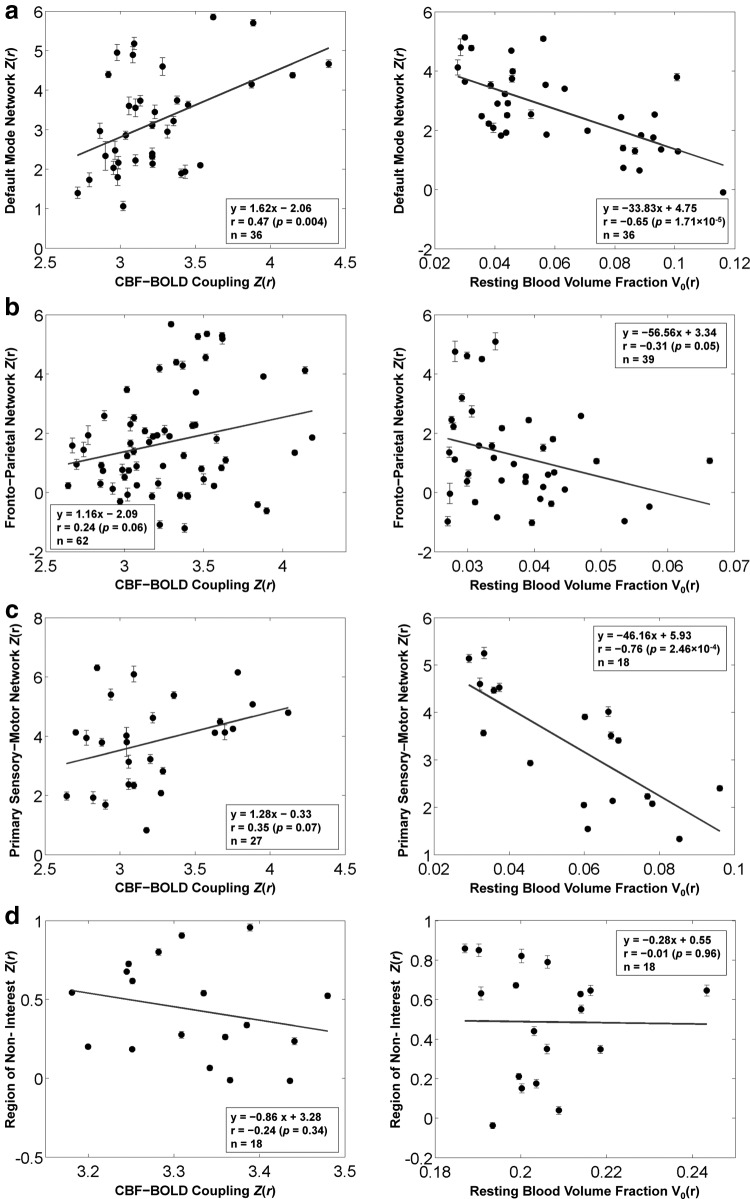
Regional associations between functional connectivity strength (seed-based) and CBF-BOLD coupling as well as macrovascular volume fraction are shown in Figure 4. The scatter plots depict the associations between two variables (regional rs-fcMRI strengths along with either regional CBF-BOLD coupling strength or macrovascular volume fraction). Increased rs-fcMRI strength is associated with increased CBF-BOLD coupling in all regions of the default mode network (r=0.47, p=0.004), the frontoparietal network (r=0.24, p=0.06), and the primary sensory-motor network (r=0.35, p=0.07). Conversely, increased macrovascular volume fraction was significantly associated with decreased rs-fcMRI strength in all networks: default mode network (r=−0.65, p=1.71×10−5), frontoparietal network (r=−0.31, p=0.05), and primary sensory-motor network (r=−0.76, p=0.0002). These associations between connectivity strength and neurovascular factors were consistently observed within the regions of resting-state networks, but not statistically significant outside of these networks.

FIG. 4.

FIG. 4.

Open in a new tab

Associations between functional connectivity strength, CBF-BOLD coupling, and macrovascular volume fraction in multiple functional networks. Functional connectivity was estimated using the conventional seed-based correlation approach. The scatter plots depict the spatial correlation between samples of two variables (connectivity strengths and either CBF-BOLD coupling or resting blood volume fraction) averaged across ROIs involved in (a) the default mode network, (b) the frontoparietal network, and (c) the primary sensory-motor (motor, auditory and visual) network. (d) As control ROIs, we selected additional ROIs outside main regions of resting-state networks. Each data point represents one ROI from one participant. The degree of functional connectivity among all network regions significantly increased as the BOLD-CBF coupling increased. In contrast, functional connectivity strength was significantly reduced as the macrovascular volume fraction increased. These associations between connectivity strength and neurovascular factors were consistently observed within the regions of resting-state networks, but not statistically significant outside of these networks.

Discussion

The role of neurovascular contributions to resting-state BOLD

While the role of CBF in generating the stimulus-evoked BOLD effect has been widely studied (Buxton et al., 1998; Davis et al., 1998), the biophysics of resting-state BOLD is far from being fully understood. The importance of understanding neurovascular contributions to resting-state BOLD is increasingly recognized, as outlined in a recent review (Liu, 2013). There is sparse but strong evidence that spontaneous CBF fluctuations in resting-state functional networks reflect neuronal activity, and CBF changes are one of the primary contributors to the intrinsic BOLD fluctuations (Chuang et al., 2008; Fukunaga et al., 2008; Liang et al., 2013; Viviani et al., 2011; Zou et al., 2009). In their previous work (Tak et al., 2014), they further showed this dynamic BOLD-CBF coupling as spatially variable (Fig. 3b), but most significant within major nodes of resting-state networks. Interestingly, this CBF-BOLD coupling also decreased as the macrovascular volume fraction increased (Tak et al., 2014). As a high macrovascular volume fraction corresponds to low neuronal specificity (Dagli et al., 1999), their observation suggests that high degrees of BOLD-CBF coupling are likely to suggest higher neuronal specificity. However, the influence of this intrinsic neurovascular involvement on the resting-state functional connectivity estimates was unclear, setting the stage for the current study.

The role of CBF-BOLD coupling in resting-state functional connectivity estimates

Along with the explosive growth in rs-fcMRI is the consensus that a better understanding of the resting-state fMRI phenomenon is essential for the interpretation of the results, as rs-fcMRI results alone can be inconsistent or ambiguous (Bright and Murphy, 2013; Murphy et al., 2009; Van Dijk et al., 2012). Specifically, as functional connectivity is a secondary measure derived from the resting-state fMRI signal itself, its interpretation from neurovascular physiology is not straightforward. In fact, non-neural factors such as respiration and head motion (Van Dijk et al., 2012) have been found to modulate rs-fcMRI estimates, calling into question the neuronal specificity of rs-fcMRI estimates.

In this work, the authors establish the role of dynamic CBF-BOLD coupling as an intrinsic factor that influences rs-fcMRI strength. The primary finding of this study is that regionally specific functional connectivity strength is significantly and positively associated with the degree of dynamic coupling between the BOLD and the CBF signal in all functional networks considered. As CBF is often viewed as a more direct measure of neuronal activity (Kim, 2012), this work attests to the neurovascular and, by extension, neuronal relevance of rs-fcMRI measures despite the many potential confounds.

The influence of large blood vessels on resting-state functional connectivity estimates

Complementing their first finding is the discovery that regions of high macrovascular content, previously found to exhibit weaker CBF-BOLD coupling, are also associated with weaker rs-fcMRI strength. As described in the earlier section, while large vessels contribute significantly to BOLD contrast, they are less specific to neuronal activity due to their location and the enhanced weighting toward physiological noise (Dalgi et al., 1999; Polimeni et al., 2010), and, therefore, may reduce the interpretability of rs-fcMRI estimates. Taken with the previous findings (Liang et al., 2013; Tak et al., 2014), their work shows that not only are regions with higher rs-fcMRI strengths associated with higher resting-state CBF and by extension, higher metabolism (Bullmore and Sporns, 2012), these regions also exhibit tighter CBF-BOLD coupling. Furthermore, rs-fcMRI estimates in such regions are least likely to be affected by non-neuronal sources such as respiration and cardiac pulsation (Birn et al., 2006; Chang and Glover, 2009; Tak et al., 2014). Therefore, it is likely that the rs-fcMRI measures observed at the heart of most known functional networks are mediated by true neuronal connections or pathways rather than by the macrovasculature (i.e., the plumbing).

Neuronal interpretation of resting-state fcMRI

This work was motivated by the important need to clarify the metabolic involvement of resting-state BOLD. To that end, Fukunaga and colleagues (2008) approximated the metabolic involvement in resting-state BOLD by the ratio of the BOLD signal to the CBF signal, and found this relationship to be similar to that observed during visual stimulation, supporting the neuronal relevance of resting-state fMRI. Using a similar approach, and adopting the Davis BOLD model (Davis et al., 1998), Wu and colleagues (2009) generated functional connectivity maps from the CMRO2 signal that resemble those based on CBF and on BOLD. Nonetheless, it is likely that these CMRO2 estimates were dominated by CBF variability, as it remains unclear whether the steady-state Davis model is appropriate for resting-state BOLD. Multimodal methods, involving simultaneous fMRI and electroencephalography for instance, may provide invaluable evidence with regard to metabolism. However, the interpretation of metabolic demand from such data is often not straightforward, and the limited spatial resolution likely precludes detailed assessment of neurovascular involvement (Laufs, 2010).

A welcome interpretation of their finding is that given that conventional preprocessing is performed, the regions with the strongest BOLD fcMRI estimates are likely not to be dominated by non-neuronal sources such as motion. Coincidentally, Liang and colleagues (2013) recently reported that higher rs-fcMRI estimates were associated with higher baseline resting CBF, further supporting a higher neuronal relevance in higher rs-fcMRI measurements. This finding can potentially translate into improved ways of thresholding rs-fcMRI maps for interpretation.

Potential caveats

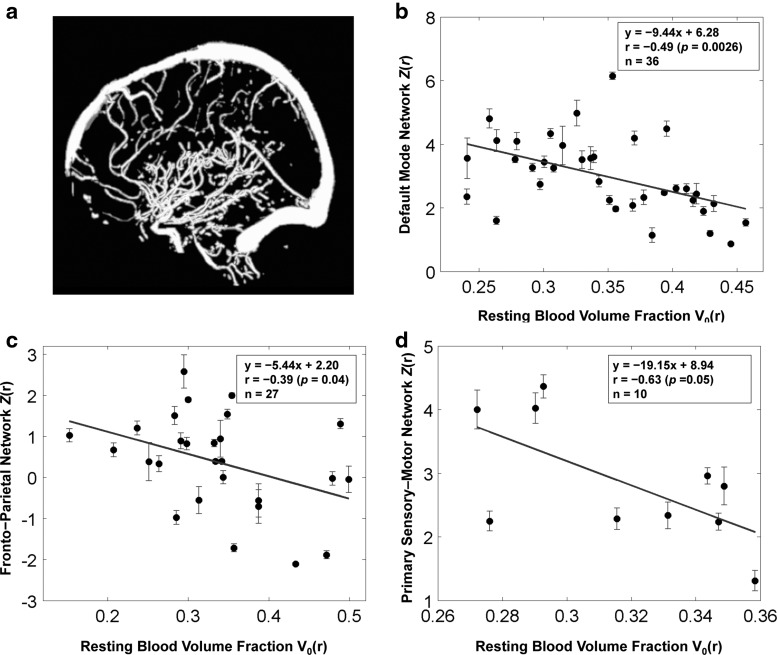
Due to limitations in the spatial resolution and sensitivity of the 3D TOF MRA technique, certain vessels may not have been clearly delineated, affecting their detectability. This may be exacerbated by suboptimal thresholding in the segmentation process. Despite potential incompleteness in their vascular segmentation, the strong correlations observed between vascular volume fraction and rs-fcMRI strength preclude the possibility of dominance by random biases. Moreover, the differences between networks could also arise from the fact that the distribution of large vessels in the brain is nonuniform (Duvernoy et al., 1981). Nonetheless, to test whether their conclusion is valid regardless of potentially miss-classified vasculatures in their MRA data, they repeated their analyses using an alternative vascular atlas, derived from the MNI digital brain phantom (Aubert-Broche et al., 2006). As shown in Figure 5, this method also produced results showing an inverse correlation between functional connectivity strength and macrovascular volume fraction within all functional networks considered. These results are consistent with those obtained from their own MRA data, and suggest that the main findings of this study are not biased by the method of segmenting MRA data.

FIG. 5.

FIG. 5.

Open in a new tab

Macrovascular volume fraction derived from the MNI digital brain phantom, and its associations with functional connectivity strength. (a) Vessels in the digital brain phantom (Aubert-Broche et al., 2006) were imaged by using Proton Density-weighted MRI, and MR angiography, and then segmented by using a multiscale geometric flow-based method. Segmented vessels include superficial vessels as well as penetrating vessels. The scatter plots depict the negative linear relationship between samples of macrovascular volume fraction and connectivity strengths averaged across all voxels of ROIs involved in (b) default mode networks, (c) frontoparietal network, and (d) primary sensory-motor cortex.

Another potential drawback of this study is the small group size in this study (n=9), limiting the statistical power (Desmond and Glover, 2002). Nonetheless, their findings regarding the physiological relationship between connectivity strength and neurovascular factors are statistically significant and consistent across the functional networks, and consistently insignificant outside the network regions, supporting the validity of their conclusions. In future work, they may explore the use of meta-analyses to boost the statistical significance and generalizability of their findings.

Conclusion

In this study, using concurrently measured BOLD and CBF time series and MRA-derived maps of macrovasculature, they explored regional associations linking dynamic CBF-BOLD coupling, resting macrovascular volume fraction, and resting-state BOLD-based rs-fcMRI estimates. They found that rs-fcMRI strength significantly increased with rising CBF-BOLD coupling strength and decreasing macrovascular volume fraction. This was true within well-known functional networks, including the default mode, frontoparietal, and primary sensory-motor networks. Their results suggest that higher rs-fcMRI strength is a sign of neuronal dominance rather than that of physiological noise.

Acknowledgments

This research was supported by the Natural Sciences and Engineering Council of Canada (NSERC) grant, National Institutes of Health (NIH) grants R01-MH080892, R01-NS081077, R01-EB014922, as well as by fellowship funding from the Rotman Research Institute of Baycrest, and the Heart and Stroke Foundation Centre for Stroke Recovery (S.T.).

Author Disclosure Statement

The authors declare no conflict of interest.

References

  1. Aubert-Broche B, Evans AC, Collins L. 2006. A new improved version of the realistic digital brain phantom. Neuroimage 32:138–145 [DOI] [PubMed] [Google Scholar]
  2. Behzadi Y, Restom K, Liau J, Liu TT. 2007. A component based noise correction method (CompCor) for BOLD and perfusion based fMRI. Neuroimage 37:90–101 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Birn RM, Diamond JB, Smith MA, Bandettini PA. 2006. Separating respiratory-variation-related fluctuations from neuronal-activity-related fluctuations in fMRI. Neuroimage 31:1536–1548 [DOI] [PubMed] [Google Scholar]
  4. Biswal B, Yetkin FZ, Haughton VM, Hyde JS. 1995. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med 34:537–541 [DOI] [PubMed] [Google Scholar]
  5. Boxerman JL, Hamberg LM, Rosen BR, Weisskoff RM. 1995. MR contrast due to intravascular magnetic susceptibility perturbations. Magn Reson Med 34:555–566 [DOI] [PubMed] [Google Scholar]
  6. Bright MG, Murphy K. 2013. Removing motion and physiological artifacts from intrinsic BOLD fluctuations using short echo data. Neuroimage 64:526–537 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Buckner RL, Krienen FM, Yeo BT. 2013. Opportunities and limitations of intrinsic functional connectivity MRI. Nat Neurosci 16:832–837 [DOI] [PubMed] [Google Scholar]
  8. Bullmore E, Sporns O. 2012. The economy of brain network organization. Nat Rev Neurosci 13:336–349 [DOI] [PubMed] [Google Scholar]
  9. Buxton RB, Wong EC, Frank LR. 1998. Dynamics of blood flow and oxygenation changes during brain activation: the balloon model. Magn Reson Med 39:855–864 [DOI] [PubMed] [Google Scholar]
  10. Chang C, Glover GH. 2009. Relationship between respiration, end-tidal CO2, and BOLD signals in resting-state fMRI. Neuroimage 47:1381–1393 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Chuang KH, van Gelderen P, Merkle H, Bodurka J, Ikonomidou VN, Koretsky AP, Duyn JH, Talagala SL. 2008. Mapping resting-state functional connectivity using perfusion MRI. Neuroimage 40:1595–1605 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Dagli MS, Ingeholm JE, Haxby JV. 1999. Localization of cardiac-induced signal change in fMRI. Neuroimage 9:407–415 [DOI] [PubMed] [Google Scholar]
  13. Dai W, Garcia D, de Bazelaire C, Alsop DC. 2008. Continuous flow-driven inversion for arterial spin labeling using pulsed radio frequency and gradient fields. Magn Reson Med 60:1488–1497 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Dale AM, Fischl B, Sereno MI. 1999. Cortical surface-based analysis: I. Segmentation and surface reconstruction. Neuroimage 9:179–194 [DOI] [PubMed] [Google Scholar]
  15. Davis TL, Kwong KK, Weisskoff RM, Rosen BR. 1998. Calibrated functional MRI: mapping the dynamics of oxidative metabolism. Proc Natl Acad Sci USA 95:1834–1839 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Desmond JE, Glover GH. 2002. Estimating sample size in functional MRI (fMRI) neuroimaging studies: statistical power analyses. J Neurosci Methods 118:115–128 [DOI] [PubMed] [Google Scholar]
  17. Duvernoy HM, Delon S, Vannson J. 1981. Cortical blood vessels of the human brain. Brain Res Bull 7:519–579 [DOI] [PubMed] [Google Scholar]
  18. Fisher RA. 1915. Frequency distribution of the values of the correlation coefficient in samples from an indefinitely large population. Biometrika 10:507–521 [Google Scholar]
  19. Fox MD, Greicius M. 2010. Clinical applications of resting state functional connectivity. Front Syst Neurosci 4:19. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. 2005. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci U S A 102:9673–9678 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Friston KJ, Ashburner JT, Kiebel SJ, Nichols TE, Penny WD. 2011. Statistical Parametric Mapping: The Analysis of Functional Brain Images. London: Academic Press [Google Scholar]
  22. Fukunaga M, Horovitz SG, de Zwart JA, van Gelderen P, Balkin TJ, Braun AR, Duyn JH. 2008. Metabolic origin of BOLD signal fluctuations in the absence of stimuli. J Cereb Blood Flow Metab 28:1377–1387 [DOI] [PubMed] [Google Scholar]
  23. Gauthier CJ, Madjar C, Desjardins-Crépeau L, Bellec P, Bherer L, Hoge RD. 2012. Age dependence of hemodynamic response characteristics in human functional magnetic resonance imaging. Neurobiol Aging 34:1469–1485 [DOI] [PubMed] [Google Scholar]
  24. Girouard H, Iadecola C. 2006. Neurovascular coupling in the normal brain and in hypertension, stroke, and Alzheimer disease. J Appl Physiol 100:328–335 [DOI] [PubMed] [Google Scholar]
  25. Greicius MD, Krasnow B, Reiss AL, Menon V. 2003. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc Natl Acad Sci U S A 100:253–258 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Hu Z, Liu C, Shi P, Liu H. 2012. Exploiting magnetic resonance angiography imaging improves model estimation of BOLD signal. PLoS One 7:e31612. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Jenkinson M, Pechaud M, Smith S. 2005. Bet2: MR-based estimation of brain, skull and scalp surfaces. In: 11th Annual Meeting of the Organization for Human Brain Mapping, Toronto, Ontario, Canada, 2005, vol. 17 [Google Scholar]
  28. Jo HJ, Saad ZS, Simmons WK, Milbury LA, Cox RW. 2010. Mapping sources of correlation in resting state FMRI, with artifact detection and removal. Neuroimage 52:571–582 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Kim SG. 2012. Perfusion MR imaging: Evolution from initial development to functional studies. Neuroimage 62:672–675 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Laufs H. 2010. Multimodal analysis of resting state cortical activity: what does EEG add to our knowledge of resting state BOLD networks? Neuroimage 52:1171–1172 [DOI] [PubMed] [Google Scholar]
  31. Liang X, Zou Q, He Y, Yang Y. 2013. Coupling of functional connectivity and regional cerebral blood flow reveals a physiological basis for network hubs of the human brain. Proc Natl Acad Sci U S A 110:1929–1934 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Liu B, Song M, Li J, Liu Y, Li K, Yu C, Jiang T. 2010. Prefrontal-related functional connectivities within the default network are modulated by COMT val158met in healthy young adults. J Neurosci 30:64–69 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Liu TT. 2013. Neurovascular factors in resting-state functional MRI. Neuroimage 80:339–348 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Liu TT, Wong EC. 2005. A signal processing model for arterial spin labeling functional MRI. Neuroimage 24:207–215 [DOI] [PubMed] [Google Scholar]
  35. Markett S, Montag C, Voigt G, Lachmann B, Rudorf S, Elger CG, Weber B. 2014. Assessing the function of the fronto-parietal attention network: Insights from resting-state fMRI and the attentional network test. Hum Brain Mapp 35:1700–1709 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Murphy K, Birn RM, Handwerker DA, Jones TB, Bandettini PA. 2009. The impact of global signal regression on resting state correlations: are anti-correlated networks introduced? Neuroimage 44:893–905 [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Otsu N. 1975. A threshold selection method from gray-level histograms. Automatica 11:23–27 [Google Scholar]
  38. Polimeni JR, Fischl B, Greve DN, Wald LL. 2010. Laminar analysis of 7T BOLD using an imposed spatial activation pattern in human V1. Neuroimage 52:1334–1346 [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Rubinov M, Sporns O. 2010. Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52:1059–1069 [DOI] [PubMed] [Google Scholar]
  40. Sepulcre J, Liu H, Talukdar T, Martincorena I, Yeo BT, Buckner RL. 2010. The organization of local and distant functional connectivity in the human brain. PLoS Comput Biol 6:e1000808. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Sled JG, Zijdenbos AP, Evans AC. 1998. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans Med Imaging 17:87–97 [DOI] [PubMed] [Google Scholar]
  42. Tak S, Wang DJJ, Polimeni JR, Yan L, Chen JJ. 2014. Dynamic and static contributions of the cerebrovasculature to the resting-state BOLD signal. Neuroimage 84:672–680 [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Tong Y, Lindsey KP, Frederick B. 2011. Partitioning of physiological noise signals in the brain with concurrent near-infrared spectroscopy and fMRI. J Cereb Blood Flow Metab 31:2352–2362 [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Toro R, Fox PT, Paus T. 2008. Functional coactivation map of the human brain. Cereb Cortex 18:2553–2559 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Van Dijk KRA, Hedden T, Venkataraman A, Evans KC, Lazar SW, Buckner RL. 2010. Intrinsic functional connectivity as a tool for human connectomics: theory, properties, and optimization. J Neurophysiol 103:297–321 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Van Dijk KRA, Sabuncu MR, Buckner RL. 2012. The influence of head motion on intrinsic functional connectivity MRI. Neuroimage 59:431–438 [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Vincent JL, Kahn I, Snyder AZ, Raichle ME, Buckner RL. 2008. Evidence for a frontoparietal control system revealed by intrinsic functional connectivity. J Neurophysiol 100:3328–3342 [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Viviani R, Messina I, Walter M. 2011. Resting state functional connectivity in perfusion imaging: correlation maps with BOLD connectivity and resting state perfusion. PLoS One 6:e27050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Wu CW, Gu H, Lu H, Stein EA, Chen JH, Yang Y. 2009. Mapping functional connectivity based on synchronized CMRO2 fluctuations during the resting state. Neuroimage 45:694–701 [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Zou Q, Wu CW, Stein EA, Zang Y, Yang Y. 2009. Static and dynamic characteristics of cerebral blood flow during the resting state. Neuroimage 48:515–524 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Brain Connectivity are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES