A Scalable Method for Molecular Network Reconstruction Identifies Properties of Targets and Mutations in Acute Myeloid Leukemia

Abstract

A key aim of systems biology is the reconstruction of molecular networks. We do not yet, however, have networks that integrate information from all datasets available for a particular clinical condition. This is in part due to the limited scalability, in terms of required computational time and power, of existing algorithms. Network reconstruction methods should also be scalable in the sense of allowing scientists from different backgrounds to efficiently integrate additional data. We present a network model of acute myeloid leukemia (AML). In the current version (AML 2.1), we have used gene expression data (both microarray and RNA-seq) from 5 different studies comprising a total of 771 AML samples and a protein–protein interactions dataset. Our scalable network reconstruction method is in part based on the well-known property of gene expression correlation among interacting molecules. The difficulty of distinguishing between direct and indirect interactions is addressed by optimizing the coefficient of variation of gene expression, using a validated gold-standard dataset of direct interactions. Computational time is much reduced compared to other network reconstruction methods. A key feature is the study of the reproducibility of interactions found in independent clinical datasets. An analysis of the most significant clusters, and of the network properties (intraset efficiency, degree, betweenness centrality, and PageRank) of common AML mutations demonstrated the biological significance of the network. A statistical analysis of the response of blast cells from 11 AML patients to a library of kinase inhibitors provided an experimental validation of the network. A combination of network and experimental data identified CDK1, CDK2, CDK4, and CDK6 and other kinases as potential therapeutic targets in AML.

1. Introduction

The knowledge of genomic changes and of other “omic” alterations in patients with acute myeloid leukemia (AML) has increased significantly over the last decade (Hoffman et al., 2012; Lawrence et al., 2014). This has not, however, resulted in the development of new effective therapies and AML still has an unfavorable prognosis for most patients (Hoffman et al., 2012). Robert Weinberg, one of the pioneers of the reductionist molecular approach to cancer research (Weinberg, 2014), recently suggested that new data-rich approaches are needed to address the complexity and heterogeneity of cancer. He, however, also pointed out that systems biology has not yet led to major advances in the understanding and treatment of malignant neoplastic disease.

A key aim of systems biology is the reconstruction of informative molecular networks, and it is becoming clear that only cell-specific and disease-specific networks are potentially able to benefit medical practice (Lefebvre et al., 2010, 2012). These networks could be used, for example, to obtain actionable information from the complex and often unique mutational cancer profiles that sequencing data provide (Lawrence et al., 2014).

More than one million gene expression datasets are available in public repositories (Baker, 2012) and biology is clearly ready for the big data computational approaches that are increasingly used in other fields of science and technology (Editorial, 2008; Schadt et al., 2010). We do not yet, however, have disease-specific networks that integrate information from most available datasets. This is in part due to the limited scalability, in terms of required computational time and power, of existing algorithms.

It is also becoming clear that integrating the growing number of datasets and the increasing amount of knowledge for a particular pathology is not a realistic task for individual research groups or even companies. Network reconstruction methods should therefore also be scalable in another sense: they should allow scientists from different groups and background to efficiently integrate additional data and progressively increase the network accuracy.

Several reviews have discussed the increasing literature on biological network reconstruction (Margolin and Califano, 2007; Marbach et al., 2012a; Csermely et al., 2013; Furlong, 2013). Among many notable articles using expression data, Basso et al. (2005) introduced ARACNE, an advanced method based on mutual information; Marbach et al. (2012b) suggested, among other components, the use of Spearman correlation for coexpression networks; and Cahan et al. (2014) very recently used a method including Pearson correlation to reconstitute stem cell regulatory networks. Other published methods, which we also use in comparisons, are TIGRESS (Haury et al., 2012), based on least angle regression, and GENIE3 (Huynh-Thu et al., 2010), which uses tree-based ensemble methods. In regard to previous AML work, Lee at al. (2009) have also used a network approach. They did not, however, provide an AML network but extracted dysregulated subnetworks (Lee et al., 2009).

In the version of the AML network we describe here (version 2.1), we have used gene expression data (both microarray and RNA-seq) from five different studies (Valk et al., 2004; Metzeler et al., 2008; Eppert et al., 2011; Macrae et al., 2013; The Cancer Genome Atlas, 2013) comprising a total of 771 AML samples. We also integrate a human protein–protein interactions dataset (Schaefer et al., 2012).

The method we present is in part based on the well-known property of gene expression correlation among interacting molecules in biological networks (Marbach et al., 2012a). A potential problem is the difficulty of distinguishing between direct and indirect interactions. We suggest a solution based on the optimization of a statistical property, the coefficient of variation, using a validated “gold-standard” dataset of direct interactions. We show that computational time is much reduced compared to other network reconstruction methods and that adding new datasets is especially easy because most computations already performed do not need to be repeated. We also suggest statistical measures that can provide the optimal correlation coefficient cutoff for the selection of significant interactions. A key feature of the method is “overlap analysis,” which is based on the study of reproducibility of interactions found in two or more independent clinical datasets.

An analysis of the most important clusters and of network properties indicated that common AML mutations have a central role in the network and that they are much closer than average to each other. This demonstrates the biological significance of the network. The network properties of kinases are consistent with a statistical analysis of the experimental response of AML primary patient cells to a kinase inhibitor library and can be combined to identify potential targets for therapeutic interventions.

2. Materials and Methods

The methods are described in Figures 1, 2, and 3 and in the Supplementary Materials (available online at www.liebertonline.com/cmb).

FIG. 1.

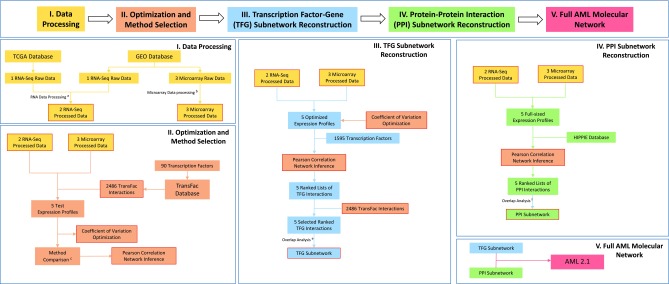
Basic workflow to generate the AML network (version 2.1). ^aOnly genes with expression level higher than 1.0 RPKM were selected and then log transformation was used to normalize the RNA-seq data. ^bThe threestep function with default setting from the affyPLM package by bioconductor was used for microarray data processing. Additionally, multiprobe to gene mapping used median probe expression. ^cFour methods were compared: Pearson correlation, Aracne, TIGRESS, and GENIE3. The methods were compared using run-time simulations and the TRANSFAC Interaction (TI) hit rate using test datasets. ^dThe average for the Poisson distribution was 2 TIs per interval. Only interactions within intervals with p-value lower than 0.10 were selected for later analysis. ^e,fOnly reproducible interactions were selected. A further selection was based on the probability of finding the same interaction multiple times only by random chance.

FIG. 2.

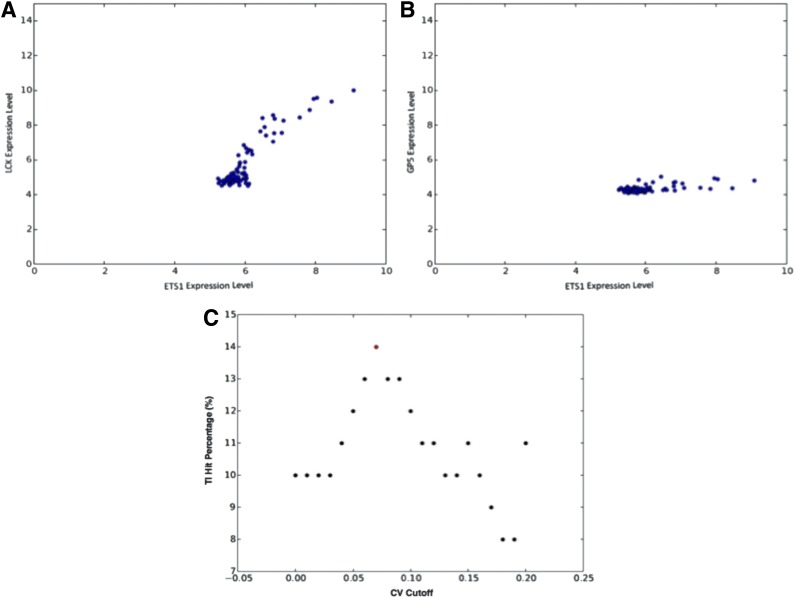
Coefficient of variation (CV) optimization. Panels (A) and (B) show an example of a retained gene target (LCK) and of an eliminated gene target (GP5) of the same transcription factor (ETS1). GP5 was eliminated from the network because of the low coefficient of variation. It is clear that the transcription factor is not likely to increase the expression of the target. Panel (C) shows an example, for one of the datasets (Eppert), of the CV optimization. The CV value is optimized to give the highest TI percentage in the top 100 interactions ranked by Pearson correlation.

FIG. 3.

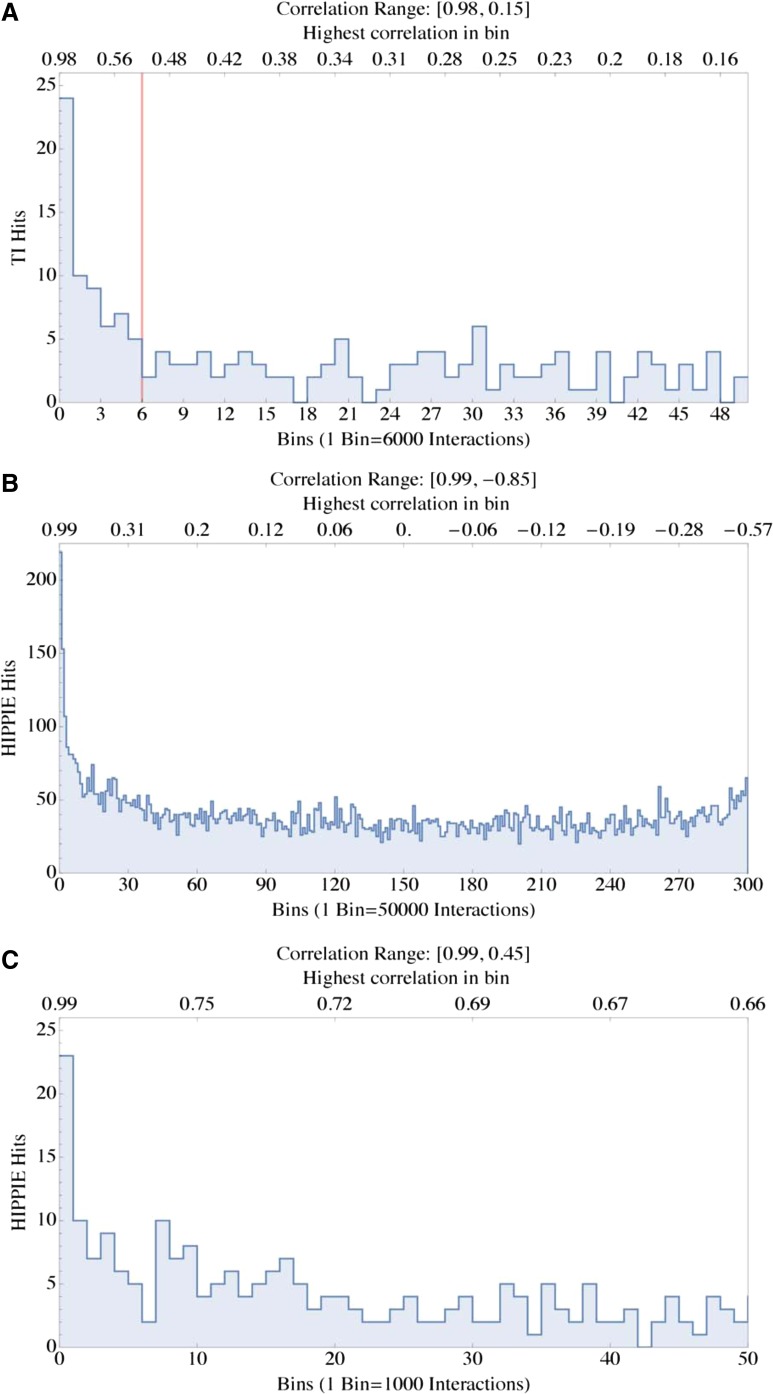
TFG and PPI interactions ranked by correlation values. (A) Poisson statistic used for the selection of TFG interactions. The panel shows the TI hits used for the Poisson distribution selection in the case of the CV-optimized Eppert dataset. Bins are ranked by correlation values, decreasing from left to right. The red line indicates the cutoff. Only interactions with correlation values above (to the left of) the cutoff were selected. These correspond to bins with a higher number of TIs, which are the validated TRANSFAC interactions. See Supplementary Figure 5S (Eppert) for the complete version of this figure, spanning all correlation values. (B) PPI interactions and HIPPIE hits. The panel shows the number of HIPPIE interaction hits within 15,000,000 random interactions from the Eppert dataset. (C) PPI interactions and HIPPIE hits. The panel shows HIPPIE interaction hits within the first bin (50,000 interactions) in (A), with finer resolution. Bins are ranked by correlation values decreasing from left to right. The analysis is from a randomly selected subset corresponding to about 10% of all possible correlations of the Eppert dataset. As for the TFG subnetwork shown in (A), also for the PPI subnetwork bins corresponding to interactions with a higher correlation coefficient contain a higher number of validated interactions obtained from the HIPPIE database.

3. Results

3.1. Methodological results

The details of the datasets we used and the corresponding numbers of genes are shown in Table 1. Supplementary Table 3S also shows the number of interactions included in AML 2.1 obtained from each of the five gene expression datasets. As expected from the more quantitative nature of RNA-seq, the datasets obtained with this technique were more informative, providing more reproducible interactions compared to the three microarray datasets, even when the number of samples was comparable or lower.

Table 1.

Expression Datasets Used for the Study, for Both the TFG and the PPI Subnetworks

Dataset	Technique	GSE ID	Number of samples	Full-size expression profile (number of genes)	Test expression profile (number of genes)	CV optimized expression profile (number of genes)
Eppert	Microarray	GSE30377	93	12,495	1208	3663
Metzeler	Microarray	GSE12417	163	12,495	1208	4535
Valk	Microarray	GSE1159	293	12,496	1208	3388
Macrae	RNA-seq	GSE49642	43	11,737	785	3154
TCGA	RNA-seq	NA	179	12,917	881	4332

Three microarray and one RNA-seq datasets were downloaded from GEO. The TCGA RNA-seq LAML dataset was downloaded from the TCGA Data Portal.

Table 2 shows that the optimized CV cutoff increased the number of validated TRANSFAC interaction (TI) hits identified in almost all cases and specifically in every case where Pearson Correlation was used. Interactions were ordered according to the measurements provided by each method, and the significance of the CV cutoff was tested using the two-tailed Student t-test of the top 100 and top 1000 interactions, before and after CV cutoff. The CV cutoff in both top 100 and top 1000 resulted in significant increases in TI hits with p<0.0001.

Table 2.

Number of TRANSFAC Interaction Hits for the Top 100 and the Top 1000 Interactions

Network inference method	Data source	Data type	Top 100 TI hit pre-CV	Top 100 TI hit post-CV	Top 1000 TI hit pre-CV	Top 1000 TI hit post-CV
Pearson correlation	Eppert	Microarray	10	13	61	67
Pearson correlation	Macrae	RNA	9	14	44	63
Pearson correlation	Metzeler	Microarray	11	19	23	62
Pearson correlation	TCGA	RNA	5	18	56	60
Pearson correlation	Valk	Microarray	12	22	35	72
Aracne	Eppert	Microarray	6	8	45	43
Aracne	Macrae	RNA	7	7	28	35
Aracne	Metzeler	Microarray	3	14	30	47
Aracne	TCGA	RNA	9	11	56	46
Aracne	Valk	Microarray	11	17	50	61
GENIE3	Eppert	Microarray	13	16	53	57
GENIE3	Macrae	RNA	11	13	53	59
GENIE3	Metzeler	Microarray	18	18	43	64
GENIE3	TCGA	RNA	13	17	67	61
GENIE3	Valk	Microarray	18	19	54	74
TIGRESS	Eppert	Microarray	9	13	43	60
TIGRESS	Macrae	RNA	5	8	52	55
TIGRESS	Metzeler	Microarray	16	17	38	56
TIGRESS	TCGA	RNA	14	15	58	54
TIGRESS	Valk	Microarray	14	19	42	70

Interactions were ordered by the values provided by the different inference methods, before and after the correlation coefficient of variation (CV) cutoff. The data were obtained using the test datasets. The table shows the increase after the CV cutoff. TI, TRANSFAC interaction.

The run times of our optimized Pearson correlation method and of three previously published network reconstruction methods, ARACNE (Basso et al., 2005; Meyer et al., 2008), TIGRESS (Haury et al., 2012), and GENIE3 (Huynh-Thu et al., 2010), were estimated using the same hardware and datasets and are shown in Supplementary Figure 2S. The comparison shows a speed advantage of several orders of magnitude for the optimized Pearson correlation method we present here. Adding another method after optimized correlation identifies 11–15% more interactions (Table 3). As shown in Supplementary Table 2S, however, these interactions are not the same for every method added. Supplementary Figure 4S shows an example of a nonlinear relationship that has been identified as a network interaction by the three additional methods listed in Table 3, but not by our method. As indicated in Table 3, these methods can miss an even larger number (14–60%) of validated interactions found by optimized correlation.

Table 3.

Additional Information Provided by the Indicated Methods Compared with Optimized Correlation

Method	TI shared with correlation	TI unique to correlation	TI discovery unique to correlation (ratio)	TI unique to other method	TI discovery unique to other method (ratio)
ARACNE	49	35	0.60	9	0.11
GENIE3	72	12	0.14	13	0.15
TIGRESS	65	19	0.24	13	0.15

The last column shows the ratio of newly identified TI to those found with the correlation method. This column shows that adding an additional method increases the number of validated interactions (TI) already found with optimized correlation only by 11–15%. The third data column shows the same ratio when optimized correlation is added to one of the other three methods.

3.2. Reproducibility results (overlap)

Table 4 shows that the reproducibility of our method (measured by the number of interactions found in more than one expression dataset) is much higher than that of randomly generated TFG and PPI subnetworks. The probability of finding the number of interactions reported 2 or more times is much lower than 0.01 for both the TFG and the PPI subnetworks. Random simulations and the exact method described in the reproducibility analysis section of the Supplementary Methods provide similar estimates. None of the interactions found in only one gene expression dataset are included in the AML 2.1 network.

Table 4A.

The Number of TFG Subnetwork Interactions That Are Found in One or More Datasets Is Compared to Those Found in Randomly Generated Subnetworks

Number of datasets where an interaction is present	Avg. interactions in random simulations	Interactions in random model	Interactions in TFG subnetwork	Interactions included in AML 2.1	Significance of number of reproducible interactions
1	179,574	179,579	129,943	0	NA
2	612	611	17,817	6117	p<10−10
3	1	1	2505	2505	p<10−10
4	0	0	1183	1183	p<10−10
5	0	0	596	596	p<10−10

None of the interactions listed in the 1 dataset row were included in AML2.1. Only part of the interactions found two times were included.

Table 4B.

The Number of PPI Subnetwork Interactions That Are Found in One or More Datasets Is Compared to Those Found in Randomly Generated Subnetworks

Number of datasets where an interaction is present	Avg. interactions in random simulations	Interactions in random model	Interactions in PPI subnetwork	Interactions included in AML 2.1	Significance of number of reproducible interactions
1	45,836	45,825	13,754	0	NA
2	3	9	6794	6794	p<10−10
3	0	0	2487	2487	p<10−10
4	0	0	1705	1705	p<10−10
5	0	0	844	844	p<10−10

None of the interactions listed in the 1 dataset row were included in AML2.1.

In addition to the reproducibility (overlap) of interactions, the TI ratio, defined as the number of TI/number of interactions, was also examined, as shown in Supplementary Table 4S, for the TFG subnetwork. This ratio was increased compared to the initial dataset (before the application of the optimized correlation selection) even for interactions present in only one dataset and increased progressively for those appearing in two or more datasets.

The full lists of overlapping interactions for the TFG and PPI subnetworks are shown in Supplementary Tables 4S and 5S. These tables also show that the average correlation is generally higher when the reproducibility increases (we show separately interactions found in 1, 2, 3, 4, or 5 datasets) but the distributions of these correlation values are not sufficient to separate the groups. In conjunction with the data already referred to in the Materials and Methods section, these findings are consistent with the rationale we have used in the optimization of the network.

We also analyzed 7 more AML microarray datasets (GSE15434, 24006, 33223, 34860, 21261, 6891, and 22845), which will be included in future version of the network, and measured the reproducibility of the interactions using all 12 datasets. The data are shown in Supplementary Table 10S.

Using the 12 datasets, we also measured the TI ratio for the first 10 overlap groups (the number of interactions was too small in groups 11 and 12). The data are presented in Supplementary Table 12S and show a monotonic (exponential) increase of the TI ratio with the number of overlaps, and therefore with the reproducibility of the interactions. We found a significant Spearman's correlation between the group number and the TI ratio with p<0.0001.

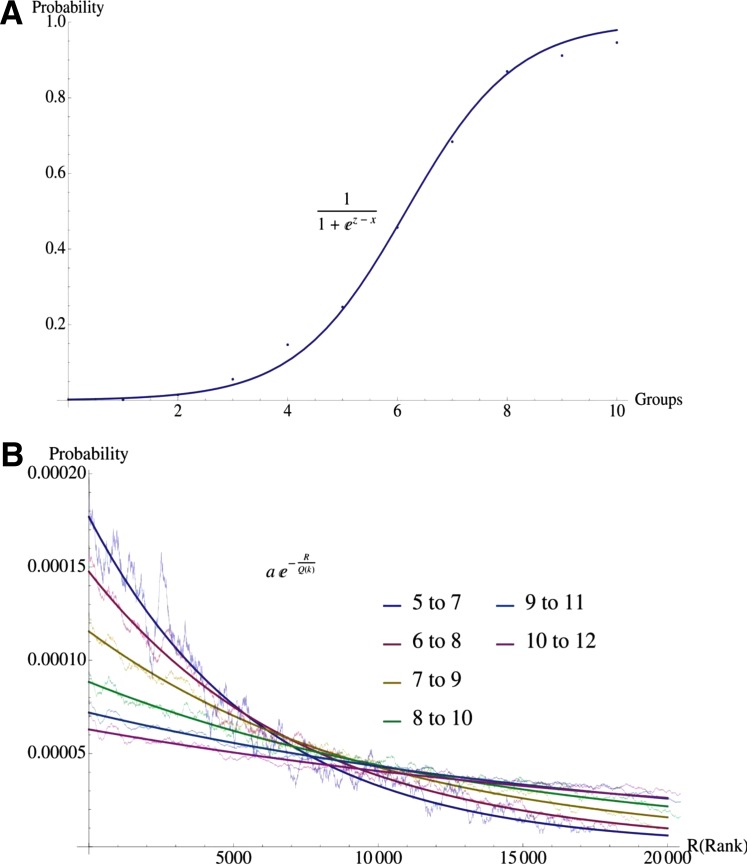
Remarkably, a similar increase as a function of the group number is also obtained when we measure, as a ratio, the interactions that, for each of the 10 overlap groups obtained from an analysis of 10 datasets, were found again twice when two more datasets were added. This ratio is a measure of the probability of reproducibility, and therefore of validity, for interactions in each group, and was found to increase monotonically from overlap group 1 to overlap group 10 (Spearman correlation had p<0.0001) (Supplementary Table 12S). This probability was found to be well approximated by a single-parameter sigmoid function of the form (1 + e^z-x)⁻¹, where x is the overlap group and the fitting parameter z=6.15609 (R²=0.9986). (See Fig. 4A.)

FIG. 4.

Reproducibility analysis. (A) Reproducibility probability in 10 groups. The figure shows the probability that a TFG interaction found in overlap group x (horizontal axis) using 10 datasets is found in group x+2 when 12 datasets are used. This probability gives an estimate of reproducibility for group 1 to group 10. The 10 points were found to be well approximated by a single-parameter sigmoid function of the form 1/[1 + Exp(z – x)], where x is the overlap group and the fitting parameter z = 6.15609 (R² = 0.9986). (B) Reproducibility probability distribution within group 2. The figure shows the distribution of the probability of reproducibility (after the addition of two more datasets) as a function of the rank R of an interaction within group 2 with k = 5 to 10 datasets. The fitting to the probability distribution is of the form P(R,k) = a Exp[−R/Q(k)], where R is the rank of the interaction within the group, and Q(k) is a characteristic decay rank that depends on the number of datasets k. The factor a takes into account the probability distribution normalization. This figure indicates that the correlation-based ranking within group 2 contains less information and is less significant when more datasets are added, since the top-ranking interactions in this group become less reproducible.

Reproducibility can also be studied within the groups shown in Figure 4A and Supplementary Table 12S. The reproducibility of interactions in the overlap 2 group, ordered by an average rank obtained from their correlation coefficient, declined monotonically. We measured the interactions in this overlap 2 group that were found again after adding all possible combinations of two more datasets. Each of the interactions originally found in two datasets could now therefore remain in overlap group 2 or could be found in overlap group 3 or 4. Assigning a value of 1 to those that progressed one step to group 3 and a value of 2 to those that progressed two steps to group 4, the average score for the top 6000 interactions was 0.268, while for the remaining interactions in the group it was only 0.068, a decrease of almost 4-fold. This difference was highly statistically significant, using both a parametric and a nonparametric test (p<0.0001 with the Mann–Whitney test).

We also studied this behavior in additional overlap 2 groups for datasets 6–10 and identified an exponential fitting that can be used to predict the distribution of the probability of reproducibility after the addition of two more datasets, as a function of the rank of an interaction within a group (Supplementary Data 11S and Fig. 4B). The probability distribution is well approximated by P(R,k) = ae^−R/Q(k), where R is the rank of the interaction within the group, and Q(k) is a characteristic decay rank that depends on the number of datasets k. Factor a takes into account the probability distribution normalization. We found that the characteristic decay rank scales with the number of possible interactions contained in each group and is well approximated by the relation 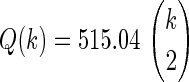(R²=0.998). Figure 4B shows that the correlation-based ranking within group 2 contains less information and is less significant when more datasets are added, since the top-ranking interactions in this group become less reproducible.

These models and analyses can assist the choice of which interactions to select when the number of datasets increases and could also be used to build weighted networks.

3.3. Biological results

3.3.1. Properties, visualization, and gene ontology cluster analysis of AML 2.1

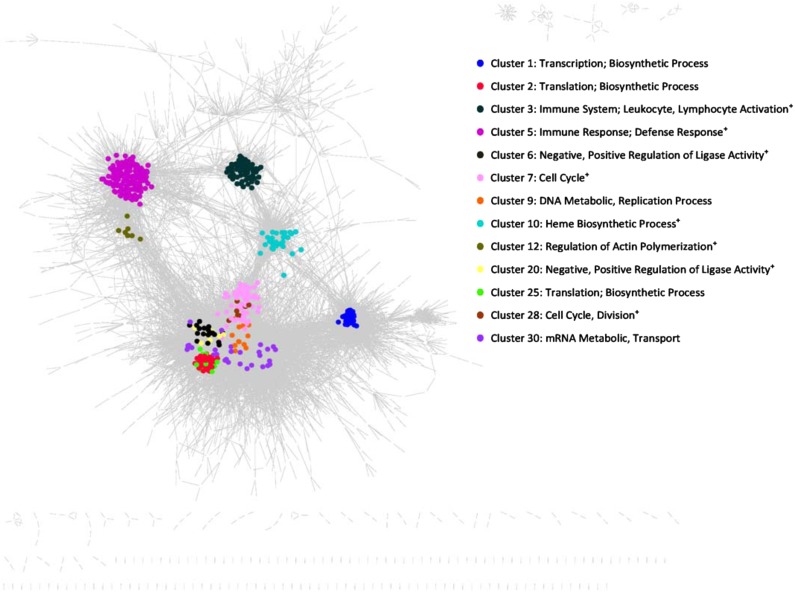
The full list of TFG and PPI interactions in AML 2.1 is shown in Supplementary Table 6S. The global network properties of AML 2.1 are shown in Table 5 (Newman, 2010). The AML 2.1 network contains the TFG and PPI subnetworks and is partially directed. MCODE clustering analysis found a total of 101 clusters. The complete list of clusters is shown in Supplementary Table 7S. Table 6A also shows the differences between normal human hematopoietic cells and AML patients for the top 13 clusters, with corresponding gene ontology (GO) functional terms, and the p-values for these differences. The Fisher's exact test and false discovery rate were performed on the clusters and 4 clusters were found to be expressed with a p-value <0.1 in either normal subjects or AML patients. Two clusters related to immune response and cell cycle were found to be highly expressed in AML patients. On the other hand, one cluster related to translation and biosynthetic process was found to be highly expressed in normal human hematopoietic cells. Figure 5 shows the AML 2.1 network with the top MCODE clusters. Figure 5 also shows several other functions that are relevant to the cells of origin of AML, for example, “leukocyte and lymphocyte activation.” Table 6B shows similar comparisons using Fisher's exact test with RECON2 (Thiele et al., 2013) metabolic pathway clustering. Eight RECON2 pathways were found to be differentially expressed.

Table 5.

Network Properties of AML 2.1

Nodes	5667
Edges	22,218
Global efficiency	0.1215
Average clustering coefficient	0.1983
Transitivity	0.2043
Betweenness centrality	0.00054

Table 6A.

Top 13 MCODE Clusters (p < 0.10)

Cluster ID	Representative GO term	Higher expression in	p
5	Immune response; defense response	AML	7.07E-18
2	Translation; biosynthetic process	Normal	8.46E-06
7	Cell cycle	AML	0.00017
1	Transcription; biosynthetic process	Normal	0.012
3	Immune system; leukocyte, lymphocyte activation	AML	0.031
20	Negative, positive regulation of ligase activity	AML	0.038
9	Dna metabolic, replication process	Normal	0.038
25	Translation; biosynthetic process	Normal	0.039
10	Heme biosynthetic process	Normal	0.061
6	Negative, positive regulation of ligase activity	AML	0.062
12	Regulation of actin polymerization	AML	0.069
28	Cell cycle, division	AML	0.069
30	mRNA metabolic, transport	Normal	0.087

The Fisher's exact test was used to compare the expression profile of AML and normal hematopoietic cells.

FIG. 5.

AML Network 2.1 with the 13 main clusters. AML 2.1 is shown with 13 functional clusters highlighted. The clusters had significant differences between AML patients and controls. See Table 8 for a detailed description of the functions associated with each cluster.

Table 6B.

Top 8 RECON2 Pathways (p < 0.10)

RECON2 pathways	Higher expression in	p
Oxidative phosphorylation	AML	0.0070
Heme synthesis	Normal	0.011
Glycolysis/gluconeogenesis	AML	0.016
Transport, lysosomal	AML	0.032
N-glycan synthesis	Normal	0.034
NAD metabolism	AML	0.038
Selenoamino acid metabolism	Normal	0.061
Pentose phosphate pathway	AML	0.065

The Fisher's exact test was used to compare the expression profile of AML and normal hematopoietic cells.

3.3.2. Receptors

We also examined the number of interactions for specific functional classes, including cellular receptors. The two most connected receptors, with degree (number of connections) higher than 200, were vitamin D receptor (VDR) and retinoid X receptor, alpha (RXRA) (Supplementary Table 8S). As we mention in the Discussion section, these are known to have important roles in AML cells. We have also analyzed the two human AML RNA-seq datasets we use in this study (Macrae et al., 2013; The Cancer Genome Atlas, 2013) and found that the coefficient of variation of receptors expression between different patients is in both cases approximately double that of other genes (p<0.0001).

3.3.3. AML mutations

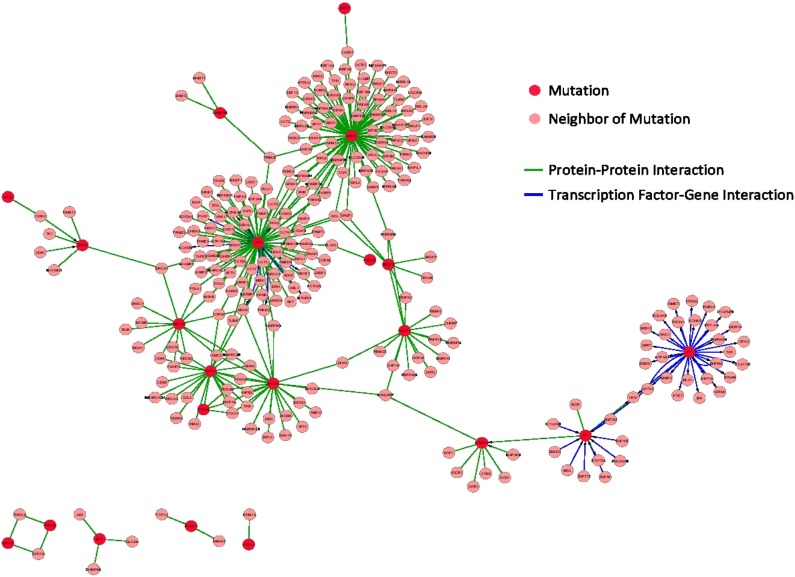
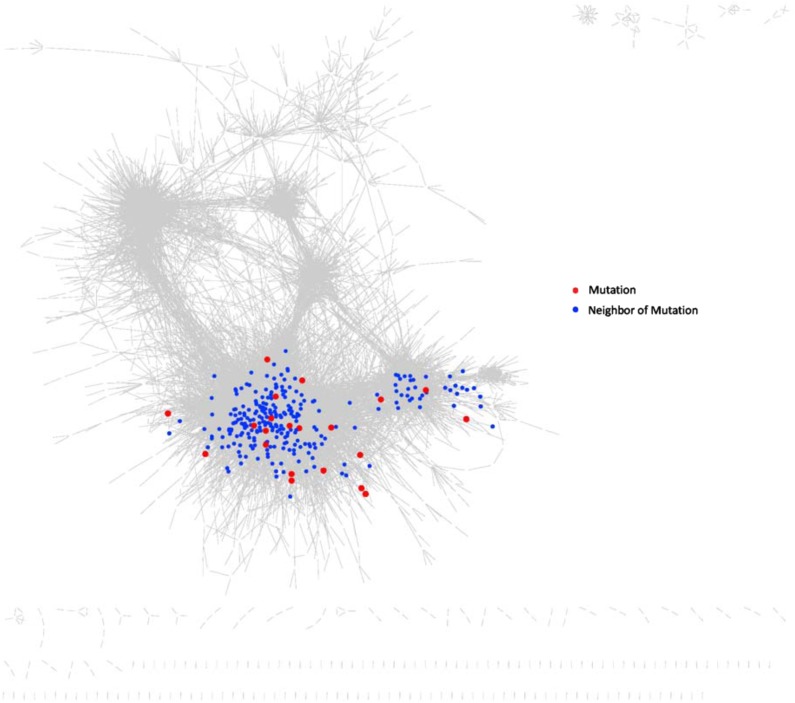
The network is significantly enriched for common known AML mutated genes. It contains 21 out of 26 significantly mutated AML genes (Lawrence et al., 2014) even though it is composed of only 5667 genes/proteins (p=2.3 × 10⁻⁸ for the enrichment). This shows that the network reconstruction method enriches for functionally relevant genes. Figure 6 shows the 21 common AML mutations included in the network and their first neighbors. This subnetwork is highly connected with a total of 5 clusters and with the largest cluster containing 16 AML mutated genes. Figure 7 shows the mutations and their first neighbors within the AML 2.1 network. Comparing Figures 5 and 7 shows that the mutations co-localize with functional clusters of known relevance to cancer, including “cell cycle” and “DNA replication.”

FIG. 6.

Mutation subnetwork. This subnetwork is composed of 21 common AML mutations and their first neighbors. The red dots are the mutations, the blue dots are their first neighbors, the blue edges are TFG interactions, and the green edges are PPI interactions.

FIG. 7.

AML Network 2.1 with the mutation subnetwork. AML 2.1 is shown with the 21 common AML mutations and their first neighbors highlighted. The red dots are the mutations and the blue dots are their first neighbors. The mutation subnetwork overlaps the region where in Figure 5 we see the clusters for cell cycle, translation, and DNA replication.

To examine the statistical significance of these measures, random subnetworks were generated. Random subnetworks consisting of 21 random genes and their first neighbors were less connected than the mutation subnetwork. They had an average of 16.2 clusters and an average size of 3.5 genes from the group of 21 in the largest cluster (p<0.0001 compared to the mutation subnetwork). Other network measurements were also computed with the same random subnetwork simulation, as shown in Table 7 and Supplementary Figure 7S. The 21 mutations also had significantly higher values of 3 network centrality measures: degree (p=0.015), betweenness centrality (p=0.02), and PageRank (p=0.01) (Newman, 2010).

Table 7.

Network Measures of the 21 AML Mutations Set Compared to Controls (Random Gene Sets of the Same Size)

Measurements	Mutations mean	Control mean	Control median	Control STD	p
Clustering coefficient	0.130	0.198	0.193	0.0664	0.846
Local efficiency	0.202	0.233	0.229	0.0723	0.648
Degree	27.952	11.799	10.619	5.338	0.015
In-degree	13.476	5.894	5.476	2.169	0.0087
Out-degree	14.476	5.905	4.952	3.753	0.0392
Betweenness centrality	0.00206	0.0005	0.0004	0.0005	0.0207
Eigen centrality	0.0027	0.0017	0.0003	0.0028	0.228
PageRank	10.942	5.313	5.0266	1.631	0.0125

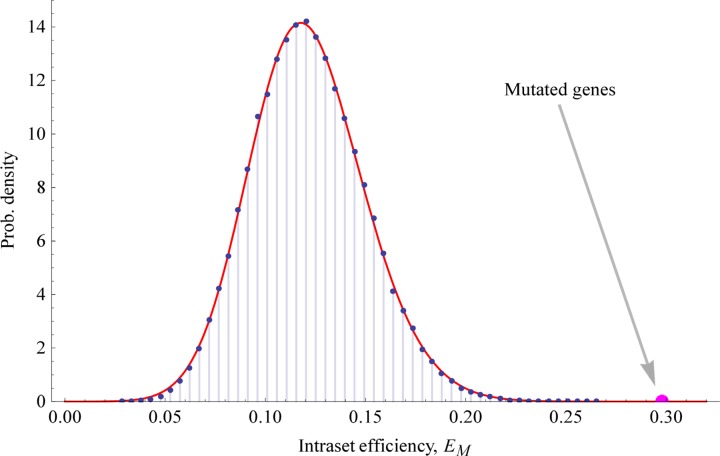
A similar conclusion, with stronger statistical significance, is obtained by examining the intraset efficiency for the 21 mutations and for random sets of 21 genes. The intraset efficiency was clearly higher for the set of 21 mutations. Figure 8 shows that a skew normal probability distribution was fitted to a histogram of the randomized sets with R²=0.99, and an approximate right-tailed p-value of 7.3 × 10⁻⁸ was obtained. This measure indicates that the paths among the mutations are much shorter than for control sets. In other words, the mutations can more easily exchange information.

FIG. 8.

Intraset efficiency. The intraset efficiency of the 21 genes commonly mutated in AML cells as well as 10 million randomly generated sets of 21 nodes for a control. The vertical axis shows the probability density. The histogram was built using 50 bins of uniform width. The red curve is the right-skewed normal distribution fitted to the random data, which has R² = 0.999982. The mutation intraset efficiency is greater than the intraset efficiency of all random sets examined.

As shown by visual inspection and comparison of Figures 5 and 7 and by calculating the clustering coefficient (Table 7 and Supplementary Fig. 7S), the mutations do not, however, form a tight cluster. That is, they do not interact mainly among themselves.

Table 8 shows a summary of the GO functional enrichment analysis of the mutation subnetwork, obtained using DAVID (Huang da et al., 2009). The full analysis is shown in Supplementary Table 8S. The mutation subnetwork is composed of 21 common AML mutations and of their first neighbors, for a total of 257 genes, but a very similar list of GO terms is obtained by analyzing the first neighbors only (Supplementary Table 8S), showing that the functional information is contained in the network and not only in the mutations. These functions are those commonly associated with cancer mutations, including DNA replication, cell cycle, and cell death.

Table 8.

GO Enrichment Analysis for the Mutation Subnetwork of AML 2.1 (Composed of 21 Common AML Mutations and Their First Neighbors, for a Total of 257 Genes)

GO term	Description	Count	p	Fold enrichment	False discovery rate
GO:0006259	DNA metabolic process	43	4.28E-16	4.47	7.55E-13
GO:0051276	Chromosome organization	42	5.06E-16	4.56	9.44E-13
GO:0006396	RNA processing	42	3.00E-14	4.04	5.08E-11
GO:0006974	Response to DNA damage stimulus	33	7.17E-13	4.66	1.22E-09
GO:0007049	Cell cycle	47	3.29E-12	3.19	5.58E-09
GO:0033554	Cellular response to stress	39	8.55E-12	3.63	1.45E-08
GO:0006281	DNA repair	27	2.79E-11	5.00	4.73E-08
GO:0016568	Chromatin modification	23	1.16E-08	4.42	1.97E-05
GO:0006260	DNA replication	18	1.20E-07	4.99	2.03E-04
GO:0016570	Histone modification	14	5.17E-07	6.04	8.77E-04
GO:0010941	Regulation of cell death	37	1.69E-06	2.39	0.0029
GO:0034621	Cellular macromolecular complex subunit organization	22	4.39E-06	3.24	0.0074
GO:0045934	Negative regulation of nucleobase, nucleoside, nucleotide, and nucleic acid metabolic process	27	4.67E-06	2.78	0.0079

3.3.4. Experimental validation using kinase inhibitors and AML primary samples

Centrality measures can be used to rank kinases in AML 2.1. These results were compared to the response of AML primary cells to a library of 244 kinase inhibitors. A method we have recently developed, based on elastic net regression applied to kinase inhibitors, the KIEN method (Tran et al., 2014), was used to identify and rank according to a score β_k (see Materials and Methods), the kinases responsible for the effects of the kinase inhibitors in primary AML cells from 11 patients.

We then calculated Pearson correlation and Spearman rank correlation on a set of 101 kinases present both in AML 2.1 and in the drug response dataset (see Materials and Methods). Table 9A shows the correlation coefficients and significance values of betweenness centrality, degree, and PageRank with the KIEN parameter β_k, using Pearson, and Table 9B shows the same three correlations using Spearman rank correlation. Betweenness centrality is significantly correlated with β_k according to both methods, while degree and PageRank were significant only with Pearson correlation.

Table 9A.

Pearson Correlation of Three Centrality Measures from AML 2.1 with Experimentally Obtained β_k for 101 Kinases

Centrality measures	Pearson correlation coefficient	p
Betweenness centrality	0.266	0.007
Degree	0.401	0.000032
PageRank	0.375	0.0001

Table 9B.

Spearman Rank Correlation of Three Centrality Measures from AML 2.1 with Experimentally Obtained β_k for 101 Kinases

Centrality measures	Spearman rank correlation coefficient	p
Betweenness centrality	0.234	0.018
Degree	0.178	0.075
PageRank	0.158	0.11

The top 10 kinases identified by the combined use of betweenness centrality and PageRank with KIEN are shown in Tables 10 and 11. The most remarkable finding is the presence of a group of four kinases, CDK1, CDK2, CDK4, and CDK6, at the top of the independent analyses based on AML 2.1 centrality measures and on experimental data analyzed by KIEN (with significance of p<10⁻⁷ for betweenness centrality, PageRank, and also degree; the details of the degree analysis are shown in the Supplementary data). The other kinases shown in Tables 10 and 11 are strong candidate targets for further experimental studies.

Table 10.

The Top 10 Kinase Targets Identified Using the Betweenness Centrality Measure from AML 2.1 and the KIEN Analysis of Experimental Data

Kinase targets	Average rank	Betweenness centrality rank	KIEN rank
CDK2	2.5	1	4
CDK1	4	7	1
CDK4	6	4	8
CDK6	9	12	6
LCK	10.5	19	2
LYN	17.5	20	15
CHEK1	18	15	21
MAP2K2	18.5	24	13
RPS6KA1	18.5	6	31
CSK	19	14	24

Table 11.

The Top 10 Kinase Targets Identified Using the PageRank Measure from AML 2.1 and the KIEN Analysis of Experimental Data

Kinase targets	Average rank	PageRank rank	KIEN rank
CDK1	2	3	1
CDK2	2.5	1	4
CDK4	5	2	8
CDK6	5.5	5	6
TYRO3	11	13	9
CHEK1	13.5	6	21
LYN	14.5	14	15
CSK	19.5	15	24
RPS6KA1	23.5	16	31
CHUK	24	23	25

Specific literature support for the involvement of these targets in AML is analyzed in more depth in the Discussion section, but an additional level of statistical confirmation of our approach is obtained by showing that the number of relevant citations for each of the 101 kinase targets mentioned above in this section (obtained by searching PubMed for the gene name and the term AML) is significantly correlated (using Spearman) with the combined average rank of the kinases obtained as shown in Tables 10 and 11. The p-value is lower than 0.0003 for ranks obtained from all three centrality measures (betweenness centrality, degree, and PageRank).

3.3.5. An additional set of networks

We have built eight additional networks based on the alternative methods of either selecting only interaction above a certain threshold (e.g., “overlap 3+”) or using the reproducibility of every group (e.g., overlap 1, 2, 3, etc.) to assign a score to each interaction. These networks use 12 AML gene expression datasets. An analysis of these networks is shown in Tables 12 and 13.

Table 12.

Dimensions and Centrality Measures for Networks Derived from 12 AML Gene Expression Datasets, with Different Cutoffs

			STD	p
	Average 2.2_2up	Median 23/26 mutations	125/175 drug targets
Degree(All)	18.8	7.0	44.6
Degree(DrugTargets)	21.2	9.0	32.1	0.24817
Degree(Mutations)	58.0	18.0	126.5	0.00300
PageRank(All)	3.3	1.7	5.3
PageRank(DrugTargets)	5.3	3.1	6.8	0.00315
PageRank(Mutation)	8.3	3.6	13.7	0.00499
Bcent(All)	0.0002	0.0000	0.0013
Bcent(DrugTargets)	0.0008	0.0000	0.0023	0.00723
Bcent(Mutations)	0.0025	0.0000	0.0095	0.00276
Nodes	9205
Edges	71,101

	2.2_2up_5k	23/26 mutations	119/175 drug targets
Degree(All)	14.2	6.0	31.2
Degree(DrugTargets)	19.0	8.0	31.7	0.06341
Degree(Mutations)	45.6	14.0	99.6	0.00161
PageRank(All)	3.8	2.2	5.9
PageRank(DrugTargets)	5.8	3.3	7.3	0.00691
PageRank(Mutation)	8.7	3.8	14.5	0.00743
Bcent(All)	0.0003	0.0000	0.0017
Bcent(DrugTargets)	0.0010	0.0001	0.0028	0.00832
Bcent(Mutations)	0.0032	0.0000	0.0114	0.00322
Nodes	7882
Edges	40,787

			STD	p
	2.2_3up	22/26 mutations	118/175 drug targets
Degree(All)	13.6	5.0	29.7
Degree(DrugTargets)	18.8	8.0	31.6	0.04567
Degree(Mutations)	44.5	16.5	89.8	0.00162
PageRank(All)	4.0	2.4	6.1
PageRank(DrugTargets)	5.9	3.4	7.5	0.00875
PageRank(Mutation)	9.3	3.8	15.1	0.00689
Bcent(All)	0.0004	0.0000	0.0019
Bcent(DrugTargets)	0.0010	0.0001	0.0029	0.00935
Bcent(Mutations)	0.0036	0.0000	0.0124	0.00308
Nodes	7483
Edges	35787

	2.2_3up_5k	21/26 mutations	114/175 drug targets
Degree(All)	12.9	5.0	27.4
Degree(DrugTargets)	18.9	8.0	31.9	0.02201
Degree(Mutations)	43.7	14.0	87.7	0.00126
PageRank(All)	4.2	2.6	6.3
PageRank(DrugTargets)	6.2	3.8	7.7	0.00990
PageRank(Mutation)	9.8	3.9	15.6	0.00710
Bcent(All)	0.0004	0.0000	0.0020
Bcent(DrugTargets)	0.0011	0.0002	0.0030	0.00685
Bcent(Mutations)	0.0036	0.0000	0.0135	0.00332
Nodes	7086
Edges	30,391

	2.2_4up	21/26 mutations	111/175 drug targets
Degree(All)	12.2	4.0	25.8
Degree(DrugTargets)	19.1	7.0	32.2	0.01088
Degree(Mutations)	39.7	13.0	73.7	0.00211
PageRank(All)	4.5	2.9	6.5
PageRank(DrugTargets)	6.4	4.2	8.0	0.01241
PageRank(Mutation)	10.1	4.0	16.2	0.00774
Bcent(All)	0.0004	0.0000	0.0021
Bcent(DrugTargets)	0.0012	0.0002	0.0031	0.00669
Bcent(Mutations)	0.0036	0.0001	0.0130	0.00369
Nodes	6674
Edges	25,390

Table 13.

Dimensions and Centrality Measures for Networks Derived from 12 AML Gene Expression Datasets, Either Unweighted or Weighted According to Reproducibility, with Two Different Levels of Stringency

	Average 2.3 unweighted	Median 26/26 mutations	STD 157/175 DrugTargets	p
Degree(All)	41.4	14.0	105.0
Degree(Mutations)	141.3	42.5	326.2	0.00095
Degree(DrugTargets)	43.7	24.0	65.6	0.36579
PageRank(All)	2.0	0.8	3.7
PageRank(Mutations)	7.3	3.2	12.4	0.00180
PageRank(DrugTargets)	4.3	2.7	5.5	0.00010
Bcent(All)	0.00011	0.00000	0.00072
Bcent(Mutations)	0.00210	0.00006	0.00906	0.00014
Bcent(DrugTargets)	0.00044	0.00009	0.00121	0.00259

	2.3 1and2	26/26 mutations	157/175 DrugTargets
Degree(All)	5.8	1.5	15.8
Degree(Mutations)	28.7	8.3	65.5	0.00015
Degree(DrugTargets)	9.7	3.4	16.3	0.00640
PageRank(All)	2.0	0.8	3.9
PageRank(Mutations)	7.8	3.2	13.9	0.00177
PageRank(DrugTargets)	4.3	2.3	5.7	0.00006
Bcent(All)	0.00018	0.00000	0.00120
Bcent(Mutations)	0.00310	0.00009	0.01181	0.00006
Bcent(DrugTargets)	0.00075	0.00009	0.00233	0.00054

	2.3 Just2	26/26 mutations	157/175 DrugTargets
Degree(All)	0.7	0.0	3.7
Degree(Mutations)	4.0	0.4	10.6	0.01069
Degree(DrugTargets)	1.5	0.1	4.0	0.03101
PageRank(All)	2.0	0.7	4.4
PageRank(Mutations)	8.6	3.3	17.7	0.00154
PageRank(DrugTargets)	4.2	1.9	6.1	0.00022
Bcent(All)	0.00035	0.00000	0.00295
Bcent(Mutations)	0.00573	0.00003	0.02251	0.00016
Bcent(DrugTargets)	0.00144	0.00007	0.00731	0.00156
Nodes	15,055
Edges	285,200

The number of nodes and edges is the same for these three networks.

The networks of Table 12 are obtained using different cutoffs, as indicated by their names. For example, 2up includes only interaction found in 2 or more datasets; 2up_5k includes only the first 5000 interactions of group 2, ordered by their correlation coefficient, and all the groups with reproducibility of 3 or more.

The networks of Table 13 are either unweighted or weighted according to reproducibility with two different levels of stringency. There is no cutoff in these networks. Reproducibility is assessed analyzing two additional independent networks and the weight of each group is assigned according to the probability of each interaction being replicated in both these additional datasets (more stringent, indicated as just 2 in the name of the network shown in Table 13) or in at least one of them (less stringent, indicated as 1 and 2 in the name of the network shown in Table 13). The weights are shown in Supplementary Table 12S.

In this analysis we have also analyzed all the drugs that are currently in active AML clinical trials, as shown in clinicaltrials.gov, and obtained a list of 175 drug targets. As can be seen from Tables 12 and 13, the drug targets have values for the three centrality measures, which are almost always significantly higher than the control values, but, in every network, never as high as the set of common AML mutations.

The analysis shows that adding the weights or using a higher cutoff often increases the significance of the p-values. Specifically, in two cases the degree of the drug targets only becomes significant using a higher cutoff or adding weights. It must be observed that using cutoffs decreases the size of the network and the coverage for the mutations and drug targets sets, which can be a disadvantage when there is an interest in a specific gene.

It is possible to argue that we should not aim for a “perfect” network, but instead should focus on the best network for a specific use. We therefore encourage users to test which network works best for their respective applications, as these networks are clearly abstract representations, still quite distant from the physical reality of the cell.

4. Discussion

We have developed a fast, reproducible, and scalable network reconstruction method, which is able to integrate biological datasets of different types. In the AML 2.1 network version we present here, both microarray and RNA-seq gene expression data and protein–protein interaction data were included.

Only interactions derived from at least two independent clinical datasets were selected for the network and some of the interactions found twice underwent further filtering. This is the only strategy that can correct for all possible types of noise, including biological, clinical, and experimental variation. As can be seen from Table 4, this led to pruning of a large number of interactions, and, most likely, to a higher quality AML network. The alternative approach of pooling all the data and performing a single analysis would be much less tractable computationally, would be less efficient when a new dataset is added, would pose severe problems of normalization among studies, and would be more prone to artifacts, because a small number of data points can greatly affect the correlation coefficient. Even in fields as diverse as particle physics (Brumfiel, 2012; Tonelli, 2013) and clinical drug development (Ioannidis, 2005; Moonesinghe et al., 2007; Casadevall and Fang, 2010; Guidance, 2010), performing multiple studies is considered a source of stronger evidence compared to pooling all resources in a single giant study.

Supplementary Figure 6S shows that networks obtained from individual datasets tend to behave similarly to the combined networks, but for several measures statistical significance was not reached at the individual level, showing the benefit of data integration.

The analysis of reproducibility in different datasets, which we call “overlap analysis,” can also provide a quantitative estimate of the probability of an interaction, based on the number of datasets in which it has been found. Figure 4B shows that, within a group with the same reproducibility measure (that is containing interactions found in the same number of datasets), the value of the correlation coefficient for an interaction could predict the probability of being identified again when additional datasets were analyzed. As shown in Figure 4A, the same was true when comparing different groups. It is therefore clear that determining which interactions to include in the network is a trade-off between maximizing the confidence in the included interactions and building a network too sparse to have sufficient statistical power for meaningful analysis. The use of a weighted network is an alternative strategy that might allow the appropriate inclusion of a larger number of links (Barrat et al., 2004).

The clustering analysis identified gene functions that are consistent with the tissue of origin of AML. The differences of AML versus normal cells gene expression for these clusters were also in the expected direction; for example, glycolysis is well known to be upregulated in cancer cells.

Among the findings supporting the biological relevance of AML 2.1 are the observations that the network is significantly enriched for common known AML driver-mutated genes (Lawrence et al., 2014) and that the mutation subnetwork is enriched for important cancer-related functions. Most notable among these are cell cycle-related genes, presently one of the most active fields of drug development in many cancer types (Malumbres and Barbacid, 2009; Diaz-Moralli et al., 2013).

The network properties of AML mutations we report are potentially useful for the understanding and therapy of cancer. It seems that mutated cancer genes not only are related to the functional categories we know well (Vogelstein et al., 2013) but also have network properties of efficient communication among the set and of centrality, therefore being able to influence many other cell functions. They do not form a close cluster, where the genes preferentially interact only among themselves. The centrality findings we obtained are consistent with previous reports of the relevance of PageRank network measures to the identification of cancer biomarkers (Winter et al., 2012).

The targets shown in Tables 10 and 11 were identified using both the AML 2.1 network properties and the KIEN analysis of experimental drug response data from AML primary cells. The four targets with higher statistical significance were CDK1, CDK2, CDK4, and CDK6. CDK 4/6 inhibitors have been shown to be effective in phase II cancer clinical trials, some of which were presented at the ASCO and AACR 2014 meetings (Brower, 2014). One of these CDK 4/6 inhibitors, palbociclib, has received the “breakthrough therapy” designation by the FDA (Sherman et al., 2013), which is intended to lead to accelerated approval. Several articles have also shown that CDK inhibitors are effective in AML cells (Wang et al., 2007; Walsby et al., 2011; Keegan et al., 2014; Placke et al., 2014).

The other targets shown in Tables 10 and 11 have also all been previously linked to AML and, in some cases, to cell cycle genes. LCK and LYN are part of the SRC family, and CSK is a kinase acting on SRC. SRC family kinases have been implicated in AML by several authors (Robinson et al., 2005; Okamoto et al., 2007) and are targets of Dasatinib, which has been shown to be active on AML cells (Dos Santos et al., 2013). LCK is also known to interact with and being phosphorylated by CDK1 (Pathan et al., 1996). TYRO3 expression has been associated with AML (Linger et al., 2008) and the expression of his ligand identifies high-risk AML patients (Whitman et al., 2014). CHEK1 is another important cell cycle gene and suggested target for cancer therapy (Lapenna and Giordano, 2009), which has been shown to sensitize AML cells to cytarabine action in an RNAi screen (Tibes et al., 2012). CHUCK (also known as IKK-alpha) is part of the cell cycle regulatory network together with CHEK1 (Barre and Perkins, 2007) and also contributes to the regulation of cell death in AML cells (Grosjean-Raillard et al., 2009). RPS6KA1 has been suggested as one of the mediators of the anti-apoptotic action of FLT3, one of the main AML mutations (Yang et al., 2005). Finally, MAP2K2 (also known as MEK2) has a very important role in regulating CDK4/6 activity (Ussar and Voss, 2004) and is often activated in AML cells (Morgan et al., 2001).

The potential of the combined use of AML 2.1 analysis and KIEN is not simply to provide a list of a few targets to be completely inhibited. We can actually identify the optimal amount of inhibition of each target, which corresponds to the coefficients of the KIEN regression equation, for a large number of kinases. This can potentially lead to the type of precise and robust distributed control that is common in biology [e.g., by transcription factors or microRNAs (Feala et al., 2012)] but until now not in pharmacology. The kinase response in vitro of primary cells is, however, in part influenced by the culture conditions, which differ from the in vivo microenvironment (Tiziani et al., 2013), and obtaining additional independent confirmation using the AML 2.1 network properties is extremely useful.

This combined approach can also be used for personalized therapy. We show that useful data using hundreds of kinase inhibitors can be obtained using primary cells, and even more precise individual targeting information could be obtained using the larger libraries [composed of up to thousands profiled kinases (Feala et al., 2012)] that several pharma companies have at their disposal. This would represent a dynamic molecular profiling of leukemic cell response, potentially much more valuable than the static snapshot of present omics techniques. The network could also be personalized further, for example, by using individual gene expression data to prune not significantly expressed gene and by giving a greater weight to mutations from a single patient and to their first neighbors within the network. An optimal kinase inhibitor combination could therefore be designed computationally (Tran et al., 2014), even in cases when the mutations would not be actionable, and then verified further by appropriate systematic testing using patient's cells (Feala et al., 2010; Kang et al., 2014).

While our increasing appreciation of the heterogeneity of cancer mutations (Wheeler and Wang, 2013), both between and within patients, is a cause of concern for the development of generally effective therapies, the identification of their shared pattern of connections raises the hope that sufficiently large and precisely calibrated combinatorial therapies designed along the principles we have discussed might benefit a wide range of patients.

The network could also be used to identify the receptors likely to have the largest effects on AML cell viability. The most connected receptors include some with well-known effects in AML cells, supporting the relevance of the network model. Among these are several interleukin receptors and the interferon gamma receptor. The top two receptors for connectivity (degree) and other network properties are VDR and RXRA. The ligands for these receptors, vitamin D3 and retinoic acid, have in fact well-known effects on AML cell proliferation and differentiation (Nowak et al., 2009; Hughes et al., 2010).

As we mentioned in the Introduction, we suggest that network reconstruction should also be socially scalable, in the sense of facilitating the integration of information from scientists of different backgrounds. This would be made easier by the adoption of the open-source model for the continuous improvement of the networks and of the related software. Open-source software is written by many (up to thousands) volunteer computer programmers publicly sharing and reviewing their work in real time as part of a self-organized community (Weber, 2004). Several fields of software development have seen the emergence of very successful open-source approaches (Weber, 2004), for example, the operating system Linux and the web server application Apache (Weber, 2004).

We report data comparing the method used for AML 2.1 with other common methods for network reconstruction (Basso et al., 2005; Meyer et al., 2008; Huynh-Thu et al., 2010; Haury et al., 2012). It is reasonable to conclude that, since all methods share most validated interactions found in our test, they might be considered as roughly equivalent, and it is certainly possible that combining multiple methods might be useful (Seni and Elder, 2010; Marbach et al., 2012a). We would need to understand more about the biological significance of the interactions that are uniquely found by each method to do a more precise comparison. Additionally, it is also possible that after adding more data all methods will eventually find essentially the same set of interactions. It is clear, however, from the run-time analysis (see also Supplementary Materials) and from considering the computational steps each method performs that the method described here is much faster. It has also been designed to be especially scalable, because most calculations do not need to be repeated when a new dataset is added. In addition, the portion of the method based on reproducibility in multiple datasets (the “overlap analysis”) is also applicable to other network reconstruction strategies.

It has been stated by leaders in artificial intelligence and data mining that “invariably, simple models and a lot of data trump more elaborate models based on less data” (Halevy et al., 2009; Mayer-Schonberger and Cukier, 2013). Thus, a case might be made for considering as our top priority the analysis of all existing gene expression datasets with the fastest and most scalable method that gives a reasonable performance in network reconstruction. We have shown that very useful information can be obtained in a study using only five datasets and it seems that we are not doing all we can for cancer patients if we leave existing data unutilized.

The present versions of the networks do not indicate if targets should be inhibited or stimulated to achieve a therapeutic effect. In the case of the kinases shown in Tables 10 and 11, we have been able to establish this using further experimental tests. The networks are, however, a framework that can be integrated with additional information derived, for example, from pathways databases like KEGG or from algorithms based on differential expression data. Examples of algorithms integrating differential expression information are MARINa (Lefebvre et al., 2010) and attractor-based signaling methods (Szedlak et al., 2014).

Planned future additions to the network include the use of HIPPIE (Schaefer et al., 2012), with the same optimization role for PPI as that played by TRANSFAC (Wingender, 2008) for TFG (expected in version 3) and the addition of microRNA–target interactions and of metabolic networks (Thiele et al., 2013) (expected in version 4). We also intend to use more AML datasets (potentially all published ones) and to explore subtypes of this acute leukemia, including pediatric AML. We then plan to extend the approach to other leukemias and eventually to other cancers and to other diseases. It will also be important to develop network models for normal cell types to assist the design of selective therapies with reduced toxicity. This will allow the development of comparative network analysis. For example, the evaluation of the general relevance of the network properties we describe for the AML mutations will be possible only when networks for many different cancer types are reconstructed using comparable methods.

We therefore present a fast and scalable method for the reconstructions of intracellular networks that can contribute to the understanding of the network role of cancer mutations and to the identification of targets for therapeutic interventions, also in combination with complementary statistical analyses of experimental data.

Acknowledgments

This work has been supported by NIH Grant R41CA174059 and NSF Grant IIP-1346482.

Author Disclosure Statement

C.P. and G.P. own equity in Salgomed Inc. The remaining coauthors have no competing financial interests.