Evidence for tunneling in base-catalyzed isomerization of glyceraldehyde to dihydroxyacetone by hydride shift under formose conditions

Significance

This paper describes experimental and computational evidence that the hydride shift that converts glyceraldehyde to dihydroxyacetone at basic pH with Ca²⁺ catalysis proceeds primarily by quantum tunneling. This answers the last question about the mechanism of the formose reaction, in which formaldehyde is converted to higher sugars under these conditions. This reaction has long been seen as an important clue to the formation of molecules needed for life under prebiotic conditions on Earth. Earlier work showed that the mechanism involved a hydride shift, not a deprotonation, and this work confirms those conclusions. It shows the critical role of tunneling, a quantum effect important in chemistry and biology, and in likely prebiotic reactions on Earth or elsewhere, one concern of astrobiology.

Abstract

Hydrogen atom transfer reactions between the aldose and ketose are key mechanistic features in formose chemistry by which formaldehyde is converted to higher sugars under credible prebiotic conditions. For one of these transformations, we have investigated whether hydrogen tunneling makes a significant contribution to the mechanism by examining the deuterium kinetic isotope effect associated with the hydrogen transfer during the isomerization of glyceraldehyde to the corresponding dihydroxyacetone. To do this, we developed a quantitative HPLC assay that allowed us to measure the apparent large intrinsic kinetic isotope effect. From the Arrhenius plot of the kinetic isotope effect, the ratio of the preexponential factors A_H/A_D was 0.28 and the difference in activation energies E_a(D) − E_a(H) was 9.1 kJ·mol⁻¹. All these results imply a significant quantum-mechanical tunneling component in the isomerization mechanism. This is supported by multidimensional tunneling calculations using POLYRATE with small curvature tunneling.

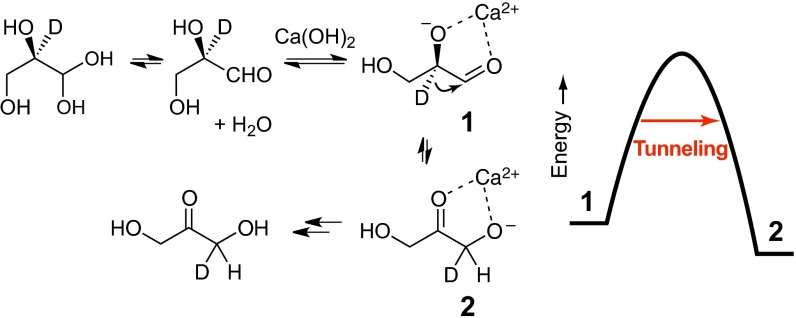
We have described a new mechanism for the formose reaction (Fig. 1) (1), essentially the same as we had proposed earlier (2) except that the isomerizations of aldose to ketose and the reversal involve a hydride shift rather than an enolization (3–7). Our evidence came from the finding that 2-deuteroglyceraldehyde was converted to 1-deuterodihydroxyacetone under conditions of the formose reaction, with catalysis by Ca²⁺ at pH 12. In 2001 Nagorski and Richard had reported an extensive study of the interconversion of glyceraldehyde and dihydroxyacetone by either enolization or hydride shift and had seen that with Zn²⁺ the hydride shift mechanism was the exclusive process, by a mechanism closely related to our more recent one (8). We also showed that the isomerization of the ketose erythrulose to the aldose aldotetrose in D₂O did not lead to deuterium incorporation, as it would have in an enolization process, so it also uses the hydride shift mechanism (1). The first study of the formose reaction in D₂O was performed by Benner, who saw that no deuterium was incorporated in the intermediates; for some reason he did not invoke hydride shift mechanisms (6).

Fig. 1.

Hydride shift mechanism for the isomerization of glyceraldehyde to dihydroxyacetone.

It should be mentioned that we saw that the presence of formaldehyde in the formose reaction in D₂O led to trapping of any enols formed; without formaldehyde, as in our previous study, there is subsequent deuterium incorporation in dihydroxyacetone, but not significant in glyceraldehyde. We saw that the glyceraldehyde was present almost entirely as its hydrate, a gem diol, but dihydroxyacetone was present mainly as the ketone. This reverses the normally accepted enolization relative rates.

Materials and Methods

In a hydride shift the distance traveled by the proton is small, comparable to the range of its wave character, so we have investigated the possibility that there is a quantum-mechanical tunneling process involved (9). We find that there is indeed tunneling accompanying thermal excitation on the way to the TS (Fig. 1). Useful criteria for tunneling have been proposed by Kim and Kreevoy (10, 11) and have been widely used by Klinman et al. in several different enzyme systems (12, 13). The important criteria are: (i) an activation energy difference E_a(D)−E_a(H) > 5.0 kJ·mol⁻¹, and (ii) a ratio of Arrhenius pre-exponential factors A_H/A_D < 0.7. Borden and Singleton and coworkers have recently emphasized the importance of A factor ratios and isotopic differences in E_a as experimental criteria for tunneling (14–16), although the numerical criteria depend on the type of reaction. The Kreevoy criteria are based on a collinear model of H-transfer. For application to a 1,2-H shift, the E_a(D)−E_a(H) criterion should be reduced to reflect the smaller loss of C-H/C-D zero point energy (ZPE) in the bent transition state (TS) (14). Nevertheless, the results reported here greatly exceed the Kreevoy criteria.

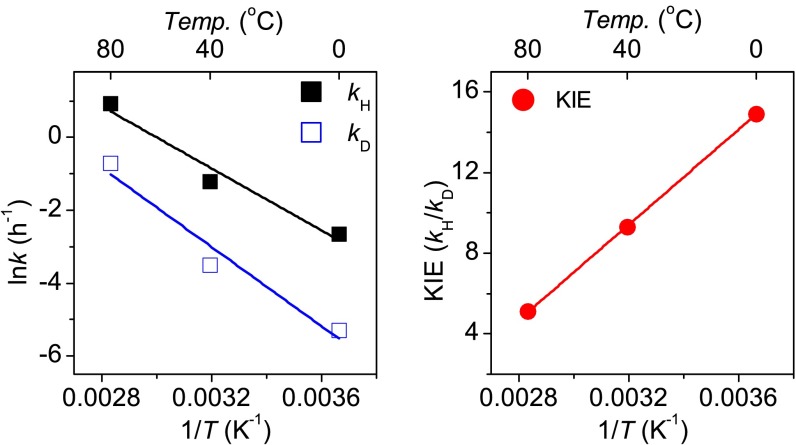
We studied the rates of conversion of 2-protioglyceraldehyde and 2-deuteroglyceraldehyde to dihydroxyacetone at three temperatures, 0 °C, 40 °C and 80 °C ± 1 °C by converting the products and starting materials to their 2,4-dinitrophenylhydrazones (2,4-DNPH) and using a quantitative HPLC assay with acetone 2,4-dinitrophenylhydrazone (Ac-2,4-DNPH) as an internal standard. We carried the reactions to only 5–10%, where the data (Table 1) fit straight lines (Fig. 2). Each point for a rate constant represents the average of at least three independent experiments. The reaction was performed with 1.0 mM glyceraldehyde, 0.6 mM Ca(OH)₂ at pH 10. The recovered 2-deuteroglyceraldehyde after 40% conversion, as its 2,4-DNPH derivative, showed 95% of one deuterium, close to that in the starting material (98%), so almost no deuterium was lost during the isomerization or the 2,4-DNPH formation.

Table 1.

Kinetic rate constants and KIEs for the isomerization of glyceraldehydes to dihydroxyacetone

Temp, °C	kH (h−1)*	kD (h−1)*	KIE (kH/kD)†
0	0.07 ± 0.02	0.005 ± 0.001	14.9 ± 4.0
40	0.30 ± 0.02	0.03 ± 0.01	9.3 ± 2.6
80	2.52 ± 0.44	0.49 ± 0.23	5.1 ± 1.8

Conditions: glyceraldehyde 1 mM, Ca(OH)₂ 0.6 mM, pH 10.

^*Results ± SEM are the average of at least three independent experiments.

^†KIE values were calculated based on unrounded rate constants.

Fig. 2.

Arrhenius plots of 2-protioglyceraldehyde (Left, filled black squares), 2-deuteroglyceraldehyde (Left, open blue squares), and intrinsic KIEs (Right, filled red circles) on the hydride transfers. The intrinsic KIEs were fitted to the Arrhenius equation (SI Appendix, Eq. S3) to obtain an isotope effect on the energy of activation [E_a(H), E_a(D)] and on the preexponential factors (A_H, A_D). Each point represents the average of at least three independent experiments. See SI Appendix for experimental details.

The kinetic isotope effects (KIEs) in Table 1 are substantial, and may indicate tunneling. E_a values were obtained from the slopes in the plots of lnk vs. 1/T in Fig. 2 using the Arrhenius equation k = A exp(−E_a/RT) (9). E_a(H) was 35.4 kJ·mol⁻¹ while E_a(D) was 44.5 kJ·mol⁻¹, so the difference of 9.1 kJ·mol⁻¹ is well in excess of 5.0 kJ·mol⁻¹, consistent with a tunneling process. For the second criterion, the ratio A_H/A_D was 0.28 (A_H = 97.9, A_D = 344.2), much less than 0.7, which implies tunneling.

This suggestion is supported by ample precedent for tunneling in 1,2-H shifts, particularly in carbenes (17–27), and also in cyclopentadienes (14). The barriers in these reactions vary from ca. 20–130 kJ·mol⁻¹. The number of examples suggests that tunneling in the formose reaction is not unreasonable.

Experimental and computational details, and full publication information for refs. 28, 29, can be found in SI Appendix, Material and Methods.

Computational Results and Discussion

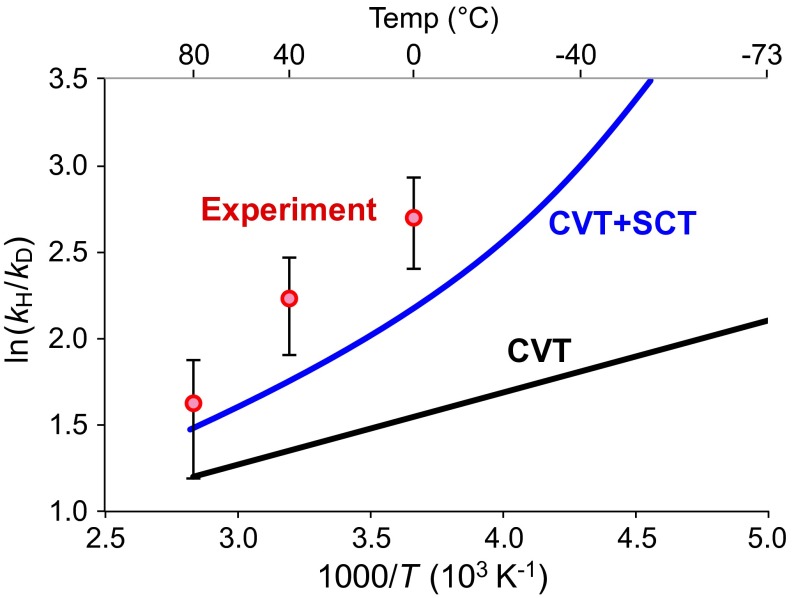
For a quantitative assessment of tunneling in the H-transfer step 1 → 2 in Fig. 1, we carried out calculations with POLYRATE (28), with the GAUSSRATE (30) interface to Gaussian 09 (29). Of the 27 density functionals tested, all overestimated E_a. The best compromise description of KIEs and E_a was given by the B3LYP density functional and 6–31++G** basis set (29) with polarized continuum model water solvation (31), with CCSD(T)/6–31++G** energy corrections (coupled cluster with single, double, and noniterative triple excitations) according to the interpolated single-point energies procedure in POLYRATE. The forward barrier is ΔH^‡ = 79.5 kJ·mol⁻¹ at 298 K, and Δ_rH° = −2.7 kJ·mol⁻¹. The rate constant without tunneling, k_CVT, is computed by canonical variational transition state theory (CVT). Multidimensional tunneling was computed by small curvature tunneling (SCT). (We examined both SCT and large curvature tunneling. SCT gives the greater amount of tunneling.) The rate constant including SCT tunneling is given by k_CVT+SCT = κ_SCT k_CVT, where κ_SCT is the SCT transmission coefficient.

The Arrhenius E_a(H) and E_a(D) for 1 → 2 computed over 0–80 °C are, respectively, 74.4 and 80.8 kJ·mol⁻¹. The difference is 6.4 kJ·mol⁻¹, in moderate agreement with experiment. The computed A_H/A_D is 0.43, and the A factors of ∼10^12.7 are in the typical unimolecular range. The observed A values of ∼10² are consistent with a large loss of entropy in forming 1 from glyceraldehyde hydrate, which was not pursued.

Fig. 3 shows Arrhenius plots of ln(KIE) vs. 1,000/T for experiment (red), and KIEs computed in the absence of tunneling (black) and inclusion of SCT tunneling (blue). [KIEs computed by CVT and CVT+SCT include a small contribution from the equilibrium isotope effect for conversion of glyceraldehyde hydrate to 1. For this equilibrium, Δ_rG°_(D) – Δ_rG°_(H) is nearly constant at 0.4 kJ/mol and is due almost entirely to enthalpy. The additive contribution to ln(KIE) in Fig. 3 ranges from 0.25 at 200 K to 0.14 at 353 K.] Whereas neither calculation agrees quantitatively with experiment, CVT+SCT is much closer than CVT. The CVT+SCT line curves upward at lower temperature where tunneling makes a greater contribution to the rate. This has been reported in other reactions in which tunneling is important (16, 32). The current calculations provide computational evidence in Fig. 3 and Table 2, amplified in SI Appendix, that tunneling dominates the reaction.

Fig. 3.

Arrhenius plots of ln(KIE) vs. 1,000/T for the H-transfer step in Fig. 1, computed by POLYRATE with the GAUSSRATE interface to Gaussian, using B3LYP/6–31++G** with PCM water solvation. Red: experimental points ± 1 SD; black: computed by canonical variational transition state theory (CVT); blue: computed by CVT+SCT.

Table 2.

CVT+SCT hydride transfer characteristics

Temp, °C	KIE*	% tun†	$E_{{\text{max}}^{\mathsf{‡}}}^H$	$E_{{\text{max}}^{\mathsf{‡}}}^D$
−73	87 (6.3)	99	43.1	72.7
−40	19 (4.9)	93	65.7	77.4
0	8.7 (3.9)	80	73.0	78.9
40	5.8 (3.3)	67	74.7	79.6
80	4.4 (2.9)	56	75.4	79.6

^*k_H/k_D computed by CVT+SCT (CVT KIEs in parentheses).

^†% tunneling = (κ_SCT – 1)/κ_SCT (shown for H only).

^‡Energy (kJ·mol⁻¹) at which H and D tunneling makes the maximum contribution to κ_SCT, relative to the ZPE-corrected energy of 1_H and 1_D as the zero of energy. H and D ZPE-corrected barriers are, respectively, 80.0 and 83.1 kJ·mol⁻¹.

Table 2 shows some important features of the reaction. The KIE predicted by CVT is only 2.9–3.9 over 0–80 °C, because in this bent TS the difference between H and D ZPE loss at the TS is only 3.1 kJ·mol⁻¹, less than the 5 kJ·mol⁻¹ expected for a linear TS (10, 11). The contribution of SCT tunneling to the rate can be estimated as (κ_SCT – 1)/κ_SCT. (More precisely, this is the fraction of the rate contributed by the quantum correction to motion along the reaction path, including transmission and reflection.) In the third column (% tunneling), these contributions range from 56% at 80 °C to 99% at −73 °C. These are similar to the contributions of CVT+SCT tunneling reported by Borden and coworkers for 1,5 sigmatropic H shifts in cyclopentadienes (14). Because the current calculation underestimates the KIEs, this column is effectively a lower bound on the contribution of tunneling.

With a large computed tunneling contribution, should Arrhenius curvature be expected at 0–80 °C? Curvature would require that the energy region over which tunneling contributes to the transmission coefficient change substantially over the experimental temperature range. The last two columns of Table 2 give the energies $E_{\max }^{\text{H}}$ and $E_{\max }^{\text{H}}$ (relative to 1_H and 1_D as the zero of energy) at which tunneling makes its maximum contribution to κ_SCT. These energies are nearly constant over 0–80 °C, consistent with a lack of obvious curvature in this temperature range, even though the tunneling contribution is large. Table 2 suggests that curvature would begin to appear around −40 °C, as $E_{\max }^{\text{H}}$ decreases by more than 7 kJ·mol⁻¹ below $E_{\max }^{\text{H}}$ at 0 °C. SI Appendix, Fig. S8 makes this clearer by showing that the entire H-tunneling region shifts dramatically to include a much larger fraction of the barrier at −40 °C than at 0 °C.

Conclusion

Our conclusion is that there is a large tunneling contribution to the hydride shift for 1 → 2 (Fig. 3). The calculations imply that at least 56–80% of the reaction occurs by tunneling over 0–80 °C. This description applies to high pH where the coordination of a calcium ion to the carbonyl group and the alkoxide ion make the hydride migration the only chemical step. It is likely that this is also true in the proposed isomerization of a ketose to an aldose in the later step of the formose reaction under those conditions. However, at neutral pH with no metal ion such a migration would need to accompany the motion of a proton in a hydrogen bond between the hydroxyl and the carbonyl, as perhaps in the triose phosphate isomerization in biochemistry. Such situations require their own investigations.