Abstract
Ab initio and density functional theory-based computations are performed to investigate the structure and stability of H3SiNgNSi and HSiNgNSi compounds (Ng = Xe, Rn). They are thermochemically unstable with respect to the dissociation channel producing Ng and H3SiNSi or HSiNSi. However, they are kinetically stable with respect to this dissociation channel having activation free energy barriers of 19.3 and 23.3 kcal/mol for H3SiXeNSi and H3SiRnNSi, respectively, and 9.2 and 12.8 kcal/mol for HSiXeNSi and HSiRnNSi, respectively. The rest of the possible dissociation channels are endergonic in nature at room temperature for Rn analogues. However, one three-body dissociation channel for H3SiXeNSi and one two-body and one three-body dissociation channels for HSiXeNSi are slightly exergonic in nature at room temperature. They become endergonic at slightly lower temperature. The nature of bonding between Ng and Si/N is analyzed by natural bond order, electron density and energy decomposition analyses. Natural population analysis indicates that they could be best represented as (H3SiNg)+(NSi)− and (HSiNg)+(NSi)−. Energy decomposition analysis further reveals that the contribution from the orbital term (ΔEorb) is dominant (ca. 67%–75%) towards the total attraction energy associated with the Si-Ng bond, whereas the electrostatic term (ΔEelstat) contributes the maximum (ca. 66%–68%) for the same in the Ng–N bond, implying the covalent nature of the former bond and the ionic nature of the latter.
Keywords: ab initio study, dissociation channels, kinetic stability, natural population analysis, electron density analysis, energy decomposition analysis
1. Introduction
Having a late break-through in 1962 with the discovery of Xe+[PtF6]−, chemistry related to the noble gas (Ng) compounds has been developing very rapidly, especially during the last two decades. This is due to the outcome of the huge efforts made by both experimentalists [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19] and theoreticians [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46] towards the syntheses and/or predictions of stable Ng-containing compounds. The first compound having the Xe–C bond was reported as XeCH3+ many years ago in 1961 by Field et al. [47], and the very next year, the same group [48] detected ArCH3+ and KrCH3+ in mass spectrum. A few years later in 1979, Turbini et al. [49] detected Xe(CF3)2 by means of mass spectroscopic techniques. Subsequently, detection of a few pentafluorophenylxenon cation [50,51,52] derivatives was also reported in 1989. Thereafter, plenty of examples with Ng–C bonds, viz. HXeCCH [53,54,55], HKrCCH [55], HXeCC [53,55], HXeCCXeH [53,55], HXeCN [5], HKrCN [5], HNgCCF [56], HCCNgF [56], ClXeCN [57], BrXeCN [57], HXeC3N [58], HKrC3N [58], HXeC4H [11] and HKrC4H [11], were made available in the literature as experimentally-detected compounds using a low temperature matrix-isolation technique. Moreover, several theoretically-predicted compounds with Ng–C bonds, some unusual highly-coordinated Ng(CCH)4 and Ng(CCH)6 clusters (Ng = Kr, Xe) [59] and polymer, H–(Xe–C2)n–Xe–H (n ≥ 1) [60], were found to be metastable species.
On the other hand, there are only a few examples of the systems having Si-Ng bonds, which were experimentally obtained or theoretically predicted to be viable. The generation of the F3SiXe+ by Grandinetti et al. [61] in an ion-molecule reaction between the protonated SiF4 and Xe, F3Si–FH+ + Xe → Xe–SiF3+ + HF, provided the first system with the Si–Ng bond. Through so-called direct addition of SiF3+ and Ng, Cunje et al. [62] were successful in producing not only XeSiF3+, but also ArSiF3+ and KrSiF3+ at room temperature and high pressure. Two other isomers of NgSiF3+ with Si–Ng–F and F–Ng–F types of linkages were also proposed [62]. The metastability of the first neutral compound, FArSiF3, with the Si–Ar chemical bond, was predicted by Cohen et al. [63]. Prompted by this study, Yockel et al. [64] found viable FKrSiF3 as the first example having the Si–Kr bond in a neutral system. Lundell and coworkers [65] further assessed the stability and bonding of FXeSiF, the first neutral compound with the Si–Xe covalent bond. Roithová et al. [66] showed that SiF32+ could behave as a superelectrophilic reagent and that NgSiF22+ (Ng = Ne, Ar) could be formed as a result of the thermal ion-molecule reaction, F3Si2+ + Ng → NgSiF22+ + F. Recently, Savoca et al. [67] detected Si4Xe+ via infrared (IR) multiple photon dissociation spectroscopy. More recently, we studied the Ng binding ability of the SiH3+ cluster, as well as the effect of H substitution of SiH3+ by halide groups (–X) on its ability in binding Ng [68].
In this manuscript, we have reported two new viable compounds, H3SiNgNSi and HSiNgNSi (Ng = Xe, Rn), with Si-Ng covalent bonds. Crabtree and coworkers [69] very recently detected highly stable silicon nitrides, H3SiNSi and HSiNSi by chirped-pulse Fourier transform microwave (CP-FTMW) spectroscopy. H3SiNSi has a C3v point group symmetry with a linear Si–N–Si moiety, whereas HSiNSi possesses a planar geometry (Cs) with a slightly bent Si–N–Si arrangement, and for both of them, the minimum energy structures have a singlet spin state. We have assessed in silico the structure, stability and the nature of bonding in H3SiNgNSi and HSiNgNSi compounds. They are found to be metastable systems. The nature of bonding therein is analyzed by natural population analysis (NPA), Wiberg bond indices (WBI) calculation [70], electron density analysis [71] and energy decomposition analysis (EDA) [72,73,74,75]. It may be noted that except for RnSiX3+ (X = H, F–Br) [68], there is no study with the compound having the Si-Rn bond. In that sense, for the first time, we reported here the neutral Rn-containing compounds, H3SiRnNSi and HSiRnNSi, with the Si–Rn covalent bond.
2. Results and Discussion
2.1. Structure and Stability
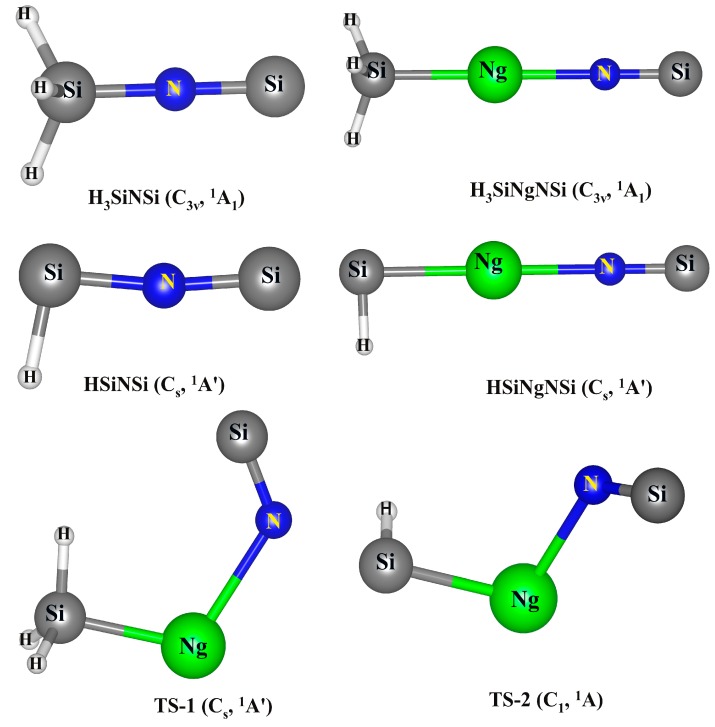
The optimized geometries of H3SiNSi and HSiNSi compounds and their Ng inserted analogues, H3SiNgNSi and HSiNgNSi, are provided in Figure 1. Similar to their mother moieties, the minimum energy structure of H3SiNgNSi corresponds to the C3v point group with the 1A1 electronic state, whereas HSiNgNSi has a planar geometry with the Cs point group and 1A' electronic state. On the other hand, the transition states (TSs) corresponding to the dissociations of H3SiNgNSi and HSiNgNSi into Ng and H3SiNSi or HSiNSi have Cs (TS-1 in Figure 1) and C1 (TS-2 in Figure 1) symmetry, respectively, in which the NSi fragment remains attached with H3SiNg or HSiNg fragments in a tilted fashion. The geometrical parameters of H3SiNgNSi and HSiNgNSi compounds obtained at the ωB97X-D/def2-QZVPPD and CCSD(T)/def2-TZVP levels are provided in Table S1 (Supplementary Information), whereas the same for the minimum energy and TS structures of H3SiNgNSi and HSiNgNSi obtained at the MP2/def2-QZVPPD level are given in Table 1. The geometrical parameters of H3SiNSi and HSiNSi are also provided in Table S2 (Supplementary Information). The Si–Ng bond distance in H3SiNgNSi is somewhat shorter than that in HSiNgNSi. This may be due to the positive charges on the Ng centers in H3SiNgNSi and HSiNgNSi compounds. The positive charge on the Ng center in H3SiNgNSi (+0.61 |e| on Xe and +0.68 |e| on Rn) is larger than that in HSiNgNSi (+0.50 |e| on Xe and +0.57 |e| on Rn). The chemical inertness of Ng atoms originates from the filled valence shell. Hence, a more positively-charged Ng center would be more effective in taking part in chemical bond formation. The larger interaction energy between H3Si and NgNSi than that between HSi and NgNSi corroborates well with the stronger bond formation in the former cases than the latter ones (vide infra).
Figure 1.
Pictorial depictions of the energy minimum structures and the transition states (TSs) of H3SiNSi, HSiNSi, H3SiNgNSi and HSiNgNSi compounds. Point groups along with their electronic states are given in parentheses. TS-1 and TS-2 are associated with the dissociation of H3SiNgNSi and HSiNgNSi, producing Ng and H3SiNSi or HSiNSi.
Table 1.
The geometrical parameters (in Å and degrees) of the optimized geometries of H3SiNgNSi and HSiNgNSi compounds (both minimum energy structures and transition states) studied at the MP2/def2-QZVPPD level.
| Nature of Stationary Points | Compounds | rH–Si | rSi–Ng | rNg–N | rN–Si | <H–Si–Ng | <Si–Ng–N | <Ng–N–Si |
|---|---|---|---|---|---|---|---|---|
| Minimum | H3SiXeNSi | 1.471 | 2.588 | 2.338 | 1.600 | 107.0 | 180.0 | 180.0 |
| Energy | H3SiRnNSi | 1.472 | 2.688 | 2.382 | 1.598 | 107.8 | 180.0 | 180.0 |
| Structures | HSiXeNSi | 1.508 | 2.653 | 2.375 | 1.603 | 88.7 | 179.5 | 178.6 |
| HSiRnNSi | 1.510 | 2.747 | 2.420 | 1.601 | 89.0 | 179.7 | 179.9 | |
| Transition | H3SiXeNSi | 1.462(3) | 2.486 | 2.683 | 1.616 | 103.9, 99.5 | 110.6 | 126.2 |
| States | H3SiRnNSi | 1.463(5) | 2.573 | 2.733 | 1.616 | 104.1, 99.3 | 103.7 | 125.9 |
| HSiXeNSi | 1.504 | 2.511 | 2.576 | 1.626 | 87.6 | 100.7 | 125.6 | |
| HSiRnNSi | 1.505 | 2.590 | 2.623 | 1.625 | 87.7 | 96.0 | 125.5 |
The N–Si bond gets slightly elongated in the Ng inserted analogues compared to those in H3SiNSi and HSiNSi. The Si–Ng–N and Ng–N–Si moieties in the H3SiNgNSi compound are linear. However, the same in the HSiNgNSi compound are slightly bent from the linear arrangement (≤0.5°). Since in TS-1 and TS-2, the NSi fragment is bonded to the Ng center in a tilted fashion, having the mode with imaginary frequency as the bending of Si–Ng–N and Ng–N–Si angles, the <Si–Ng–N and <Ng–N–Si get shortened (96.0°–126.2°) compared to those in the corresponding minimum energy structures (~180.0°). In the TSs, the Si–Ng bond distance is found to decrease by about 0.1 Å, while the Ng–N bond distance increases by 0.3–0.2 Å compared to those in the corresponding minimum energy structures.
The stability of these Ng inserted compounds is understood by computing ZPE-corrected dissociation energy (D0), as well as dissociation enthalpy (ΔH) and free energy change (ΔG) at 298 K for different possible dissociation channels. We have considered the higher spin states of all of the dissociated products. The spin state, which gives the lowest energy, is taken into consideration. We have computed ΔG values for the different possible dissociation channels of H3SiNgNSi and HSiNgNSi at both the MP2/def2-QZVPPD (see Table S3 in the Supplementary Information) and ωB97X-D/def2-QZVPPD levels (see Table 2), and those for the D0 and ΔH are given in Tables S4 and S5 (Supplementary Information). We found that the D0, ΔH and ΔG values obtained at the MP2 level are larger than those obtained at the ωB97X-D level in most cases, particularly in Xe analogues. In some cases, this provides qualitatively wrong results. For example, with respect to most of the dissociation channels, the Xe inserted compounds are less likely to be dissociated than those of the Rn analogues, implying larger stability of the former compounds than the latter ones. However, in general, it is expected that due to larger polarizability, Rn would make a somewhat stronger bond than that of Xe. It was already reported in the literature that the MP2 level of computation can produce inaccurate dissociation energy diagrams for the Ng inserted compounds [76]. Our results corroborate that the stability of Ng inserted compounds should not be analyzed based on MP2 results alone. Therefore, we have given special emphasis to the results obtained at the ωB97X-D level to assess the stability of these studied compounds with respect to the different dissociation channels.
Table 2.
Free energy change (ΔG, kcal/mol) at 298 K for different dissociation channels of H3SiNgNSi and HSiNgNSi compounds at the ωB97X-D/def2-QZVPPD level.
| Processes | ΔG | Processes | ΔG | ||
|---|---|---|---|---|---|
| Xe | Rn | Xe | Rn | ||
| H3SiNgNSi → H3SiNg+ + NSi− | 105.3 | 110.7 | HSiNgNSi → HSiNg+ + NSi− | 99.1 | 103.8 |
| H3SiNgNSi → H3Si− + NgNSi+ | 165.2 | 166.1 | HSiNgNSi → HSiNg + NSi | −3.6 | 3.8 |
| H3SiNgNSi → H3SiNSi + Ng | −119.3 | −110.5 | HSiNgNSi → HSi− + NgNSi+ | 163.6 | 163.9 |
| H3SiNgNSi → H3Si + Ng + NSi | −0.2 | 8.6 | HSiNgNSi → HSiNSi + Ng | −121.1 | −113.0 |
| H3SiNgNSi → H3Si+ + Ng + NSi− | 122.0 | 130.8 | HSiNgNSi → HSi + Ng + NSi | −5.8 | 2.4 |
| H3SiNgNSi → H3Si− + Ng + NSi+ | 201.6 | 210.4 | HSiNgNSi → HSi+ + Ng + NSi− | 112.9 | 121.1 |
| H3SiNgNSi → H2Si + NgH + NSi | 64.4 | 73.0 | HSiNgNSi → HSi− + Ng + NSi+ | 199.9 | 208.1 |
| H3SiNgNSi → H2Si+ + NgH + NSi− | 206.6 | 215.2 | HSiNgNSi → Si + NgH + NSi | 87.7 | 95.7 |
| H3SiNgNSi → H2Si− + NgH + NSi+ | 271.9 | 280.6 | HSiNgNSi → Si + NgH+ + NSi− | 220.2 | 221.9 |
| H3SiNgNSi → H2Si + NgH+ + NSi− | 196.9 | 199.2 | ΔG‡a | 9.2 | 12.8 |
| H3SiNgNSi → H2Si− + NgH+ + NSi | 236.9 | 239.2 | − | − | − |
| H3SiNgNSi → HSi + HNgH + NSi | 149.4 | 149.8 | − | − | − |
| H3SiNgNSi → HSi+ + HNgH + NSi− | 268.1 | 268.4 | − | − | − |
| H3SiNgNSi → HSi− + HNgH + NSi+ | 355.1 | 355.5 | − | − | − |
| ΔG‡a | 19.3 | 23.3 | − | − | − |
ΔG‡a is the activation free energy barrier for the processes, H3SiNgNSi → H3SiNSi + Ng and HSiNgNSi → HSiNSi + Ng.
We have considered two-body (2-B) as well as three-body (3-B) dissociation channels comprising both neutral and ionic fragments. For H3SiNgNSi, except for the 2-B dissociation channel producing H3SiNSi and Ng, all other dissociation channels are endergonic in nature at room temperature. Though dissociation of H3SiNgNSi into H3SiNSi, and Ng is exergonic by −119.3 kcal/mol for Xe and −110.5 kcal/mol for Rn, the dissociation is kinetically protected by 19.3 and 23.3 kcal/mol for Xe and Rn analogues, respectively. For H3SiXeNSi, except this 2-B dissociation, another 3-B dissociation producing H3Si, Ng and NSi is slightly exergonic in nature (−0.2 kcal/mol) at room temperature. However, it becomes endergonic (2.6 kcal/mol) at a slightly lower temperature (250 K), as the contribution from the favorable ΔS term becomes smaller at a lower temperature.
In the case of HSiRnNSi, except for the dissociation into HSiNSi and Rn, all other dissociation channels are endergonic in nature. However, for HSiXeNSi, in addition to the dissociation into HSiNSi and Xe, two other 2-B and 3-B dissociations are slightly exergonic in nature at 298 K. In both Xe and Rn analogues, the dissociation producing HSiNSi and Ng is highly exergonic, being −121.1 kcal/mol for Xe and −113.0 kcal/mol for Rn. This dissociation is found to be kinetically protected by the free energy barrier of 9.2 kcal/mol for Xe and 12.8 kcal/mol for Rn analogues. The 2-B dissociation of HSiXeNSi producing HSiXe and NSi and the 3-B dissociation producing HSi, Xe and NSi are exergonic by −3.6 and −5.8 kcal/mol, respectively, at 298 K. We have computed ΔG values at a lower temperature and have found that at 180 K, ΔG values become slightly positive (0.5 and 0.2 kcal/mol for 2-B and 3-B dissociations, respectively), and at 150 K, it becomes 1.6 kcal/mol for the 2-B dissociation and 1.7 kcal/mol for the 3-B dissociation. It may be noted that activation free energy barriers obtained at the MP2 level are quite close to those obtained at the ωB97X-D level (see Table S3).
Hu and co-workers [77] argued that to have a half-life in the order of ~102 s at 100, 200 and 300 K, a system of type XNgY must have a minimum energy barrier of 6, 13 and 21 kcal/mol, respectively. Therefore, H3SiNgNSi could be detected at as high as a 250–300 K temperature range, whereas HSiNgNSi could be detected around the 150–200 K temperature range.
2.2. Nature of Bonding
The NPA charge at each atomic center and the WBI values of Si–Ng and Ng–N bonds are tabulated in Table 3. The H and N centers are electronegative in nature, while Si and Ng centers are electropositive in nature. The Si center attached to N (0.77–0.80 |e|) carries a slightly more positive charge than that of Si in the –SiH3 fragment (0.51–0.63 |e|). On the other hand, N attains a large negative charge of −1.50 |e| for Xe analogues and −1.52(4) |e| for Rn analogues. Note that the net charge on the NSi fragment ranges from −0.71 |e| to −0.75 |e|. Therefore, they could be best represented as (H3SiNg)+(NSi)− and (HSiNg)+(NSi)−. Obviously, the Ng–N bond would be of the ionic type. The low WBI values (~0.2) for the Ng–N bonds dictate their ionic nature of interaction. In contrast, the quite high WBI values (~0.65) for the Si–Ng bonds imply that the bonds are of the covalent type, and almost a single bond is formed therein.
Table 3.
Natural population analysis (NPA) charge on each atomic center (qk, au) and Wiberg bond indices (WBI) values of Si–Ng and Ng–N bonds computed at the MP2/def2-QZVPPD level.
| Compounds | qk | WBI | |||||
|---|---|---|---|---|---|---|---|
| H | Si | Ng | N | Si | Si–Ng | Ng–N | |
| H3SiXeNSi | −0.17 | +0.63 | +0.61 | −1.50 | +0.79 | 0.64 | 0.22 |
| H3SiRnNSi | −0.17 | +0.56 | +0.68 | −1.52 | +0.80 | 0.65 | 0.22 |
| HSiXeNSi | −0.33 | +0.56 | +0.50 | −1.50 | +0.77 | 0.63 | 0.18 |
| HSiRnNSi | −0.33 | +0.51 | +0.57 | −1.54 | +0.79 | 0.66 | 0.17 |
Electron density analysis [71] provides additional insight into the nature of bonding. Different topological descriptors of electron density and electron localization function (ELF) computed at the bond critical points (BCPs) of Si–Ng and Ng–N bonds are given in Table 4. The concentration and depletion of electron density at the BCPs are indicated by the negative and positive values of ∇2ρ(rc), respectively. In general, the occurrence of electron density concentration and depletion at the BCPs indicates the covalent and noncovalent type of bonding, respectively. However, many failures ([71,78,79,80,81,82,83] pp. 312–314) of this descriptor in representing a covalent bond, especially for the systems with heavy atoms, are documented in the literature. The local electron energy density (H(rc)), which is the sum of local kinetic energy density (G(rc)) and local potential energy density (V(rc)), is also commonly applied to interpret the nature of a bond.
Table 4.
Calculated topological properties (au) at the bond critical points of Ng–Si and Ng–N bonds obtained from the .wfn files generated at the MP2/def2-QZVPPD level.
| Compounds | ρ(rc) | ∇2ρ(rc) | G(rc) | V(rc) | H(rc) | ELF |
|---|---|---|---|---|---|---|
| H3Si__●__XeNSi | 0.078 | −0.093 | 0.016 | −0.055 | −0.039 | 0.868 |
| H3SiXe__●__NSi | 0.073 | 0.140 | 0.057 | −0.079 | −0.022 | 0.295 |
| H3Si__●__RnNSi | 0.075 | −0.061 | 0.018 | −0.051 | −0.033 | 0.824 |
| H3SiRn__●__NSi | 0.073 | 0.139 | 0.058 | −0.081 | −0.023 | 0.284 |
| HSi__●__XeNSi | 0.069 | −0.056 | 0.017 | −0.049 | −0.032 | 0.786 |
| HSiXe__●__NSi | 0.068 | 0.137 | 0.053 | −0.072 | −0.019 | 0.278 |
| HSi__●__RnNSi | 0.066 | −0.042 | 0.017 | −0.045 | −0.028 | 0.769 |
| HSiRn__●__NSi | 0.068 | 0.132 | 0.053 | −0.073 | −0.020 | 0.276 |
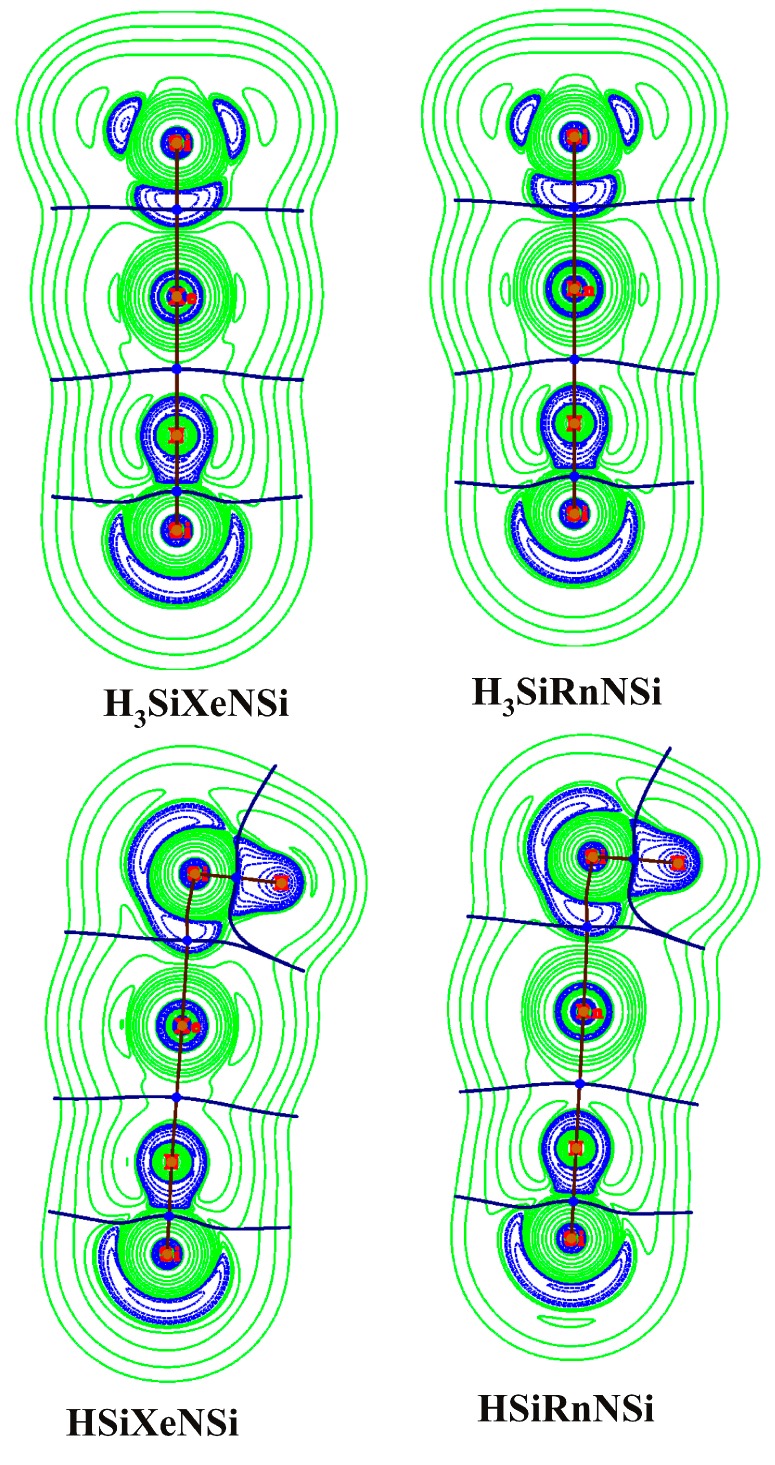
Even if ∇2ρ(rc) > 0, but H(rc) < 0, then also the bond might be considered as a covalent type [84]. In our cases, ∇2ρ(rc) is negative in the Si–Ng bonds, implying their covalent nature. However, H(rc) is negative in both Si–Ng and Ng–N bonds and slightly more negative in Si–Ng bonds than that in Ng–N bonds. The contour plots of ∇2ρ(r) are displayed in Figure 2.
Figure 2.
Contour plots of the Laplacian of the electron density of H3SiXeNSi and HSiXeNSi clusters at a particular plane computed at the MP2/def2-QZVPPD/WTBS level (WTBS is used for Xe and Rn; The green-colored region shows the area of ∇2ρ(r) > 0, whereas the blue-colored region shows the area of ∇2ρ(r) < 0).
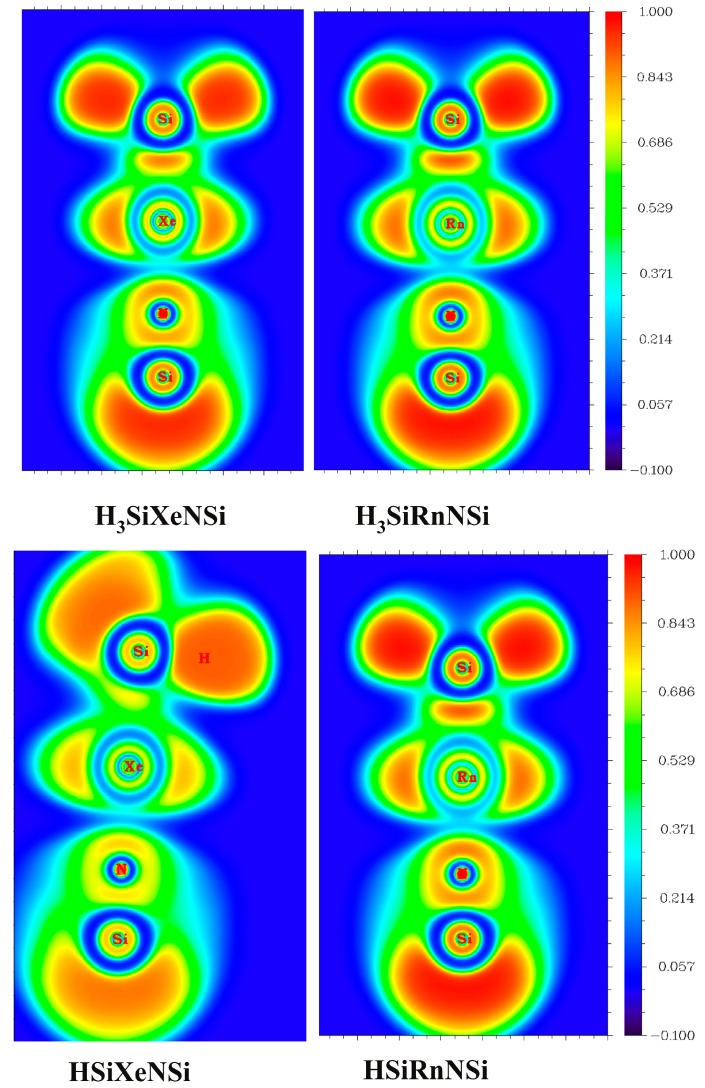
In between Si and Ng centers, a well-defined region having ∇2ρ(r) < 0 is developed, whereas in between Ng and N centers, the valence orbitals only undergo slight deformation in their shapes. Note that though H(rc) is negative in Ng–N bonds, the charge distribution shows that it would be better to consider them as ionic bonds rather than the covalent ones. To prove this, we have further computed ELF [85] at the BCPs of Si–Ng and Ng–N bonds, and the corresponding color-filled maps of ELF are provided in Figure 3. Generally, a high value of ELF at a certain point is an indicator of the localized electrons therein. It further implies the existence of covalent bonds or lone pairs or core electrons.
Figure 3.
Color-filled maps of the electron localization function of H3SiXeNSi and HSiXeNSi clusters at a particular plane computed at the MP2/def2-QZVPPD/WTBS level (WTBS is used for Xe and Rn).
A typical covalent bond possesses a large ELF value in between two bonded centers, whereas in the case of an ionic bond, the ELF value at the interstitial positions of the two atoms is very low. In our cases, the ELF values at the BCPs of Si–Ng bonds are quite high (~0.8) being close to the limiting value of 1.0 for a perfect localization case, whereas they are quite small (~0.3) for the Ng–N cases, corroborating well with their ionic nature. The color-filled maps of ELF further dictate the large degree of electron localization in between Si and Ng centers, whereas it is very small in between Ng and N centers (see Figure 3).
The total interaction energy (ΔEint) is divided into the Pauli repulsion (ΔEpauli), electrostatic (Eelstat), orbital (ΔEorb) and dispersion (ΔEdisp) energy terms in EDA to get further insight into the nature of Si–Ng and Ng–N bonds (see Table 5). The NPA charge on each atomic center is used as a guiding tool to impose the charges on the fragments used in our energy partitioning schemes. Since H3SiNgNSi and HSiNgNSi could be best represented as (H3SiNg)+(NSi)− and (HSiNg)+(NSi)−, we have used [H3SiNg]+ or [HSiNg]+ and [NSi]− as two fragments to know the nature of the Ng–N bond. As Tonner and Frenking [86] argued, when two different fragmentation schemes are possible, the most favorable one is given by the smallest size of the ΔEorb term. Therefore, we also performed EDA following the radical fragmentation scheme, and indeed, the ionic fragmentation gives a smaller ΔEorb value than that of the radical one. On the other hand, since the total charges on the fragments, [H3Si] or [HSi] and [NgNSi], are well below 0.5 |e|, we have partitioned H3SiNgNSi and HSiNgNSi into neutral [H3Si] or [HSi] and [NgNSi] fragments to explore the nature of Si–Ng bond, as the total charges on them are below 0.5 |e|.
Table 5.
Energy decomposition analysis (EDA) results of the H3SiNgNSi and HSiNgNSi molecules studied at the revPBE-D3/TZ2P//MP2/def2-QZVPPD level. All of the energy terms are in kcal/mol.
| Compounds | Fragments | ΔEint | ΔEpauli | ΔEelstat | ΔEorb | ΔEdisp |
|---|---|---|---|---|---|---|
| H3SiXeNSi | [H3Si] + [XeNSi] | −46.0 | 210.4 | −82.0 (32.0%) | −172.6 (67.3%) | −1.7 (0.7%) |
| [H3SiXe]+ + [NSi]− | −128.1 | 111.6 | −159.4 (66.5%) | −78.6 (32.8%) | −1.7 (0.7%) | |
| H3SiRnNSi | [H3Si] + [RnNSi] | −49.9 | 198.8 | −80.0 (32.2%) | −166.9 (67.1%) | −1.8 (0.7%) |
| [H3SiRn]+ + [NSi]− | −132.9 | 113.0 | −166.6 (67.7%) | −77.4 (31.5%) | −1.9 (0.8%) | |
| HSiXeNSi | [HSi] + [XeNSi] | −37.8 | 169.6 | −51.0 (24.6%) | −155.4 (74.9%) | −1.0 (0.5%) |
| [HSiXe]+ + [NSi]− | −120.4 | 103.4 | −148.0 (66.2%) | −74.0 (33.1%) | −1.7 (0.8%) | |
| HSiRnNSi | [HSi] + [RnNSi] | −41.0 | 163.9 | −50.9 (24.8%) | −153.0 (74.7%) | −1.1 (0.5%) |
| [HSiRn]+ + [NSi]− | −123.7 | 105.3 | −154.4 (67.4%) | −72.7 (31.7%) | −1.9 (0.8%) |
(The percentage values within the parentheses show the contribution towards the total attractive interaction ΔEelstat + ΔEorb + ΔEdisp).
In the Ng–N bonds, the contribution from ΔEelstat towards the total attraction is the maximum ranging within 66%–68%. ΔEorb contributes around 31%–33% towards the total attraction in these bonds. In cases of Si–Ng bonds, ΔEorb is the largest contributor towards the total attraction (ca. 67%–75%), implying their covalent nature. In both Ng–N and Si–Ng bonds, ΔEdisp is found to be less important, as it contributes the least.
3. Experimental Section
The geometry optimization and the frequency calculation are performed at several levels, viz. ωB97X-D/def2-QZVPPD [87,88], MP2/def2-QZVPPD [89] and CCSD(T)/def2-TZVP [90], to ensure that the results obtained are not an artifact of the calculation at a particular level. For the core electrons of Xe and Rn, a quasi-relativistic pseudopotential is used [91]. At both the ωB97X-D/def2-QZVPPD and MP2/def2-QZVPPD levels, H3SiNgNSi and HSiNgNSi (Ng = Ar–Rn) are found to be minima on the potential energy surface (PES). However, at the CCSD(T)/def2-TZVP level, the calculations for Ar and Kr inserted analogues do not converge; rather, the compounds dissociate into two fragments during optimization. Hence, we exclude those systems from the discussion. The occurrence of only one imaginary frequency with a mode, which leads to the desired products, implies the transition states (TSs) corresponding to the dissociations of H3SiNgNSi and HSiNgNSi into Ng and H3SiNSi or HSiNSi. All of these computations are performed by using the Gaussian 09 program package [92]. The atoms-in-molecules (AIM) analysis [71] is carried out by using Multiwfn software [93] at the MP2/def2-QZVPPD/WTBS level. All of electron WTBS [94,95] basis set is used for Xe and Rn.
The energy decomposition analysis (EDA) [72,73,74,75] is performed at the revPBE-D3/TZ2P//MP2/def2-QZVPPD [96,97,98] level using the ADF (2013.01) program package [99]. Scalar relativistic effects are considered for the heavier atoms using the zeroth-order regular approximation (ZORA) [100,101,102].
4. Conclusions
H3SiNgNSi and HSiNgNSi (Ng = Xe, Rn) could be considered as metastable compounds. The 2-B dissociation pathways producing Ng and H3SiNSi or HSiNSi are found to be highly exergonic in nature at room temperature. However, they are found to be kinetically stable along the same dissociation channel due to their activation free energy barriers of 19.3 and 23.3 kcal/mol for H3SiXeNSi and H3SiRnNSi, respectively, and 9.2 and 12.8 kcal/mol for HSiXeNSi and HSiRnNSi, respectively. The Rn analogues have thermochemical stability with respect to all other possible dissociation channels. However, for H3SiXeNSi, another 3-B dissociation channel producing H3Si, Xe and NSi is slightly exergonic in nature at 298 K, but at a slightly low temperature (250 K), it turns out to be endergonic in nature. On the other hand, for HSiXeNSi one 2-B (HSiNg and NSi) and 3-B (HSi, Ng and NSi) dissociation paths are slightly exergonic in nature at room temperature. At low temperature (around 150–180 K), they become endergonic. The rest of the dissociation paths are not feasible. According to the argument of Hu et al. [77], H3SiNgNSi could be stable enough to be detected at the 250–300 K temperature range, whereas HSiNgNSi needs a lower temperature (150–200 K) to be detected. The NPA charge suggests that they could be best represented as (H3SiNg)+(NSi)− and (HSiNg)+(NSi)−. Consequently, the WBI values for the Ng–N bonds are found to be quite low (~0.2), whereas the same for the Ng–Si bonds are quite large (~0.65), signifying the covalent nature of the bond. Large ELF values (~0.8) and negative values of ∇2ρ(rc) at the Si–Ng bond critical points further imply its covalent character. As expected from the ionic nature of Ng–N bonds, the maximum contribution in the total attraction energy comes from the ΔEelstat (ca. 66%–68%). On the other hand, ΔEorb is the main contributing term (ca. 67%–75%) in the total attraction energy of Si–Ng bonds, showing their covalent nature.
Acknowledgments
Pratim K. Chattaraj would like to thank Department of Science & Technology, New Delhi, for the Jagadish Chandra Bose National Fellowship. Sudip Pan and Ranajit Saha thank Council of Scientific & Industrial Research and University Grants Commission, New Delhi, for their fellowships. We would like to thank Tamal Goswami for his help.
Supplementary Materials
Supplementary materials can be found at http://www.mdpi.com/1422-0067/16/03/6402/s1.
Author Contributions
Sudip Pan performed the computations and wrote the manuscript. Ranajit Saha helped in preparing the manuscript. Pratim K. Chattaraj guided throughout the work, analyzed the results and reviewed the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Bartlett N. Xenon hexafluoroplatinate (V) Xe+[PtF6]−. Proc. Chem. Soc. 1962;218 doi: 10.1039/PS9620000197. [DOI] [Google Scholar]
- 2.Pettersson M., Lundell J., Räsänen M. Neutral rare-gas containing charge-transfer molecules in solid matrices. II. HXeH, HXeD, and DXeD in Xe. J. Chem. Phys. 1995;103:205. doi: 10.1063/1.469632. [DOI] [Google Scholar]
- 3.Pettersson M., Nieminen J., Khriachtchev L., Räsänen M. The mechanism of formation and infrared-induced decomposition of HXeI in solid Xe. J. Chem. Phys. 1997;107:8423. doi: 10.1063/1.475042. [DOI] [Google Scholar]
- 4.Pettersson M., Lundell J., Khriachtchev L., Isoniemi E., Räsänen M. HXeSH, the first example of a xenon-sulfur bond. J. Am. Chem. Soc. 1998;120:7979–7980. doi: 10.1021/ja981032d. [DOI] [Google Scholar]
- 5.Pettersson M., Lundell J., Khriachtchev L., Räsänen M. Neutral rare-gas containing charge-transfer molecules in solid matrices. III. HXeCN, HXeNC, and HKrCN in Kr and Xe. J. Chem. Phys. 1998;109:618. doi: 10.1063/1.476599. [DOI] [Google Scholar]
- 6.Pettersson M., Khriachtchev L., Lundell J., Räsänen M. A chemical compound formed from water and xenon: HXeOH. J. Am. Chem. Soc. 1999;121:11904–11905. doi: 10.1021/ja9932784. [DOI] [Google Scholar]
- 7.Khriachtchev L., Pettersson M., Runeberg N., Lundell J., Räsänen M. A stable argon compound. Nature. 2000;406:874–876. doi: 10.1038/35022551. [DOI] [PubMed] [Google Scholar]
- 8.Khriachtchev L., Pettersson M., Lignell A., Räsänen M. A more stable configuration of HArF in solid argon. J. Am. Chem. Soc. 2001;123:8610–8611. doi: 10.1021/ja016197s. [DOI] [PubMed] [Google Scholar]
- 9.Khriachtchev L., Pettersson M., Lundell J., Tanskanen H., Kiviniemi T., Runeberg N., Räsänen M. A neutral xenon-containing radical, HXeO. J. Am. Chem. Soc. 2003;125:1454–1455. doi: 10.1021/ja029024r. [DOI] [PubMed] [Google Scholar]
- 10.Khriachtchev L., Tanskanen H., Cohen A., Gerber R.B., Lundell J., Pettersson M., Kiljunen H., Räsänen M. A gate to organokrypton chemistry: HKrCCH. J. Am. Chem. Soc. 2003;125:6876–6877. doi: 10.1021/ja0355269. [DOI] [PubMed] [Google Scholar]
- 11.Tanskanen H., Khriachtchev L., Lundell J., Kiljunen H., Räsänen M. Chemical compounds formed from diacetylene and rare-gas atoms: HKrC4H and HXeC4H. J. Am. Chem. Soc. 2003;125:16361–16366. doi: 10.1021/ja038610x. [DOI] [PubMed] [Google Scholar]
- 12.Feldman V.I., Sukhov F.F. Formation and decay of transient xenon dihydride resulting from hydrocarbon radiolysis in a xenon matrix. Chem. Phys. Lett. 1996;225:425–430. doi: 10.1016/0009-2614(96)00346-6. [DOI] [Google Scholar]
- 13.Feldman V.I., Sukhov F.F., Orlov A.Y. Further evidence for formation of xenon dihydride from neutral hydrogen atoms: A comparison of ESR and IR spectroscopic results. Chem. Phys. Lett. 1997;280:507–512. doi: 10.1016/S0009-2614(97)01208-6. [DOI] [Google Scholar]
- 14.Thompson C.A., Andrews L. Noble gas complexes with BeO: Infrared spectra of NG–BeO (NG = Ar, Kr, Xe) J. Am. Chem. Soc. 1994;116:423–424. doi: 10.1021/ja00080a069. [DOI] [Google Scholar]
- 15.Thompson C.A., Andrews L. Reactions of laser ablated Be atoms with O2: Infrared spectra of beryllium oxides in solid argon. J. Chem. Phys. 1994;100:8689. doi: 10.1063/1.466724. [DOI] [Google Scholar]
- 16.Cooke S.A., Gerry M.C.L. XeAuF. J. Am. Chem. Soc. 2004;126:17000–17008. doi: 10.1021/ja044955j. [DOI] [PubMed] [Google Scholar]
- 17.Michaud M., Gerry M.C.L. XeCu covalent bonding in XeCuF and XeCuCl, characterized by fourier transform microwave spectroscopy supported by quantum chemical calculations. J. Am. Chem. Soc. 2006;128:7613–7621. doi: 10.1021/ja060745q. [DOI] [PubMed] [Google Scholar]
- 18.Brock D.S., Mercier H.P.A., Schrobilgen G.J. [H(OXeF2)n][AsF6] and [FXeII(OXeIVF2)n][AsF6] (n = 1, 2); Examples of xenon(IV) hydroxide fluoride and oxide fluoride cations and the crystal structures of [F3Xe---FH][Sb2F11] and [H5F4][SbF6]·2[F3Xe---FH][Sb2F11] J. Am. Chem. Soc. 2013;135:5089–5104. doi: 10.1021/ja312493j. [DOI] [PubMed] [Google Scholar]
- 19.Debackere J.R., Mercier H.P.A., Schrobilgen G.J. Noble-gas difluoride complexes of mercury(II): The syntheses and structures of Hg(OTeF5)2·1.5NgF2 (Ng = Xe, Kr) and Hg(OTeF5)2. J. Am. Chem. Soc. 2014;136:3888–3903. doi: 10.1021/ja412193z. [DOI] [PubMed] [Google Scholar]
- 20.Collins J.R., Frenking G. Are there neutral helium compounds which are stable in their ground state?: A theoretical investigation of HeBCH and HeBeO. Chem. Phys. Lett. 1986;132:330–333. doi: 10.1016/0009-2614(86)80134-8. [DOI] [Google Scholar]
- 21.Koch W., Frenking G., Gauss J., Cremer D., Collins J.R. Helium chemistry: Theoretical predictions and experimental challenge. J. Am. Chem. Soc. 1987;109:5917–5934. doi: 10.1021/ja00254a005. [DOI] [Google Scholar]
- 22.Frenking G., Koch W., Gauss J., Cremer D. Stabilities and nature of the attractive interactions in HeBeO, NeBeO, and ArBeO and a comparison with analogs NGLiF, NGBN, and NGLiH (NG = He, Ar). A theoretical investigation. J. Am. Chem. Soc. 1988;110:8007–8016. doi: 10.1021/ja00232a009. [DOI] [Google Scholar]
- 23.Koch W., Liu B., Frenking G. Theoretical investigations of small multiply charged cations. III. NeN2+ J. Chem. Phys. 1990;92:2464. doi: 10.1063/1.457989. [DOI] [Google Scholar]
- 24.Frenking G., Koch W., Reichel F., Cremer D. Light noble gas chemistry: Structures, stabilities, and bonding of helium, neon, and argon compounds. J. Am. Chem. Soc. 1990;112:4240–4256. doi: 10.1021/ja00167a020. [DOI] [Google Scholar]
- 25.Jiménez-Halla C.Ó., Fernández I., Frenking G. Is it possible to synthesize a neutral noble gas compound containing a Ng–Ng bond? A theoretical study of H–Ng–Ng–F (Ng = Ar, Kr, Xe) Angew. Chem. Int. Ed. 2009;48:366–369. doi: 10.1002/anie.200803252. [DOI] [PubMed] [Google Scholar]
- 26.Fernández I., Frenking G. Neutral noble gas compounds exhibiting a Xe-Xe bond: Structure, stability and bonding situation. Phys. Chem. Chem. Phys. 2012;14:14869–14877. doi: 10.1039/c2cp41244f. [DOI] [PubMed] [Google Scholar]
- 27.Frohn H.-J., Bilir V., Westphal U. Two new types of xenon–carbon species: The zwitterion, 1-(Xe+)C6F4−4-(BF3−), and the dication, [1,4-(Xe)2C6F4]2+ Inorg. Chem. 2012;51:11251–11258. doi: 10.1021/ic3017112. [DOI] [PubMed] [Google Scholar]
- 28.Pan S., Contreras M., Romero J., Reyes A., Merino G., Chattaraj P.K. C5Li7+ and O2Li5+ as noble gas trapping agents. Chem. Eur. J. 2013;19:2322–2329. doi: 10.1002/chem.201203245. [DOI] [PubMed] [Google Scholar]
- 29.Pan S., Jalife S., Romero J., Reyes A., Merino G., Chattaraj P.K. Attractive Xe-Li interaction in Li-decorated clusters. Comput. Theor. Chem. 2013;1021:62–69. doi: 10.1016/j.comptc.2013.06.026. [DOI] [Google Scholar]
- 30.Pan S., Jalife S., Kumar R.M., Subramanian V., Merino G., Chattaraj P.K. Structure and stability of (NG)nCN3Be3+ clusters and comparison with (NG)BeY0/+ (NG = Noble Gas and Y = O, S, Se, Te) ChemPhysChem. 2013;14:2511–2517. doi: 10.1002/cphc.201300357. [DOI] [PubMed] [Google Scholar]
- 31.Khatua M., Pan S., Chattaraj P.K. Confinement induced binding of noble gas atoms. J. Chem. Phys. 2014;140:164306. doi: 10.1063/1.4871800. [DOI] [PubMed] [Google Scholar]
- 32.Pan S., Moreno D., Cabellos J.L., Romero J., Reyes A., Merino G., Chattaraj P.K. In quest of strong Be–Ng bonds among the neutral Ng-Be complexes. J. Phys. Chem. A. 2014;118:487–494. doi: 10.1021/jp409941v. [DOI] [PubMed] [Google Scholar]
- 33.Pan S., Moreno D., Cabellos J.L., Merino G., Chattaraj P.K. Ab initio study on the stability of NgnBe2N2, NgnBe3N2 and NgBeSiN2 Clusters. ChemPhysChem. 2014;15:2618–2625. doi: 10.1002/cphc.201402101. [DOI] [PubMed] [Google Scholar]
- 34.Pan S., Gupta A., Mandal S., Moreno D., Merino G., Chattaraj P.K. Metastable behavior of noble gas inserted tin and lead fluorides. Phys. Chem. Chem. Phys. 2015;17:972–982. doi: 10.1039/C4CP03856H. [DOI] [PubMed] [Google Scholar]
- 35.Ansbacher T., Gerber R.B. New organic noble molecules: Energetics, stability and potential energy surfaces of HCCXeCCH and HCCKrCCH. Phys. Chem. Chem. Phys. 2006;8:4175–4181. doi: 10.1039/b606478g. [DOI] [PubMed] [Google Scholar]
- 36.Khriachtchev L., Räsänen M., Gerber R.B. Noble-gas hydrides: New chemistry at low temperatures. Acc. Chem. Res. 2009;42:183–191. doi: 10.1021/ar800110q. [DOI] [PubMed] [Google Scholar]
- 37.Feldman V.I., Kobzarenko A.V., Baranova I.A., Danchenko A.V., Sukhov F.F., Tsivion E., Gerber R.B. Direct visualization of the H–Xe bond in xenon hydrides: Xenon isotopic shift in the IR spectra. J. Chem. Phys. 2009;131:151101. doi: 10.1063/1.3250426. [DOI] [PubMed] [Google Scholar]
- 38.Lockyear J.F., Douglas K., Price S.D., Karwowska M., Fijałkowski K.J., Grochala W., Remeš M., Roithová J., Schröder D. Generation of the ArCF22+ dication. J. Phys. Chem. Lett. 2010;1:358–362. doi: 10.1021/jz900274p. [DOI] [Google Scholar]
- 39.Grochala W. A metastable He–O bond inside a ferroelectric molecular cavity: (HeO)(LiF)2. Phys. Chem. Chem. Phys. 2012;14:14860–14868. doi: 10.1039/c2cp42321a. [DOI] [PubMed] [Google Scholar]
- 40.Kurzydłowski D., Zaleski-Ejgierd P., Grochala W., Hoffmann R. Freezing in resonance structures for better packing: XeF2 becomes (XeF+)(F−) at large compression. Inorg. Chem. 2011;50:3832–3840. doi: 10.1021/ic200371a. [DOI] [PubMed] [Google Scholar]
- 41.Borocci S., Bronzolino N., Grandinetti F. From OBeHe to H3BOBeHe: Enhancing the stability of a neutral helium compound. Chem. Phys. Lett. 2005;406:179–183. doi: 10.1016/j.cplett.2005.02.096. [DOI] [Google Scholar]
- 42.Antoniotti P., Bottizzo E., Operti L., Rabezzana R., Borocci S., Grandinetti F. F3Ge-Xe+: A xenon-germanium molecular species. J. Phys. Chem. Lett. 2010;1:2006–2010. doi: 10.1021/jz100676g. [DOI] [Google Scholar]
- 43.Operti L., Rabezzana R., Turco F., Borocci S., Giordani M., Grandinetti F. Xenon–nitrogen chemistry: Gas-phase generation and theoretical investigation of the xenon–difluoronitrenium ion F2N-Xe+ Chem. Eur. J. 2011;17:10682–10689. doi: 10.1002/chem.201101395. [DOI] [PubMed] [Google Scholar]
- 44.Jayasekharan T., Ghanty T.K. Prediction of metastable metal-rare gas fluorides: FMRgF (M = Be and Mg; Rg = Ar, Kr and Xe) J. Chem. Phys. 2008;128:144314. doi: 10.1063/1.2899015. [DOI] [PubMed] [Google Scholar]
- 45.Sirohiwal A., Manna D., Ghosh A., Jayasekharan T., Ghanty T.K. Theoretical prediction of rare gas containing hydride cations: HRgBF+ (Rg = He, Ar, Kr, and Xe) J. Phys. Chem. A. 2013;117:10772–10782. doi: 10.1021/jp4064824. [DOI] [PubMed] [Google Scholar]
- 46.Manna D., Ghosh A., Ghanty T.K. Theoretical prediction of XRgCO+ ions (X = F, Cl, and Rg = Ar, Kr, Xe) J. Phys. Chem. A. 2013;117:14282–14292. doi: 10.1021/jp410631y. [DOI] [PubMed] [Google Scholar]
- 47.Field F.H., Franklin J.L. Reactions of gaseous ions. X. Ionic reactions in xenon-methane mixtures. J. Am. Chem. Soc. 1961;83:4509–4515. doi: 10.1021/ja01483a004. [DOI] [Google Scholar]
- 48.Field H., Head H.N., Franklin J.L. Reactions of gaseous ions. XI. Ionic reactions in krypton-methane and argon-methane mixtures. J. Am. Chem. Soc. 1962;84:1118–1122. doi: 10.1021/ja00866a011. [DOI] [Google Scholar]
- 49.Turbini L.J., Aikman R.E., Lagow R.J. Evidence for the synthesis of a stable sigma-bonded xenon-carbon compound: Bis(trifluoromethyl)xenon. J. Am. Chem. Soc. 1979;101:5833–5834. doi: 10.1021/ja00513a066. [DOI] [Google Scholar]
- 50.Naumann D., Tyrra W.T. The first compound with a stable xenon-carbon bond: 19F- and 129Xe-n.m.r. spectroscopic evidence for pentafluorophenylxenon(II) fluoroborates. J. Chem. Soc. Chem. Commun. 1989 doi: 10.1039/C39890000047. [DOI] [Google Scholar]
- 51.Frohn H.J., Jacobs S., Henkel G. The Acetonitrile(pentafluorophenyl)xenon(II) cation, [MeCN-Xe–C6F5]: The first structural characterization of a xenon-carbon bond. Angew. Chem. Int. Ed. 1989;28:1506–1507. doi: 10.1002/anie.198915061. [DOI] [Google Scholar]
- 52.Frohn H.J., Jakobs S. The pentafluorophenylxenon(II) cation: [C6F5Xe]+: The first stable system with a xenon-carbon bond. J. Chem. Soc. Chem. Commun. 1989 doi: 10.1039/C39890000625. [DOI] [Google Scholar]
- 53.Khriachtchev L., Tanskanen H., Lundell J., Pettersson M., Kiljunen H., Räsänen M. Fluorine-free organoxenon chemistry: HXeCCH, HXeCC, and HXeCCXeH. J. Am. Chem. Soc. 2003;125:4696–4697. doi: 10.1021/ja034485d. [DOI] [PubMed] [Google Scholar]
- 54.Domanskaya A., Kobzarenko A.V., Tsivion E., Khriachtchev L., Feldman V.I., Gerber R.B., Räsänen M. Matrix-isolation and ab initio study of HXeCCH complexed with acetylene. Chem. Phys. Lett. 2009;481:83–87. doi: 10.1016/j.cplett.2009.09.072. [DOI] [Google Scholar]
- 55.Tanskanen H., Khriachtchev L., Lundell J., Räsänen M. Organo-noble-gas hydride compounds HKrCCH, HXeCCH, HXeCC, and HXeCCXeH: Formation mechanisms and effect of 13C isotope substitution on the vibrational properties. J. Chem. Phys. 2004;121:8291. doi: 10.1063/1.1799611. [DOI] [PubMed] [Google Scholar]
- 56.Khriachtchev L., Domanskaya A., Lundell J., Akimov A., Räsänen M., Misochko E. Matrix-isolation and ab initio study of HNgCCF and HCCNgF molecules (Ng = Ar, Kr, and Xe) J. Phys. Chem. A. 2010;114:4181–4187. doi: 10.1021/jp1001622. [DOI] [PubMed] [Google Scholar]
- 57.Arppe T., Khriachtchev L., Lignell A., Domanskaya A.V., Räsänen M. Halogenated xenon cyanides ClXeCN, ClXeNC, and BrXeCN. Inorg. Chem. 2012;51:4398–4402. doi: 10.1021/ic3002543. [DOI] [PubMed] [Google Scholar]
- 58.Khriachtchev L., Lignell A., Tanskanen H., Lundell J., Kiljunen H., Räsänen M. Insertion of noble gas atoms into cyanoacetylene: An ab initio and matrix isolation study. J. Phys. Chem. A. 2006;110:11876–11885. doi: 10.1021/jp063731f. [DOI] [PubMed] [Google Scholar]
- 59.Sheng L., Gerber R.B. High coordination chemically bound compounds of noble gases with hydrocarbons: Ng(CCH)4 and Ng(CCH)6, (Ng = Xe or Kr) J. Chem. Phys. 2006;124:231103. doi: 10.1063/1.2217734. [DOI] [PubMed] [Google Scholar]
- 60.Lundell J., Cohen A., Gerber R.B. Quantum chemical calculations on novel molecules from xenon insertion into hydrocarbons. J. Phys. Chem. A. 2002;106:11950–11955. doi: 10.1021/jp026777r. [DOI] [Google Scholar]
- 61.Cipollini R., Grandinetti F. The gaseous trifluorosilylxenon cation, F3SiXe+: A stable species with a silicon–xenon bond. J. Chem. Soc. Chem. Commun. 1995 doi: 10.1039/C39950000773. [DOI] [Google Scholar]
- 62.Cunje A., Baranov V., Ling Y., Hopkinson A., Bohme D.K. Bonding of rare-gas atoms to Si in reactions of rare gases with SiF3+ J. Phys. Chem. A. 2001;105:11073–11079. doi: 10.1021/jp011908u. [DOI] [Google Scholar]
- 63.Cohen A., Lundell J., Gerber R.B. First compounds with argon-carbon and argon-silicon chemical bonds. J. Chem. Phys. 2003;119:6415. doi: 10.1063/1.1613631. [DOI] [Google Scholar]
- 64.Yockel S., Garg A., Wilson A.K. The existence of FKrCF3, FKrSiF3, and FKrGeF3: A theoretical study. Chem. Phys. Lett. 2005;411:91–97. doi: 10.1016/j.cplett.2005.06.014. [DOI] [Google Scholar]
- 65.Lundell J., Panek J., Latajka Z. Quantum chemical calculations on FXeSiF. Chem. Phys. Lett. 2001;348:147–154. doi: 10.1016/S0009-2614(01)01099-5. [DOI] [Google Scholar]
- 66.Roithová J., Schröder D. Silicon compounds of neon and argon. Angew. Chem. Int. Ed. 2009;48:8788–8790. doi: 10.1002/anie.200903706. [DOI] [PubMed] [Google Scholar]
- 67.Savoca M., Langer J., Harding D.J., Dopfer O., Fielicke A. Incipient chemical bond formation of Xe to a cationic silicon cluster: Vibrational spectroscopy and structure of the Si4Xe+ complex. Chem. Phys. Lett. 2013;557:49–52. doi: 10.1016/j.cplett.2012.12.020. [DOI] [Google Scholar]
- 68.Pan S., Moreno D., Merino G., Chattaraj P.K. Stability of noble-gas-bound SiH3+ clusters. ChemPhysChem. 2014;15:3554–3564. doi: 10.1002/cphc.201402370. [DOI] [PubMed] [Google Scholar]
- 69.Crabtree K.N., Martinez O., Jr., McCarthy M.C. Detection of two highly stable silicon nitrides: HSiNSi and H3SiNSi. J. Phys. Chem. A. 2013;117:11282–11288. doi: 10.1021/jp4068119. [DOI] [PubMed] [Google Scholar]
- 70.Wiberg K.B. Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane. Tetrahedron. 1968;24:1083–1096. doi: 10.1016/0040-4020(68)88057-3. [DOI] [Google Scholar]
- 71.Bader R.F.W. Atoms in Molecules: A Quantum Theory. Clarendon Press; Oxford, UK: 1990. [Google Scholar]
- 72.Morokuma K. Why do molecules interact? The origin of electron donor-acceptor complexes, hydrogen bonding and proton affinity. Acc. Chem. Res. 1977;10:294–300. doi: 10.1021/ar50116a004. [DOI] [Google Scholar]
- 73.Ziegler T., Rauk A. On the calculation of bonding energies by the hartree Fock Slater Method. Theor. Chim. Acta. 1977;46:1–10. doi: 10.1007/BF02401406. [DOI] [Google Scholar]
- 74.Ziegler T., Rauk A., Baerends E.J. On the calculation of multiplet energies by the Hartree-Fock-Slater Method. Theor. Chim. Acta. 1977;43:261–271. doi: 10.1007/BF00551551. [DOI] [Google Scholar]
- 75.Von Hopffgarten M., Frenking G. Energy decomposition analysis. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012;2:43–62. doi: 10.1002/wcms.71. [DOI] [Google Scholar]
- 76.Lignell A., Khriachtchev L., Lundell J., Tanskanen H., Räsänen M. On theoretical predictions of noble-gas hydrides. J. Chem. Phys. 2006;125:184514. doi: 10.1063/1.2378624. [DOI] [PubMed] [Google Scholar]
- 77.Li T.-H., Liu Y.-L., Lin R.-J., Yeh T.-Y., Hu W.-P. On the stability of noble gas molecules. Chem. Phys. Lett. 2007;434:38–41. doi: 10.1016/j.cplett.2006.11.108. [DOI] [Google Scholar]
- 78.Cioslowski J., Mixon S.T. Universality among topological properties of electron density associated with the hydrogen–hydrogen nonbonding interactions. Can. J. Chem. 1992;70:443–449. doi: 10.1139/v92-064. [DOI] [Google Scholar]
- 79.Cioslowski J., Mixon S.T. Topological properties of electron density in search of steric interactions in molecules: Electronic structure calculations on ortho-substituted biphenyls. J. Am. Chem. Soc. 1992;114:4382–4387. doi: 10.1021/ja00037a053. [DOI] [Google Scholar]
- 80.Poater J., Visser R., Solà M., Bickelhaupt F.M. Polycyclic benzenoids: Why kinked is more stable than straight. J. Org. Chem. 2007;72:1134–1142. doi: 10.1021/jo061637p. [DOI] [PubMed] [Google Scholar]
- 81.Cerpa E., Krapp A., Vela A., Merino G. The implications of symmetry of the external potential on bond paths. Chem. Eur. J. 2008;14:10232–10234. doi: 10.1002/chem.200800934. [DOI] [PubMed] [Google Scholar]
- 82.Macchi P., Proserpio D.M., Sironi A.J. Experimental electron density in a transition metal dimer: Metal-metal and metal-ligand Bonds. J. Am. Chem. Soc. 1998;120:13429–13435. doi: 10.1021/ja982903m. [DOI] [Google Scholar]
- 83.Macchi P., Garlaschelli L., Martinengo S., Sironi A.J. Charge density in transition metal clusters: Supported vs. unsupported metal-metal interactions. J. Am. Chem. Soc. 1999;121:10428–10429. doi: 10.1021/ja9918977. [DOI] [Google Scholar]
- 84.Cremer D., Kraka E. Chemical bonds without bonding electron density—Does the difference electron-density analysis suffice for a description of the chemical bond? Angew. Chem. Int. Ed. 1984;23:627–628. doi: 10.1002/anie.198406271. [DOI] [Google Scholar]
- 85.Becke A.D., Edgecombe K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990;92:5397. doi: 10.1063/1.458517. [DOI] [Google Scholar]
- 86.Tonner R., Frenking G. Divalent carbon(0) chemistry, Part 1: Parent compounds. Chem. Eur. J. 2008;14:3260–3272. doi: 10.1002/chem.200701390. [DOI] [PubMed] [Google Scholar]
- 87.Chaim J.-D., Head-Gordon M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008;10:6615–6620. doi: 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
- 88.Weigend F., Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005;7:3297–3305. doi: 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- 89.Møller C., Plesset M.S. Note on an approximation treatment for many-electron systems. Phys. Rev. 1934;46:618–622. doi: 10.1103/PhysRev.46.618. [DOI] [Google Scholar]
- 90.Pople J.A., Head-Gordon M., Raghavachari K. Quadratic configuration interaction. A general technique for determining electro correlation energies. J. Chem. Phys. 1987;87:5968. doi: 10.1063/1.453520. [DOI] [Google Scholar]
- 91.Peterson K.A., Figgen D., Goll E., Stoll H., Dolg M. Systematically convergent basis sets with relativistic pseudopotentials. II. Small-core pseudopotentials and correlation consistent basis sets for the post-d group 16–18 elements. J. Chem. Phys. 2003;119:11113. doi: 10.1063/1.1622924. [DOI] [Google Scholar]
- 92.Frisch M.J., Truck G.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R., Scalmani G., Barone V., Mennucci B., Petersson G.A., et al. Gaussian 09, Revision C.01. Gaussian, Inc.; Wallingford, CT, USA: 2010. [Google Scholar]
- 93.Lu T., Chen F.W. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012;33:580–592. doi: 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- 94.Huzinaga S., Miguel B. A comparison of the geometrical sequence formula and the well-tempered formulas for generating GTO basis orbital exponents. Chem. Phys. Lett. 1990;175:289–291. doi: 10.1016/0009-2614(90)80112-Q. [DOI] [Google Scholar]
- 95.Huzinaga S., Klobukowski M. Well-tempered Gaussian basis sets for the calculation of matrix Hartree—Fock wavefunctions. Chem. Phys. Lett. 1993;212:260–264. doi: 10.1016/0009-2614(93)89323-A. [DOI] [Google Scholar]
- 96.Zhang Y., Yang W. Comment on “Generalized Gradient Approximation Made Simple”. Phys. Rev. Lett. 1998;80:890. doi: 10.1103/PhysRevLett.80.890. [DOI] [Google Scholar]
- 97.Grimme S., Antony J., Ehrlich S., Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010;132:154104. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- 98.Van Lenthe E., Baerends E.J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003;24:1142–1156. doi: 10.1002/jcc.10255. [DOI] [PubMed] [Google Scholar]
- 99.Baerends E.J., Ziegler T., Autschbach J., Bashford D., Bérces A., Bickelhaupt F.M., Bo C., Boerrigter P.M., Cavallo L., Chong D.P., et al. ADF 2013.01, SCM, Theoretical Chemistry. Vrije Universiteit; Amsterdam, The Netherlands: 2013. [Google Scholar]
- 100.Van Lenthe E., Ehlers A., Baerends E-J. Geometry optimizations in the zero order regular approximation for relativistic effects. J. Chem. Phys. 1999;110:8943. doi: 10.1063/1.478813. [DOI] [Google Scholar]
- 101.Van Lenthe E., Snijders J.G., Baerends E.J. The zero-order regular approximation for relativistic effects: The effect of spin–orbit coupling in closed shell molecules. J. Chem. Phys. 1996;105:650592. [Google Scholar]
- 102.Van Lenthe E., Baerends E.J., Snijders J.G. Relativistic total energy using regular approximations. J. Chem. Phys. 1994;101:9783. doi: 10.1063/1.467943. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.