Bridging Systems Medicine and Patient Needs

Abstract

While there is widespread consensus on the need both to change the prevailing research and development (R&D) paradigm and provide the community with an efficient way to personalize medicine, ecosystem stakeholders grapple with divergent conceptions about which quantitative approach should be preferred. The primary purpose of this position paper is to contrast these approaches. The second objective is to introduce a framework to bridge simulation outputs and patient outcomes, thus empowering the implementation of systems medicine.

Traditional approaches to biomedical research and pharmaceutical innovation have patently failed to make an optimal use of the vast quantity of knowledge available in the scientific literature. Serendipity, rather than the knowledge of disease-perturbed dynamical biological networks, is still the major driver of therapeutic innovation, and the dearth of truly innovative treatments reaching the market each year is a prime example of our failure to employ the principles of systems medicine.1 However, novel and effective diagnostic techniques and therapeutic modalities as well as a more efficient use of available treatments will come from the deployment of the many new strategies and technologies of systems medicine. The emergent application of quantitative and systems-driven sciences to biomedical research provides a structured context to improve translational research.

In their attempts to improve drug research and development (R&D) and come up with a practical approach to personalizing medical decisions, ecosystem stakeholders (academia, drug producers, regulators, and payers) grapple with divergent conceptions about which quantitative approach should be preferred. The essence of this controversy lies in the current deployment of large population-driven clinical studies—where, for example, 30,000 patients are given drug or placebo and the results are abstracted into curves that inform one about how the average population behaves and how successful the drug has been. This averages patients who differ strikingly both genetically and in their environmental exposures. Systems medicine analyzes the dynamic data cloud that surrounds each patient and uses this to derive “actionable possibilities” that can improve wellness or avoid disease for each patient. Once 30,000 individual data clouds have been analyzed they can be aggregated into groups that are relevant to drug responsiveness or other features—and this analysis is based on each individual and not an averaged population.2

These divergent conceptions are further fueled by a number of factors: the paucity of epistemological thinking pervading the ecosystem, the growing clout of computer science in biopharmaceutical R&D (blind applications of big data without the relevant domain expertise), the absence to date of an established standard to bridge in silico simulation outputs and clinical outcomes, a lack of emphasis on the importance of optimizing wellness for the individual, the poor understanding of the comparative merits of current biosimulation techniques, as well as the large number of terms denoting overlapping activities (bioinformatics, systems biology, systems medicine, pharmacometrics, systems pharmacology, model-informed drug development, etc.).

The primary purpose of this position paper is to contrast these approaches by explaining their respective limitations. The second objective is to introduce a standard framework to bridge simulation outputs and patient outcomes, thus empowering the implementation of systems medicine by combining the best elements of existing approaches into an integrated one. In the first part of the article, we briefly review the emergence of systems thinking in biomedical sciences from a historical perspective (more thorough reviews have previously been published3). The second section gives an overview of current approaches and their conceptual limitations. The third section details the hallmarks of human biology in systems thinking. The fourth section introduces the original approach based on the Effect Model law, which bridges the gap between systems medicine and patient needs. The penultimate section provides an application of this framework to coronary heart disease. The final section outlines perspectives of this new approach in the context of drug R&D.

QUANTITATIVE APPROACHES IN A HISTORICAL PERSPECTIVE

When the limitations of reductionism in biology became obvious,4 researchers started to show growing interest in modeling and computer-based applications in support of a paradigm shift. In 2001 Hood and colleagues advocated a systems approach to biology. In their view, a systems-based deciphering of a living organism needs insight into its structure—gene interactions, biochemical pathways, mechanisms by which they arrange cellular properties and intercellular interactions—its dynamics, how it behaves over time—and its controlling mechanisms, its design.5

In the late 1990s, thanks to advances in genome exploration and expression technology, Hood and others paved the way for functional genomics.6 Years before that, Hood had foreseen that technology would eventually streamline the process to the point where a single test would enable the exploration of the whole body functioning.7 The idea was to look beyond gene structure and arrangement to account for their functions. This marked the birth of “omics.” The discovery of the role of regulatory gene networks in the development of organisms led to the view that genes governed the functioning of living systems.8

More recently, Hood and colleagues have argued that healthcare embodies both optimizing wellness and avoiding disease—and that the most effective way to achieve these goals is to generate virtual data clouds for each individual of billions of data points from many different types of data (molecular, cellular, physiological, phenotypic, etc.) that can be integrated to create insights into the “actionable possibilities” that for each patient will optimize wellness and avoid disease.2,9 Along these lines, a group of 107 patients were put through a 10-month longitudinal wellness study with complete genome sequences and blood, stool, and urine assays taken every 3 months. The integrative data from these studies appears transformational. This study embodies all of the principles of P4 medicine—predictive, preventive, personalized, and participatory. A key point is that this type of study will also show the earliest disease transitions—and create the possibility for early diagnostics and therapeutics to change them for each individual from a disease back to a wellness trajectory.

At the same time as Hood's plea in the late 1990s, Noble emphasized the need to bridge biochemistry and the whole organism.10 Furthermore, he noted that the functioning of living systems does not stem only from genes.11 Noble's intuition was later confirmed by an in silico experiment, which also proved that living organisms share at least one property with complex systems: their global functioning is different (more or less) than the sum of their components functions.12,13

Years later, once these early visions had begun to be put in practice and genome exploration techniques had tremendously improved, efforts emerged in favor of the P4 principle: predictive, preventive, personalized, and participatory medicine. This extension of systems biology was coined systems medicine.14 In the intervening period, the term systems physiopathology had been proposed by Boissel et al. for modeling and in silico experimentation of disease mechanisms.15

Biologists and pharmacologists did not wait for the emergence of systems biology, systems physiopathology, predictive pharmacology, or systems medicine to represent quantitative dynamic basal biological phenomena with mathematical symbolism: receptor–ligand interaction, hemoglobin dissociation, enzyme–substrate reaction, compartment model for xenobiotic elimination, to quote a few, have been modeled during the first half of the 20^th century. Later, mathematical models of more complicated biological processes have fostered tremendous progress in the interpretation of experimental data,16 the deciphering of biological enigma,17 of the mechanism of drug cardiac toxicity,18 as well as the understanding of biological systems19 and diseases, either with a phenomenological20 or a mechanistic approach,21 and the discovery, development, and management of drugs,22 including preclinical in silico testing of rare although potentially lethal toxicity.17 There is now mounting empirical evidence that in silico approaches incorporating disease models with pharmacokinetic/ pharmacodynamic (PK-PD) models add value to current R&D methods.22,23

However, challenges have evolved. The issue now goes well beyond the representation of a single biological phenomenon where two biological entities are interacting or a first-order elimination process is at play. Rather, it is to capture in a manageable way thousands of interacting biological entities exhibiting a number of distinctive properties, with various levels of integration, from gene expression up to population, with differing time-scales.

CONCEPTUAL LIMITATIONS OF CURRENT APPROACHES

These commendable efforts point in the same direction: an improvement of our understanding of disease mechanisms to support biomedical research. There is no doubt that, thanks to the development of omics technologies, these efforts have generated a wealth of new knowledge that has led to profound revisions to biological thinking, our understanding of how life functions and diseases occur. Nevertheless, in the context of pharmaceutical innovation, drug R&D and the progress towards more personalized medicine, they exhibit a number of fundamental limitations and have led to misunderstandings between the various stakeholders involved. For instance, Schmidt acknowledges that the exploitation of omics data yields great promise, but as of today has largely failed to rise up to its claims.24

First, contemporary medicine focuses on the study of patients suffering from well-advanced disease. The new systems medicine allows a strategy for looking at the earliest transition of wellness to disease—and opens the possibility of developing new diagnostic and therapeutic reagents to terminate a disease trajectory for each individual early, returning them to wellness.

Second, these approaches rely on data as the primary modeling material, not knowledge. While they often get mixed up, there is a clear differentiation between data and knowledge. The latter is extracted from the former, after analysis, interpretation, and crosschecking. An illustration of a piece of knowledge would be: “Myxobacteria communicate with each other by direct cell contact through a biochemical circuit known as the C-signaling system,” quoted from Tomlin and Axelrod.25 In this particular instance, data were, among others, the reversal frequencies with two doses of C-factor and control in cell aggregation experiments (as shown in figure 5 of ref. 26). This short example underlines that, as in many cases, knowledge derives from data. However, data and knowledge are not used with the same tools. For instance, statistical regression cannot be applied to knowledge, whereas it is quite a standard technique to analyze data. Beyond exploitation tools, data and knowledge have different status and scope. The former have a validity, which is, strictly speaking, limited to the setting they were collected in. The context therefore severely constrains the ability to draw generic conclusions. On the contrary, knowledge can reach a much more general validity status. If new data confirm it, it may well become a scientific fact, which is no longer debated. However, the gap between data and knowledge is not as wide as it would seem. Techniques employed to extract knowledge from data integrate some knowledge. Even a simple linear regression is not fitted to data without prior knowledge of the studied phenomenon. Nevertheless, it remains that data and knowledge do not have the same properties, the same potential, nor do they operate in the same way.

The attention of biologists has focused essentially on collecting ever more data, with little regard for exploiting available knowledge.27 Because data are heavily time- and context-dependent, it makes for a less reliable material to model human biology. We would favor the rigorous analysis and curating of knowledge available in the scientific literature, which is doubling in quantity every decade since the 1950s.26 A lot of information is already out there, scattered across multiple publications in heterogeneous fields of expertise. The postmortem evaluation of a number of avoidable R&D failures makes for a fascinating, if eminently frustrating, lesson, as illustrated by neuroprotective agents for the treatment of acute ischemic stroke.28

Third, they are unable to disentangle correlation and causality. Kitano noted: “Although clustering analysis provides insight into the ‘correlation' among genes and biological phenomena, it does not reveal the ‘causality' of regulatory relationships.”19 If an association between a gene variant and the occurrence of a disease can be viewed as a causal relation (with the interplay of other factors most of the time), provided the chronology criterion is met, a similar association between a tumor mutation and lack of disease progression in treated cancer patients should not be considered as proof of interaction between the treatment and the gene product. A new target based on such a shortcut may well prove a failure. There are plenty of examples in the cardiovascular domain where a number of agents lowering blood cholesterol do not prevent the associated clinical events (e.g., fibrates). The difference between association and causality is central to any successful interpretation of biological mechanisms. In this context, big data and bioinformatics statistical models are valid and predictive only when applied to the same dataset as the one used to design the model in the first place. In the absence of a structured effort to represent available knowledge in a mechanistic way, such models are bound to yield predictions of questionable reliability. A fundamental principle of systems medicine is that the experimental systems (e.g., animal models or stem cells) must be perturbed to verify mechanisms and avoid the ambiguity of correlations that arise from big data.

Fourth, these approaches are based on a bottom-up approach: from genes to population.5 Schmidt stressed that current modeling approaches of pathways and networks miss the ultimate objective, which is to predict clinical outcomes.15 As noted by Noble, there are two opposing strategies to modeling diseases,29 bottom-up and top-down. The former starts at the lowest organizational level (e.g., genes) with the detailed components of the system, their properties and their interactions. Higher levels are constructed from this lowest level, by assembling its components and accounting for interactions between levels. This approach assumes that, in order to understand the functioning of the system, it is first necessary to decipher its lowest organizational levels. The implicit thinking is that living systems are built from a limited number of standard parts, each amenable to standard formal models and that interactions between levels are encoded in the lower levels.30 This is the assumption behind traditional systems biology. This excessive reductionism is exemplified in a study devoted to explaining the poor correlation between genomic data and disease outcome, where the success rate is only around 10.8%, which proposes to describe this “missing inheritance” as “phantom heritability.”31 Such a shortcut, which demonstrates the failure to account for causal mechanisms at every abstraction layer, poses a threat when predictions are applied in clinical research.

On the contrary, the top-down strategy does not make any assumption of that sort. Instead, it postulates that the outcome one wants to predict should be considered from the outset. Thus, modeling starts at the highest level in accordance with the modeling process objective, and focuses on functions rather than entities. Then the modeler replaces each functional block with a model of the mechanism that implements it. In fact, many systems biologists are beginning to use the middle-down and middle-up approach—starting at an integrated data position that avoids many of the pitfalls of a bottom-up approach.

HALLMARKS OF HUMAN BIOLOGY IN SYSTEMS THINKING

Myocardial infarction (refer to Table 1) illustrates the large number of genes, molecules, signals, cell types, organs, and phenomena involved in most human diseases. Living organisms are inherently complex and variable. Complexity, a signature of life, can be defined as a mix of redundancy and feedbacks.32 Even when all of a system's constituent parts are known, failure to account for their quantitative interactions results in the impossibility to predict its behavior. Disease mechanisms exhibit complexity at each layer and in all the interactions between these layers.

Table 1.

A mechanistic understanding of myocardial infarction from pathways to clinical events

Diseases span over multiple layers of complex mechanisms, from impaired signaling pathways to clinical events. Myocardial infarction is a typical illustration.
• From arterial wall cell dysfunction to sudden death, a large number of genes, molecular species, cell types, endocrine and paracrine, as well as neurological regulations, are involved, with feedback loops and redundancies.
• Atherosclerosis is a disease located at discrete sites of the arterial tree. To this date, the triggering event is not fully established. A recent theory defines the entry of monocytes into the arterial wall as the primary cause. But this yields little explanation as to why these monocytes pass through the endothelium in the first place. Nevertheless, it has been established that atherogenesis involves several molecular species and cells: circulating lipoproteins and their oxidized derivatives, endothelial cells, circulating monocytes, macrophages, smooth muscle cells, and extracellular proteins (elastin, collagens, enzymes such as metalloproteases).
• Biological phenomena as diverse as inflammation, cell migration, free radical production, ageing, etc., are also involved. Plaque anatomy and arterial wall structure, as well as phenotypes and proportions of the aforementioned components, are playing a role in the ultimate event, the plaque rupture.
• Critical to the rupture process are fatigue (arterial wall, plaque fibrous cap) and stress-related mechanical phenomena (shear, pulse). Plaque rupture eventually enables interactions between plaque and blood components, leading to the occurrence of a clot. The clot may obstruct the arterial lumen leading to a global ischemia of the downstream tissues, migrate to block a smaller artery or stay in its initial location and end up being incorporated in the plaque after its fibrous organization.
• A coronary plaque rupture can thus result in a variety of outcomes: sudden death, acute coronary infarction, unstable angina, silent infarction, or increased coronary stenosis. When the artery lumen is narrow enough, effort angina or heart failure can occur. Heart failure can also be caused by healed myocardial infarction(s). While atherosclerotic plaque takes decades to build up, its rupture and ischemic consequences develop over a short timespan.

In addition to its sheer complexity, life is a time-dependent process. Time is an unavoidable dimension both in chronic and acute diseases. Fundamental biological phenomena occurring at the outset of any biological process, such as enzyme–substrate interaction, protein synthesis, protein decay, gene expression, cell contraction, cell moving, etc., develop over time. Integration of the fundamental phenomena in systems, either at a lower level (pathways) or at higher ones (tissue, body), with molecule diffusion, signal transduction through molecular networks, cell–cell interactions, neuronal or hormonal signal processing, needs time to be completed. The order of magnitude of the time-constants of the integrating processes, whatever they are, is well above those of fundamental biological processes. Elimination outside the body of xenobiotics or autobiotics, and water, amino acids, carbon, oxygen, and energy supply through feeding and breathing are time-dependent processes spanning over longer horizons. And finally, the occurrence of somatic mutations, mechanical fatigue (blood vessels, joints, bones), multiple-hit processes, etc., which are part of aging and chronic diseases, evolve over an even longer time scale.

Further obstacles arise from the varying time scales of submechanisms involved in any given disease. For myocardial infarction, signaling pathway abnormalities developing over nanoseconds can result in a clinical event occurring years or even decades after the first abnormal molecular functioning. A cascade of dysfunctions, provided enough signals that need to be operating together to sustain a healthy physiological state end up to become ineffective, eventually leads to the clinical event. Multiple interventions are then needed in order to restore synergistic interactions.

Lastly, physiopathology is multiscale in nature. Since all levels are intertwined, the alteration of the behavior of one element at a particular level is likely to have an impact on all other levels, below and above. In this context, statistical or computational biology analyses alone provide only limited assistance to foresee the end results of those alterations. In this sense, Brenner's criticism is relevant: “I contend that this approach will fail because deducing models of function from the behavior of a complex system is an inverse problem that is impossible to solve.”33 But we would disagree with his reasoning, which is that “the essence of all biological systems is that they are encoded as molecular descriptions in their genes and since genes are molecules and exert their functions through other molecules, the molecular explanation must constitute the core of understanding biological systems. We then solve the forward problem of computing the behavior of the system from its components and their interactions.” In our view, this also will fail, as Brenner himself admitted in the Novartis Foundation meeting in 2001: “I know one approach that will fail, which is to start with genes, make proteins from them and to try to build things bottom-up.”34 The solution must include multilevel interactions in an integrative approach.35,36 Thus, systems medicine should go beyond the realm of the intracellular layer to integrate upper physiological layers, including all time and complexity level components.

AN ORIGINAL FRAMEWORK TO BRIDGE SYSTEMS MEDICINE AND PATIENT NEEDS

We propose to enrich the operational framework of systems medicine by combining top-down and bottom-up approaches to empower practical middle-out studies.10 Systems medicine, which purports to design multiscale mathematical disease models, must become the missing link to bridge systems biology and patient outcomes, i.e., patient needs. The systems medicine-driven modeling approach includes all the biological components that are thought to play a role in the course of a disease process, up to clinical events. However, accounting for all of these biological components is not enough to generate reliable clinical outcome predictions.

Systems medicine aims at predicting the course of a disease in a given patient and how far it can be altered by available therapies. Thus, the main object of the prediction should be the absolute benefit (AB), i.e., the difference between two probabilities, the event rate without treatment, and the event rate with a given treatment. Note that AB is time-dependent. The optimal patient-level outcome is obtained by selecting the treatment corresponding to the largest predicted benefit. In practice, the decision paradigm should also account for toxicity and compliance issues.

The fundamental principle of systems medicine should thus be the prediction of benefit–risk for a single subject, a group, or a population. To bridge the gap between simulation outputs and clinical outcomes, an original framework, which is initiated based on top-down modeling principles, then combined with data from bottom-up approaches, thus enabling AB prediction is proposed. It is summarized in Figure 1 and will be discussed further below. Tables 2, 3, 4, 5 and Figure 2 in the next section give an illustration based on research funded by the EU (PL962640). Some results have been published,37 others are still being worked on.

Figure 1.

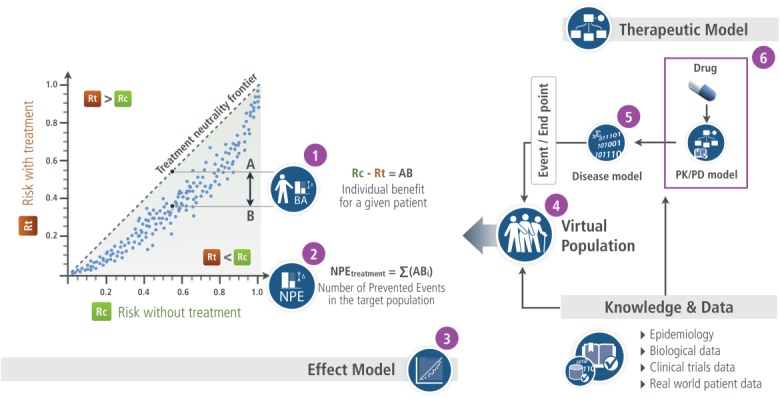
The Effect Model law visual illustration.

Table 3.

Models

Current thoughts on the mechanism of angina pectoris attack assume that the thoracic pain and simultaneous specific EKG changes are due to an imbalance between O2 needs of myocardium and supply by the coronary arteries caused by a reduction of the maximum blood flow. Maximum coronary flow is a function, among others, of the surface of the coronary artery lumen that is reduced when an atherosclerotic plaque induces a coronary stenosis. Angina attack occurs when coronary reserve goes down below a threshold. Further, such a plaque can rupture, leading to a clot and an ischemic clinical event.
Angina pectoris was modeled with a series of algebraic equations that translated heart functioning as a pump, integrating factors that modify stroke volume and heart flow (Q). Heart rate is a major factor. Coronary flow was a function of heart flow and coronary stenosis (d).
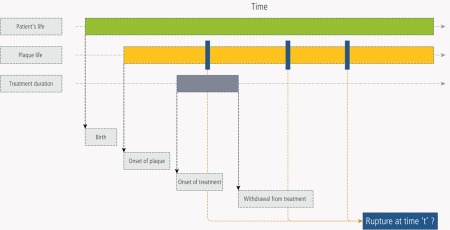
Plaque rupture was assumed to be primarily a mechanical event: rupture occurs when the instantaneous mechanical stress (shear stress) on the plaque can no longer be afforded by its mechanical properties. The latter decrease as a result of fatigue. Fatigue is a function of cumulative systolic stress and plaque components and status, among which the most important is the lipid core. Other factors of plaque mechanical properties are: plaque cap thickness, inflammation, plaque duration, patient age and sex. Fatigue is a life-long process. The dynamic of the whole process should be accounted for (see the figure below). Several sub-models, with specific level of details and mathematical solutions were considered: fluid-structure interactions (one dimensional model, incremental boundary iteration method for the fluid-wall interaction), plaque structure, arterial wall motion (a solid model, a finite-element method) inflammation, fatigue (plaque structure is assumed to be an homogeneous metal, with average properties changing with plaque composition, of which the lipid core is a major component). All of these submodels were considered at a phenomenological level of granularity (i.e. at an upper abstraction level than the molecular one).
The entry in both models was the concentration of ivabradine at its site of action. It was assumed that the main activity of the drug is a reduction of heart rate through a modulation of an atrial potassium channel. The connection between orally given amount of ivabradine and concentration at the drug target site was a PK-PD model fitted to real data with NONMEM. Other models were computed with SAS and Mathematica.
Equations of the angina pectoris attack model: Systolic blood pressure: SBP(t) = 101.1 + 0.74*HR(t) Left ventricle contractility: S(t) = λ (S)*HR(t) Duration of diastole: DD(t) = (60/HR(t))0.5 *[(60/HR(t))0.5 –k] Left ventricular volume: DV(t) = (Vr-C* PV) exp(DD(t)/C* R) – C* PV With: Vr = end-systolic ventricular volume C = ventricular compliance at relax status R = resistances due to viscosity PV = venous pressure From the Starling law, the stroke volume is: SV(t) = S(t)*(DV(t)/SBP(t)) Heart flow: Q(t) = HR(t)*SV(t) Coronary flow: QCOR(t) = α*Q(t) Perfusion pressure through the coronary stenosis: PP(t) = (1.8*QCOR(t)/60*d4) + 6.1*(QCOR(t)2/3600*d4) With: d, diameter (mm) of the artery lumen Coronary reserve: CR(t) = 1 – (PP(t)/(SBP(t) - PV))
Plaque rupture: dynamics of the process
Plaque rupture model flow chart

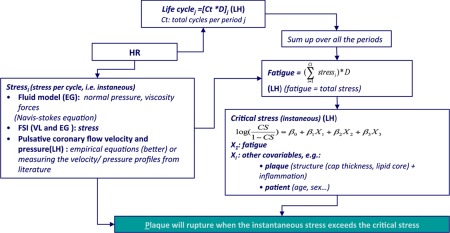Table 4.

Virtual populations

Questions 1 to 4
A database of 1,706 case records of subjects without angina pectoris with a 24-hour recording of heart and blood pressure during normal life. To each case record, values of pharmacokinetic parameters, degree of coronary lumen stenosis, bottom value for coronary reserve, were randomly allocated.
Questions 5 to 8
A 1,000 virtual patient population was designed. Patient descriptor values were randomly drawn from distributions of patient age and sex, heart rate without treatment, instantaneous shear stress, lipid core volume, fibrous cap thickness, high sensitive CRP. All of these descriptors have corresponding model parameters. In addition, fatigue was computed for each patient as a result of plaque age.

Table 5.

Validation: a few examples

Validation of the angina pectoris model
Solid line: real 24-hour heart recording in one patient. Dotted line: simulated 24-hour heart rate recording in the same patient with 40 mg ivabradine bid [from figure 4 in ref. (37)].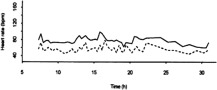
Does-effect relations predicted in-silico (solid lines) versus observed results (bars) produced ex-post.
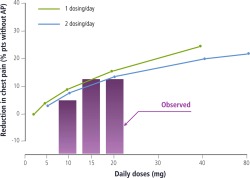Validation of the simulated coronary velocity
Real-life coronary blood velocity profiles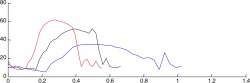
Simulated coronary velocity profiles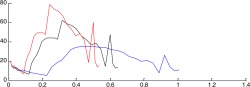
Predicted efficacy compared to efficacy observed in clinical trial.
In the Beautiful randomized trial, in patients with heart rate >70 bpm at baseline, the ratio of rates of admission to hospital for fatal or nonfatal myocardial infraction in patients with ivabradine and patients on placebo was 0.64 after a median follow-up of 19 months. The simulated ratio was 0.66.

Figure 2.

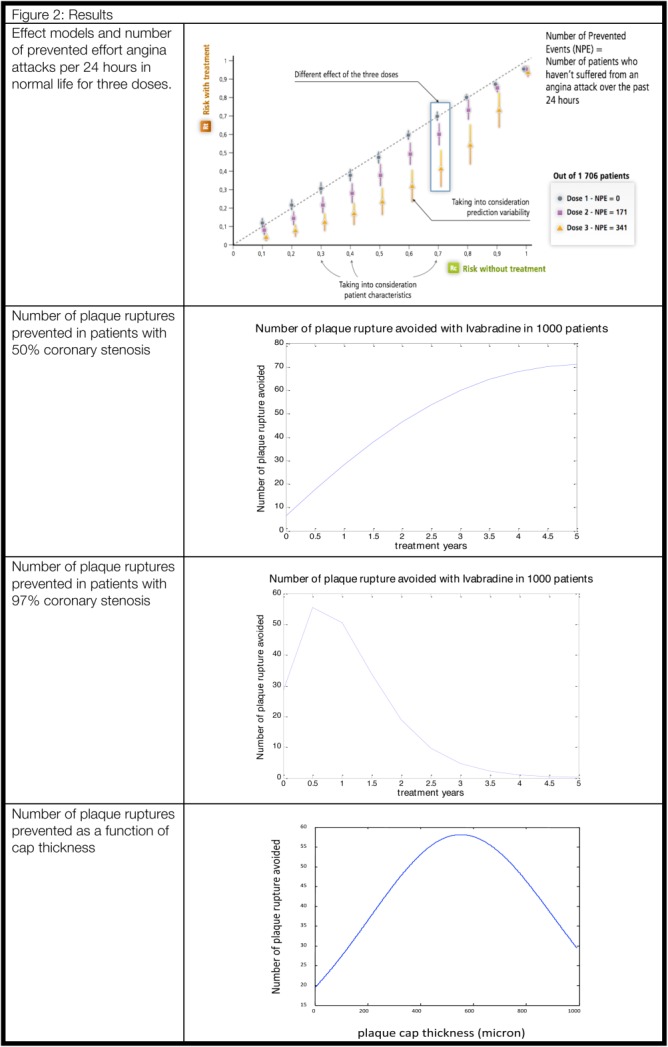
Results.

The cornerstone of this original framework is the Effect Model law37 (#3 in Figure 1, arranged from figure 3 in ref. 38). It refers to the relation between the risk of a clinical event without and with the therapy being developed or available to patients.39 The difference between the two risks gives the absolute benefit ABi for a given patient (i) (#1 in Figure 1). The Effect Model is an emergent property whenever a disease model coupled with a pharmacological model is combined with a virtual population of patients. As such, it is never explicitly modeled.

The number of prevented events (NPE) yields the predicted efficacy at the population or group level (Figure 2). It is equal to the sum of the predicted absolute benefits AB_i for each patient (i) of the population or group (#2 in Figure 1). AB and NPE, which measure the expected clinical benefit, are predictors of individual- and, respectively, population-level effects of the intervention being investigated. They therefore operate as standardized metrics bridging biological alterations with clinical outcomes. AB is the metric for comparing the expected benefits of available interventions for a given individual (personalized medicine or personalized prevention40). NPE is the metric that enables the comparison and selection of available interventions for a group or a population, new targets, or drug under development with comparator(s).

The virtual population represents the population or the group of interest (#4 in Figure 1 and Table 4). Each virtual patient of the population is characterized by a vector of descriptors that translates biological and environmental parameters involved in the course of the disease and interactions between the drug or any intervention and the body. By applying the disease model or the therapeutic model (see below) over the virtual population, one can simulate the patient outcome without or with treatment, and obtain the Effect Model, AB, and NPE. This virtual population can be realistic, i.e., derived from a real population (first virtual population in Table 4). In such a case, some39,41 or all42 descriptors are built from epidemiological and/or clinical trial data. Virtual populations can also be designed from scratch, through the translation of model parameters in virtual patient descriptors (second virtual population in Table 4). In such a case, their distributions are drawn from knowledge extracted from the literature or based on reasonable assumptions. Certain patient descriptors highly correlated with the outcome are potential biomarkers.

The disease model is a mathematical representation of biological entities, physiology, and abnormalities leading to the clinical event (#5 in pharmacological model (#6 in Figure 1 and Table 3) represents what is known about the intervention, i.e., its mode of action—site(s) at which it connects with the body to alter its functioning, affinity to this or these site(s)—and all other interactions with the body: absorption process, transfers, metabolism, etc. This model is continuously updated on the basis of new data accumulated throughout in vitro and in vivo experiments. It connects to the disease model at the target site (Table 3). This enables the exploration of the consequences of alterations, e.g., the dose of the ligand or the compliance of the patient, on the disease progression. The combination of the pharmacological model and the disease model yields the global therapeutic model.

Computing the Effect Model is a two-step process: first, one applies the disease model to the virtual population to generate the distribution of the base (or control) risk (Rc) of suffering from the clinical event under investigation in the population of interest. Then the global therapeutic model is applied to the same virtual population to generate the risk modified by the treatment or drug candidate (Rt). For each patient, AB is the arithmetic difference between Rc and Rt.

Two final comments are worth mentioning. First, while disease models are deterministic, patient genotypic and phenotypic variability is accounted for at the virtual population level. Second, there are as many Effect Models as treatments (or drug candidates) and patient populations or groups.

ILLUSTRATION

This original framework based on the Effect Model law has wide-reaching implications for therapeutic innovation, comparative effectiveness analyses of drug products, and personalized medicine.

One of the key benefits of this approach is its consistency. Regardless of the therapeutic area or real patient population being investigated, AB and NPE operate as standardized metrics to guide decision-making in a variety of settings (e.g., selecting new targets, profiling optimal responders, transposing randomized controlled trial [RCT] results in real-world outcomes, comparing treatment effectiveness on the same population, tailoring treatment strategies to idiosyncratic patient risk profiles).

In the example37 shown in the above and below (Tables 2-5 and Figure 1), there was no integration of omics data, since the model could answer the questions to be addressed without accounting for lower systems levels than physiology. However, there are neither conceptual nor technical barriers to modifying the model in such a way that lower levels of structuring and functional biological components are included. For instance, if Question 7 (Q7) in Table 2 becomes “Are arterial endothelial, smooth muscle cells and neutrophils functional status and extracellular matrix molecules as seen in remodeling arterial tissue factors that can modify the number of prevented plaque ruptures?” then cellular, molecular, and even gene levels would be incorporated. Relevant knowledge from networks and pathways resulting from omics analysis would be used to design these new submodels and data from omics databases required for calibration and validation.

Table 2.

Problem and questions

Problem
Heart rate is a causative cofactor of several vital physiological phenomena: average cardiac output, arterial beat, average myocardial energy consumption. Some diseases or clinical events are mechanistically dependent of these phenomena. Thus, one can question whether modulation of heart rate can alter the course of these diseases.
Leading hypothesis
Funny channel (If) is highly expressed in the sino-atrial node, the atrio-ventricular node, and the Purkinje fibers of conduction tissue. Through its action on the ionic exchanges during the cardiac beat, it controls the rate of spontaneous activity of sinoatrial myocytes, hence the cardiac rate. Ivabradine is a drug that inhibits If activity. Thus it reduces heart rate with, as far as it was known at the time, little or no other activity.
Questions
Q1	Can ivabradine, a heart rate moderator, prevent effort angina pectoris attack?
Q2	If yes, is once a day better than b.i.d.?
Q3	If yes, what is the dose-effect relation?
Q4	What is the expected number of prevented attacks per day?
Q5	Can heart rate reduction (with, e.g., ivabradine) prevent atherosclerotic plaque rupture?
Q6	What would be the number of prevented plaque ruptures?
Q7	What are the factors influencing the number of prevented plaque ruptures?
Q8	How these factors modify the number of prevented plaque ruptures?

This consideration of a possible extension of the number of complexity levels accounted for in the heart rate reduction model illustrates another major advantage of this approach, its flexibility or “Lego–like” nature.

As illustrated by the myocardial infarction example (Table 1), collecting and editing all relevant knowledge is the key demanding step in any modeling process. It consists of a careful analysis of review articles and published original works, knowledge bases, and published models.43

PERSPECTIVES

The middle-out approach we propose is designed to integrate findings from bottom-up and top-down approaches as needed to answer specific biomedical questions. Its standard nature makes it applicable both to personalized medicine (predicting the absolute benefit ABi for a particular patient i) and drug R&D (predicting the NPE to guide decision-making).

Both the myocardial infarction and the ivabradine37 use cases illustrate the potential of this approach in drug R&D decision-making. Provided that a disease model and a virtual population are available, and assuming further that the disease model was rigorously validated and that the procedure to continuously update the model and the virtual population based on emerging knowledge and data is applied properly, the scope of applications to drug R&D is vast. In early research, the maximization of the NPE can serve as the guiding metric to identify new vectors of potential targets. In clinical development, with the coupling of the pharmacological model of the drug under investigation with the disease model, the approach can help identify optimal responders (patients from the virtual population with the largest predicted AB, which can then be compared to actual patient populations), identify companion biomarkers (parameters of the disease model most highly correlated with the maximized NPE), determine the optimal regimen (the one which maximizes the NPE), design dose–effect search or phase III pivotal trial(s), explore the interaction with best of evidence treatment of the condition. Upon completion of phase III trials, relative effectiveness analyses can be performed by benchmarking the product's NPE against the NPE of standard-of-care competitors (the latter computed by switching the relevant pharmacological models). The distribution of ABs and value of NPE in the target population can be explored for marketing purposes, with or without comparison against competitor products. Finally, throughout R&D, exploring the relations between model components and virtual population descriptors on one hand and AB and NPE values on the other can help identify lacking or uncertain knowledge. Designing experiments to close these gaps and feeding back the newly generated knowledge would result in improved predictive capabilities.

This integrated framework promises to identify novel treatment modalities, accelerate the generation of proof-of-concept based on the prediction of a drug's efficacy on carefully characterized patient populations, reduce development costs by focusing spending on the most promising avenues, and bring time to market down thanks to better-designed trials.

The proposed approach, while yielding significant potential, suffers from a major bottleneck, which is the amount of resources (chiefly biomodeler time) required to build knowledge-based multiscale models of diseases. This is essentially due to the time necessary to scan scientific articles to identify, extract, curate, and arrange knowledge about a given pathophysiology. The issue is one of resources as much as it is behavioral in nature, rather than technological. Indeed, researchers of all stripes customarily collect, edit, and manage knowledge. Furthermore, useful knowledge bases such as Ensembl and Uniprot exist. Unfortunately, their form and structure are seldom aligned with modeling objectives and constraints. Making biomedical information useful (i.e., curated, structured, and distributed) for modeling purposes is a major challenge going forward.

Limitations to this approach are fairly generic in the context of complex systems modeling. First, some diseases and biological systems suffer from a limited understanding of their mechanisms. One can argue that even in such cases, a mathematical representation of what little is known is likely to bring value over and above nonquantitative approaches. Second, there are systems for which the mathematical representation is extremely complicated and/or require large computing power. Solutions already exist, such as parallel computing or decreasing the system's complexity without increasing significantly the risk of missing the modeling objective.

All things considered, the major limitation pertains to the paucity of available knowledge either on the mechanism of the disease of interest or the biology and physiology of the systems involved. The latter case is extremely rare. While the former is more common, it is always feasible to build a phenomenological model of what little is known. And it will always be possible to formulate assumptions regarding the mechanism and test them in silico.

CONCLUSION

To be of any help to researchers, practitioners, and patients, P4 systems medicine needs to identify clearly what it is aiming for. We believe the key wording here is the prediction of individual as well as population benefit of interventions, i.e., the gain in disease outcome rates and burden the interventions can provide. The optimization of wellness is a key to maximizing human potential for each individual—improving physiological as well as psychological performances. This is the very essence of the personalized P in P4 medicine. This prediction is the cornerstone of both improved R&D and ethical, practical, and efficient personalized medicine. It cannot rely solely on clinical or omics assessments of individuals, but must integrate them within the physiological and pharmacological framework described above. Thus, clinical and environmental information should be integrated in the prediction algorithm. This algorithm should be designed with all the relevant knowledge abundant in the scientific literature. It should be calibrated and validated with data. This requires easy access to curated and annotated knowledge thanks to an appropriate knowledge management process. Access to databases where data have been checked and annotated is also a prerequisite. Eventually, systems medicine will vastly improve innovation capabilities as well as enable the better use of existing treatments, the repositioning of drugs, the definition of target populations, and the combination of treatments, by integrating methods, data, and knowledge from systems biology, physiology, epidemiology, and clinical studies. This is one of the key objectives of the European Union research framework program “Horizon 2020.” The Effect Model framework introduced in this article is being applied to the management of chronic lung allograft dysfunction, with the objective to provide clinicians with personalized medicine capabilities in order to improve postlung-transplantation survival.44

Conflict of Interest

FHB is Chief Executive Officer of Novadiscovery. JPB is Chief Scientific Officer of Novadiscovery.