Constant pH Molecular Dynamics of Proteins in Explicit Solvent with Proton Tautomerism

Abstract

pH is a ubiquitous regulator of biological activity, including protein-folding, protein-protein interactions and enzymatic activity. Existing constant pH molecular dynamics (CPHMD) models that were developed to address questions related to the pH-dependent properties of proteins are largely based on implicit solvent models. However, implicit solvent models are known to underestimate the desolvation energy of buried charged residues, increasing the error associated with predictions that involve internal ionizable residue that are important in processes like hydrogen transport and electron transfer. Furthermore, discrete water and ions cannot be modeled in implicit solvent, which are important in systems like membrane proteins and ion channels. We report on an explicit solvent constant pH molecular dynamics framework based on multi-site λ-dynamics (CPHMD^MSλD). In the CPHMD^MSλD framework, we performed seamless alchemical transitions between protonation and tautomeric states using multi-site λ-dynamics, and designed novel biasing potentials to ensure that the physical end-states are predominantly sampled. We show that explicit solvent CPHMD^MSλD simulations model realistic pH-dependent properties of proteins such as the Hen-Egg White Lysozyme (HEWL), binding domain of 2-oxoglutarate dehydrogenase (BBL) and N-terminal domain of ribosomal L9 (NTL9), and the pK_a predictions are in excellent agreement with experimental values, with a RMSE ranging from 0.72 to 0.84 pK_a units. With the recent development of the explicit solvent CPHMD^MSλD framework for nucleic acids, accurate modeling of pH-dependent properties of both major class of biomolecules – proteins and nucleic acids is now possible.

1. INTRODUCTION

pH is one of the critical regulators of biological activity. Enzymatic activity is optimized within a narrow pH range,¹ often requiring the participation or presence of ionizable residues such as aspartic acid, glutamic acid and/or histidine in the active site,² and accurate measurement of their pK_a values is crucial in understanding the catalytic mechanism.^3–5 In recent years, the role of pH regulation in nucleic acid systems has been acknowledged,^6,7 where parallels to proteins can be drawn, such as the catalytic activity of ribozymes (ribonucleic acid enzyme),^8–11 demonstrating the ubiquity of pH regulation in biological processes. Apart from its influence on catalytic activity, pH regulation has been observed in numerous other processes including protein folding,^12–15 protein-protein interactions,¹⁶ protein-substrate binding,^17,18 translational recoding,¹⁹ and aberrant pH regulation has even been implicated in cancer-related physiology.²⁰ As such, specific examples of pH-dependent properties encompass a wide variety of systems, such as the catalytic mechanism of dihydrofolate reductase,²¹ proton gradient driven ATP synthesis,²² activity of the U6 intramolecular stem-loop of the spliceosome complex²³ and the influenza virus haemagglutinin.²⁴

While the pK_a values of amino acid monomers have been known for decades, the microenvironment around the residue located in a protein environment may alter its pK_a value. Thus, the ability to measure the microscopic pK_a of a site-specific residue is invaluable in identifying key titrating residues and understanding the mechanism of these pH-dependent biological processes. Using staphylococcal nuclease and its mutants as a model system, Garcia-Moreno and co-workers undertook a series of comprehensive investigations into the effect that the local microenvironment has on the perturbation of the pK_a values of protein residues.^25–28 Their effort has cumulated in a joint collaboration between experimentalist and theoreticians, where the current state-of-the-art computational methods for predicting protein pK_a values were evaluated against experimentally measured pK_a values.^29,30

One major physics-based approach that has emerged over the years to treat electrostatics in proteins and nucleic acids is the Poisson-Boltzmann (PB) equation methodology, which has achieved reasonable success in predicting protein pK_a values.³¹ A key limitation of initial PB methods was the lack of conformational flexibility, although this has been partially addressed using approaches like tuning the effective protein dielectric constant³² and including representations of multiple conformations.^33,34 The need for conformational flexibility led to the development of the other major physics-based approach in computational pK_a predictions, which is based on molecular dynamics (MD) simulation. Warshel and co-workers were the first to demonstrate the use of free energy calculations to calculate the pK_a values of protein residues.^35–38 Subsequent developments in the MD community have sought to couple the protonation state of the titrating residue with the dynamics of the protein itself. Such pH-coupled simulations, which have been termed constant pH molecular dynamics (CPHMD), are uniquely suited to model realistic pH-dependent responses, even in systems where there is limited experimental data because no a priori information on the identity of key titrating residues and their protonation state is required.

The CPHMD methodology has been implemented using two distinct approaches, which vary in the manner in which the titration coordinates are treated – either discretely or continuously.³⁹ In the discrete CPHMD variant, the MD sampling of atomic coordinates is combined with the Monte Carlo (MC) sampling of protonation states. At regular intervals during a typical MD simulation, a MC step is performed to determine the change of the protonation state. Discrete CPHMD was first reported by Bürgi et. al.,⁴⁰ which was computationally expensive at that time and suffered from convergence issues, owing to the fact that it was performed in explicit solvent and used the more expensive thermodynamic integration approach to calculate the energies used in the MC evaluation step. Baptista and co-workers reported a similar discrete CPHMD implementation but used the Poisson-Boltzmann finite-difference method to calculate the energies used in the MC evaluation step.^41–43 With the advances in implicit solvation models around this time,^44,45 and the initial convergence issues reported for explicit solvent CPHMD,⁴⁰ subsequent developments in discrete CPHMD by Dlugosz and Antosiewicz,^46,47 and Mongan et. al.,⁴⁸ were implemented using a Generalized-Born (GB) implicit solvent model. More recent improvements in the discrete CPHMD community have been focused on achieving better sampling by enhanced sampling techniques, such as Accelerated Molecular Dynamics by Williams et. al.⁴⁹ and replica exchange strategies by Roitberg and co-workers.^50–52 Others in the field, namely Warshel and co-workers have focused on developing a more physically realistic form of CPHMD,⁵³ using time-dependent MC sampling of the proton transfer process,⁵⁴ and the empirical valence bond (EVB) framework to simulate proton transfer between solute and solvent.⁵⁵

By contrast, in the continuous CPHMD variant, which were first reported by Baptista et. al.⁵⁶ and Borjesson et. al.,⁵⁷ titration coordinates can be treated as mixed states. In the continuous CPHMD variant developed by Brooks and co-workers, the titration coordinate represents an instantaneous microstate, and it is propagated continuously between the protonated and unprotonated states using the λ dynamics approach.^58–60 Continuous CPHMD allows one to avoid sudden jumps in potential energy that occur after a successful MC move in the discrete CPHMD variant, and potentially avoids artifacts that may be caused by the MC moves in titration coordinates. Additionally, continuous CPHMD facilitates coupled proton moves, which would need to be engineered as specific move types in the MC-based variant. Continuous CPHMD was originally implemented in implicit solvent,⁶¹ improved to account for proton tautomerism,⁶² and it provided the first demonstration of using enhanced sampling strategies to accelerate sampling and convergence in CPHMD simulations.⁶³ The effectiveness of continuous CPHMD has been demonstrated on numerous pH-dependent systems, including of protein folding,^64,65 aggregation of Alzheimer's beta-amyloid peptides,⁶⁶ pH-triggered chaperon activity of HdeA dimers,⁶⁷ electrostatic effects on protein stability,⁶⁸ self-assembly of spider silk proteins,⁶⁹ and RNA silencing in the carnation italian ringspot virus.⁷⁰ Other investigators in the field have also seen a number of successes using discrete CPHMD simulations.^71–73

While the move to implicit solvent CPHMD has obvious advantages in sampling and convergence, a number of unresolved issues have emerged over the years. It has been reported that the generalized Born implicit solvent model underestimates the desolvation of buried charge-charge interactions,⁶³ causing a systematic overstabilization of the ionized form⁷⁴ and consequently increasing the error of predicted pK_a values. In addition, these models are known to cause structural compaction which may distort the overall structure,^68,75 introducing another source of error to the pK_a calculations. Furthermore, in systems such as ion channels^76–78 and some transmembrane proteins,⁷⁹ where the microscopic interactions of discrete ions and water with the protein are important, the use of an explicit solvent representation of the solvent environment is desirable. Thus, recent developments in the continuous CPHMD community have been focused on re-introducing explicit solvent into the CPHMD framework. Wallace and Shen were the first to report a hybrid solvent CPHMD model, and showed that using an explicit solvent representation of the protein’s conformational dynamics can reduce the errors introduced by the GB implicit model.⁷⁵ Around the same time, the first “pure” explicit solvent CPHMD was reported by Grubmüller and co-workers, with a proof of concept demonstration for model amino acid compounds.⁸⁰ Brooks and co-workers subsequently reported another “pure” explicit solvent constant pH MD simulation, termed as CPHMD^MSλD as it is based on the newer multi-site λ-dynamics (MSλD) framework.^81,82 CPHMD^MSλD was developed initially for investigating pH-dependent behavior of nucleic acid systems and it has been validated on both model nucleotides⁸³ and larger RNA systems.⁸⁴ The initial challenges associated with convergence in explicit solvent were noted by practitioners in the field,^80,83 and have been addressed to some extent using enhanced sampling strategies.^75,85 More recent developments in enhanced sampling methods, such as Orthogonal Space Random Walk by Yang and co-workers have demonstrated that accurate pK_a calculations for buried protein residues in explicit solvent simulations can be achieved,⁸⁶ indicating that practical challenges first encountered by Bürgi et. al. over a decade ago will be resolved eventually.

In this article, we will adopt the explicit solvent CPHMD^MSλD framework and extend its application to include proteins. We apply the multi-site λ-dynamics (MSλD) algorithm to seamlessly perform alchemical reactions between protonation and tautomeric states, and develop a novel biasing potential to ensure that the physical end-states are adequately sampled. The quality of the CPHMD^MSλD model for proteins will be demonstrated by its ability to reproduce the pK_a values of model compounds, simulate coupled pH-dependent behavior of dipeptides, and to accurately reproduce experimental pK_a values of proteins, such as the hen egg-white lysozyme (HEWL), the binding domain of 2-oxoglutarate dehydrogenase (BBL) and the N-terminal of ribosomal L9 protein (NTL9).

2. THEORY

2.1 Constant pH Molecular Dynamics Simulations in Explicit Solvent

We briefly review the theory behind constant pH molecular dynamics (CPHMD). In CPHMD, the protonation state of the titrating residue is described by a continuous variable, λ. The dynamics of λ is described according to multi-site λ-dynamics (MSλD),^81,82 a formalism that couples the dynamics of λ to the dynamics of the protein system. The simulation is under the influence of a hybrid Hamiltonian and its potential energy is described by:

$$U_{\mathit{\text{tot}}}(X,\{x\},\{\lambda \})=U_{\mathit{\text{env}}}(X)+\sum _{\alpha =1}^{N_{\mathit{\text{sites}}}}[{\lambda }_{\alpha ,1}(U(X,x_{\alpha ,1}))+{\lambda }_{\alpha ,2}(U(X,x_{\alpha ,2})\left)\right]$$ (1)

where N_sites is the total number of titrating residues, X represents the coordinates of the environment atoms (i.e., the parts of the protein that are not titrating), and x_α,1 and x_α,2 represent the coordinates of atoms in residue α that are associated with the protonated and unprotonated states, respectively. λ serves as a scaling factor that is associated with each titrating residue α and its value describes the physically relevant protonated (λ_α,1 = 1) and unprotonated (λ_α,2 = 1) states. Details about the theoretical and methodological treatment of λ dynamics can be found in the following references.^81,82

CPHMD simulations are calibrated on model compounds (i.e., amino acids) to reproduce the external pH environment. Modeling of the external pH is achieved by introducing a fixed biasing potential parameter (${\mathrm{F}}_{\alpha ,2}^{\text{fixed}}$) to the unprotonated state, which results in the biased potential energy function:

$$U_{\mathit{\text{tot}}}(X,\{x\},\{\lambda \})=U_{\mathit{\text{env}}}(X)+\sum _{\alpha =1}^{N_{\mathit{\text{sites}}}}\left[{\lambda }_{\alpha ,1}\right(U(X,x_{\alpha ,1}))+{\lambda }_{\alpha ,2}(U(X,x_{\alpha ,2})-F_{\alpha ,2}^{\mathit{\text{fixed}}}\left)\right]$$ (2)

The free energy of protonation (ΔG_protonation) is used to calibrate the biasing potential (${\mathrm{F}}_{\alpha ,2}^{\text{fixed}}$) that simulates the effect of an external pH environment. By setting the value of ${\mathrm{F}}_{\alpha ,2}^{\text{fixed}}$ to ΔG_protonation, approximately equal populations of protonated and unprotonated states are sampled in the simulation. Under this condition, the external pH environment is equal to the pK_a value of the model compound. To change the pH of the simulation, ${\mathrm{F}}_{\alpha ,2}^{\text{fixed}}$ can be adjusted by the following equation:

$$F_{\alpha ,2}^{\mathit{\text{fixed}}}=\mathrm{\Delta }{\mathrm{G}}_{\text{protonation}}+\text{ln}\left(10\right)k_{B}T(\mathrm{p}{\mathrm{K}}_{\mathrm{a}}-\mathrm{p}\mathrm{H}),$$ (3)

where pH is the external pH of the simulation and pK_a is the experimental pK_a of the model compound. The fixed biasing potential is pre-calculated and its value, corresponding to the specified external pH, is universally applied to all residues of the same type regardless of the protein environment it is in. In explicit solvent CPHMD simulations, when the titration coordinates are allowed to propagate dynamically, the two end points that correspond to physical protonation states may not be sufficiently sampled to yield converged estimates of the pK_a shifts. To ameliorate this issue, the inclusion of an extra variable biasing potential (F^var) is introduced, which can be adjusted to tune the sampling efficiency of titration coordinates and the fraction of physical protonation states:

$$F_{\alpha ,i}^{\text{var}}=\{\begin{array}{cc}\hfill k_{\mathit{\text{bias}}}{({\lambda }_{\alpha ,i}-0.8)}^2;\hfill & \hfill \mathit{\text{if}}{\lambda }_i<0.8\hfill \\ \hfill 0;\hfill & \hfill \mathit{\text{otherwise}}\hfill \end{array}$$ (4)

Thus, in the CPHMD treatment, titratable groups in proteins may be viewed as model compounds that are perturbed by the introduction of the protein environment. Further details on the implementation and calibration of explicit solvent CPHMD^MSλD can be obtained from the following reference.⁸³

2.2 pH Replica Exchange Sampling Protocol

The potential for slow convergence of protonation state sampling in CPHMD simulations has been well documented, and is exacerbated for residues with conformationally-coupled pK_a values, where they undergo a local conformation change that causes them to sample different electrostatic environments yielding distinct microscopic pK_a values.^49,84,87 Early work by Brooks and co-workers on protein CPHMD simulations has demonstrated that the introduction of a temperature replica exchange (T-REX) protocol can significantly accelerate sampling to address such issues.⁶³ However, using T-REX in explicit solvent MD simulations typically incurs a large computational expense, for example, a moderate sized protein of ~100 residues (40k atoms when solvated) requires at least 20 replicas to achieve reasonable exchange rates between adjacent temperature replicas, and when simulating CPHMD across a reasonable pH range (e.g., pH 5 to 9), the total number of replicas required increases to ~100. Therefore, in this paper, we used a pH replica exchange (pH-REX) sampling strategy instead, and the pH-REX sampling protocol implemented in our work is based on the work of Wallace and Shen,⁷⁵ where simulations performed at various pH conditions are exchanged based on the following Metropolis criterion:

$$P=\{\begin{array}{cc}\hfill 1;\hfill & \hfill \text{if}\mathrm{\Delta }\le 0\hfill \\ \hfill \text{exp}(-\mathrm{\Delta });\hfill & \hfill \text{otherwise}\hfill \end{array}\text{where}\mathrm{\Delta }=\beta [\begin{array}{c}{U}^{\mathrm{p}\mathrm{H}}(\{{\lambda }_i\};\mathrm{P}\mathrm{H}\text{'})+U^{\mathrm{p}\mathrm{H}}(\{{\lambda }_i\text{'}\};\mathrm{p}\mathrm{H})\hfill \\ -U^{\mathrm{p}\mathrm{H}}(\{{\lambda }_i\};\mathrm{p}\mathrm{H})-U^{\mathrm{p}\mathrm{H}}(\{{\lambda }_i\text{'}\};\mathrm{p}\mathrm{H}\text{'})\hfill \end{array}]$$ (5)

where β is 1/k_bT, the first two terms, U^pH({λ_i};pH') and U^pH ({λ _i'};pH) are the pH-biasing potential energies for the two adjacent replicas after the exchange, and the next two terms, U^pH({λ_i};pH') and U^pH ({λ _i'};pH') are the corresponding energies for the respective replicas before the exchange.

3. METHODS

3.1 Generating Input Structures

Input structures of the peptide compounds were generated from the CHARMM topology files using the IC facility in CHARMM.⁸⁸ The input structure for the protein hen egg-white lysozyme (HEWL), the 45-residue binding domain of 2-oxoglutarate dehydrogenase multienzyme complex (BBL) and the 56-residue N-terminal domain of ribosomal L9 protein (NTL9) were generated from the PDB file (accession codes: 2LZT, 1W4H, 1CQU respectively). Hydrogen atoms were added using the HBUILD facility in CHARMM. Model compounds (single amino acids), test compounds (dipeptide sequences) and the proteins were solvated in a cubic box of explicit TIP3P water⁸⁹ using the convpdb.pl tool from the MMTSB toolset.⁹⁰ For each protein, the system was first neutralized, before an appropriate number of Na⁺ and Cl⁻ counterions was added to match the experimental ionic strength of 100mM NaCl. All systems were capped at the N-terminus and C-terminus using CHARMM’s ACE and CT2 patches. Additional patches were constructed to represent the protonated forms of Asp, Glu, His and Lys. All of the associated bonds, angles and dihedrals were explicitly defined in the patch. Each titratable residue was simulated as a hybrid model that explicitly included atomic components of both the protonated and unprotonated forms. The CHARMM parameters for the partial charges of aspartic acid, glutamic acid and lysine used in this study were reported previously by Lee et. al.⁶¹ Partial charges for the three protonation states of histidine were obtained without modification from the HSP, HSE and HSD residues as reported in the CHARM22 all-atom force field for proteins.⁹¹

3.2 Simulation Details

MD simulations were performed within the CHARMM macromolecular modeling program (version c36a6) using the CHARMM22 all-atom force field for proteins⁹¹ and TIP3P water.⁸⁹ The SHAKE algorithm⁹² was used to constrain the hydrogen-heavy atom bond lengths. The Leapfrog Verlet integrator was used with an integration time step of 2 fs. A non-bonded cutoff of 12 Å was used with an electrostatic force shifting function and a van der Waals switching function. While group-based 8 Å cutoffs investigated in the 1990s were notoriously poor in reproducing accurate dynamics of biomolecules relative to the Ewald summation technique,^93,94 modern atom-based cutoff schemes with sufficiently long cutoff distances (12 Å),⁹⁵ such as those employed in this study, has been shown to be comparable to the Ewald summation technique in modeling the dynamics of both proteins⁹⁶ and nucleic acids.⁹⁷ Titration was performed in the multi-site λ-dynamics framework (MSλD)^81,82 within the BLOCK facility, using the λ^Nexp functional form for λ (FNEX) with a coefficient of 5.5.^81,82 The titratable fragment included the protonation site and adjacent atoms whose partial charge differed according to the protonation state. The environment atoms were defined as all atoms that were not included in the titratable fragments. Linear scaling by λ was applied to all energy terms except bond, angle and dihedral terms, which were treated at full strength regardless of λ value to retain physically reasonable geometries. Each θ_α was assigned a fictitious mass of 12 amu•Å₂ and λ values were saved every 10 steps. The temperature was maintained at 298K by coupling to a Langevin heatbath using a frictional coefficient of 10ps⁻¹. After an initial minimization, the system was heated for 100 ps and equilibrated for 100ps (for amino acid compounds and dipeptides) or 400 ps (for HEWL, BBL and NTL9). This was followed by a production run of 3 ns (for amino acid compounds, dipeptides and NTL9), 5 ns (for BBL) or 20 ns (for HEWL). CPHMD^MSλD simulations were performed across the pH range, with integer value pH spacing, as indicated in the titration curves (see Results and Discussion), from pH 1 to 7 for Asp and Glu, pH 4 to 9 for His, pH 7 to 12 for Lys, pH 0 to 8 for HEWL, and pH 0 to 5 for BBL and NTL9. In the pH-REX simulations, exchange attempts were made at every 1 ps. All CPHMD^MSλD simulations were performed in triplicate.

3.3 Calculation of pK_a value

The populations of unprotonated (N^unprot) and protonated (N^prot) states are defined as the total number of times in the trajectory where conditions λ_α,1 > 0.8 and λ_α,2 > 0.8 are satisfied respectively. They are used in the calculation of the fraction of physical states, which is the ratio of N^unprot and N^prot states over all states (which include intermediate λ values). The unprotonated fraction (S^unprot) is calculated for each pH window:

$$S^{\mathit{\text{unprot}}}(\mathrm{p}\mathrm{H})=\frac{N^{\mathit{\text{unprot}}}(\mathrm{p}\mathrm{H})}{N^{\mathit{\text{unprot}}}(\mathrm{p}\mathrm{H})+N^{\mathit{\text{prot}}}(\mathrm{p}\mathrm{H})}$$ (6)

S^unprot values computed across the entire pH range, were then fitted to a generalized version of the Henderson-Hasselbalch (HH) formula⁹⁸ to obtain a single pK_a value:

$$S^{\mathit{\text{unprot}}}(\mathrm{p}\mathrm{H})=\frac{1}{1+{10}^{-n(pH-pKa)}}$$ (7)

To illustrate the effect of coupled titrating residues, CPHMD^MSλD simulations on several dipeptides (see Supporting Information for discussion) were also performed. For these dipeptide simulations, the protonation state statistics for a specific residue may not be associated with the titrating residue, because the symmetry of the system may render the environment around each titrating residue to be similar. Therefore, the pK_a calculation has to be performed using a modified version of eqn. 7, where the combined S^unprot ratio for all i residues is fitted to the following equation:

$$\sum _i^N{S}_i^{\mathit{\text{unprot}}}(\mathrm{p}\mathrm{H})=\sum _i^N\frac{1}{1+{10}^{-(pH-pK{a}_i)}}$$ (8)

In this study, the reported pK_a value and its uncertainty correspond to the mean and standard deviation calculated from 3 sets of independent runs.

4. RESULTS & DISCUSSION

4.1 Optimization of Model Potential Parameters for 2-State Titrations

As with the previous implementation of CPHMD^MSλD for nucleic acids,⁸³ we used the free energy of deprotonation as the fixed biasing potential (F^fixed) in our simulation. The free energy of deprotonation was calculated for each isolated model compound embedded in explicit solvent using traditional λ-dynamics at zero ionic strength. In order to facilitate transitions between the two protonation states, we optimized the force constant (k^bias) on the variable biasing potential (F^var) that was applied to each model compound, and targeted to achieve a maximal value of the transition rate in λ-space (i.e., titration coordinate sampling), while maintaining a high fraction of physical ligands. The optimized parameters for the model potentials are reported in Table I. Calculation of the sampling statistics (see Table S1) indicates that the fraction of physical states was maintained at ~70% and transitions in λ-space were ~50 transitions/ns. The sampling properties of our model amino acids are comparable to previous work performed on model nucleosides in explicit solvent.⁸³

Table I.

Parameters for the Model Potential for 2-state Titrations

Residue	ΔGprotonation (kcal/mol)	Fvar (kcal/mol)	Ref pKa
		kbias
Asp	43.71	34.00	4.00
Glu	46.00	34.25	4.40
His-δ	−3.58	26.00	7.00
His-ε	−12.26	26.00	6.60
Lys	−23.02	29.50	10.40

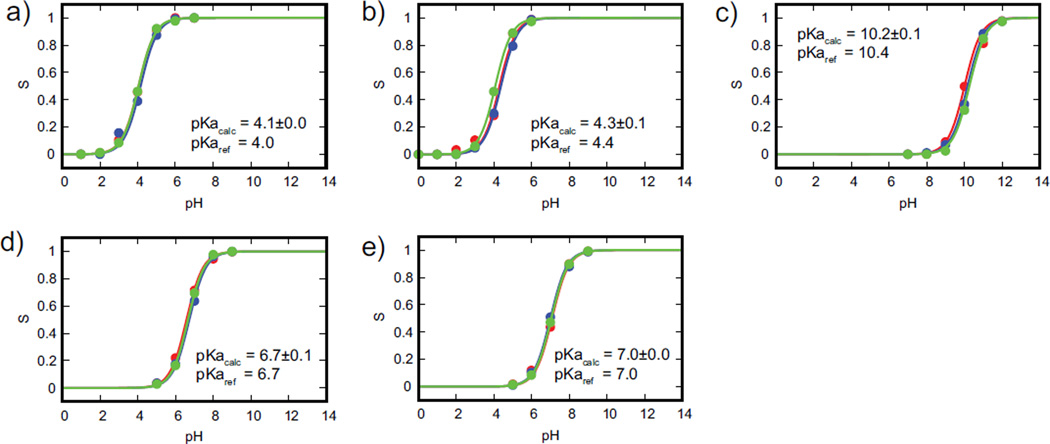
Next, we performed a 2-state titration simulation, where only two titrating states (protonated and unprotonated) were simulated, and tautomers for each protonation state were not explicitly modeled. The titration curves for our model compounds are illustrated in Figure 1. The calculated pK_a of aspartic and glutamic acid for a two-state titration (i.e., without proton tautomerism) was 4.1 and 4.3 pK_a respectively, which is within ±0.1 pK_a units from their experimental pK_a values of 4.0 and 4.4 respectively.⁹⁹ For the two-state titration of histidine, where either Nδ or Nε was titrated, the pK_a values obtained were 6.7 and 7.0 respectively,¹⁰⁰ which is identical to their experimental pK_a values. Finally, the calculated pK_a of lysine was 10.2, which is in close agreement with the experimental pK_a value of 10.4.⁹⁹ The excellent agreement between our model compounds calculated pK_a values and their experimental values indicate that the sampling of titration coordinates in our CPHMD^MSλD simulations was sufficient to yield accurate results.

Figure 1.

Titration curve of model compounds: (a) aspartic acid, (b) glutamic acid, (c) lysine, (d) (d) histidine-δ and (e) histidine-ε. Calculated pK_a values of model compounds are in excellent agreement with experimental pK_a values. Colors represent the results from the triplicate runs.

4.2 Optimization of Model Potential Parameters for 3-State Titrations

The original form of the F^var potential assumed the existence of only two states. When accounting for proton tautomerism and thus three states, the original form was not suitable because it frequently sampled an intermediate state of the two tautomers. This intermediate state is typically characterized by λ_α,1 ≈ 0, λ_α,2 ≈ 0.5 and λ_α,3 ≈ 0.5, which corresponds to a half proton on both the Nδ and Nε protonation sites (using His as an example), and this represents an unphysical state whose sampling should be minimized. The existence of the intermediate state can be rationalized by considering that the free energy barrier for conversion between the two protonation states would be larger than the conversion between the two tautomers, as in the former process there is a change in the net charge of the system and a greater reorganization of the distribution of partial charges. The combined functional form of the original F^var potential that uses the same 0.8 cutoff in the definition of physical protonation states (see Methods section) as expressed in eqn. 9, where λ_α,1, λ_α,2 and λ_α,3 denote the alchemical scaling factors associated with each of the 3 states for some residue α, does not account for the uneven barrier height of the different alchemical reactions.

$$F_{\alpha }^{\text{var}}=k_1{({\lambda }_{\alpha ,1}-0.8)}^2+k_1{({\lambda }_{\alpha ,2}-0.8)}^2+k_1{({\lambda }_{\alpha ,3}-0.8)}^2$$ (9)

To avoid the intermediate tautomeric states, we modified the existing F^var potential by including additional cross terms (k₂ expressions) to account for uneven barrier heights, and a final term (k₃ expressions) was added to ensure that the relative free energy of the end-states were not altered. The resulting functional form as outlined in eqn. 10 results in a more versatile biasing potential that is suited to address the asymmetry of the potential energy surface associated with changes in both protonation and tautomeric states.

$$F_{\alpha }^{\text{var}}=k_1{({\lambda }_{\alpha ,1}-0.8)}^2+k_1{({\lambda }_{\alpha ,2}-0.8)}^2+k_1{({\lambda }_{\alpha ,3}-0.8)}^2+k_2{({\lambda }_{\alpha ,1}-{\lambda }_{\alpha ,2})}^2{k}_2{({\lambda }_{\alpha ,1}-{\lambda }_{\alpha ,3})}^2-k_3\left({\lambda }_{\alpha ,2}\right)-k_3\left({\lambda }_{\alpha ,3}\right)$$ (10)

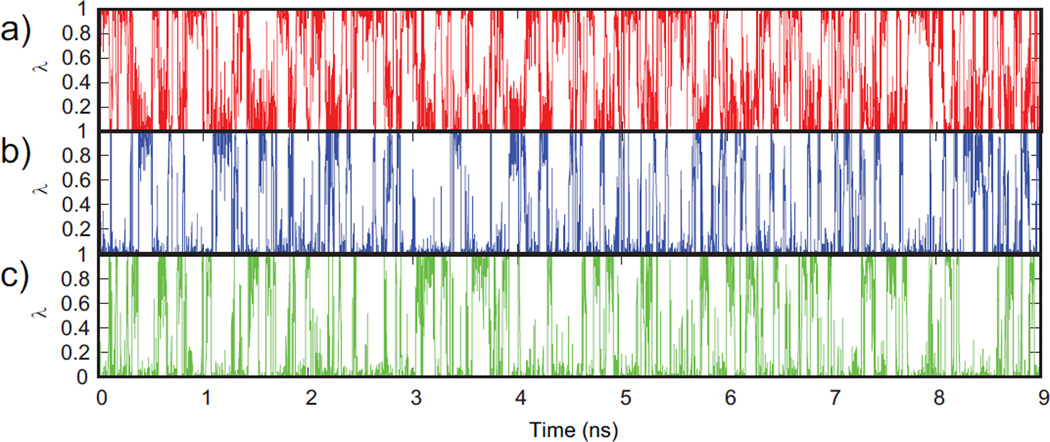
An iterative grid search strategy was used in testing various combinations of the force constants (k₁, k₂, k₃), and the optimal combination is reported in Table II. As illustrated in Figure 2, which shows the time-evolution of λ, all 3 end states for the model compounds were well sampled. Calculation of the sampling statistics as summarized in Table III indicates that the fraction of physical states was maintained above 70%, confirming that the modified F^var potential does not trap λ in an unphysical intermediate state. The transitions in λ-space were ~50 transitions/ns, which is comparable to the statistics obtained from 2-state titrations of the model compounds.

Table II.

Parameters for the Model Potential for 3-state Titrations

Residue	ΔGprotonation (kcal/mol)	Fvar (kcal/mol)			Ref pKa
		k1	k2	k3
Asp-T	43.30	−16.5	18.5	−18.5	4.00
Glu-T	45.59	−16.0	18.5	−18.5	4.40
His-T	−3.58/−12.26	8.0	6.0	−6.0	6.45

Figure 2.

Titration coordinate transitions of aspartic acid at pH 4 for (a) unprotonated state, (b) protonated tautomer #1 and (c) protonated tautomer #2 shows that the physical end states are well sampled.

Table III.

Sampling characteristics of 3-state titration simulations performed at the pH closest to the model compound’s pK_a value. Using pH-REX greatly accelerates sampling of titration coordinates with minimal loss in the fraction of physical states (FPS).

Residue	pH	Normal MD		pH-REX
		FPS	Transition(ns−1)	FPS	Transition(ns−1)
Asp-T	4	0.78 ± 0.01	50 ± 1	0.78 ± 0.01	294 ± 16
Glu-T	4	0.76 ± 0.01	46 ± 7	0.75 ± 0.00	322 ± 21
His-T	7	0.81 ± 0.02	60 ± 6	0.81 ± 0.01	298 ± 12

While the sampling efficiency in λ-space of model compounds allows us to reproduce the pK_a values of the model compounds, the transition rate is nevertheless limited to ~50 transitions/ns. In our previous evaluation of explicit solvent CPHMD^MSλD simulations of larger nucleic acid structures, slower pK_a convergence was observed,⁸⁴ and it is likely that protein systems will encounter similar issues as well. The sampling of titration and spatial coordinates can be accelerated using a pH-REX sampling strategy.⁸⁵ Therefore, we have applied pH-REX sampling, and as illustrated in Table III, it resulted in a 6-fold improvement in λ-space sampling of model compounds with effectively no loss in the fraction of physical states. As pH-REX sampling confers significant improvement over straightforward MD simulations and requires negligible overhead in terms of computational cost, the results presented in the subsequent sections are obtained from pH-REX CPHMD^MSλD simulations unless specified otherwise.

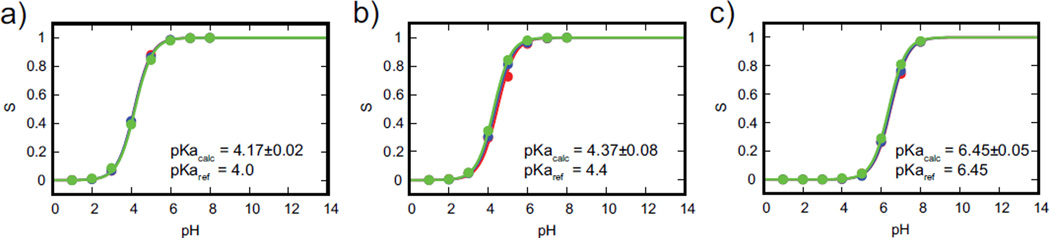
We performed a 3-state titration on the model compounds, where alchemical transformations across different protonation states and across different tautomers of the same protonation state were explicitly modeled. The tautomeric titrations of aspartic and glutamic yielded a pK_a of 4.4 and 4.8 respectively, which matches well with the macroscopic pK_a of 4.35 and 4.70 when the double degeneracy of the protonated states is taken into account.⁶² However, since the experimental pK_a measured does not distinguish between the tautomeric forms, we recalibrated the fixed biasing potential in our CPHMD^MSλD simulations to reproduce the experimentally measured macroscopic pK_a values. This was achieved by reducing the biasing potential at pH=pK_a by k_bTln(2) = 0.41 kcal/mol, which accounts for the degeneracy of the tautomeric protonated states. Our approach is different from that of Khandogin and co-workers,⁶² where a post-correction factor of 0.3 pK_a units was applied to tautomeric residues. However, the net result in both approaches is the same, in the sense that the final pK_a value calculated accounts for tautomer degeneracy. The titration curves for our model compounds with proton tautomerism are illustrated in Figure 3. The calculated pK_a of aspartic and glutamic acid was 4.17 and 4.37 respectively, which is good agreement with experimental pK_a values. For histidine tautomeric titration, no re-calibration was performed because the pK_a measured by experiments were microscopic pK_a associated with the titration at the Nε and Nδ sites, and the fixed biasing potential applied to each tautomer was identical to those used in the 2-state titration setup. Our calculated pK_a for the histidine tautomer was 6.45, which is identical to the expected macroscopic pK_a value of 6.45.⁶²

Figure 3.

Titration curve of model compounds with proton tautomerism: (a) aspartic acid, (b) glutamic acid and (c) histidine. Calculated pK_a values of model compounds show excellent agreement with experimental pK_a values. Colors represent the results from the triplicate runs.

4.3 pK_a Calculations of Proteins: Hen-Egg White Lysozyme (HEWL)

The HEWL protein is a well-studied protein system that contains the 3 most common titrating residues (Asp, Glu, His) with microscopic pK_a values for each residue that have been measured in a number of experimental studies.^101–106 It is perhaps the closest thing to a “universal benchmark” system that has been evaluated by numerous CPHMD implementations over the years.^{43,48,49,51,63,75,107} To the best of our knowledge, all existing “pure” explicit solvent CPHMD simulations reported in the literature have only been demonstrated on small peptide compounds⁸⁰ and simple organic molecules.¹⁰⁸ We performed a 20 ns pH-REX CPHMD^MSλD simulation of HEWL, which is the first example of explicit solvent CPHMD simulation on a full protein to be reported.

pK_a calculations over 5 ns interval segments of our pH-REX CPHMD^MSλD trajectory show that good convergence is achieved within 20 ns (Table S3). The difference in pK_a values across our triplicate runs is small, typically between 0.2 to 0.3 pK_a units, demonstrating that our results are robust and reproducible. The accuracy of our calculated pK_a values are then compared to experimental measurements from consensus NMR titrations.¹⁰⁶ As summarized in Table IV and Figure S3, the calculated pK_a values are in good agreement with experiment, with a root-mean-square-error (RMSE) of 0.85 pK_a units and an average unsigned error (AUE) of 0.68 pK_a units. Nielson and co-workers previously estimated that experimental pK_a values reported in the literature on average may vary by 0.5 pK_a units depending on the experimental method and/or protocol used to make the measurements.¹⁰⁶ This suggests that the accuracy of our pH-REX CPHMD^MSλD simulations are approaching the uncertainty of experimental pK_a values. Next, we identified the residues that had errors in their calculated pK_a values, which we defined as having more than 1.0 pK_a unit difference between calculated and experimental values. Asp-119 was underpredicted by −1.9 pK_a units, which suggests that the unprotonated state is overstabilized in our simulations. Analysis of its microenvironment indicates that persistent hydrogen bond interactions between the carboxylic oxygens of Asp-119 and the amide backbone hydrogen of Gln-121 and Ala-122 were present even in a low pH environment (Figure S4), which accounts for the extra stabilization of the unprotonated state of Asp-119. Similar underprediction of Asp pK_a values has been documented in other CPHMD work, where salt bridge interactions were responsible.⁴⁹ When non-salt-bridge configurations were sampled, it resulted in more accurate pK_a results.⁴⁹ This suggests that the apparent error in the Asp-119 pK_a value could be a sampling issue, and more extensive sampling or more aggressive sampling methods may be required when dealing with residues that are “locked” to their initial conformation by strong interactions like hydrogen bonds or salt bridges.

Table IV.

pK_a values of HEWL calculated using implicit and hybrid solvent pH-REX CPHMD simulations as reported by Wallace and Shen,⁷⁵ compared to pK_a values calculated using explicit solvent pH-REX CPHMD^MSλD simulations in this work. Calculated pK_a values with error greater than 1.0 pK_a unit relative to experimental values based on consensus NMR titrations¹⁰⁶ are identified in red.

Residue	Exp pKa	Implicit CPHMD		Hybrid CPHMD		Explicit CPHMDMSλD
		pKa	Error	pKa	Error	pKa	Error
GLU-7	2.6 ± 0.2	2.6 ± 0.1	0.0	2.7 ± 0.0	0.1	2.7 ± 0.1	0.1
HIS-15	5.5 ± 0.2	5.3 ± 0.5	−0.2	6.6 ± 0.1	1.1	6.0 ± 0.2	0.5
ASP-18	2.8 ± 0.3	2.9 ± 0.0	0.1	3.1 ± 0.1	0.3	2.1 ± 0.2	−0.7
GLU-35	6.1 ± 0.4	4.4 ± 0.2	−1.8	7.2 ± 0.2	1.1	7.0 ± 0.3	0.9
ASP-48	1.4 ± 0.2	2.8 ± 0.2	1.4	1.6 ± 0.5	0.2	1.3 ± 0.0	−0.1
ASP-52	3.6 ± 0.3	4.6 ± 0.0	1.0	2.9 ± 0.1	−0.7	4.5 ± 0.3	0.9
ASP-66	1.2 ± 0.2	1.2 ± 0.4	−0.1	1.5 ± 0.6	0.3	1.5 ± 0.1	0.3
ASP-87	2.2 ± 0.1	2.0 ± 0.1	−0.2	1.5 ± 0.4	−0.7	1.3 ± 0.0	−0.9
ASP-101	4.5 ± 0.1	3.3 ± 0.3	−1.2	3.0 ± 0.1	−1.5	5.1 ± 0.5	0.6
ASP-119	3.5 ± 0.3	2.5 ± 0.1	−1.1	2.9 ± 0.1	−0.7	1.6 ± 0.0	−1.9
RMSE		0.94		0.80		0.84
AUE		0.70		0.66		0.68

We compared the performance of explicit solvent pH-REX CPHMD^MSλD simulations to CPHMD models implemented in other solvation models. A number of CPHMD variations have been implemented in AMBER⁴⁸ and GROMACS.⁴³ However, they will not be included our analysis as deconvoluting the effects originating from force field differences to those arising from solvation model differences is not straightforward. Instead, we will focus our analysis on CPHMD variations implemented in CHARMM. The original CPHMD in CHARMM was implemented with a GB implicit solvent model,⁶¹ and we have used the HEWL pK_a values reported by Wallace and Shen for comparison.⁷⁵ Since that work was reported using a pH-REX sampling strategy, we have also eliminated the effects of using different sampling strategies. At the time of writing, there is no “pure” explicit solvent CPHMD based on the CHARMM force field that has been tested on the HEWL protein. However, a close comparison can be made with Shen’s hybrid solvent CPHMD model.⁷⁵ The key methodological difference between explicit and hybrid solvent models is that the evaluation of free energies of deprotonation and the forces on the fictitious λ particles that govern the titration coordinates are calculated using a GB implicit solvent model in Shen’s hybrid solvent CPHMD model, whereas in our explicit solvent CPHMD^MSλD model there is no use of the GB implicit solvent model in any part of the calculation. Unfortunately, the use of such hybrid sampling means there is no clear Hamiltonian for this system and correspondence to results from any specific statistical mechanical cannot be demonstrated. Lastly, the sampling of titration coordinates in implicit solvent is typically ~2000 transitions/ns,⁵¹ which is an order of magnitude higher than those obtained in our explicit solvent simulations. Therefore, to compensate for the differential sampling speed associated with different solvent models, we compared the results of our 20 ns pH-REX CPHMD^MSλD trajectories to the previously reported 2 ns pH-REX trajectories that uses the implicit and hybrid CPHMD model.

As summarized in Table IV, in terms of overall pK_a predictive performance, our explicit solvent CPHMD^MSλD results had a RMSE error of 0.84 pK_a units. This is an improvement from the results obtained using implicit solvent CPHMD (RMSE = 0.94), and our model performance is close to that of the hybrid solvent CPHMD (RMSE = 0.80). A similar trend was also noted using alternative error metrics, such as the average unsigned error (AUE). We then identified the number of residues that had errors of more than 1.0 pK_a unit relative to experimental values. Our explicit solvent CPHMD^MSλD model had only 1 such residue (i.e., Asp-119) compared to the implicit and hybrid solvent CPHMD models which had 5 and 3 residues respectively. Notable improvements in moving from a hybrid solvent to a “pure” explicit solvent model can be observed in His-15, where the overestimation of its pK_a value is reduced from 1.1 to 0.5 pK_a units. Similarly, the hybrid solvent CPHMD model incorrectly predicted the direction of pK_a shift for residue Asp-101, whereas the explicit solvent CPHMD^MSλD model not only predicted the right direction of pK_a shift, but the magnitude of error was also smaller (−1.5 vs +0.6). Our findings suggest that when corrected for differences in titrating coordinates sampling, the explicit solvent CPHMD^MSλD model produces more accurate pK_a predictions than the original implicit solvent CPHMD.

4.4 pK_a Calculations of Proteins: Other Proteins, BBL and NTL9

Lastly, to demonstrate that the pK_a calculations obtained from the CPHMD^MSλD framework for proteins is not specific to HEWL protein, we performed pK_a calculations on two additional proteins, the BBL and NTL9 protein. Given that we have only investigated a single His residue in a protein environment, for BBL we only titrated the two His residues. NTL9 has no His residues, and the Glu and Asp residues that have experimental pK_a measurements were titrated. As summarized in Table V and Figure S5 the calculated pK_a values have are reasonably accurate (RMSE = 0.72, AUE = 0.59).^109,110 From the experimental data, most of the residues titrate close to the pK_a of their reference compounds, but two residues had more than a 1.0 pH unit shift. For His-166 of BBL, the residue is buried and its experimental pK_a is 5.4. For Asp-8 of NTL9, its experimental pK_a of 3.0 can be traced to the salt bridge interactions it forms with the amide backbone of adjacent residues. Our calculated pK_a values demonstrate a similar downward shift, although in both cases the extent of the shift tends to be overestimated. We suggest that this overestimation may be due to the lack of sampling stemming from the shorter 3 to 5 ns simulations performed for these systems. In other proteins like staphylococcal nuclease, residues with shifted pK_a values are known to undergo local conformational changes,^26,28 and sampling these states will be required to improve the accuracy of pK_a calculations. Together with our observations for Asp-119 in HEWL, our work suggests that while short pH-REX CPHMD^MSλD simulations are capable of reproducing experimental pK_a values of most protein residues, accurate reproduction of highly shifted pK_a values (e.g., buried charged residues) or those involving salt-bridge or similarly strong interactions remains a challenge that may be better addressed with more aggressive conformational sampling techniques.

Table V.

pK_a values of BBL and NTL9 calculated using explicit solvent pH-REX CPHMD^MSλD simulations in this work. Calculated pK_a values with error greater than 1.0 pK_a unit relative to experimental values^109,110 based are identified in red.

Residue	Explicit CPHMDMSλD
	Exp pKa	pKa	Error
BBL
HIS-142	6.5	6.6 ± 0.1	0.1
HIS-166	5.4	4.8 ± 0.0	−0.6
NTL9
ASP-8	3.0	1.5 ± 0.1	−1.5
GLU-17	3.6	4.0 ± 0.5	0.4
ASP-23	3.1	3.7 ± 0.2	0.6
GLU-38	4.0	3.9 ± 0.2	−0.1
GLU-48	4.2	3.4 ± 0.3	−0.8
GLU-54	4.2	3.6 ± 0.2	−0.6
RMSE			0.72
AUE			0.59

5. CONCLUSION

In conclusion, we have demonstrated the use of the constant pH molecular dynamics framework based on multi-site λ-dynamics (CPHMD^MSλD) to simulate realistic pH-dependent properties of proteins. In the CPHMD^MSλD framework, we performed seamless alchemical transitions between protonation and tautomeric states using multi-site λ-dynamics, and designed a novel biasing potential to ensure that only the physical end-states are predominantly sampled. Then, we applied explicit solvent CPHMD^MSλD simulations to the proteins HEWL, BBL and NTL9, which are the first examples of a “pure” explicit solvent CPHMD on full protein systems to be reported. Our pK_a calculations for HEWL protein are in excellent agreement with experimental values, with a RMSE of 0.84 pK_a units, and this is close to the uncertainty of 0.50 pK_a units associated with experimental measurements. Our pK_a calculations on the other model protein systems, BBL and NTL9 also provide similarly good agreement with experiments. In addition, comparison with implicit solvent CPHMD shows that explicit solvent CPHMD^MSλD produces results that are more accurate, reducing the number of residues with large errors in their pK_a predictions from 5 to 1. With the development of explicit solvent CPHMD^MSλD for proteins, it will finally allow us to confidently address questions related to pH-dependent properties of membrane proteins and ion channels, where discrete representation of ions and water is important. Coupled with the explicit solvent CPHMD^MSλD framework for nucleic acids, accurate modeling of pH-dependent properties for all major classes of biomolecules – proteins, nucleic acids and even protein-nucleic acid complexes is now a reality.