Abstract
A recently engineered mutant of cyan fluorescent protein (WasCFP) that exhibits pH-dependent absorption suggests that its tryptophan-based chromophore switches between neutral (protonated) and charged (deprotonated) states depending on external pH. At pH 8.1 the latter gives rise to green fluorescence as opposed to the cyan color of emission that is characteristic for the neutral form at low pH. Given the high energy cost of deprotonating the tryptophan at the indole nitrogen, this behavior is puzzling, even if the stabilizing effect of the V61K mutation in the proximity of the protonation/deprotonation site is considered. Due to its potential to open new avenues for the development of optical sensors and photoconvertible fluorescent proteins, a mechanistic understanding of how the charged state in WasCFP can possibly be stabilized is, thus, important. Attributed to the dynamic nature of proteins, such understanding often requires knowledge of the various conformations adopted, including transiently populated conformational states. Transient conformational states triggered by pH are of emerging interest, and have been shown to be important whenever ionizable groups interact with hydrophobic environments. Using a combination of the weighted-ensemble sampling method and explicit solvent constant pH molecular dynamics (CPHMDMSλD) simulations, we have identified a solvated transient state, characterized by a partially open β-barrel where the chromophore pKa of 6.8 is shifted by over 20 units from that in the closed form (6.8 and 31.7, respectively). This state contributes a small population at low pH (12% at pH 6.1), but becomes dominant at mildly basic conditions, contributing as much as 53% at pH 8.1. This pH-dependent population shift between neutral (at pH 6.1) and charged (at pH 8.1) forms is thus responsible for the observed absorption behavior of WasCFP. Our findings demonstrate the conditions necessary to stabilize the charged state of the WasCFP chromophore (namely, local solvation at the deprotonation site and a partial flexibility of the protein β-barrel structure) and provide the first evidence that transient conformational states can control optical properties of fluorescent proteins.
INTRODUCTION
Expanding the palette of genetically encodable fluorescent proteins (FPs) with spectral properties that can be modulated by pH is a well-appreciated challenge due to their wide applicability as non-invasive pH sensors1–5 and optical highlighters for super-resolution imaging of living cells.6–9 The majority of such proteins developed to date belong to the green fluorescent protein (GFP) family and owe their pH-sensitive optical behavior to a tyrosine-based chromophore that can interconvert between the neutral (protonated) and deprotonated (charged) states depending on the hydrogen-bonding environment surrounding its phenolic group.7 Rational design of new pH-sensitive variants requires both (i) a fundamental understanding of how the proteins with tyrosine-based chromophores function at the atomic level, as well as (ii) going beyond and looking at the FPs with chromophores other than tyrosine as potential candidates (e.g. tryptophan or phenylalanine/histidine-based chromophores, as in the case of cyan and blue fluorescent proteins). While a second approach has long been overlooked, the first one has been quite successful resulting in a number of useful pH sensors (e.g. pHluorins,3,5 phRed2) and optical highlighters (e.g. Kaede8,9). The efforts in this direction, however, have mostly been focused on targeting the residues in the vicinity of the chromophore that affect its spectral characteristics through electronic effects, and largely neglected the importance of characterizing the conformational ensemble of the protein.7
In recent years, a large body of evidence has emerged suggesting that understanding the mechanisms underlying protein functions depends on our ability to characterize its dynamic ensemble.10–12 Due to the nature of conventional biophysical techniques that primarily probe the most stable protein conformers, our understanding has long been limited to the information regarding highly populated ground conformational states. However, such states often represent only one of the functional forms, and higher-energy physiologically-relevant conformers can be transiently populated (~10% or less) when initiated by external stimuli, such as substrate binding, pH changes, or thermal fluctuations.12,13 While low-energy ground-state conformers residing at the bottom of the conformational energy landscape are normally separated by very small kinetic barriers and interconvert between one another within pico- to nanoseconds, the barriers between them and higher energy structures are larger and associated with micro-to millisecond timescale or longer. Recent advances in relaxation dispersion NMR spectroscopy11,14 and room temperature X-ray crystallography15 have made the detection of such transient conformational states possible, demonstrating their ubiquitous role in enzyme catalysis,10 protein folding,13,14 and ligand binding.16 Transiently populated conformational states triggered by pH are of particular importance since pH regulates the biological activity of many proteins, and the role of pH-dependent transient states is an emerging discovery that has been recently reported to influence membrane fusion,17 folding pathways,18 and, more generally, the dynamics of buried ionizable groups.19
In this paper, we demonstrate that pH-dependent transient conformational states can tune the absorption profile of cyan fluorescent protein (CFP)20 – a blue-shifted variant of the green fluorescent protein (GFP) family used for multicolor labeling and fluorescence resonance energy transfer (FRET) applications – which to our knowledge is the first precedent of such a mechanism. In particular, we provide a theoretical explanation for the non-monotonic pH-dependent absorption of a recently engineered CFP mutant (WasCFP; see Figure 1A). While the vast majority of the pH-sensitive fluorescent proteins reported to date2,3,5 exhibit monotonic changes in optical signals (e.g. absorption, emission, excitation), the WasCFP mutant does not conform to such a monotonic behavior. It reversibly interconverts between cyan-emitting and green-emitting forms, with the latter form dominant at pH 8.1 (and 25°C), above which the green signal drops.21 Part of this behavior has been attributed to the deprotonation of the tryptophan-based chromophore (Figure 1B) at mildly basic pH, which is accompanied by a 60 nm bathochromic shift in absorption.
Figure 1.
A: Structure of WasCFP showing Cα positions of mutated residues (V61K, D148G, Y151N, L207Q). B: Structure of Trp66-based WasCFP chromophore covalently bound to β-barrel at positions showed with dashed lines (Leu64 and Val68). C: Deprotonation of CRF. CRF-H and CRF− are neutral (protonated) and charged (deprotonated) forms of the synthetic chromophore, respectively.
Even though the observed effect is a highly unusual scenario as the pKa of an analogous indole is high (16.2 in H2O; 21.0 in DMSO), Sarkisyan et al.21 have shown that a synthetic CFP chromophore (hereon referred to as CRF), which is a truncated version of that in the protein, undergoes a similar pH-dependent absorption red-shift in both protic and aprotic solvents, and its pKa is depressed to 12.4 due to the more efficient delocalization of the negative charge over the extended π-system (see Figure 1C).
The same shift has been observed in a wild-type CFP variant mCerulean denatured in 5M NaOH. In addition, analogous pH-dependent bathochromic shifts, attributed to the deprotonation at phenolic oxygen, have been previously detected in various members of the GFP family with tyrosine-based chromophores (e.g. yellow, red and green fluorescent proteins).22 In WasCFP, a key V61K substitution positions a Lys residue in close proximity to the indole nitrogen of the chromophore (see Figure 1B), and this was proposed to stabilize its deprotonated state.
The pKa of the WasCFP chromophore, however, could not be directly measured and the atomic level details of its pH-dependent absorption remained unknown. Moreover, no explanation for the non-monotonic optical properties of WasCFP, specifically the signal drop in the green fluorescent form above pH 8.1 has been proposed..
To elucidate the mechanism of the unusual pH-dependent spectral behavior of WasCFP, we probed it with a combination of two computational techniques: the weighted-ensemble sampling method23 using a novel hydration order parameter;24 and explicit solvent constant pH molecular dynamics simulations (CPHMDMSλD),25 which has been used successfully to interrogate the pH-dependent dynamics of several biological systems.19,26–28 Among our key findings is the existence of a low pKa (6.8) solvated state characterized by a partially open β-barrel, which, in combination with a high pKa (31.7) closed conformation, governs the pH-dependent properties of WasCFP. In particular, we have shown that even in the presence of the stabilizing V61K mutation, the free energy cost of deprotonating the chromophore is still high and does not allow for the existence of the charged state of WasCFP even at high pH. The protein has to adopt a partially open conformation allowing a few water molecules to access to the chromophore. This conformation is transiently populated at low pH but becomes dominant under mildly basic conditions. The pH-dependent shift between the closed and open form is thus responsible for the observed bathochromic shift in WasCFP.
RESULTS AND DISCUSSION
First, to determine the plausibility for WasCFP (hereon referred to as, simply, WAS) to exist in the charged deprotonated state, we modeled the absorption properties of CRF at the TDDFT//B3LYP/6-31+G* level, both in gas phase and in implicit solvent. As shown in Table 1, the vertical excitation energy of the lowest-energy transition (ground to first excited electronic state; S0→S1) for the neutral CRF is in good agreement with both experiment21 and previous computations,29,30 and the direction of the bathochromic shift between the neutral and anionic form is qualitatively reproduced. We note that the latter is quantitatively underestimated due to well-known systematic errors produced by TDDFT methods for anions.29,31
Table 1.
TDDFT//B3LYP/6-31+G* vertical excitation energies and oscillator strengths for the lowest-energy (S0→S1) transition of the CRF-H and CRF−:
| λamax (comp.), nm | λamax (exp.), nm | fS0→S1 | |
|---|---|---|---|
| Neutral | 391a (375 b) | 400 | 0.7a (0.6b) |
| Charged | 415a (400b) | 460 | 0.9a, b |
– in implicit solvent,
– in the gas phase
Nevertheless, the computed oscillator strengths support the qualitative picture and demonstrate that the S0→S1 transition for the charged form is stronger than that for the neutral one, making plausible the existence of a charged state in the CRF.
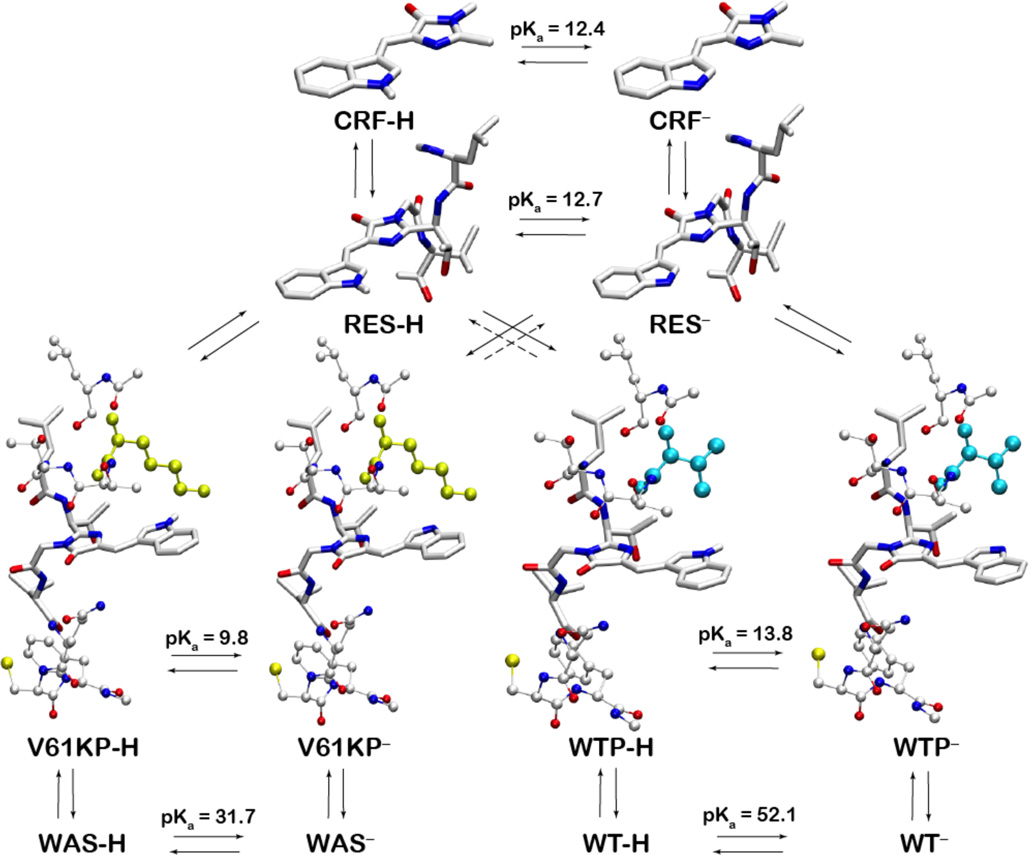
Next, we constructed a model compound (RES; denoting the model compound “residue”), which is an extended CFP chromophore consisting of the CRF moiety covalently bound to Leu64 and Val68 (see Figure 1B and Figure 2) to serve as a reference for our explicit solvent CPHMDMSλD simulations.25 Using a model pKa of 12.7 (calculated using thermodynamic integration based on the CRF), we initially computed the pKa values of the model wild type and mutant peptides (WTP and V61KP, respectively) that consist of 10 residues including a key position 61, before proceeding to the wild type and mutant proteins (WT and WAS, respectively) – all using a thermodynamic cycle depicted in Figure 2.
Figure 2.
Thermodynamic cycle that shows alchemical transformations considered in this study. Cyan and yellow-colored side chains correspond to V61 and K61 in WTP and V61KP peptides, respectively. pKa values computed from CPHMDMSλD simulations are highly elevated in both WT and WAS and, thus, are not responsible the observed pH-dependent absorption of WasCFP.
As shown in Figure 2, while an alchemical transformation of CRF to RES barely alters the pKa of the titrating moiety, perturbation by the peptide and protein environment (WTP and WT) shifts its pKa by 1.1 and 39.4 units, respectively. Such large pKa shifts have been reported when ionizable groups are transferred into a hydrophobic environment,32 and demonstrates the sensitivity of the chromophore pKa to the extent of local solvation at the protonation site. In our case, the solvation is high in the peptide and low inside the hydrophobic β-barrel of WAS, which is not surprising considering that nature selected the cylindrical β-barrel for fluorescent proteins in order to prevent the fluorescence quenching by either water or oxygen.7 Using the thermodynamic cycle in Figure 2 and the pKa values computed using the CPHMDMSλD method, we calculated that the positive charge of Lys61 introduced in a close proximity to the indole group of RES stabilizes V61KP by 5.4 kcal/mol with respect to WTP, and WAS – by 27.9 kcal/mol relative to WT. This cost is also solvation-dependent and leads to the downshift of the RES pKa in a peptide by 4 units, while depressing the pKa in the protein by 20.4. Even though our simulations clearly show that positive charge in the vicinity of the protonation site stabilizes the anionic form of RES, both neutral WT and charged WAS species are extremely stable, with pKas of 52.1 and 31.7 that are comparable to those of the so-called “super-bases” in a low dielectric environment.33 Therefore, the deprotonation at the indole nitrogen does not happen in such “closed” state conformations in the experimental pH range of 6–10, and the computed pKa values do not account for the observed pH-dependent absorption properties of WAS.
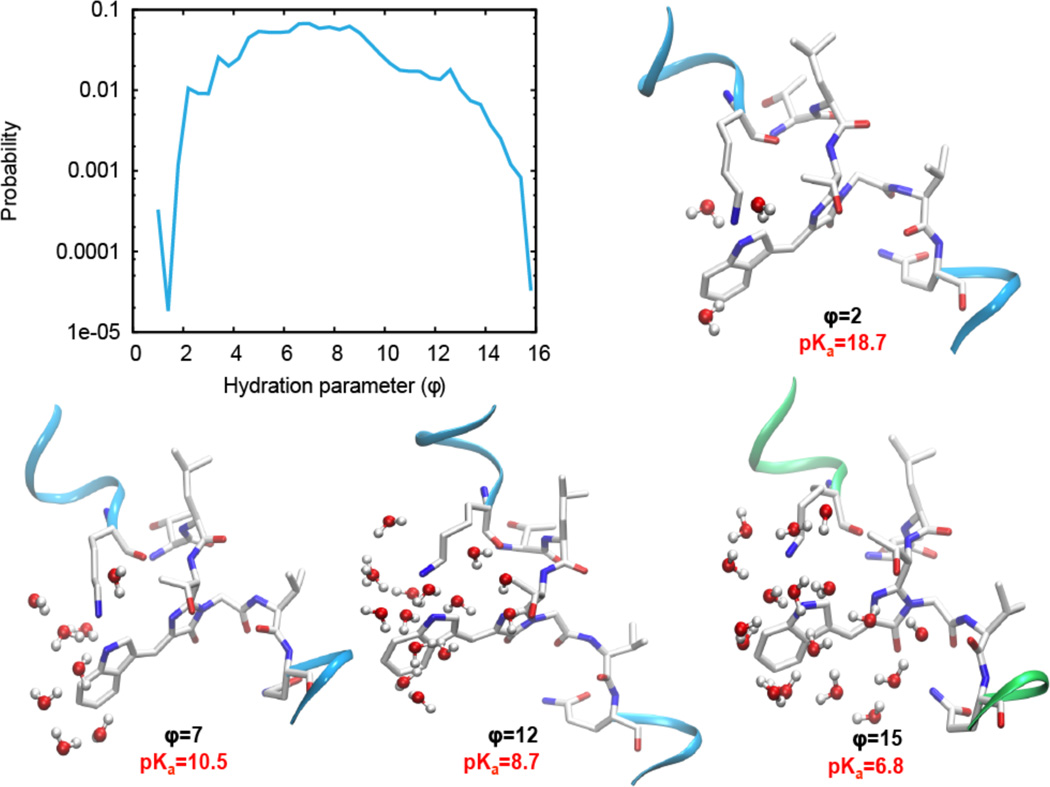
Numerous studies of conformational plasticity of proteins, however, have demonstrated the importance of characterizing the dynamic ensemble of their states, including those that are only transiently populated.10–13,16 Moreover, partially open, solvated pH-dependent transient states have been hypothesized to be of general importance in systems with buried ionizable groups.19 However, capturing the transition between ground and transient conformational states often requires simulation timescales currently not accessible to the version of the CPHMD used in our work. Therefore, guided by the observation of a significantly diminished pKa in a well-solvated peptide vs. “dry” high-pKa closed conformation of the protein, we chose a hydration of the chromophore as our reaction coordinate and performed a search for an alternative WAS conformation using the weighted-ensemble sampling method23 that allows the escape from deep local minima (high probability regions) and provides enhanced sampling of low probability, transient states. Guided by the observation of a significantly diminished pKa in a well-solvated peptide vs. “dry” high-pKa closed conformation of the protein, we chose a hydration of the chromophore as our reaction coordinate Figure 3A shows a sampling of WAS configuration space along a hydration parameter (φ), which posits the existence of transiently populated states, characterized by the partially open β-barrel and local solvation at the protonation site. The pKa values of the RES chromophore were subsequently computed for four representative WAS structures, extracted from the four regions in the histogram (φ=1.5–2.5; 5.5–8.0; 12.0–13.0 and 14.5–15.0), and structural changes influencing its pKa were analyzed.
Figure 3.
A: Probability distribution of the hydration parameter of RES in the WAS protein shows transiently populated states with large hydration parameters. B: Snapshots of the chromophore environment in four different conformations of WAS corresponding to hydration parameters φ=2, 7, 12, and 15. Number of water molecules within 7Å of nitrogen of the chromophore (3, 8, 15, and 17, respectively) and the corresponding pKa values computed using CPHMDMSλD simulations are shown for each conformation.
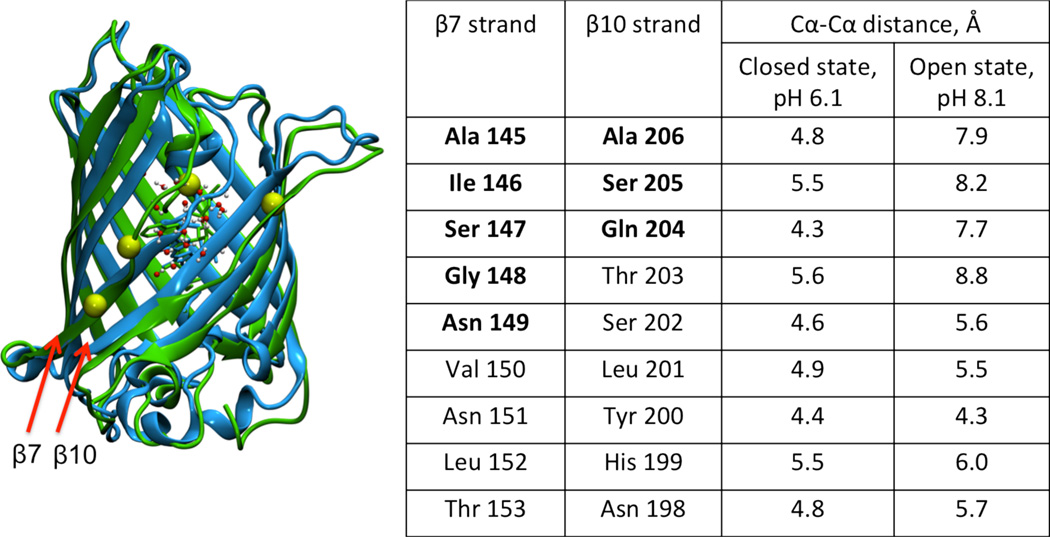
We discovered that opening of the β7–β10 channel (up to 1.58Å backbone RMSD with respect to the crystal structure of WT; see Figures 3B), which has been previously shown to be rather flexible in both wild type CFP34 and in the study of the oxygen diffusion pathway in red fluorescent protein, mCherry,35 facilitates local solvation (i.e. an increase in the number of water molecules within a 7 Å radius) at the indole nitrogen. Our calculations suggest that the pKa of the chromophore can be as low as 6.8 for a structure with a high hydration parameter φ =15 that corresponds to as many as 17 water molecules within 7Å of the indole nitrogen of the chromophore (see Figure 3). Based on the structural data provided from our simulations, the residues on strands β7 and β10 undergo local unfolding into an unstructured loop. Notably, as illustrated in Figure 4, residues 145–149 of β7 and 204–206 of β10 lose their secondary structure (also refer to Figure S4 for Cα-Cα distances between β7 and β10 for all four structures in Figure 3). We note that these structural changes can be monitored by examining the carbon (Cα) chemical shifts in these regions as one titrates WasCFP from pH 8 to pH 6. We predict that these shifts would report a change from a mixed fraction of open and closed conformational states at pH 8 to a predominantly closed conformational state at pH 6. It is also worth noting that the chromophore in the open state is still significantly more rigid than it is in solution (see Figure S6).
Figure 4.
Distances between Cα-Cα atoms of residues in β7 and β10 strands in the open state (dominant at pH=8.1) vs. the closed state (dominant at pH=6.1).
As WasCFP itself is a relatively recent construct, there is a lack of experimental data that measures its fluorescent properties as a function of its dynamics. However, parallels can be drawn between CFP and the related GFP, which, despite their differences in the chromophore, do share significant sequence similarity and may have similar conformational properties. Interestingly, prior studies of the unfolding of green fluorescent protein GFP have revealed a stable fluorescent intermediate that retained considerable secondary and tertiary geometry with displaced β7 and β10 strands and access of the water molecules to the chromophore,36 It has also been noted that chromophore formation in fluorescent proteins occurs in a partially structured intermediate state, although this structure had reduced fluorescence. These experimental observations for GFP suggest that partially open conformations of the protein, similar to the transient state we observed in our simulations, can exist. In addition, in two companion papers, where the effect of pressure on the quenching of fluorescence was examined, Weber and co-workers37 and Krylov and co-workers38 reported that mCherry and mStrawberry are both highly fluorescent at standard pressure (0.1MPa) even though their chromophore are partially solvated. In fact, the extent of local solvation in our open state is similar to what the authors’ computations predict for ambient conditions. In the context of our findings, it raises the possibility that non-ground state protein conformations may play a role in modulating spectral properties of fluorescent proteins.
Lastly, to explain the unusual pH-dependent absorption behavior of WAS, we constructed a model based on the assumption that WAS interconverts between the hydrated transient (open) state that we identified and its original closed configuration. Previously, we developed a two-state model to explain the protonation equilibrium of SNase mutants with buried ionizable groups,19 which allows one to compute the fraction of open state (Fopen) as a function of pH based on the ratio of the open and closed state populations (Roc) deduced from the simulations.
| (1) |
| (2) |
This ratio (please see the derivation of (2) in Section S4 of the SI) is calculated using the computed microscopic pKa values of both forms (pKopen=6.8 and pKclosed=31.7) and the apparent pKa value estimated based on available experimental data (pKapp=7.8) (see Section S4 of the SI).
To test the validity of the model, we compared the computed Fopen values with those that can be found directly from experiment reported in ref. 21. As a basis for our analysis, we used the pH-dependent absorption data for WasCFP recorded by Sarkisyan et al.21 at 25°C (see Figures S2a and S2b of the Supplemental material in the original reference). The spectrum presented in their work differs from a typical pH-dependent absorption profile where one would expect for a mixture of conjugated acid and base, where one form is largely dominant at low pH, while the other one dominates under high pH conditions. In the case of WasCFP, the signal at 494 nm, corresponding to the charged (deprotonated) chromophore, grows with pH up to pH=8.1, but then its intensity decreases – due to titration of a nearby Lys61, as suggested by the authors of the paper. In addition, the signal of the protonated form consists of two peaks – a bonafide spectral feature of all cyan fluorescent proteins, the origin of which is still a subject of a great controversy.20,29 While the authors do not mention any open states or fraction of the open states in their work and discuss the signals at 436 and 494 nm as arising from the protonated and deprotonated forms of the chromophore in the same protein conformation, our simulations suggest that chromophore can only exist in its deprotonated form when protein conformation is partially open allowing a few water molecules access to the deprotonation site. Therefore, for the remainder of this study, we will use the terms deprotonated and open states interchangeably and express the fraction of open state, Fopen, using the following information only: (1) extinction coefficients at 436 and 494 nm (ε436, HA and ε494, A−); (2) absorbance of the protonated (closed) form at the lowest pH, Abs436, low pH (neglecting a small absorption signal at 494 nm); and (3) absorbance of the deprotonated (open) form, Abs494 – which is the only variable in our final equation for Fopen, presented below, that changes with pH (all taken from the data in ref.21).
Derivation of expression for Fopen from experiment
The concentrations of protonated (HA) and deprotonated (A−) forms can be written in terms of the absorbances of the protein chromophore at the appropriate wavelengths (436 and 494 nm, respectively) using the Beer’s-Lambert law:
| (3) |
| (4) |
The sum of those concentrations represents the total concentration of all species, which remains constant at any pH:
| (5) |
At low pH, the protonated form dominates, so that CHA = CT. Similarly, at high pH there is predominantly deprotonated form, and CA− = CT. Knowing that, we can express the absorbances at low pH and high pH as follows:
| (6) |
| (7) |
From equation (6) we obtain CT and by substitution of (8) into (7), the absorbance at high pH can be expressed in the following way:
| (8) |
By dividing Eq. (4) by Eq. (7), we obtain the fraction of the deprotonated state, which varies with pH:
| (10) |
Both extinction coefficients are available from experiment: ε436, HA = 28000 M−1cm−1 and ε494, A− = 51000 M−1cm−1
The value of absorbance of pure HA at low pH, Abs436, low pH, remains the same across the entire pH range, and the only parameter that varies is the absorbance of the A− form at 494 nm (Abs494), which can be calculated directly from the intensity of the peak. Table 2 provides all the information necessary to estimate Fopen at different pH using the information from the pH-dependent absorption spectrum at 25°C recorded by Sarkisyan et al.21
Table 2.
Fopen derived from experimental data in ref. 21
| pH | Abs494 | Fopen | |
|---|---|---|---|
| ε436, HA = 28000 M−1cm−1 | 6.1 | 0.16 | 0.09 |
| ε494, A− = 51000 M−1cm−1 | 6.5 | 0.28 | 0.15 |
| Abs436, low pH = 1.00 | 7.0 | 0.54 | 0.30 |
| 8.1 | 1.00 | 0.55 | |
| 8.5 | 0.91 | 0.50 | |
| 9.5 | 0.75 | 0.41 | |
| 9.9 | 0.45 | 0.25 | |
Two-state model: experiment vs. simulations
As shown in Figure 5B, our two-state model provides a moderate correlation with experimental Fopen values up to pH 8.1. However, it does not fully describe the system at higher pH (see Figure 5A), where Lys61 presumably deprotonates, as mentioned above. Therefore, we introduced a third state that accounts for a neutral Lys61 and partially re-protonated chromophore at high pH, whose pKa is approximated by that in the V61KP peptide found from our simulations (which is also in agreement with the experimentally suggested value of 9.8).
Figure 5.
pH-dependent Fopen computed using two (A) and three (C) state model. Correlation with Fopen estimated from the pH-dependent absorption data is in (B) and (D), respectively.
Three-state model: experiment vs. simulations
The states in our three-state model are defined as follows: (i) [RES-H/Lys+]closed – a closed state with neutral RES chromophore and protonated Lys61 (pKclosed=31.7); (ii) [RES/Lys+]open – an open state with deprotonated chromophore and protonated Lys61 (pKopen=6.8); and (iii) [RES-H/Lys]open – an open state with re-protonated chromophore (pKRES=9.8), and deprotonated Lys, whose pKa (pKLys) was calculated from additional CPHMDMSλD simulations where both the chromophore and Lys61 were simultaneously titrating.
Due to the complexity of thermodynamic treatment of three different conformations, two of which have residues with strongly coupled protonation states (that of the chromophore and that of the nearby Lys61), we simplified the treatment of the three-state system into an effective two-state system. In our analysis, this effective two-state system corresponds to the bottom two arms of the thermodynamic cycle depicted in Figure 6, where the open state conformations are collectively represented by states (ii) and (iii) and where the protonation states of the chromophore and Lys61 are tightly coupled.
Figure 6.
Schematic illustration of the three-state model. Kprot and Kdeprot are equilibrium constants corresponding to the pH-independent conformational transitions between open and closed states.
Using the microscopic pKa calculated for states (i) and (ii), as well as the experimental apparent pKapp (7.8), we calculated that if the pKa of the second state was shifted to 9.8 (which is the value representing state (iii) in the three-state model), it would result in a shift of pKapp to 10.8. Thus, the pKapp changes from 7.8 to 10.8 depending on the identity of the second state, which is primarily determined by the protonation state of Lys61. In other words, we assumed that the protonation state of Lys61 is coupled to the protonation state of the chromophore, which is justified because that is the only titrating residue in its vicinity. Hence, we interpolated the shift in the pKapp and pKopen by accounting for the fraction of the unprotonated Lys61. Thus, the corresponding pKapp and pKopen are expected to vary as a function of pH and we can substitute these pH-dependent terms to Eq. 2 to derive a ratio of the open to closed states for the three-state model. This ratio is then approximated using a modified Eq. (11) for Roc:
| (11) |
Where both pKpHopen and pKpHclosed are pH-dependent and differ from their corresponding values in the two-state model (pKopen=6.8 and pKclosed=31.7) by the delta term, used to interpolate the pKa of the open conformation from state (ii) to state (iii) by accounting for the coupling between protonation states of the chromophore and Lys61.
| (12) |
| (13) |
| (14) |
As shown in Figure 5D, our three-state model not only improves the correlation with experimental observables (with R2=0.86), but also captures, both qualitatively and quantitatively, the unusual bell-shaped pH-dependent absorption profile of WAS (see Figure 5C). Thus, our results show that the open state, collectively represented by the two locally solvated configurations and a partially open β-barrel, is transiently populated and contributes a small fraction at low pH (up to 12% at pH 6.1). This state becomes dominant (as much as 53%) at mildly basic conditions (pH=8.1), and gives rise to a strong absorption at 494 nm (and, thus, green fluorescence), which then titrates with a pKa of 9.8 at higher pH values.
Lastly, our three-state model provides some useful insights into engineering pH-sensitive cyan fluorescent protein based on WasCFP. For example, to engineer a mutant that does not possess the residual cyan fluorescence at high pH, one may target the electrostatic environment in the vicinity of Lys61 in a manner to prevent its re-protonation at mildly basic conditions. Such a design would suppress the population of the third state in our three-state model by reducing the mechanism of the engineered mutant to two interconverting states, and this will increase the fraction of the open state with pKopen=6.8 (that only reaches a maximum of 53% at pH=8.1 in the current WasCFP design).
CONCLUSIONS
In conclusion, we have applied a combination of the weighted-ensemble sampling method23 with a novel hydration parameter and explicit solvent constant pH molecular dynamics (CPHMDMSλD)25 to elucidate the origin of the unusual non-monotonic pH-dependent absorption behavior of a recently engineered CFP mutant that features a pH-dependent shift between cyan and green fluorescent forms. In earlier experimental observations, this optical property was proposed to be controlled by the charged anionic state of its tryptophan-containing chromophore.21 Our calculations demonstrate that even in the presence of the stabilizing V61K mutation, the free energy cost of deprotonating the chromophore is still high and does not allow for the existence of the charged state of WasCFP even at basic pH. Instead, we propose the following explanation: The distribution between two transiently populated conformational states characterized by a partially open β-barrel with local solvation around the chromophore (that have pKa values of 6.8 and 9.8), relative to the ground state crystallographic structure (that has pKa of 31.7), is able to fully recapitulate both qualitatively and quantitatively the unusual non-monotonic pH-dependent properties of WasCFP. In this model, the open state is transiently populated at low pH, but reaches a population of 53% under mildly basic conditions, before losing its dominance and reverting to a transient state under highly basic conditions, and such mechanistic understanding may be used to further engineer the pH-sensitive fluorescent properties of WasCFP. Therefore, our work not only validates that tryptophan can be deprotonated in a biological system at mildly basic pH, but, more importantly, shows that pH-dependent transient conformational states are functionally relevant, and that they can tune the optical properties of fluorescent proteins. Such an outlook will have implications in the rational design of fluorescent proteins with pH-dependent optical properties.
MATERIALS AND METHODS
Calculating absorption properties
The geometries of the neutral (protonated) and charged (deprotonated) synthetic chromophore, referred to in this study as CRF, were first optimized both in gasphase and in implicit solvent of high polarity (water) using a polarizable continuum model (PCM)39 at the B3LYP/6-31+G* level, which has previously been widely applied to model excitation properties of chromophores in various fluorescent proteins.29,30,40 The calculations of vertical excitation energies and oscillator strengths for the five lowest energy transitions were then performed on the optimized geometries using the TDDFT method. Several scenarios considered during the optimization are reported in the Supporting Information (SI), Table S1.
Building input structures
The structures of a synthetic CRF chromophore, along with its extended version RES (see Figure 1B and Figure S1), were built using Avogadro.41 Both residues were parameterized, as described in the SI (see Section S2a). The RES structure, which is comprised of the CRF covalently bound to Leu64 and Val68 of the protein, was further selected as a model compound for CPHMDMSλD simulations.25 The wild type peptide (WTP) was built based on the mCerulean crystallographic structure (PDBID: 2WSO)20 using Leu60–Val61–Thr62–Thr63–RES–Gln69–Cys70–Phe71 fragment. To generate a mutant peptide (V61KP), Val in position 61 was mutated to Lys using Pymol.42 Protein models were built in the same fashion, with three additional substitutions (D148G, Y151N, L207Q) incorporated in the mutant protein (WAS) relative to the wild type (WT) form. Hydrogen atoms were added using the HBUILD facility in CHARMM43 and the structures were then solvated in a cubic box of explicit TIP3P water molecules using convpdb.pl of the MMTSB44 toolset with a 12Å cutoff. The appropriate number of Na+ and Cl− ions was added to maintain neutrality. The terminal ends of both peptides and proteins were capped using ACE and CT3 patches.
An additional patch was constructed to represent the charged (deprotonated) form of CRF. The same patch was used in all subsequent TI and CPHMDMSλD calculations. Atoms included in the patch were those that differed in partial charges between protonated and deprotonated forms of CRF (see Section S2, Figure S1). Those atoms constitute the so-called titratable fragment. All corresponding bond, angle and dihedral terms were explicitly specified in the patch. A titratable residue was simulated as a hybrid ligand with dual topology, built using the BLOCK facility in CHARMM, and included all components of the neutral and charged forms. Atoms not included in the patch were considered environment atoms and were the same for both neutral and charged forms.
Calculating pKa of the model compound RES
In order to obtain the pKa of RES, which was used as a model compound in all CPHMDMSλD simulations, we performed thermodynamic integration (TI)45 calculations, for the two deprotonation reactions (CRF-H/CRF− and RES-H and RES−), as schematically shown in Figure 2 and S2. A hybrid ligand containing patched atoms of the titratable fragment was constructed for each case using the procedure described above, and the simulations were run for 3 ns using nine discrete λ-windows (λ = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9) following a procedure similar to the one previously used by Knight and Brooks.46 Distance restraints were applied to the pairs of atoms of the titratable fragment using a force constant of 100 kcal/mol/Å2 with a zero target distance between atoms in order to keep the two (dual topology) fragments occupying the same volume. Each system was first minimized using two rounds of 200 steps using Steepest Descent (SD) method, followed by 2000 steps of Adopted Basis Newton-Raphson, with weak harmonic restraints on heavy atoms (force constants of 2.0 and 0.1 kcal/mol/Å2 for each run, respectively) that were released prior to the heating stage. The minimized system was then gradually heated from 100K to 298K for 100 ps. During both the 1 ns-long equilibration and 2 ns-long production runs the temperature was maintained at 298 K by coupling to a Langevin heat bath using a friction coefficient of 10 ps−1. In all simulations hydrogen heavy-atom bond lengths were constrained using the SHAKE47 algorithm. The equations of motion were integrated using the Leapfrog-Verlet algorithm47 with a time step of 2 fs. A non-bonded cutoff of 12 Å was used with an electrostatic force switching (“fswitch”) and a van der Waals switching (“vswitch”) functions between 10 Å and 12 Å.
All simulations were done within the BLOCK facility in CHARMM.48 All energy terms were scaled by λ, except for the bonds, angles and dihedrals, which remained at full strength regardless of the λ-value to retain physically reasonable geometries. The post-processing of the trajectories was done in CHARMM and the free energies of deprotonation for each system (ΔGRES and ΔGCRF) were calculated by combining the dU/dλ values from all λ-windows of the corresponding deprotonation reaction. The pKaRES was then calculated based on the computed ΔΔG as follows:
| (15) |
| (16) |
Details of the CPHMDMSλD method
In our explicit-solvent constant pH molecular dynamics approach (CPHMDMSλD),25 the titration coordinate is represented by λ, which serves as a scaling factor for each titratable residue α, and is propagated continuously between the physically relevant protonated (λα,1 = 1) and unprotonated (λα,1 = 0) states. In CPHMDMSλD the dynamics of the λ-variable is described using the multi-site λ-dynamics approach (MSλD)49 that enables a coupling between λ and the atomic coordinates. As such, in CPHMDMSλD, titratable residues are model compounds perturbed by the protein environment via non-bonded interactions. For more details about the theory behind CPHMDMSλD simulation we refer our readers to the following references.25,50
The simulation setup for CPHMDMSλD simulations is similar to the one used in the TI (see above)45. Only those aspects that are different are reported below. In particular, the BLOCK facility was used with the λNexp functional form of λ (FNEX) and a coefficient of 5.5. A fictitious mass of 12 amu•Å2 was assigned to each θα value. The threshold value for assigning λα,i = 1 was λα,i ≥ 0.8. The values of the Ffixed and Fvar biasing potentials (see Table S3) were parameterized using the same method as reported previously, and were targeted to maintain both (i) good sampling efficiency throughout the simulations (> 50 transitions per ns; see Figure S2) and (ii) a high fraction of physical ligand (~0.8).
To facilitate the convergence of sampling of protonation states, we have also employed the pH-based replica exchange protocol, which allows the exchange between replicas representing different pH conditions. The pKa values for each relevant structure were computed by combining the populations of the unprotonated (Nunprot) and protonated (Nprot) states in multiple runs and by fitting their ratio (Sunprot) to the modified Henderson-Hasselbalch equation:
| (17) |
The protocol described above was applied to compute the pKa values of the wild type and mutant peptides (WTP and V61KP, respectively), as well as wild type and mutant proteins (WT and WAS, respectively). The pH range varied depending on the system: while the wild-type and mutant peptides (WTP and V61KP, respectively), were titrated in the pH range 1 to 16 (with an increment of 1), the high-pKa closed wild-type and mutant protein conformations (WT and WAS) were sampled across the extended pH range (1 to 56 and 1 to 40, respectively). The pKa of the open state was calculated using 16 pH replicas (1 to 16). In all cases the calibrated RES with a pKa=12.7 was used as a model compound, and peptide/protein environments were assumed to perturb the pKa via non-bonded interactions only. The full thermodynamic cycle considered in this study can be found in Figure 2.
Sampling transiently populated states
The weighted ensemble algorithm (WE)23 enhances sampling of transiently populated states by defining a set of regions, and encouraging equal sampling in each region. This is achieved by evolving a group of trajectories (replicas) forward in time (in parallel) and periodically redistributing trajectories between the regions using cloning and merging steps. To ensure physical sampling, each trajectory has a statistical probability (or weight, wi) associated with it such that the sum of all weights equals to one. During cloning, weights of the parent trajectory are divided equally amongst the clones. When two trajectories A and B are merged, the resulting replica has a weight of wA+wB, and it takes on the structure of replica A with probability wA/(wA+wB), and otherwise takes on the structure of replica B.
Here the number of replicas is constant at 48, and regions are defined using a novel hydration parameter, φ, defined as follows:
| (18) |
Where the sum is over all water molecules i, and pi is defined as:
| (19) |
Here, di is the closest distance from atom N28 of the chromophore (RES) to an atom in the water molecule i. Regions were defined along this parameter with a spacing of 0.2, and were defined dynamically over the course of the WE simulation. A “cycle” consists of 20 ps of sampling for all 48 walkers followed by cloning and merging steps, and the simulation was continued for 490 cycles, at which point region discovery had slowed almost to a halt. The aggregate simulation time employed is thus 9.8 ns per walker, or 470 ns. Sampling was performed using CHARMM, implemented on graphics processing units using OpenMM5.2.51 Otherwise the simulation is implemented as specified above.
Before computing the histogram of WAS in Figure 3, a weight is computed for each sampling region using a matrix-based weight balancing algorithm, which finds the vector of region weights (R) by solving the equation TR = R, where T is the transition matrix.24 The histogram is then built using a list of replica weights and hydration parameter values collected during the WE simulation, where the replica weights are multiplied by factor m, which is defined as:
| (20) |
Where ri is the region weight determined by the matrix equation, and the denominator is the sum of the weights of all replicas in the list that are in region i.
To obtain starting structures for subsequent CPHMDMSλD simulations, a set of regions of the histogram with significant probabilities (p > 0.001) is chosen that represents a spectrum of hydration values: 1.5–2.5, 5.5–8.0, 12–13 and 14.5–15. We then use as a starting point the structure recorded with the largest replica weight.
Supplementary Material
ACKNOWLEDGMENT
This work was supported by grants from NIH (GM037554 and GM057513), and the Howard Hughes Medical Institute (HHMI International Student Research Fellowship). E.N.L. would like to thank Dr. Mike Ryazantsev for useful discussions of related spectroscopic issues.
Footnotes
ASSOCIATED CONTENT
Supporting Information
Details of a computational protocol. This material is available free of charge via the Internet at http://pubs.acs.org
The authors declare no competing financial interests.
REFERENCES
- 1.Wang T-M, Holzhausen LC, Kramer RH. Nat. Neurosci. 2014;17:262–268. doi: 10.1038/nn.3627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Tantama M, Hung YP, Yellen G. J. Am. Chem. Soc. 2011;133:10034–10037. doi: 10.1021/ja202902d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ashby MC, Ibaraki K, Henley JM. Trends Neurosci. 2004;27:257–261. doi: 10.1016/j.tins.2004.03.010. [DOI] [PubMed] [Google Scholar]
- 4.Llopis J, McCaffery JM, Miyawaki A, Farquhar MG, Tsien RY. Proc. Natl. Acad. Sci. USA. 1998;95:6803–6808. doi: 10.1073/pnas.95.12.6803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Miesenbock G, De Angelis DA, Rothman JE. Nature. 1998;394:192–195. doi: 10.1038/28190. [DOI] [PubMed] [Google Scholar]
- 6.Shcherbakova DM, Sengupta P, Lippincott-Schwartz J, Verkhusha VV. Annu. Rev. Biophys. 2014;43:303–329. doi: 10.1146/annurev-biophys-051013-022836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chudakov DM, Matz MV, Lukyanov S, Lukyanov KA. Physiol. Rev. 2010;90:1103–1163. doi: 10.1152/physrev.00038.2009. [DOI] [PubMed] [Google Scholar]
- 8.Hatta K, Tsujii H, Omura T. Nat. Protoc. 2006;1:960–967. doi: 10.1038/nprot.2006.96. [DOI] [PubMed] [Google Scholar]
- 9.Ando R, Hama H, Yamamoto-Hino M, Mizuno H, Miyawaki A. Proc. Natl. Acad. Sci. USA. 2002;99:12651–12656. doi: 10.1073/pnas.202320599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sekhar A, Kay LE. Proc. Natl. Acad. Sci. USA. 2013;110:12867–12874. doi: 10.1073/pnas.1305688110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Baldwin AJ, Kay LE. Nat. Chem. Biol. 2009;5:808–814. doi: 10.1038/nchembio.238. [DOI] [PubMed] [Google Scholar]
- 12.Korzhnev DM. J. Mol. Biol. 2013;425:17–18. doi: 10.1016/j.jmb.2013.05.029. [DOI] [PubMed] [Google Scholar]
- 13.Korzhnev DM, Religa TL, Banachewicz W, Fersht AR, Kay LE. Sci. 2010;329:1312–1316. doi: 10.1126/science.1191723. [DOI] [PubMed] [Google Scholar]
- 14.Vallurupalli P, Hansen DF, Stollar E, Meirovitch E, Kay LE. Proc. Natl. Acad. Sci. USA. 2007;104:18473–18477. doi: 10.1073/pnas.0708296104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fraser JS, van den Bedem H, Samelson AJ, Lang PT, Holton JM, Echols N, Alber T. Proc. Natl. Acad. Sci. USA. 2011;108:16247–16252. doi: 10.1073/pnas.1111325108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tzeng S-R, Kalodimos CG. Nat. Chem. Biol. 2013;9:462–465. doi: 10.1038/nchembio.1250. [DOI] [PubMed] [Google Scholar]
- 17.Lorieau JL, Louis JM, Schwieters CD, Bax A. Proc. Natl. Acad. Sci. USA. 2012;109:19994–19999. doi: 10.1073/pnas.1213801109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Long D, Bouvignies G, Kay LE. Proc. Natl. Acad. Sci. USA. 2014 doi: 10.1073/pnas.1405011111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Goh GB, Laricheva EN, Brooks CL. J. Am. Chem. Soc. 2014 doi: 10.1021/ja5012564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lelimousin M, Noirclerc-Savoye M, Lazareno-Saez C, Paetzold B, Le Vot S, Chazal R, Macheboeuf P, Field MJ, Bourgeois D, Royant A. Biochemistry. 2009;48:10038–10046. doi: 10.1021/bi901093w. [DOI] [PubMed] [Google Scholar]
- 21.Sarkisyan KS, Yampolsky IV, Solntsev KM, Lukyanov SA, Lukyanov KA, Mishin AS. Sci. Rep. 2012;2:1–5. doi: 10.1038/srep00608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Shaner NC, Campbell RE, Steinbach PA, Giepmans BNG, Palmer AE, Tsien RY. Nat Biotech. 2004;22:1567–1572. doi: 10.1038/nbt1037. [DOI] [PubMed] [Google Scholar]
- 23.Huber GA, Kim S. Biophys. J. 1996;70:97–110. doi: 10.1016/S0006-3495(96)79552-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dickson A, Warmflash A, Dinner AR. J. Chem. Phys. 2009;131 doi: 10.1063/1.3244561. -. [DOI] [PubMed] [Google Scholar]
- 25.Goh GB, Hulbert BS, Zhou H, Brooks CL. Proteins: Struct. Funct. Bioinf. 2014 doi: 10.1002/prot.24499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Goh GB, Knight JL, Brooks CL. J. Phys. Chem. Lett. 2013;4:760–766. doi: 10.1021/jz400078d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Goh GB, Knight JL, Brooks CL. J. Chem. Theory Comput. 2013;9:935–943. doi: 10.1021/ct300942z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Nikolova EN, Goh GB, Brooks CL, Al-Hashimi HM. J. Am. Chem. Soc. 2013;135:6766–6769. doi: 10.1021/ja400994e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Demachy I, Ridard J, Laguitton-Pasquier H, Durnerin E, Vallverdu G, Archirel P, Lévy B. J. Phys. Chem. B. 2005;109:24121–24133. doi: 10.1021/jp054656w. [DOI] [PubMed] [Google Scholar]
- 30.Nifosí R, Amat P, Tozzini V. J. Comput. Chem. 2007;28:2366–2377. doi: 10.1002/jcc.20764. [DOI] [PubMed] [Google Scholar]
- 31.Wanko M, Hoffmann M, Strodel P, Koslowski A, Thiel W, Neese F, Frauenheim T, Elstner M. J. Phys. Chem. B. 2005;109:3606–3615. doi: 10.1021/jp0463060. [DOI] [PubMed] [Google Scholar]
- 32.Kütt A, Leito I, Kaljurand I, Sooväli L, Vlasov VM, Yagupolskii LM, Koppel IA. J. Org. Chem. 2006;71:2829–2838. doi: 10.1021/jo060031y. [DOI] [PubMed] [Google Scholar]
- 33.Vazdar K, Kunetskiy R, Saame J, Kaupmees K, Leito I, Jahn U. Angew. Chem. Int. Ed. 2014;53:1435–1438. doi: 10.1002/anie.201307212. [DOI] [PubMed] [Google Scholar]
- 34.Goedhart J, von Stetten D, Noirclerc-Savoye M, Lelimousin M, Joosen L, Hink MA, van Weeren L, Gadella TWJ, Royant A. Nat. Commun. 2012;3:751. doi: 10.1038/ncomms1738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Regmi CK, Bhandari YR, Gerstman BS, Chapagain PP. J. Phys. Chem. B. 2013;117:2247–2253. doi: 10.1021/jp308366y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Huang J, Craggs TD, Christodoulou J, Jackson SE. J. Mol. Biol. 2007;370:356–371. doi: 10.1016/j.jmb.2007.04.039. [DOI] [PubMed] [Google Scholar]
- 37.Pozzi EA, Schwall LR, Jimenez R, Weber JM. J. Phys. Chem. B. 2012;116:10311–10316. doi: 10.1021/jp306093h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Laurent AD, Mironov VA, Chapagain PP, Nemukhin AV, Krylov AI. J. Phys. Chem. B. 2012;116:12426–12440. doi: 10.1021/jp3060944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tomasi J, Mennucci B, Cammi R. Chem. Rev. 2005;105:2999–3094. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
- 40.Nemukhin AV, Topol IA, Burt SK. J. Chem. Theory Comput. 2005;2:292–299. doi: 10.1021/ct050243n. [DOI] [PubMed] [Google Scholar]
- 41.Hanwell Marcus D, Curtis Donald E, Lonie David C, Vandermeersch Tim, Z E, H GR. J. Cheminform. 2012;4:1–17. doi: 10.1186/1758-2946-4-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. The PyMOL Molecular Graphics System, Version 1.2r3pre [Google Scholar]
- 43.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. J. Comput. Chem. 1983;4:187–217. [Google Scholar]
- 44.Feig M, Karanicolas J, Brooks CL., III J. Mol. Graph. Model. 2004;22:377–395. doi: 10.1016/j.jmgm.2003.12.005. [DOI] [PubMed] [Google Scholar]
- 45.Mezei M, Beveridge DL. Ann. N. Y. Acad. Sci. 1986;482:1–23. doi: 10.1111/j.1749-6632.1986.tb20933.x. [DOI] [PubMed] [Google Scholar]
- 46.Knight JL, Brooks CL. J. Comput. Chem. 2009;30:1692–1700. doi: 10.1002/jcc.21295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mezei M, Beveridge DL. J. Comp. Phys. 1977;23:327–341. [Google Scholar]
- 48.Brooks BR, Brooks CL, Mackerell AD, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, Caflisch A, Caves L, Cui Q, Dinner AR, Feig M, Fischer S, Gao J, Hodoscek M, Im W, Kuczera K, Lazaridis T, Ma J, Ovchinnikov V, Paci E, Pastor RW, Post CB, Pu JZ, Schaefer M, Tidor B, Venable RM, Woodcock HL, Wu X, Yang W, York DM, Karplus M. J. Comput. Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Knight JL, Brooks CL. J. Chem. Theory Comput. 2011;7:2728–2739. doi: 10.1021/ct200444f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Goh GB, Knight JL, Brooks CL. J. Chem. Theory Comput. 2011;8:36–46. doi: 10.1021/ct2006314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Eastman P, Friedrichs MS, Chodera JD, Radmer RJ, Bruns CM, Ku JP, Beauchamp KA, Lane TJ, Wang L-P, Shukla D, Tye T, Houston M, Stich T, Klein C, Shirts MR, Pande VS. J. Chem. Theory Comput. 2012;9:461–469. doi: 10.1021/ct300857j. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.