Multiple intermediates, diverse conformations, and cooperative conformational changes underlie the catalytic hydride transfer reaction of dihydrofolate reductase

Abstract

It has become increasingly clear that protein motions play an essential role in enzyme catalysis. However, how exactly these motions are related to an enzyme’s chemical step is still intensely debated. This chapter examines the possible role of protein motions that display a hierarchy of timescales in enzyme catalysis. The linkage between protein motions and catalysis is investigated in the context of a model enzyme, E. coli dihydrofolate reductase (DHFR) that catalyzes the hydride transfer reaction in the conversion of dihydrofolate to tetrahydrofolate. The results of extensive computer simulations probing the protein motions that are manifest during different steps along the turnover cycle of DHFR are summarized. Evidence is presented that the protein motions modulate the catalytic efficacy of DHFR by generating a conformational ensemble conducive to the hydride transfer. The alteration of the equilibrium conformational ensemble rather than any protein dynamical effects is found to be sufficient to explain the rate-diminishing effects of mutation on the kinetics of the enzyme. These data support the view that the protein motions facilitate catalysis by establishing reaction competent conformations of the enzyme, but they do not directly couple to the chemical reaction itself. These findings have broad implications for our understanding of enzyme mechanisms and the design of novel protein catalysts.

1. Introduction

Enzymes are specialized proteins that catalyze life-sustaining biochemical reactions inside cells. Enzymes permit a reaction that could take years to complete in a solution to be accomplished within a matter of seconds with typically more than a million-fold increase in the reaction rate compared to the uncatalyzed reaction [1, 2]. Deciphering how enzymes achieve such enormous increase in the rate of the reaction over similar uncatalyzed reactions in the solution is the holy grail of biochemistry. A detailed understanding of enzyme mechanisms can yield great benefits both scientifically and commercially in applications such as the design of biological catalysts and the development of targeted therapeutics to name a few [3, 4]. Therefore many experimental and theoretical investigations over the decades have been focused on gaining deeper understanding of enzyme mechanisms (cf. refs [5, 6] and references therein). While these studies have collectively provided significant insights into enzyme function, our understanding of various key mechanisms that enzymes employ to significantly speedup biochemical reactions remains rudimentary [7, 8]. This is evident from our inability to synthesize biological catalysts that can match the efficiency of enzymes produced through natural evolutionary processes [9, 10].

The way an enzyme speeds up a chemical reaction is often a complex, multi-step process. First, the ligand binds to the enzyme. Second, a conformational change occurs that is mostly associated with ligand binding. This transitions the enzyme-subtrate complex from an inactive to active state (“induced-fit” model [11]) or simply stabilizes the pre-existing minor population of the enzyme’s active state (“population-shift” model [12, 13]). Third, an actual chemical reaction occurs. Fourth, following chemistry, the product is released and the enzyme returns to its initial substrate-free conformation for the next cycle to begin.

A full and quantitative understanding of the catalytic power of enzymes requires the detailed knowledge of the dynamical changes and the underlying energy landscape (i.e., free energy barriers and minima) as an enzyme progresses through different stages of the catalytic cycle. However, gathering this information is a challenging problem whose solution requires a combination of theory, simulation, and experiment. While the ground state structures combined with kinetic studies provide crucial information on possible mechanisms of enzyme catalysis, they do not unravel atomically detailed transition pathways and the multidimensional energy landscape required to explain the catalytic prowess of enzymes. Theory and simulation can provide complementary information to experiments [14–18]. When data from such simulations is interpreted with a careful attention to the inherent limitations of the methodology, valuable information on atomically detailed conformational transition pathways, reaction intermediates and the discrete local energy minima of the high dimensional energy landscape of enzyme underlying conformational changes, i.e., conformational substates [12], can be elucidated to gain a quantitative understanding of enzyme function [19, 20].

This review will present advances in our understanding of enzyme catalysis, primarily exemplified through our group’s work in the application of the range of computational methods to quantitatively investigate protein conformational changes and the chemical transformation event in catalysis of a model enzyme dihydrofolate reductase (DHFR) [21–28]. DHFR catalyzes the reduction of 7,8-dihydrofolate (DHF) to 5,6,7,8-tetrahydrofolate (THF) utilizing the nucleotide cofactor 5,10-methylenetetrahydrofolate reductase (NADPH). The reduction of DHF is initiated through a protonation of the N5 atom of DHF, which is followed by a hydride transfer from the cofactor NADPH to the C6 atom in dihydrofolate.

Following a brief introduction into DHFR structure and function, we describe key results of equilibrium molecular dynamics (MD) simulations, which provide information on the local conformational fluctuations of the enzyme that may impact the chemical reaction. We then describe insights into factors modulating the chemical reactivity of the enzyme and mediating the rate differences between wild type and debilitating mutants of DHFR obtained through the examination of equilibrium ensembles of activation energies for the key hydride transfer step as well as the distributions of structural parameters in the different protein isoforms. Following, we discuss insights gained from simulations into the role of protein conformational changes in facilitating the protonation of dihydrofolate that precedes the hydride transfer event in the chemical transformation step. We then describe atomic and energetic details of large-scale conformational reorganization of the enzyme between functional states and the role such conformational changes play in the organization of the reactive groups for efficient catalysis. The features of enzyme catalysis investigated in a model enzyme DHFR may well provide insight regarding the general mechanisms by which enzyme activity is modulated. We note that comprehensive reviews on related topics have appeared that will be of use to interested reader [29, 30], this brief review makes no attempt at a complete review of the literature.

2. DHFR structure and function

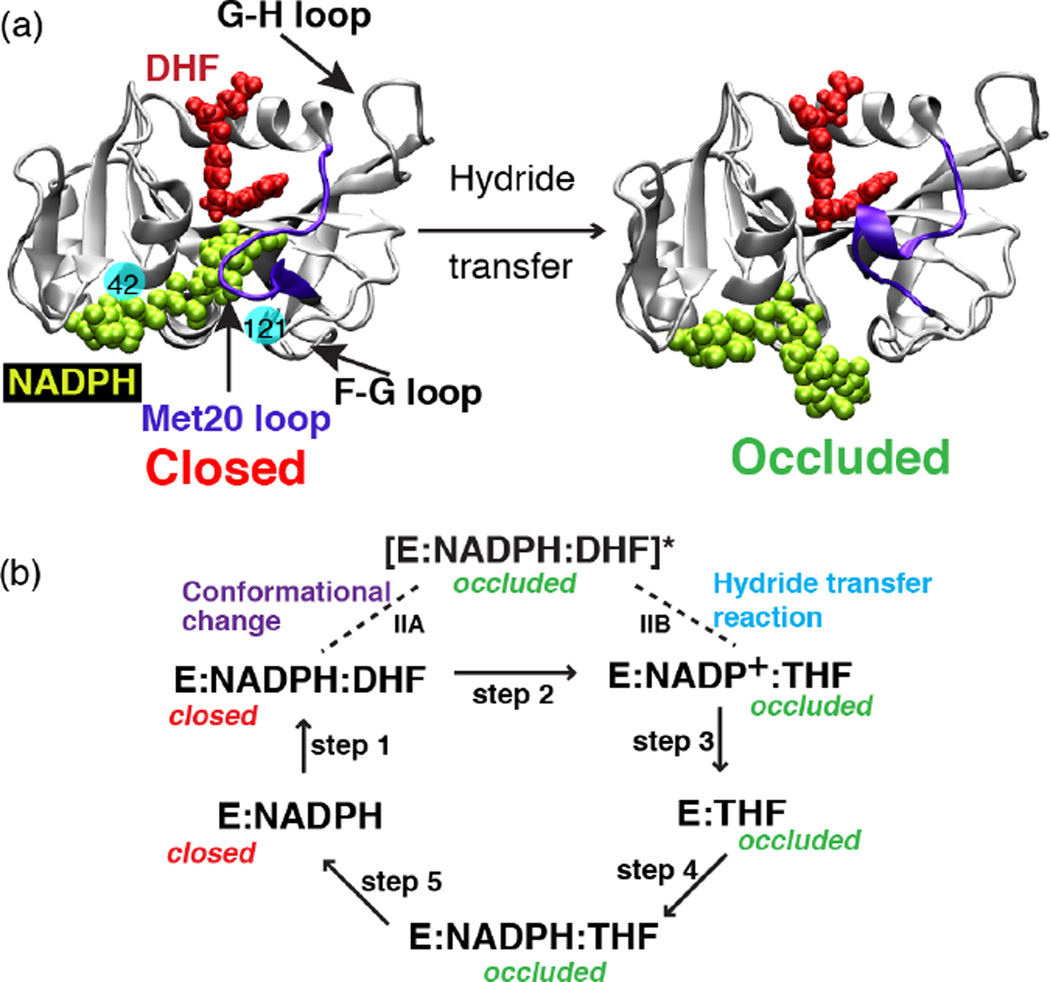
DHFR catalyzes the reduction of dihydrofolate (DHF) to tetrahydrofolate (THF) with help of a cofactor nicotinamide adenine dinucleotide phosphate (NADPH) [31]. The product of this reaction, THF, is a precursor of cofactors required for purine, pyrimidine and amino acid synthesis. Given its biological significance, DHFR has been subject of several theoretical [21–28, 32–35] and experimental investigations [36–54]. Based on the multiple crystal structures [55] and kinetic data [56] a catalytic cycle for DHFR has been deduced (Fig. 1). These studies suggest that during catalysis, DHFR cycles through five major intermediates: E:NADPH, E:NADPH:DHF, E:NADP+:THF, E:THF and E:NADPH:THF and undergoes significant conformational changes during this process. Analysis of these structures reveals that the large conformational changes of DHFR are concentrated in its Met20 loop (residues 14–24). Thus depending upon the conformation of the Met20 loop, different DHFR states along the catalytic pathway are characterized as open, closed or occluded. In the closed state the Met20 loop stacks against the nicotinamide ring while in the occluded state the Met20 loop sterically hinders the cofactor from binding in the active site (Fig. 1). The conformation of the Met20 loop in turn seems to depend on the ligands bound in the substrate and cofactor binding sites. In the holoenzyme E:NADPH and the Michaelis Menten complex E:NADPH:DHF, the Met20 loop adopts the closed conformation. While in the other three product complexes along the DHFR catalytic pathway, E:NADP+, E:THF and E:NADPH:THF, the Met20 loop assumes an occluded conformation. To determine how conformational changes on wide ranging timescales within the enzyme complex relate to its catalytic efficiency, we have generated a conformational and catalytic energy landscape of DHFR. Results of these computational explorations are reviewed in the following sections.

Fig. 1.

The structure of E. coli DHFR and the conformational changes that take place during the catalytic process. (a) Crystal structure of DHFR in the closed (PDB ID: 1RX2) and the occluded (PDB ID: 1RX6) states. In the closed state, the Met20 loop stacks against the nicotinamide ring of the cofactor (NADPH) while in the occluded state the loop prevents cofactor from accessing the active site pocket. Solid balls illustrate the locations of mutated residues 42 and 121. (b) Schematic representation of the catalytic pathway of DHFR as deduced from several kinetic and structural studies. In the holoenzyme E:NADPH and the Michaelis Menten complex E:NADPH:DHF, the Met20 loop adopts the closed conformation. In the three product complexes, E:NADP⁺, E:THF and E:NADPH:THF, the Met20 loop occurs in the occluded conformation. We have performed simulations capturing the enzyme’s transition between the closed and occluded state (step IIA, above). (Fig. 1 of Arora K and Brooks, C. L. (2009), J. Amer. Chem. Soc. 131:5642, Copyright © 2007, The American Chemical Society.

3. Correlated motion and the effect of distal mutations in hydride transfer

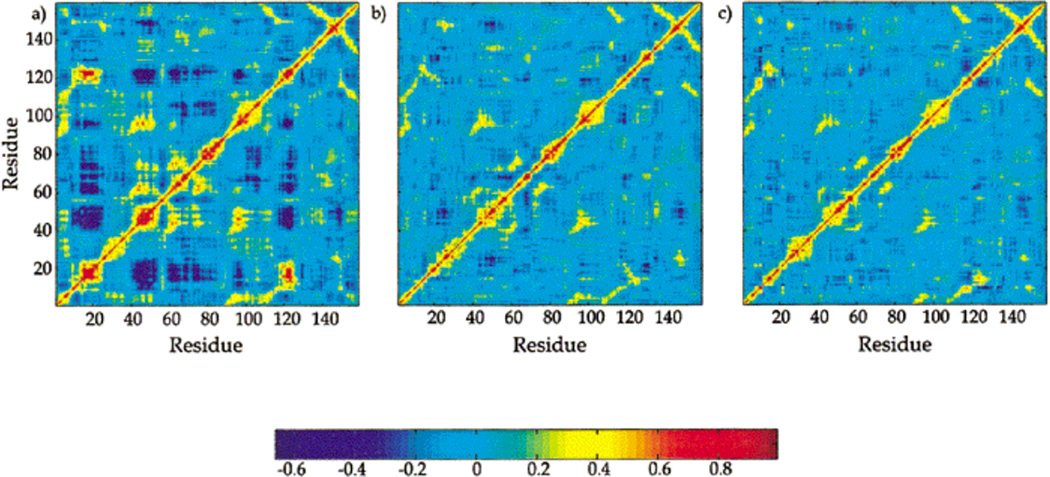
Proteins are intrinsically dynamic and protein internal motions can play a key role in their biological function [57, 58]. Initial understanding of the role of such protein motions in DHFR catalysis was derived from the equilibrium molecular dynamics (MD) simulations of wild type DHFR as well as distal mutants of DHFR implicated in modulating the hydride transfer rate by experimental kinetic and mutagenesis studies [32, 42, 59]. Classical MD simulations and correlated motions analysis of the corresponding MD trajectories for three ternary wild type complexes: DHFR/DHF/ NADPH (DH), DHFR/THF/NADP+ (TP), and DHFR/THF/NADPH (TH) from the DHFR catalytic cycle have provided residue-based maps of correlated motions [24]. As shown in Fig. 2, the results of correlated motion analysis reveal that spatially and sequentially separated residues in DHFR are coupled, displaying strongly “correlated” motions. However, strongly correlated motions present in the reactant Michaelis complex (DH) structure are abrogated in the product complexes with NADP+ (TP) or NADPH and H4F (TH).

Fig. 2.

Residue–residue based map of correlated motions. Red and yellow indicate regions of positive correlation, and dark blue indicates regions of anti-correlation. (a) DHFR/DHF/NADPH, (b) DHFR/THF/NADP⁺, (c) DHFR/THF/NADPH. (Figure 5 of Radkiewicz JL, Brooks III CL (2000) J. Am. Chem. Soc. 122: 225, Copyright © 2003, The American Chemical Society)

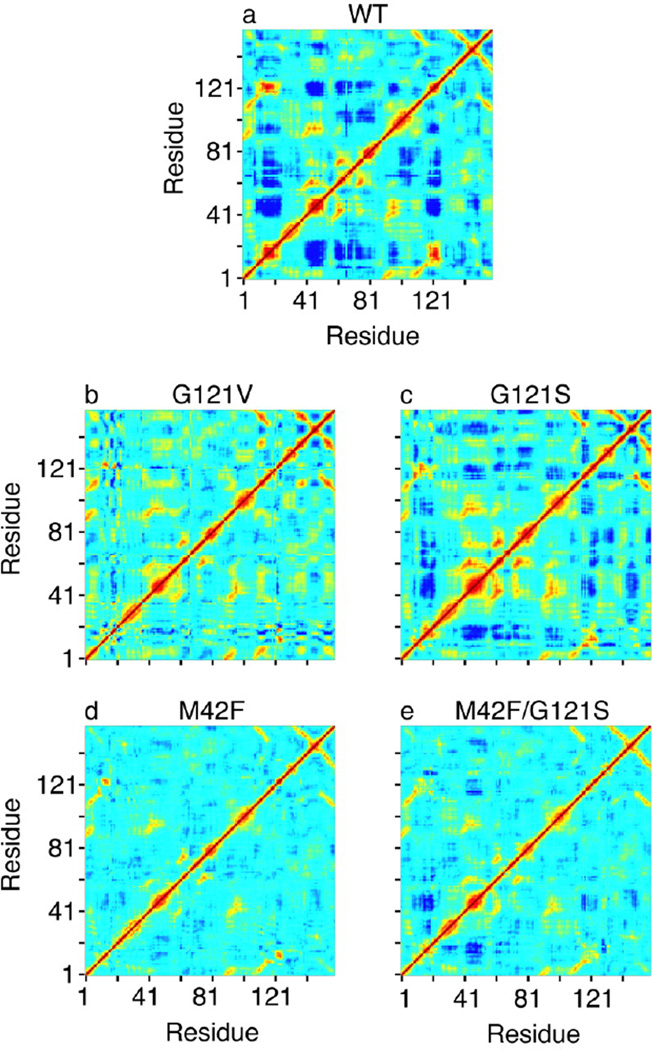
Motivated by earlier investigation of wild type DHFR, MD simulations were performed on reactant Michaelis complexes of G121S, G121V, M42F, and M42F/G121S mutants in which the position of mutations is located far away from the active site [28]. Interestingly, results of this analysis show that compared to wild type DHFR the correlated motions are reduced in all mutant complexes (Fig. 3), correlating somewhat with the reduction in the experimental hydride transfer rates [42]. As shown in Fig. 3, particularly, correlated fluctuations of the Met20 loop with several regions of the enzyme are strongly affected by mutations, suggesting that these motions may be relevant to the catalytic efficacy of the enzyme. The question then arose, if and how diminished correlated fluctuations upon distal mutations would manifest in the structural changes of the enzyme?

Fig. 3.

Covariance matrix for the fluctuations of the C_α atoms in wild type DHFR and various mutants. Yellow and red regions indicate that the C_α atoms move in a concerted way (positively correlated movements), and dark blue means they move opposite to each other (anticorrelated movements). The scale goes from −0.6 (dark blue) to 1 (red). We note that we get the same qualitative picture for the correlated motions if all heavy atoms are included in the calculation of the covariance matrix. (Figure 3 of Rod TH, Radkiewicz JL, Brooks III CL (2003) Proc. Nat. Acad. Sci. USA 100: 6980, Copyright © 2003, National Academy of Sciences USA)

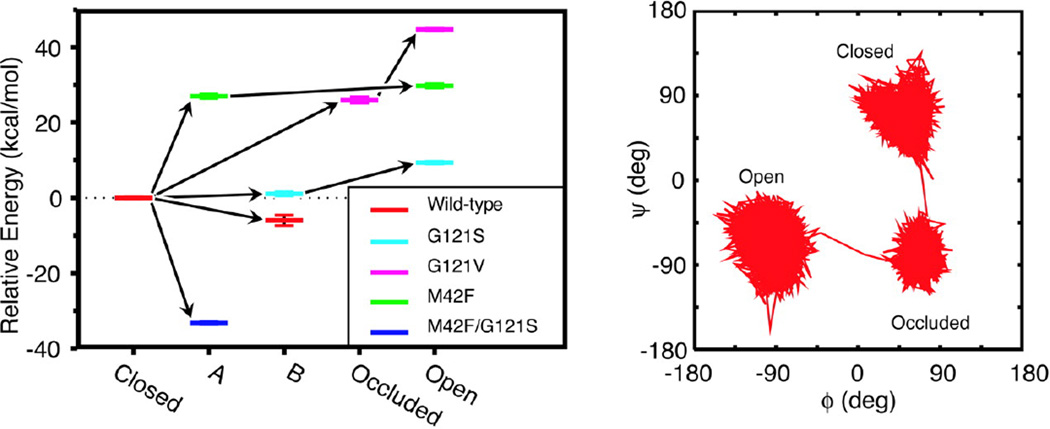
Answers were sought by performing cluster analysis of MD trajectories on the Met20 loop backbone conformations based on their ϕ/ψ dihedral angles for G121S, G121V, M42F, and M42F/G121S mutants and wild type DHFR [24]. Specifically, Met20 loop conformations were clustered since the correlated fluctuations of the Met20 loop with the rest of the enzyme are most affected upon mutations (Fig. 4). The results of cluster analysis show that the simulations sample five different well-defined clusters, which include the closed, open, and occluded conformations of the Met20 loop. As shown in Fig. 4, the wild type enzyme mostly samples the closed conformation of the Met20 loop. However, the mutants sample multiple conformations of the Met20 loop that include intermediate conformations between crystallographically observed open, closed, and occluded states. Furthermore, results of cluster analysis show that the mutations change the relative energy among the different Met20 loop conformations (Fig. 4). The shift in the energy levels for different conformations of the Met20 loop sampled in the simulations of wild type and mutants indicates that the structural changes occur near the active site, even if the mutation is distant from the site of chemical transformation. These long-range structural perturbations in the vicinity of the active site center of the enzyme may influence the hydride transfer reaction, rationalizing the experimentally observed rate-diminishing effects of distal mutations. How are these structural perturbations manifesting in the energy barrier of the hydride transfer? Answers were sought by performing hybrid quantum mechanics molecular mechanics (QM/MM) simulations capable of capturing bond breaking and formation in the chemical reaction [60, 61], which is beyond the reach of classical MD simulations discussed above. In the next section, we present results of QM/MM investigations of the hydride transfer event in wild type DHFR as well as the G121S and G121V mutants that provide quantitative insights into the affect of mutations outside the active site on the hydride transfer barrier height.

Fig. 4.

(Left) Shown are the energy levels for different conformations of the Met20 loop sampled in the simulations of native and mutant Michaelis complexes of DHFR, relative to the closed conformation. Each color represents a particular mutant, and the five different conformations found from our cluster analysis are shown along the horizontal axis. The energies are the average energies calculated by using a generalized Born implicit solvent model from snapshots from the portions of the trajectories belonging to particular loop conformations. The error bars represent the standard errors about these averages. The arrows indicate the progression in time. (Right) Shown is a representative trajectory in ϕ−ψ space for loop residue Gly-17 in the G121V mutant to illustrate the extent to which different conformations may be differentiated. (Figure 4 of Rod TH, Radkiewicz JL, Brooks III CL (2003) Proc. Nat. Acad. Sci. USA 100: 6980, Copyright © 2003, National Academy of Sciences USA)

In summary, equilibrium MD simulations of wild type and distal mutants of DHFR show that there are specific correlated motions in the reactive ternary complex of the enzyme that are abolished in the ternary product complex and reduced in the mutants. The changes in the patterns of correlated motions simply reflect structural changes of the catalytically important Met20 loop, which in turn may affect the hydride transfer rate.

4. Conformational substates modulate the barrier to hydride transfer

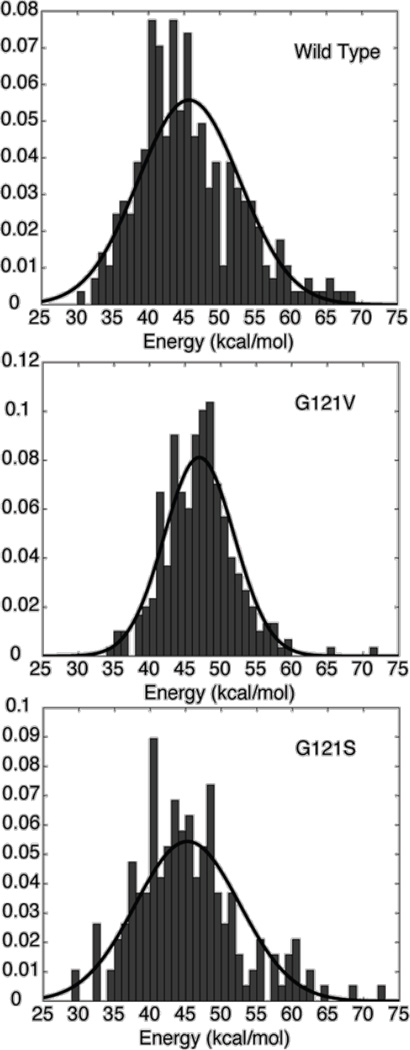
Insights into how structural changes of the Met20 loop can be manifest in the energy barrier of the hydride transfer have emerged from QM/MM calculations of the distributions of activation energies for the hydride transfer reaction in wild type as well as the G121S and G121V variants of DHFR [23]. In these studies, taking into account the possibility that the enzyme may exist as a distribution of conformations [62], the distributions of energy barriers were computed from the corresponding fixed protein structures extracted from the different time-course of MD simulations trajectories. The results of QM/MM simulations show that wide ranges of hydride transfer energy barriers exist for the wild type and the G121V and G121S mutants (see Fig. 5). This result establishes that the energy barrier for hydride transfer, and consequently, reaction rate, in DHFR fluctuates in a time-dependent manner. Time-dependent variations in the energy barriers for an enzyme-catalyzed reaction have been demonstrated in both theoretical studies [63] and single molecule experiments [64, 65] by other researchers. In the single molecule experiments, time-dependent variation in the reaction rate was interpreted as a toggling of protein between different conformers, each associated with a distinct reaction rate [64]. However, additional theoretical analyses have revealed that such observations are consistent with the presence of the two or more conformers of a protein with distinct reaction rates [63]. This suggests that the QM/MM calculations of activation energy barriers initiated from several snapshots of the MD simulations are analogous to single molecule experiments demonstrating time-dependent variation in the reaction rate of individual enzyme molecules [65]. Further, this occurrence suggests that the computationally observed variation in the hydride transfer barriers can be attributed to the existence of the enzyme in multiple distinct conformational substates which modify the potential energy surface, each giving rise to a unique energy barrier for the hydride transfer.

Fig. 5.

Histograms of calculated hydride transfer energy barrier distributions for (a) wild type, (b) G121V, and (c) G121S enzymes. The lines represent a Gaussian fit to the data. (Figure 2 of Thorpe IF, Brooks III CL (2003) J. Phys. Chem. B 107: 14042, Copyright 2003, © The American Chemical Society)

Comparison of the activation energy distributions present in DHFR and its variants demonstrates that the ensemble of energy barriers differs in each system studied (see Fig. 5). Subsets of structures extracted from MD simulations were employed to calculate the activation free energy for the hydride transfer following the free-energy perturbation approach. These calculations focused on the properties of the reactant states, with an assumption that the corresponding transition states reflect a small perturbation of the reactant-state configurations [66]. Furthermore, to account for the inadequate sampling of low hydride-transfer energy barriers at either side of the distribution, Gaussian approximant was used to model the distribution of the energy barriers for the three enzyme systems. Resulting, effective activation free energies for the wild type, G121S, and G121V distributions are 13.7 (33.4), 12.9 (32.0), and 26.6 (37.6) kcal/mol, respectively [23]. Values in the parentheses correspond to the estimated barriers without Gaussian approximant. The free energy barrier differences among the three protein systems agree qualitatively with the experimental estimates. The relative ordering of the calculated free energies shows that the energy barrier for the G121V mutant is greater than the wild type, as expected based on experimentally determined rate constants. However, the energy barrier for G121S mutant is not very different from the wild type DHFR. Experimentally, however, the G121S hydride transfer rate differs from that measured for the wild type protein.

How then is the hydride transfer barrier height modulated? To find answers, the hydride barrier distributions of wild type DHFR and its mutants were analyzed for the variability of hydride transfer barriers [22]. The variability of hydride transfer barriers reflects the ground state conformational space explored by an enzyme. In addition, quasi-harmonic (QH) analysis [67] was performed to measure the impact of the Met20 loop conformations on the fluctuations of the ligand and cofactor molecules in the active site. Together these analyses reveal that for the G121S mutant that has a similar free energy as the wild type protein, the variability of hydride transfer barriers is similar to the wild type protein but the flexibility of the ligand and cofactor molecules in the active site is enhanced compared to the wild type protein. This is an unexpected result, as one would anticipate that increased flexibility of the ligands would generate an increase in the variability of the energy barrier distribution. These observations suggest that although the ligand and cofactor sample more conformational space than in the wild type protein, the additional conformational space explored is not directed toward generating configurations conducive to the hydride transfer, and the corresponding energy barrier distributions are unaffected. Thus, while conformations giving rise to low hydride transfer barriers still exist; such conformations comprise only a small fraction of all conformations accessible to the G121S mutant. This would explain the reduction in the effective hydride transfer rates observed for this mutant. In contrast, for the G121V mutant which has a much higher hydride transfer barrier than the wild type protein, similar analysis shows decreased variability of hydride transfer barriers as well as the reduced flexibility of ligand and cofactor molecules in the active site compared to wild type protein. These observations suggest that the G121V mutant samples very different conformational space from the wild type DHFR and conformations conducive to hydride transfer are not sampled. Taken together, results show that although there is a subtle difference in the mechanism, eventually for both mutants the decrease in the effective hydride transfer rate arises due to a decrease in the relative amount of conformational substates favorable for hydride transfer to take place compared to the wild type DHFR.

Computational studies by Hammes-Schiffer and coworkers have provided evidence for a network of coupled motions that correlate with the progress of the hydride transfer reaction in DHFR and the G121V mutant [68]. In these studies, thermally averaged geometric properties that may be related to the hydride transfer were computed. We examined the wild type and mutant conformational ensembles for a similar set of representative distances presented by Hammes-Schiffer and co-workers [21–23]. This analysis shows that there are significant differences in the key geometric parameters that correlate well with the progress of the reaction for the wild type and mutant systems. These results highlight differences in the wild type and mutant structural ensembles that may be the origin of the observed variation in the distributions of hydride transfer energy barriers and corresponding variations in the reaction rate among the wild type and mutant systems studied. Further, analysis of key geometric parameters reveals that there is a significant qualitative agreement with the earlier study of Hammes-Schiffer and coworkers despite the fact that we employed equilibrium distributions of static protein conformations to calculate the hydride transfer barriers. This finding suggests that the changes in the geometric parameters arise due to the progress of the catalytic reaction itself and not due to the fluctuations of the protein. Furthermore, the network of coupled motions observed throughout the protein and ligand by Hammes-Schiffer and coworkers reflect changes in the equilibrium conformational distribution of the protein.

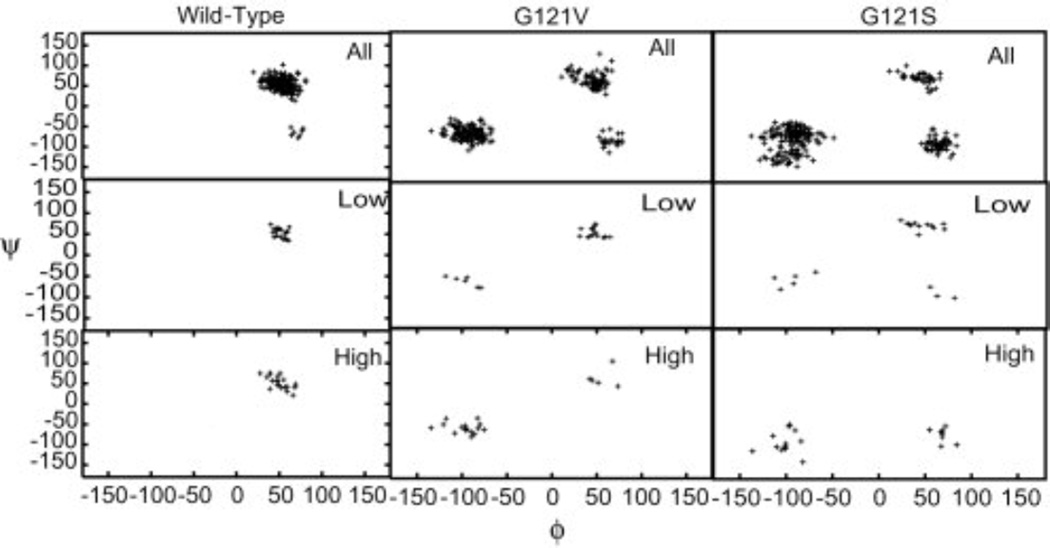
In addition to the key geometric parameters presented by Hammes-Schiffer and coworkers, the detailed examination of the wild type and mutants structural ensembles has revealed a select set of ϕ/ψ dihedral angles that correlate with the presence of protein conformations giving rise to low hydride transfer barriers [22]. As shown in Fig. 6, mutants exhibit dihedral angle values for residues within the Met20 loop not observed in wild type DHFR. These alternate dihedral angle values correspond to the Met20 loop conformations that are not suited for hydride transfer to take place and are generally associated with high hydride transfer energy barriers. These results imply that the configuration of the Met20 loop, which abuts the site of hydride transfer, is one of the important components of a low energy conformational substate. Mutations act to change the structure of this mobile Met20 loop leading to a redistribution of conformational substates present in the protein and thereby impact the hydride transfer rate.

Fig. 6.

Backbone ϕ/ψ angles for glutamate 17. The first row in each panel corresponds to the entire trajectory, while the second and third rows correspond to structures giving rise to low and high transfer barriers, respectively. Dihedral angles are exhibited by the mutant proteins that are not observed in wild type DHFR. These alternate dihedral values are generally associated with higher barriers. Glutamate 17 is observed to be primarily in the region ϕ 50°/ψ 50° for the wild type protein and for the low-barrier structures of the two mutants. Structures giving rise to higher barriers in the mutant proteins are found in the vicinity of ϕ −100°/ψ −50°. (Figure 5 of Thorpe IF, Brooks III CL (2004) Proteins: Struct. Funct. Bioinf. 57: 444, Copyright 2004, © The Protein Society)

Additional computational studies have emphasized that time-dependent displacement of groups within the active site of the enzyme can directly contribute energy to the reactive event (henceforth referred to as “dynamical coupling”). This phenomenon has been suggested to exist for several enzymatic reactions [69, 70]. However, our results do not support dynamic coupling as a key factor influencing the rate of hydride transfer in DHFR [23]. This is because if the time-dependent conformational fluctuations of the protein groups were directly contributing energy to induce a reactive event, one would expect to see no differences in the energy barriers computed using static snapshots from MD trajectories. Clearly, as discussed above, simulations have demonstrated that differences in the energy barrier distributions exist, even though static snapshots from MD simulations were used for the calculations of the activation energy barriers, suggesting against any role of dynamical coupling in modulating the hydride transfer energy barrier (see Fig. 5). Moreover, differences in the energy barrier distributions that qualitatively agree with the experimentally determined reaction rates suggest that the modulation of the conformational ensemble rather than dynamic coupling is one of the main factors influencing the hydride transfer barriers, and consequently, reaction rate. This suggestion is in agreement with the recent kinetic isotope effect (KIE) study of wild type and N23PP/S148A mutant of DHFR [71]. According to this study, the magnitude and temperature dependence of the KIEs on hydride transfer are unaffected by mutation, suggesting that there is likely no dynamic coupling of protein motions to the hydride transfer step itself.

Other features that could have an impact on the chemical reaction barrier have also been suggested. Theoretical studies by Hammes-Schiffer and coworkers have shown that the protein motions could affect the rate of barrier re-crossing for the hydride transfer step and hence influence the reaction rate [68]. These studies also suggest that in addition to the effect of protein motions on the barrier re-crossing rate, the incorporation of quantum dynamical effects should further reduce the barrier to hydride transfer by 2–3 kcal/mol [68]. However, subsequent investigation revealed that both barrier re-crossing and quantum dynamical effects are almost identical for the wild type and mutants suggesting that they are not responsible for differences in the relative reaction rates [72]. Yet another factor that could influence the reactivity of DHFR is the pK_a of the bound substrate, dihydrofolate [36]. The closed ternary complex can affect hydride transfer, which is believed to follow the substrate protonation at position N5. The substrate protonation is considered to be responsible for the observed pH dependence of the hydride transfer [36]. In the next section, we present results of simulations probing the affect of the protein conformational changes in modulating the pK_a of the bound substrate and consequently hydride transfer rate.

In summary, results of QM/MM investigations show that the energy barrier of hydride transfer in wild type, G121V and G121S variants fluctuates in a time-dependent manner. The features of these energy barrier distributions are consistent with experimentally determined reaction rates for the three proteins and support observations of single molecule experiments demonstrating time-dependent variation in the reaction rate of individual enzyme molecules. Further, the results show that the fluctuations of hydride transfer energy barriers primarily arise due to the modulation of the equilibrium ensemble of the protein conformations. The configuration of the Met20 loop is an important component of this equilibrium structural ensemble as indicated by the correlation between the change in the dihedral angles populated by residues within the Met20 loop and the concomitant change in the ensemble of hydride transfer barriers. The mutations at position 121 acts to disrupt the equilibrium distributions of the Met20 loop that is adjacent to the site of chemistry in the enzyme and thus impact the hydride transfer rate. Collectively, these results suggest that the alteration of the ensemble of conformational substates populated by the protein rather than dynamical coupling is the key factor influencing the rate constants for the hydride transfer reaction in DHFR.

5. Met20 loop facilitates the protonation of the substrate

The chemical step of DHFR's catalytic cycle involves a hydride transfer from the cofactor to the substrate with concomitant protonation of N5 atom of the substrate. Experiments have shown that this chemical step is pH dependent [36] and this pH dependency primarily arises due to the substrate protonation that is best described with a single pK_a value of 6.5 [36, 73, 74]. The pK_a value of the substrate in solution is 2.6, implying that DHFR increases the pK_a value by ~4 pK_a units. The key question for investigation is how does an enzyme facilitate the protonation of the substrate?

Answers were sought by performing the pK_a calculations for the key enzyme conformations, those involving the closed and occluded configurations for the Met20 loop [26]. The pK_a values of 7.1 and 7.7 were reported for the closed and occluded Michaelis complexes, respectively. These results confirm that indeed, the enzyme facilitates the protonation of the N5 atoms of the substrate. Further, analysis revealed that the side chain of Asp27 in the active site that forms hydrogen bonds to the substrate remains ionized in both occluded and closed complexes to properly coordinate the substrate, thus further stabilizing the substrate protonated state. Together these results suggest that DHFR promotes protonation by enclosing the N5 atom in a hydrophobic pocket together with the negatively charged Asp27 residue. However, in these preliminary investigations the effect of the Met20 loop conformational change in the enzyme on the substrate pK_a and consequently its implications to catalysis were not explored.

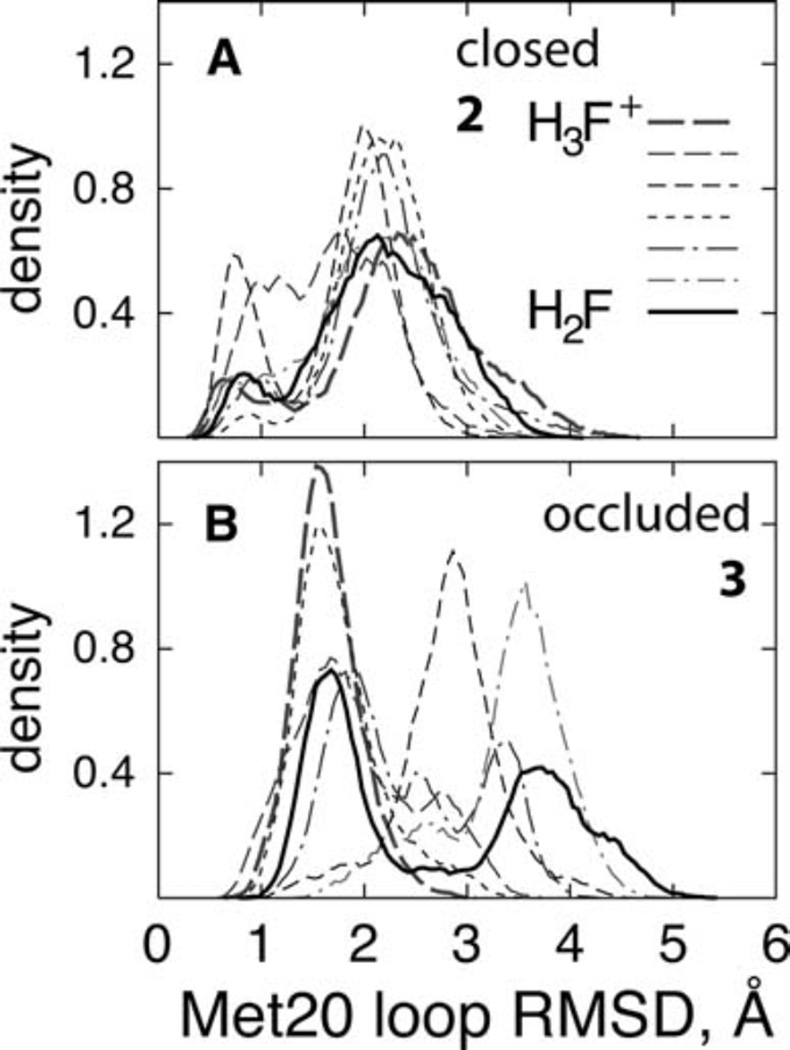
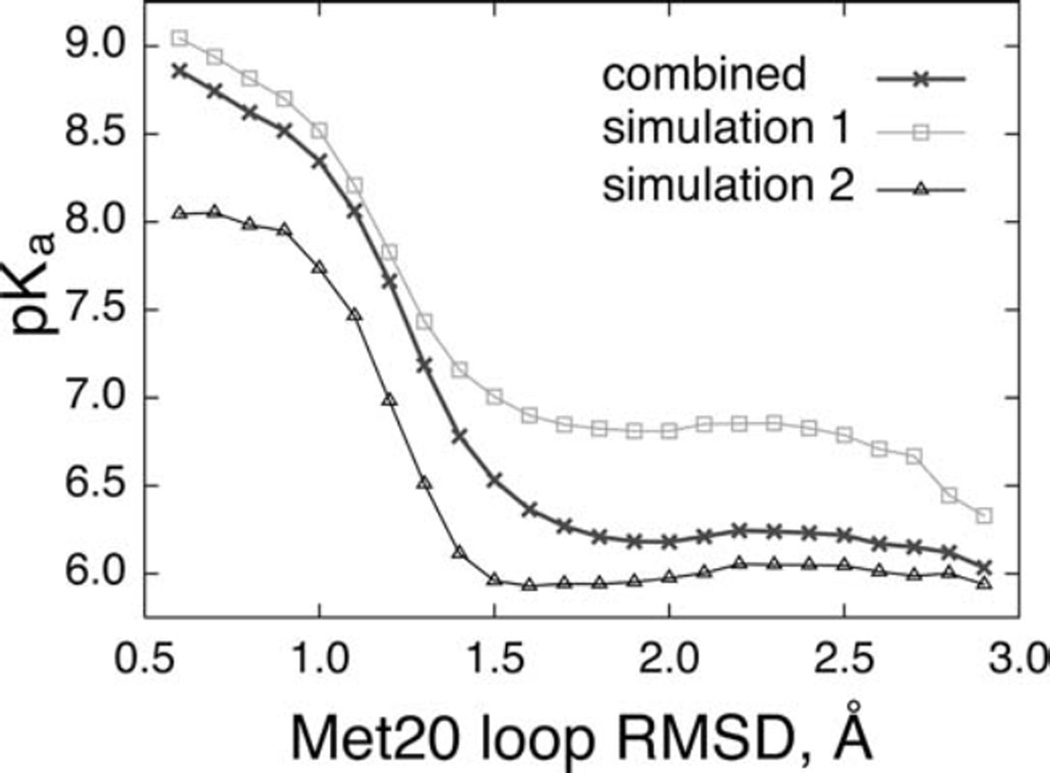
Insights into how the conformational change from occluded to closed state enhances the substrate pK_a in the reactive complex have emerged from combined free energy perturbation and molecular dynamics simulations (FEP/MD) for the closed and occluded Michaelis complexes. In this study, initially the flexibility of the Met20 loop was quantified by measuring the C_α root mean square deviation (RMSD) of the Met20 loop with respect to the X-ray closed and occluded complexes. As shown in Fig. 7, the Met20 loop is quite flexible in the occluded complex compared to the closed complex. Furthermore, in the closed complex two major loop states are visible: a small population of “tightly-closed” state (RMSD 0.25 to 1.0 Å) and a larger population of the “partial closed/open” state (RMSD 1.5 to 3.5 Å). Subsequently, the Met20 loop flexibility was related to the substrate pK_a by plotting the pK_a of the substrate as a function of the Met20 loop RMSD. As shown in Fig. 8, the pK_a of the Met20 loop strongly modulates the substrate pK_a in the closed Michaelis complex, with the dependence having a characteristic sigmoidal shape. In the “tightly closed” state of closed complex, the computed pK_a is in the 8.0–9.0 unit range that is substantially larger than that in the “partially closed/open” state and the corresponding final pK_a. Further, analysis of the trajectories have revealed that the tight closing of the Met20 loop enhances the interactions of the cofactor and the substrate with the Met20 side chain and aligns the nicotinamide ring of the cofactor coplanar with the pterin ring of the substrate, thus facilitating the protonation.

Fig. 7.

The distributions of the Met20 loop RMSD in (Å) the closed complex and (B) the occluded complex. All FEP windows are shown (thin lines), along with the endpoint states (thick lines) to illustrate the overlap between the windows. (Figure 5 of Khavrutskii IV, Price DJ, Lee J, Brooks III CL (2007) Protein Sci. 16: 1087, Copyright © 2007, The Protein Society)

Fig. 8.

The substrate pKa in the closed complex, as a function of the Met20 loop RMSD. The three curves refer to the results from the independent simulations 1 (squares) and 2 (triangles) with different initial velocities and the combined (crosses) result. (Figure 6 of Khavrutskii IV, Price DJ, Lee J, Brooks III CL (2007) Protein Sci. 16: 1087, Copyright © 2007, The Protein Society)

In summary, results demonstrate that the conformational change of the Met20 loop is coupled to change in the substrate pK_a and may enhance hydride transfer catalysis. These results supplement studies discussed in the previous sections, which show that the equilibrium sampling of the Met20 loop configurations conducive to the hydride transfer is a major factor influencing the catalytic rate.

6. Conformational dynamics of the Met20 loop on a free energy surface

Studies discussed so far have suggested that the configuration of the Met20 loop may be an important component of a conformational substate in DHFR that engenders an environment favorable to hydride transfer. However, these conclusions are derived from the equilibrium dynamics simulations that tend to explore localized regions of conformational space around the ground state structures of the enzyme. Therefore a clear link between the conformational reorganization of the Met20 loop between different functional states and the modulation of the chemical environment is missing. This missing dynamics picture has emerged from the elucidation of the conformational transition pathway between closed and occluded states of the enzyme and the corresponding free energy profile using enhanced sampling simulations [27]. These calculations show that the free energy barriers separating occluded and closed states of the Met20 loop in the Michaelis Menten complex of DHFR are small and the transition between these states occurs via an intermediate ‘open’ conformation along the pathway (see Fig. 9). The highest free energy barrier corresponding to this conformational change is 5 ± 1 kcal/mol. This value of barrier height is much lower than the transition-state theory estimate of 16.0 kcal/mol obtained from the experimental kinetic data [43, 49]. However, the calculated free energy difference between the closed and occluded states (3.3 ± 1 kcal/mol) is in good agreement with experiments, suggesting that the value for the free energy barrier height obtained from simulations is also probably correct. Moreover, activation barriers estimated by using transition-state theory represent extreme upper limits given the limitation of the theory to describe diffusive processes such as protein folding and protein conformational changes [75].

Fig. 9.

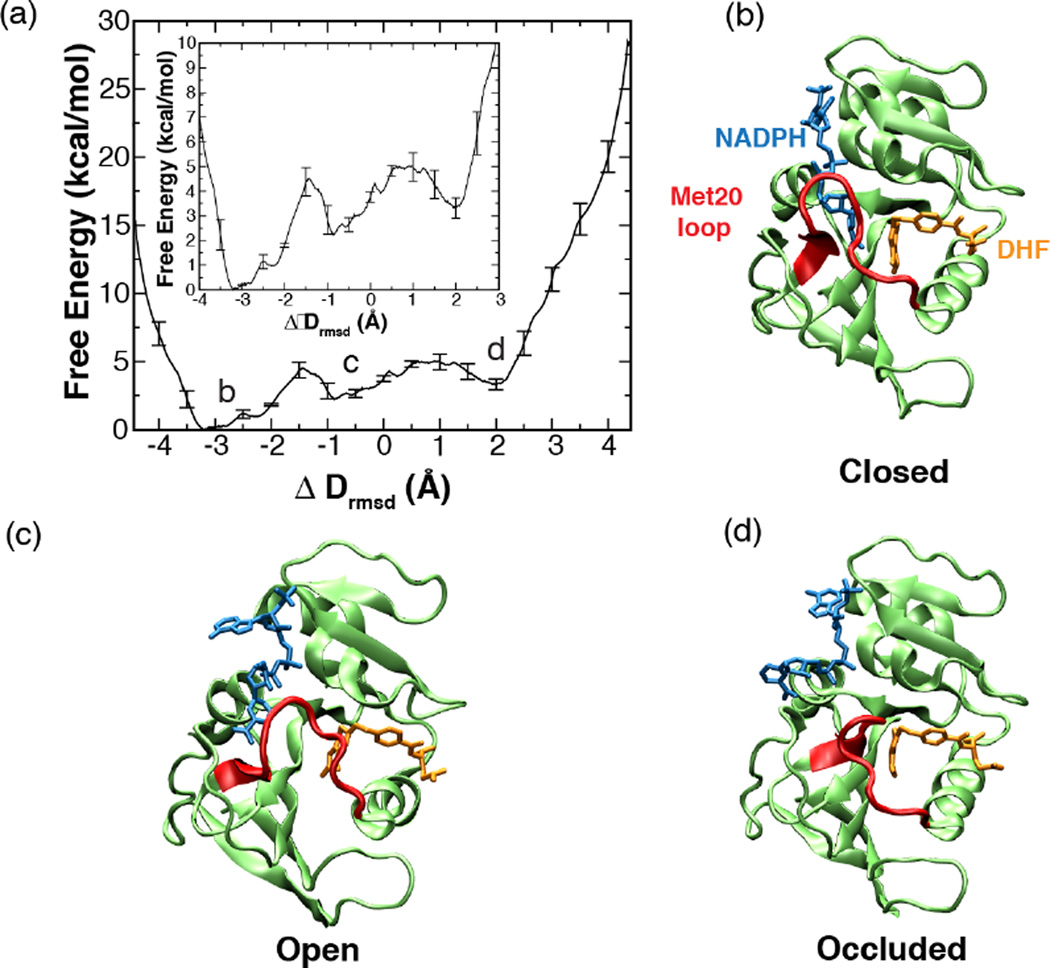
One-dimensional free energy profile along the ΔD_rmsd order parameter. The error bars represent the standard deviation in the energy values determined from the set of three umbrella sampling MD simulations with different initial velocities. Inset depicts the enlarged view of the same plot. (a, c, and d) Representative structures, closed, open and occluded (top right to bottom right) corresponding to the three free energy minima (a, top left) along DHFR’s conformational change pathway. (Fig. 2 of Arora K and Brooks, C. L. (2009), J. Amer. Chem. Soc. 131:5642, Copyright © 2007, The American Chemical Society)

How does one reconcile the calculated small ~5 kcal/mol free energy barrier with the slow kinetics of the Met20 loop transitions observed in NMR studies? Kramer's reaction rate theory that incorporates the dynamical fluctuations of the enzyme missing in the transition-state theory estimate of rate constant can be used to estimate the reaction rate of diffusive motions in enzymes [76]. Kramer’s rate model assumes that the dynamics of the system can be represented as a diffusive process on a low-dimensional free energy surface and has been successfully applied earlier to predict rates of protein folding [77, 78]. To deduce the kinetics of the Met20 loop transitions by using Kramer’s reaction rate theory, the position dependent diffusion constants along the Met20 loop conformational transition pathway were computed. The computed diffusion constant values together with the barrier height obtained from the free energy profile were then incorporated in Kramer's reaction rate equation. Interestingly, the calculated rate of transition from the closed state using Kramer’s rate relationship agrees very well with the rate of the Met20 loop transitions provided by NMR dispersion experiments [47]. Thus, simulations show that the slow dynamics of the system arises due to the small diffusion constant on a rugged energy landscape and not due to high-energy barriers separating different conformational states.

The small free energy barriers separating the functionally important conformational states imply that the system can populate alternate conformations via thermal fluctuations. As shown in Fig. 9, when the cofactor is out of the binding pocket, the enzyme can frequently sample open and occluded conformations because of a small (~3 kcal/mol) free energy barrier between the two states. However, when the cofactor is in the binding pocket, the closed conformation is thermodynamically most favored [27]. These results suggest that every possible conformation of the protein is present at all times, although with different population distributions that can be modulated via interaction with the specific substrate. This mechanistic picture emerging from the thermodynamic and kinetic analysis of the Met20 loop fluctuations is consistent with the population-shift model of ligand binding, which postulates that the ligand binding merely stabilizes the pre-existing minor population of the enzyme’s active state in the conformational ensemble [13]. This viewpoint is also consistent with the perspective of conformational dynamics in DHFR informed by NMR dispersion experiments; according to which each intermediate in the catalytic cycle samples low-lying excited states whose conformations resemble the ground state structures of the preceding and following intermediates [49].

The detailed examination of the closed state conformational ensemble has revealed that only a few selected conformations of the Met20 loop from the ensemble have an active site geometry conducive to the hydride transfer reaction (see Fig. 10). This phenomenon was noticed in the previous studies of this system. As discussed in Section 5, simulations exploring the role of the Met20 loop conformations in modulating the substrate protonation have shown that in the closed state two substates can be distinguished, namely the “partially closed” and “tightly-closed’’ conformation of the Met20 loop [26]. However, only the tightly-closed state has the correct pKa of the substrate conducive to protonation. Taken together, these results reaffirm the earlier conclusions drawn from the equilibrium simulations that the enzyme can populate an ensemble of substates with differentially preorganized protein environments in the vicinity of the enzyme’s active site.

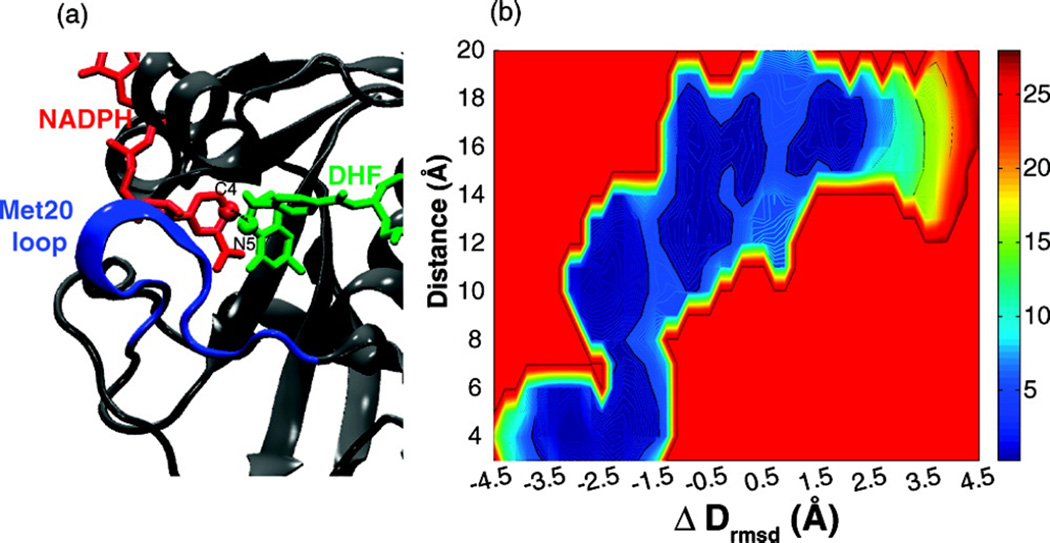
Fig. 10.

View of the active site and Met20 loop corresponding to the closed state depicting atoms involved in the hydride transfer reaction. (b) The two-dimensional free energy surface along the ΔD_rmsd order parameter versus hydride transfer distance between the atom N5 of DHF and C4 of NADPH. In the closed state (ΔD_rmsd ≈ −3.5 Å), the distance between the cofactor and substrate fluctuates in the range of 3–4 Å, suitable for promotion of the hydride transfer reaction. (Fig. 3 of Arora K and Brooks, C. L. (2009), J. Amer. Chem. Soc. 131:5642, Copyright © 2007, The American Chemical Society)

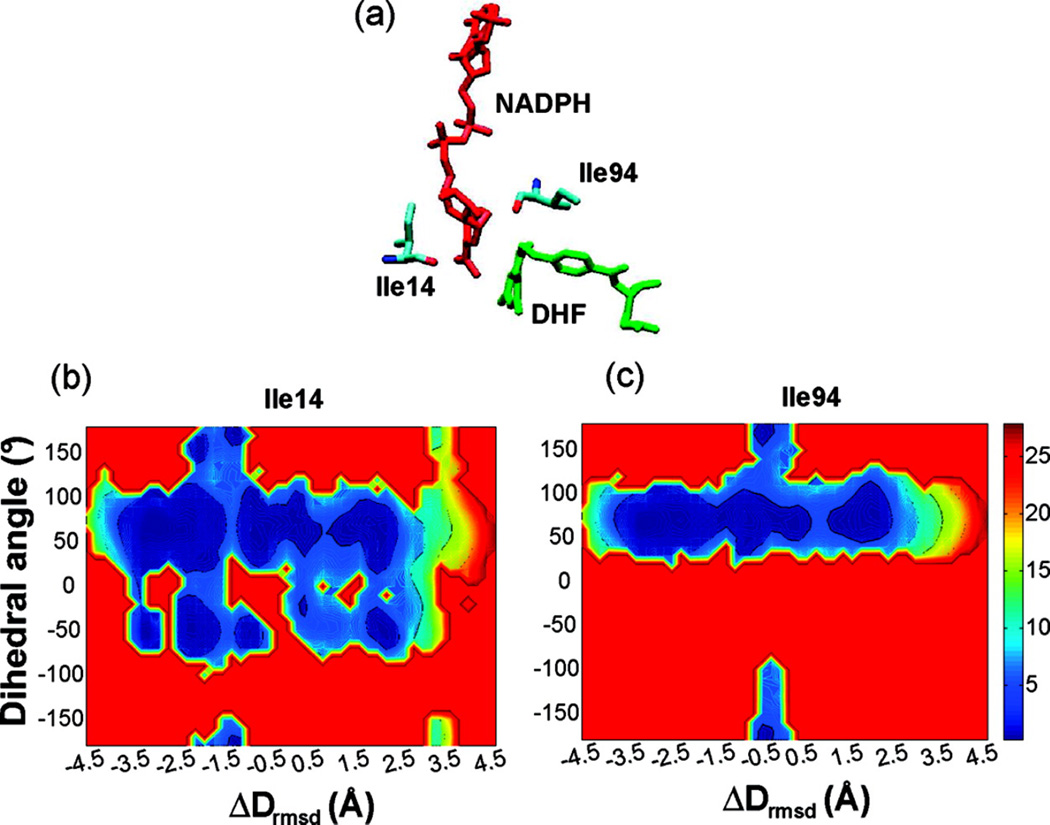
Local side chain motions have been proposed to be important for hydride transfer in several enzymes [79, 80]. For DHFR catalysis, hydrophobic active site residues Ile14 and Ile94, which in the crystal structure are in van der Waals contact with the substrate and cofactor, are of particular interest. NMR studies have demonstrated that the side chains of residues Ile14 and Ile94 populate both trans and gauche⁺ rotamers about the χ₁ dihedral angle in solution. However, only the gauche⁺ conformation of these side chains is observed in the occluded and closed crystal structures. Further, modeling has suggested that in the trans rotameric state, the side chains of these residues would sterically clash with the atoms of the cofactor and pterin rings, respectively. Therefore in order for residue Ile14 to exist as a trans rotamer, the nicotinamide ring would have to be displaced towards the pterin ring. To test this hypothesis, we computed the free energy surfaces corresponding to the χ₁ dihedral angle of the residues Ile14 and Ile94 along the reaction coordinate, as part of the conformational change of the Met20 loop [27]. As shown in Fig. 11, the trans rotamer population is observed only in the open state and in high-energy conformations leading to the occluded state of that loop. Only the gauche⁺ and a small amount of gauche⁻ populations are present in the closed, reaction competent state. Interestingly, the position of the trans population along the reaction coordinate coincides with a decrease in the hydride transfer distance. These simulation results are consistent with the hypothesis that favors a mechanism in which residues Ile14 and Ile94 guide the cofactor and substrate toward a reactive configuration for subsequent hydride transfer reaction and thus facilitate catalysis. Corrobrating these findings, recent studies examining the relationship between the hydride-donor acceptor distance (DAD) and its distribution and dynamics to the rate of hydride transfer and the temperature dependence of intrinsic KIEs has provided evidence that residue Ile14 participates in the restrictive active-site motions that modulate the DAD and thus assist the hydride transfer [81].

Fig. 11.

View of the active site showing the side chains of residues Ile14 and Ile94 near the cofactor and the substrate, respectively. (b and c) Two-dimensional free energy surface corresponding to the χ₁ rotameric dihedral angle (N-C_α-C_β-C_γ1) along the reaction coordinate for residues Ile14 (middle) and Ile94 (right). Both residues explore a minor trans conformation near the barrier region (see Fig. 9). In the trans rotameric state these residues interact unfavorably with the substrate and cofactor bringing the two reactants close to each other. (Fig. 4 of Arora K and Brooks, C. L. (2009), J. Amer. Chem. Soc. 131:5642, Copyright © 2007, The American Chemical Society)

In summary, characterization of microsecond-millisecond time scale conformational fluctuations that precede the chemical transformation step of DHFR show that the largest conformational changes are concentrated in the Met20 loop of the enzyme implicated in modulating the hydride transfer efficacy. The free energy profile corresponding to the conformational transition pathway reveals that the free barriers separating the functional states of enzyme are small and rough, suggesting rapid sampling of conformers. Furthermore, results show that the slow kinetics of the enzyme suggested by NMR dispersion experiments arises due to the diffusive motions of the Met20 loop on the rough energy landscape rather than the large reorganization energy barrier as suggested by the application of transition-state theory to estimate barrier heights from the experimental kinetics data. Finally, these studies also emphasize the role of the assembly of enzyme side chains to achieve optimal geometry for chemistry.

7. Concluding remarks

The simulations discussed above have provided detailed quantitative insights into the DHFR reaction mechanism not currently accessible to experiments. As demonstrated, equilibrium MD simulations of DHFR show that there are specific correlated motions in the reactive ternary complex of the enzyme that are abrogated in the ternary product complex and reduced in the mutants, suggesting that these motions are relevant to the catalytic efficacy of the enzyme. These correlated fluctuations of the enzyme manifest as the distinct conformational substates that are correlated with modulations in the hydride transfer barrier height as indicated by the examination of equilibrium ensembles of activation energies for the key hydride transfer step as well as the distributions of structural parameters in the different protein isoforms. Backbone conformations of the Met20 loop are important components of these conformational substates as illustrated by the link between dihedral angle values exhibited by residues within the Met20 loop and modulation of the hydride transfer barrier height. The backbone ϕ/ψ dihedral angles of wild type DHFR predominantly occupy regions of conformational space that are conducive to hydride transfer, while the mutant proteins visit alternative conformations generally associated with high barriers. Clearly, the mutations act to disrupt the equilibrium distribution of the Met20 loop that abuts the site of chemistry. This alteration of the static, equilibrium distribution of the Met20 loop conformations is sufficient to explain the influence of mutations on the rate of the hydride transfer. The above discussion clearly suggests that the Met20 loop of DHFR serves as a master regulator of catalysis due to its ability to adapt to mutations by assuming alternate conformations that lead to redistribution of conformational substates present in the protein and consequently give rise to distinct hydride transfer barriers.

In recent papers, the question of whether protein motions are coupled to the chemical transformation has been hotly debated. Although it is broadly accepted that the conformational movements of proteins are indispensable to enzyme function in substrate binding and product release, the question of whether protein motions play a direct role in the chemical step of enzymatic catalysis is controversial with arguments for and against such coupling [34, 51, 82, 83]. For example, in the case of DHFR, recent experimental studies reported a “dynamic knockout” caused by mutations suggesting that the conformational fluctuations can influence the chemical step of enzyme catalysis [51]. In these studies, mutations were made that both prevent formation of the occluded conformation through loss of hydrogen bonding between the Met20 and GH loops of DHFR and to impair millisecond timescale motions of the Met20 loop in the Michaelis complex. This N23PP/S148A DHFR mutant displayed a reduced rate constant for hydride transfer compared to wild type and it was suggested that this was a consequence of the loss of conformational flexibility. However, subsequent computational [34] and experimental [71] KIE studies of the N23PP/S148A variant of DHFR reached quite the opposite conclusion than that reached by the previous investigation [51]. In the latter studies, it was suggested that the role of flexibility in catalysis is negligible and that the largest contribution to catalysis comes from the pre-organization of the active site, which is a long-standing concept [84, 85] that has been implicated in function of other enzymes [86]. Consistent with these suggestions, based on the understanding of DHFR’s reaction mechanism emerging from our own computational investigations as discussed above, we suggest that the decrease in the hydride transfer rate constant of N23PP/S148A variant likely arises due to modulation of the equilibrium conformational ensemble as the result of the structural perturbations to the reactive distance in the active site.

In summary, our picture of the enzyme mechanism, as assembled from the quantitative investigation of conformational changes and chemical transformation of DHFR, reveals that alteration of conformational equilibrium rather than dynamical coupling is the key factor influencing the rate of the reaction. Protein fluctuations are important in establishing the structural ensembles conducive to the chemical reaction but do not directly couple to the chemical reaction itself. This view of enzyme catalysis is also supported by other calculations and experiments and has been discussed elsewhere in the literature [29, 87]. Finally, we conclude by mentioning that DHFR is an amazing molecular machine, in which conformational heterogeneity, cooperative conformational changes, and multiple intermediates are integral to its catalytic function.