EPIDEMIOLOGICAL CONSEQUENCES OF IMPERFECT VACCINES FOR IMMUNIZING INFECTIONS

Abstract

The control of some childhood diseases has proven to be difficult even in countries that maintain high vaccination coverage. This may be due to the use of imperfect vaccines and there has been much discussion on the different modes by which vaccines might fail. To understand the epidemiological implications of some of these different modes, we performed a systematic analysis of a model based on the standard SIR equations with a vaccinated component that permits vaccine failure in degree (“leakiness”), take (“all-or-nothingness”) and duration (waning of vaccine-derived immunity). The model was first considered as a system of ordinary differential equations, then extended to a system of partial differential equations to accommodate age structure. We derived analytic expressions for the steady states of the system and the final age distributions in the case of homogenous contact rates. The stability of these equilibria are determined by a threshold parameter R_p, a function of the vaccine failure parameters and the coverage p. The value of p for which R_p = 1 yields the critical vaccination ratio, a measure of herd immunity. Using this concept we can compare vaccines that confer the same level of herd immunity to the population but may fail at the individual level in different ways. For any fixed R_p > 1, the leaky model results in the highest prevalence of infection, while the all-or-nothing and waning models have the same steady state prevalence. The actual composition of a vaccine cannot be determined on the basis of steady state levels alone, however the distinctions can be made by looking at transient dynamics (such as after the onset of vaccination), the mean age of infection, the age distributions at steady state of the infected class, and the effect of age-specific contact rates.

1. Introduction

The mechanics of vaccine-preventable childhood diseases depend on the underlying disease process and the nature of the vaccine. Different types of vaccines can have different impacts on population-level dynamics. Consider three candidate imperfect vaccines:

1. Vaccine 1: Reduces the probability of infection upon exposure by a factor ε.

2. Vaccine 2: Provides no protection to a fraction ε of the vaccinees and perfect lifetime immunity to the remainder.

3. Vaccine 3: Provides perfect protection to each vaccinee for an exponentially distributed “waning time,” after which the vaccinee becomes as susceptible as unvaccinated individuals. The probability of immunity waning within a vaccinated host's lifetime is given by ε.

These examples illustrate the three different avenues of vaccine failure that are commonly considered in the literature. McLean and Blower [14] introduced the following terminology: when a vaccine only reduces the probability of infection upon exposure but does not eliminate it as in the case of vaccine 1, this is called failure in degree. When a vaccine has no effect on some individuals but confers complete protection in others as in the case of vaccine 2, this is called failure in take. When the protection conferred wanes over time as with vaccine 3, this is termed failure in duration. Halloran et al. [6] used the term leaky vaccine (inspired by the literature on malaria) to describe a vaccine that only exhibits failure in degree, and all-or-nothing vaccine for one that demonstrates failure in take. A vaccine that only displays failure in duration is called a waning vaccine. Farrington et al. [4] lists the vaccine for pertussis as a possibly leaky vaccine, those for measles and rubella as all-or-nothing vaccines, and that for cholera as a waning vaccine.

Vaccines 1, 2 and 3 are examples of leaky, all-or-nothing and waning vaccines, respectively. The direct effects of these vaccines at the individual level are given in their descriptions, but the indirect protection that they confer as a result of reduction in disease transmission (herd immunity) is not so easily surmised from individual effects. It is important to examine this as it may have significant implications in the control of the disease at the population level. Conversely, it might also be possible to deduce information on the individual-level effects from population data on disease incidence. Using a susceptible-infectious-recovered (SIR) model with a vaccine component, we can compare the dynamics of vaccines 1–3. Under the same assumptions on the disease, it can be shown that the critical proportion of the model population that needs to be vaccinated in order to drive the disease to extinction is the same for all three. Furthermore if the coverage is maintained below the critical ratio then the disease remains endemic in the model population at a higher level for vaccine 1, while the levels for vaccines 2 and 3 are equal. These results follow from our investigation of the model in 2–4. Different transient dynamics and contrasting age distributions of the infected class are also discussed in these sections. Numerical simulations indicate that vaccines 1 and 3 may display a significant “honeymoon period,” a temporary period of very low disease incidence after the initiation of vaccination programs. On the other hand, vaccine 2 appears to display a more stable transition from pre-vaccine to vaccine-era steady states.

In this paper we present a systematic analysis of a general model of an imperfect vaccine. We begin by considering an unstructured population described by a system of ordinary differential equations (ODEs) similar to that presented by McLean and Blower [14]. It is assumed that the disease follows standard SIR dynamics. A vaccinated class is added with connections that represent the three avenues of vaccine failure. We also extend this into an age-structured model using the McKendrick-Von Förster formalism [13, 19]. The age-structured equations consist of a system of partial differential equations (PDEs) which allows for age-specific transmission. We establish the well-posedness of this system, find expressions for the disease-free and endemic steady states, and derive a threshold parameter R_p (the basic reproduction number incorporating the effects of vaccination) that determines the stability of these equilibria. We also provide conditions for which different types of vaccines have the same steady state values and prove that a purely leaky model results in the highest level of endemic infection among all models with the same efficacy. Finally we also show that the three special cases (leaky, all-or-nothing and waning) have distinct transient dynamics following the inception of mass vaccination, and distinct age distributions at steady state of the infected class (even in the case of homogenous transmission) which may adjust in contrasting ways to changes in vaccination coverage. To illustrate our results we present figures that compare the steady state infection level, mean age of infection and age distributions for vaccines 1–3.

Models of vaccines exhibiting failures in degree, take and duration have been studied before in the literature [1, 4, 5, 14]. These models have typically consisted of systems of ODEs or integral equations. Arino et al. [1] analyzed a general ODE model similar to that presented here but their model also accounts for the waning of disease-induced immunity as well as the vaccination of susceptibles (not only as newborns). They applied a result by Li and Muldowney [11] to prove global results under certain conditions. Depending on the norm used in the proof, global stability can be confirmed in different subsets of the parameter space. However in all of these subsets the mean duration of the infectious period is required to be longer than the other time scales in the model such as the expected lifetime. Arino et al. [1] also showed that backward bifurcations can occur when vaccine-induced immunity lasts longer than disease-induced immunity. With childhood diseases we generally expect the infectious period to be much shorter than our other time scales, and expect disease-induced immunity to last longer than vaccine-derived protection. In our model we keep the focus on vaccination programs for newborns only and make the simplifying assumption that disease-induced immunity is permanent. This leads to a less complicated model which still incorporates the different facets of vaccine failure and allows for a more complete characterization of their effects on population-level dynamics.

The distinction between the modes of vaccine failure is also relevant in unambiguously measuring vaccine total effectiveness from individual efficacy. Halloran et al. [6] defined efficacy to be the relative change in the susceptibility of vaccinated individuals to a specified amount of exposure to infection. In our example, vaccines 1 and 2 clearly have an efficacy of 1 − ε. Similarly, we can define the efficacy of vaccine 3 to also be 1 − ε since the chance of getting infected within a lifetime is reduced by this amount. Realizing that all three candidates have the same efficacy makes it easy to see why they all have the same critical proportion of vaccination. However, since vaccine 1 leads to higher level of prevalence when coverage is not high enough for eradication, this vaccine is less effective than the other two. We also note that the focus of clinical trials is typically to measure the effectiveness of vaccines within a limited time period. It would be difficult to measure the efficacy of waning vaccines without extended follow-up on trial participants [20].

This paper is divided as follows: In 2 we present a derivation of our model with general parameters. In 3 we consider the dynamics of an ODE model that incorporates the three modes of vaccine failure. In 4 we extend the ODE model into an age-structured model and analyze the resulting system of PDEs. Using these models we examine the differences in the dynamics of the disease at the population level by considering both stationary states and transient behaviour generated by the different modes of failure. For the age-structured system we also illustrate how the age distribution of the steady state infected class, under the assumption of both constant and age-specific contact rates, changes with increasing vaccination coverage. We summarize our results and give some concluding remarks in 5.

2. An ODE model of an imperfect vaccine

The model is illustrated in Figure 2.1. Let V (t) be the fraction of the total population that is in the vaccinated state. By this state we mean the proportion of the population that was vaccinated and enjoys some protection from the vaccine (the vaccine did not fail in take in these individuals and their immunity has not waned yet). Let S(t) be the fraction that is in the susceptible class. This includes the vaccinated individuals for whom the vaccine had no effect from the beginning, as well as those whose immunity has waned by time t. The remaining compartments are I(t) and R(t), fractions of the total population in the infectious and recovered states respectively. To be consistent with these definitions we require that V (t) + S(t) + I(t) + R(t) = 1 for all t ≥ 0.

Fig. 2.1.

A model of imperfect vaccine immunity incorporating three possible modes of failure: degree (blue), take (green) and duration (red).

Suppose that the model population has equal birth and death rates of μ. Most of the connections in Figure 2.1 between S, I and R are from the standard Kermack-McKendrick SIR model [9, 18] (the symbols used for the different parameters are given in Table 2.1). We expand upon the SIR model by adding the vaccinated class V with connections to S and I. For all t ≥ 0, a constant fraction p of the newborns are assumed to be vaccinated. Of this fraction, a proportion ε_A ∈ [0, 1) (the all-or-nothing parameter) exhibit failure in take and go directly instead to the susceptible class. The individuals in the vaccinated class experience a reduction by ε_L ∈ [0, 1) (the leakiness parameter) in the probability of getting infected. Vaccine protection is also assumed to wane at a rate of $\alpha =\frac{\mu {\epsilon }_W}{1-{\epsilon }_W}$. This parametrization was chosen so that the parameter ε_W is the probability that the vaccine protection of individuals in the V class wanes within a lifetime given that they do not get infected first.

$${\epsilon }_W=\frac{\alpha }{\alpha +\mu }=\frac{\text{rate at which vaccine protection wanes}}{\text{rate at which individuals leave the}V\text{class if}{\epsilon }_L=0}.$$ (2.1)

The choice of ε_W also results in this parameter having the same range of ε_W ∈ [0, 1) and the same weight in determining the stability of the disease-free equilibrium as both ε_L and ε_A. This will be shown later on when we define the basic reproduction number of this system R_p.

Table 2.1.

Description of parameters and list of default values used for simulations unless otherwise indicated in the figures

Symbol	Parameter	Default value for plots
μ	Birth and death rate	$\frac{1}{70}{\mathrm{yr}}^{-1}$
γ	Recovery rate	20 yr–1
β	Transmission rate	400 yr–1
p	Infant vaccination probability	0.85
ε L	Factor by which the probability that an individual will get infected after exposure is reduced after vaccination	0.2 or 0
ε A	Probability of not getting protected after vaccination	0.2 or 0
ε W	Probability that protection wanes in the case given that one does not get infected first	0.2 or 0
α	Waning rate of vaccine-derived immunity	μεW/(1 – εw)
φ	Vaccine impact parameter	0.80

Going back to the three vaccines we considered in 1, vaccine 1 is given by (ε_L, ε_A, ε_W ) = (ε, 0, 0), vaccine 2 by (ε_L, ε_A, ε_W ) = (0, ε, 0) and vaccine 3 by (ε_L, ε_A, ε_W ) = (0, 0, ε). The waning rate of vaccine 3 is $\alpha \frac{\mu \epsilon }{1-\epsilon }$ which translates to a waning rate that is exponentially distributed with mean equal to $\frac{1-\epsilon }{\epsilon }$ times the expected host lifetime. Definition 2.1 presents the full set of model equations for a general imperfect vaccine that can take on any value of (ε_L, ε_A, ε_W ) ∈ [0, 1)³.

Definition 2.1. Let μ ≥ 0, γ > 0, β > 0, p ∈ [0, 1] and (ε_L, ε_A, ε_W) ∈ [0, 1)³. The imperfect vaccine ODE model is given by the following system of ODEs,

$$\frac{dV}{dt}=(1-{\epsilon }_A)p\mu -{\epsilon }_L\beta VI-\alpha V-\mu V,$$ (2.2a)

$$\frac{dS}{dt}=(1-(1-{\epsilon }_A)p)\mu -\beta SI+\alpha V-\mu S,$$ (2.2b)

$$\frac{dI}{dt}=\beta SI+{\epsilon }_L\beta VI-\gamma I-\mu I,$$ (2.2c)

$$\frac{dR}{dt}=\gamma I-\mu R.$$ (2.2d)

for t ≥ 0 where $\alpha =\frac{\mu {\epsilon }_W}{1-{\epsilon }_W}$ and the initial conditions satisfy

$$V\left(0\right)+S\left(0\right)+I\left(0\right)+R\left(0\right)=1.$$ (2.3)

We call (ε_L, ε_A, ε_W ) the vaccine failure parameters. In the case when ε_L > 0 and ε_A = ε_W = 0 we call this the leaky ODE model. In the case when ε_A > 0 and ε_L = ε_W = 0 we call this the all-or-nothing ODE model. In the case when ε_W > 0 and ε_L = ε_A = 0 we call this the waning ODE model. We also define φ, a measure of vaccine impact by

$$\phi =(1-{\epsilon }_L)(1-{\epsilon }_A)(1-{\epsilon }_W),$$

and the basic reproduction number for this model by

$$R_p=\frac{\beta (1-(1-{\epsilon }_L)(1-{\epsilon }_A)(1-{\epsilon }_W)p)}{\mu +\gamma }=R_0(1-\phi p),$$

where $R_0=\frac{\beta }{\mu +\gamma }$ is the basic reproduction number in the absence of vaccination (p = 0).

The definition of the vaccine impact parameter φ is the same as the $\phi =\frac{\epsilon \psi \mu }{\mu +\alpha }$ in McLean and Blower [14] if their ε is replaced by 1 − ε_L, ψ by 1 − ε and α by $\frac{\mu {\epsilon }_W}{1-{\epsilon }_W}$. It is also consistent with the vaccine efficacy VE defined by Farrington [4] for more general types of leaky and all-or-nothing vaccines where $\mathrm{VE}=\frac{\mathrm{PE}}{p}$ and $\mathrm{PE}=1-\frac{R_p}{R_0}$ is the projected effectiveness of the vaccine. In our example, vaccines 1–3 all have φ = 1 − ε, consistent with the values for efficacy discussed in 1. The parameters of the model and their default values used in simulations and sample plots are summarized in Table 2.1. The default value of the recovery and transmission rates were chosen to have the infectious period and basic reproduction number of pertussis. The special cases of the imperfect vaccine model that we consider in our simulations are summarized in Table 2.2.

Table 2.2.

Special cases of the imperfect vaccine model

Name	Vaccine parameter values (εL,εA,εW)	Default value for plots
Leaky model	(ε, 0, 0)	(0.2, 0, 0)
All-or-nothing model	(0, ε, 0)	(0, 0.2, 0)
Waning model	(0, 0, ε)	(0, 0, 0.2)
Combined model	$(1-\sqrt[3]{1-\epsilon },1-\sqrt[3]{1-\epsilon },1-\sqrt[3]{\epsilon })$	(0.072, 0.072, 0.072)

3. Dynamics and properties of the ODE model

In this section we examine the properties of the imperfect vaccine ODE model (Definition 2.1) with a focus on its equilibria. In Proposition 3.1 the well-posedness of the model and the invariance of solutions in the positive orthant are established. We also derive expressions for the disease-free and endemic equilibria, and establish the threshold property of the basic reproduction number R_p in determining the existence and stability of these steady states. The critical vaccination ratio p_c is defined in Definition 3.1 to be the minimum vaccination probability required to drive the disease to extinction, if this is possible. We also state Propositions 3.2–3.3 which present results on the equality of the steady states for different combinations of the vaccine failure parameters (ε_L, ε_A, ε_W ) and prove that for a fixed value of φ, the purely leaky model provides an upper bound on the steady state level of infection. At the end of the section we show plots of the steady states of the special cases as different parameters are varied (Figure 3.1). We also present some interesting transient dynamics displayed by the leaky and waning vaccines models at the onset of a vaccination program (Figure 3.2).

Fig. 3.1.

Bifurcation of the I steady state of the leaky (ε_L, ε_A, ε_W ) = (ε, 0, 0), all-or-nothing (ε_L, ε_A, ε_W ) = (ε, 0, 0) and waning (ε_L, ε_A, ε_W ) = (0, 0, ε) models as parameters are varied. We vary p ∈ [0, 1] in (a), ε ∈ [0, 1) in (b) β and ∈ [0, 1600] in (c). Default values of the parameters that are not being varied are given in Table 2.1. The values of the steady state for the all-or-nothing model overlap with those for waning immunity model. The imaginary part of the complex conjugate eigenvalue pair of the Jacobian matrix from part of the bifurcation diagram in (c) is shown in (d). Here the values for the leaky model is slightly below the overlapping plots for the all-or-nothing and waning models.

Proposition 3.1. The vaccine failure model in Definition 2.1 has the following properties.

1. The system of equations is well-posed and invariant in the set $\mathcal{D}=\{(V,S,I,R)\in {[0,1]}^4:V+S+I+R=1\}\subset {\mathbb{R}}_{+}^4$.

2. If R_p ≤ 1 then the only steady state of the system in $\mathcal{D}$ is the disease-free equilibrium,

   $$(V^0,S^0,I^0,R^0)=((1-{\epsilon }_A)(1-{\epsilon }_W)p,1-(1-{\epsilon }_A)(1-{\epsilon }_W)p,0,0).$$
3. If R_p > 1 then there are two steady states in $\mathcal{D}$, the disease-free equilibrium V ⁰, S⁰, I⁰, R⁰ and the endemic equilibrium given by

   $$(V^{\ast },S^{\ast },I^{\ast },R^{\ast })=\left(V^{\ast },\frac{1}{R_0}-{\epsilon }_L{V}^{\ast },\frac{\mu }{\beta }\left(R_0(1-(1-{\epsilon }_L)V^{\ast }\right)-1),\frac{\gamma }{\beta }(R_0(1-(1-{\epsilon }_L)V^{\ast })-1)\right),$$

   where if ε_L > 0 then

   $$V^{\ast }=\frac{{\epsilon }_L(1-{\epsilon }_W)(R_0-1)+1\sqrt{{({\epsilon }_L(1-{\epsilon }_W)(R_0-1)+1)}^2-4R_0{\epsilon }_L(1-{\epsilon }_W)}\phi p}{2R_0{\epsilon }_L(1-{\epsilon }_L)(1-{\epsilon }_W)},$$ (3.1)

   and if ε_L = 0 then instead

   $$V^{\ast }=(1-{\epsilon }_A)(1-{\epsilon }_W)p.$$

4. If R_p < 1 then the disease-free equilibrium of the vaccine failure ODE model is (at least) locally asymptotically stable. If the stronger condition R₀ < 1 holds then the disease-free equilibrium is globally asymptotically stable, i.e. for any set of non-negative initial conditions the solutions satisfy (V (t), S(t), I(t), R(t)) → V ⁰, S⁰, I⁰, R⁰ as t → ∞ .

5. If R_p > 1 then the disease-free equilibrium is unstable and only initializations with I(0) = 0 will approach this equilibrium. In this case the endemic equilibrium (V * , S* , I* , R* ) is locally asymptotically stable.

Proof. The proof of item 1 is standard. The proof of items 2–3 is trivial for the ε_L = 0 case. For the ε_L > 0 case, we derive a quadratic equation (A.1) for V * from the system of equations and the manipulations are given in the appendix. The only root of the quadratic equation that can lead to $V^{\ast },S^{\ast },I^{\ast },R^{\ast })\in \mathcal{D}$ is given in (3.1). We also show that (V * , S* , I* , R* ) = V ⁰, S⁰, I⁰, R⁰ when R_p = 1. For all allowable parameter values, V * > 0, but the non-negativity of all components of the endemic equilibrium only occurs when R_p ≥ 1(refer to Proposition A.3).

Another way to write the endemic equilibrium expression for I* in the case when ε_L > 0 is

$$I^{\ast }=\frac{\mu }{\beta }\left[\frac{{\epsilon }_L(1-{\epsilon }_W)(R_0-1)-1+\sqrt{{({\epsilon }_L(1-{\epsilon }_W)(R_0-1)-1)}^2+4{\epsilon }_L(1-{\epsilon }_W)(R_p-1)}}{2{\epsilon }_L(1-{\epsilon }_W)}\right].$$ (3.2)

It is possible to show ε_L(1 − ε_W )(R₀ − 1) − 1 ≤ 0 when R_p = 1. Thus it is clear from (3.2) that R_p = 1 is the point at which I* changes sign.

The basic reproduction number R_p as a function of vaccination rate p of the system (2.2) was derived using the next-generation matrix method (refer to [18] for a discussion of this method). This guarantees the local asymptotic stability of the disease-free equilibrium in the case when R_p < 1 and instability when R_p > 1. Global asymptotic stability in the case when R₀ < 1 can be proven using a Lyapunov function $\mathcal{L}\left(I\left(t\right)\right)=I\left(t\right)$.

$$\frac{d}{dt}\mathcal{L}\left(I\left(t\right)\right)=[\beta (S+{\epsilon }_{L}V)-(\mu +\gamma )]I=(\mu +\gamma )(R_0(S+{\epsilon }_{L}V)-1)I.$$

Since S + ε_LV ≤ S + V ≤ 1 then the derivative is negative-definite in the case when R₀ < 1. For the proof of local asymptotic stability of the endemic equilibrium for R_p > 1 we prove that the dominant eigenvalue of the Jacobian matrix evaluated at this steady state lies on the left half of the complex plane (see Proposition A.4).

From the threshold property of R_p we may be able to derive the critical proportion of the population that needs to be vaccinated in order to achieve eradication of the disease. This critical proportion may not exist if the vaccine impact parameter φ is too small.

Definition 3.1. The critical vaccination proportion p_c is given by

$$p_c=\left(1-\frac{1}{R_0}\right)\frac{1}{\phi },$$

if this expression is less than or equal to one.

By Proposition 3.1, if p > p_c then R_p < 1 and the disease-free equilibrium is locally asymptotically stable. For the same disease, the critical vaccination ratio depends only on φ and hence is the same for vaccines 1–3 in our example from 1.

In Proposition 3.2 we derive conditions on the vaccine failure parameters that lead to the same steady state values. We also prove that for a fixed value of φ, the leaky model provides an upper bound on the infection level in Proposition 3.3. Applied to our example vaccines, these results show that the disease-free and endemic steady states of vaccines 2 and 3 are identical while vaccine 1 results in a larger infection at the endemic steady state.

Proposition 3.2. Suppose that P ⁽¹⁾ is the set of parameter values with vaccine failure parameters $({\epsilon }_L,{\epsilon }_A,{\epsilon }_W)=({\epsilon }_L^{\left(1\right)},{\epsilon }_A^{\left(1\right)},{\epsilon }_W^{\left(1\right)})$ and P is another set with $({\epsilon }_L,{\epsilon }_A,{\epsilon }_W)=({\epsilon }_L^{\left(2\right)},{\epsilon }_A^{\left(2\right)},{\epsilon }_W^{\left(2\right)})$. All other parameters are the same in P ⁽¹⁾ and P ⁽²⁾. Then,

1. The component values at the disease-free equilibrium are the same for either parameter set independent of the value of ${\epsilon }_L^{\left(1\right)}$ and ${\epsilon }_L^{\left(2\right)}$ as long as

   $$(1-{\epsilon }_A^{\left(1\right)})(1-{\epsilon }_W^{\left(1\right)})=(1-{\epsilon }_A^{\left(2\right)})(1-{\epsilon }_W^{\left(2\right)}).$$
2. The component values at the endemic equilibrium are the same for either parameter set as long as ${\epsilon }_L^{\left(1\right)}={\epsilon }_L^{\left(2\right)}={\epsilon }_L$, and either (i) in the case when ε_L > 0,

   $$\frac{1}{1-{\epsilon }_W^{\left(1\right)}}-\sqrt{{({\epsilon }_L(R_0-1)+\frac{1}{1-{\epsilon }_W^{\left(1\right)}})}^2-4R_0{\epsilon }_L(1-{\epsilon }_L)(1-{\epsilon }_A^{\left(1\right)})p}=\frac{1}{1-{\epsilon }_W^{\left(2\right)}}-\sqrt{{({\epsilon }_L(R_0-1)+\frac{1}{1-{\epsilon }_W^{\left(2\right)}})}^2-4R_0{\epsilon }_L(1-{\epsilon }_L)(1-{\epsilon }_A^{\left(2\right)})p},$$

   or (ii) in the case when ε_L = 0,

   $$(1-{\epsilon }_A^{\left(1\right)})(1-{\epsilon }_W^{\left(1\right)})=(1-{\epsilon }_A^{\left(2\right)})(1-{\epsilon }_W^{\left(2\right)}).$$

Proof. These statements follow from the expressions derived in Proposition 3.1.

Proposition 3.3. For a fixed vaccine impact parameter φ such that R_p > 1, the vaccine failure parameter set (ε_L, ε_A, ε_W) that leads to the highest value of the endemic steady state value of the infected class is (1 − φ, 0, 0) (the leaky model).

Proof. Suppose that φ is fixed and set ${\epsilon }_A=1-\frac{\phi }{(1-{\epsilon }_L)(1-{\epsilon }_W)}$. Let x = ε_L (1 − ε_W ) ∈ [0, 1]. From (3.2) in Proposition 3.1 the endemic steady-state infected class can be written as

$${\mathcal{I}}^{\ast }\left(x\right)=\frac{\mu }{2\beta }\left[R_0-1-\frac{1}{x}+\sqrt{{\left(R_0-1-\frac{1}{x}\right)}^2+\frac{4}{x}(R_p-1)}\right].$$ (3.3)

Since we are keeping φ fixed, R_p is also fixed. The derivative of this with respect to x is

$$\frac{d}{dx}{\mathcal{I}}^{\ast }\left(x\right)=\frac{\mu }{2\beta x^2}\left[1+\frac{R_0-1-\frac{1}{x}-2(R_p-1)}{\sqrt{{(R_0-1-\frac{1}{x})}^2+\frac{4}{x}(R_p-1)}}\right]=\frac{\mu }{2\beta x^2}\left[1+\frac{a-b}{\sqrt{a^2+c}}\right].$$ (3.4)

where $a=R_0-1-\frac{1}{x}$, b = 2 (R_p − 1) and $c=\frac{4}{x}(R_p-1)$. We claim that $\frac{d}{dx}{\mathcal{I}}^{\ast }\left(x\right)\ge 0$ for all x > 0. When a ≥ b this is clearly true so consider the case when a < b. Since c > b > 0,

$$1+\frac{a-b}{\sqrt{a^2+c}}\ge 0,\iff \frac{a^2-2ab+b^2}{a^2+c}\le 1\iff b^2-2ab-c\le 0\iff -4R_0\phi p(R_p-1)\le 0.$$

The last inequality is clearly true when R_p > 1, and it follows that the value of the endemic steady state increases with x. Thus the maximum occurs when ε_L = 1 − φ and ε_A = ε_W = 0.

In the bifurcation diagrams and sample simulations that we present in this paper, we use vaccines 1, 2 and 3 as examples for the leaky, all-or-nothing (denoted by AON) and waning models, respectively. When ε is not being varied we set ε = 0.2 (refer to Table 2.2). In Figure 3.1(a)–(c) we plot the infected class steady state I* against different model parameters. When any parameter is fixed and its value is not indicated in the figure then it is set to the default value in Table 2.1. In Figure 3.1(d) we plot the imaginary part of the eigenvalues of the Jacobian matrix against the parameter β and show that the value is slightly smaller for the leaky model. This indicates that the leaky model has a slightly longer period for small oscillations, at least for the parameter ranges that we have chosen. Although not shown, this statement is supported by simulations of stochastic versions of the models and deriving the dominant frequencies.

It is clear from Proposition 3.2 and Figure 3.1 that we cannot uniquely identify the parameters of vaccine failure using steady state data alone. In particular, we cannot distinguish between the all-or-nothing and waning model by just looking at the equilibrium values of the components. Furthermore, in practice we may only have data on I* and/or R* available and it would be difficult to determine how the remaining population splits up between S* (which includes vaccinated individuals whose immunity has waned) and V * .

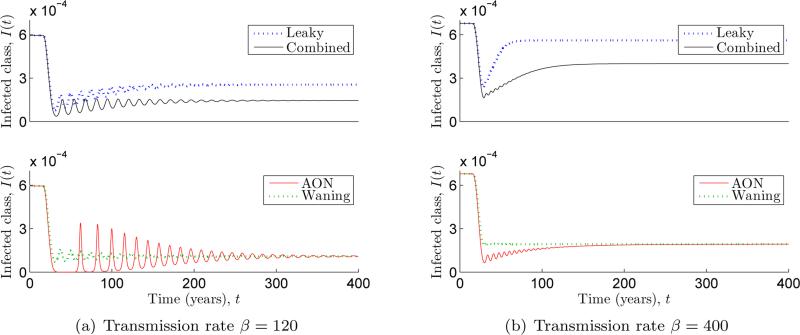
Since the vaccine failure parameters may be indeterminable from steady state data, we turn our attention to transient dynamics. In Figure 3.2 numerical simulations were used to compare the behaviour of solutions after the start of vaccination programs employing the three special cases of vaccines. Here we finally observe a clear distinction between the dynamics of an all-or-nothing model and a waning model with the same value of φ. Simulations such as the one shown indicate that the latter displays an initial drop to low disease prevalence after the start of vaccination, then recovers to have the same steady state value as the all-or-nothing model. This temporary period of low disease prevalence is called the honeymoon period. For the set of parameter values that we chose, the all-or-nothing model does not appear to display a significant honeymoon period while the leaky model does. These are important considerations for vaccination programs. Furthermore, these observations present an alternative explanation for the observed “resurgence” of some diseases like pertussis in highly vaccinated regions. The documented rise in incidence may just be signaling the end of the honeymoon period, and the observed disease outbreaks may be transient oscillations such as those we see in Figure 3.2(a).

Fig. 3.2.

Simulations showing what happens when the system is initially at the zero vaccination endemic steady state, then vaccination is gradually increased from p = 0 at t = 15 to p = 0.85 at t = 30. In (a) the waning model displays a honeymoon period of about 30 years. Afterward the solution oscillates as it approaches equilibrium yielding initially large outbreaks every 15 years. When is increased in (b), the oscillations get smaller.

Simulations using different combinations of (ε_L, ε_A, ε_W ) for which φ = 0.8 appear to display behavior that is intermediate between the extremes of the special cases that are being combined. In Figure 3.2, we include a simulation of the combined model with $({\epsilon }_L,{\epsilon }_A,{\epsilon }_W)=(1-\sqrt[3]{1-\epsilon },1-\sqrt[3]{1-\epsilon },1-\sqrt[3]{1-\epsilon })$ which displays transient behavior that is bounded above by the leaky model and below by the waning model. One can also check that a simulation with $({\epsilon }_L,{\epsilon }_A,{\epsilon }_W)=(1-\sqrt[2]{1-\epsilon },1-\sqrt[2]{1-\epsilon },1-\sqrt[2]{1-\epsilon },0)$ shows intermediate behavior between the leaky and all-or-nothing models.

4. An age-structured PDE model of an imperfect vaccine

In this section we introduce age structure to the model using an extension of the McKendrick-Von Förster population model [13, 19]. This extension is standard and is also used by Inaba [8] and Thieme [17]. A formal definition of the imperfect vaccine PDE model is given in Definition 4.1. The equations have been set up so that adding up the components yields the basic McKendrick-Von Förster population model. This is consistent with an assumption that the total population dynamics is not affected by the disease. To keep the focus on the different modes of vaccine failure we also assume that the total population is already at its equilibrium age distribution. The existence of a classical solution to the system (in the sense of an abstract Cauchy problem) as well as the consistency of the above assumptions with the model statement is established in Proposition 4.1. In the special case where homogenous transmission rates are used, it is shown in Remark 4.1 that integrating the PDE system over all ages lead to the original ODE system in Definition 2.1. Expressions for the steady states age distributions are also derived and presented in Proposition 4.2. We end this section with plots showing the different steady state mean ages of infection and age distributions of the special cases of the model as parameters are varied.

Definition 4.1. Let μ > 0, γ > 0, p ∈ [0, 1], (ε_L, ε_A, ε_W ) ∈ [0, 1)³. Let $b\in L^{\infty }({\mathbb{R}}_{+}^3\to {\mathbb{R}}_{+})$ (an essentially bounded function). The imperfect vaccine PDE model is given∈ by the system following of PDEs,

$$\frac{\partial v(t,a)}{\partial t}+\frac{\partial v(t,a)}{\partial a}=-{\epsilon }_L{\lambda }_i(t,a)v(t,a)-\alpha v(t,a)-\mu v(t,a),$$ (4.1a)

$$\frac{\partial s(t,a)}{\partial t}+\frac{\partial s(t,a)}{\partial a}=\alpha v(t,a)-{\lambda }_i(t,a)s(t,a)-\mu s(t,a),$$ (4.1b)

$$\frac{\partial i(t,a)}{\partial t}+\frac{\partial i(t,a)}{\partial a}={\lambda }_i(t,a)(s(t,a)+{\epsilon }_{L}v(t,a))-\gamma i(t,a)-\mu i(t,a),$$ (4.1c)

$$\frac{\partial r(t,a)}{\partial t}+\frac{\partial r(t,a)}{\partial a}=\gamma i(t,a)-\mu r(t,a).$$ (4.1d)

for t ≥ 0 where $\alpha =\frac{\mu {\epsilon }_W}{1-{\epsilon }_W},{\lambda }_i(t,a)$ is given by

$${\lambda }_i(t,a)={\int }_0^{\infty }b(t,a,x)i(t,x)dx.$$ (4.2)

For t ≥ 0 we require the following boundary conditions,

$$v(t,0)=\mu (1-{\epsilon }_A)p,s(t,0)=\mu (1-(1-{\epsilon }_A)p),i(t,0)=0,r(t,0)=0,$$ (4.3)

and initial conditions,

$$v(0,a)={\psi }_v\left(a\right),s(0,a)={\psi }_s\left(a\right),i(0,a)={\psi }_i\left(a\right),r(0,a)={\psi }_r\left(a\right).$$ (4.4)

where ψ_v, ψ_s, ψ_i and ${\psi }_r\in L^1([0,\infty ),{\mathbb{R}}^{+})$ are absolutely continuous functions. We assume that the total population is already in equilibrium at t = 0 so the initial conditions are required to satisfy

$${\psi }_v\left(a\right)+{\psi }_s\left(a\right)+{\psi }_i\left(a\right)+{\psi }_r\left(a\right)=\mu e^{-\mu a},$$

as well as,

$${\psi }_v\left(0\right)=\mu (1-{\epsilon }_A)p,{\psi }_s\left(0\right)=\mu (1-(1-{\epsilon }_A)p),{\psi }_i\left(0\right)=0,{\psi }_r\left(0\right)=0.$$

The function b(t, a, x) incorporates the contact and transmission rate between individuals of ages a and x at time t. The initial age distribution given in (4.4) guarantees that the total population is already at a steady state age distribution but each component is not necessarily at equilibrium. This is discussed further in Proposition 4.1.

Proposition 4.1. There exists a unique classical solution to the system (4.1) which is defined for t ≥ 0. Furthermore, for t ≥ 0,

$$v(t,a)+s(t,a)+i(t,a)+r(t,a)=\mu e^{-\mu a},{\int }_0^{\infty }[v(t,a)+s(t,a)+i(t,a)+r(t,a)]da=1.$$

Proof. Local existence and uniqueness follows from setting up the PDE problem (4.1) as an abstract semilinear Cauchy problem in the Banach space $L^1([0,\infty ),{\mathbb{R}}_{+}^4)$ as in [8]. Non-negativity of the solution follows from applying the formula for integration along characteristics for v and s, then writing the equation for i as an abstract Cauchy problem (see [8]).

Let n(t, a) = v(t, a) + s(t, a) + i(t, a) + r(t, a) and consider the system

$$\frac{\partial n(t,a)}{\partial t}+\frac{\partial n(t,a)}{\partial a}=-\mu n(t,a),n(t,0)=\mu ,n(0,a)=\mu e^{-\mu a},$$

which is derived from (4.1)–(4.3). Using the method of characteristics, the solution is

$$n(t,a)=\{\begin{array}{cc}\mu e^{-\mu a},\hfill & t>a,\hfill \\ n(0,a-t)e^{-\mu t},\hfill & t\le a.\hfill \end{array}\phantom{\}}$$ (4.5)

Initial conditions state that n(0, a − t) = μe^−μ(a−t) so n(t, a) = μe^−μa follows. Also,

$${\int }_0^{\infty }[v(t,a)+s(t,a)+i(t,a)+r(t,a)]da={\int }_0^{\infty }\mu e^{-\mu a}da=1.$$

Global existence and uniqueness of the solution follow from the positivity and boundedness of the solutions for all t ≥ 0.

It is clear that for a constant contact rate b(t, a, x) = β, integrating the PDE system (4.1) over all ages yields the original ODE system (2.2).

Remark 4.1. Let b(t, a, x) = β > 0 and the initial conditions in the ODE system (2.2) and the PDE system (4.1) satisfy

$$V\left(0\right)={\int }_0^{\infty }v(0,a)da,S\left(0\right)={\int }_0^{\infty }s(0,a)da,I\left(0\right)={\int }_0^{\infty }i(0,a)da,R\left(0\right)={\int }_0^{\infty }r(0,a)da.$$

Then for all t ≥ 0,

$$V\left(t\right)={\int }_0^{\infty }v(t,a)da,S\left(t\right)={\int }_0^{\infty }s(t,a)da,I\left(t\right)={\int }_0^{\infty }i(t,a)da,R\left(t\right)={\int }_0^{\infty }r(t,a)da.$$

In the next proposition we derive expressions for the disease-free and endemic steady states of the model when b(t, a, x) = β. We also state the threshold property of R_p in determining the existence and stability of the steady states. This last result simply follows from the previous proposition and the results in the previous section.

Proposition 4.2. Let b(t, a, x) = > 0. The disease-free equilibrium of the PDE model is given by

$$v^0\left(a\right)=\mu p(1-{\epsilon }_A)e^{-\mu a},s^0\left(a\right)=\mu (1-(1-{\epsilon }_A)p)e^{-\mu a},i^0\left(a\right)=0,r^0\left(a\right)=0.$$ (4.6)

Let β(t, a, x) = , a constant. If ε_L = α = 0 (the all-or-nothing case) then endemic steady state distributions are given by

$$v^{\ast }\left(a\right)=\mu (1-{\epsilon }_A)p{e}^{-\mu a},$$ (4.7a)

$$s^{\ast }\left(a\right)=\mu (1-(1-{\epsilon }_A)p)e^{-(\mu +{\lambda }^{\ast })a},$$ (4.7b)

$$i^{\ast }\left(a\right)=\frac{\mu {\lambda }^{\ast }(1-(1-{\epsilon }_A)p)e^{-\mu a}}{\gamma -{\lambda }^{\ast }}\left(e^{-{\lambda }^{\ast }a}-e^{\gamma a}\right),$$ (4.7c)

$$r^{\ast }\left(a\right)=\frac{\mu (1-(1-{\epsilon }_A)p)e^{-\mu a}}{\gamma -{\lambda }^{\ast }}\left(\gamma (1-e^{-{\lambda }^{\ast }a})-{\lambda }^{\ast }(1-e^{-\gamma a})\right).$$ (4.7d)

If ε_L and are not both zero the endemic steady state distributions are given by

$$v^{\ast }\left(a\right)=\mu (1-{\epsilon }_A)p{e}^{-(\mu +{\epsilon }_L{\lambda }^{\ast }+\alpha )a},$$ (4.8a)

$$s^{\ast }\left(a\right)=\mu e^{-\mu a}\left[(1-q)e^{-{\lambda }^{\ast }a}+\frac{\alpha q}{{\lambda }^{\ast }(1-{\epsilon }_L)}{e}^{-({\epsilon }_L{\lambda }^{\ast }+\alpha )}a\right],$$ (4.8b)

$$i^{\ast }\left(a\right)=\mu {\lambda }^{\ast }{e}^{-\mu a}\left[\frac{q({\epsilon }_L{\lambda }^{\ast }+\alpha )}{{\lambda }^{\ast }(\gamma -{\epsilon }_L{\lambda }^{\ast }-\alpha )}\left(e^{-({\epsilon }_L{\lambda }^{\ast }+\alpha )a}-e^{-\gamma a}\right)+\frac{1-q}{\gamma -{\lambda }^{\ast }}\left(e^{-{\lambda }^{\ast }a}-e^{-\gamma a}\right)\right],$$ (4.8c)

$$r^{\ast }\left(a\right)=\mu \gamma {\lambda }^{\ast }{e}^{-\mu a}\left[\frac{q({\epsilon }_L{\lambda }^{\ast }+\alpha )}{{\lambda }^{\ast }(\gamma -{\epsilon }_L{\lambda }^{\ast }-\alpha )}\left(\frac{1-e^{-({\epsilon }_L{\lambda }^{\ast }+\alpha )a}}{{\epsilon }_L{\lambda }^{\ast }+\alpha }-\frac{1-e^{-\gamma a}}{\gamma }\right)+\frac{1-q}{\gamma -{\lambda }^{\ast }}\left(\frac{1-e^{-{\lambda }^{\ast }a}}{{\lambda }^{\ast }}-\frac{1-e^{-\gamma a}}{\gamma }\right)\right].$$ (4.8d)

where λ* = βI* , I* is as given in Proposition 3.1 and $q={\lambda }^{\ast }\frac{(1-{\epsilon }_L)\left(1{\epsilon }_A\right)p}{(1-{\epsilon }_L){\lambda }^{\ast }-\alpha }=\frac{{\lambda }^{\ast }\phi p}{(1-{\epsilon }_L)(1-{\epsilon }_W){\lambda }^{\ast }-\mu {\epsilon }_W}$. If ε_L = α = 0 this simplifies to λ* = μ (R_p − 1). Another way to solve for λ* when ε_L and α are not both zero is to solve the equation

$$1=\frac{\mu }{\mu +{\lambda }^{\ast }}{R}_0\left(1-\frac{\mu \varpi p}{\mu +{\epsilon }_L(1-{\epsilon }_W){\lambda }^{\ast }}\right).$$ (4.9)

The existence and stability of the disease-free and endemic equilibria of the system (4.1) is determined by R_p as in Proposition 3.1.

Proof. The steady states are found by setting all derivatives with respect to time in (4.1) equal to zero. To find the disease-free equilibrium we set i(t, a) = 0. This leads to an ODE system that has solutions given by (4.6) and this exists for all allowable parameter values.

In the homogenous case, the steady state expression for λ_i(t, a) is independent of t and a. To solve for the endemic equilibrium, the expressions (4.7) and (4.8) can be derived by performing the integration with a fixed λ_i(t, a) = λ*.

With the endemic steady state expression i* (a) known then it is possible to solve for λ* . The expression for λ* for the all-or-nothing case is easy to derive. When ε_L and are not both zero, simplifying ${\lambda }^{\ast }=\beta {\int }_0^{\infty }{i}^{\ast }\left(x\right)dx$ leads to (4.9). Solving for a nonzero λ* and substituting λ* = βz yields the solution z = I* as in (3.2) in Proposition 3.1. From this earlier result the existence, uniqueness and positivity of the endemic equilibrium is guaranteed when R_p > 1.

The proof of local stability is straightforward. If R_p < 1, Proposition 3.1 states that if the initial conditions are close enough to the disease-free equilibrium, $I\left(t\right)={\int }_0^{\infty }i(t,a)da\to 0$ and λ_i(t, a, x) = βI(t) → 0 as t → ∞. Thus as t ∞, (4.1), approach a linear system that can be solved integration along the characteristics starting from a = 0. From this derive that (v(t, a), s(t, a), i(t, a), r(t, a)) → v⁰(a), s⁰(a), i⁰(a), r⁰(a) as t → ∞. Similarly, if R_p > 1 and we start close to the endemic equilibrium, λ_i(t, a, x) → λ* and we can show that (v(t, a), s(t, a), i(t, a), r(t, a)) → (v* (a), s* (a), i* (a), r* (a)) as t → ∞.

Remark 4.2. In all cases where ε_L = 0 (which is true for any combination of all-or-nothing and waning model), we have the steady state force of infection λ* = μ (R_p 1). To determine the mean age of infection in the case when b(t, a, x) = β, we divide the expression

$${\int }_0^{\infty }a.i^{\ast }\left(a\right)da=\frac{\mu {\lambda }^{\ast }}{{(\mu +\gamma )}^2}\left[\frac{q({\epsilon }_L{\lambda }^{\ast }+\alpha )}{{\lambda }^{\ast }}\left(\frac{2\mu +\gamma +{\epsilon }_L{\lambda }^{\ast }+\alpha }{{(\mu +{\epsilon }_L{\lambda }^2+\alpha )}^2}\right)+(1-q)\left(\frac{2\mu +\gamma +{\lambda }^{\ast }}{{(\mu +{\lambda }^{\ast })}^2}\right)\right],$$ (4.10)

by I* which is given in (3.2). For fixed φ = 1 − ε, the leaky and all-or-nothing models have the same mean age of infection at λ* = 0 (corresponding to R_p = 1), and the gap between that and the mean age of the waning model is given by $\frac{p\epsilon }{(\mu +\epsilon )(\mu (1-p)+\epsilon )}$.

In Figure 4.1 we plot λ* and the mean age of infection as a function of β when the transmission rate is fixed at b(t, a, x) = β. These are shown for the standard three special cases as well as for a combined model where $({\epsilon }_L,{\epsilon }_A,{\epsilon }_W)=(1-\sqrt[3]{0.8},1-\sqrt[3]{0.8},1-\sqrt[3]{0.8})$. The values could be analytically calculated using the steady state expressions in Proposition 4.2. The mean age of infection at steady state plots show that the lowest mean age of infection occurs in vaccine 2, the all-or-nothing example. This is followed by vaccine 1, the leaky example, then the combined model. Unsurprisingly, vaccine 3, the purely waning model has the highest mean age of infection. This plot shows another observable distinction between vaccines 2 and 3 which could not be differentiated using the steady state data without age structure.

Fig. 4.1.

The value of λ* and the mean age of the infective class at steady state for the leaky, all-or-nothing, waning and combined models (refer to Table 2.2). For this figure we set b(t, a, x) = β with ∈ [0, 500]. The value of λ* for the all-or-nothing and waning models overlap.

In Figure 4.2 we plot the age distribution of the infected class (divided into school age classes) for the three special cases as a function of the infant vaccination probability p. These plots are shown for both homogenous b(t, a, x) = β and age-specific b(t, a, x) based on the contact structure matrix presented in Mossong et al. [15]. This matrix features assortative mixing with school children and young adults more likely to contact people of similar age. We normalized the contact matrix so that it has a mean value that is the same as β. In the case with homogenous contact rates the distributions can be analytically calculated from the expressions in Proposition 4.2. In the case with age-specific contacts the steady states were numerically evaluated. It is clear from Proposition 4.2 that different vaccine failure parameters will lead to different distributions even with the same φ. Interestingly the distributions of the age classes respond in different manners as p is increased. In particular we note that in the case with age-structured contacts, as p is increased the proportion of the infected class aged 1–7 appear to grow for the leaky case, remain roughly the same for the all-or-nothing case and decrease for the waning case.

Fig. 4.2.

Illustration of the proportions of the infected class within the age ranges [0, 1), [1, 7), [7, 11), [11, 20) and [20, ∞) years at the endemic steady state of (4.1) for homogenous transmission β = 400 and age-specific transmission based on the contact structure described in [15].

5. Summary and conclusions

Clinical trials focus on the benefits that vaccines provide at the individual level. In these controlled experiments the effects on herd immunity cannot be measured directly. Using models we can extrapolate from individual to population-level effects, and determine the epidemiological ramifications of using different types of imperfect vaccines. We considered a mathematical model of an imperfect vaccine that may exhibit failures in degree (“leak-iness”), take (“all-or-nothingness”) and duration (waning of vaccine-derived immunity). Vaccines 1, 2 and 3, described in 1, are special cases corresponding to the leaky, all-or-nothing and waning models, respectively. The ODE equations, given in Definition 2.1, were derived in 2 with the underlying assumption that the disease without vaccination follows SIR dynamics. In the same section we defined a vaccine impact parameter φ consistent with other definitions of vaccine effectiveness in [4] and [14]. Based on this we showed how vaccines 1–3 are comparable to each other in terms of vaccine individual-level efficacy.

In 3 we examined the dynamics of the ODE model. In Proposition 3.1 the disease-free and endemic steady states of the model were derived. The stability of these steady states depend on the value of the basic reproduction number R_p which depends on φ. When the endemic equilibrium is stable we showed in Proposition 3.2 that the vaccine parameters cannot be uniquely determined based on steady state data alone. The all-or-nothing model and the waning model exhibit the same steady state values for the same value of φ.

For a fixed value of φ, we showed in Proposition 3.3 that the highest level of infection is obtained if all of the vaccine failure stems from leakiness. There have been other studies that point towards this result. White et al. [20] and Smith et al. [16] compared the efficacy of leaky and all-or-nothing vaccines and concluded that a leaky vaccine performs worse than an all-or-nothing vaccine. However in these papers the comparisons were done assuming a constant force of infection. In Proposition 3.3 we compared the vaccine models in the case when the force of infection actually depends on the choice of vaccine.

At the end of 3 we presented graphs of the steady states of the special cases of the vaccines from 1. The all-or-nothing and waning models were shown to have the same steady states (consistent with Proposition 3.2) while the leaky model had a higher level of infection at endemic state (consistent with Proposition 3.3). The leaky model was also observed to have a longer period for small oscillations compared to the other two.

Sample simulations of the onset of a vaccination program were also included to show how transient dynamics can highlight the difference between the models even when they have matching steady state data. Leaky and waning models appear to both exhibit a “honeymoon period” after the onset of vaccination which the all-or-nothing model does not display. Although these are transient dynamics, they can have important implications for vaccination programs. Moreover these provide an alternative explanation for the observed “resurgence” of some diseases like pertussis in regions that have maintained high vaccination coverage. The rise in incidence may just be due to the end of the honeymoon period, and the occurrence of large disease outbreaks may be transient oscillations during a slow transition to a vaccine-era steady state.

In 4 we extended the ODE model into an age-structured PDE model given in Definition 4.1. The well-posedness of the equations and the consistency of the model assumptions were established in Proposition 4.1. When the transmission rate is assumed to be constant, integrating the PDE system with respect to age leads back to the original ODE model (Remark 4.1). In this case the disease-free and endemic steady states can be analytically derived and the stability of this equilibrium is also determined by R_p. This is presented in Proposition 4.2 where the steady state age distributions of the model are also given. The formula shows that the distributions are distinct for different sets of values of the vaccine failure parameters. Other steady state measures can also be derived from these equations that provide useful information about the dynamics and allow us to distinguish between the different vaccines. One such measure is the mean age at infection, which in our example is highest for the waning model, followed by the leaky model and lowest for the all-or-nothing model.

The age distributions of the infected class under the assumption of age-specific transmission were also examined numerically. Figure 4.2 shows how the proportion of the different age groups for the different vaccines may respond differently to changes in vaccine coverage. For our choice of parameter values the contrast was particularly pronounced for the group between the ages of 1–7.

Our results suggest that there is enough difference in the epidemiological signatures of imperfect vaccines to determine the parameters of the vaccine used in a region where the disease is endemic despite significant vaccination coverage. It would be interesting to use the available incidence time series data on a disease like pertussis to see if an imperfect vaccine model can adequately explain the honeymoon period and resurgence of the disease, without imposing any change in the underlying disease and vaccine dynamics. One way that we plan to test this hypothesis is to fit the parameters of a stochastic imperfect vaccine model to pertussis data using maximum likelihood estimation as in the studies by Blackwood et al. [3] and Lavine et al. [10].

To our knowledge the age-structured PDE system given in Definition 4.1 has not been analyzed before. A paper by Arino et al. [2] considers an integro-differential equation model of the different types of vaccine failure (with a general waning function) derived from an age-structured system. In that paper the authors focused on the system without age-structure and did not explore the effects of the vaccine failure parameters on the age distributions of the infected class.

In this study we did not examine the role of seasonality in transmission rates. We also used exponentially distributed waiting times (transfer times between components) for simplicity. This can be improved by dividing each relevant model component into multiple compartments. For example the I class could be split up into a sequence of ${\left\{I_i\right\}}_{i=1}^n$ compartments and this would result in a gamma-distributed infective period with shape parameter of n [12]. This will be more important later on when we start fitting our model to data. The infective period is generally expected to have less dispersion than described by an exponential distribution. On the other hand, estimates of the waning time of vaccine-derived immunity appear to have more variation than the infective period so an exponential distribution may already be a fair approximation for this. There are studies that have introduced a continuity of vaccine states to allow for more general distribution of the waning period as well as a continuum of vaccine failure parameters [2, 4]. Transient dynamics such as the honeymoon period and outbreaks after the start of vaccination (illustrated in Figure 3.2) can be affected by the distribution of the waning period. Heffernan and Keeling [7] demonstrated that an SEIR model with both waning, boosting of immunity and multiple disease compartments may generate sustained cycles of disease outbreaks. They noted that these cycles are not maintained when assuming exponential waning time. We observe this as well in the decaying magnitude of the outbreaks in Figure 3.2(a).

Models of imperfect infection-derived immunity, like those of imperfect vaccines, are often formulated as waning immunity models. In this paper we focused on the population-level effects of a continuous range of vaccine types. A more general disease model would be one that allows for failure in degree, take and duration in both infection and vaccine-derived immunity. We also did not consider the possibility that when vaccinated individuals get infected, they are less infective than they would have been without vaccination. This has been considered in the literature dealing with vaccine efficacy on infectiousness [4]. These extensions of the model and their complex effects are topics for future work.

Appendix A. Proofs

To determine the steady states of the ODE model we set the right-hand-sides of (2.2) equal to zero and derive the following quadratic equation,

$$P\left(z\right)=R_0{\epsilon }_L(1-{\epsilon }_L)(1-{\epsilon }_W)z^2-({\epsilon }_L(1-{\epsilon }_W)(R_0-1)+1)z+(1-{\epsilon }_A)(1-{\epsilon }_W)p=0.$$ (A.1)

The solution to P (z) = 0 satisfying z ∈ [0, 1] is given by V * in Proposition 3.1. In Appendix B we prove that V * does indeed have the required properties and that the other root to this equation does not yield physical equilibrium values.

Proposition A.1. The discriminant of the quadratic equation (A.1) satisfies,

$$\text{discriminant}={(1-{\epsilon }_W)}^2\left[{\left({\epsilon }_L(R_0-1)+\frac{1}{1-{\epsilon }_W}\right)}^2-4R_0{\epsilon }_L(1-{\epsilon }_L)(1-{\epsilon }_A)p\right]\ge 0,$$

for all μ ≥ 0, > 0, > 0, p ∈ [0, 1] and (ε_L, ε_A, ε_W) ∈ [0, 1)³.

Proof. The discriminant can be rewritten as (1 − ε_W )² times the following expression,

$${\left({\epsilon }_L(R_0-1)+\frac{1}{1-{\epsilon }_W}\right)}^2-4R_0{\epsilon }_L(1-{\epsilon }_L)(1-{\epsilon }_A)p={\left[{\epsilon }_L{R}_0-\left(\frac{1}{1-{\epsilon }_W}-{\epsilon }_L\right)\right]}^2+4R_0{\epsilon }_L\left[(1-{\epsilon }_L)(1-(1-{\epsilon }_A)p)+\frac{{\epsilon }_W}{1-{\epsilon }_W}\right].$$ (A.2)

Clearly the last line is always non-negative due to the range of allowable parameter values.

Proposition A.2. The roots of the the quadratic equation (A.1) are V * (given in (3.1)) and Q where

$$Q=\frac{{\epsilon }_L(1-{\epsilon }_W)(R_0-1)+1\sqrt{{({\epsilon }_L(1-{\epsilon }_W)(R_0-1)+1)}^2-4{R_0}_L(1-{\epsilon }_W)}\phi p}{2R_0{\epsilon }_L(1-{\epsilon }_L)(1-{\epsilon }_W)},$$

and Q satisfies Q > 1 for all μ ≥ 0, γ > 0, β > 0, p ∈ [0, 1], (ε_L, ε_A, ε_W ) ∈ [0, 1)³ with ε_L > 0.

Proof. It is clear that Q ≥ 0. By Proposition A.1, the discriminant satisfies

$$\sqrt{\text{discriminant}}\ge (1-{\epsilon }_W)\mid {\epsilon }_L{R}_0-\left(\frac{1}{1-{\epsilon }_W}-{\epsilon }_L\right)\mid =\{\begin{array}{cc}{\epsilon }_L(1-{\epsilon }_W)(R_0+1)-1,\hfill & \text{if}{\epsilon }_L(R_0+1)-\frac{1}{1-{\epsilon }_W}\ge 0,\hfill \\ 1-{\epsilon }_L(1-{\epsilon }_W)(R_0+1),\hfill & \text{if}{\epsilon }_L(R_0+1)-\frac{1}{1-{\epsilon }_W}<0.\hfill \end{array}\phantom{\}}$$

It follows that

$$Q\ge \frac{{\epsilon }_L(1-{\epsilon }_W)(R_0-1)+(1-{\epsilon }_W)\mid {\epsilon }_L{R}_0-\left(\frac{1}{1-{\epsilon }_W}-{\epsilon }_L\right)\mid }{2R_0{\epsilon }_L(1-{\epsilon }_L)(1-{\epsilon }_W)}=\{\begin{array}{cc}\frac{1}{1-{\epsilon }_L},\hfill & \text{if}{\epsilon }_L(R_0+1)-\frac{1}{1-{\epsilon }_W}\ge 0,\hfill \\ \frac{1-{\epsilon }_L(1-{\epsilon }_W)}{R_0{\epsilon }_L(1-{\epsilon }_L)(1-{\epsilon }_W)},\hfill & \text{if}{\epsilon }_L(R_0+1)-\frac{1}{1-{\epsilon }_W}<0.\hfill \end{array}\phantom{\}}$$

In the case when ${\epsilon }_L(R_0+1)-\frac{1}{1-{\epsilon }_W}<0$, let x = ε_L (1 − ε_W. Then $x\in (0,\frac{1}{R_0+1})$. The function $\frac{1-x}{R_0(1-{\epsilon }_L)x}$ decreases with x. Thus,

$$\frac{1-{\epsilon }_L(1-{\epsilon }_W)}{R_0{\epsilon }_L(1-{\epsilon }_L)(1-{\epsilon }_W)}\ge \frac{1-\frac{1}{R_0+1}}{R_0(1-{\epsilon }_L)\frac{1}{R_0+1}}=\frac{1}{1-{\epsilon }_L}.$$

Hence $Q\ge \frac{1}{1-{\epsilon }_L}>1$ in all cases.

Proposition A.3. In Proposition 3.1, V * ∈ [0, 1] and S* ∈ [0, 1]. The expressions for I* and R* are in [0, 1] if and only if R_p ≤ 1 with I* = R* = 0 occurring only when R_p = 1.

Proof. By the positivity of the discriminant, V * > 0 is obvious. The results on I* and R* follows if we prove that R₀ (1 − (1 − ε_L)V * ) − 1 ≥ 0 occurs when R_p ≤ 0 with the equality only occurring at R_p = 1. This proof is simple and is omitted. The result on S* follows from V * +S* +I* +R* = 1.

Proposition A.4. The endemic steady state is locally asymptotically stable when R_p > 1.

Proof. The proof of this proposition is similar to the proof of local stability in Arino et al. [1]. Consider the system (2.2) in terms of three independent variables (V, S, I). The Jacobian J and its second additive component J^[2] (defined in [11]) evaluated at the endemic steady state is

$$\begin{array}{cc}\hfill J=& \left[\begin{array}{ccc}\hfill -{\epsilon }_L\beta I^{\ast }-\mu -\alpha \hfill & \hfill 0\hfill & \hfill -{\epsilon }_L\beta V^{\ast }\hfill \\ \hfill \alpha \hfill & \hfill -\beta I^{\ast }-\mu \hfill & \hfill -\beta S^{\ast }\hfill \\ \hfill {\epsilon }_L\beta I^{\ast }\hfill & \hfill \beta I^{\ast }\hfill & \hfill 0\hfill \end{array}\right],\hfill \\ \hfill J^{\left[2\right]}=& \left[\begin{array}{ccc}\hfill -{\epsilon }_L\beta I^{\ast }-2\mu -\alpha -\beta I^{\ast }\hfill & \hfill -\beta S^{\ast }\hfill & \hfill {\epsilon }_L\beta V^{\ast }\hfill \\ \hfill \beta I^{\ast }\hfill & \hfill -{\epsilon }_L\beta I^{\ast }-\mu -\alpha \hfill & \hfill 0\hfill \\ \hfill -{\epsilon }_L\beta I^{\ast }\hfill & \hfill \alpha \hfill & \hfill -\beta I^{\ast }-\mu \hfill \end{array}\right].\hfill \end{array}$$

Let λ₁, λ₂ and λ₃ be the eigenvalues of J ordered such that $\Re \left({\lambda }_1\right)\le \Re \left({\lambda }_2\right)\le \Re \left({\lambda }_3\right)$. It is trivial to show that Tr(J) < 0 and Det(J) < 0. This allows for four possibilities:

1. $({\lambda }_1,{\lambda }_2,{\lambda }_3)\in {\mathbb{R}}^3\text{and}{\lambda }_1\le {\lambda }_2\le {\lambda }_3<0$.

2. $({\lambda }_1,{\lambda }_2,{\lambda }_3)\in {\mathbb{R}}^3,{\lambda }_1<0<{\lambda }_2\le {\lambda }_3,{\lambda }_1+{\lambda }_2<0\text{and}{\lambda }_1+{\lambda }_3<0$

3. ${\lambda }_2\in \mathbb{R}\text{and}{\lambda }_3={\stackrel{‒}{\lambda }}_2\in \mathbb{C}\text{with}{\lambda }_1<0\text{and}\Re \left({\lambda }_2\right)<0$

4. ${\lambda }_1\in \mathbb{R}\text{and}{\lambda }_3={\stackrel{‒}{\lambda }}_2\in \mathbb{C}\text{with}{\lambda }_1<-2\Re \left({\lambda }_2\right)\text{and}\Re \left({\lambda }_2\right)\ge 0$.

The eigenvalues of J^[2] are λ_i + λ_j, 1 ≤ i < j ≤ 3, thus Det(J^[2]) = (λ₁ + λ₂) (λ₁ + λ₃) (λ₂ + λ₃). It is also possible to show that if R_p > 1 then Det(J^[2]) < 0 (proof omitted). Since this inequality cannot hold in cases 2 and 4, only case 1 and 3 are allowed. Thus $\Re \left({\lambda }_i\right)<0$ for i = 1, 2, 3. This proves that the endemic equilibrium is locally asymptotically stable.