Dynamic properties of small-scale solar wind plasma fluctuations

Abstract

The paper presents the latest results of the studies of small-scale fluctuations in a turbulent flow of solar wind (SW) using measurements with extremely high temporal resolution (up to 0.03 s) of the bright monitor of SW (BMSW) plasma spectrometer operating on astrophysical SPECTR-R spacecraft at distances up to 350 000 km from the Earth. The spectra of SW ion flux fluctuations in the range of scales between 0.03 and 100 s are systematically analysed. The difference of slopes in low- and high-frequency parts of spectra and the frequency of the break point between these two characteristic slopes was analysed for different conditions in the SW. The statistical properties of the SW ion flux fluctuations were thoroughly analysed on scales less than 10 s. A high level of intermittency is demonstrated. The extended self-similarity of SW ion flux turbulent flow is constantly observed. The approximation of non-Gaussian probability distribution function of ion flux fluctuations by the Tsallis statistics shows the non-extensive character of SW fluctuations. Statistical characteristics of ion flux fluctuations are compared with the predictions of a log-Poisson model. The log-Poisson parametrization of the structure function scaling has shown that well-defined filament-like plasma structures are, as a rule, observed in the turbulent SW flows.

1. Introduction

Significant progress in studying the solar wind (SW) turbulence has been achieved during the past decades (e.g. the reviews [1,2], reviews in the current issue [3–7] and references therein). The main aim of these investigations is to understand the general process of energy exchange in the course of nonlinear interaction between the structures of different time and spatial scales. Another problem important for space physics is to estimate SW plasma heating in these processes. The SW spectra of fluctuations are consistent with the properties of multifractallity and self-similarity over all scales (e.g. [8] and references therein). The most comprehensive study of SW turbulence properties is provided in the low frequency range, the so-called inertial scale (see the reviews by [2,9–11], and references therein). The majority of these investigations observe a power spectrum of interplanetary magnetic field (IMF) fluctuations at scales lower than 10⁻¹ Hz and demonstrate that the slope of these spectra is on average close to −5/3, corresponding to the Kolmogorov spectrum [12]. Few papers (e.g. [13–17]) have observed similar spectra of SW flux and electron density fluctuations. The less steep spectrum of SW velocity (the slope is approx. −3/2) has been found in e.g. [18–21]. High-resolution measurements of IMF have been available for a long time, so the high-frequency range (known in the literature as the range of dissipation scales) of IMF fluctuations has been well enough studied (e.g. the reviews by [1,2] and references therein). It was shown in different experiments that the spectra in the high-frequency range are significantly steeper than in the low frequency one. Chen et al. [22] have shown the existence of a similar steepening in the high-frequency range (up to 10 Hz) of the spectra of electron density fluctuations in the measurements made by the ARTHEMIS satellite. These findings were performed using the indirect method based on the data of a spacecraft's potential fluctuations. We discuss these results in §3. High-resolution plasma data were earlier accomplished up to 13.3 Hz by SW flux measurements in the OGO- 5 experiment [17], up to approximately 5 Hz by electron density measurements in ISEE-1 and ISEE-2 experiments [13,14] and up to 2.5 Hz by electron density measurements on the CLUSTER experiment [16]. However, these authors did not note the steepening of the spectra. The systematic experimental investigation of the high-frequency range of plasma fluctuations became feasible only after the launch of the BMSW experiment. The first study of SW turbulence in [23] has shown that the frequency spectra of the density, velocity and thermal velocity exhibit the same behaviour at the magnetohydrodynamic (MHD) scale, but their spectra are remarkably different at the kinetic scale. The results of further studies of ion flux fluctuations are presented in this paper.

The standard approach usually does not take into account the intermittency of SW fluctuations at small scales (see reviews [1,2,6]). It implies that intermittent fluctuations should demonstrate non-Gaussian, scale-dependent statistics [24,25]. Intermittency and a self-similarity are responsible for the memory effect and large-scale correlations in space plasma (e.g. the review [26]). Intermittency leads to a local destruction of turbulence homogeneity and can contribute to the dissipation of turbulence [4,6]. So, the analysis of intermittency properties is important for fundamental understanding of the statistical properties of turbulence, and of the transport process in this turbulent plasma. The intermittency of density fluctuations in the SW at kinetic scales has been examined using high time resolution Faraday cup measurements from the SPECTR-R spacecraft [27]. The authors found that the probability distribution functions (PDFs) of the fluctuations are highly non-Gaussian over this range, but they do not show large changes in shape with scale, statistically similar to those of the magnetic fluctuations. We also need to take into account the strong anisotropy of turbulence in the SW (see [7,28–31]), which can finally lead to different deviations from the Kolmogorov model often observed in experiments. Here, we present some new results concerning turbulent properties of small-scale SW ion flux fluctuations on the basis of the SPECTR-R measurements with the record high time resolution up to 32 Hz.

2. Basic features of the measurement technique

The plasma spectrometer BMSW is installed onboard the high-apogee SPECTR-R satellite. This spacecraft was launched on 18 July 2011, and its orbit has apogee of approximately 350 000 km, perigee of approximately 5000–500 00 km and orbital period of 8.5 days. The BMSW instrument has operated practically permanently since 5 August 2011 [32]. Such orbit allows regular measurements of plasma parameters to be carried out in both SW and Earth's magnetosheath during the March–November period of each year for 7–8 days per orbit.

The BMSW instrument was specially designed for measuring some SW plasma parameters with very high time resolution (see [33–35]). The main axis of the BMSW instrument is permanently directed to the Sun within the limits of 5–10° deviation. The instrument is equipped with its own solar sensor that allows one to know the orientation of instrument axes relative to the Sun's direction with accuracy of 1°. The BMSW instrument includes a set of six sensors—Faraday cups (FCs):

• — three integral cups having various orientation and designed for the determination of the ion flux vector (the flux value and direction) with time resolution up to 31 ms;

• — three cups aligned with the main axis of the instrument, but having different control voltages. This allows one to measure the energy distribution of ions with time resolution of 3 s and to determine the bulk velocity, ion density and ion temperature of a SW flux with time resolution 3 s or 0.03 s (depending on the mode).

The BMSW device can operate in two different modes:

• — Sweeping mode: the control voltages change by the saw tooth law. This mode is used for measurements of energetic spectra with 3 s time resolution.

• — Adaptive mode: the control voltages are slaved automatically for keeping the fixed proportions between currents of three cups aligned with the main axis. This mode is used for the determination of the main parameters of energetic spectrum (density, velocity and temperature) with record resolutions of 31 ms.

So, a set of some SW plasma parameters can be measured with resolution of approximately 3 s for 50% of the time, and for another 50% with resolution of 31 ms, whereas the integral ion flux is measured always with the highest time resolution in 31 ms (the ion flux data of BMSW instrument used in this paper is available at http://www.plasma-f.cosmos.ru/bmsw/ion-flux). The first results provided by this instrument are published in [23,34–38].

3. Observations of fast variations of solar wind ion flux and their Fourier spectra

Fluctuations with different temporal scales are typical for observations of SW plasma parameters. The BMSW measurements allow us to investigate the ion flux fluctuations with temporal scales up to 31 ms. Figure 1 presents 10 h (panel a), 17 min (panel b) and 40 s (panel c) time intervals with 31 ms time resolution of ion flux measurements for 27/09/2011–28/09/2011. It clearly demonstrates the high variability of the intensity of SW ion flux over all scales. The flux variations are even observed during time intervals shorter than 1 s. Such multiscale structure of SW is described in numerous papers (e.g. [39]).

Figure 1.

Typical turbulent fluctuations of SW ion flux (high-resolution BMSW measurements): 27–28/09/2011 23:00–09:00 UT (a) 28/09/2011 03:08–03:24 UT, (b) 28/09/2011 03:15:35–03:16:15 UT (c).

In this section, we present the spectral analysis of high-resolution BMSW measurements. We use the method of fast Fourier transform with window of ‘Hamming’ in the frequency domain for smoothing. Figure 2a presents an example of the spectrum of ion flux turbulent fluctuations measured by BMSW instrument at 28/09/2011 from 03:08 to 03:25 UT (the ion flux variations for this period are shown on figure 1b) in the range 0.01–16 Hz for a 17 min interval. In general, the spectrum has a power law shape (straight lines in logarithmic coordinates) with two characteristic slopes at lower and higher frequencies: the low-frequency (in literature named ‘inertial range’) range from approximately 10⁻² to approximately 1 Hz and the high-frequency one (in literature named ‘dissipation range’) from approximately 1 to approximately 10 Hz. The solid lines in figure 2a show the power law approximation for each region. The dashed line corresponds to the −5/3 Kolmogorov slope. The quantitative estimates of spectral indices for both regions provide for their slopes P₁=−1.69±0.05 and P₂=−3.23±0.06. The boundary between these regions is determined as the point of intersection of these two linear approximations, and we call it a ‘break frequency’ of the ion flux spectrum (F_b). For the example above, this value is F_b=1.93±0.5 Hz. It should be noted that some flattening in all ion flux spectra obtained by BMSW can be seen at frequencies of 10–15 Hz. The level of fluctuations is rather low in this frequency range, the signal-to-noise ratio is approximately 10 for these cases, and the spectrum becomes flatter owing to the noise influence on this range. The mixing of frequencies was excluded, because the amplifiers of the BMSW Faraday cups were equipped with Bessel's filters at the Nyquist frequency [34]. The laboratory tests and analysis of in-flight calibration intervals have shown that the noise of BMSW amplifiers can spoil the ion flux frequency spectra above 8–10 Hz [27,34] when the level of the ion flux fluctuations is very low, thus the reasonable estimate for the upper boundary of the range of SW ion flux variations is about 10 Hz. The spectra of some other SW plasma parameters (density, velocity and temperature) can be obtained by measurements carried in the ‘adaptive mode’ [34].

Figure 2.

(a) Power spectrum of ion flux fluctuation values in SW 28/09/2011 03:08–03:25 UT. (b) Power spectrum of ion density fluctuations on 15/07/2012 12:00–15:00 UT.

The presence of the break qualitatively corresponds to the prediction of fractal model (see [40]). Following this model, the plasma flow with high beta values tends to be organized in clusters with considerable fine structure separated producing intermittent manifestations in observed time series of plasma and magnetic field parameters. The Fourier spectrum has two characteristic domains: the one which is the result of collective convectional motion of quasi-static fractal structures interacting with current carrying particles and the higher frequency one with significantly steeper power law spectrum which is controlled by nonlinear interactions effectively dissipating the fluctuation energy. This hypothesis has been confirmed earlier only by the IMF measurements (e.g. [24,41]), by the SW electron density measurements on ARTHEMIS spacecraft (e.g. [22]) and, at present, by the first results of fast BMSW measurements of some plasma parameters [23,27]. So, the BMSW measurements show, for the first time, the presence of a break point approximately 1 Hz in spectra of some direct plasma parameters fluctuations. Note here that the fluctuations of the bulk and thermal speeds are similar to each other, but the spectral indices differ from those determined for the density fluctuations, thus a location of the break point of the ion flux can differ from other SW parameters.

We described above the typical spectra of fluctuations, but, in reality, particular spectra can look very different. For example, the spectra with spectral flattening between these low- and high-frequency parts can be observed rather frequently (see [37]). An example of such spectra for 15/07/2012 from 12:00 to 15:00 UT is shown in figure 2b. We need to note that in figure 2b the spectrum of density fluctuation is presented (as in [37]), but the ion flux fluctuations are mainly density fluctuations, so the spectrum of ion flux fluctuations will look similar to the spectrum of density fluctuations for the same time periods. There are no clear break points between the low frequency, high frequency and plateau parts of the spectrum (the transition region are rather smooth), but the spectrum can be approximately fitted by three straight lines. The values of the slopes and the frequencies of point intersections of these lines (breakpoint 1 and breakpoint 2 in the figure) are shown in figure 2b, together with the slope of the Kolmogorov spectrum −5/3 (dashed line). A similar spectrum with flattening around ion scales was first observed in [13,14,16,17,42]. Safrnakova et al. [37] have shown that the breakpoint locations are controlled by the gyro-frequency.

Even if the spectrum has two branches with a well-defined break point, the slopes of the branches and the position of the break can differ quite strongly from spectrum to spectrum. Figure 3 presents the statistics of spectral indices P₁ (a), P₂ (b) and break frequency F_b (c), for the set of the cases with two branches. Statistics combines the results of analysis of 363 spectra calculated during approximately 17 min overlapped intervals. Statistics includes rather broad ranges of SW plasma parameters: density approximately 1–30 cm⁻³, velocity approximately 250–700 km s⁻¹, temperature approximately 1–60 eV. All spectral indices also change in a wide range. The maximum of distributions of the P₁ slope are approximately −(1.6 to 1.7), and of the P₂∼−(2.6 to 2.8). The average values of the slope of the low frequency range 〈P₁〉=−1.6±0.2 are in a good agreement with the numerous experimental results of plasma and IMF parameters in SW obtained earlier (see the reviews [1,2] and references therein) and correspond approximately to the slope of the Kolmogorov model spectrum in the inertial range [12]. The average values of the slope at high-frequency range are equal 〈P₂〉=−2.9±0.2. Our predecessor has shown very close results: the spectral index P₂∼2.8 for IMF in the SW (e.g. [41,43]), and approximately 2.7 for indirect measurements of electron density in the SW [22]. The possible reasons of spectral steepening at high frequencies were discussed e.g. by [5,44–47] and other related papers. One can see that such numerical values of slopes in the inertial and dissipation parts of fluctuation spectra are typical both for SW plasma and for IMF parameters. So, such shapes of spectra with these values of slopes represents the fundamental property of SW plasma flow.

Figure 3.

The distribution of the spectral indices P₁ (a), P₂ (b) and of the break frequencies F_b (c) for ion flux fluctuation spectra in SW (BMSW measurements).

Now, let us discuss the break frequency in the case of two branch spectra. The maximum of its distribution is at approximately 1.5–2.5 Hz, the average value 〈F_b〉=1.9±0.8 Hz. It is comparable to the frequency of a break point (equal approx. 1 Hz) for indirect measurements of electron density published in [22], taking into account the large dispersion of the values of break points. Therefore, it is quite clear that electron and ion density variations can, in principle, be qualitatively different. It is important to note that the frequency of the break point for ion flux spectra is approximately two to five times higher than one for IMF spectra (which is equal in experiments near to approx. 0.1–0.7 Hz (see review in [1])). It is interesting that the additional analysis of the spectra of velocity and density fluctuation (in adaptive mode of BMSW measurements) shows that the break frequency is equal to approximately 1.6 Hz for density (close to our results for ion flux presented here, and the results of Chen et al. [22]) and approximately 0.4 Hz for velocity (which is also close to numerous results of IMF analysis; see the review [1] and references therein).

It is important to note the high level of variability of break frequencies. It is equal to approximately 40% of their mean value. We need to draw readers' attention to the break points in cases of spectra with ‘plateau’ that are observed separately and are presented in [37]. The broad range of spectral break values can be explained by complicated processes of their formation, including the nonlinear interaction of waves and kinetic plasma instabilities of different nature (e.g. the review [3] and the references therein). In [23], it was shown that the break frequency weakly depends on proton cyclotron frequency and the value of inertial interval length, which confirms the previous results [48]. However, the large dispersion of experimental points indicates that other numerous factors can also influence the value of a break frequency.

4. Intermittency of small-scale ion flux fluctuations

(a). The analysis of probability distribution functions

A local breaking of the inhomogeneity of turbulence, when active regions coexist with passive (quasi-laminar) ones, is called intermittency, and was considered for the first time by Novikov & Stewart [49]. The intermittency phenomenon is observed both in turbulent hydrodynamic flows in neutral media and in turbulent magnetized plasmas (see e.g. review [26] and other related papers), both having moderate (less than 10³) and high Reynolds numbers ≫10³). Random fluctuations of the velocity, fields, fluxes and other parameters of a turbulent flow obey a non-Gaussian statistics in an intermittent media. The universality of intermittency properties for hydrodynamics and magnetofluids was considered in a number of publications (e.g. [26]).

The non-Gaussian PDF of small-scale SW fluctuations in the MHD inertial range scale demonstrates the high level of intermittency (see [50,51]). The experiment shows the growth of the intermittency level of IMF fluctuations from the large to the small scale (e.g. [24,25,52,53]. Small-scale fluctuations of the SW velocity are observed to be highly intermittent too (e.g. [21,53]). The high intermittency of ion flux fluctuations on a scale of approximately 1 s was observed in our earlier works based on INTERBALL-1 measurements (see [54–56]).

An example in figure 1 demonstrates that highly disturbed periods could alternate with the rather calm ones. The examples of PDFs of ion flux fluctuations on the 0.1 s scale measured by BMSW instrument (figure 4a,b) demonstrate the strong deviation from Gaussian distributions. Both symmetric (figure 4a) and asymmetric (figure 4b) PDFs can be observed for small-scale fluctuations in SW flows.

Figure 4.

An example of the PDF of ion flux SW variations on scale 0.1 s (solid line shows BMSW results) and corresponding Gaussian distribution based on the standard deviation on the observed signal (dashed line). (a) Symmetric distribution for period 28/09/2011 03:59–04:16 UT and (b) asymmetric distribution for period 28/09/2011 03:16–03:33 UT.

The deviation of PDF from the Gaussian distribution can be estimated by the flatness, fourth-order moment of distribution: , where the structure function , τ is the length scale of the ion flux variation and X is the investigated parameter. The flatness corresponds to the sharpness of the peak of the distribution, and thus is a measure of the intermittency level (see [53]).

The flatness is equal to 3 for non-intermittent periods described by the Gaussian distribution function. Figure 5 shows the dependence of the flatness from the time scale F∼1/τ (Hz) and the corresponding frequency spectrum of ion flux fluctuations for the period presented in figure 1a. Flatness grows when one moves from large to small time scales up to 0.1 s (scale of the noise influence). So, the level of intermittency becomes significantly lager for small scales. The time scale approximately 10 Hz can be correspondingly characterized as the most intermittent. This dependence confirms and supplements our previous results of analysis of 1 Hz ion flux measurements received earlier in the frame of Interball-1 project with the similar but less advanced instrumentation (see [55,56]). So, now we are able to extend and obtain dependencies to 10-fold in the high-frequency range. The different departure of PDF from the Gaussian shape for different time scales leads to a break of the trivial self-similarity. It drives the non-trivial self-similarity and the intermittency.

Figure 5.

Flatness (fourth-order of moment) coefficient for ion flux fluctuations in the range 0.03–100 s (BMSW results) calculated on period 27–28/09/2011 23:00–09:00 UT and corresponding spectrum of ion flux fluctuations (grey points and the black line (averaged spectrum)). The noise influence is strong on the right side of the dashed vertical line.

(b). The description by using Tsallis statistics

The heavy power law tails of PDFs can be related to the Tsallis theory (the generalization of the Boltzmann–Gibbs (BG) statistics) and its q-extension of the central limit theorem (CLT) (e.g. [57,58]). Nonlinear interactions can create fractal structuring of the phase space and produce global correlations in the entire multiscale system. According to Milovanov & Zelenyi [59], Tsallis entropy can be rigorously obtained as the solution of a nonlinear functional equation referred to the spatial entropies. The complexity of dynamics is far beyond the simple ergodic complexity and can be described by non-extensive Tsallis statistics based on the extended concept of q-entropy [57]:

4.1

Equation (4.1) is the basis of Tsallis non-extensive statistics and the Tsallis entropy E_q is a measure of the complexity of the system, whereas the parameter q measures the degree of non-extensivity of the system. For two probabilistically independent systems A and B, the relation given by equation (4.1) transforms into

4.2

The first part of E_q(A+B) is additive, whereas the second part is multiplicative, describing the long-range interactions between the two systems. For q〈1,q=1,q〉1, equation (4.2) holds for superadditivity, additivity and subadditivity, respectively. Tsallis index q≠1 means also deviation from normal CLT. In particular, the normal CLT concerns with Gaussian random variables x_i for which the sum gradually tends to a Gaussian process as , whereas its fluctuations tend to zero, in contrast to the possibility of non-equilibrium fluctuations with long-range correlations. Using the Fourier transform (FT) q-extension, we can prove that q-independence means independence for q=1 (normal CLT), but for q≠1 it means strong correlation (q-extended CLT). In this case (q≠1), the number of allowed states W_A1+A2+⋯+AN in a system composed of (A₁,A₂,…,A_N) subsystems is expected to be less than , where W_A1,W_A2,…,W_AN are the possible states of the subsystems. This means self organization of dynamics for q≠1 and development of long-range correlations in space and time. In figure 6, we present the q-Gaussian distribution (solid line), where the difference between the q-Gaussian and the Gaussian PDF (dotted line) in long tails is clearly depicted. The open circles correspond to the experimental time series (detrended with a first difference filter). The estimation of the Tsallis q-Gaussian is based on the estimation of Tsallis q entropic index referred to as stationary q=q_stat which corresponds to the maximization of Tsallis entropy E_q. In particular, Tsallis q_stat entropic index is connected with the Tsallis q-Gaussian distribution given by

4.3

Figure 6.

An example of the PDF of ion flux SW variations (open points) for period 26/09/2011 09:40–10:57 UT in comparison with the Gaussian distribution (dashed line) and the approximation of Tsallis statistic distributions (solid line).

where e_q=[1+(1−q)x]^1/(1−q) is the q-exponential, β is a positive number and C_q is a normalization constant, namely figure 6 demonstrates the good agreement of experimental PDF measured by BMSW and PDF predicted by Tsallis approach. So, the approach of Tsallis approximation of PDFs can rather successfully be applied for the investigation of dynamics of SW turbulent properties. Extensive description of Tsallis theory and its application in various time series as well as analysis of SW at quiet and disturbed periods is presented in the papers [60,61]. In particular, concerning the analysis of SW time series (corresponding to ion flux BMSW measurements), the results show clearly the non-extensive statistical character of SW during quiet or shock periods. The summary results obtained by application of the Tsallis non-extensive statistical theory give for quiet periods q_stat=1.37±0.05 and for shock periods q_stat=1.61±0.01. So, the non-extensive character of statistics was found to be gradually enhancing passing from the calm period to the shock state. Finally, non-extensive statistical mechanics include the q-analogue (extensions) of the classical CLT and a-stable distributions corresponding to dynamical statistics of globally correlated systems. The q-extension of CLT leads to the definition of statistical q-parameters of which the most significant is the q-triplet (q_sen, q_rel, q_stat), where the abbreviations sen, rel and stat stand for sensitivity (to the initial conditions), relaxation and stationary (state) in non-extensive statistics, respectively [58,62]. In particular, the q_sen describes the production of E_q entropy, the q_rel describes the relaxation of the dynamics at stationary states and the q_stat describes the q-extension of statistics and the statistical distribution of the q-correlation random variables at stationary states, produced by the extremization of Tsallis q-entropy (E_q). In the case of Gaussian processes, the q-triplet takes the values (q_sen=q_rel=q_stat=1). The results concerning the Tsallis q-triplet (q_sen, q_rel, q_stat) for SW time series are presented, among others, in a recent paper by Pavlos et al. [61], which further support the hypothesis of Tsallis non-extensive statistics in SW plasma dynamics. Conclusively, the value q_stat>1 suggests the presence of long-range interactions, a characteristic feature of open far from equilibrium complex systems, whose underlying dynamics can generate non-Gaussian (q-Gaussian) distributions. In this case, it is the maximization of Tsallis entropy which is responsible for the observed q-Gaussian distribution in contrast to BG formalism which is connected with exponential distributions. Thus, the system's dynamics evolves through a sequence of metastable stationary states which are described by a Tsallis q-Gaussian distribution with an entropic index q>1. In addition, in this case the system's entropy in all cases is subadditive meaning that the entropy of the whole system is smaller than the sum of its parts.

(c). The analysis of high-order structure functions

The intermittency and scale-invariance are also studied in detail by analysing the high-order structure functions S_q(τ)=〈|δ_τX(t)|^q〉 (moments of the PDF, 〈…〉 is an ensemble average of increments δ_τX(t)=X(t+τ)−X(t), q is the order of this moment, τ is the length scale of variation) of different orders versus spatial or temporal separation (Eulerian statistics).

Structure functions are sensitive to correlation and contribution of great intensity events. Statistical self-similarity of the type S_q(τ)∼τ^ζ(q) can be expected in the inertial range. The Kolmogorov (K41 model) assumed that all statistically averaged moments (the q-th order structure functions S(q,l)∼〈|δυ_l|^q〉, δυ_l=υ(x+l)−υ(x)) at scale l depend only on the mean dissipation rate and l with the scaling 〈|δυ_l|^q〉∼l^ζ(q). Scaling ζ(q)=q/3 was found in the K41 model for fully developed isotropic turbulence. Nonlinear behaviour of the structure function scaling ζ(q) was observed in SW by Burlaga [63]. Examples of structure function of high orders (with orders up to 9) for SW ion flux (BMSW measurements) are presented in figure 7. The linear dependence S_q(τ)∼τ^Hq, where H=const, is observed only in a limited range of scales (less than 0.1 s): dependence ζ(q) is obviously nonlinear.

Figure 7.

Structure functions of high orders q from the time scale τ. SW ion flux, BMSW measurements 28.09.2011 02:39–03:05 UT.

For intermittent turbulence in the usual fluid [64], it was found that the log–log plot of structure functions S_q(l) versus S_p(l) (moments of different order) lies on a straight line in a range which is much wider than the log–log plot of S_q(l) versus l itself. This empirical fact was called extended self-similarity (ESS). Such behaviour of generalized self-similarity holds even at moderate Reynolds numbers over the range which is substantially longer than the inertial one. The extended self-similarity corresponds to the scaling in a turbulent cascade not with respect to the usual distance, but with respect to an effective scale defined by the third order moment of the velocity field. Hidden statistical symmetries of the motion equations, hierarchy of moments and multifractality are behind the property of the ESS. The ESS is observed in turbulent systems such as usual fluid, space plasma, plasma of fusion devices (see review in [26]). The ESS property is observed also in SW ion flux data from the BMSW instrument: the dependence of S_q(τ) on S₃(τ) is seen to be linear (figure 8). This ESS plot is obtained from figure 7 by using S_q(τ) over almost three orders of magnitude in time. Similar results of PDF analysis of high-frequency BMSW data of SW ion density fluctuations are also published in [27]. The ESS demonstrates the presence of statistical symmetry in the system that ensures the invariance of the process over a wide range of scales, up to the dissipative one. The observations of the ESS in the intermittent turbulence can be interpreted in terms of the log-Poisson turbulence model (see below).

Figure 8.

Extended self-similarity plot: structure functions S_q(τ) versus S₃(τ). SW ion flux, BMSW measurements 28.09.2011 02:39–03:05 UT.

(d). Parametrization of the structure functions by the log-Poisson model

Log-Poisson models generalize the previous fractal models of intermittent turbulence [65,66]. In log-Poisson models, the logarithm of the energy dissipation obeys the Poisson statistics characterized by special scale-invariance properties. The Poisson distribution describes the probability of an anisotropic energy division between the splitting sub-eddies in the turbulent cascade. The log-Poisson model of She–Leveque–Dubrulle [65,66] assumes the existence of the limiting energy rate value associated with singular dissipative structures (with scaling , where the parameter Δ is associated with the geometry of dissipative structures) and adopts the self-similarity hypothesis. It is assumed that such properties arise from the hidden dilatation symmetries (scale-invariance) of the governing equations (the Navier–Stokes equations in hydrodynamics and MHD equations in plasma physics). In the frame of She–Leveque–Dubrulle implementation of the log-Poisson model, one can derive the scaling

4.4

The parameter β characterizes the degree of intermittency (for non-intermittent homogeneous developed turbulence in, for example, the K41 model β=1). This scaling has two adjustable parameters Δ and β that could be estimated from experimental data.

The log-Poisson model reproduces experimental and numerical results in hydrodynamic and plasma turbulence rather well (see review [26]). For three-dimensional isotropic hydrodynamic turbulence She & Leveque (SL [66]) proposed that Δ=β=2/3.

The example of the time dependence of β and Δ from BMSW data is presented in figure 9. The example presents the rather typical period (02/08/2012 09:00–22:50 UT)) of large (up to several times) and sharp (shorter than several minutes) SW ion flux changes. Each set of coefficients is calculated on 50 000 samples (approx. 26 min of 32 Hz measurements) overlapped with each other. The intermittency level is high during most of this interval (β∼0.05–0.3). It decays only at the very end of it (β∼0.7−1). Values of Δ between 0.1 and 0.3 are found during the entire period. There are deviations from the values β=Δ=2/3, which characterize three-dimensional isotropic turbulence in the She–Leveque version of the log-Poisson model. The interpretation of experimental results requires a systematization of the extended statistics. Such dissipative structures are likely to have complicated fractal topology instead of a trivial Euclidean one. This issue can be investigated in detail by considering an anisotropic stochastic cascade (see [26,67]).

Figure 9.

The time variation of β (rhombus) and Δ (triangles). The solid line—the value of SW ion flux (in arb. units). t is the time in seconds from the beginning of the interval of BMSW data 02/08/2012 09:00–22:50 UT.

The distribution of β and Δ coefficients on 207 intervals with 26 min duration is presented in figure 10. The distribution of β values (figure 10a) has two peaks and shows that a high level of intermittency is observed in the majority of intervals (the median of distribution is equal 0.1). A low level of intermittency is observed in approximately 10% of intervals (the right peak of distribution in figure 10a). The distribution of Δ values (figure 10b) demonstrates that in the majority of intervals Δ change from 0.1 to 0.25, with the mean value of 0.2.

Figure 10.

The distributions of β (a) and Δ (b) values for SW ion flux data measured by BMSW instrument.

Figure 11 presents the comparison of the properties of intermittent (β<0.1) and non-intermittent (β>0.9) intervals. The significant difference is observed between density and velocity parameters for these two regions. The density is an average of approximately 12–14 cm⁻³ (figure 11a), and the velocity is approximately 300–400 km s⁻¹ for the intermittent periods (most part of the entire statistics). For the non-intermittent periods, the values of parameters are the density is equal on average to approximately 4–6 cm⁻³ (figure 11a), and the velocity is on average approximately 550–600 km s⁻¹ (figure 11b). There is practically no difference in temperature (figure 11c) for both intermittent and non-intermittent intervals. The typical temperature of our dataset is of the order of approximately 2–4 eV, we do not show here the intervals with temperature more than 16 eV, because our statistics are not representative in this case. More statistical data are necessary for detailed analysis of this question including sufficient numbers of the intervals with high temperatures. So, one can conclude that typically the low level of intermittency can be observed in the fast SW or in the case of low SW density (sometimes both conditions together), whereas the high level of intermittency is often observed in the slow SW or in the case of high SW density. The dependence of the intermittency level on the value of SW velocity was obtained also for IMF fluctuations [28,51,53].

Figure 11.

The distributions of proton density (a), velocity (b) and temperature (c) of intermittent β<0.1 (light bins) and non-intermittent β≥0.9 (dark bins) intervals in SW.

The scaling properties depend on the topology of singular dissipative structures (see review [26]). In the She–Leveque model of three-dimensional isotropic hydrodynamics, dissipative structures are considered as one-dimensional filaments. The traditional approach using Iroshnikov–Kraichnan phenomenology for plasma has been generalized by Biskamp & Mueller [68]. In the Biskamp–Mueller model (BM model) of three-dimensional isotropic MHD turbulence, dissipative structures are assumed to be two-dimensional current sheets. To determine the anisotropic statistics of the cascade strength Biskamp & Mueller [68] considered the following scaling:

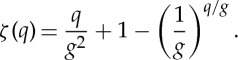4.5

Anomalous scaling that captures one-dimensional filament-like structures was proposed by Budaev [67]:

4.6

The quantities g and g_f express the cascade efficiency relative to the K41 model supposing scaling of velocity differences over scale l as δ_lυ∼l^l/g and assuming a constant cascade energy rate in the arbitrary anisotropic cascade (see [26]):

• (i) g,g_f=3 corresponds cascade efficiency the same as in the K41 model,

• (ii) g,g_f>3 corresponds to the cascade enhancement,

• (iii) g,g_f<3 corresponds to the cascade depletion.

The g and g_f are evaluated from experimental scaling of structure functions ζ(q) (see, for example, figure 12) by the wavelet transform modulus maxima method procedure [26] which allows the scaling ζ(q) estimation up to q=9 by using of approximately 50 000 data points. Experimental data should be tested by scalings (4.5) and (4.6) for choosing either g or g_f that is the closest to 3.

Figure 12.

The deviation of experimental scaling from Kolmogorov (K41) scaling (dashed line—q/3) for SW ion flux fluctuations. BMSW data 02/08/2012 09:00–22:50 UT (the curves of different signs for several different subintervals). Solid line—the She–Leveque log-Poisson model (SL) with Δ=β=2/3. Dashed-dotted line—Biskamp–Mueller (BM) model.

The time dependence of the coefficients g and g_f for the same example, which is shown in figure 9, can be seen in figure 13. The values of g∼ 2.3–2.6, whereas g_f∼ 2.7–3, i.e. the values of g_f are close to 3. So, it can be interpreted that filament-like structures dominate in the process. It can also be proved by statistical analysis of all 209 selected intervals (figure 14), which presents the distributions of g (figure 14a) and g_f (figure 14b). The mean values of these parameters for the distributions shown in figure 14 are 〈g〉=2.4 and 〈g_f〉=2.8. This fact is in a good agreement with the ‘flux tubes’ approach to the SW structure [69,70]. Apparently, filamentary structures are the most stable and, therefore, could dominate in the dynamics of SW turbulence.

Figure 13.

Parameters g (reverse triangles) and g_f (crosses). The solid line is the value of SW ion flux (in arb. units). t is the time in seconds from the beginning of the interval. BMSW data 02/08/2012 09:00–22:50 UT.

Figure 14.

The distributions of g (a) and g_f (b) values, SW ion flux BMSW data.

Experimental scaling ζ(q)/ζ(3) for several 26 min subintervals during the period 02/08/2012, 09:00–22:50 UT are shown in figure 12. All intervals demonstrate the deviation from Kolmogorov scaling (q/3) for isotropic developed turbulence. The scalings also deviate from the log-Poisson-type model by Biskamp & Mueller [68] treating dissipative structures as two-dimensional current sheets with scaling given by equation (4.5). As was discussed above, the properties of the experimental scaling are most adequately described by the log-Poisson model including one-dimensional dissipative structures with the scaling described by the equations (4.6).

5. Conclusion

Fast variations of the SW ion flux in the relatively high-frequency range 0.03–10 Hz have been poorly investigated before the launch of the SPECTR-R spacecraft. High-resolution ion flux measurements onboard the SPECTR-R spacecraft demonstrated the permanent presence of significant variations up to scale of approximately 10 Hz. SW ion flux fluctuations measured by the BMSW instrument have been studied both by spectral and statistical methods. The analysis of spectra and PDFs of ion flux fluctuations in the frequency range (10⁻² to 10 Hz), performed in this paper, allows the following conclusions to be drawn:

• — the frequencies spectra of the ion flux fluctuations in SW have a complicated form. The spectrum shape often has two branches with different slopes, but sometimes the plateau can be observed between low and high frequency branches of spectra as was already observed for electron density fluctuations [13,22], etc;

• — the value of the spectral index (spectral slope) in the low frequency range (approx. 10⁻² to 1 Hz) is 1.6±0.2. The value of the spectral index in the high-frequency range (approx. −10 Hz) is 2.9±0.2, in agreement with magnetic field turbulent spectra [1]. The spectral indices are obtained using statistics of 363 17 min intervals of high-resolution BMSW measurements of SW ion flux;

• — the boundary between these two branches (named ‘break frequency’) occurs at the frequency 1.9±0.8 Hz. The break frequency is about an order of magnitude higher than the estimated ion gyro-frequency for our conditions;

• — we did not find a distinct dependence between variations of spectral parameters two slopes and the break points of ion flux fluctuations and variations of SW plasma parameters (density, velocity, temperature). We think that these investigations should be continued with more abundant statistics;

• — usually, PDFs of SW ion flux fluctuations in the frequency range approximately 0.1–10 Hz deviate significantly from the Gaussian distribution and represent the high level of intermittency. The level of intermittency grows to the smallest scales;

• — the analysis of high-order structure functions demonstrates the ESS properties of SW turbulence;

• — the shape of the PDF was compared with PDF predicted by Tsallis statistics, and this analysis confirmed the non-extensive statistical nature of SW ion flux fluctuations. Deviations from the Boltzman statistics become larger during the disturbed periods;

• — statistical characteristics of ion flux fluctuations are compared with predictions of different models and the best fit was found for the log-Poisson model. Analysis of the structure functions scaling in the frame of the log-Poisson approach has shown the dominant contribution of filament-like structures to the turbulent process in the SW; and

• — the log-Poisson parametrization has shown that the high level of the intermittency of small-scale SW ion flux fluctuations was observed in the majority of intervals, predominantly in SW with low velocity or high-density values. In contrast, the low level of intermittency was observed only in 10% of intervals in SW with high values of velocity or low values of density.