Abstract
Ptychography is a coherent diffraction imaging (CDI) method for extended objects in which diffraction patterns are acquired sequentially from overlapping coherent illumination spots. The object’s complex transmission function can be reconstructed from those diffraction patterns at a spatial resolution limited only by the scattering strength of the object and the detector geometry. Most experiments to date have positioned the illumination spots on the sample using a move-settle-measure sequence in which the move and settle steps can take longer to complete than the measure step. We describe here the use of a continuous “fly-scan” mode for ptychographic data collection in which the sample is moved continuously, so that the experiment resembles one of integrating the diffraction patterns from multiple probe positions. This allows one to use multiple probe mode reconstruction methods to obtain an image of the object and also of the illumination function. We show in simulations, and in x-ray imaging experiments, some of the characteristics of fly-scan ptychography, including a factor of 25 reduction in the data acquisition time. This approach will become increasingly important as brighter x-ray sources are developed, such as diffraction limited storage rings.
OCIS codes: (100.5070) Phase retrieval, (100.3010) Image reconstruction techniques, (180.5810) Scanning microscopy, (180.7460) X-ray microscopy
1. Introduction
Ptychography is an imaging method in which a limited-size coherent illumination probe is moved sequentially across an extended object, while the resulting diffraction patterns are collected [1]. With sufficient overlap between these illumination spots [2], one can use an iterative algorithm to reconstruct the object’s complex transmission function [3–5], and thus obtain images with a spatial resolution not limited by optics but rather by the object’s scattering strength [6] and the geometry of the pixelated detector. The probe function is reconstructed along with the object [3, 5, 7], with the consequence that ptychography can be used for characterizing nanofocused beams [8,9].
While ptychography can be used over a broad spectrum of wavelengths including visible light [2, 10], it has proven to be especially popular in x-ray microscopy. X-ray ptychography has been used to image radiation-hard materials at sub-10 nm resolution [11–13], and biological specimens at sub-30 nm resolution [14,15]. The object’s complex transmission function delivers quantitative phase contrast images [16] which, if combined with angular projections, can be used to generate tomographic reconstructions with 3D quantitative measurements of electron density [17]. For example, ptychography has been used for 3D imaging of a mouse femur at 100 nm resolution [18], and nanoporous glass at 16 nm resolution [19].
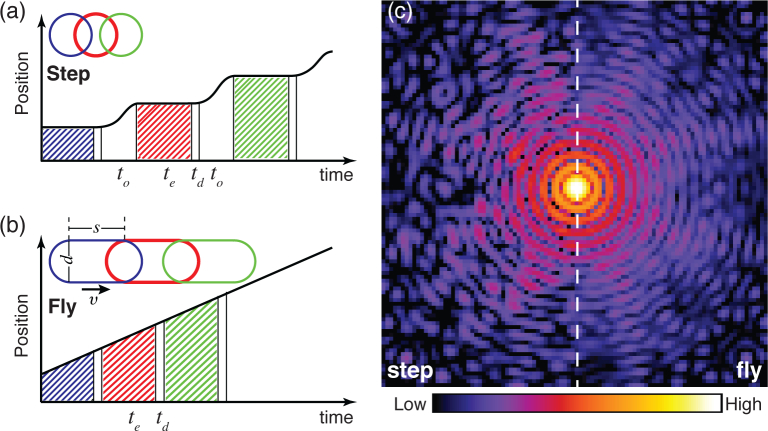
Most ptychography experiments employ a move-settle-measure mode for data acquisition, which is often referred to as a step-scan mode. In this mode the sample is moved to place the illumination probe on a specified position and the position is allowed to stabilize (with a total move-settle overhead time to), after which a measurement is made over an exposure time te followed by a detector dead time td for data transfer (see Fig. 1(a)). The fraction of “wasted” time when signal is not being acquired in step scans is
| (1) |
Fig. 1.
Comparison of step-scan and fly-scan ptychography. In step-scan mode (a), the probe moves relative to the sample in a move-settle-acquire sequence, where no signal is collected during the move-settle overhead time to; the diffraction pattern is then collected over an exposure time of te, after which the detector becomes inactive for a dead time td for data transfer. In fly-scan mode (b), the probe moves at a constant velocity to the sample while data is acquired over exposure times te followed by brief detector dead times td. Outlines of both step-scan and fly-scan total beam footprints (assuming a round coherent probe with a diameter d) are shown as insets, with s representing the probe motion distance corresponding to the per-flyscan-point acquisition time te. (c) The diffraction intensities measured for scanning the same region in the two scan modes. Speckle visibility is reduced in fly-scan mode.
While some ptychography experiments have used exposure times as long as te = 30 seconds [8] which dwarf any overhead time to and also the readout time of detectors such as the Pilatus with td = 2.3 msec [20], more recent experiments with high brightness sources and fast-readout detectors (such as the Eiger with td = 3 μsec [21]) have used exposure times te = 200 msec and move-settle overhead times of to=150 msec [22], so that the wasted time fraction is wstep = 43%. With diffraction limited storage rings on the horizon with hundredfold gains in coherent flux [23], exposure times te will decrease accordingly so the wasted time fraction could approach wstep = 99%, which is grossly inefficient.
An alternative approach of “fly-scan” ptychography was recently proposed [24] and then demonstrated [25] independently by several teams, including ours (as discussed in this paper). In scanning optical [26] and probe microscopes, it is common to perform scans where the probe moves relative to the object at constant velocity within a scan line, rather than in a move-settle-measure fashion (Fig. 1). One can then mark the increment from one pixel to the next by using a timing signal, or use the output of a position feedback system such as a laser interferometer to do position-based scan clocking. This approach has long been used in soft x-ray scanning microscopes, and has recently been implemented for hard x-ray scanning fluorescence microscopes as well [27]. Fly scans can have very low wasted time fraction
| (2) |
especially when considering detectors such as the Eiger with dead time as small as td = 3 μs. With incoherent imaging modalities, such as fluorescence imaging, the effect of a fly scan is to convolve the probe with a line with the width of a pixel, so that there is little effect on the recorded data even if the pixel size approaches the resolution of the probe. However, ptychography is a coherence-based imaging process, and the coherent diffraction intensity distribution produced by one illumination region is different to that produced by a slightly different region. One must therefore think of the effects of combining diffraction intensities from these different regions in ptychography.
An important recent development in ptychography has shown that the redundancy of information provided by overlapping probe positions offers the opportunity to reconstruct multiple modes of the object and/or probe [28]. This allows one to use partially coherent illumination, since it can be represented by a small number of self-coherent, but mutually incoherent, optical modes [29, 30]; it also allows one to deal with some degree of sample vibration in step-scan ptychography [31]. Since fly-scan ptychography involves the integration of diffraction patterns over the illumination area, it is natural to consider that fly scans can be thought of as representing the combination of the object with a set of probe modes [24, 25]. We show here that this is indeed the case, so that ptychography can be implemented in fly-scan mode to dramatically speed up data acquisition while high quality images are obtained by using multiple probe modes in the reconstruction.
2. Theory of fly-scan ptychography
In ptychography, the far-field propagated wave can be described as the Fourier transform of the exit surface wave. For step-scan ptychography, the diffraction intensity Ij(k) collected from a static sample at a position rj is given by
| (3) |
where ℱ represents a Fourier transform, r is the real space coordinate, ψj is the exit surface wave when sample is moved to position rj, P(r) is the probe function, and O(r) is the object transmission function. In fly-scan ptychography, each diffraction pattern is collected while the probe is moving relative to the object at a velocity v during an exposure time of te, so that the total diffraction intensity for one measurement interval te becomes
| (4) |
The total beam footprint on the sample is extended along the scan line by a distance s = vte (named fly-scan pixel size), so one diffraction recording involves an integrated probe coverage of
| (5) |
which has a length in the moving direction of l = s + d, where d is the beam diameter (see the inset of Fig. 1(b)).
Provided that the observation time is much longer than the coherence time of the incident beam, the diffraction pattern can be approximated by an incoherent sum of intensities produced from N discrete positions with measurement times separated by a sufficiently small time interval ∆t [24]. In this case, Eq. (4) becomes
| (6) |
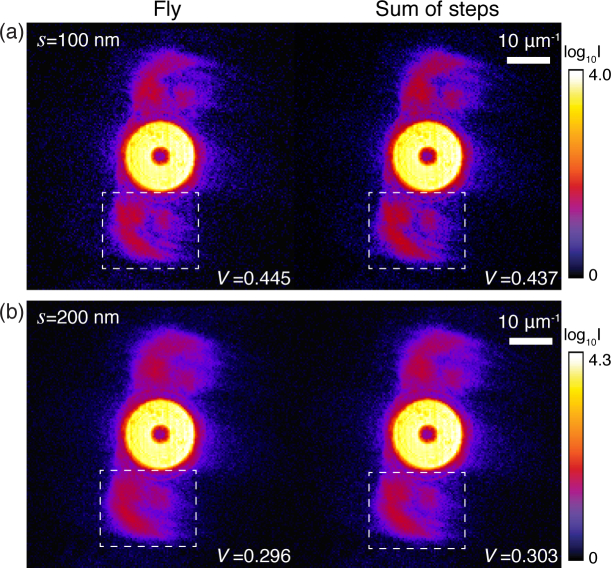
To test the equivalence of Eqs. (4) and (6), we show in Fig. 2 the diffraction patterns obtained from step and fly scans acquired from the same region of a test pattern (experimental details are in Sec. 4). The fly-scan data described by Eq. (4) are seen to be quite similar to the sum of fine-increment step scans as described by Eq. (6). This implies that fly-scan data can be treated as mixture states of the object interacting with a number of probe modes [24]. To quantify any differences, the speckle visibility V [32] is calculated within the indicated regions as
| (7) |
where the analyzed region is an M×N matrix, and Imn is the value of intensity at each pixel. The deterioration of speckle visibility in fly-scan diffraction pattern is similar to a degradation of spatial coherence [28]. Therefore, fly-scan ptychography reconstructions can be performed by a modified algorithm using multiple probe modes.
Fig. 2.
Comparison of fly-scan diffraction patterns (Eq. (4); left) with the summed intensity of discrete step-scan diffraction patterns (Eq. (6); right). Data from the same region of an Au test pattern were acquired using 5.2 keV x-rays (Sec. 4). The illumination probe (produced by the focus of a Fresnel zone plate) was measured to have a full-width at half-maximum (FWHM) size of 103 nm. In (a), a fly-scan diffraction (left) was acquired while the sample was continuously moving over a distance of s = 100 nm during a time of te = 400 ms; step-scan diffraction patterns were recorded at 10 discrete positions each with 10 nm step size and te = 40 ms exposure time within the same scan region as the fly scan, so that their sum as shown at right contains the same number of photons. In (b), a similar procedure was followed using s = 200 nm with te=800 sec for the fly scan, and 20 discrete positions each with 10 nm step size and te = 40 sec. The speckle visibility V (Eq. (7)) was analyzed on the regions bounded by white dash-line boxes.
3. Simulating fly scans
To numerically evaluate fly-scan ptychography reconstructions and determine the largest tolerable fly-scan pixel size (s), we simulated a series of fly scans for a range of values of s. In the simulations, an Airy disk pattern with a FWHM of d = 100 nm was chosen to be the probe. An image of a mandrill was used as the sample, with real space pixel size of 10 nm. With a vertical step size of 50 nm, fly-scan diffraction patterns of scans with different s were simulated using Eq. (6).
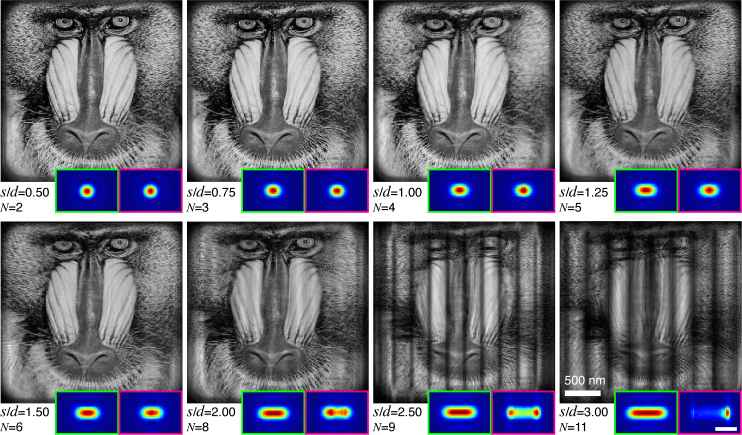
With simulated data in hand, we used a modified version of the ePIE algorithm [33] incorporating multiple-probe-mode recovery [28] for image reconstruction. (We note that there are analytical approaches for non-iterative reconstruction from coherent x-ray diffraction patterns [34], but we are not aware of their adaptation to multiple probe mode ptychography as of yet). The code was implemented in a way that it can use graphical processing units (GPU) for speedup on individual nodes, and parallelized so that separate regions of the overall scan could be reconstructed on separate nodes and then recombined [35]. Reconstruction results for different s are shown in Fig. 3. As expected, with the increase in s, more probe modes are needed in reconstructions. When the sample moves less than 200 nm (twice the beam diameter of d = 100 nm, giving s/d = 2.00) in one fly-scan interval, the sample images are successfully retrieved; the summed intensity of reconstructed probes is also consistent with the expected beam footprint. However, the reconstructions fail to produce faithful images when s/d >2.00, and the recovered footprints are no longer consistent with the expected footprint. The vertical stripe artifacts seen to appear on the failure images are attributed to the weak overlap in the horizontal direction, even though there is sufficient vertical overlap. For s/d = 2.00, the relative linear overlap percentage between neighboring footprints in horizontal direction is about 33% which is close to the overlap percentage of 29% that has been suggested to be a minimum for for step-scan ptychography using a circular beam [2].
Fig. 3.
Reconstructions of simulated data with different values of the fly-scan pixel size s relative to an Airy beam FWHM of d = 100 nm, indicated by s/d. The probe mode number N shown here is the number above which the error of reconstruction (Eq. (8)) doesn’t decrease further. The inset at each panel shows the expected (green box) and recovered (magenta box) footprint (∝ s) of beam on the sample. The expected footprint was obtained through Eq. (5), while the recovered footprint is the sum of intensities of the reconstructed probe modes. Each reconstruction ran for 500 iterations. The scale bar for the footprints (lower right magenta box) is 200 nm.
To overcome the limitation of fly-scan pytchography with fly-scan pixel size s larger than twice the beam diameter d, we have tested two scan geometries to increase the overlap in the horizontal direction. Figure 4(a) shows a scan geometry of two scans with a displacement of s/2 in the vertical direction. The diffraction patterns from the two scans are then combined together for one reconstruction. The reconstruction results show that the vertical stripes are removed, which is attributed to the increase of the horizontal overlap. Even though this method can provide sufficient horizontal overlap with (s/2 +d)/(s +d) > 50%, it starts to break down with obvious artifacts when s/d is about 5.00. This is probably due to the greatly deteriorated diffraction patterns associated with too many coherent modes for the algorithm to disentangle. The second scan geometry is a single scan but with a displacement between odd and even scan lines (Fig. 4(b)). The horizontal overlap of neighboring footprints in adjacent scan lines is improved. However, the increasing overlap percentage of this second scan geometry is smaller than that of the two-scan approach. Even so, in this approach one can even use s/d = 3.00 (Fig. 4(b)), and obtain an image which is recognizable even though it contains some artifacts. One can presumably obtain improved results by reducing the scan step size in the vertical direction.
Fig. 4.

Alternative scan geometries tested to overcome the limit of fly-scan pixel size s in fly-scan ptychography with a beam diameter d = 100 nm, indicated by s/d. In the doubled scan approach (a), two ptychographic fly scans are acquired with a horizontal displacement of s/2 between them. The probe intensity is halved in these two scans to yield equivalent intensity on the sample as in other fly scans. Images with high fidelity are obtained with s/d = 2.50, while scans with s/d = 3.00 also show good contrast and visibility though some light stripes appear on the image. In the offset scan approach (b), a single scan is acquired with a displacement between odd and even scan lines. In this case, scans with s/d = 2.50 show fairly good results, while some artifacts begin to appear when using s/d = 3.00. In all cases the vertical step size is 50 nm, the same as in aforementioned fly scans. The insets show the expected (green box) and recovered (magenta box) footprints of the beam on the sample. The scale bar for the footprints (lower right magenta box) is 200 nm.
Since the true object O(r) is known in simulations, the quality of above fly-scan reconstructions Of (r) can be evaluated directly using a normalized error metric [33] of
| (8) |
with
| (9) |
Figure 5 shows that the error of reconstructions is fairly small when s/d is less than 2.00, but that it quickly increases when s/d > 2.00 (vertical stripe artifacts appear on the images). The alternative scan geometries suggested in Fig. 4 are helpful to reduce the reconstruction error for the scans with large s/d. The required probe mode number for simulated data with different s is also shown in Fig. 5. This number increases linearly as a function of s/d until s/d > 2.00 where the reconstructions break down.
Fig. 5.
Normalized error E0 of the reconstructions (Eq. (8)), and required probe mode number N, for simulated data with different fly-scan pixel sizes s using a beam size of d = 100 nm. Shown here are the errors for the reconstructions of Fig. 3 (red), and also for the doubled scan mode of Fig. 4(a) (green) and the offset scan mode of Fig. 4(c) (blue). The black square markers show the probe mode number N needed for the convergence of the reconstruction with a specific s.
4. Experimental data and image reconstruction
In order to test these ideas experimentally, we used the Bionanoprobe [36] at the Advanced Photon Source (APS) at Argonne National Laboratory. A 5.2 keV x-ray beam was focused by a Fresnel zone plate with 85 nm theoretical Rayleigh resolution onto a gold test pattern with 30 nm finest feature. A Delta Tau Turbo PMAC2 Ultralite VME system was used for motion control. The far-field diffraction patterns were recorded using a PILATUS 100K photon-counting pixel array detector placed 2.2 m downstream of the sample; while this detector has 195×487 square pixels 172 μm across, only 195 × 256 pixels were used—with zero-padding to 256×256 array size—for our reconstructions.
We began by carrying out step-scan ptychography with a scan grid of 81×61 positions with 50 nm step size and an exposure time of te = 100 msec (the move-settle overhead time was to = 400 msec, yielding wstep = 80%). Figure 6 shows the reconstructed phase image of the test pattern as well as the single-mode probe. The retrieved probe (Fig. 6(b)) has a FWHM of about 103 nm with a profile near the center similar to that of the Airy function used in simulations (see Fig. 6(c)).
Fig. 6.
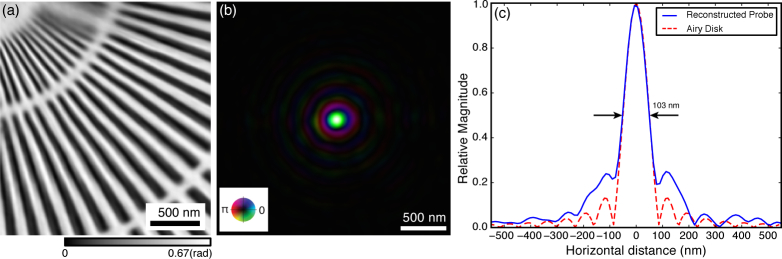
Reconstruction results of step-scan ptychography. (a) Phase of the reconstructed complex transmission function of the gold test pattern. (b) Retrieved probe function, the horizontal line profile of which is shown in (c). The measured probe has a FWHM size of 103 nm, with a profile close to the expected Airy pattern (with d ≃ 100 nm) at higher intensities.
For fly-scan ptychography, the scan region and vertical step size were kept the same as in the step scan. The scan speed in the horizontal direction was changed, generating a series of fly-scans with different s; the same exposure time te = 100 ms was used in each case, so that the fluence was reduced as s−1 (see Table 1). In fly-scan mode, the Delta Tau controller generated a constant velocity motion profile based on selected scan parameters, and the sample stage was moved according to this profile. During a continuous scan line, hardware triggers were generated at constant spatial intervals using a nanometer-resolution laser interferometer system, and these position triggers were used to trigger detector readout.
Table 1.
Parameters for fly-scan ptychography data recording. The field of view was the same (4 μm×3 μm) as in the step scan. The exposure time per frame was 100 ms, and the focused flux was of the order of 3 × 108 photons/s.
| s (nm) | Scan grid (H×V) | Footprint horizontal overlap (%) | Fluence (photons/μm2) |
|---|---|---|---|
| (step) | 81×61 | 51.5 | 1.24×1010 |
| 50 | 81×61 | 67.3 | 1.24×1010 |
| 75 | 54×61 | 57.8 | 8.24×109 |
| 100 | 41×61 | 50.7 | 6.25×109 |
| 125 | 33×61 | 45.2 | 5.03×109 |
| 150 | 27×61 | 40.7 | 4.12×109 |
| 200 | 20×61 | 34.0 | 3.05×109 |
| 250 | 16×61 | 29.2 | 2.44×109 |
| 300 | 13×61 | 25.6 | 1.98×109 |
Figure 7 shows the image reconstructed from a fly-scan ptychography dataset with s =250 nm and d ≃ 100 nm. The single-probe-mode reconstruction (Fig. 7(a)) shows considerable artifacts, as expected. As the number of probe modes are increased (Fig. 7(b)–(d)), the reconstruction quality is improved. The finest structures of 30 nm on the gold test pattern are well resolved by using 15 probe modes in the reconstruction (Fig. 7(d)), with an appearance similar to the step-scan ptychographic image of Fig. 7(e). The summed intensity of those 15 probe modes (Fig. 7(f)) yields a beam footprint on the sample with a horizontal size of l ≃ 350 nm, consistent with the expected value of l = s+d = 250+100 nm. While s/d ≤ 2.00 was required for best results in the simulations, the fact that s/d = 2.50 works well in experiment is probably due to the increased signal outside the central Airy disk in the experimental probe compared to the simulated one.
Fig. 7.

The improvement of fly-scan reconstruction quality using multiple probe modes. Shown here are the phases of reconstructed transmission function of a gold test pattern. Images (a)–(d) were reconstructed from the same fly-scan dataset with s/d ≃ 2.50 (assuming d ≃ 100 nm) by using 1, 5, 10 and 15 probe modes, respectively. The first 5 individual probe modes in (d) case are shown in (f), along with the summed intensity of the total 15 modes at right (revealing the scan footprint). Even with s/d = 2.50, the fly-scan reconstruction (d) is similar in quality to the step scan image (e).
The reconstruction results of fly scans with different values of s/d (and d ≃ 100 nm) are shown in Fig. 8. For s/d in a range of 0.50–2.50, the test pattern phase images are nicely recovered (the 30 nm finest features are well resolved). With the increase in s/d, more probe modes are needed, which is consistent with the simulations. The sum of reconstructed probe modes shows the expected scan footprint with different s. The reconstruction starts to break down when s/d is larger than 2.50, producing vertical stripes on the images and incorrect footprint due to the weak overlap in the horizontal direction. As noted above, scans with s/d = 2.50 succeed in experiment, presumably because the experimental probe function has more energy outside of the central Airy disk than the simulated probe does.
Fig. 8.
Experimental fly-scan ptychography reconstructions with different s using multiple probe modes, all with d ≃ 100 nm. The fly-scan datasets were acquired with the same vertical step size of 50 nm, but with different s/d in horizontal direction as indicated. N shows the probe mode number needed for the convergence of the reconstruction, which we found to be N=2, 3, 4, 4, 6, 9, 12, and 15 in correspondence with the increased values of s/d. The insets are the sum of intensities of reconstructed probes, which represent the beam footprint on the sample. The scale bar for the footprints is 200 nm.
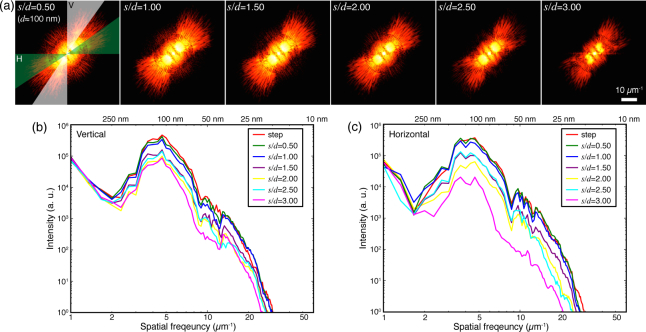
To assess the quality and the spatial resolution of fly-scan ptychography reconstruction, we calculated the power spectral density (PSD) of the reconstructed images shown in Fig. 8. Figure 9(a) shows the 2D PSD of the reconstruction results for these scans with d ≃ 100 nm. The power density is distributed around 45° due to the orientation of the spokes on the reconstructed images (see Fig. 6). As s increases, the power density behaves differently in the vertical and horizontal directions. Instead of a conventional method of azimuthally averaging the power density over all angles, we calculated the vertical and horizontal PSD by azimuthally averaging the power density over two angular regions (labeled as ‘V’ and ‘H’ in Fig. 9(a)) respectively. Due to the sufficient vertical overlap, the vertical features in the image can be recovered even for large s, so the vertical PSD (Fig. 9(b)) doesn’t degrade significantly as s increases. The degradation in high spatial frequency information is mainly attributed to the reduced fluence on the sample as shown in Table 4. Fig. 9(c) shows the horizontal PSD which is affected by both fluence and horizontal overlap. For s/d > 1.00, the horizontal overlap starts to be less than 50% (used in step scan), so that the horizontal PSD shows larger degradation compared to the vertical PSD; it deteriorates significantly at s/d = 3.00 due to insufficient horizontal overlap. For large s, methods of increasing the horizontal overlap as proposed in Fig. 4 can be used to improve the reconstructions.
Fig. 9.
Power spectrum of the reconstruction results for different s/d, with d ≃ 100 nm. (a) 2D power spectrum of the images shown in Fig. 8. (b) Vertical azimuthal power spectrum analyzed on the white region (azimuthal angle 30°) shown in (a). (c) Horizontal azimuthal power spectrum on the green region (azimuthal angle 30°) shown in (a).
A proper fly-scan pixel size s is one that provides sufficient overlap between adjacent footprints; that is, when s/d ≤ 2.00. This limit plays an important role in the success of fly-scan ptychography, while the scan speed determines the fluence on the sample that affects the achieved resolution. Figure 10 shows a series of fly-scan ptychography reconstructions with s/d = 1.00 but with different scan speeds quantified by the exposure time. The sample was well recovered from these scans at different scan speeds. The slight degradation of image quality as exposure time decreases is due to the reduced fluence on the sample.
Fig. 10.
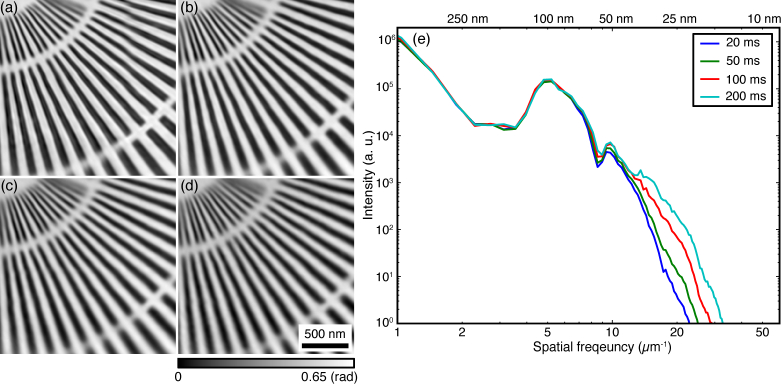
Fly-scan ptychography reconstructions (s/d =1.00 with d ≃ 100 nm) with different scan speed characterized by the per-fly-scan pixel collection time te = 200 msec (a), 100 msec (b), 50 msec (c), and 20 msec (d). (e) Azimuthally averaged power spectra of reconstructed images (a)–(d).
5. Conclusion
The ability to extend ptychography to work in fly-scan mode allows for faster data acquisition, which will become increasingly important as brighter x-ray sources are developed; this is because with modern, low-dead-time detectors, there is almost no wasted time over a continuous scan line. In addition, while in step-scan ptychography the separation between illumination points should be no more than 70% of the beam diameter [2], fly-scan ptychography is successful even with s/d = 2.00. This means that a fly-scan can have fewer scan points for the same scan region, bringing some advantages in computational requirement since it involves smaller array sizes and less computational steps than are involved with a larger number of diffraction pattern recordings. In our experiments, fly scans with s/d = 2.50 are about 25 times faster to acquire than the step scan equivalents. This factor can become even larger using smaller exposure time with lower emittance, higher brightness sources, such as are anticipated with multibend achromat storage rings [23]. (As a counter-example, full-field imaging systems need to fill as many spatially coherent modes as there are pixels in the detector, so to first approximation they suffer rather than benefit from the development of intrinsically coherent sources). The speedup in coherent imaging that fly-scan ptychography can provide will become especially important when ptychography is used to obtain 2D projections which are then combined over many angles to yield a tomographic three-dimensional view of the sample [18,19], as well as fly scan modes in x-ray fluorescence imaging which can be combined with ptychography [14]. We expect that fly-scan ptychography will find widespread adoption across different imaging domains using x-rays, electrons and visible light.
Acknowledgments
We thank R. Mak and Y. Sun for valuable discussions, K. Brister, C. Roehrig, J. VonOsinkski, and M. Bolbat for help during the experiments. We thank NIH NIGMS for support of this work under R01 grant GM104530. The Bionanoprobe is funded by NIH/ NCRR High End Instrumentation (HEI) grant (1S10RR029272-01) as part of the American Recovery and Reinvestment Act (ARRA). Use of the Advanced Photon Source, an Office of Science User Facility operated for the U.S. Department of Energy ( DOE) Office of Science by Argonne National Laboratory, was supported by the U.S. DOE under Contract No. DE-AC02-06CH11357.
References and links
- 1.Hoppe W., “Diffraction in inhomogeneous primary wave fields. 1. principle of phase determination from electron diffraction interference,” Acta Crystallogr. A 25, 495–501 (1969). 10.1107/S0567739469001045 [DOI] [Google Scholar]
- 2.Bunk O., Dierolf M., Kynde S., Johnson I., Marti O., Pfeiffer F., “Influence of the overlap parameter on the convergence of the ptychographical iterative engine,” Ultramicroscopy 108, 481–487 (2008). 10.1016/j.ultramic.2007.08.003 [DOI] [PubMed] [Google Scholar]
- 3.Faulkner H. M. L., Rodenburg J., “Movable aperture lensless transmission microscopy: A novel phase retrieval algorithm,” Phys. Rev. Lett. 93, 023903 (2004). 10.1103/PhysRevLett.93.023903 [DOI] [PubMed] [Google Scholar]
- 4.Rodenburg J., Hurst A., Cullis A., Dobson B., Pfeiffer F., Bunk O., David C., Jefimovs K., Johnson I., “Hard-x-ray lensless imaging of extended objects,” Phys. Rev. Lett. 98, 034801 (2007). 10.1103/PhysRevLett.98.034801 [DOI] [PubMed] [Google Scholar]
- 5.Thibault P., Dierolf M., Menzel A., Bunk O., David C., Pfeiffer F., “High-resolution scanning x-ray diffraction microscopy,” Science 321, 379–382 (2008). 10.1126/science.1158573 [DOI] [PubMed] [Google Scholar]
- 6.Schropp A., Schroer C. G., “Dose requirements for resolving a given feature in an object by coherent x-ray diffraction imaging,” New J. Phys.. 12, 035016 (2010). 10.1088/1367-2630/12/3/035016 [DOI] [Google Scholar]
- 7.Thibault P., Dierolf M., Bunk O., Menzel A., Pfeiffer F., “Probe retrieval in ptychographic coherent diffractive imaging,” Ultramicroscopy 109, 338–343 (2009). 10.1016/j.ultramic.2008.12.011 [DOI] [PubMed] [Google Scholar]
- 8.Kewish C. M., Thibault P., Dierolf M., Bunk O., Menzel A., Vila-Comamala J., Jefimovs K., Pfeiffer F., “Ptychographic characterization of the wavefield in the focus of reflective hard x-ray optics,” Ultramicroscopy 110, 325–329 (2010). 10.1016/j.ultramic.2010.01.004 [DOI] [PubMed] [Google Scholar]
- 9.Schropp A., Boye P., Feldkamp J. M., Hoppe R., Patommel J., Samberg D., Stephan S., Giewekemeyer K., Wilke R. N., Salditt T., Gulden J., Mancuso A. P., Vartanyants I. A., Weckert E., Schöder S., Burghammer M., Schroer C. G., “Hard x-ray nanobeam characterization by coherent diffraction microscopy,” Appl. Phys. Lett. 96, 091102 (2010). 10.1063/1.3332591 [DOI] [Google Scholar]
- 10.Zheng G., Horstmeyer R., Yang C., “Wide-field, high-resolution Fourier ptychographic microscopy,” Nature Photon. 7, 739–745 (2013). 10.1038/nphoton.2013.187 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Vila-Comamala J., Diaz A., Guizar-Sicairos M., Mantion A., Kewish C. M., Menzel A., Bunk O., David C., “Characterization of high-resolution diffractive X-ray optics by ptychographic coherent diffractive imaging,” Opt. Express 19, 21333–21344 (2011). 10.1364/OE.19.021333 [DOI] [PubMed] [Google Scholar]
- 12.Takahashi Y., Suzuki A., Zettsu N., Kohmura Y., Senba Y., Ohashi H., Yamauchi K., Ishikawa T., “Towards high-resolution ptychographic x-ray diffraction microscopy,” Phys. Rev. B 83, 214109 (2011). 10.1103/PhysRevB.83.214109 [DOI] [Google Scholar]
- 13.Shapiro D. A., Yu Y.-S., Cabana Jordi, Celestre R., Chao W., Kaznatcheev K., Kilcoyne A. L. D., Marchesini Stefano, Meng Y. S., Warwick T., Yang L. L., Padmore H. A., “Chemical composition mapping with nanometre resolution by soft X-ray microscopy,” Nature Photon. 8, 765–769 (2014). 10.1038/nphoton.2014.207 [DOI] [Google Scholar]
- 14.Vine D. J., Pelliccia D., Holzner C., Baines S., Berry A., McNulty I., Vogt S., Peele A. G., Nugent K., “Simultaneous x-ray fluorescence and ptychographic microscopy of Cyclotella meneghiniana,” Opt. Express 20, 18287–18296 (2012). 10.1364/OE.20.018287 [DOI] [PubMed] [Google Scholar]
- 15.Wilke R. N., Priebe M., Bartels M., Giewekemeyer K., Diaz A., Karvinen P., Salditt T., “Hard X-ray imaging of bacterial cells: nano-diffraction and ptychographic reconstruction,” Opt. Express 20, 19232–19254 (2012). 10.1364/OE.20.019232 [DOI] [PubMed] [Google Scholar]
- 16.Thibault P., Dierolf M., Kewish C. M., Menzel A., Bunk O., Pfeiffer F., “Contrast mechanisms in scanning transmission x-ray microscopy,” Phys. Rev. A 80, 043813 (2009). 10.1103/PhysRevA.80.043813 [DOI] [Google Scholar]
- 17.Diaz A., Trtik P., Guizar-Sicairos M., Menzel A., Thibault P., Bunk O., “Quantitative x-ray phase nanotomography,” Phys. Rev. B 85, 020104 (2012). 10.1103/PhysRevB.85.020104 [DOI] [Google Scholar]
- 18.Dierolf M., Menzel A., Thibault P., Schneider P., Kewish C., Wepf R., Bunk O., Pfeiffer F., “Ptychographic x-ray computed tomography at the nanoscale,” Nature 467, 436–439 (2010). 10.1038/nature09419 [DOI] [PubMed] [Google Scholar]
- 19.Holler M., Diaz A., Guizar-Sicairos M., Karvinen P., Farm E., Harkonen E., Ritala M., Menzel A., Raabe J., Bunk O., “X-ray ptychographic computed tomography at 16 nm isotropic 3D resolution,” Sci. Rep.. 4, 3857 (2014). 10.1038/srep03857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bech M., Bunk O., David C., Kraft P., Brönnimann C., Eikenberry E., Pfeiffer F., “X-ray imaging with the PILATUS 100k detector,” Appl. Radiat. Isot. 66, 474–478 (2008). 10.1016/j.apradiso.2007.10.003 [DOI] [PubMed] [Google Scholar]
- 21.Dinapoli R., Bergamaschi A., Henrich B., Horisberger R., Johnson I., Mozzanica A., Schmid E., Schmitt B., Schreiber A., Shi X., Theidel G., “Eiger: Next generation single photon counting detector for x-ray application,” Nucl. Instr. Meth. Phys. Res. A 650, 79–83 (2011). 10.1016/j.nima.2010.12.005 [DOI] [Google Scholar]
- 22.Guizar-Sicairos M., Johnson I., Diaz A., Holler M., Karvinen P., Stadler H. C., Dinapoli R., Bunk O., Menze A., “High-throughput ptychography using Eiger: scanning X-ray nano-imaging of extended regions,” Opt. Express 22, 14859–14870 (2014). 10.1364/OE.22.014859 [DOI] [PubMed] [Google Scholar]
- 23.Eriksson M., van der Veen J. F., Quitmann C., “Diffraction-limited storage rings–a window to the science of tomorrow,” J. Synchrotron Rad. 21, 837–842 (2014). 10.1107/S1600577514019286 [DOI] [PubMed] [Google Scholar]
- 24.Clark J. N., Huang X., Harder R. J., Robinson I. K., “Continuous scanning mode for ptychography,” Opt. Lett. 39, 6066–6069 (2014). 10.1364/OL.39.006066 [DOI] [PubMed] [Google Scholar]
- 25.Pelz P. M., Guizar-Sicairos M., Thibault P., Johnson I., Holler M., Menzel A., “On-the-fly scans for x-ray ptychography,” Appl. Phys. Lett. 105, 251101 (2014). 10.1063/1.4904943 [DOI] [Google Scholar]
- 26.Young J. Z., Roberts F., “A flying-spot microscope,” Nature 167, 231 (1951). 10.1038/167231a0 [DOI] [PubMed] [Google Scholar]
- 27.Lombi E., Jonge M. D., Donner E., Ryan C. G., Paterson D., “Trends in hard x-ray fluorescence mapping: environmental applications in the age of fast detectors,” Anal. Bioanal. Chem. 400, 1637–1644 (2011). 10.1007/s00216-011-4829-2 [DOI] [PubMed] [Google Scholar]
- 28.Thibault P., Menzel A., “Reconstructing state mixtures from diffraction measurements,” Nature 494, 68–74 (2013). 10.1038/nature11806 [DOI] [PubMed] [Google Scholar]
- 29.Mandel L., Wolf E., Optical Coherence and Quantum Optics (Cambridge University, 1995). 10.1017/CBO9781139644105 [DOI] [Google Scholar]
- 30.Flewett S., Quiney H. M., Tran C. Q., Nugent K. A., “Extracting coherent modes from partially coherent wavefields,” Opt. Lett. 34, 2198–2200 (2009). 10.1364/OL.34.002198 [DOI] [PubMed] [Google Scholar]
- 31.Clark J., Huang X., Harder R., Robinson I., “Dynamic imaging using ptychography,” Phys. Rev. Lett. 112, 113901 (2014). 10.1103/PhysRevLett.112.113901 [DOI] [PubMed] [Google Scholar]
- 32.Inoue I., Shinohara Y., Watanabe A., Amemiya Y., “Effect of shot noise on x-ray speckle visibility spectroscopy,” Opt. Express 20, 26878–26887 (2012). 10.1364/OE.20.026878 [DOI] [PubMed] [Google Scholar]
- 33.Maiden A., Rodenburg J., “An improved ptychographical phase retrieval algorithm for diffractive imaging,” Ultramicroscopy 109, 1256–1262 (2009). 10.1016/j.ultramic.2009.05.012 [DOI] [PubMed] [Google Scholar]
- 34.Podorov S. G., Pavlov K. M., Paganin D. M., “A non-iterative reconstruction method for direct and unambiguous coherent diffractive imaging,” Opt. Express 15, 9954–9962 (2007). 10.1364/OE.15.009954 [DOI] [PubMed] [Google Scholar]
- 35.Nashed Y., Vine D., Peterka T., Deng J., Ross R., Jacobsen C., “Parallel ptychographic reconstruction,” Opt. Express 22, 32082–32097 (2014). 10.1364/OE.22.032082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chen S., Deng J., Yuan Y., Flachenecker C., Mak R., Hornberger B., Jin Q., Shu D., Lai B., Maser J., Roehrig C., Paunesku T., Gleber S., Vine D., Finney L., Von Osinski J., Bolbat M., Spink I., Chen Z., Steele J., Trapp D., Irwin J., Feser M., Snyder E., Brister K., Jacobsen C., Woloschak G., Vogt S., “The Bionanoprobe: hard x-ray fluorescence nanoprobe with cryogenic capabilities,” J. Synchrotron Rad. 21, 66–75 (2014). 10.1107/S1600577513029676 [DOI] [PMC free article] [PubMed] [Google Scholar]